A Robust and High-Precision Three-Step Positioning Method for an Airborne SAR Platform
Abstract
:1. Introduction
2. Positioning Method
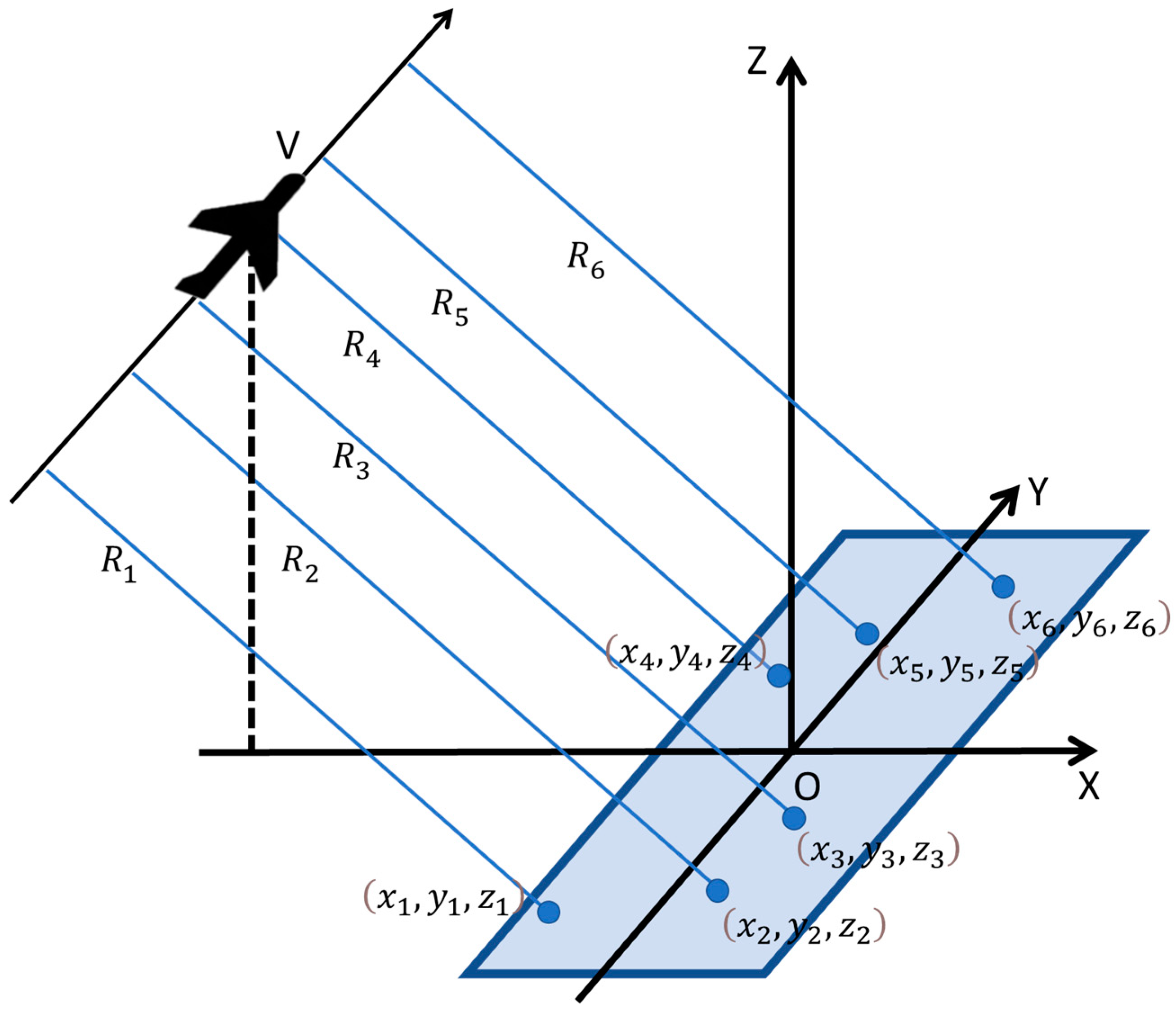
2.1. Platform Positioning Model
2.2. Three-Step Solution Method
2.2.1. Gauss–Newton Iteration
2.2.2. Singular Value Decomposition
2.2.3. Three-Step Robust Solution
- 1.
- In the first step, the six parameters are roughly estimated by the slant range equation.
- 2.
- In the second step, the three parameters are accurately estimated by the Doppler equation, namely, the position estimation at zero time.
- 3.
- In the third step, the three parameters are accurately estimated by the Doppler equation, namely, the average velocity estimation in three directions.
3. Error Analysis
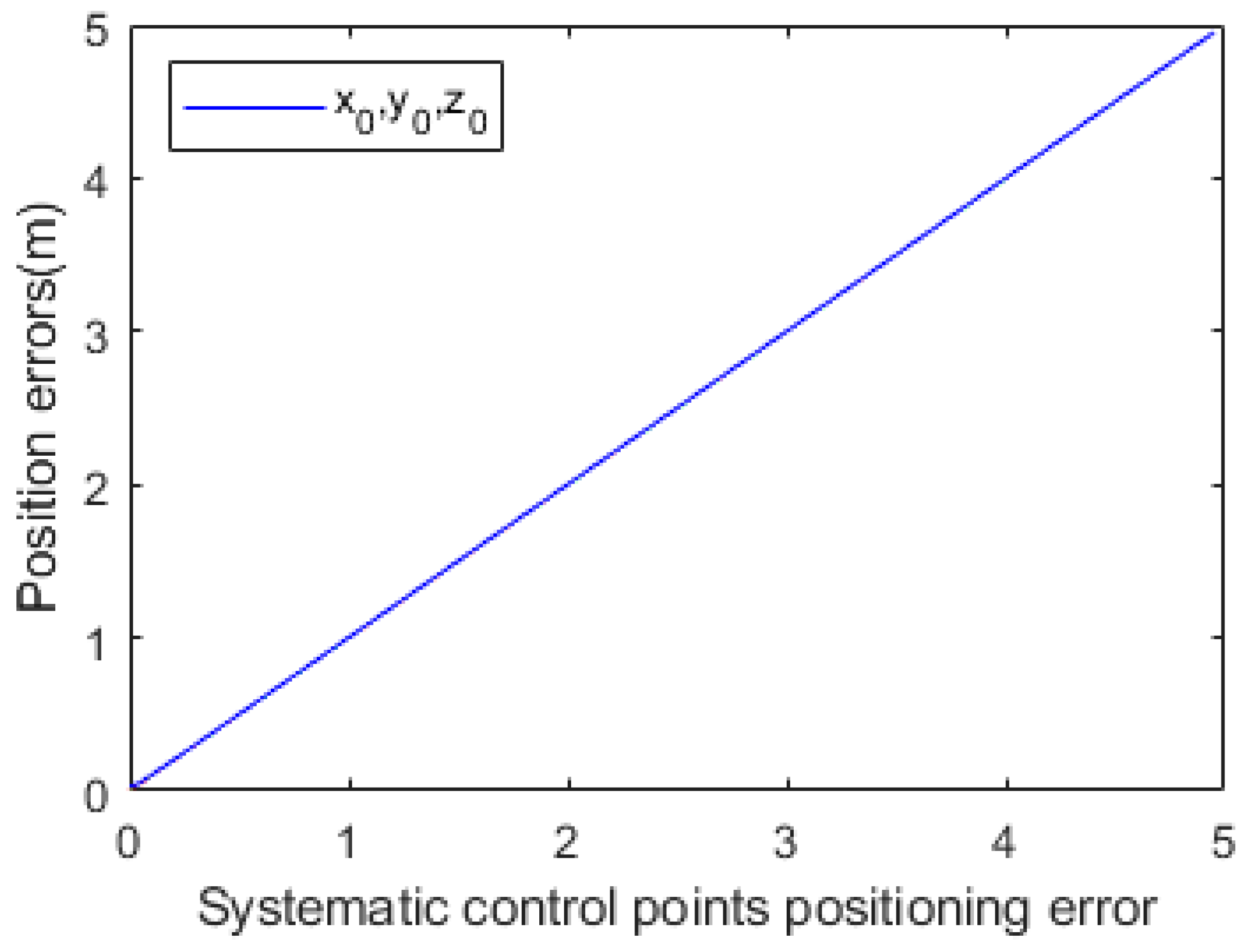
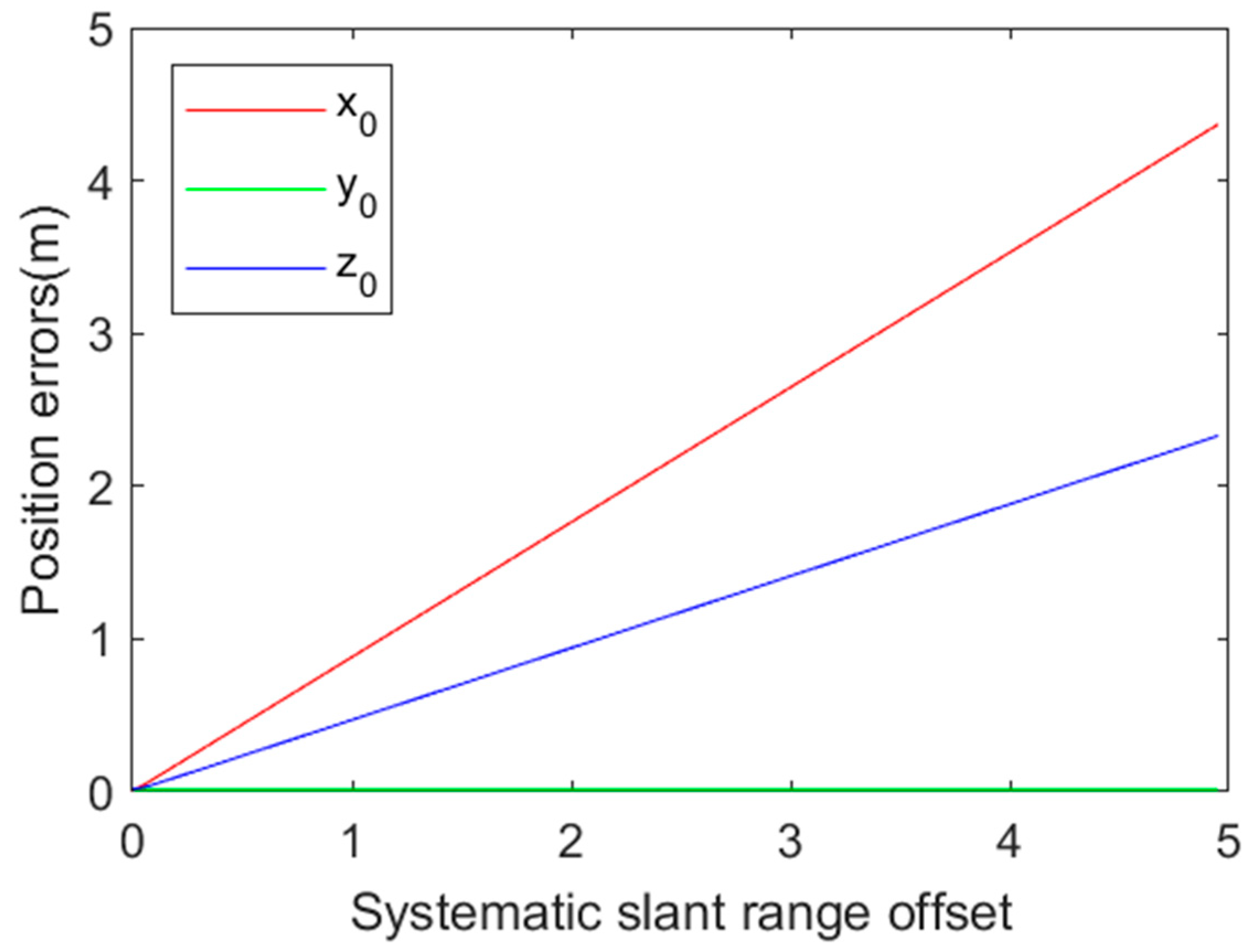
3.1. Analysis of Systematic Errors
3.1.1. Systematic Slant Range Error
3.1.2. Systematic Control-Point Positioning Error
3.1.3. Doppler Shift
3.2. Random Error Analysis
3.2.1. Error Analysis of Slant Range Equation
- (1)
- Slant range random error : assuming that the slant range random error of each control point follows an independent zero-mean Gaussian distribution , represents an N × N identity matrix.
- (2)
- Random error indirectly caused by control points’ positioning: linearize the slant range equation for each target point coordinate.
3.2.2. Doppler Equation Position Estimation Error Analysis
- (1)
- Assuming that the three-directional random error of each control point follows an independent zero-mean Gaussian distribution , the error is as follows.
- (2)
- Error indirectly caused by inaccurate velocity estimates: linearize the Doppler equation for the three-directional velocity:
3.2.3. Doppler Equation Velocity Estimation Error Analysis
4. Results
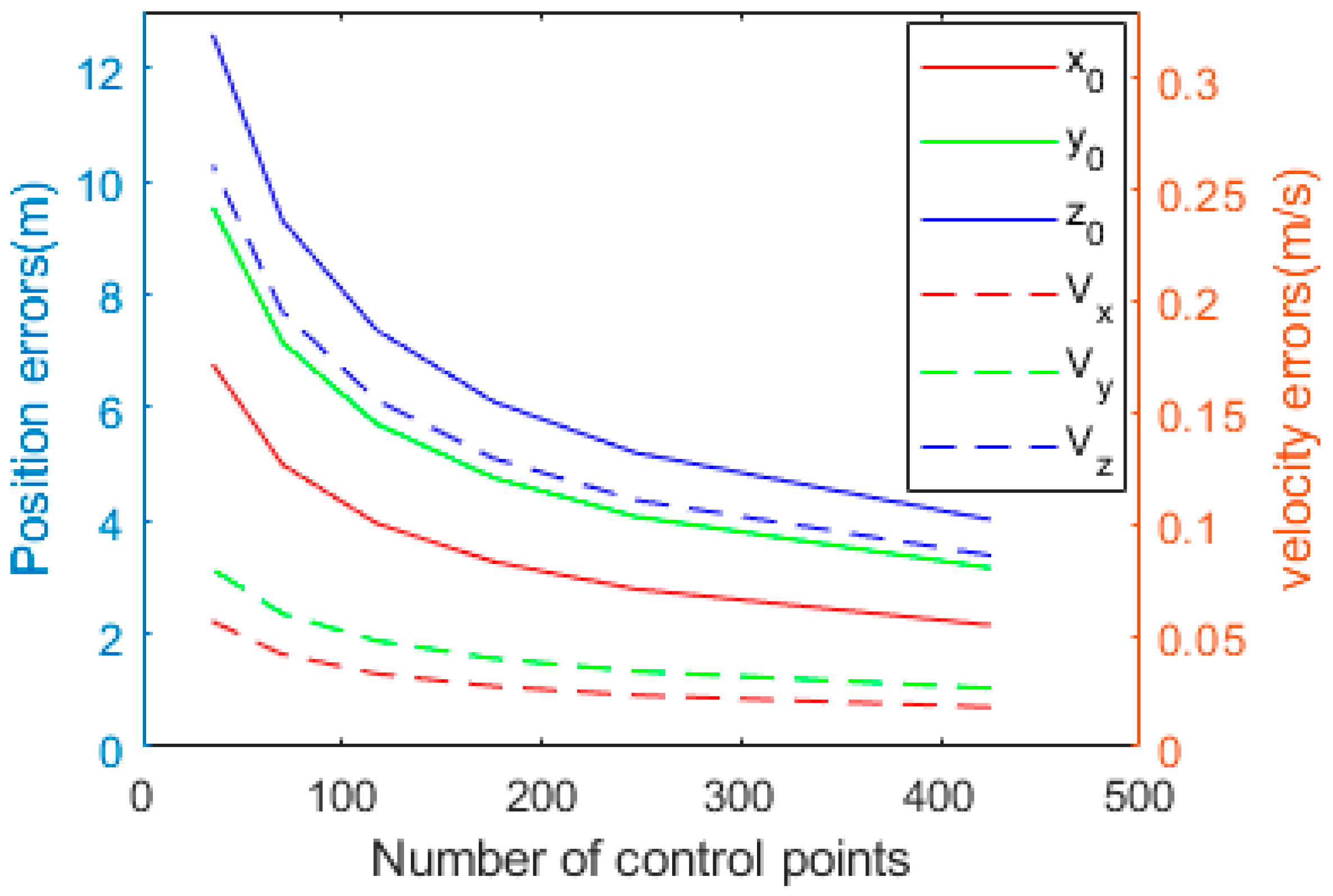
4.1. Error Propagation Curve
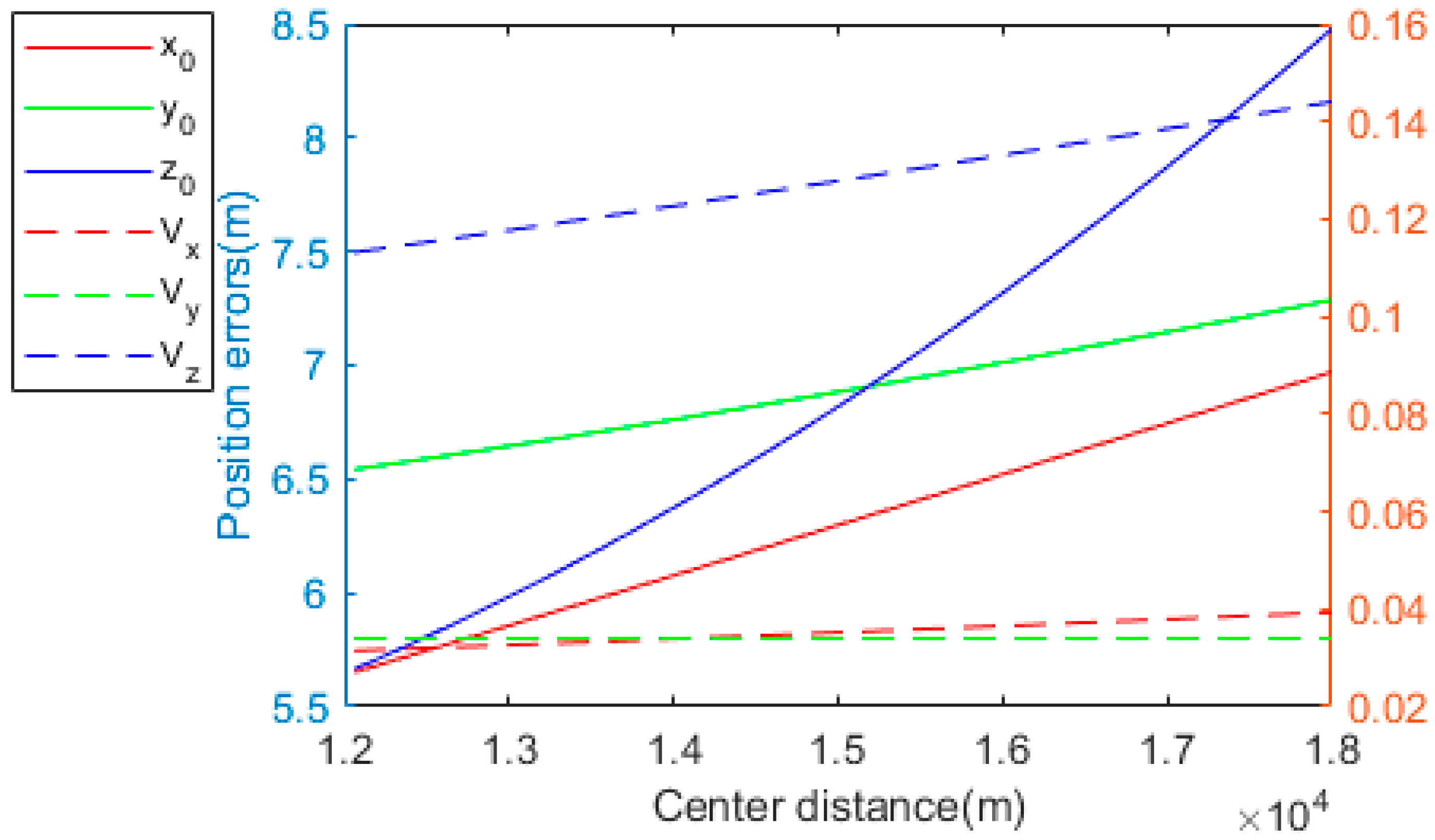
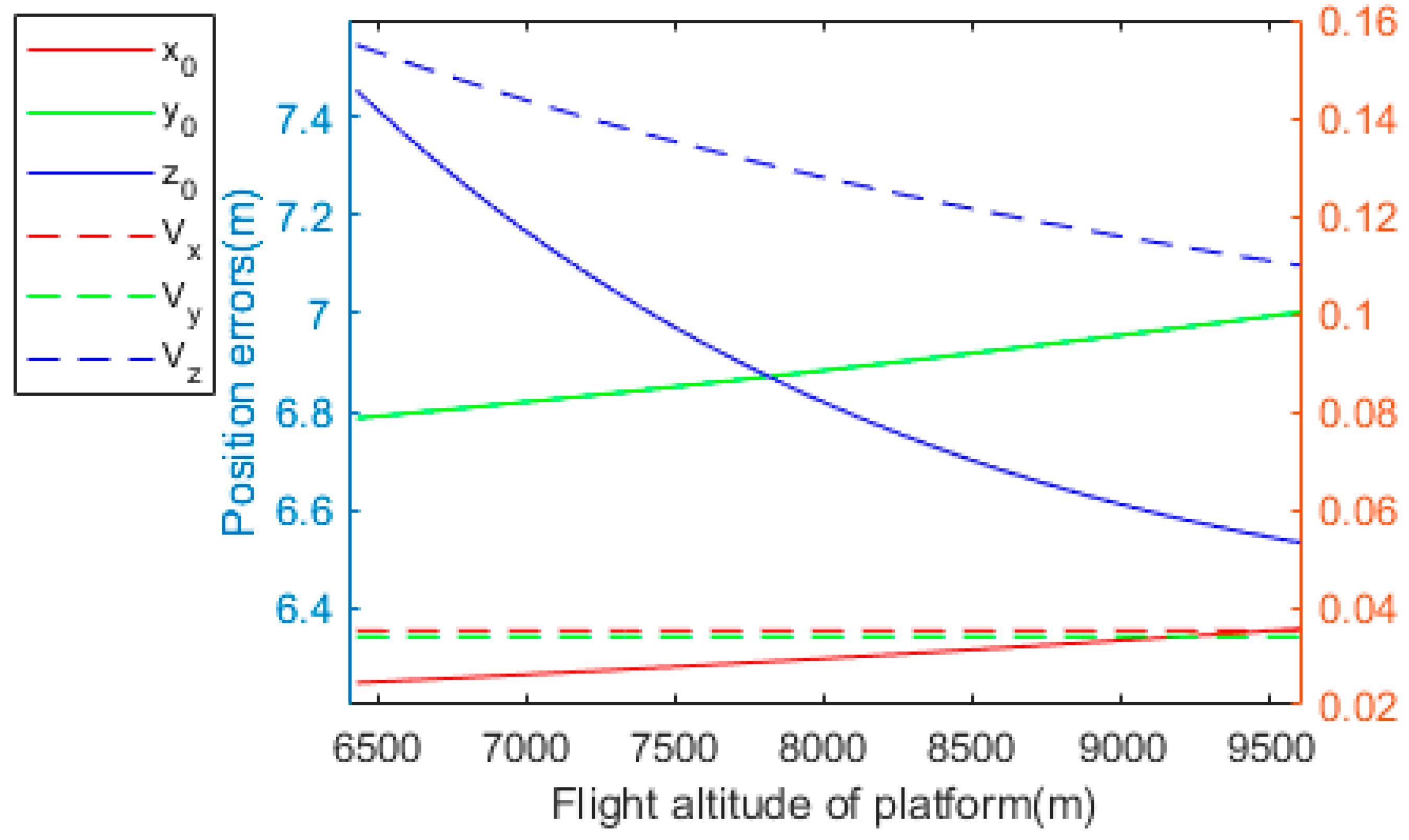
4.2. System Parameter Effects on Positioning Error
4.3. Semi-Physical Simulation Verification
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Moreira, A.; Hounam, D. Foreword to the special issue on synthetic aperture radar (sar) technologies and techniques. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3303–3305. [Google Scholar] [CrossRef]
- Seo, J.; Lee, J.G. Application of nonlinear smoothing to integrated GPS/INS navigation system. J. Glob. Position. Syst. 2005, 4, 88–94. [Google Scholar] [CrossRef]
- Greco, M.; Querry, S.; Pinelli, G. SAR-based augmented integrity navigation architecture. In Proceedings of the 2012 13th International Radar Symposium, Warsaw, Poland, 9 July 2012. [Google Scholar] [CrossRef]
- White, T.; Wheeler, J. Gps-Denied Navigation Using Sar Images and Neural Networks. In Proceedings of the ICASSP 2021—2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6 June 2021. [CrossRef]
- Lu, J.; Ye, L. A deep fusion method based on ins/sar integrated navigation and sar bias estimation. IEEE Sens. J. 2020, 20, 10057–10070. [Google Scholar] [CrossRef]
- Nitti; Davide, O. Feasibility of Using Synthetic Aperture Radar to Aid UAV Navigation. Sensors 2015, 15, 18334–18359. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qing, Y.; Li, H. Missile location based on SAR seeker. Acta Electron. Sin. 2009, 31, 121–124. [Google Scholar]
- Qing, Y.; Huang, Z. Missile Geo-Location Using INS and Dual-Antenna Missile-Borne SAR. Acta Electron. Sin. 2009, 37, 1216–1221. [Google Scholar]
- Fu, X. Study on the Technology of Scene Matching and Missile Location for Bistatic Missile-Borne SAR. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2015. [Google Scholar]
- Deng, H. Study on Imaging and Positioning of Missile-Borne Monostatic/Bistatic SAR with Curve Tracks. Ph.D. Thesis, Xidian University, Xi’an, China, 2018. [Google Scholar]
- Li, Y.; Lan, J. Positioning of Missile with Terminal Guide SAR System and Analysis. J. Telem. Track. Command. 2004, 25, 29–33. [Google Scholar]
- Li, Y.; Lv, X.L. Research on positioning and measuring speed in the high speed SAR system based on high precision map matching. Syst. Eng. Electron. 2007, 29, 1851–1855. [Google Scholar]
- Chen, S.; Liu, X. SAR Positioning Method based on High-precision Scene Matching. J. Natl. Univ. Def. Technol. 2016, 38, 121–126. [Google Scholar]
- Chen, S.; Liu, X. SAR Platform Location Method based on Scene Matching and Inertial Navigation System Information. J. Natl. Univ. Def. Technol. 2017, 39, 105–109. [Google Scholar]
- Cheng, H.; Lu, W. SAR Platform Geo-location Based on Least Squares Support Vector Machines. J. Astronaut. 2010, 31, 489–494. [Google Scholar]
- Toss, T.; Dämmert, P. Navigation with SAR and 3D-map aiding. In Proceedings of the 2015 18th International Conference on Information Fusion (Fusion), Washington, DC, USA, 14 October 2015. [Google Scholar]
- Chen, J.; Li, W. Convergence of Gauss-Newton’s method and uniqueness of the solution. Appl. Math. Comput. 2005, 170, 686–705. [Google Scholar] [CrossRef]
- Wu, J.; Li, M. Ill Matrix and Regularization Method in Surveying Data Processing. J. Geod. Geodyn. 2010, 30, 102–105. [Google Scholar]
- An, T. Research on SAR/INS Intergraded Velocity and Position Measurement Technology. Master’s Thesis, National University of Defense Technology, Changsha, China, 2012. [Google Scholar]
- Wang, Z.; Yu, A. A Fast Registration Method for Optical and SAR Images Based on SRAWG Feature Description. Remote Sens. 2022, 14, 5060. [Google Scholar] [CrossRef]
- Wang, Z.; Yu, A. Performance Evaluation of Interest Point Detectors for Heterologous Image Matching. Remote Sens. 2022, 14, 724. [Google Scholar] [CrossRef]


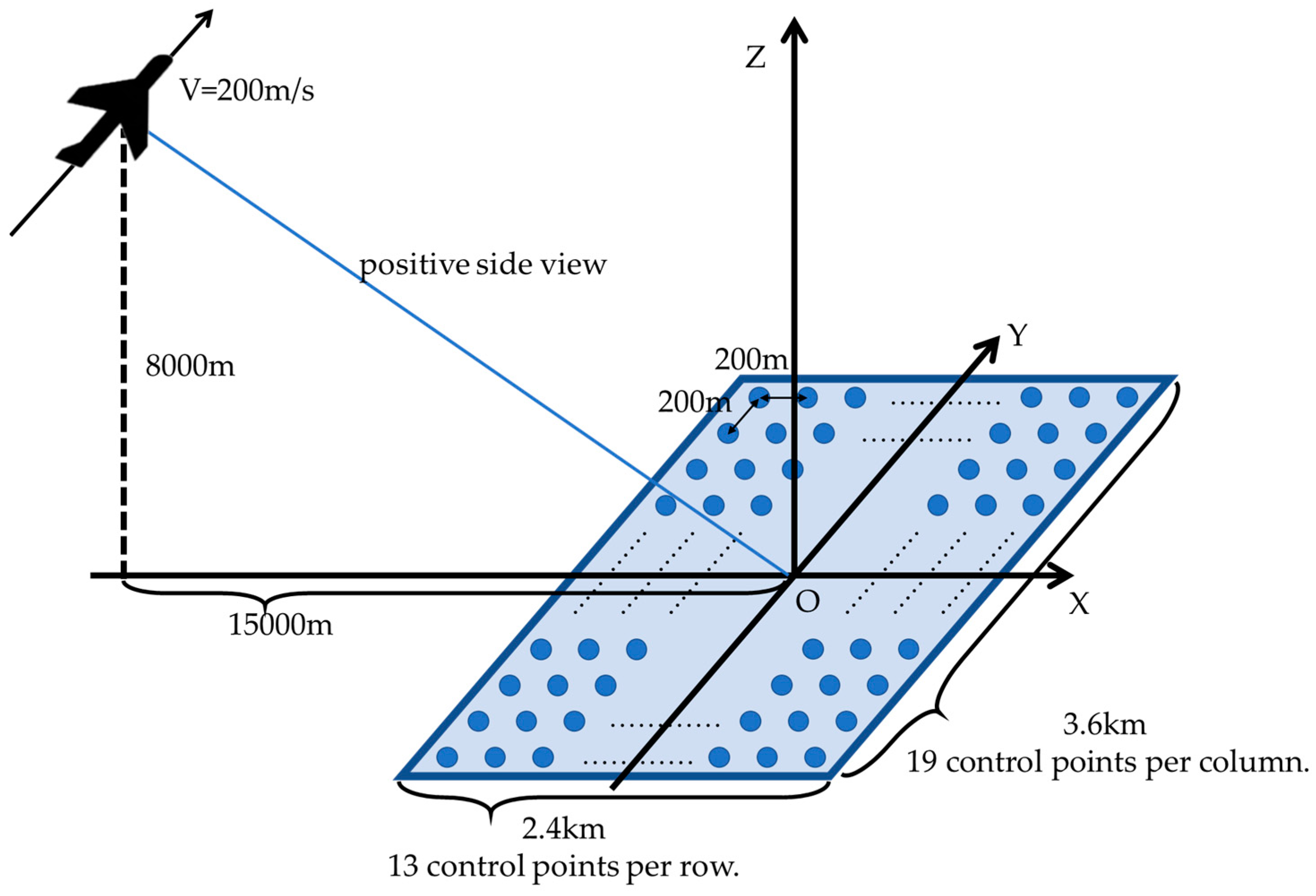





| Parameters | Value |
|---|---|
| Flight altitude of platform | 8000 m |
| Center distance | 15,000 m |
| Flight speed | 200 m/s |
| Imaging area | 3.6 × 2.4 km |
| Number of control points | 247 |
| Simulation Errors | Value |
|---|---|
| Systematic slant range offset | 3 m |
| Systematic control points positioning error | 3 m |
| Systematic Doppler bias | 2 Hz |
| Random slant range error | 2 m |
| Random control points positioning error | 2 m |
| Parameters | Value |
|---|---|
| Flight altitude of platform | 4908.5 m |
| Center distance | 34,196.9 m |
| Flight speed | 51.8 m/s |
| Resolution | 0.3 m |
| Imaging area | 2905 m × 4404 m |
| Image size | 11,200 × 14,336 |
| Number of control points | 200 |
| Simulation Errors | Value |
|---|---|
| Systematic slant range offset | 3 m |
| Systematic control points positioning error | 3 m |
| Systematic Doppler bias | 2 Hz |
| Random slant range error | 1 m |
| Random control points positioning error | 1 m |
| Parameters | (m) | (m) | (m) | (m/s) | (m/s) | (m/s) |
|---|---|---|---|---|---|---|
| Estimation errors | 5.87 | 17.1 | 4.0 | 0.0296 | 0.0008 | 0.2080 |
| Theoretical errors | 5.96 | 17.0 | 3.7 | 0.0296 | 0.0008 | 0.2115 |
| Parameters | (m) | (m) | (m) | (m/s) | (m/s) | (m/s) |
|---|---|---|---|---|---|---|
| Estimation errors | 3.16 | 4.94 | 22.19 | 0.00321 | 0.00519 | 0.0571 |
| Theoretical errors | 3.20 | 4.86 | 22.46 | 0.00325 | 0.00512 | 0.0573 |
| Parameters | (m) | (m) | (m) | (m/s) | (m/s) | (m/s) |
|---|---|---|---|---|---|---|
| Estimation errors | 6.51 | 17.64 | 22.54 | 0.0299 | 0.00526 | 0.213 |
| 6.76 | 17.68 | 22.76 | 0.0297 | 0.00518 | 0.219 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, W.; Yu, A.; Zhang, K.; Dong, Z. A Robust and High-Precision Three-Step Positioning Method for an Airborne SAR Platform. Remote Sens. 2023, 15, 3897. https://doi.org/10.3390/rs15153897
Tong W, Yu A, Zhang K, Dong Z. A Robust and High-Precision Three-Step Positioning Method for an Airborne SAR Platform. Remote Sensing. 2023; 15(15):3897. https://doi.org/10.3390/rs15153897
Chicago/Turabian StyleTong, Wenhao, Anxi Yu, Keke Zhang, and Zhen Dong. 2023. "A Robust and High-Precision Three-Step Positioning Method for an Airborne SAR Platform" Remote Sensing 15, no. 15: 3897. https://doi.org/10.3390/rs15153897





