SRTM DEM Correction Using Ensemble Machine Learning Algorithm
Abstract
:1. Introduction
2. Study Areas and Datasets
2.1. Study Areas
2.2. Datasets
2.2.1. SRTM DEM
2.2.2. Reference Elevation Data
2.2.3. Ancillary Data
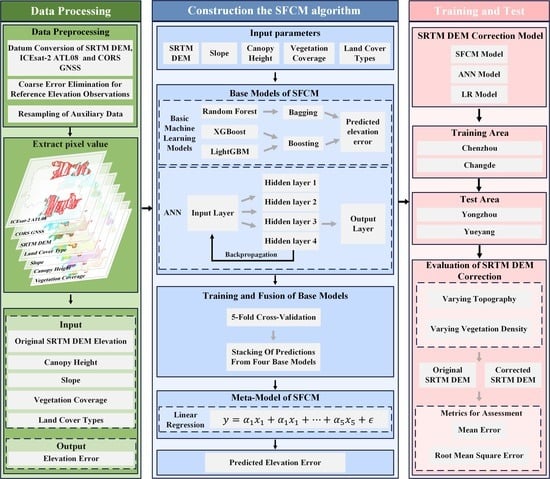
3. Method
3.1. Stacking Fusion Correction Model (SFCM) Construction
3.1.1. Base Models of the SFCM
3.1.2. Meta-Models of the SFCM
3.1.3. SRTM DEM Correction Using SFCM
4. Results and Discussion
4.1. SFCM-Based SRTM DEM Correction
4.2. Accuracy Evaluation of the SFCM-Corrected SRTM DEMs
4.3. Performance Comparisons between the SFCM and the Classical Algorithms
4.3.1. Comparison of Overall Accuracy
4.3.2. Accuracy Comparison with Respect to Slopes
4.3.3. Accuracy Comparison with Respect to Vegetation Coverage
4.3.4. Accuracy Comparison with Respect to Land Cover Types
4.3.5. Time Cost Comparison
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Miliaresis, G.C.; Paraschou, C.V.E. Geoinformation. Vertical accuracy of the SRTM DTED level 1 of Crete. Int. J. Appl. Earth Obs. Geoinf. 2005, 7, 49–59. [Google Scholar]
- Wilson, J.P. Environmental Applications of Digital Terrain Modeling; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Wolock, D.M.; Price, C.V. Effects of digital elevation model map scale and data resolution on a topography-based watershed model. Water Resour. Res. 1994, 30, 3041–3052. [Google Scholar] [CrossRef]
- Okolie, C.J.; Smit, J.L. A systematic review and meta-analysis of Digital elevation model (DEM) fusion: Pre-processing, methods and applications. ISPRS J. Photogramm. Remote Sens. 2022, 188, 1–29. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef] [Green Version]
- Hirt, C.; Filmer, M.S.; Featherstone, W.E. Comparison and validation of the recent freely available ASTER-GDEM ver1, SRTM ver4.1 and GEODATA DEM-9S ver3 digital elevation models over Australia. Aust. J. Earth Sci. 2010, 57, 337–347. [Google Scholar] [CrossRef] [Green Version]
- Tadono, T.; Nagai, H.; Ishida, H.; Oda, F.; Naito, S.; Minakawa, K.; Iwamoto, H. Generation of the 30 M-mesh global digital surface model by ALOS PRISM. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 157–162. [Google Scholar]
- Fahrland, E.; Paschko, H.; Jacob, P.; Kahabka, D.H. Copernicus DEM Product Handbook. Available online: https://spacedata.copernicus.eu/documents/20126/0/GEO1988-CopernicusDEM-SPE-002_ProductHandbook_I1.00.pdf (accessed on 25 June 2022).
- Mukherjee, S.; Joshi, P.K.; Mukherjee, S.; Ghosh, A.; Garg, R.; Mukhopadhyay, A. Geoinformation. Evaluation of vertical accuracy of open source Digital Elevation Model (DEM). Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 205–217. [Google Scholar]
- Berry, P.; Garlick, J.; Smith, R. Near-global validation of the SRTM DEM using satellite radar altimetry. Remote Sens. Environ. 2007, 106, 17–27. [Google Scholar] [CrossRef]
- Li, Y.; Fu, H.; Zhu, J.; Wu, K.; Yang, P.; Wang, L.; Gao, S. A Method for SRTM DEM Elevation Error Correction in Forested Areas Using ICESat-2 Data and Vegetation Classification Data. Remote Sens. 2022, 14, 3380. [Google Scholar] [CrossRef]
- Magruder, L.; Neuenschwander, A.; Klotz, B. Digital terrain model elevation corrections using space-based imagery and ICESat-2 laser altimetry. Remote Sens. Environ. 2021, 264, 112621. [Google Scholar] [CrossRef]
- O’Loughlin, F.; Paiva, R.; Durand, M.; Alsdorf, D.; Bates, P. A multi-sensor approach towards a global vegetation corrected SRTM DEM product. Remote Sens. Environ. 2016, 182, 49–59. [Google Scholar] [CrossRef] [Green Version]
- Su, Y.; Guo, Q. A practical method for SRTM DEM correction over vegetated mountain areas. ISPRS J. Photogramm. Remote Sens. 2014, 87, 216–228. [Google Scholar] [CrossRef]
- Su, Y.; Guo, Q.; Ma, Q.; Li, W. SRTM DEM Correction in Vegetated Mountain Areas through the Integration of Spaceborne LiDAR, Airborne LiDAR, and Optical Imagery. Remote Sens. 2015, 7, 11202–11225. [Google Scholar] [CrossRef] [Green Version]
- Yamazaki, D.; Ikeshima, D.; Tawatari, R.; Yamaguchi, T.; O’Loughlin, F.; Neal, J.C.; Sampson, C.C.; Kanae, S.; Bates, P.B. A high-accuracy map of global terrain elevations. Geophys. Res. Lett. 2017, 44, 5844–5853. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Su, Y.; Hu, T.; Chen, L.; Gao, S.; Wang, R.; Jin, S.; Guo, Q. A global corrected SRTM DEM product for vegetated areas. Remote Sens. Lett. 2018, 9, 393–402. [Google Scholar] [CrossRef]
- Zhou, C.; Zhang, G.; Yang, Z.; Ao, M.; Liu, Z.; Zhu, J. An Adaptive Terrain-Dependent Method for SRTM DEM Correction Over Mountainous Areas. IEEE Access 2020, 8, 130878–130887. [Google Scholar] [CrossRef]
- Preety, K.; Prasad, A.K.; Varma, A.K.; El-Askary, H. Accuracy Assessment, Comparative Performance, and Enhancement of Public Domain Digital Elevation Models (ASTER 30 m, SRTM 30 m, CARTOSAT 30 m, SRTM 90 m, MERIT 90 m, and TanDEM-X 90 m) Using DGPS. Remote Sens. 2022, 14, 1334. [Google Scholar] [CrossRef]
- Shastry, A.; Durand, M. Water Surface Elevation Constraints in a Data Assimilation Scheme to Infer Floodplain Topography: A Case Study in the Logone Floodplain. Geophys. Res. Lett. 2020, 47, e2020GL088759. [Google Scholar] [CrossRef]
- Hawker, L.; Neal, J.; Bates, P. Accuracy assessment of the TanDEM-X 90 Digital Elevation Model for selected floodplain sites. Remote Sens. Environ. 2019, 232, 111319. [Google Scholar] [CrossRef]
- Mason, D.C.; Trigg, M.; Garcia-Pintado, J.; Cloke, H.L.; Neal, J.C.; Bates, P.D. Improving the TanDEM-X Digital Elevation Model for flood modelling using flood extents from Synthetic Aperture Radar images. Remote Sens. Environ. 2016, 173, 15–28. [Google Scholar] [CrossRef] [Green Version]
- Durand, M.; Andreadis, K.M.; Alsdorf, D.E.; Lettenmaier, D.P.; Moller, D.; Wilson, M. Estimation of bathymetric depth and slope from data assimilation of swath altimetry into a hydrodynamic model. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Hawker, L.; Bates, P.; Neal, J.; Rougier, J. Perspectives on Digital Elevation Model (DEM) Simulation for Flood Modeling in the Absence of a High-Accuracy Open Access Global DEM. Front. Earth Sci. 2018, 6, 233. [Google Scholar] [CrossRef] [Green Version]
- Kulp, S.; Strauss, B.H. Global DEM errors underpredict coastal vulnerability to sea level rise and flooding. Front. Earth Sci. 2016, 4, 36. [Google Scholar] [CrossRef]
- Wendi, D.; Liong, S.-Y.; Sun, Y.; Doan, C.D. An innovative approach to improve SRTM DEM using multispectral imagery and artificial neural network. J. Adv. Model. Earth Syst. 2016, 8, 691–702. [Google Scholar] [CrossRef] [Green Version]
- Hawker, L.; Uhe, P.; Paulo, L.; Sosa, J.; Savage, J.; Sampson, C.; Neal, J. A 30 m global map of elevation with forests and buildings removed. Environ. Res. Lett. 2022, 17, 024016. [Google Scholar] [CrossRef]
- Kasi, V.; Yeditha, P.K.; Rathinasamy, M.; Pinninti, R.; Landa, S.R.; Sangamreddi, C.; Agarwal, A.; Radha, P.R.D. A novel method to improve vertical accuracy of CARTOSAT DEM using machine learning models. Earth Sci. Inform. 2020, 13, 1139–1150. [Google Scholar] [CrossRef]
- Kim, D.E.; Liong, S.-Y.; Gourbesville, P.; Andres, L.; Liu, J. Simple-Yet-Effective SRTM DEM Improvement Scheme for Dense Urban Cities Using ANN and Remote Sensing Data: Application to Flood Modeling. Water 2020, 12, 816. [Google Scholar] [CrossRef] [Green Version]
- Meadows, M.; Wilson, M. A Comparison of Machine Learning Approaches to Improve Free Topography Data for Flood Modelling. Remote Sens. 2021, 13, 275. [Google Scholar] [CrossRef]
- Nguyen, N.S.; Kim, D.E.; Jia, Y.; Raghavan, S.V.; Liong, S.Y. Application of Multi-Channel Convolutional Neural Network to Improve DEM Data in Urban Cities. Technologies 2022, 10, 61. [Google Scholar] [CrossRef]
- Chen, C.; Yang, S.; Li, Y. Accuracy Assessment and Correction of SRTM DEM using ICESat/GLAS Data under Data Coregistration. Remote Sens. 2020, 12, 3435. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: Berlin/Heidelberg, Germany, 2013; Volume 26. [Google Scholar]
- Polikar, R. Applications. In Ensemble Learning; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1–34. [Google Scholar]
- Bui, D.T.; Tsangaratos, P.; Ngo, P.-T.T.; Pham, T.D.; Pham, B.T. Flash flood susceptibility modeling using an optimized fuzzy rule based feature selection technique and tree based ensemble methods. Sci. Total Environ. 2019, 668, 1038–1054. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Peng, L.; Hong, H. A comparative study of heterogeneous ensemble-learning techniques for landslide susceptibility mapping. Int. J. Geogr. Inf. Sci. 2021, 35, 321–347. [Google Scholar] [CrossRef]
- Fu, B.; He, X.; Yao, H.; Liang, Y.; Deng, T.; He, H.; Fan, D.; Lan, G.; He, W. Comparison of RFE-DL and stacking ensemble learning algorithms for classifying mangrove species on UAV multispectral images. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102890. [Google Scholar] [CrossRef]
- Rabus, B.; Eineder, M.; Roth, A.; Bamler, R. The shuttle radar topography mission—A new class of digital elevation models acquired by spaceborne radar. ISPRS J. Photogramm. Remote Sens. 2003, 57, 241–262. [Google Scholar] [CrossRef]
- Rodríguez, E.; Morris, C.S.; Belz, J.E. A Global Assessment of the SRTM Performance. Photogramm. Eng. Remote Sens. 2006, 72, 249–260. [Google Scholar] [CrossRef] [Green Version]
- Jarvis, A.; Guevara, E.; Reuter, H.I.; Nelson, A.D. Hole-filled SRTM for the globe Version 4: Data grid. CGIAR Consort. Spat. Inf. 2008, 15, 5. [Google Scholar]
- Reuter, H.I.; Nelson, A.; Jarvis, A. An evaluation of void-filling interpolation methods for SRTM data. Int. J. Geogr. Inf. Sci. 2007, 21, 983–1008. [Google Scholar] [CrossRef]
- Florinsky, I.; Skrypitsyna, T.; Luschikova, O. Comparative accuracy of the AW3D30 DSM, ASTER GDEM, and SRTM1 DEM: A case study on the Zaoksky testing ground, Central European Russia. Remote Sens. Lett. 2018, 9, 706–714. [Google Scholar] [CrossRef]
- Ao, M.; Dong, M.; Chu, B.; Zeng, X.; Li, C. Revealing the User Behavior Pattern Using HNCORS RTK Location Big Data. IEEE Access 2019, 7, 30302–30312. [Google Scholar] [CrossRef]
- Snay, R.A.; Soler, T. Continuously operating reference station (CORS): History, applications, and future enhancements. J. Surv. Eng. 2008, 134, 95–104. [Google Scholar] [CrossRef]
- Teunissen, P.J.; Odijk, D.; Zhang, B. PPP-RTK: Results of CORS network-based PPP with integer ambiguity resolution. J. Aeronaut. Astronaut. Aviat. Ser. A 2010, 42, 223–230. [Google Scholar]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The Ice, Cloud, and land Elevation Satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Guenther, E.; White, J.C.; Duncanson, L.; Montesano, P. Validation of ICESat-2 terrain and canopy heights in boreal forests. Remote Sens. Environ. 2020, 251, 112110. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Pitts, K. The ATL08 land and vegetation product for the ICESat-2 Mission. Remote Sens. Environ. 2019, 221, 247–259. [Google Scholar] [CrossRef]
- Liu, A.; Cheng, X.; Chen, Z. Performance evaluation of GEDI and ICESat-2 laser altimeter data for terrain and canopy height retrievals. Remote Sens. Environ. 2021, 264, 112571. [Google Scholar] [CrossRef]
- Satgé, F.; Bonnet, M.; Timouk, F.; Calmant, S.; Pillco, R.; Molina, J.; Lavado-Casimiro, W.; Arsen, A.; Crétaux, J.; Garnier, J. Accuracy assessment of SRTM v4 and ASTER GDEM v2 over the Altiplano watershed using ICESat/GLAS data. Int. J. Remote Sens. 2015, 36, 465–488. [Google Scholar] [CrossRef]
- Wessel, B.; Huber, M.; Wohlfart, C.; Marschalk, U.; Kosmann, D.; Roth, A. Accuracy assessment of the global TanDEM-X Digital Elevation Model with GPS data. ISPRS J. Photogramm. Remote Sens. 2018, 139, 171–182. [Google Scholar] [CrossRef]
- Liu, X.; Su, Y.; Hu, T.; Yang, Q.; Liu, B.; Deng, Y.; Tang, H.; Tang, Z.; Fang, J.; Guo, Q. Neural network guided interpolation for mapping canopy height of China’s forests by integrating GEDI and ICESat-2 data. Remote Sens. Environ. 2022, 269, 112844. [Google Scholar] [CrossRef]
- Song, W.; Mu, X.; Ruan, G.; Gao, Z.; Li, L.; Yan, G. Estimating fractional vegetation cover and the vegetation index of bare soil and highly dense vegetation with a physically based method. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 168–176. [Google Scholar] [CrossRef]
- Brovelli, M.A.; Molinari, M.E.; Hussein, E.; Chen, J.; Li, R. The First Comprehensive Accuracy Assessment of GlobeLand30 at a National Level: Methodology and Results. Remote Sens. 2015, 7, 4191–4212. [Google Scholar] [CrossRef] [Green Version]
- Wu, T.; Zhang, W.; Jiao, X.; Guo, W.; Hamoud, Y.A. Evaluation of stacking and blending ensemble learning methods for estimating daily reference evapotranspiration. Comput. Electron. Agric. 2021, 184, 106039. [Google Scholar] [CrossRef]
- Wen, L.; Hughes, M. Coastal Wetland Mapping Using Ensemble Learning Algorithms: A Comparative Study of Bagging, Boosting and Stacking Techniques. Remote Sens. 2020, 12, 1683. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Saritas, M.M.; Yasar, A. Performance analysis of ANN and Naive Bayes classification algorithm for data classification. Int. J. Intell. Syst. Appl. Eng. 2019, 7, 88–91. [Google Scholar] [CrossRef] [Green Version]
- Dou, J.; Yunus, A.P.; Bui, D.T.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.-W.; Han, Z.; Pham, B.T. Improved landslide assessment using support vector machine with bagging, boosting, and stacking ensemble machine learning framework in a mountainous watershed, Japan. Landslides 2019, 17, 641–658. [Google Scholar] [CrossRef]
- Zhang, H.; Li, J.-L.; Liu, X.-M.; Dong, C. Multi-dimensional feature fusion and stacking ensemble mechanism for network intrusion detection. Futur. Gener. Comput. Syst. 2021, 122, 130–143. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- Buffington, K.J.; Dugger, B.D.; Thorne, K.M.; Takekawa, J.Y. Statistical correction of lidar-derived digital elevation models with multispectral airborne imagery in tidal marshes. Remote Sens. Environ. 2016, 186, 616–625. [Google Scholar] [CrossRef] [Green Version]
- Pham, H.T.; Marshall, L.; Johnson, F.; Sharma, A. A method for combining SRTM DEM and ASTER GDEM2 to improve topography estimation in regions without reference data. Remote Sens. Environ. 2018, 210, 229–241. [Google Scholar] [CrossRef]
- Kulp, S.A.; Strauss, B.H. CoastalDEM: A global coastal digital elevation model improved from SRTM using a neural network. Remote Sens. Environ. 2018, 206, 231–239. [Google Scholar] [CrossRef]
- Akyol, K. Stacking ensemble based deep neural networks modeling for effective epileptic seizure detection. Expert Syst. Appl. 2020, 148, 113239. [Google Scholar] [CrossRef]
- Ribeiro, M.H.D.M.; dos Santos Coelho, L. Ensemble approach based on bagging, boosting and stacking for short-term prediction in agribusiness time series. Appl. Soft Comput. 2020, 86, 105837. [Google Scholar] [CrossRef]
- Maulud, D.; Abdulazeez, A. A review on linear regression comprehensive in machine learning. J. Appl. Sci. Tech. Trends 2020, 1, 140–147. [Google Scholar] [CrossRef]
- Gorokhovich, Y.; Voustianiouk, A. Accuracy assessment of the processed SRTM-based elevation data by CGIAR using field data from USA and Thailand and its relation to the terrain characteristics. Remote Sens. Environ. 2006, 104, 409–415. [Google Scholar] [CrossRef]
- Satge, F.; Denezine, M.; Pillco, R.; Timouk, F.; Pinel, S.; Molina, J.; Garnier, J.; Seyler, F.; Bonnet, M.-P. Absolute and relative height-pixel accuracy of SRTM-GL1 over the South American Andean Plateau. ISPRS J. Photogramm. Remote Sens. 2016, 121, 157–166. [Google Scholar] [CrossRef]









| Topography | Region | Area (km2) | Mean Elevation (m) | Mean Slope (°) | Mean Canopy Height (m) | Vegetation Coverage (%) | Number of CORS Observations | Number of ATL08 Observations |
|---|---|---|---|---|---|---|---|---|
| Mountainous | Chenzhou | 19,387 | 493.3 | 14.9 | 8.1 | 71.8 | 219,439 | 12,569 |
| Yongzhou | 22,400 | 434.3 | 14.5 | 7.5 | 70.2 | 125,442 | 7185 | |
| Low-relief | Changde | 18,200 | 159.3 | 9.2 | 5.8 | 59.4 | 240,009 | 13,747 |
| Yueyang | 14,858 | 133.5 | 7.9 | 5.6 | 58.7 | 157,117 | 8999 |
| Slope Thresholds (°) | SRTM DEM | SFCM-Corrected | ANN-Corrected | LR-Corrected | ||||
|---|---|---|---|---|---|---|---|---|
| ME (m) | RMSE (m) | ME (m) | RMSE (m) | ME (m) | RMSE (m) | ME (m) | RMSE (m) | |
| 0–5 | 2.70 | 10.7 | −0.03 | 6.1 | −0.01 | 7.5 | −0.38 | 9.9 |
| 5–10 | 4.91 | 11.5 | 0.05 | 6.4 | −0.12 | 7.9 | −0.05 | 10.2 |
| 10–20 | 7.73 | 13.1 | 0.07 | 7.3 | 0.03 | 8.8 | 0.02 | 10.9 |
| 20–30 | 10.10 | 16.4 | −0.08 | 10.2 | 0.15 | 11.4 | 0.21 | 14.3 |
| ≥30 | 12.45 | 18.6 | 0.43 | 11.5 | 0.02 | 13.0 | 0.77 | 16.9 |
| Vegetation Coverage Thresholds (%) | SRTM DEM | SFCM-Corrected | ANN Corrected | LR Corrected | ||||
|---|---|---|---|---|---|---|---|---|
| ME (m) | RMSE (m) | ME (m) | RMSE (m) | ME (m) | RMSE (m) | ME (m) | RMSE (m) | |
| 0–25 | 2.27 | 6.8 | 0.03 | 3.9 | 0.09 | 4.6 | −0.03 | 6.0 |
| 25–50 | 3.56 | 8.4 | 0.06 | 4.9 | 0.10 | 6.1 | 0.08 | 6.1 |
| 50–75 | 4.90 | 9.2 | −0.02 | 5.2 | 0.10 | 6.4 | 0.03 | 7.7 |
| 75–100 | 8.00 | 12.0 | 0.05 | 6.6 | −0.03 | 7.6 | −0.20 | 9.2 |
| Land Cover Types | CORS GNSS | ICEsat-2 ATL08 |
|---|---|---|
| Cultivated Land | 407,669 | 17,188 |
| Forest | 192,769 | 16,301 |
| Grasslands | 58,099 | 4106 |
| Wetlands | 611 | 36 |
| Water Bodies | 17,186 | 1008 |
| Artificial Surfaces | 65,634 | 3848 |
| Bare Land | 39 | 13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouyang, Z.; Zhou, C.; Xie, J.; Zhu, J.; Zhang, G.; Ao, M. SRTM DEM Correction Using Ensemble Machine Learning Algorithm. Remote Sens. 2023, 15, 3946. https://doi.org/10.3390/rs15163946
Ouyang Z, Zhou C, Xie J, Zhu J, Zhang G, Ao M. SRTM DEM Correction Using Ensemble Machine Learning Algorithm. Remote Sensing. 2023; 15(16):3946. https://doi.org/10.3390/rs15163946
Chicago/Turabian StyleOuyang, Zidu, Cui Zhou, Jian Xie, Jianjun Zhu, Gui Zhang, and Minsi Ao. 2023. "SRTM DEM Correction Using Ensemble Machine Learning Algorithm" Remote Sensing 15, no. 16: 3946. https://doi.org/10.3390/rs15163946
APA StyleOuyang, Z., Zhou, C., Xie, J., Zhu, J., Zhang, G., & Ao, M. (2023). SRTM DEM Correction Using Ensemble Machine Learning Algorithm. Remote Sensing, 15(16), 3946. https://doi.org/10.3390/rs15163946