Self-Adaptive Filtering for Ultra-Large-Scale Airborne LiDAR Data in Urban Environments Based on Object Primitive Global Energy Minimization
Abstract
1. Introduction
- i)
- Point clouds filtering is transformed as global energy minimization, which can be solved using graph cuts automatically.
- ii)
- A mode graph is constructed using the mode points instead of raw LiDAR points, which will reduce the computation load and speed up the implementation efficiency of the method.
- iii)
- Filtering thresholds can be calculated self-adaptively according to the constantly updated coarse ground surface, so as to protect terrain details and obtain higher filtering accuracy.
2. Methodology
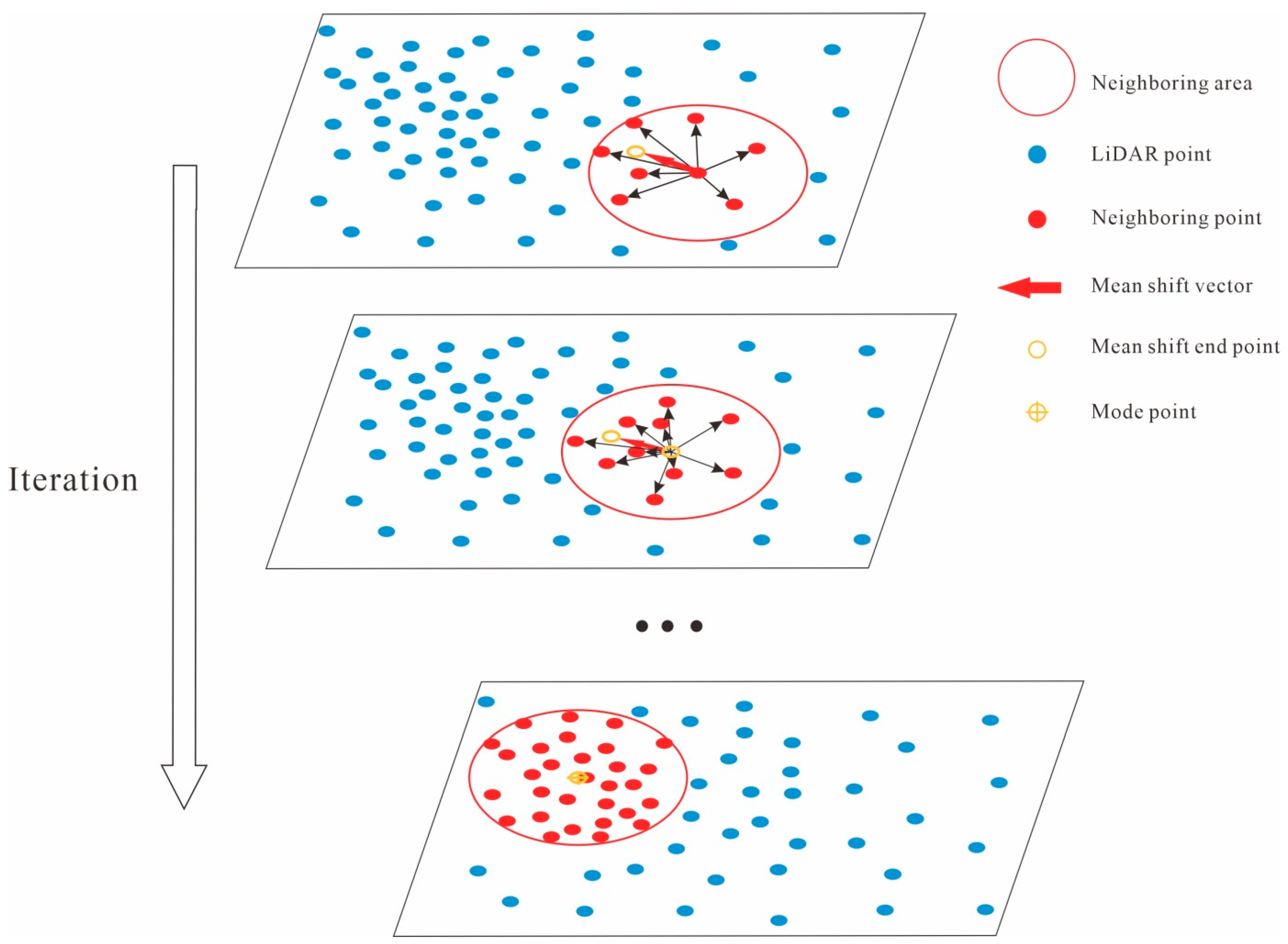
2.1. Mode Graph Construction
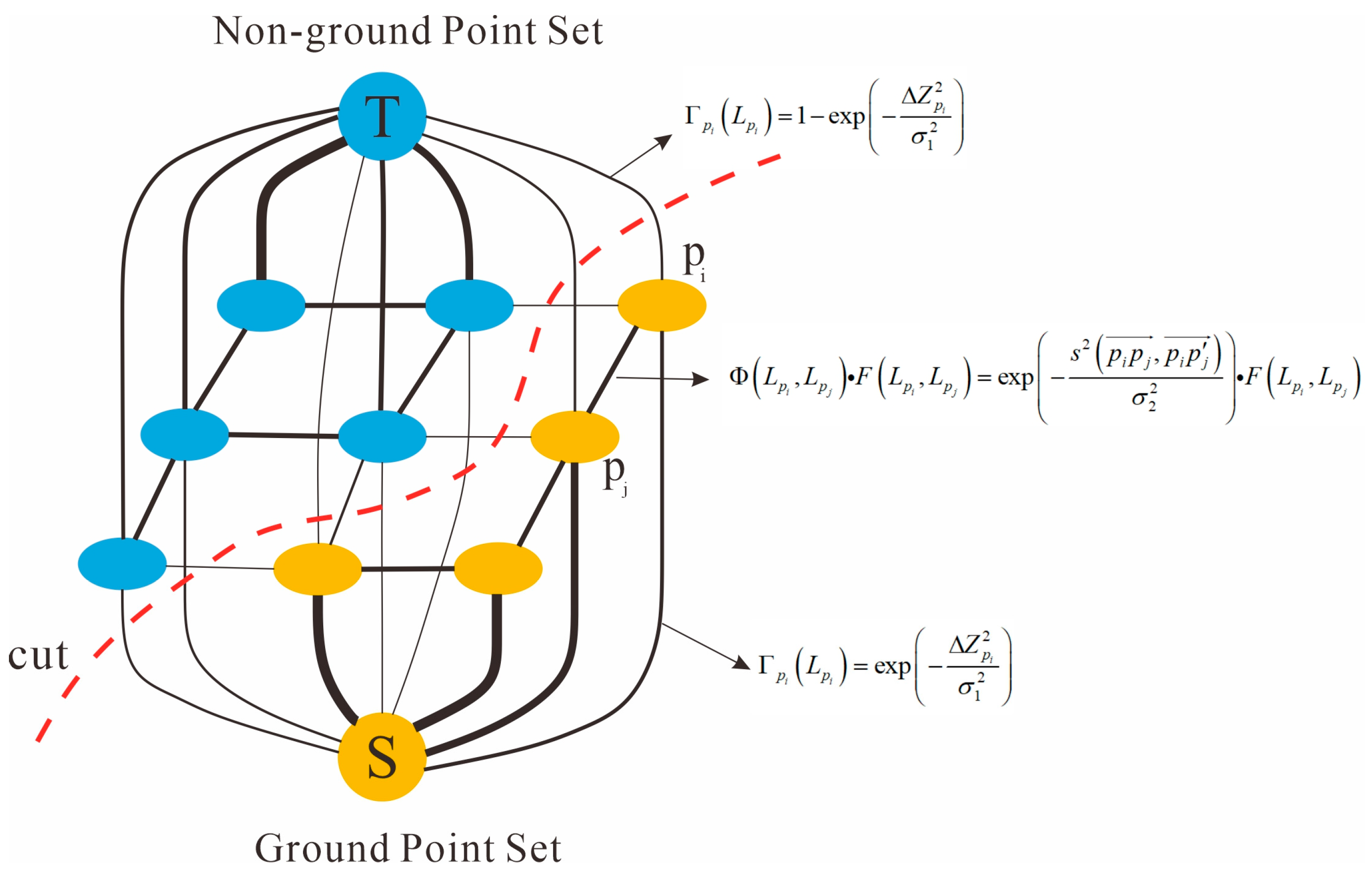
2.2. Global Energy Minimization
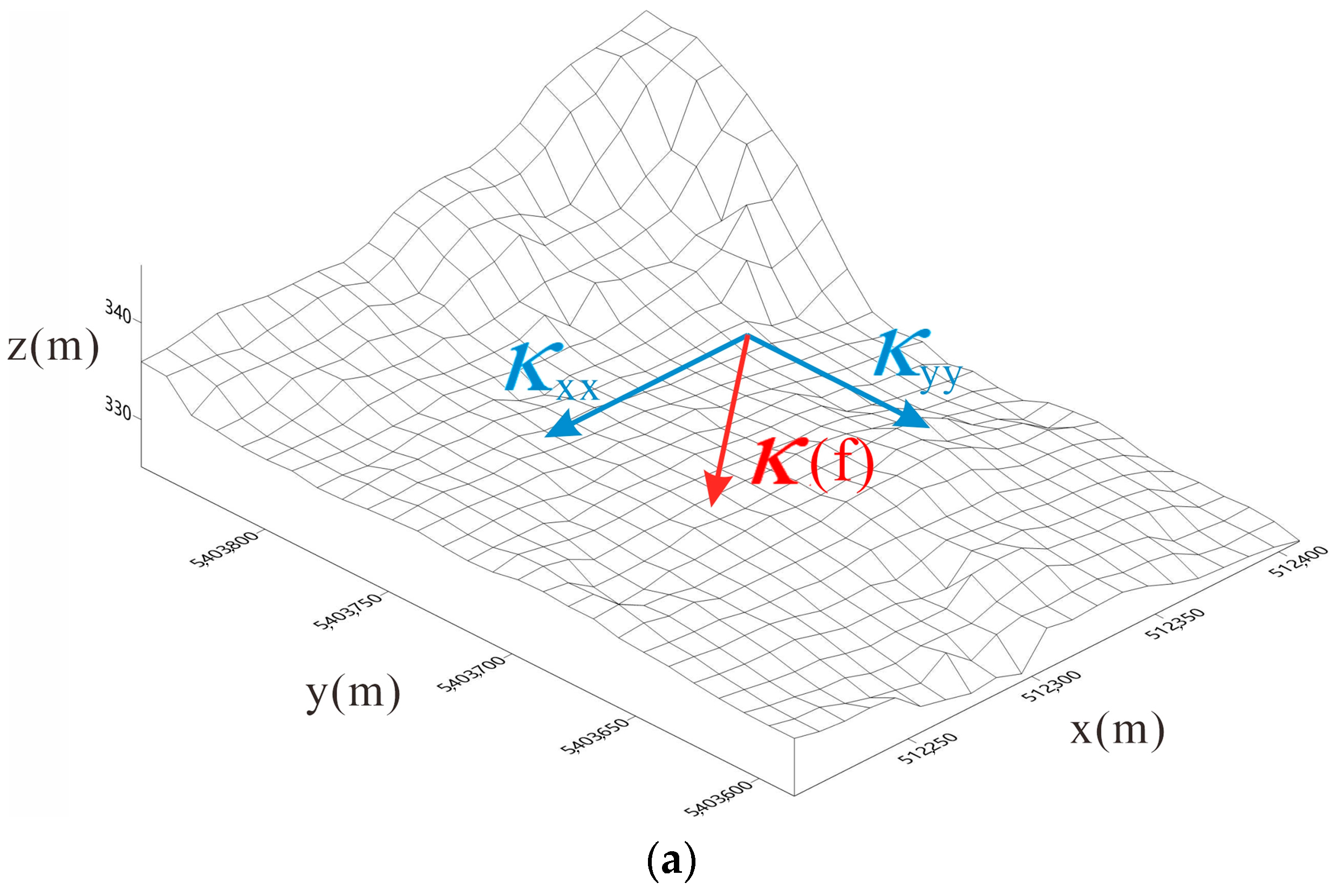
2.3. Self-Adaptive Progressive Filtering
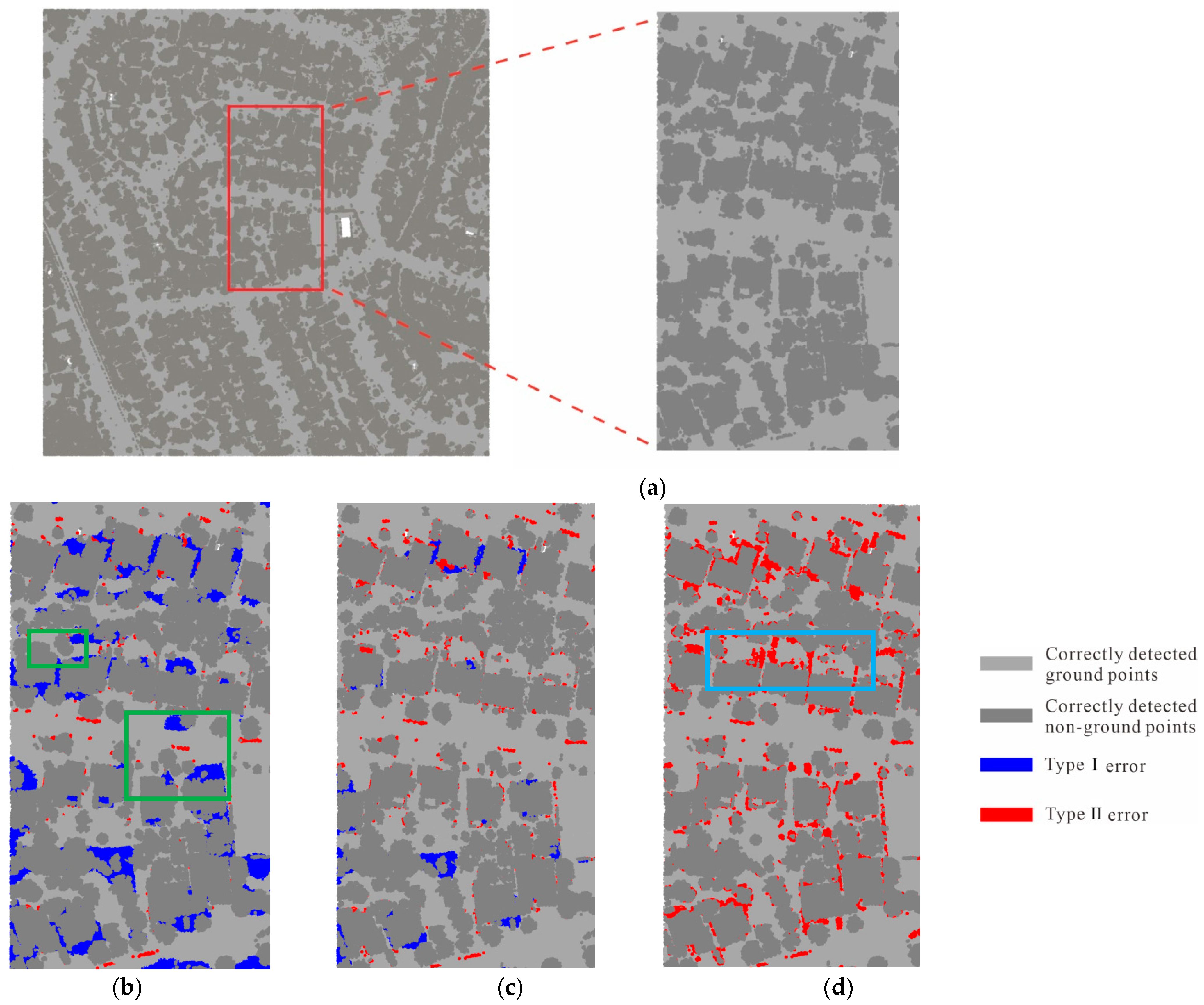
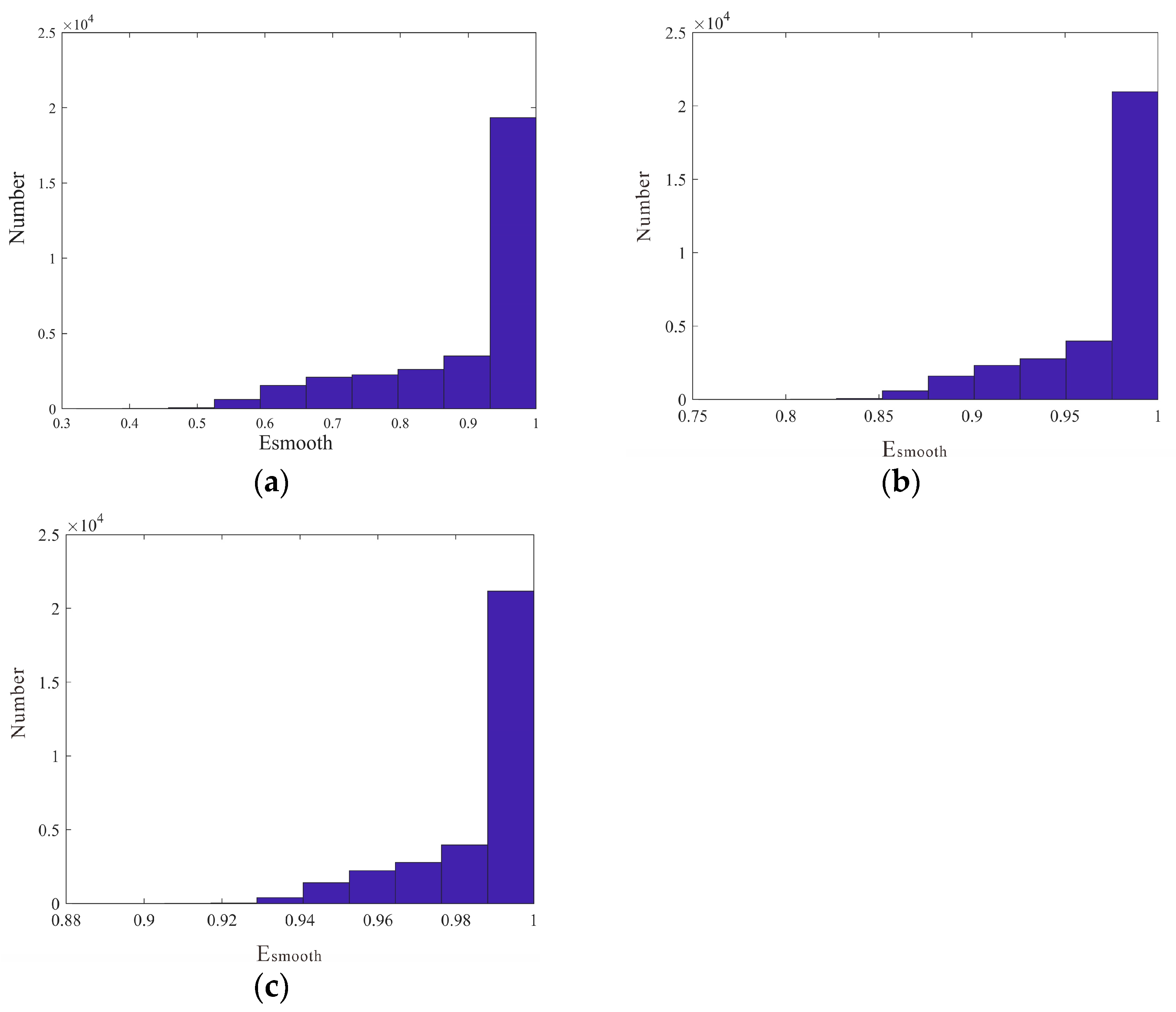
3. Experimental Results and Analysis
3.1. Data Description
3.2. Experimental Results and Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jia, J.; Sun, H.; Jiang, C.; Karila, K.; Karjalainen, M.; Ahokas, E.; Khoramshahi, E.; Hu, P.; Chen, C.; Xue, T.; et al. Review on active and passive remote sensing techniques for road extraction. Remote Sens. 2021, 13, 4235. [Google Scholar] [CrossRef]
- Cai, Z.; Ma, H.; Zhang, L. A building detection method based on semi-suppressed fuzzy c-means and restricted region growing using airborne LiDAR. Remote Sens. 2019, 11, 848. [Google Scholar] [CrossRef]
- You, H.; Li, S.; Xu, Y.; He, Z.; Wang, D. Tree extraction from airborne laser scanning data in urban areas. Remote Sens. 2021, 13, 3428. [Google Scholar] [CrossRef]
- Xue, F.; Lu, W.; Chen, Z.; Webster, C.J. From LiDAR point cloud towards digital twin city: Clustering city objects based on gestalt principles. ISPRS J. Photogramm. 2020, 167, 418–431. [Google Scholar] [CrossRef]
- Zhao, H.; Xi, X.; Wang, C.; Pan, F. Ground surface recognition at voxel scale from mobile laser scanning data in urban environment. IEEE Geosci. Remote Sens. Lett. 2020, 17, 317–321. [Google Scholar] [CrossRef]
- Cai, S.; Zhang, W.; Liang, X.; Wan, P.; Qi, J.; Yu, S.; Yan, G.; Shao, J. Filtering airborne LiDAR data through complementary cloth simulation and progressive TIN densification filters. Remote Sens. 2019, 11, 1037. [Google Scholar] [CrossRef]
- Vosselman, G. Slope Based Filtering of Laser Altimetry Data; IAPRS: Amsterdam, The Netherlands, 2000; Volume XXXIII. [Google Scholar]
- Meng, X.; Wang, L.; Silván-Cárdenas, J.L.; Currit, N. A multi-directional ground filtering algorithm for airborne LIDAR. ISPRS J. Photogramm. 2009, 64, 117–124. [Google Scholar] [CrossRef]
- Susaki, J. Adaptive slope filtering of airborne LiDAR data in urban areas for digital terrain model (DTM) generation. Remote Sens. 2012, 4, 1804–1819. [Google Scholar] [CrossRef]
- Rashidi, P.; Rastiveis, H. Extraction of ground points from LiDAR data based on slope and progressive window thresholding (SPWT). Earth Obs. Geomat. Eng. 2018, 2, 36–44. [Google Scholar]
- Chen, C.; Guo, J.; Wu, H.; Li, Y.; Shi, B. Performance comparison of filtering algorithms for high-density airborne LiDAR point clouds over complex landscapes. Remote Sens. 2021, 13, 2663. [Google Scholar] [CrossRef]
- Zhang, K.; Chen, S.; Whitman, D.; Shyu, M.; Yan, J.; Zhang, C. A progressive morphological filter for removing nonground measurements from airborne LiDAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 872–882. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An easy-to-use airborne LiDAR data filtering method based on cloth simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Pingel, T.J.; Clarke, K.C.; McBride, W.A. An improved simple morphological filter for the terrain classification of airborne LIDAR data. ISPRS J. Photogramm. 2013, 77, 21–30. [Google Scholar] [CrossRef]
- Hui, Z.; Hu, Y.; Yevenyo, Y.Z.; Yu, X. An improved morphological algorithm for filtering airborne LiDAR point cloud based on multi-Level kriging interpolation. Remote Sens. 2016, 8, 35. [Google Scholar] [CrossRef]
- Axelsson, P. DEM generation from laser scanner data using adaptive TIN models. Int. Arch. Photogramm. Remote Sens. 2000, 33, 110–111. [Google Scholar]
- Zhang, J.; Lin, X. Filtering airborne LiDAR data by embedding smoothness-constrained segmentation in progressive TIN densification. ISPRS J. Photogramm. 2013, 81, 44–59. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Y.; Cheng, L.; Yao, M.; Deng, S.; Li, M.; Cai, D. Airborne laser scanning point clouds filtering method based on the construction of virtual ground seed points. J. Appl. Remote Sens. 2017, 11, 16032. [Google Scholar] [CrossRef]
- Mongus, D.; Žalik, B. Parameter-free ground filtering of LiDAR data for automatic DTM generation. ISPRS J. Photogramm. 2012, 67, 1–12. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y.; Li, W.; Dai, H. A multiresolution hierarchical classification algorithm for filtering airborne LiDAR data. ISPRS J. Photogramm. 2013, 82, 1–9. [Google Scholar] [CrossRef]
- Cheng, P.; Hui, Z.; Xia, Y.; Ziggah, Y.Y.; Hu, Y.; Wu, J. An improved skewness balancing filtering algorithm based on thin plate spline interpolation. Appl. Sci. 2019, 9, 203. [Google Scholar] [CrossRef]
- Melzer, T. Non-parametric segmentation of ALS point clouds using mean shift. J. Appl. Geodesy. 2007, 3, 159–170. [Google Scholar] [CrossRef]
- Boykov, Y.; Funka-Lea, G. Graph Cuts and Efficient N-D Image Segmentation. Int. J. Comput. Vis. 2006, 70, 109–131. [Google Scholar] [CrossRef]
- Qin, N.; Tan, W.; Ma, L.; Zhang, D.; Li, J. OpenGF: An ultra-large-scale ground filtering dataset built upon open ALS point clouds around the world. In Proceedings of the IEEE/CVF Conference on CVPR Workshop, Virtual Event, 19–25 June 2021; pp. 1–11. [Google Scholar]
- Pacific Northwest Research Station USDA Forest Service. Available online: https://forsys.sefs.uw.edu/FUSION/fusionlatest.html (accessed on 27 July 2023).






| Input: Mode Points and Mode Graph |
| Step 1: Achieve initial coarse ground surface . |
| Step 2: Calculate the distance from each point to the surface (). |
| Step 3: Calculate probability according to Equation (5). |
| Step 4: Construct energy function using Equations (4) and (6). |
| Step 5: Energy minimization based on graph cuts as shown in Figure 4. |
| Step 6: Obtain the labeling results and update the coarse ground surface . |
| Step 7: if |
| obtain the final ground surface as |
| break |
| else |
| and go to S2 |
| end |
| Step 8: Calculate the self-adaptive filtering threshold based on the ground surface. |
| Output: Filtering Results: |
| Area | Ground Points | Non-Ground Points | Size (m2) | Density (Points/m2) | Objects |
|---|---|---|---|---|---|
| S1 | 1,306,153 | 1,498,883 | 500 × 500 | 11 | Large buildings, cars, overpass, low vegetation, trees. |
| S2 | 1,783,541 | 3,690,842 | 500 × 500 | 21 | Dense buildings, cars, bridges, low vegetation, trees. |
| S3 | 137,033 | 119,707 | 500 × 500 | 1 | Middle-size buildings, cars, low vegetation, trees. |
| S4 | 388,303 | 375,554 | 500 × 500 | 3 | Dense middle-size buildings, low vegetation, trees. |
| Area | Method | Type I (%) | Type II (%) | Total (%) | (%) |
|---|---|---|---|---|---|
| S1 | PM | 13.81 | 3.87 | 8.5 | 82.83 |
| CSF | 3.05 | 2.34 | 2.67 | 94.63 | |
| Fusion | 3.4 | 14.04 | 9.09 | 81.89 | |
| The proposed method | 0.49 | 3.19 | 1.94 | 96.12 | |
| S2 | PM | 17.56 | 4.68 | 8.87 | 79.38 |
| CSF | 5.65 | 3.76 | 4.38 | 90.09 | |
| Fusion | 1.46 | 4.86 | 3.75 | 91.65 | |
| The proposed method | 0.67 | 5.21 | 3.73 | 91.72 | |
| S3 | PM | 3.37 | 8.65 | 5.83 | 88.25 |
| CSF | 4.7 | 7.42 | 5.97 | 87.79 | |
| Fusion | 3.49 | 7.55 | 5.39 | 89.16 | |
| The proposed method | 2 | 6.92 | 4.29 | 91.35 | |
| S4 | PM | 5.01 | 6.18 | 5.58 | 88.82 |
| CSF | 11.04 | 3.6 | 7.38 | 85.25 | |
| Fusion | 14.36 | 2.87 | 8.71 | 82.61 | |
| The proposed method | 2.08 | 3.79 | 2.92 | 94.15 |
| Type I Error (%) | Type II Error (%) | Total Error (%) | Kappa (%) | |
|---|---|---|---|---|
| 2 | 2.59 | 3.76 | 3.17 | 93.67 |
| 4 | 2.08 | 3.79 | 2.92 | 94.15 |
| 6 | 1.60 | 5.53 | 3.53 | 92.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hui, Z.; Li, Z.; Li, D.; Xu, Y.; Wang, Y. Self-Adaptive Filtering for Ultra-Large-Scale Airborne LiDAR Data in Urban Environments Based on Object Primitive Global Energy Minimization. Remote Sens. 2023, 15, 4013. https://doi.org/10.3390/rs15164013
Hui Z, Li Z, Li D, Xu Y, Wang Y. Self-Adaptive Filtering for Ultra-Large-Scale Airborne LiDAR Data in Urban Environments Based on Object Primitive Global Energy Minimization. Remote Sensing. 2023; 15(16):4013. https://doi.org/10.3390/rs15164013
Chicago/Turabian StyleHui, Zhenyang, Zhuoxuan Li, Dajun Li, Yanan Xu, and Yuqian Wang. 2023. "Self-Adaptive Filtering for Ultra-Large-Scale Airborne LiDAR Data in Urban Environments Based on Object Primitive Global Energy Minimization" Remote Sensing 15, no. 16: 4013. https://doi.org/10.3390/rs15164013
APA StyleHui, Z., Li, Z., Li, D., Xu, Y., & Wang, Y. (2023). Self-Adaptive Filtering for Ultra-Large-Scale Airborne LiDAR Data in Urban Environments Based on Object Primitive Global Energy Minimization. Remote Sensing, 15(16), 4013. https://doi.org/10.3390/rs15164013






