Spatial Statistical Prediction of Solar-Induced Chlorophyll Fluorescence (SIF) from Multivariate OCO-2 Data
Abstract
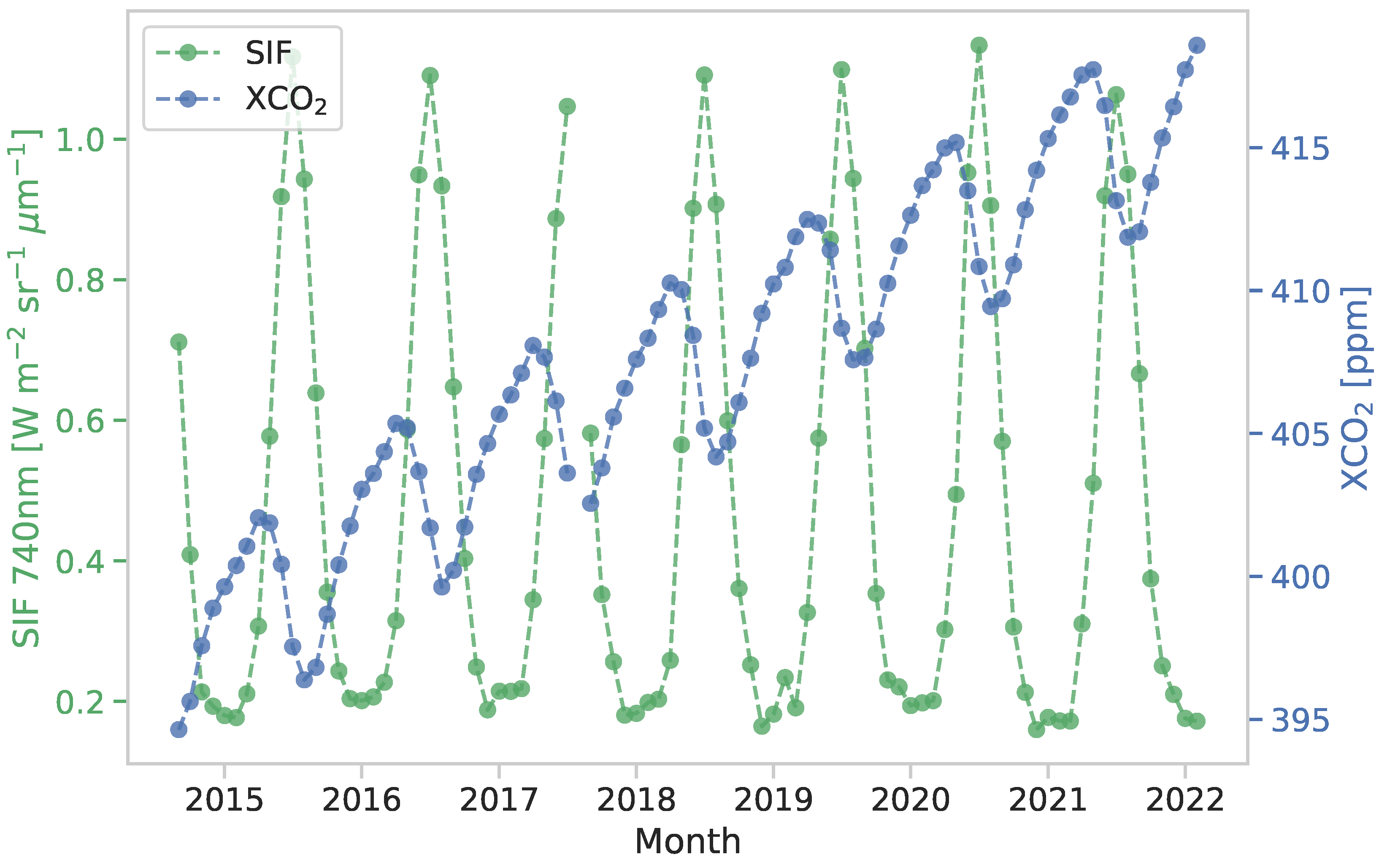
:1. Introduction
2. Materials and Methods
2.1. Datasets Used
- Observational Datasets: OCO-2 SIF and XCO
- Auxiliary Dataset: MODIS LCC
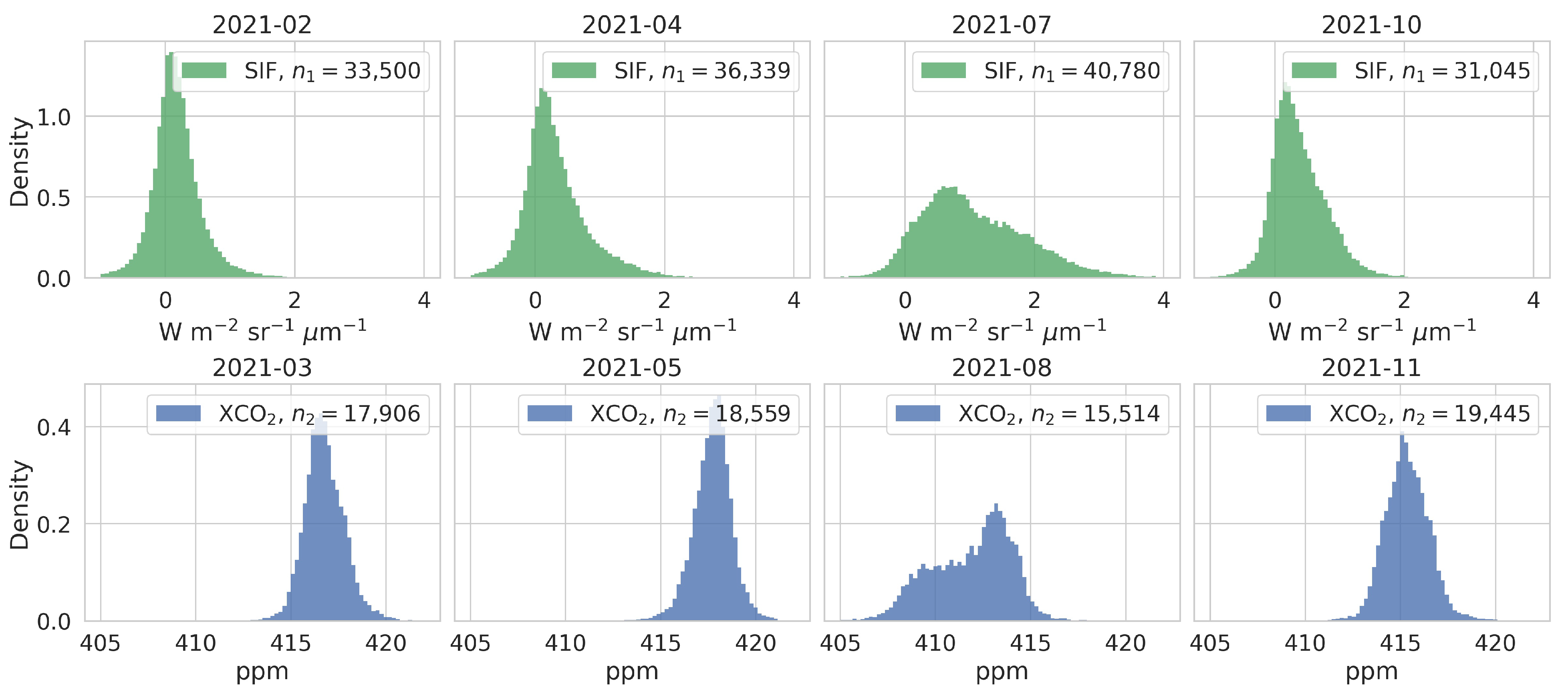
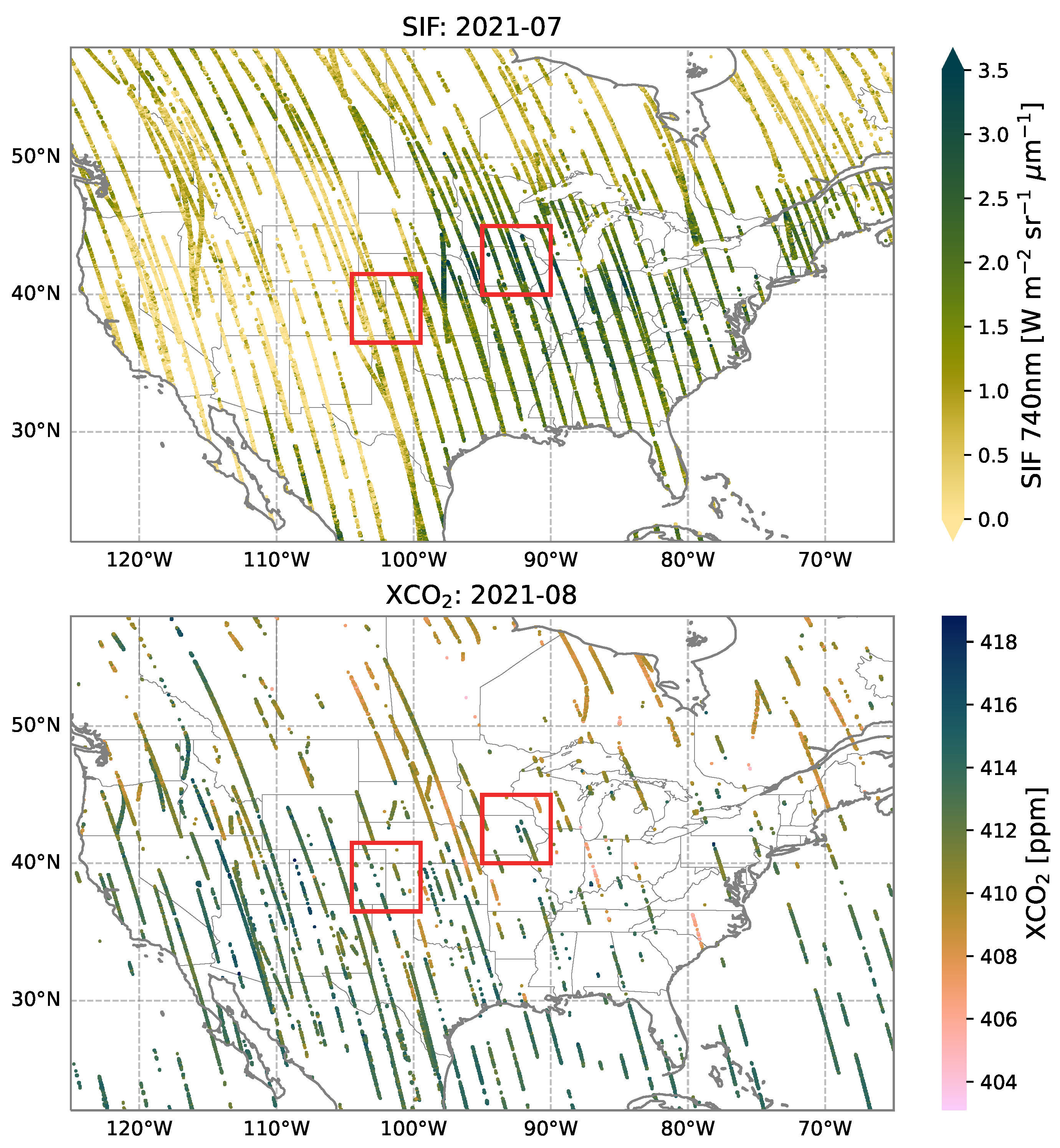
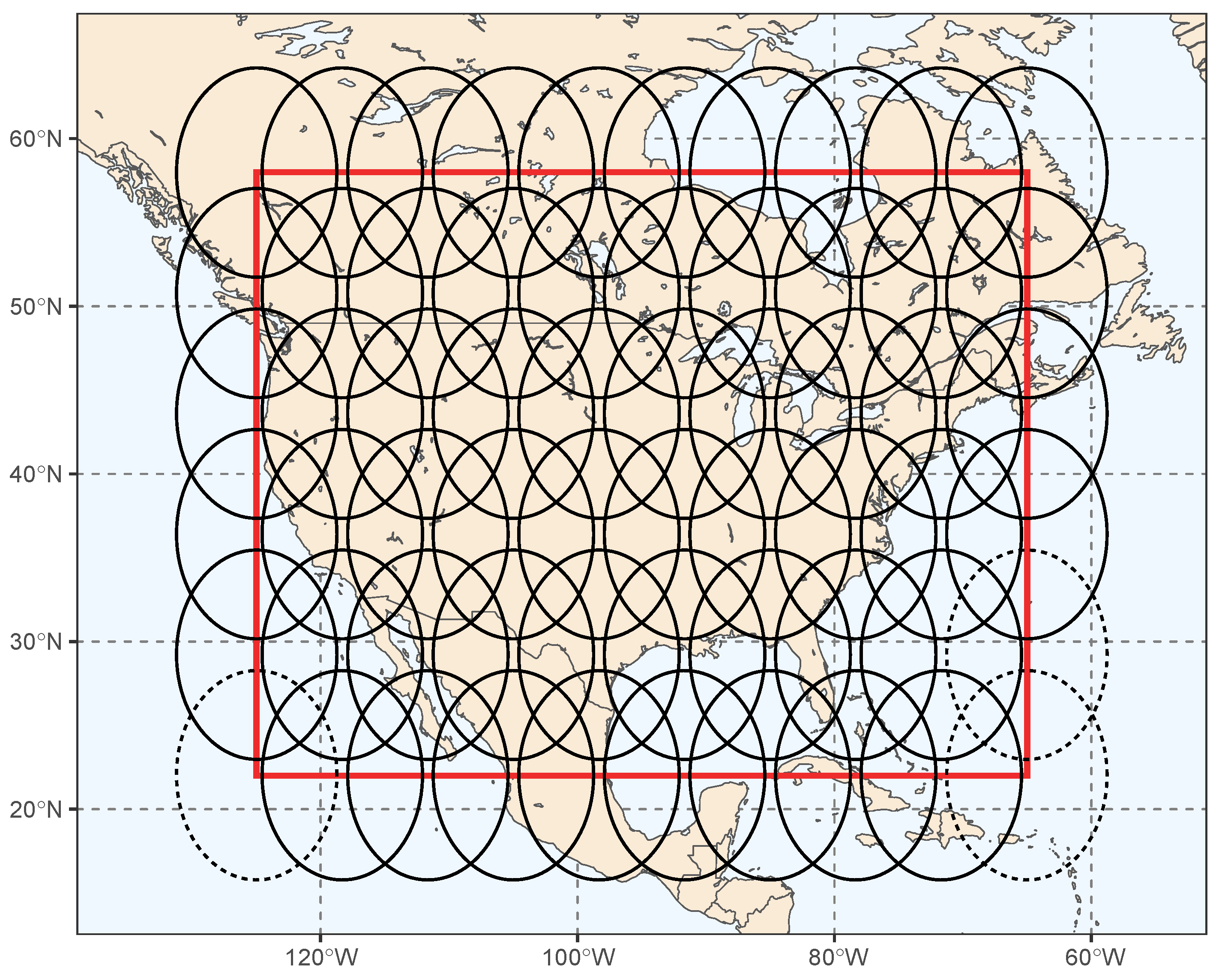
2.2. Data Preparation
2.3. Modeling Multivariate Spatial Dependence between SIF and XCO
2.4. Generating the Spatially Contiguous coSIF Data Product with Quantified Uncertainties Based on Cokriging
2.5. Statistical Validation of the coSIF Data Product
3. Results and Discussion
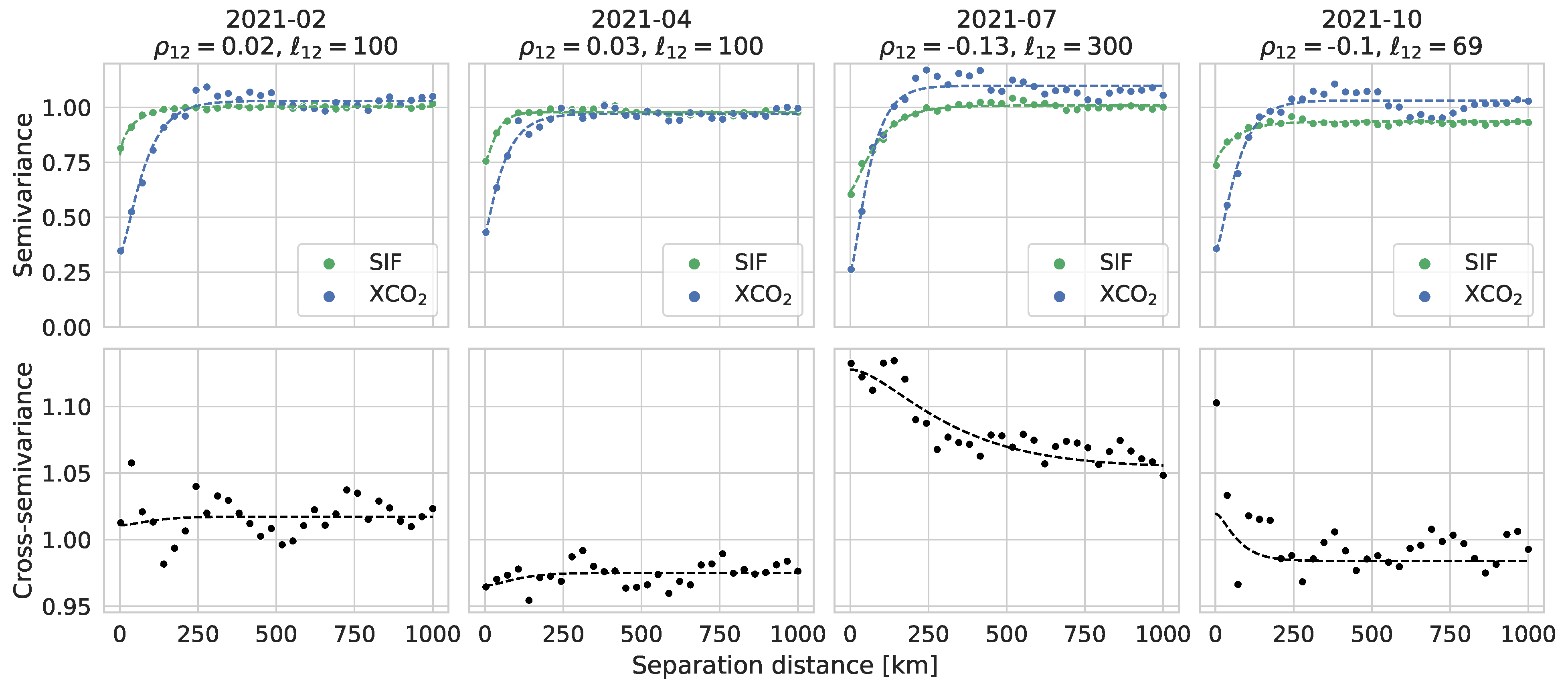
3.1. Evaluation of Fitted Spatial Models
3.2. Level 3 coSIF Predictions and Quantified Uncertainties
3.3. Validation of coSIF and Comparison with Simpler Methods
4. Conclusions, Limitations, and Future Research
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BIAS | Average Prediction Error |
| CMG | Climate Modeling Grid |
| CO | Carbon Dioxide |
| DSS | Dawid-Sebastiani Score |
| GES DISC | Goddard Earth Sciences Data and Information Services Center |
| GPP | Gross Primary Production |
| IGBP | International Geosphere-Biosphere Programme |
| INT | Interval Score |
| LCC | Land-Cover Classification |
| MDSS | Multivariate Dawid-Sebastiani Score |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| MSPE | Mean Squared Prediction Error |
| NASA | National Aeronautics and Space Administration (United States) |
| OCO-2 | Orbiting Carbon Observatory-2 |
| RASPE | Root-Average-Squared Prediction Error |
| RMSPE | Root-Mean-Squared Prediction Error |
| SIF | Solar-Induced Chlorophyll Fluorescence |
| TROPOMI | Tropospheric Monitoring Instrument |
| XCO | Column-Averaged Atmospheric Carbon Dioxide Concentrations |
Appendix A. Methodological Detail
Appendix A.1. Parameter Estimation: Fitting (Cross-) Semivariograms
Appendix A.2. Kriging and Trend-Surface-Only Prediction for Validation Comparisons
Appendix A.3. Multivariate Predictive Covariance Matrix Approximation
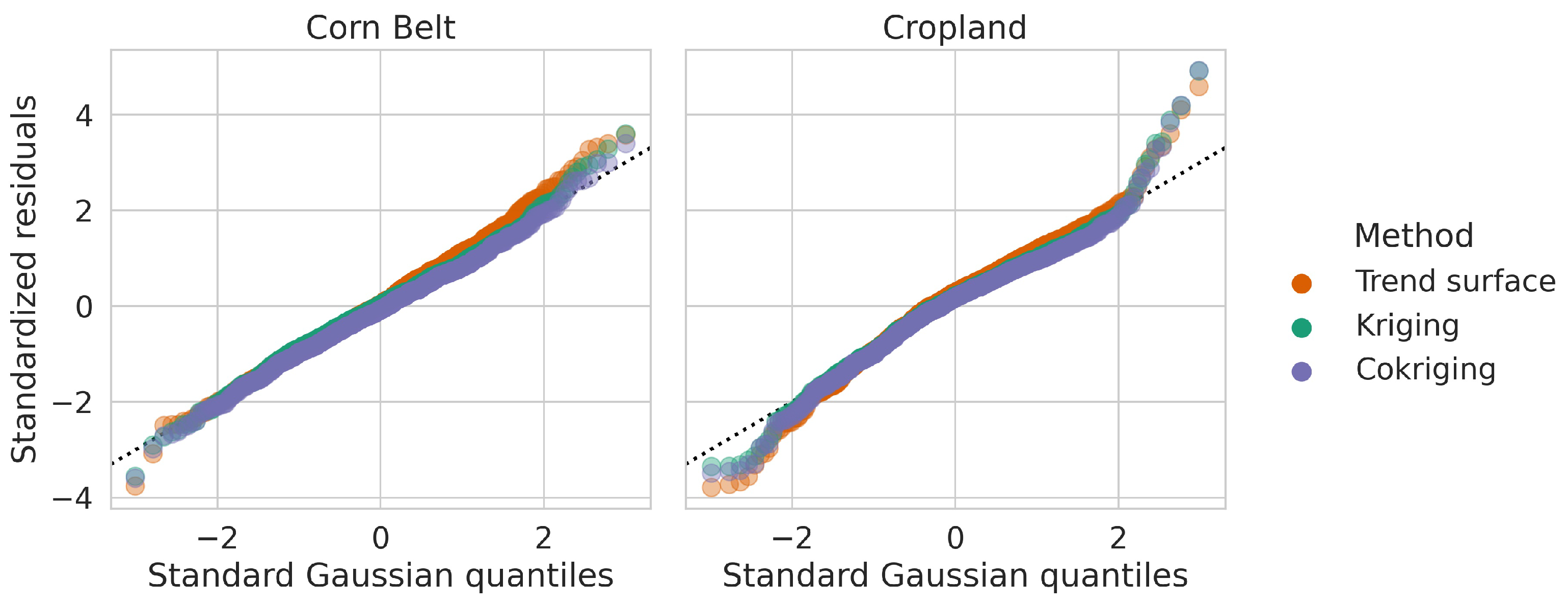
Appendix B. Model Diagnostics

References
- Frankenberg, C.; O’Dell, C.; Berry, J.; Guanter, L.; Joiner, J.; Köhler, P.; Pollock, R.; Taylor, T.E. Prospects for Chlorophyll Fluorescence Remote Sensing from the Orbiting Carbon Observatory-2. Remote Sens. Environ. 2014, 147, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Frankenberg, C.; Wood, J.D.; Schimel, D.S.; Jung, M.; Guanter, L.; Drewry, D.T.; Verma, M.; Porcar-Castell, A.; Griffis, T.J.; et al. OCO-2 Advances Photosynthesis Observation from Space via Solar-Induced Chlorophyll Fluorescence. Science 2017, 358, eaam5747. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Frankenberg, C.; Jung, M.; Joiner, J.; Guanter, L.; Köhler, P.; Magney, T. Overview of Solar-Induced Chlorophyll Fluorescence (SIF) from the Orbiting Carbon Observatory-2: Retrieval, Cross-Mission Comparison, and Global Monitoring for GPP. Remote Sens. Environ. 2018, 209, 808–823. [Google Scholar] [CrossRef]
- Li, X.; Xiao, J.; He, B.; Altaf Arain, M.; Beringer, J.; Desai, A.R.; Emmel, C.; Hollinger, D.Y.; Krasnova, A.; Mammarella, I.; et al. Solar-Induced Chlorophyll Fluorescence Is Strongly Correlated with Terrestrial Photosynthesis for a Wide Variety of Biomes: First Global Analysis Based on OCO-2 and Flux Tower Observations. Glob. Chang. Biol. 2018, 24, 3990–4008. [Google Scholar] [CrossRef] [PubMed]
- Frankenberg, C.; Berry, J. Solar Induced Chlorophyll Fluorescence: Origins, Relation to Photosynthesis and Retrieval. In Comprehensive Remote Sensing; Liang, S., Ed.; Elsevier: Oxford, UK, 2018; pp. 143–162. [Google Scholar] [CrossRef]
- Porcar-Castell, A.; Tyystjärvi, E.; Atherton, J.; van der Tol, C.; Flexas, J.; Pfündel, E.E.; Moreno, J.; Frankenberg, C.; Berry, J.A. Linking Chlorophyll a Fluorescence to Photosynthesis for Remote Sensing Applications: Mechanisms and Challenges. J. Exp. Bot. 2014, 65, 4065–4095. [Google Scholar] [CrossRef]
- Sun, Y.; Wen, J.; Gu, L.; Joiner, J.; Chang, C.Y.; van der Tol, C.; Porcar-Castell, A.; Magney, T.; Wang, L.; Hu, L.; et al. From Remotely-Sensed Solar-Induced Chlorophyll Fluorescence to Ecosystem Structure, Function, and Service: Part II—Harnessing Data. Glob. Chang. Biol. 2023, 29, 2893–2925. [Google Scholar] [CrossRef] [PubMed]
- Baker, N.R. Chlorophyll Fluorescence: A Probe of Photosynthesis in Vivo. Annu. Rev. Plant Biol. 2008, 59, 89–113. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guanter, L.; Alonso, L.; Gómez-Chova, L.; Amorós-López, J.; Vila, J.; Moreno, J. Estimation of Solar-Induced Vegetation Fluorescence from Space Measurements. Geophys. Res. Lett. 2007, 34, L08401. [Google Scholar] [CrossRef]
- Frankenberg, C.; Fisher, J.B.; Worden, J.; Badgley, G.; Saatchi, S.S.; Lee, J.E.; Toon, G.C.; Butz, A.; Jung, M.; Kuze, A.; et al. New Global Observations of the Terrestrial Carbon Cycle from GOSAT: Patterns of Plant Fluorescence with Gross Primary Productivity. Geophys. Res. Lett. 2011, 38, L17706. [Google Scholar] [CrossRef] [Green Version]
- Joiner, J.; Yoshida, Y.; Vasilkov, A.P.; Yoshida, Y.; Corp, L.A.; Middleton, E.M. First Observations of Global and Seasonal Terrestrial Chlorophyll Fluorescence from Space. Biogeosciences 2011, 8, 637–651. [Google Scholar] [CrossRef] [Green Version]
- Mohammed, G.H.; Colombo, R.; Middleton, E.M.; Rascher, U.; van der Tol, C.; Nedbal, L.; Goulas, Y.; Pérez-Priego, O.; Damm, A.; Meroni, M.; et al. Remote Sensing of Solar-Induced Chlorophyll Fluorescence (SIF) in Vegetation: 50 Years of Progress. Remote Sens. Environ. 2019, 231, 111177. [Google Scholar] [CrossRef]
- Doughty, R.; Kurosu, T.P.; Parazoo, N.; Köhler, P.; Wang, Y.; Sun, Y.; Frankenberg, C. Global GOSAT, OCO-2, and OCO-3 Solar-Induced Chlorophyll Fluorescence Datasets. Earth Syst. Sci. Data 2022, 14, 1513–1529. [Google Scholar] [CrossRef]
- Parazoo, N.C.; Frankenberg, C.; Köhler, P.; Joiner, J.; Yoshida, Y.; Magney, T.; Sun, Y.; Yadav, V. Towards a Harmonized Long-Term Spaceborne Record of Far-Red Solar-Induced Fluorescence. J. Geophys. Res. Biogeosci. 2019, 124, 2518–2539. [Google Scholar] [CrossRef] [Green Version]
- Köhler, P.; Frankenberg, C.; Magney, T.S.; Guanter, L.; Joiner, J.; Landgraf, J. Global Retrievals of Solar-Induced Chlorophyll Fluorescence with TROPOMI: First Results and Intersensor Comparison to OCO-2. Geophys. Res. Lett. 2018, 45, 10456–10463. [Google Scholar] [CrossRef] [Green Version]
- Guanter, L.; Bacour, C.; Schneider, A.; Aben, I.; van Kempen, T.A.; Maignan, F.; Retscher, C.; Köhler, P.; Frankenberg, C.; Joiner, J.; et al. The TROPOSIF Global Sun-Induced Fluorescence Dataset from the Sentinel-5P TROPOMI Mission. Earth Syst. Sci. Data 2021, 13, 5423–5440. [Google Scholar] [CrossRef]
- Duveiller, G.; Cescatti, A. Spatially Downscaling Sun-Induced Chlorophyll Fluorescence Leads to an Improved Temporal Correlation with Gross Primary Productivity. Remote Sens. Environ. 2016, 182, 72–89. [Google Scholar] [CrossRef]
- Duveiller, G.; Filipponi, F.; Walther, S.; Köhler, P.; Frankenberg, C.; Guanter, L.; Cescatti, A. A Spatially Downscaled Sun-Induced Fluorescence Global Product for Enhanced Monitoring of Vegetation Productivity. Earth Syst. Sci. Data 2020, 12, 1101–1116. [Google Scholar] [CrossRef]
- Turner, A.J.; Köhler, P.; Magney, T.S.; Frankenberg, C.; Fung, I.; Cohen, R.C. A Double Peak in the Seasonality of California’s Photosynthesis as Observed from Space. Biogeosciences 2020, 17, 405–422. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Huang, Y.; Nie, C.; Zhang, S.; Wang, G.; Chen, S.; Chen, Z. A Long-Term Reconstructed TROPOMI Solar-Induced Fluorescence Dataset Using Machine Learning Algorithms. Sci. Data 2022, 9, 427. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Biederman, J.A.; Knowles, J.F.; Scott, R.L.; Turner, A.J.; Dannenberg, M.P.; Köhler, P.; Frankenberg, C.; Litvak, M.E.; Flerchinger, G.N.; et al. Satellite Solar-Induced Chlorophyll Fluorescence and near-Infrared Reflectance Capture Complementary Aspects of Dryland Vegetation Productivity Dynamics. Remote Sens. Environ. 2022, 270, 112858. [Google Scholar] [CrossRef]
- Gentine, P.; Alemohammad, S.H. Reconstructed Solar-Induced Fluorescence: A Machine Learning Vegetation Product Based on MODIS Surface Reflectance to Reproduce GOME-2 Solar-Induced Fluorescence. Geophys. Res. Lett. 2018, 45, 3136–3146. [Google Scholar] [CrossRef] [PubMed]
- Wen, J.; Köhler, P.; Duveiller, G.; Parazoo, N.; Magney, T.; Hooker, G.; Yu, L.; Chang, C.; Sun, Y. A Framework for Harmonizing Multiple Satellite Instruments to Generate a Long-Term Global High Spatial-Resolution Solar-Induced Chlorophyll Fluorescence (SIF). Remote Sens. Environ. 2020, 239, 111644. [Google Scholar] [CrossRef]
- Gensheimer, J.; Turner, A.J.; Köhler, P.; Frankenberg, C.; Chen, J. A Convolutional Neural Network for Spatial Downscaling of Satellite-Based Solar-Induced Chlorophyll Fluorescence (SIFnet). Biogeosciences 2022, 19, 1777–1793. [Google Scholar] [CrossRef]
- Zhang, Y.; Joiner, J.; Alemohammad, S.H.; Zhou, S.; Gentine, P. A Global Spatially Contiguous Solar-Induced Fluorescence (CSIF) Dataset Using Neural Networks. Biogeosciences 2018, 15, 5779–5800. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Xiao, J. A Global, 0.05-Degree Product of Solar-Induced Chlorophyll Fluorescence Derived from OCO-2, MODIS, and Reanalysis Data. Remote Sens. 2019, 11, 517. [Google Scholar] [CrossRef] [Green Version]
- Yu, L.; Wen, J.; Chang, C.Y.; Frankenberg, C.; Sun, Y. High-Resolution Global Contiguous SIF of OCO-2. Geophys. Res. Lett. 2019, 46, 1449–1458. [Google Scholar] [CrossRef]
- Zammit-Mangion, A.; Cressie, N.; Shumack, C. On Statistical Approaches to Generate Level 3 Products from Satellite Remote Sensing Retrievals. Remote Sens. 2018, 10, 155. [Google Scholar] [CrossRef] [Green Version]
- Tadić, J.M.; Qiu, X.; Yadav, V.; Michalak, A.M. Mapping of Satellite Earth Observations Using Moving Window Block Kriging. Geosci. Model Dev. 2015, 8, 3311–3319. [Google Scholar] [CrossRef] [Green Version]
- Tadić, J.M.; Qiu, X.; Miller, S.; Michalak, A.M. Spatio-Temporal Approach to Moving Window Block Kriging of Satellite Data v1.0. Geosci. Model Dev. 2017, 10, 709–720. [Google Scholar] [CrossRef] [Green Version]
- Myers, D.E. Pseudo-Cross Variograms, Positive-Definiteness, and Cokriging. Math. Geol. 1991, 23, 805–816. [Google Scholar] [CrossRef]
- Ver Hoef, J.M.; Cressie, N. Multivariable Spatial Prediction. Math. Geol. 1993, 25, 219–240, Errata in Math. Geol. 1994, 26, 273–275. [Google Scholar] [CrossRef]
- Eldering, A.; Wennberg, P.O.; Crisp, D.; Schimel, D.S.; Gunson, M.R.; Chatterjee, A.; Liu, J.; Schwandner, F.M.; Sun, Y.; O’Dell, C.W.; et al. The Orbiting Carbon Observatory-2 Early Science Investigations of Regional Carbon Dioxide Fluxes. Science 2017, 358, eaam5745. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Crisp, D.; Pollock, H.R.; Rosenberg, R.; Chapsky, L.; Lee, R.A.M.; Oyafuso, F.A.; Frankenberg, C.; O’Dell, C.W.; Bruegge, C.J.; Doran, G.B.; et al. The On-Orbit Performance of the Orbiting Carbon Observatory-2 (OCO-2) Instrument and Its Radiometrically Calibrated Products. Atmos. Meas. Tech. 2017, 10, 59–81. [Google Scholar] [CrossRef] [Green Version]
- OCO-2 Science Team; Gunson, M.; Eldering, A. OCO-2 Level 2 Bias-Corrected Solar-Induced Fluorescence and Other Select Fields from the IMAP-DOAS Algorithm Aggregated as Daily Files, Retrospective Processing V10r. 2020. Available online: https://disc.gsfc.nasa.gov/datasets/OCO2_L2_Lite_SIF_10r/summary (accessed on 1 March 2022). [CrossRef]
- OCO-2 Science Team; Gunson, M.; Eldering, A. OCO-2 Level 2 Bias-Corrected XCO2 and Other Select Fields from the Full-Physics Retrieval Aggregated as Daily Files, Retrospective Processing V10r. 2020. Available online: https://disc.gsfc.nasa.gov/datasets/OCO2_L2_Lite_FP_10r/summary (accessed on 1 March 2022). [CrossRef]
- Friedl, M.; Sulla-Menashe, D. MODIS/Terra+Aqua Land Cover Type Yearly L3 Global 0.05Deg CMG V061. 2022. Available online: https://lpdaac.usgs.gov/products/mcd12c1v061/ (accessed on 1 March 2022). [CrossRef]
- Cressie, N.; Johannesson, G. Fixed Rank Kriging for Very Large Spatial Data Sets. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2008, 70, 209–226. [Google Scholar] [CrossRef]
- Zammit-Mangion, A.; Cressie, N. FRK: An R Package for Spatial and Spatio-Temporal Prediction with Large Datasets. J. Stat. Softw. 2021, 98, 1–42. [Google Scholar] [CrossRef]
- Cressie, N. Statistics for Spatial Data, revised ed.; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar] [CrossRef]
- Gneiting, T.; Kleiber, W.; Schlather, M. Matérn Cross-Covariance Functions for Multivariate Random Fields. J. Am. Stat. Assoc. 2010, 105, 1167–1177. [Google Scholar] [CrossRef]
- Apanasovich, T.V.; Genton, M.G.; Sun, Y. A Valid Matérn Class of Cross-Covariance Functions for Multivariate Random Fields with Any Number of Components. J. Am. Stat. Assoc. 2012, 107, 180–193. [Google Scholar] [CrossRef]
- Matérn, B. Spatial Variation—Stochastic Models and Their Application to Some Problems in Forest Surveys and Other Sampling Investigations; Meddelanden från Statens Skogsforskningsinstitut: Stockholm, Sweden, 1960; Volume 49. [Google Scholar]
- Stein, M.L. Interpolation of Spatial Data: Some Theory for Kriging; Springer Series in Statistics; Springer: New York, NY, USA, 1999. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables, 9th ed.; Dover Books on Mathematics; Dover Publications: New York, NY, USA, 1965. [Google Scholar]
- Jeong, J.; Jun, M.; Genton, M.G. Spherical Process Models for Global Spatial Statistics. Stat. Sci. 2017, 32, 501–513. [Google Scholar] [CrossRef]
- Cressie, N. Fitting Variogram Models by Weighted Least Squares. J. Int. Assoc. Math. Geol. 1985, 17, 563–586. [Google Scholar] [CrossRef]
- Cressie, N. Change of Support and the Modifiable Areal Unit Problem. Geogr. Syst. 1996, 3, 159–180. [Google Scholar]
- Arlot, S.; Celisse, A. A Survey of Cross-Validation Procedures for Model Selection. Stat. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]
- Roberts, D.R.; Bahn, V.; Ciuti, S.; Boyce, M.S.; Elith, J.; Guillera-Arroita, G.; Hauenstein, S.; Lahoz-Monfort, J.J.; Schröder, B.; Thuiller, W.; et al. Cross-Validation Strategies for Data with Temporal, Spatial, Hierarchical, or Phylogenetic Structure. Ecography 2017, 40, 913–929. [Google Scholar] [CrossRef] [Green Version]
- Gneiting, T.; Raftery, A.E. Strictly Proper Scoring Rules, Prediction, and Estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- Dawid, A.P.; Sebastiani, P. Coherent Dispersion Criteria for Optimal Experimental Design. Ann. Stat. 1999, 27, 65–81. [Google Scholar] [CrossRef]
- Gneiting, T.; Katzfuss, M. Probabilistic Forecasting. Annu. Rev. Stat. Its Appl. 2014, 1, 125–151. [Google Scholar] [CrossRef]
- Crameri, F. Scientific Colour Maps. Zenodo. 2023. Available online: https://zenodo.org/record/8035877 (accessed on 14 June 2023). [CrossRef]
- Johnson, R.A.; Wichern, D.W. Applied Multivariate Statistical Analysis, 6th ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]

| Block | Method | BIAS | RASPE | INT | DSS | MDSS |
|---|---|---|---|---|---|---|
| Corn Belt | Cokriging | −0.06 | 0.58 | 2.85 | −0.13 | −311.94 |
| Kriging | −0.01 | 0.59 | 2.93 | −0.12 | −308.63 | |
| Trend surface | 0.03 | 0.62 | 3.03 | 0.03 | 21.32 | |
| Cropland | Cokriging | 0.01 | 0.56 | 2.95 | −0.22 | −356.18 |
| Kriging | 0.03 | 0.56 | 2.93 | −0.20 | −355.44 | |
| Trend surface | 0.07 | 0.60 | 3.05 | −0.08 | −57.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jacobson, J.; Cressie, N.; Zammit-Mangion, A. Spatial Statistical Prediction of Solar-Induced Chlorophyll Fluorescence (SIF) from Multivariate OCO-2 Data. Remote Sens. 2023, 15, 4038. https://doi.org/10.3390/rs15164038
Jacobson J, Cressie N, Zammit-Mangion A. Spatial Statistical Prediction of Solar-Induced Chlorophyll Fluorescence (SIF) from Multivariate OCO-2 Data. Remote Sensing. 2023; 15(16):4038. https://doi.org/10.3390/rs15164038
Chicago/Turabian StyleJacobson, Josh, Noel Cressie, and Andrew Zammit-Mangion. 2023. "Spatial Statistical Prediction of Solar-Induced Chlorophyll Fluorescence (SIF) from Multivariate OCO-2 Data" Remote Sensing 15, no. 16: 4038. https://doi.org/10.3390/rs15164038
APA StyleJacobson, J., Cressie, N., & Zammit-Mangion, A. (2023). Spatial Statistical Prediction of Solar-Induced Chlorophyll Fluorescence (SIF) from Multivariate OCO-2 Data. Remote Sensing, 15(16), 4038. https://doi.org/10.3390/rs15164038






