Radar Anti-Jamming Decision-Making Method Based on DDPG-MADDPG Algorithm
Abstract
:1. Introduction
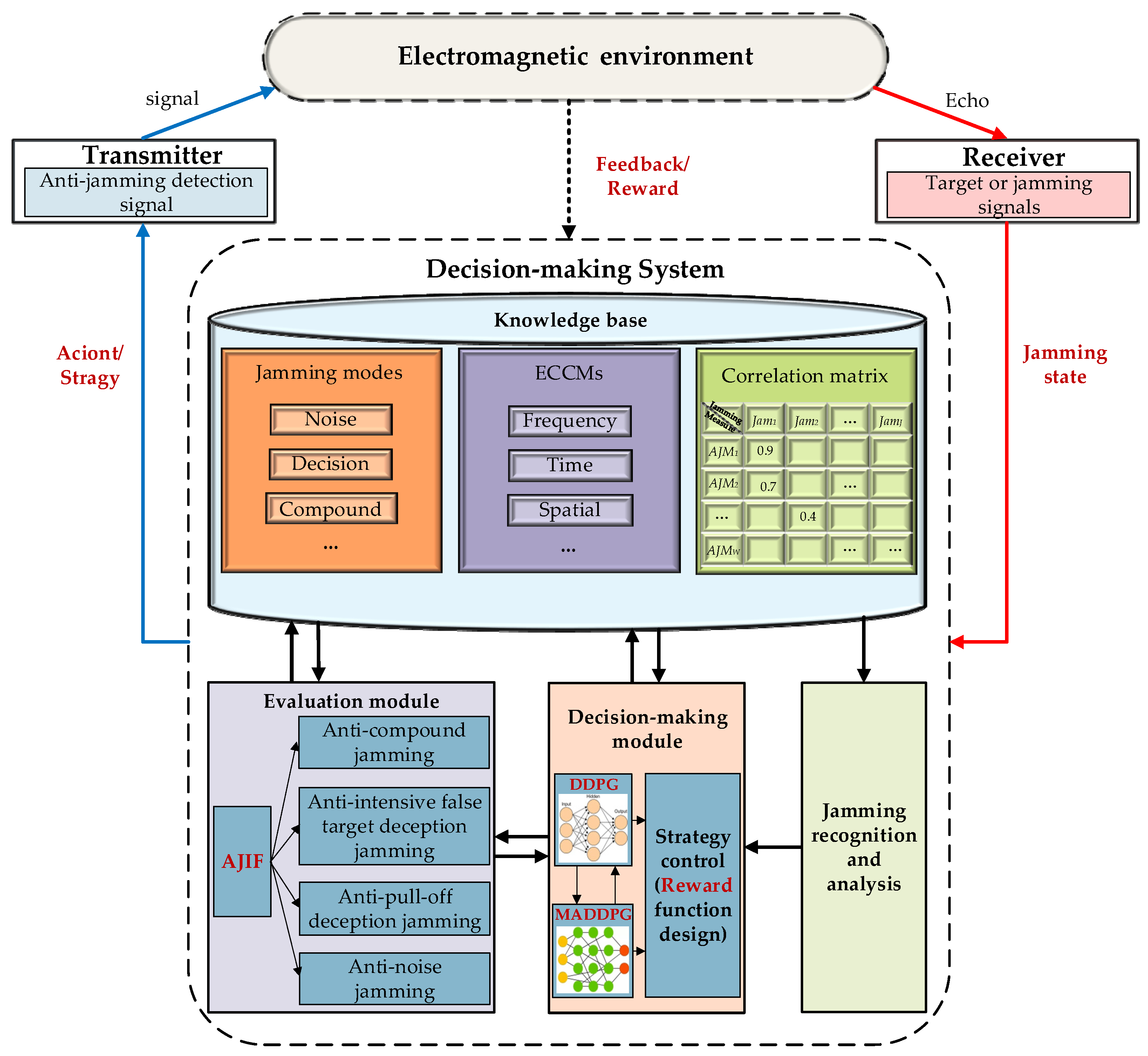
- We established a typical electronic radar and jamming countermeasure scenario and divided various jamming modes and ECCMs according to different categories. Therefore, the dimension of the radar anti-jamming knowledge base was reduced by layering. According to the dynamic interaction process between radar and jamming, we proposed an intelligent radar anti-jamming decision-making model. By defining the anti-jamming decision-making elements of the radar, the radar anti-jamming decision-making process was formulated. This is the basis for the design of the anti-jamming decision-making algorithm.
- An anti-jamming improvement factor was designed to evaluate the performance of ECCMs, which can provide feedback to the decision-making algorithm. Based on the anti-jamming improvement factor, we established the correlation matrix of jamming and ECCM, which provides prior knowledge for the decision-making algorithm. Then, according to the limitation of radar anti-jamming resources, we designed four decisioned objectives and constraints to verify the performance of the anti-jamming decision-making algorithm.
- We designed the DDPG-MADDPG algorithm to generate anti-jamming strategies, which includes the outer DDPG algorithm and the inner MADDPG algorithm. Through the hierarchical selection and joint optimization of two layers, this not only reduces the dimensionality of the action space, but also finds the global optimal solution in a shorter convergence time. Simulation results proved that this method has better robustness, a shorter convergence time, higher decision making accuracy, and better generalization performance.
2. Materials
2.1. Working Scenario of Radar and Jamming
2.2. Intelligent Radar Anti-Jamming Decision-Making Model
3. Methods
3.1. Anti-Jamming Improvement Factor and Decision-Making Objectives
3.1.1. Anti-Jamming Improvement Factor
3.1.2. Decision-Making Objectives and Constraints
3.2. Anti-Jamming Decision-Making Algorithm Based on DDPG-MADDPG
3.2.1. Preliminaries
3.2.2. DDPG-MADDPG Algorithm
| Algorithm 1: DDPG-MADDPG algorithm. |
| Initialize parameters. Initialize replay buffer and . For to sample length do: Initialize a random process and with Gumbel Softmax distribution. Receive initial state , . For (DDPG) to the decision-making cycle do: Sample action from Gumbel Softmax distribution according to the current policy and exploration noise . Determine whether is in ; if so, set , and return to the previous step. Otherwise, go to the next step. Execute actions and observe reward and observe new state . Store transition in replay buffer . Sample a random minibatch of transitions from . Set . Update critic by minimizing the loss: . Update the actor policy using the sampled policy gradient: . Update target network parameters: , . End for for (MADDPG) to sample length do: for each sub-agent , sample action from Gumbel Softmax distribution according to the current policy and exploration noise . Execute actions and observe reward and new state . Store transition in replay buffer . for sub-agent to do Sample a minibatch of samples from . Set . Update critic by minimizing the loss: . Update actor using the sampled policy gradient: . End for Update target network parameters for each sub-agent : . end for end for |
4. Results
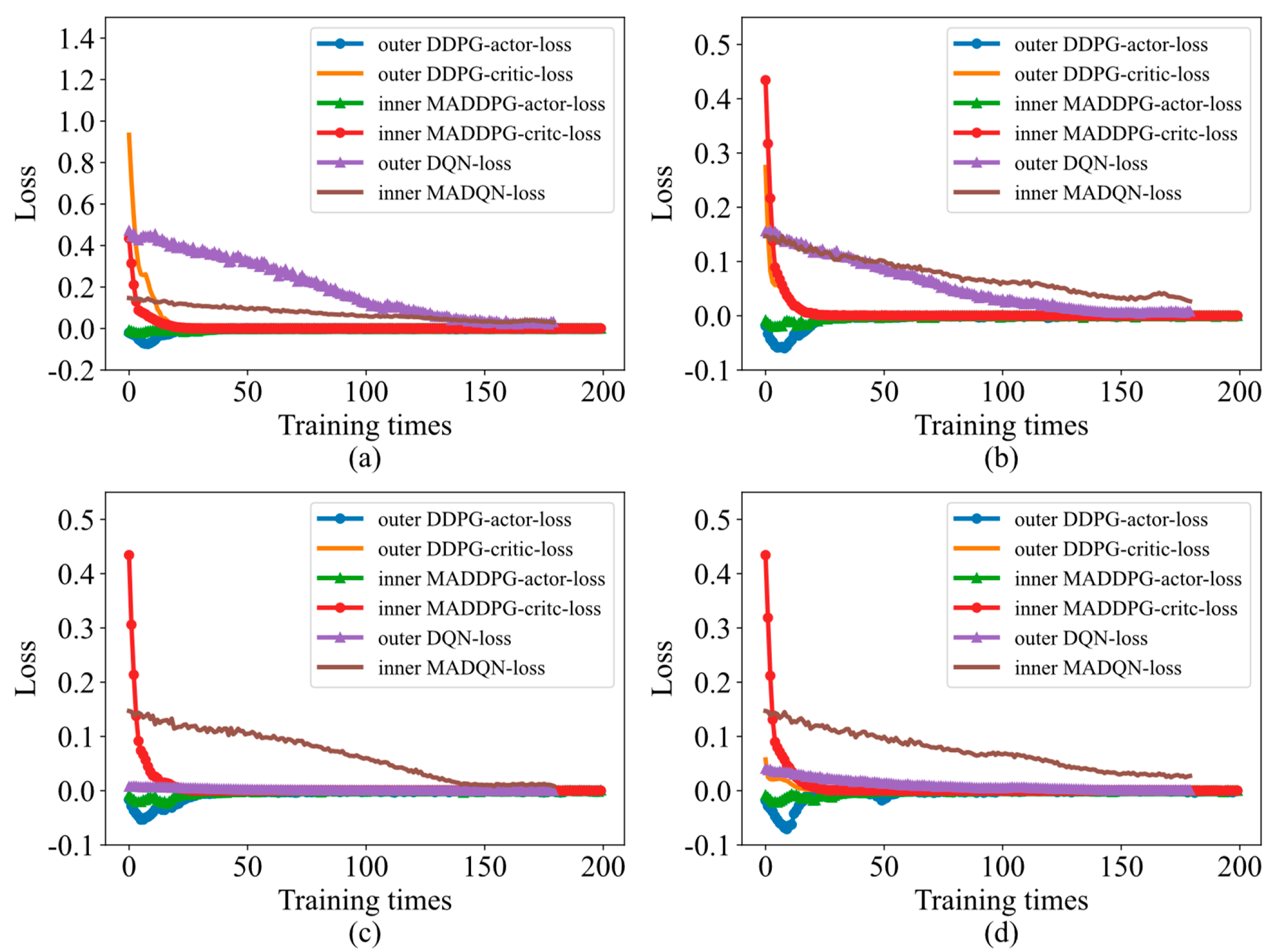
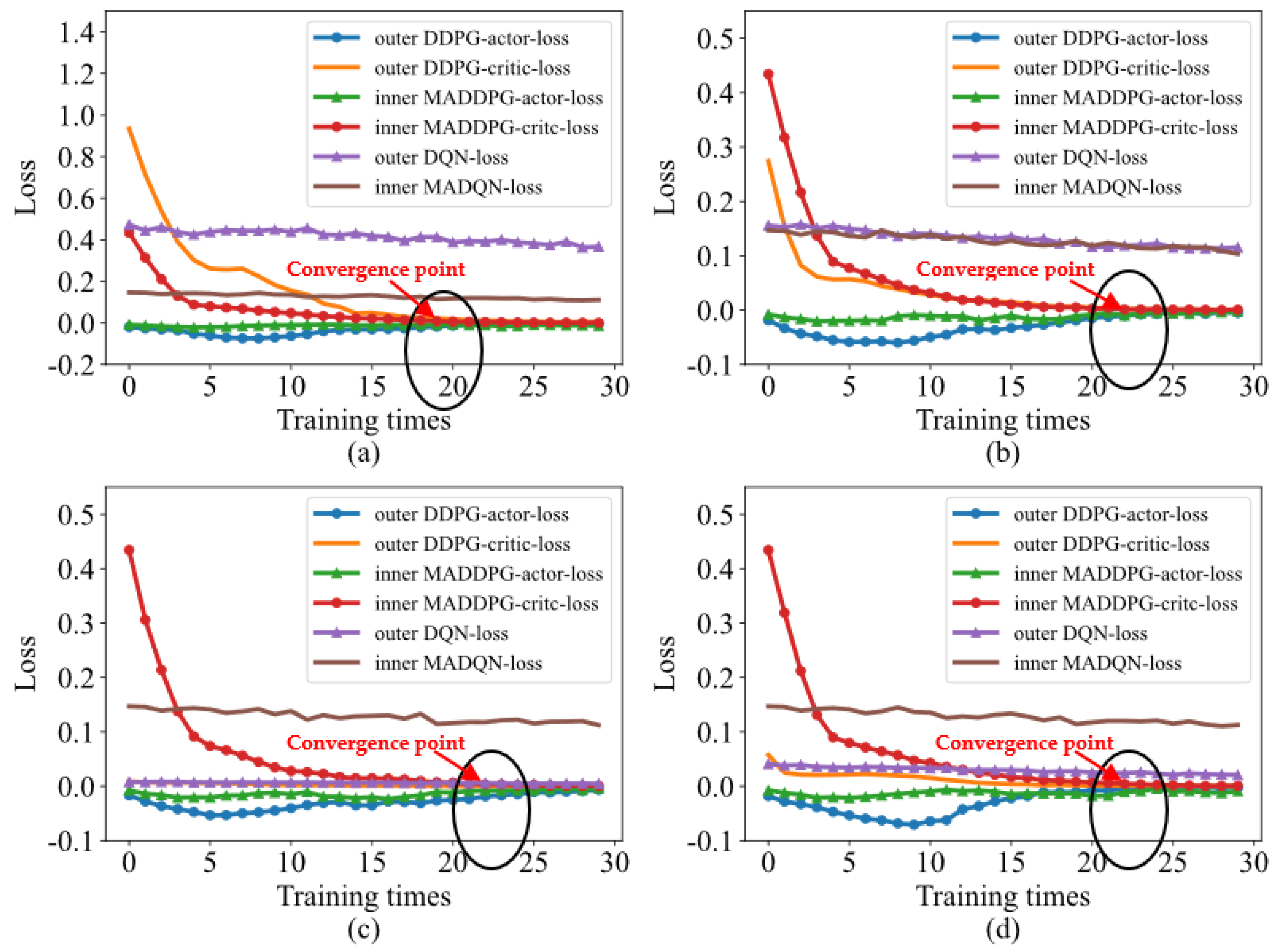
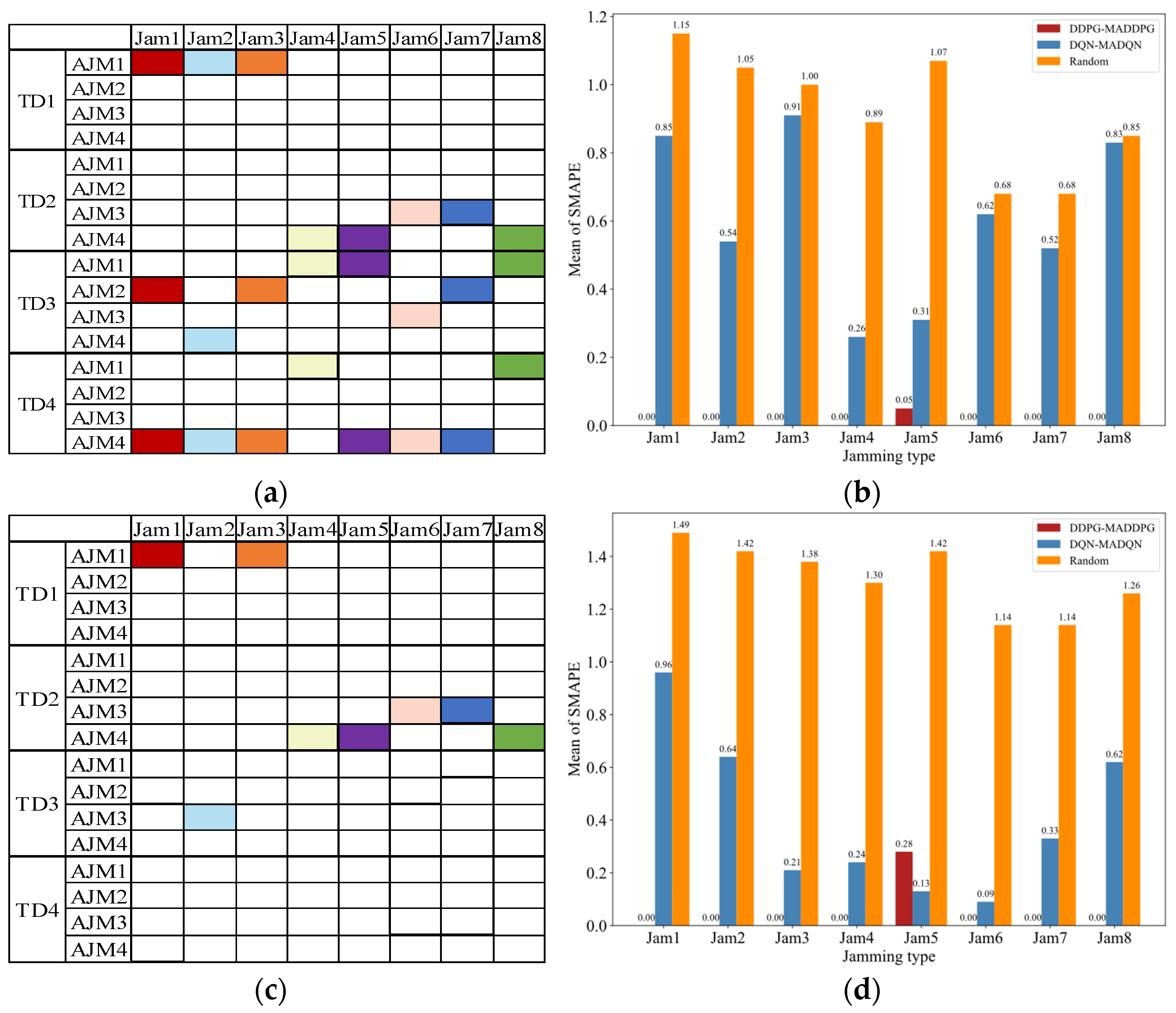
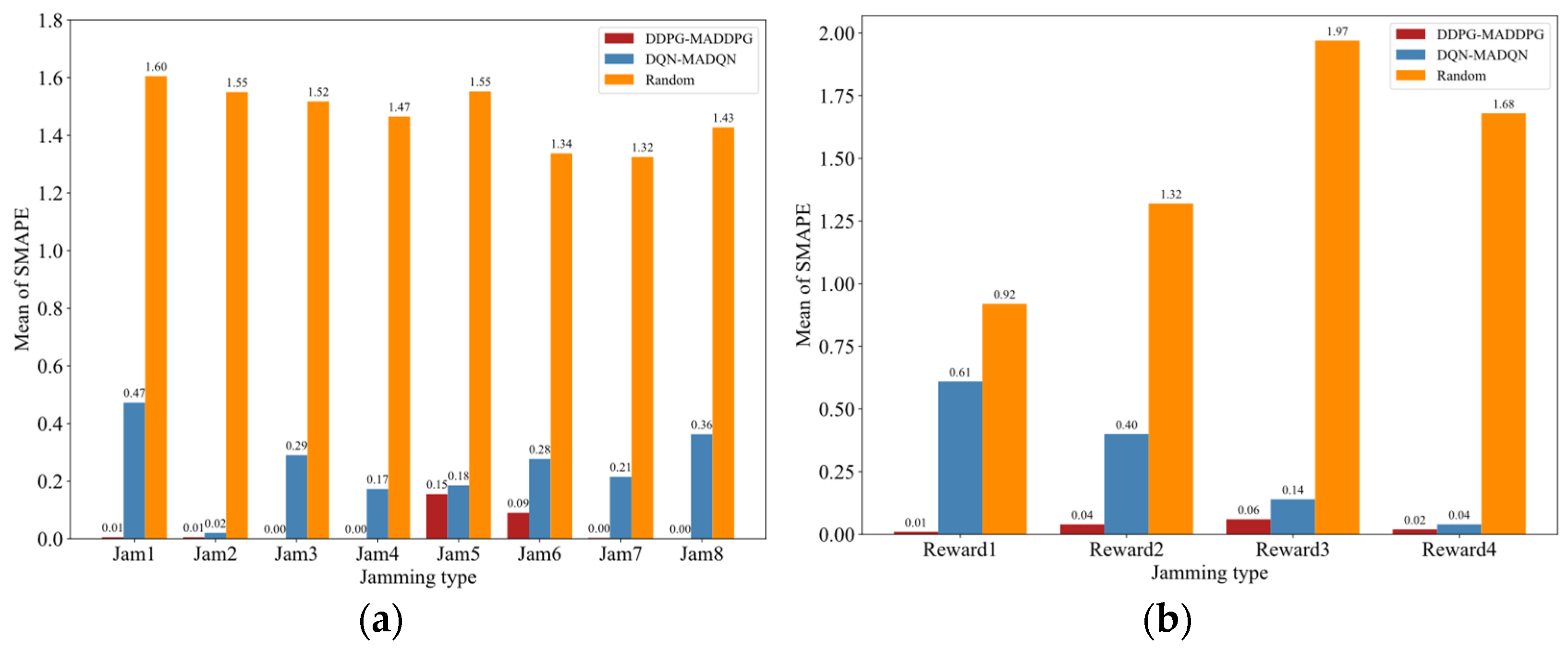
4.1. Robust Performance Based on the Loss Function
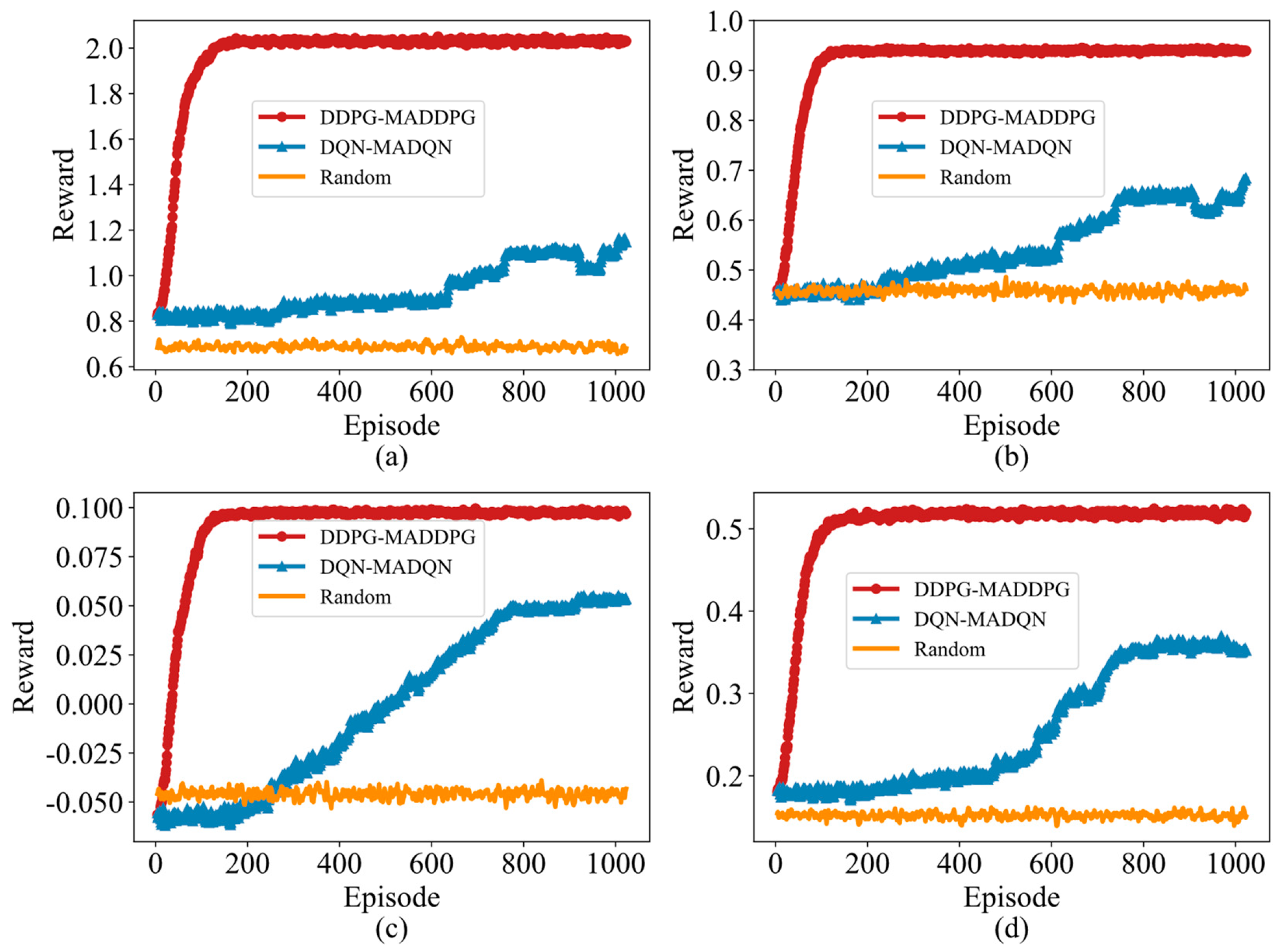
4.2. Convergence Performance Based on Reward Function
4.3. Decision Accuracy Performance Based on SMAPE
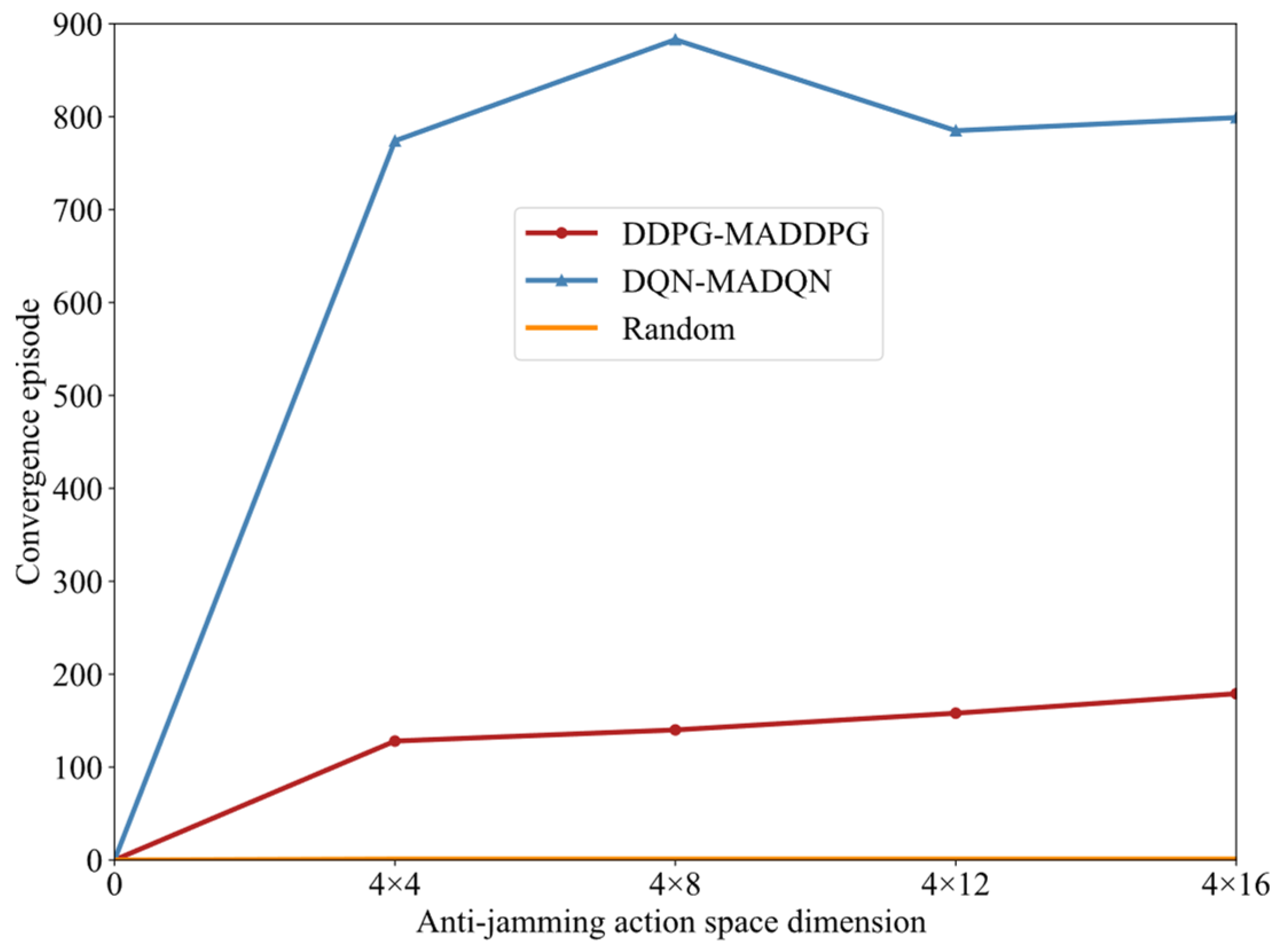
4.4. Generalization Performance Based on Large Action Space
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Geng, J.; Jiu, B.; Li, K.; Zhao, Y.; Liu, H.; Li, H. Radar and Jammer Intelligent Game under Jamming Power Dynamic Allocation. Remote Sens. 2023, 15, 581. [Google Scholar] [CrossRef]
- Li, K.; Jiu, B.; Pu, W.; Liu, H.; Peng, X. Neural Fictitious Self-Play for Radar Antijamming Dynamic Game with Imperfect Information. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 5533–5547. [Google Scholar] [CrossRef]
- Li, K.; Jiu, B.; Liu, H. Game Theoretic Strategies Design for Monostatic Radar and Jammer Based on Mutual Information. IEEE Access 2019, 7, 72257–72266. [Google Scholar] [CrossRef]
- Feng, X.; Zhao, Z.; Li, F.; Cui, W.; Zhao, Y. Radar Phase-Coded Waveform Design with Local Low Range Sidelobes Based on Particle Swarm-Assisted Projection Optimization. Remote Sens. 2022, 14, 4186. [Google Scholar] [CrossRef]
- Jin, M.H.; Yeo, S.-R.; Choi, H.H.; Park, C.; Lee, S.J. Jammer Identification Technique based on a Template Matching Method. J. Position. Navig. Timing 2014, 3, 45–51. [Google Scholar] [CrossRef]
- Yu, W.; Sun, Y.; Wang, X.; Li, K.; Luo, J. Modeling and Analyzing of Fire-Control Radar Anti-Jamming Performance in the Complex Electromagnetic Circumstances. In Proceedings of the International Conference on Man-Machine-Environment System Engineering, Jinggangshan, China, 21–23 October 2017; Springer: Singapore, 2017. [Google Scholar] [CrossRef]
- Guo, W.; Zhang, S.; Wang, Z. A method to evaluate radar effectiveness based on fuzzy analytic hierarchy process. In Proceedings of the 2008 Chinese Control and Decision Conference, Yantai, China, 2–4 July 2008. [Google Scholar] [CrossRef]
- Xia, X.; Hao, D.; Wu, X. Optimal Waveform Design for Smart Noise Jamming. In Proceedings of the 7th International Conference on Education, Management, Information and Mechanical Engineering, Shenyang, China, 28–30 April 2017. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Q.; Li, K. A Smart Noise Jamming Suppression Method Based on Atomic Dictionary Parameter Optimization Decomposition. Remote Sens. 2022, 14, 1921. [Google Scholar] [CrossRef]
- Liu, Y.-X.; Zhang, Q.; Xiong, S.-C.; Ni, J.-C.; Wang, D.; Wang, H.-B. An ISAR Shape Deception Jamming Method Based on Template Multiplication and Time Delay. Remote Sens. 2023, 15, 2762. [Google Scholar] [CrossRef]
- Dai, H.; Zhao, Y.; Su, H.; Wang, Z.; Bao, Q.; Pan, J. Research on an Intra-Pulse Orthogonal Waveform and Methods Resisting Interrupted-Sampling Repeater Jamming within the Same Frequency Band. Remote Sens. 2023, 15, 3673. [Google Scholar] [CrossRef]
- Zhan, H.; Wang, T.; Guo, T.; Su, X. An Anti-Intermittent Sampling Jamming Technique Utilizing the OTSU Algorithm of Random Orthogonal Sub-Pulses. Remote Sens. 2023, 15, 3080. [Google Scholar] [CrossRef]
- Han, B.; Qu, X.; Yang, X.; Li, W.; Zhang, Z. DRFM-Based Repeater Jamming Reconstruction and Cancellation Method with Accurate Edge Detection. Remote Sens. 2023, 15, 1759. [Google Scholar] [CrossRef]
- Kirk, B.H.; Narayanan, R.M.; Gallagher, K.A.; Martone, A.F.; Sherbondy, K.D. Avoidance of Time-Varying Radio Frequency Interference with Software-Defined Cognitive Radar. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1090–1107. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Liang, X.; Zhao, D.; Huang, J.; Xu, X.; Dai, B.; Miao, Q. Deep Reinforcement Learning: A Survey. IEEE Trans. Neural Networks Learn. Syst. 2022, 1–15. [Google Scholar] [CrossRef]
- Feng, S.; Haykin, S. Cognitive Risk Control for Anti-Jamming V2V Communications in Autonomous Vehicle Networks. IEEE Trans. Veh. Technol. 2019, 68, 9920–9934. [Google Scholar] [CrossRef]
- Lotfi, I.; Niyato, D.; Sun, S.; Dinh, H.T.; Li, Y.; Kim, D.I. Protecting Multi-Function Wireless Systems from Jammers with Backscatter Assistance: An Intelligent Strategy. IEEE Trans. Veh. Technol. 2021, 70, 11812–11826. [Google Scholar] [CrossRef]
- Pourranjbar, A.; Kaddoum, G.; Ferdowsi, A.; Saad, W. Reinforcement Learning for Deceiving Reactive Jammers in Wireless Networks. IEEE Trans. Commun. 2021, 69, 3682–3697. [Google Scholar] [CrossRef]
- Xiao, L.; Jiang, D.; Xu, D.; Zhu, H.; Zhang, Y.; Poor, H.V. Two-dimensional anti-jamming mobile communication based on reinforcement learning. IEEE Trans. Veh. Technol. 2018, 67, 9499–9512. [Google Scholar] [CrossRef]
- Ailiya; Yi, W.; Varshney, P.K. Adaptation of Frequency Hopping Interval for Radar Anti-Jamming Based on Reinforcement Learning. IEEE Trans. Veh. Technol. 2022, 71, 12434–12449. [Google Scholar] [CrossRef]
- Thornton, C.E.; Kozy, M.A.; Buehrer, R.M.; Martone, A.F.; Sherbondy, K.D. Deep Reinforcement Learning Control for Radar Detection and Tracking in Congested Spectral Environments. IEEE Trans. Cogn. Commun. Netw. 2020, 6, 1335–1349. [Google Scholar] [CrossRef]
- Liu, P.; Liu, Y.; Huang, T.; Lu, Y.; Wang, X. Decentralized Automotive Radar Spectrum Allocation to Avoid Mutual Interference Using Reinforcement Learning. IEEE Trans. Aerosp. Electron. Syst. 2020, 57, 190–205. [Google Scholar] [CrossRef]
- Selvi, E.; Buehrer, R.M.; Martone, A.; Sherbondy, K. Reinforcement Learning for Adaptable Bandwidth Tracking Radars. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3904–3921. [Google Scholar] [CrossRef]
- Feng, C.; Fu, X.; Wang, Z.; Dong, J.; Zhao, Z.; Pan, T. An Optimization Method for Collaborative Radar Antijamming Based on Multi-Agent Reinforcement Learning. Remote Sens. 2023, 15, 2893. [Google Scholar] [CrossRef]
- Li, K.; Jiu, B.; Liu, H.; Liang, S. Reinforcement learning based anti-jamming frequency hopping strategies design for cognitive radar. In Proceedings of the 2018 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Qingdao, China, 14–16 September 2018; pp. 1–5. [Google Scholar]
- Li, K.; Jiu, B.; Liu, H. Deep Q-Network based anti-Jamming strategy design for frequency agile radar. In Proceedings of the International Radar Conference (RADAR), Toulon, France, 23–27 September 2019. [Google Scholar] [CrossRef]
- Ak, S.; Brüggenwirth, S. Avoiding Jammers: A Reinforcement Learning Approach. In Proceedings of the 2020 IEEE International Radar Conference (RADAR), Washington, DC, USA, 28–30 April 2020; pp. 321–326. [Google Scholar]
- Li, K.; Jiu, B.; Wang, P.; Liu, H.; Shi, Y. Radar active antagonism through deep reinforcement learning: A Way to address the challenge of mainlobe jamming. Signal Process. 2021, 186, 108130. [Google Scholar] [CrossRef]
- Li, K.; Jiu, B.; Liu, H.; Pu, W. Robust Antijamming Strategy Design for Frequency-Agile Radar against Main Lobe Jamming. Remote Sens. 2021, 13, 3043. [Google Scholar] [CrossRef]
- Geng, J.; Jiu, B.; Li, K.; Zhao, Y.; Liu, H. Reinforcement Learning Based Radar Anti-Jamming Strategy Design against a Non-Stationary Jammer. In Proceedings of the 2022 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xi’an, China, 25–27 October 2022. [Google Scholar] [CrossRef]
- He, X.; Liao, K.; Peng, S.; Tian, Z.; Huang, J. Interrupted-Sampling Repeater Jamming-Suppression Method Based on a Multi-Stages Multi-Domains Joint Anti-Jamming Depth Network. Remote Sens. 2022, 14, 3445. [Google Scholar] [CrossRef]
- Sharma, H.; Kumar, N.; Tekchandani, R. Mitigating Jamming Attack in 5G Heterogeneous Networks: A Federated Deep Reinforcement Learning Approach. IEEE Trans. Veh. Technol. 2023, 72, 2439–2452. [Google Scholar] [CrossRef]
- Du, Y.; Zandi, H.; Kotevska, O.; Kurte, K.; Munk, J.; Amasyali, K.; Mckee, E.; Li, F. Intelligent multi-zone residential HVAC control strategy based on deep reinforcement learning. Appl. Energy 2021, 281, 116117. [Google Scholar] [CrossRef]
- Zehni, M.; Zhao, Z. An Adversarial Learning Based Approach for 2D Unknown View Tomography. IEEE Trans. Comput. Imaging 2022, 8, 705–720. [Google Scholar] [CrossRef]
- Peng, H.; Shen, X. Multi-Agent Reinforcement Learning Based Resource Management in MEC- and UAV-Assisted Vehicular Networks. IEEE J. Sel. Areas Commun. 2021, 39, 131–141. [Google Scholar] [CrossRef]
- Johnston, S.L. The ECCM improvement factor (EIF)–Illustrative examples, applications, and considerations in its utilization in radar ECCM performance assessment. In Proceedings of the International Conference on Radar, Nanjing, China, 4–7 November 1986. [Google Scholar]
- Liu, X.; Yang, J.; Hou, B.; Lu, J.; Yao, Z. Radar seeker performance evaluation based on information fusion method. SN Appl. Sci. 2020, 2, 674. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, S.; Zhu, L.; Chen, S.; Zhao, H. Research on anti-Narrowband AM jamming of Ultra-wideband impulse radio detection radar based on improved singular spectrum analysis. Measurement 2022, 188, 110386. [Google Scholar] [CrossRef]
- Li, T.; Wang, Z.; Liu, J. Evaluating Effect of Blanket Jamming on Radar Via Robust Time-Frequency Analysis and Peak to Average Power Ratio. IEEE Access 2020, 8, 214504–214519. [Google Scholar] [CrossRef]
- Xing, H.; Xing, Q.; Wang, K. Radar Anti-Jamming Countermeasures Intelligent Decision-Making: A Partially Observable Markov Decision Process Approach. Aerospace 2023, 10, 236. [Google Scholar] [CrossRef]
- Wang, F.; Liu, D.; Liu, P.; Li, B. A Research on the Radar Anti-jamming Evaluation Index System. In Proceedings of the 2015 International Conference on Applied Science and Engineering Innovation, Jinan, China, 30–31 August 2015. [Google Scholar]
- Lillicrap, T.; Hunt, J.; Pritzel, A. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Watkins, C.J.C.H.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Lowe, R.; Wu, Y.; Tamar, A.; Harb, J.; Abbeel, P.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Jang, E.; Gu, S.; Poole, B. Categorical reparameterization with gumbel-softmax. arXiv 2016, arXiv:1611.01144. [Google Scholar]
- Rasheed, F.; Yau, K.-L.A.; Low, Y.-C. Deep reinforcement learning for traffic signal control under disturbances: A case study on Sunway city, Malaysia. Futur. Gener. Comput. Syst. 2020, 109, 431–445. [Google Scholar] [CrossRef]



| Category | Jamming Mode | Number |
|---|---|---|
| Noise jamming | Blocking jamming | |
| Aiming jamming | ||
| Sweep jamming | ||
| False target deception jamming | Range false target deception jamming | |
| Sample-and-modulation deception jamming | ||
| Intensive false target deception jamming | ||
| Pull-off deception jamming | Range pull-off jamming | |
| Velocity pull-off jamming | ||
| Range–velocity simultaneous pull-off jamming | ||
| Compound jamming | Noise jamming + false target deception jamming | |
| Noise jamming + pull-off deception jamming | ||
| False target deception jamming + pull-off deception | ||
| … |
| Transform Domain | ECCM | ||
|---|---|---|---|
| Name | Number | Name | Number |
| Time domain | Linear filter design | ||
| LFM waveform parameter design | |||
| … | … | ||
| Frequency domain | Carrier frequency fixed mode agility | ||
| Carrier frequency random agility | |||
| … | |||
| … | … | ||
| Space domain | Space–time adaptive filtering | ||
| Adaptive beamforming | |||
| Sidelobe cancellation | |||
| … | |||
| … | … | … | |
| Name | Variable |
|---|---|
| Agent | Radar |
| Environment | Electromagnetic jamming environment |
| State | Jamming mode |
| Action | : transform domains, : ECCMs. |
| Reward | Anti-jamming evaluation result |
| The policy | The probability that radar chooses and |
| Decision-making cycle | 200 pulse repetition intervals (PRIs) |
| Jamming Category | Evaluation Indicator |
|---|---|
| Noise jamming | SINR |
| False target deception jamming | The number of real targets found |
| Pull-off deception jamming | Tracking accuracy error |
| Compound jamming | The mathematical accumulation of evaluation indicators of each single jamming |
| Parameter | Value |
|---|---|
| Jamming modes | 8 |
| Transform sub-domains | 4 |
| ECCMs | 4 |
| The number of combinations | 15 |
| The number of in | 4 |
| Decision-making cycle | 200 |
| Discount factor | 0.9 |
| Learning rate of the critic network | 0.002 |
| Learning rate of the actor network | 0.001 |
| Replay buffer and | 2048 |
| samples in one minibatch | 64 |
| Sample length | 1024 |
| Training time (the number of minibatches) | 200 |
| Transform Domain | ECCM | Jamming Mode | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| … | ||||||||||
| 0.99 | 0.6 | 0.99 | 0.3 | 0.2 | 0.3 | 0.92 | 0.5 | … | ||
| 0.9 | 0.5 | 0.97 | 0.2 | 0.1 | 0.2 | 0.9 | 0.4 | … | ||
| 0.1 | 0.11 | 0.1 | 0.65 | 0.85 | 0.9 | 0.3 | 0.6 | … | ||
| 0.1 | 0.07 | 0.12 | 0.6 | 0.75 | 0.8 | 0.2 | 0.55 | … | ||
| … | … | … | … | … | … | … | … | … | … | |
| 0 | 0.01 | 0.1 | 0.7 | 0.6 | 0.88 | 0.89 | 0.7 | … | ||
| 0 | 0 | 0.05 | 0.73 | 0.65 | 0.8 | 0.81 | 0.73 | … | ||
| 0.1 | 0.03 | 0.15 | 0.9 | 0.7 | 0.95 | 0.96 | 0.91 | … | ||
| 0 | 0.01 | 0.17 | 0.95 | 0.73 | 0.87 | 0.88 | 0.96 | … | ||
| … | … | … | … | … | … | … | … | … | … | |
| 0.5 | 0.6 | 0.8 | 0.6 | 0.97 | 0 | 0.5 | 0.65 | … | ||
| 0.6 | 0.7 | 0.95 | 0.55 | 0.1 | 0 | 0.6 | 0.6 | … | ||
| 0.6 | 0.99 | 0.8 | 0 | 0 | 0 | 0.3 | 0.1 | … | ||
| 0.55 | 0.99 | 0.77 | 0 | 0 | 0 | 0.32 | 0.05 | … | ||
| … | … | … | … | … | … | … | … | … | … | |
| 0 | 0.1 | 0.1 | 0.4 | 0.2 | 0.5 | 0.75 | 0.82 | … | ||
| 0 | 0.05 | 0.2 | 0.15 | 0.2 | 0.6 | 0.8 | 0.8 | … | ||
| 0.1 | 0.13 | 0.2 | 0.3 | 0.45 | 0.6 | 0.7 | 0.4 | … | ||
| 0.15 | 0.18 | 0.2 | 0.35 | 0.5 | 0.7 | 0.8 | 0.35 | … | ||
| … | … | … | … | … | … | … | … | … | … | |
| … | … | … | … | … | … | … | … | … | … | … |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, J.; Wei, Y.; Yu, L.; Xu, R. Radar Anti-Jamming Decision-Making Method Based on DDPG-MADDPG Algorithm. Remote Sens. 2023, 15, 4046. https://doi.org/10.3390/rs15164046
Wei J, Wei Y, Yu L, Xu R. Radar Anti-Jamming Decision-Making Method Based on DDPG-MADDPG Algorithm. Remote Sensing. 2023; 15(16):4046. https://doi.org/10.3390/rs15164046
Chicago/Turabian StyleWei, Jingjing, Yinsheng Wei, Lei Yu, and Rongqing Xu. 2023. "Radar Anti-Jamming Decision-Making Method Based on DDPG-MADDPG Algorithm" Remote Sensing 15, no. 16: 4046. https://doi.org/10.3390/rs15164046
APA StyleWei, J., Wei, Y., Yu, L., & Xu, R. (2023). Radar Anti-Jamming Decision-Making Method Based on DDPG-MADDPG Algorithm. Remote Sensing, 15(16), 4046. https://doi.org/10.3390/rs15164046







