Solid Precipitation and Visibility Measurements at the Centre for Atmospheric Research Experiments in Southern Ontario and Bratt’s Lake in Southern Saskatchewan
Abstract
:1. Introduction
2. Materials and Methods
2.1. CARE Site
2.2. Bratt’s Lake Site
2.3. The Gauge Data Analysis
2.4. Precipitation Intensity, Type, and Fall Velocity
2.5. Visibility and Solid Precipitation Intensity Data Analysis
3. Results
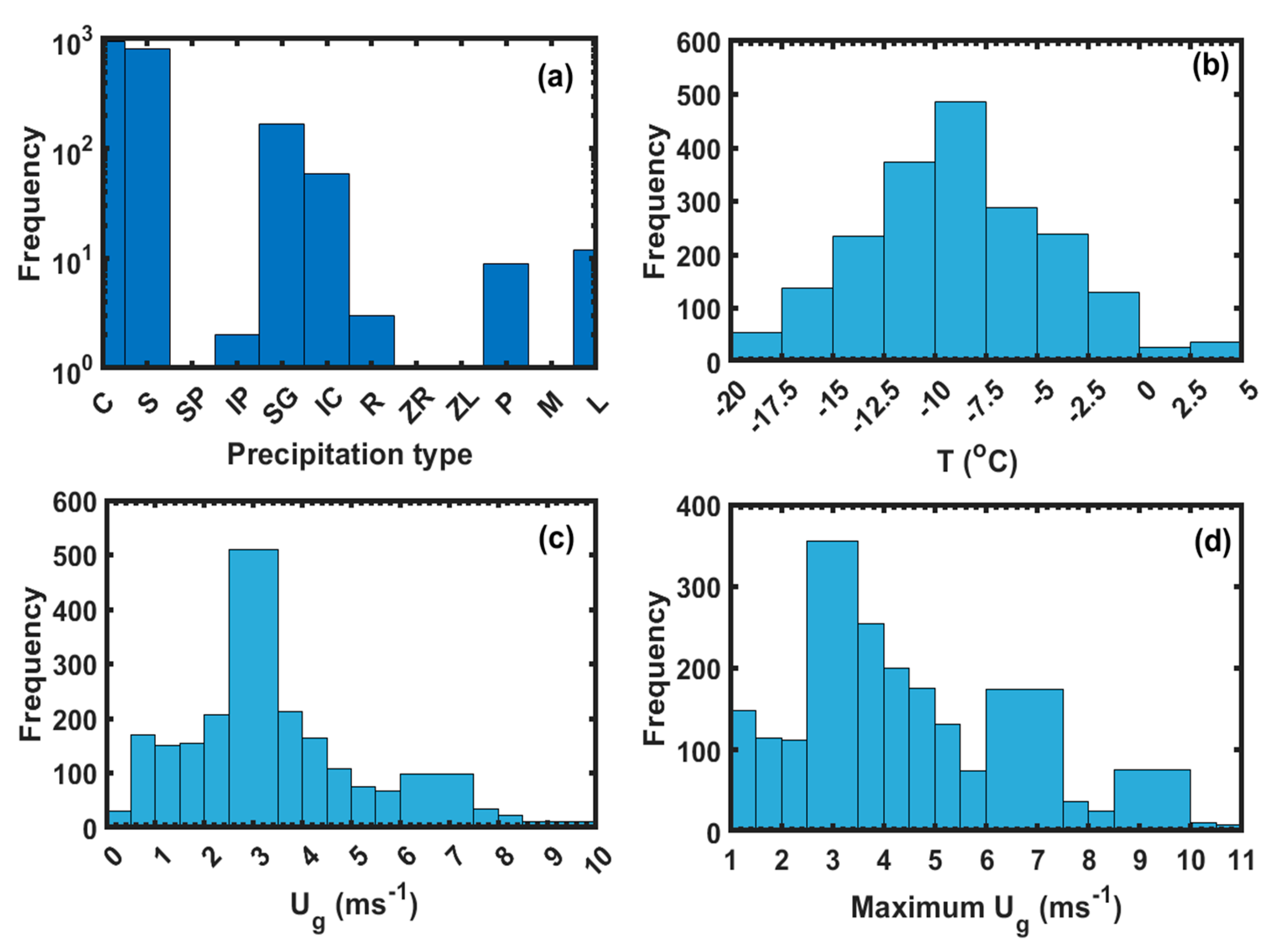
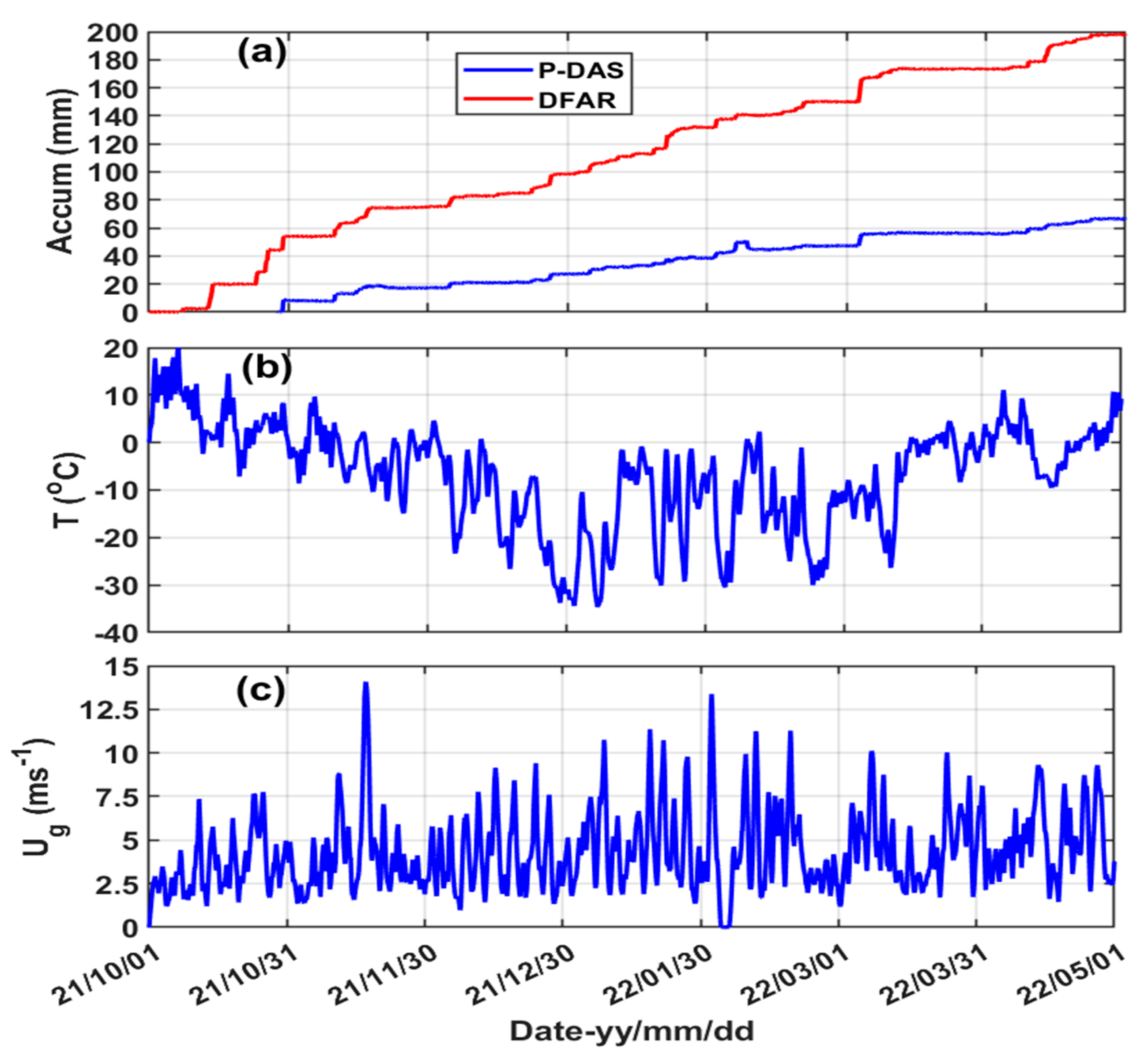
3.1. Precipitation Type and Temeprature at CARE Site
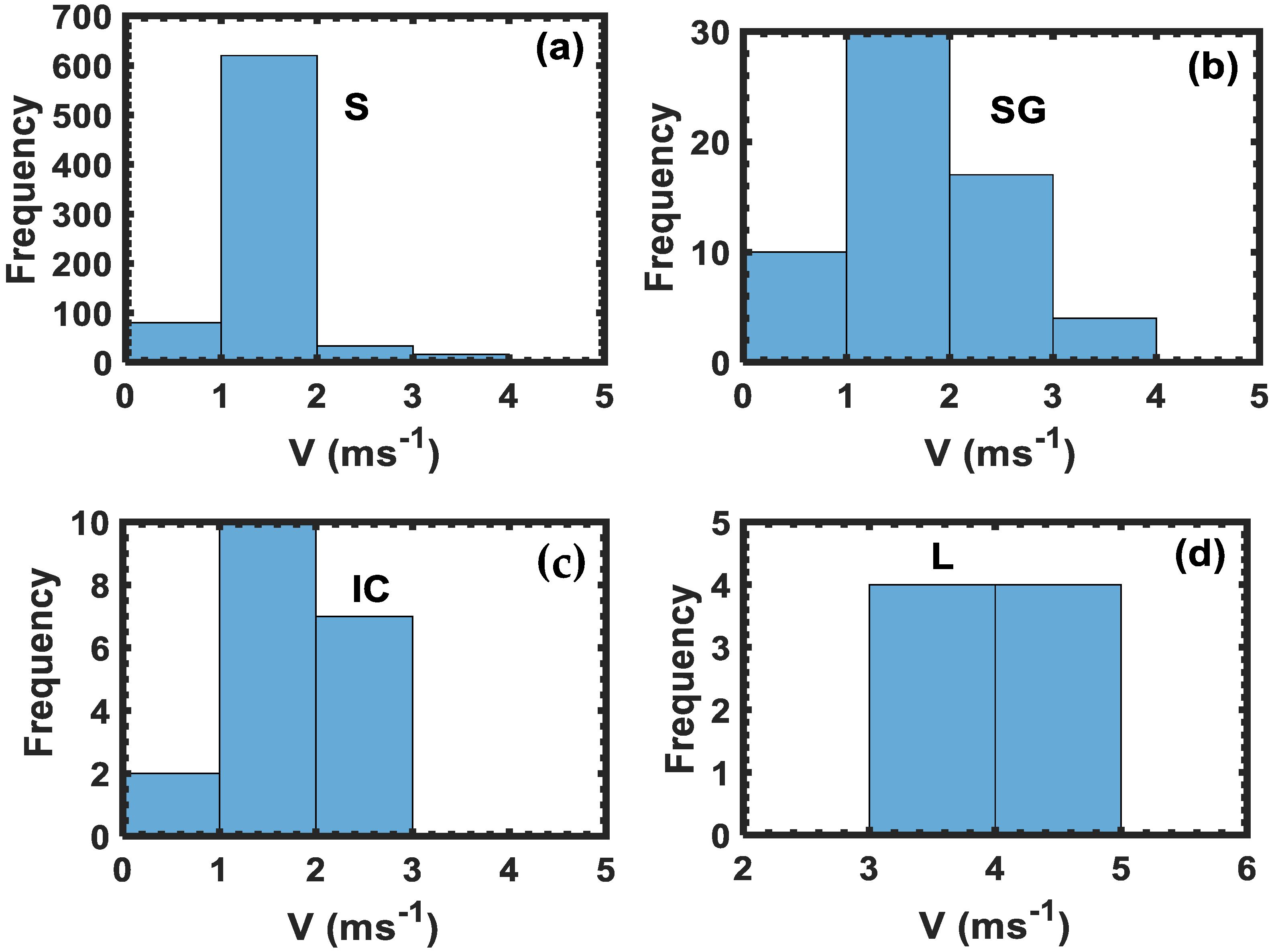
3.2. Fall Velocity
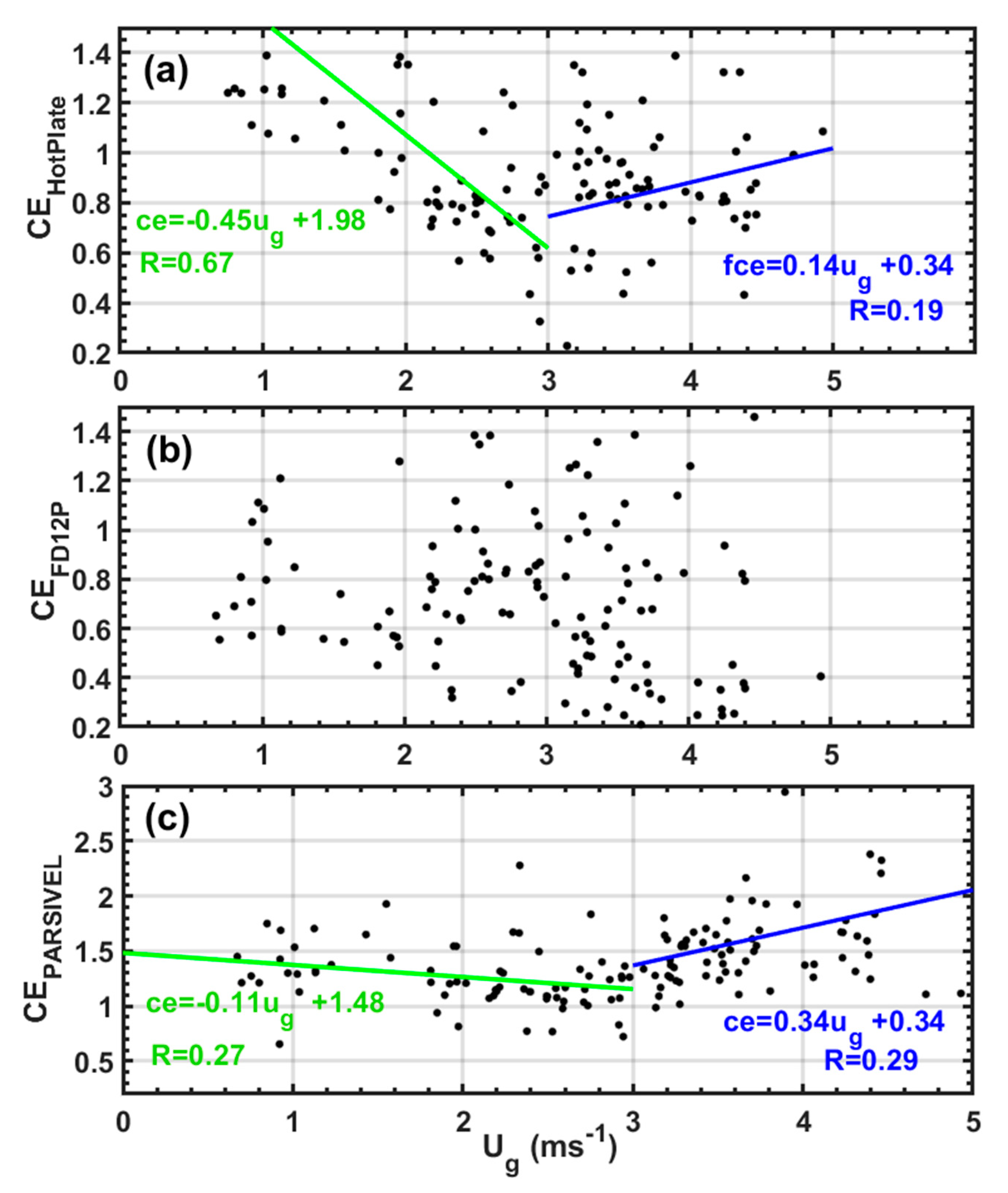
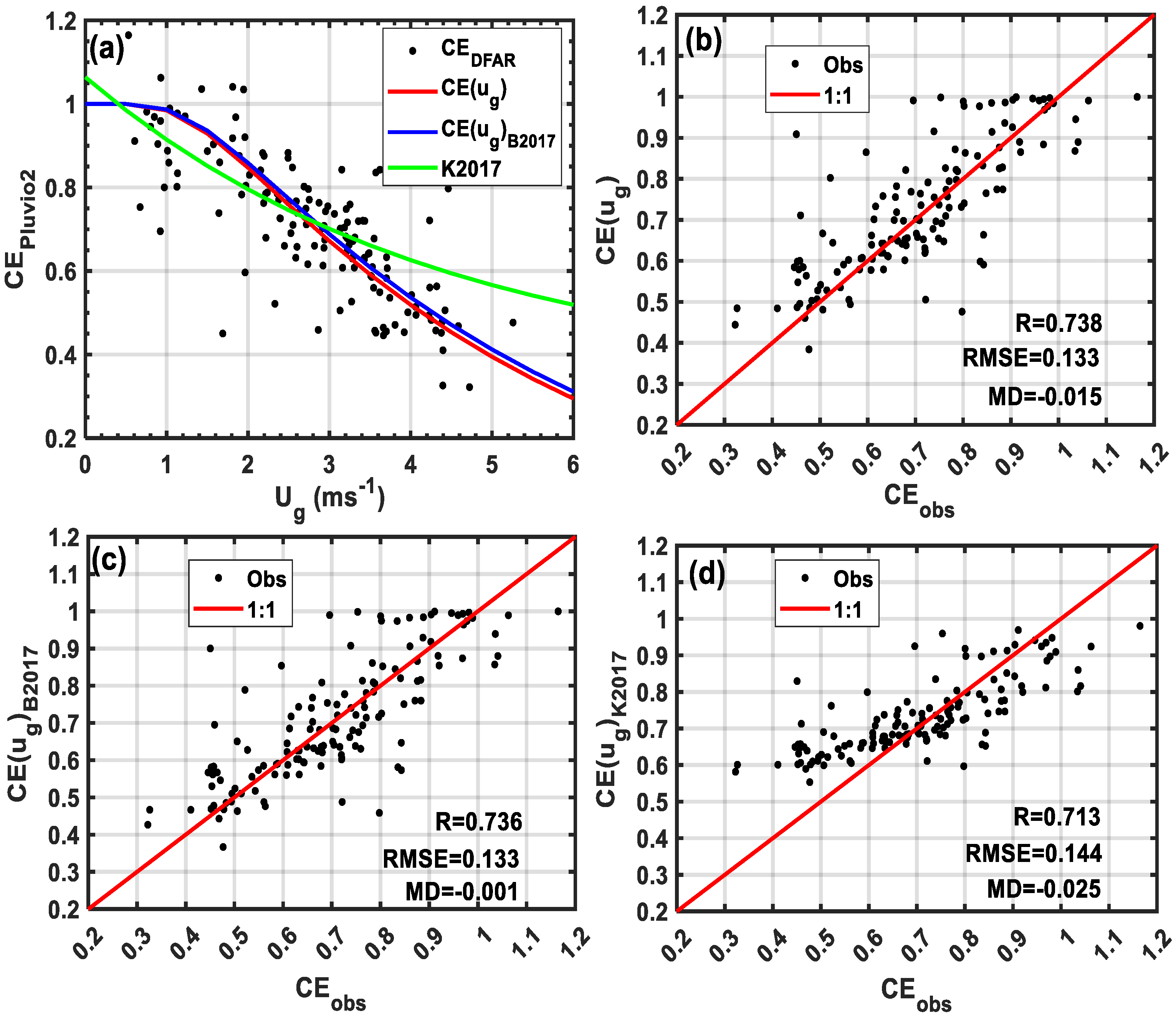
3.3. Solid Precipitation and Collection Efficiency of Geonor Gauge at CARE Site
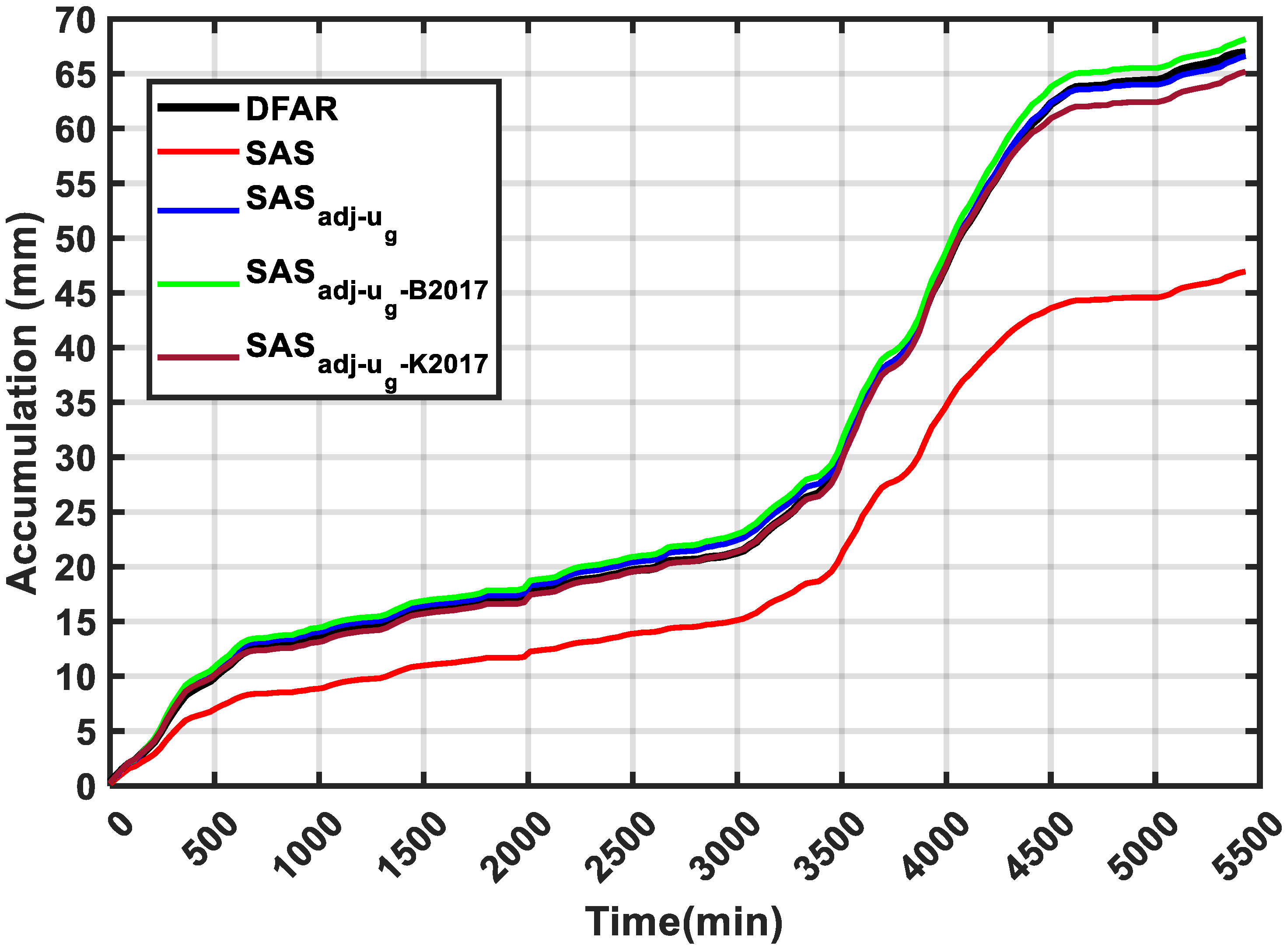
3.4. Solid Precipitation and Collection Efficiency of Pluvio2 Gauge at CARE Site
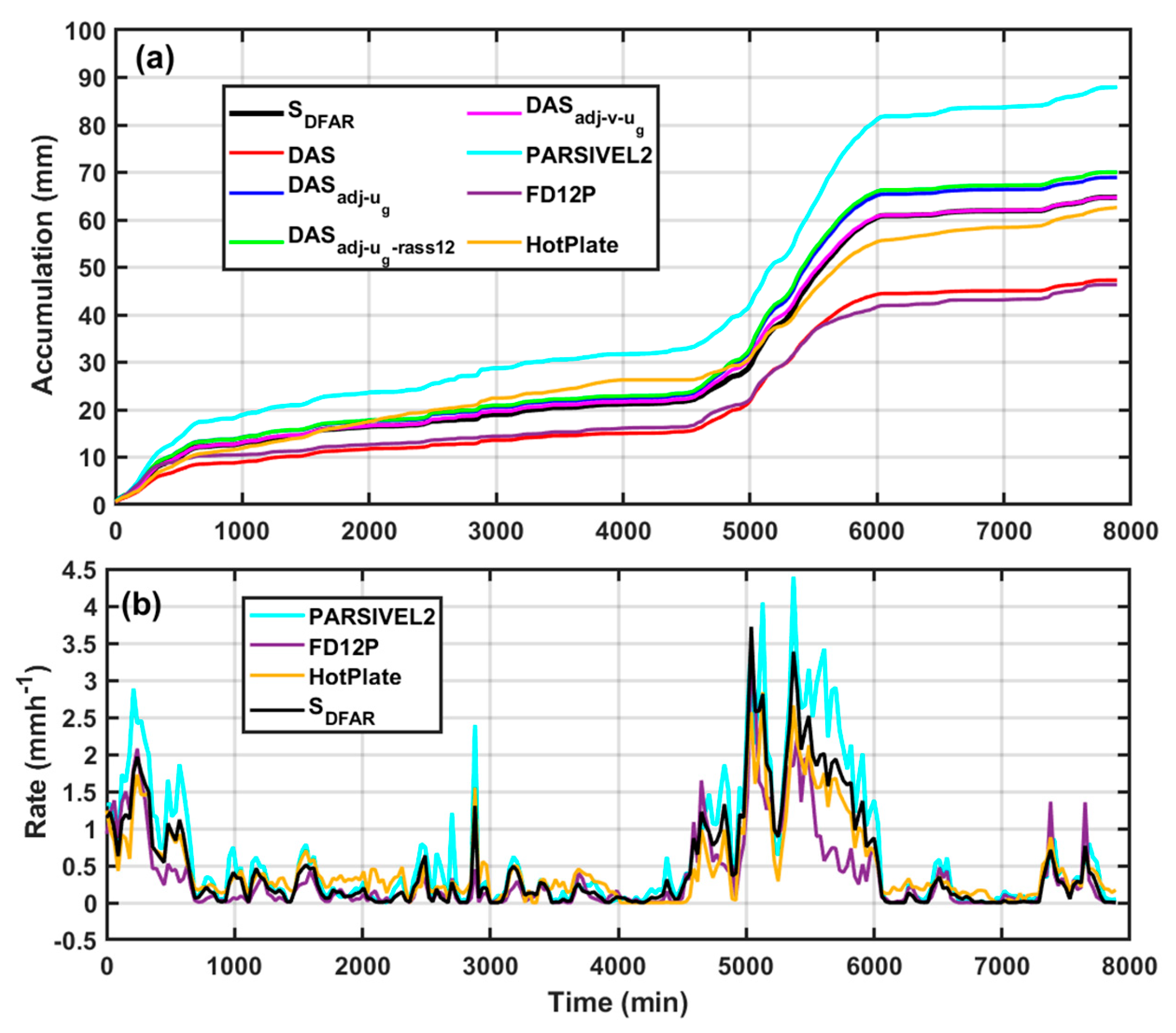
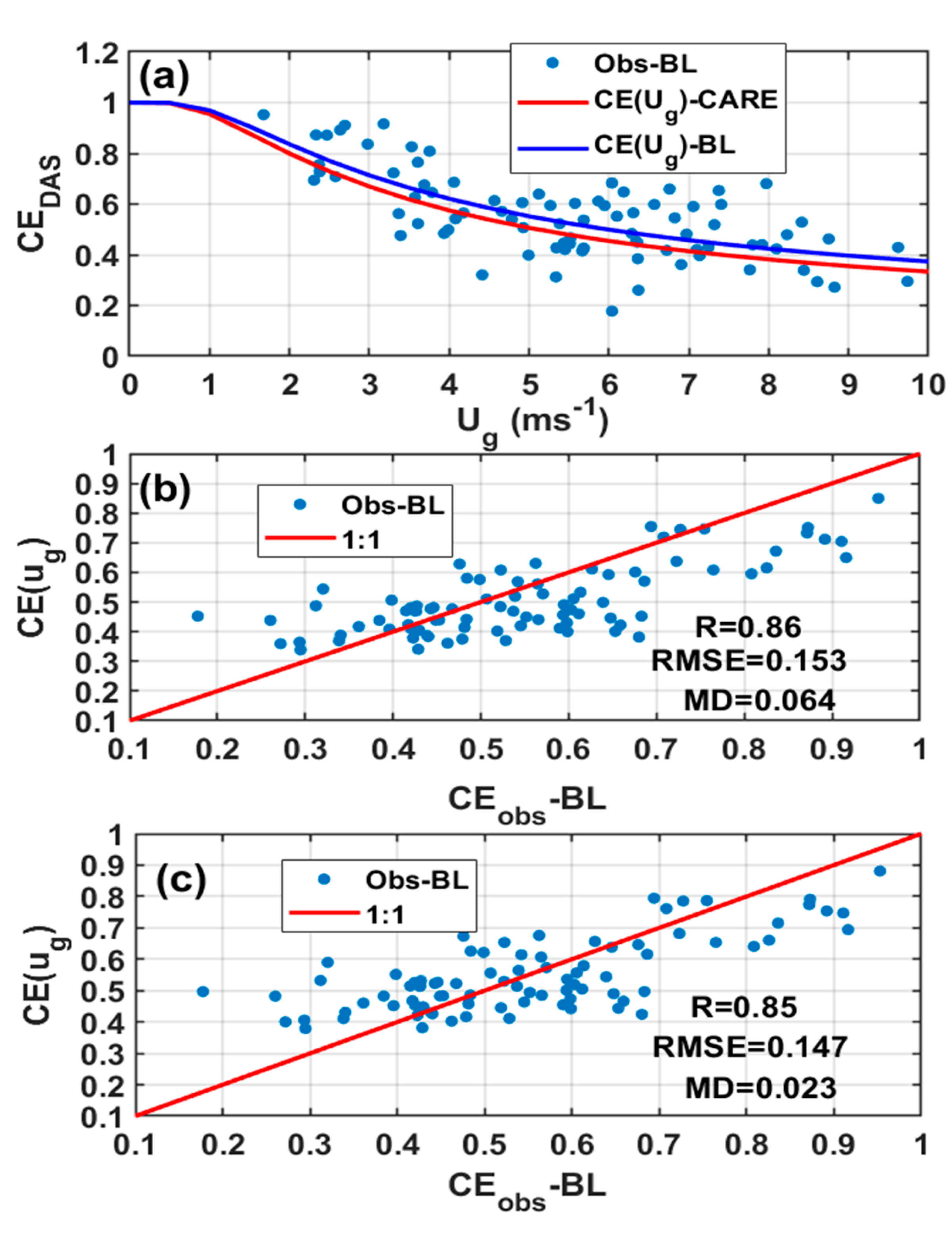
3.5. Bratt’s Lake Data
3.6. Comparisons of Transfer Function Based on Bratt’s Lake and CARE Data
3.7. Visibility and Precipitation Intensity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. The Description of the Geonor T-200B3
Appendix A.2. The Description of the Pluvio2 Gauge
Appendix A.3. The Descrption of the Vaisala FD12P Presnt Weather Senor
Appendix A.4. The Descrption of the OTT PARSIVEL2 Disdrometer
Appendix A.5. The Descrption of the HotPlate Instrument
References
- Ballesteros, J.A.A.; Hitchens, N.M. Meteorological Factors Affecting Airport Operations during the Winter Season in the Midwest. Weather. Clim. Soc. 2018, 10, 307–322. [Google Scholar] [CrossRef]
- Das, S.; Brimley, K.B.; Lindheimer, E.T.; Zupancich, M. Association of reduced visibility with crash outcomes. IATSS Res. 2018, 42, 143–151. [Google Scholar] [CrossRef]
- Eisenberg, D.; Warner, E.K. Effects of Solid precipitations on Motor Vehicle Collisions, Injuries, and Fatalities. Am. J. Public Health 2005, 95, 120–124. [Google Scholar] [CrossRef] [PubMed]
- Rasmussen, R.M.; Vivekanandan, J.; Cole, J.; Myers, B.; Masters, C. The estimation of solid precipitation rate using visibility. J. Appl. Meteor. 1999, 38, 1542–1563. [Google Scholar] [CrossRef]
- Boudala, F.S.; Isaac, G.A. Parameterization of visibility in snow: Application in numerical weather prediction models. J. Geophys. Res. 2009, 114, D19202. [Google Scholar] [CrossRef]
- Gultepe, I.; Milbrandt, J.; Zhou, B.-B. Visibility parameterization for forecasting model applications. In Proceedings of the 5th International Conference onFog, Fog Collection and Dew, Münster, Germany, 25–30 July 2010; pp. 227–230. [Google Scholar]
- Falconi, M.T.; von Lerber, A.; Ori, D.; Marzano, F.S.; Moisseev, D. Solid precipitation retrieval at X, Ka and W bands: Consistency of backscattering and microphysical properties using BAECC ground-based measurements. Atmos. Meas. Tech. 2018, 11, 3059–3079. [Google Scholar] [CrossRef]
- Goodison, B.E.; Louie, P.Y.T.; Yang, D. WMO Solid Precipitation Measurement Intercomparison. In World Meteorological Organization, Instruments and Observing Methods; Report No. 67, WMO/TD—No. 872; 1998; 88p. Available online: https://library.wmo.int/doc_num.php?explnum_id=9694 (accessed on 9 August 2023).
- Goodison, B.E.; Yang, D. In-situ measurement of solid precipitation in high latitudes: The need for correction. In Proceedings of the ACSYS Solid Precipitation Climatology Project Workshop, Reston, VA, USA, 12–15 September 1995; WMO/TD- No.739, WMO, 1–12. Available online: https://library.wmo.int/doc_num.php?explnum_id=9637 (accessed on 9 August 2023).
- Kochendorfer, J.; Nitu, R.; Wolffm, M.; Mekis, E.; Rasmussen, R.; Baker, B.; Earle, M.E.; Reverdin, A.; Wong, K.; Smith, C.; et al. Analysis of single- Alter-shielded and unshielded measurements of mixed and solid precipitation from WMO-SPICE. Hydrol. Earth Syst. Sci. 2017, 21, 3525–3542. [Google Scholar] [CrossRef]
- Kochendorfer, J.; Rasmussen, R.; Wolff, M.; Baker, B.; Hall, M.E.; Meyers, T.; Landolt, S.; Jachcik, A.; Isaksen, K.; Brækkan, R.; et al. The quantification and correction of windinduced precipitation measurement errors. Hydrol. Earth Syst. Sci. 2017, 21, 1973–1989. [Google Scholar] [CrossRef]
- Kochendorfer, J.; Earle, M.; Rasmussen, R.; Smith, C.; Yang, D.; Morin, S.; Mekis, E.; Buisan, S.; Roulet, Y.-A.; Landolt, S.; et al. How well are we measuring snow post-SPICE. Am. Meteorol. Soc. 2022, 103, 370–378. [Google Scholar] [CrossRef]
- Smith, C.D.; Yang, D. An assessment of the Geonor T-200B used with a large octagonal double fence wind shield as an automated reference for the gauge measurement of solid precipitation. In Proceedings of the 90th AMS Annual Meeting/15th SMOI, Atlanta, GA, USA, 16–21 January 2010; Available online: https://ams.confex.com/ams/pdfpapers/158669.pdf (accessed on 9 August 2023).
- Pierre, A.; Jutras, S.; Kochendorfer, J.; Smith, C.; Fortin, V.; Anctil, F. Evaluation of catch efficiency transfer functions for unshielded and single-Alter-shielded solid precipitation measurements. J. Atmos. Ocean. Technol. 2019, 36, 865–881. [Google Scholar] [CrossRef]
- Køltzow, M.; Casati, B.; Haiden, T.; Valkonen, T. Verification of Solid Precipitation Forecasts from Numerical Weather Prediction Models in Norway. Wea. Forecasting. 2020, 35, 2279–2292. [Google Scholar] [CrossRef]
- Kochendorfer, J.; Nitu, R.; Wolff, M.; Mekis, E.; Rasmussen, R.; Baker, B.; Earle, M.E.; Reverdin, A.; Wong, K.; Smith, C.D.; et al. Testing and development of transfer functions for weighing precipitation gauges in WMO-SPICE, Hydrol. Earth Syst. Sci. 2020, 22, 1437–1452. [Google Scholar] [CrossRef]
- Wolff, M.A.; Isaksen, K.; Petersen-Øverleir, A.; Ødemark, K.; Reitan, T.; Brækkan, R. Derivation of a new continuous adjustment function for correcting wind-induced loss of solid precipitation: Results of a Norwegian field study. Hydrol. Earth Syst. Sci. 2015, 19, 951–967. [Google Scholar] [CrossRef]
- Colli, M.; Stagnaro, M.; Lanza, L.G.; Rasmussen, R.; Thériault, J.M. Adjustments for Wind-Induced Undercatch in Snowfall Measurements Based on Precipitation Intensity. J. Hydrometeorol. 2020, 21, 1039–1050. [Google Scholar] [CrossRef]
- Rasmussen, R.M.; Baker, B.; Kochendorfer, J.; Meyers, T.; Landolt, S.; Fischer, A.P.; Black, J.; Thériault, J.M.; Kucera, P.; Gochis, D.; et al. How well are we measuring snow: The NOAA/FAA/NCAR winter precipitation test bed. Bull. Amer. Meteor. Soc. 2012, 93, 811–829. [Google Scholar] [CrossRef]
- Leroux, N.R.; Thériault, J.M.; Rasmussen, R. Improvement of snow gauge collection efficiency through a knowledge of solid precipitation fall speed. J. Hydrometeor. 2021, 22, 997–1006. [Google Scholar] [CrossRef]
- Hoover, J.; Earle, M.E.; Joe, P.I.; Sullivan, P.E. Unshielded precipitation gauge collection efficiency with wind speed and hydrometeor fall velocity. Hydrol. Earth Syst. Sci. 2021, 25, 5473–5491. [Google Scholar] [CrossRef]
- Thériault, J.M.; Rasmussen, R.; Ikeda, K.; Landolt, S. Dependence of snow gauge collection efficiency on snowflake characteristics. J. Appl. Meteor. Climatol. 2012, 51, 745–762. [Google Scholar] [CrossRef]
- Smith, C.D.; Yang, D.; Ross, A.; Barr, A. The Environment and Climate Change Canada solid precipitation intercomparison data from Bratt’s Lake and Caribou Creek, Saskatchewan. Earth Syst. Sci. 2019, 11, 1337–1347. [Google Scholar] [CrossRef]
- Nitu, R.; Roulet, Y.-A.; Wolff, M.; Earle, M.; Reverdin, A.; Smith, C.; Kochendorfer, J.; Morin, S.; Rasmussen, R.; Wong, K.; et al. WMO Solid Precipitation Intercomparison Experiment (SPICE) (2012–2015); Instruments and Observing Methods Report No. 131; World Meteorological Organization: Geneva, Switzerland, 2018. [Google Scholar]
- Smith, C.D.; Ross, A.; Kochendorfer, J.; Earle, M.E.; Wolff, M.; Buisán, S.; Roulet, Y.-A.; Laine, T. Evaluation of the WMO Solid Precipitation Intercomparison Experiment (SPICE) transfer functions for adjusting the wind bias in solid precipitation measurements. Hydrol. Earth Syst. Sci. 2020, 24, 4025–4043. [Google Scholar] [CrossRef]
- Nitu, R. Proposed configuration of intercomparison sites and of the field references. In Second Session of the International Organization Committee for the WMO Solid Precipitation Intercomparison Experiment; World Meteorological Organization: Boulder, CO, USA, 2012. [Google Scholar]
- Boudala, F.S.; Hudak, D.; Boodoo, S.; Donaldson, N.; Nitu, R.; Wong, K. Improved Algorithms for Radar Remote Sensing of Solid precipitation Rate Using Dual Polarization C Band Radar. In Proceedings of the 17th International Conference on Clouds and Precipitation, ICCP 2016, Manchester, UK, 25–29 July 2016. [Google Scholar]
- Boudala, F.S.; Isaac, G.A.; Filman, P.; Crawford, R.; Hudak, D. Performance of Emerging Technologies for Measuring Solid and Liquid Precipitation in Cold Climate as Compared to the Traditional Manual Gauges. J. Atmos. Oceanic Technol. 2017, 34, 167–184. [Google Scholar] [CrossRef]
- Haavasoja, T.; Nnqvist, J.L.; Nylander, P. ‘Present Weather and Fog Detection for Highways. In Proceedings of the Seventh Road Conference, Seefeld, Austria, 21–22 March 1994. [Google Scholar]
- Loffler-Mang, M.; Joss, J. An optical Disdrometer for measuring size and velocity of hydrometeors. J. Atmos. Oceanic Technol. 2000, 17, 130–139. [Google Scholar] [CrossRef]
- Battaglia, A.; Rustemeier, E.; Tokay, A.; Blahak, U.; Simmer, C. Parsivel snow observations: A critical assessment. J. Atmos. Ocean. Tech. 2010, 27, 333–344. [Google Scholar] [CrossRef]
- Boudala, F.S.; Isaac, G.A.; Rasmussen, R.; Cober, S.; Scott, B. Comparisons of snowfall measurements in complex terrain made during the 2010 Winter Olympics in Vancouver. Pure Appl. Geophys. 2014, 171, 113. [Google Scholar] [CrossRef]
- Boudala, F.S.; Rasmussen, R.; Isaac, G.A.; Scott, B. Performance of hot plate for measuring solid precipitation in complex terrain during the 2010 Vancouver Winter Olympics. J. Atmos. Oceanic Technol. 2014, 31, 437–446. [Google Scholar] [CrossRef]
- Rasmussen, R.M.; Hallett, J.; Purcell, R.R.; Landolt, S.D.; Cole, J. The hotplate precipitation gauge. J. Atmos. Oceanic Technol. 2011, 28, 148–164. [Google Scholar] [CrossRef]
- Transport Canada (TC), 2020–2021. Transport Canada Holdover Time (HOT) Guidelines Winter 2020–2021. Available online: https://tc.canada.ca/en/aviation/general-operating-flight-rules/holdover-time-hot-guidelines-icing-anti-icing-aircraft (accessed on 9 August 2023).
- Boudala, F.S.; Isaac, G.A.; Crawford, R.; Reid, J. Parameterization of runway visual range as a function of visibility: Application in in numerical weather prediction models. J. Atmos. Ocean. Technol. 2012, 29, 177–191. [Google Scholar] [CrossRef]
- Boudala, F.S.; Wu, D.; Isaac, G.A.; Gultepe, I. Seasonal and Microphysical Characteristics of Fog at a Northern Airport in Alberta, Canada. Remote Sens. 2022, 14, 4865. [Google Scholar] [CrossRef]
- Leroux, 2022. Guide to Aircraft Deicing. Available online: https://www.sae.org/works/committeeResources.do?resourceID=900393 (accessed on 9 August 2023).
- Mitchell, D.L. Use of mass- and area-dimensional power laws for determining precipitation particle terminal velocities. J. Atmos. Sci. 1996, 53, 1710–1723. [Google Scholar] [CrossRef]
- Thériault, J.M.; Rasmussen, R.; Petro, E.; Colli, M.; Lanza, L. Impact of wind direction, wind speed and particle characteristics on the collection efficiency of the Double Fence Intercomparison. J. Appl. Met. Clim. 2015, 54, 1918–1930. [Google Scholar] [CrossRef]
- Mellor, M. Light scattering and particle aggregation in snow-storms. J. Glaciol. 1966, 6, 237–248. [Google Scholar] [CrossRef]
- Warner, C.; Gunn, K.L.S. Measurement of solid precipitation by optical attenuation. J. Appl. Meteorol. 1969, 8, 110–121. [Google Scholar] [CrossRef]
- O’Brien, H.W. Visibility and light attenuation in falling snow. J. Appl. Meteorol. 1970, 9, 671–683. [Google Scholar] [CrossRef]
- Stallabrass, J.R. Measurements of the concentration of falling snow. Tech. Memo. 140. In Proceedings of the Snow Property Measurements Workshop, Lake Louise, AB, Canada, 1–3 April 1985. [Google Scholar]
- Fujiyoshi, Y.; Wakahamam, G.; Endoh, T.; Irikawa, S.; Konishi, H.; Takeuchi, M. Simultaneous observation of solid precipitation intensity and visibility in winter at Saporro. Low Temp. Sci. 1983, 42A, 147–156. [Google Scholar]
- Bisyarin, V.P.; Bisyarina, I.P.; Rubash, V.K.; Sokolov, A.K. Attenuation of 10.6 and 0.63 mm laser radiation in atmospheric precipitation. Radio Eng. Electron. Phys. 1971, 16, 1594. [Google Scholar]
- Muench, H.S.; Brown, H.A. Measurement of Visibility and Radar Reflectivity during Snowstorms in the AFGL Mesonet; Project 8628; 1977. Available online: https://apps.dtic.mil/sti/citations/ADA049258 (accessed on 15 May 2023).





| Sources | Catch Efficiency Parameterization | RMSE |
|---|---|---|
| In this work-Geonor double Alter shield, at CARE site | 0.074 | |
| In this work at CARE site | 0.07 | |
| Rasmussen et al., 2012 based on data at Marshall site, USA [19] | 0.09 |
| Sources | Catch Efficiency Parameterization | RMSE |
|---|---|---|
| In this work at CARE site | 0.13 | |
| Boudala et al., (2017) in Cold Lake Alberta [28] | 0.13 | |
| Kochendorfer et al., (2017a) [10] Based on 8 different sites | 0.14 |
| Source | Parameterization |
|---|---|
| This work -Vis(S) | ) |
| Boudala and Isaac, 2009 (BI09(S)) [5] | |
| This work -Vis(S,T) | |
| Boudala and Isaac, 2009 (BI09(S,T) [5] | |
| Mellor (1966) (M66) [41] | |
| Warner and Gunn (1969) [42] | |
| O’Brien (1970) (OB70) [43] | |
| Gultepe et al. (2010) (G10) [44] | |
| Stallabrass (1985) (S85) | |
| Fujiyoshi et al. (1983) [45] | |
| Bisyarin et al. (1971) (B71) [46] | |
| Muench and Brown (1977) (MB77) [47] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boudala, F.S.; Milbrandt, J.A. Solid Precipitation and Visibility Measurements at the Centre for Atmospheric Research Experiments in Southern Ontario and Bratt’s Lake in Southern Saskatchewan. Remote Sens. 2023, 15, 4079. https://doi.org/10.3390/rs15164079
Boudala FS, Milbrandt JA. Solid Precipitation and Visibility Measurements at the Centre for Atmospheric Research Experiments in Southern Ontario and Bratt’s Lake in Southern Saskatchewan. Remote Sensing. 2023; 15(16):4079. https://doi.org/10.3390/rs15164079
Chicago/Turabian StyleBoudala, Faisal S., and Jason A. Milbrandt. 2023. "Solid Precipitation and Visibility Measurements at the Centre for Atmospheric Research Experiments in Southern Ontario and Bratt’s Lake in Southern Saskatchewan" Remote Sensing 15, no. 16: 4079. https://doi.org/10.3390/rs15164079
APA StyleBoudala, F. S., & Milbrandt, J. A. (2023). Solid Precipitation and Visibility Measurements at the Centre for Atmospheric Research Experiments in Southern Ontario and Bratt’s Lake in Southern Saskatchewan. Remote Sensing, 15(16), 4079. https://doi.org/10.3390/rs15164079






