The Uncertainty Analysis of the Entrance Pupil Irradiance for a Moon-Based Earth Radiation Observation Instrument
Abstract
:1. Introduction
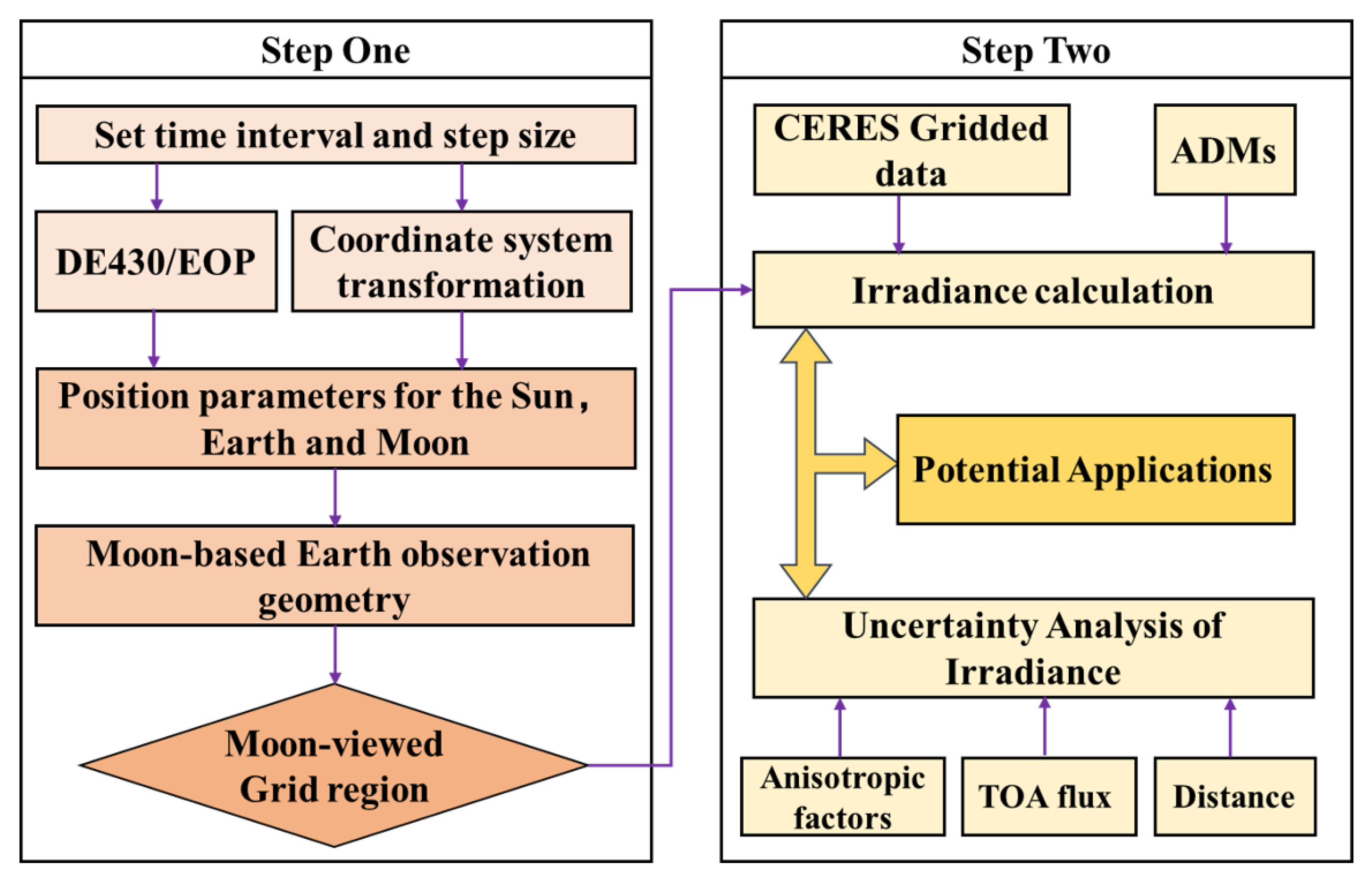
2. Materials and Methods
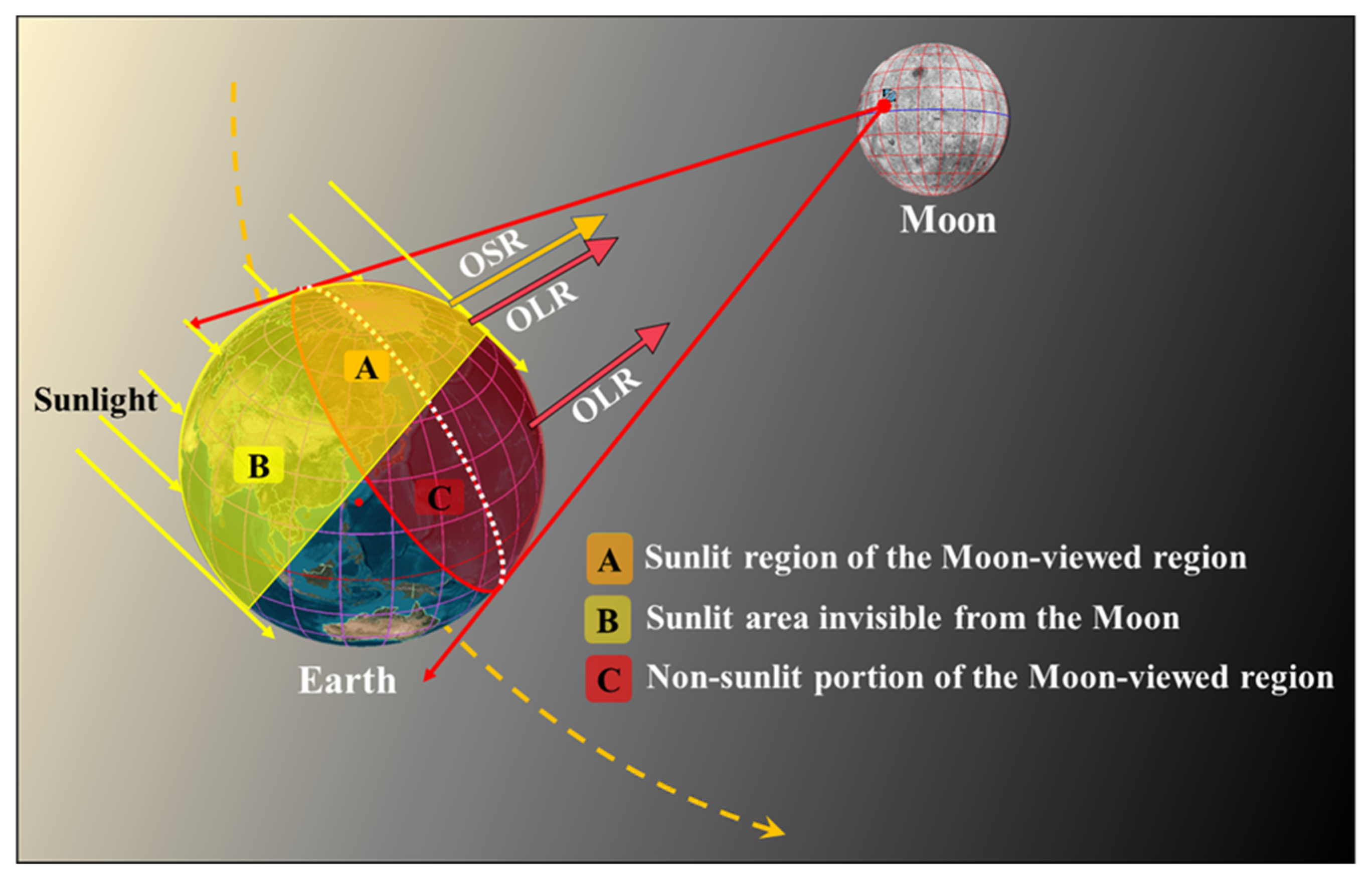
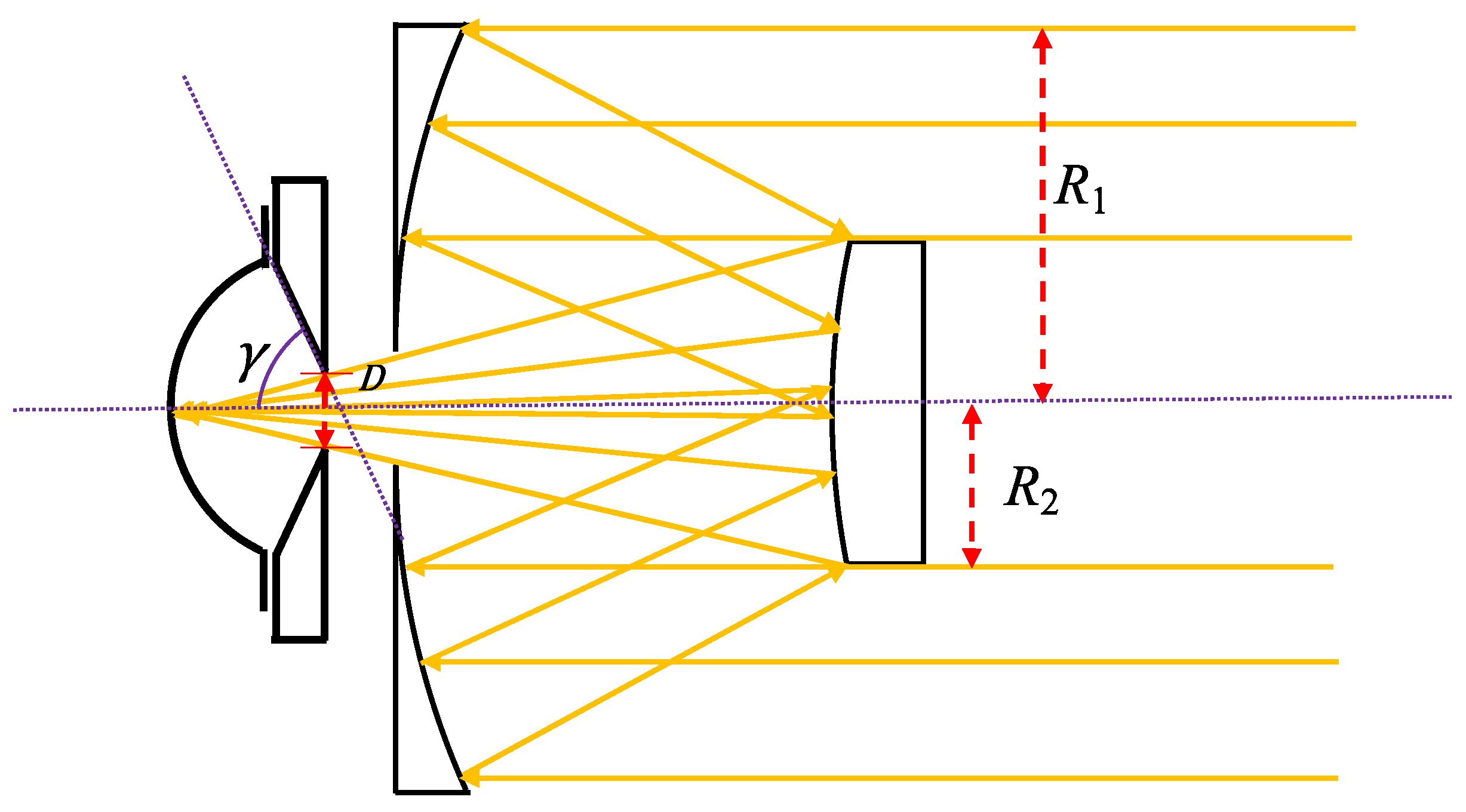
2.1. Observation Geometry
2.2. Radiation Transfer Function
2.3. The Analysis of Uncertainty
3. Results
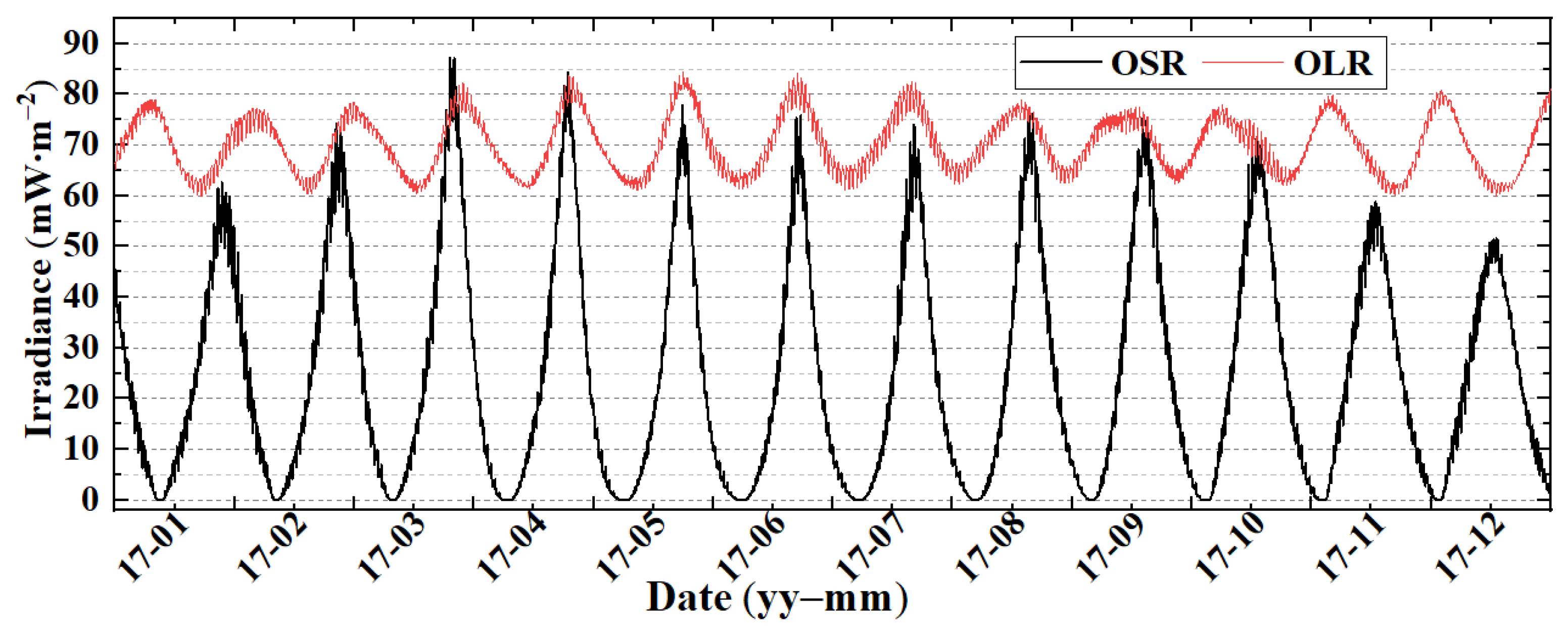
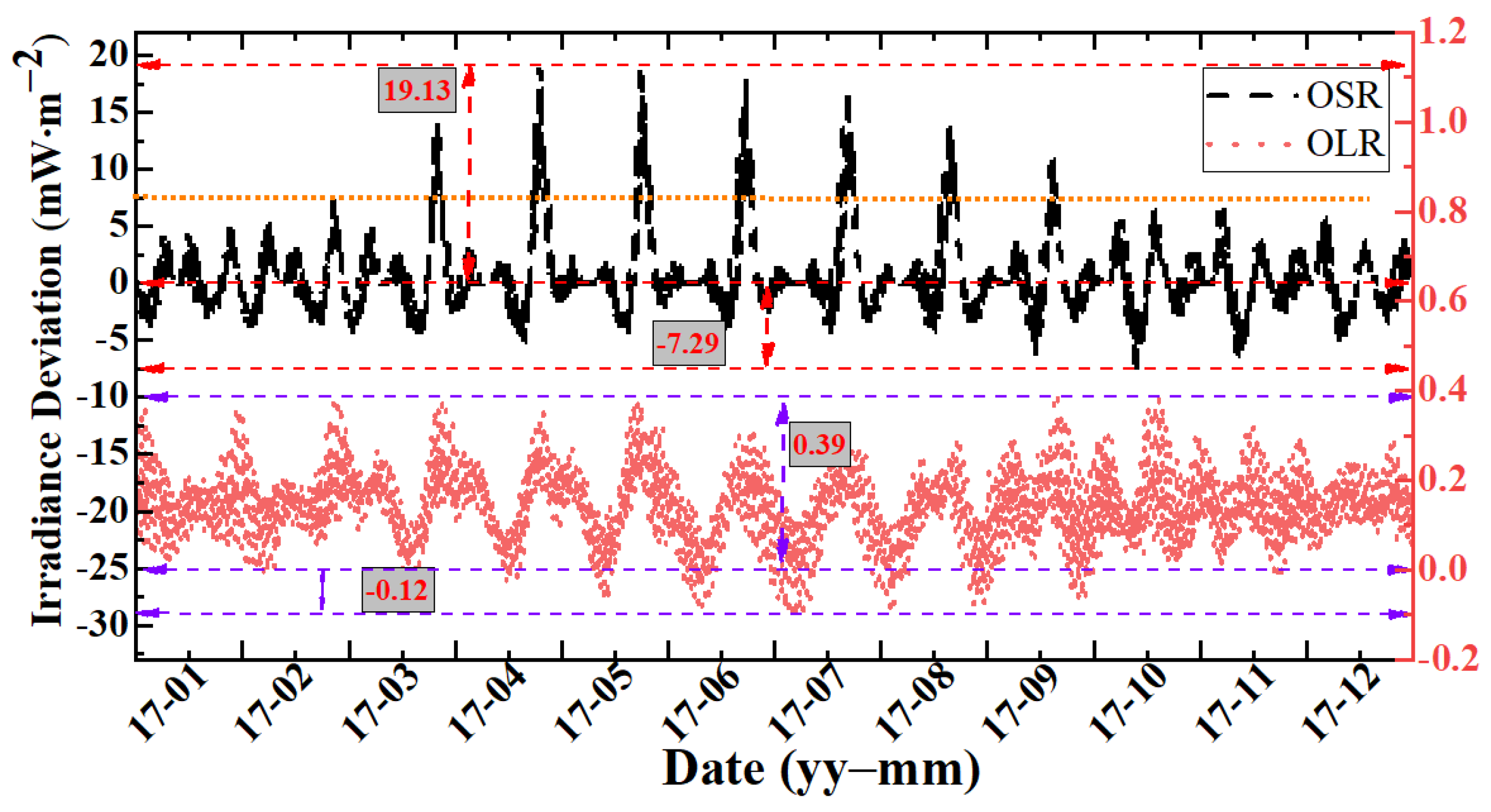
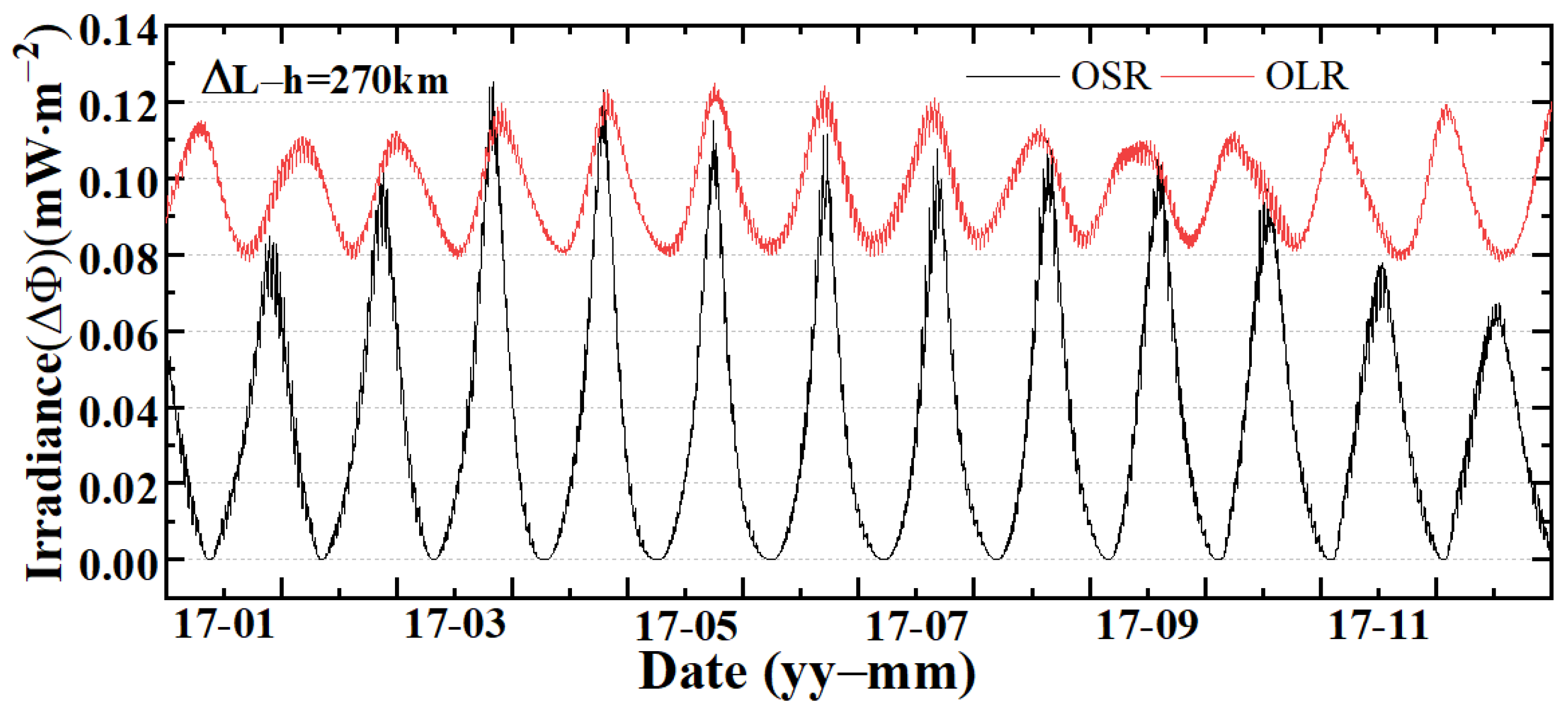
3.1. The Origin Simulated EPI Time Series
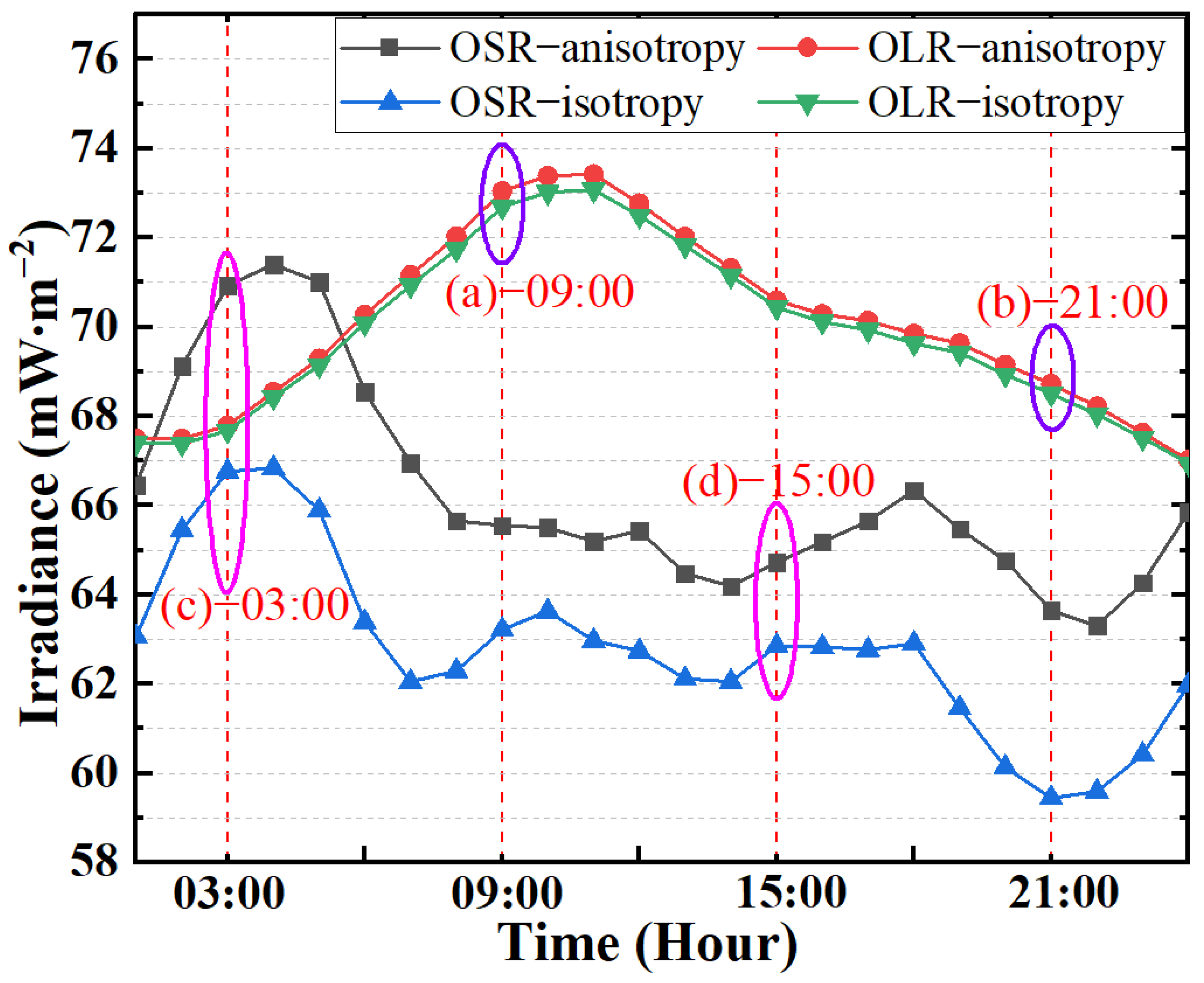
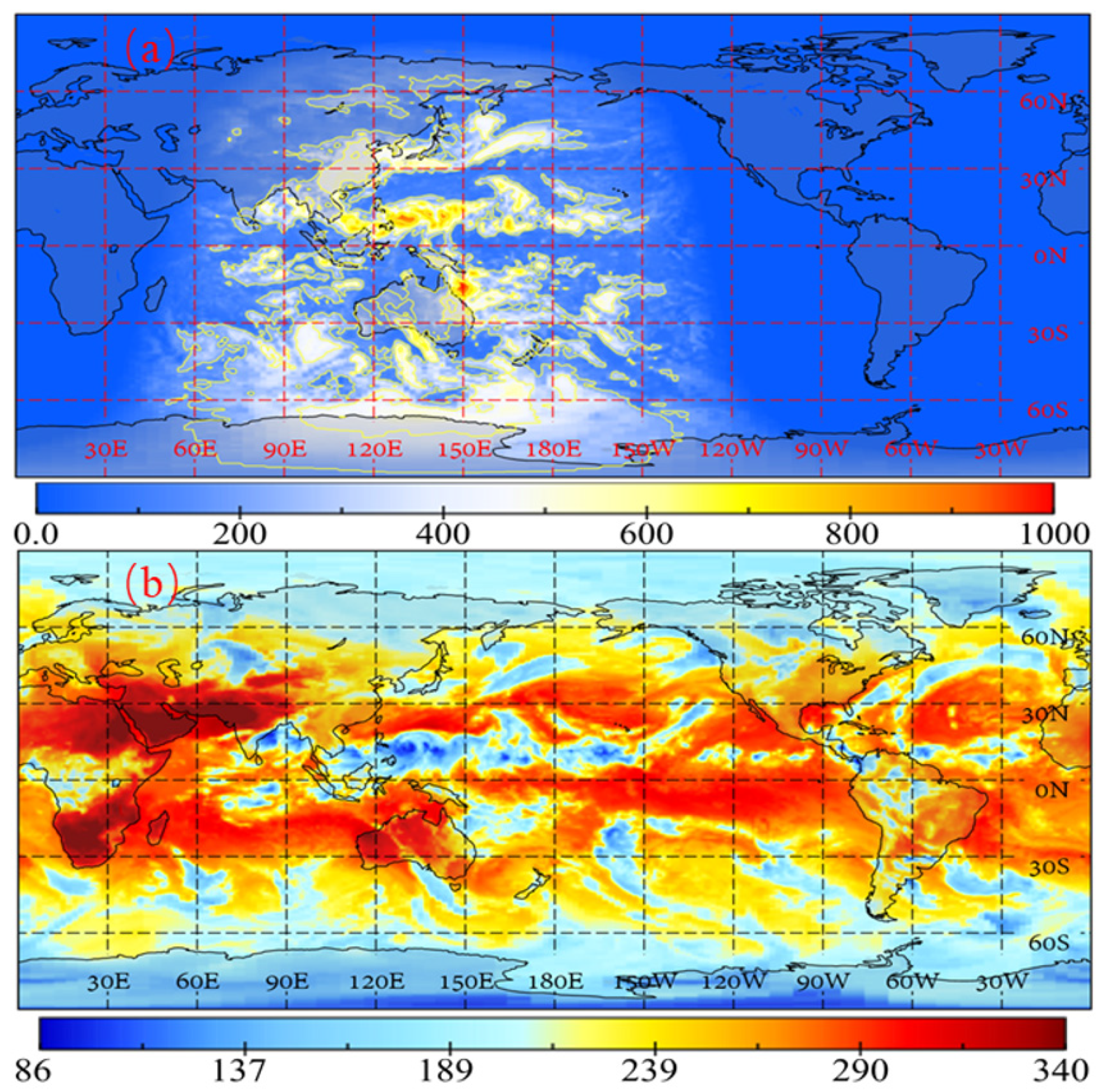
3.2. The Effects of ADMs
3.3. The Effects of TOA Flux
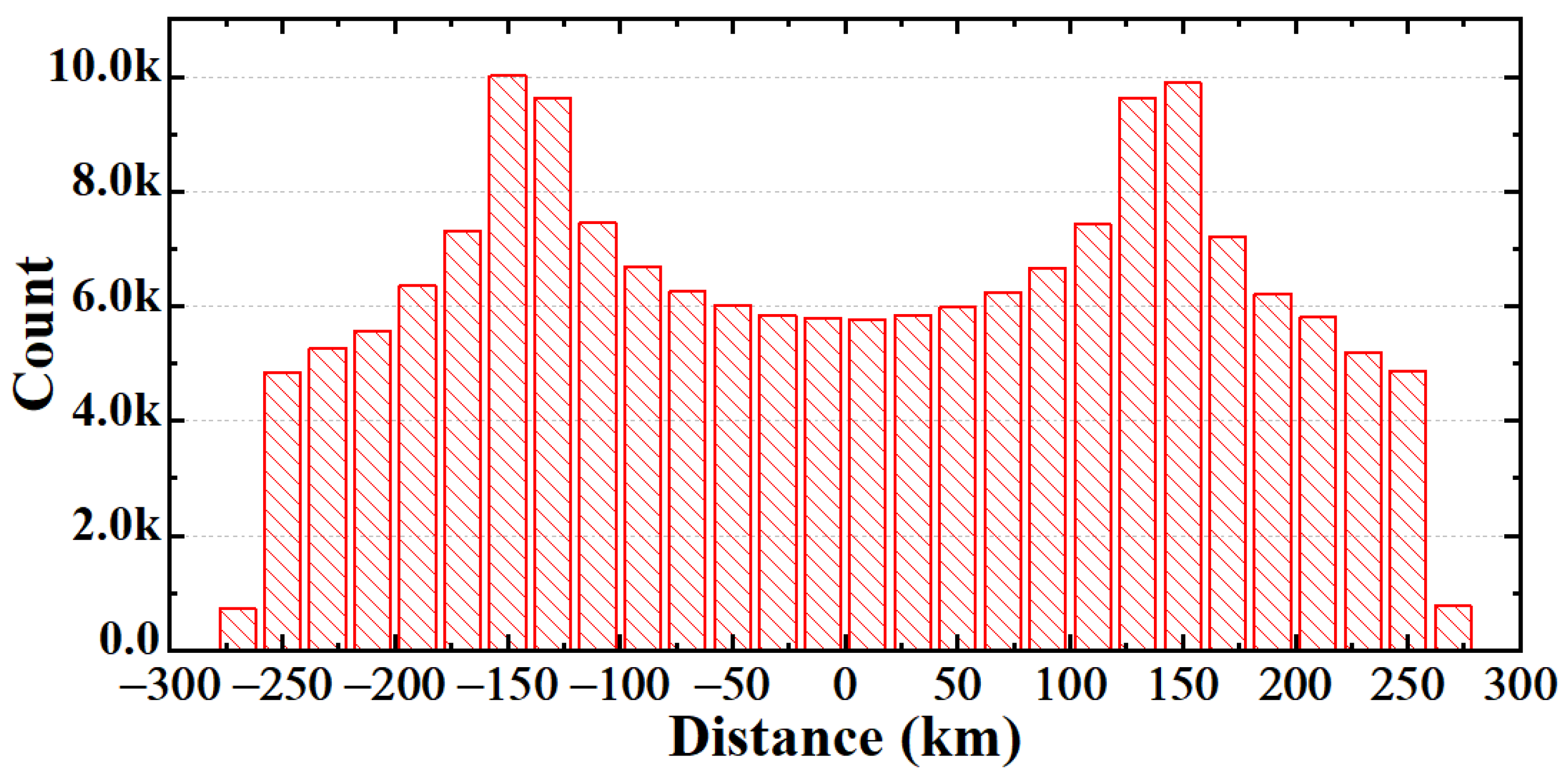
3.4. The Effect of the Earth–Moon Distance
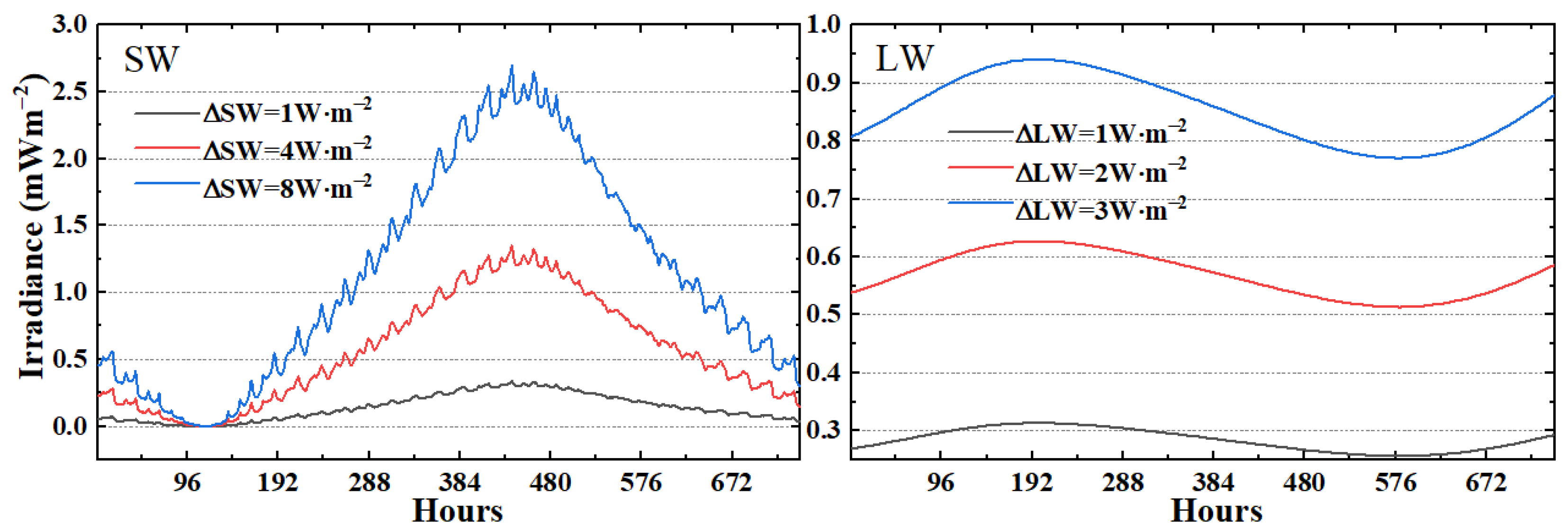
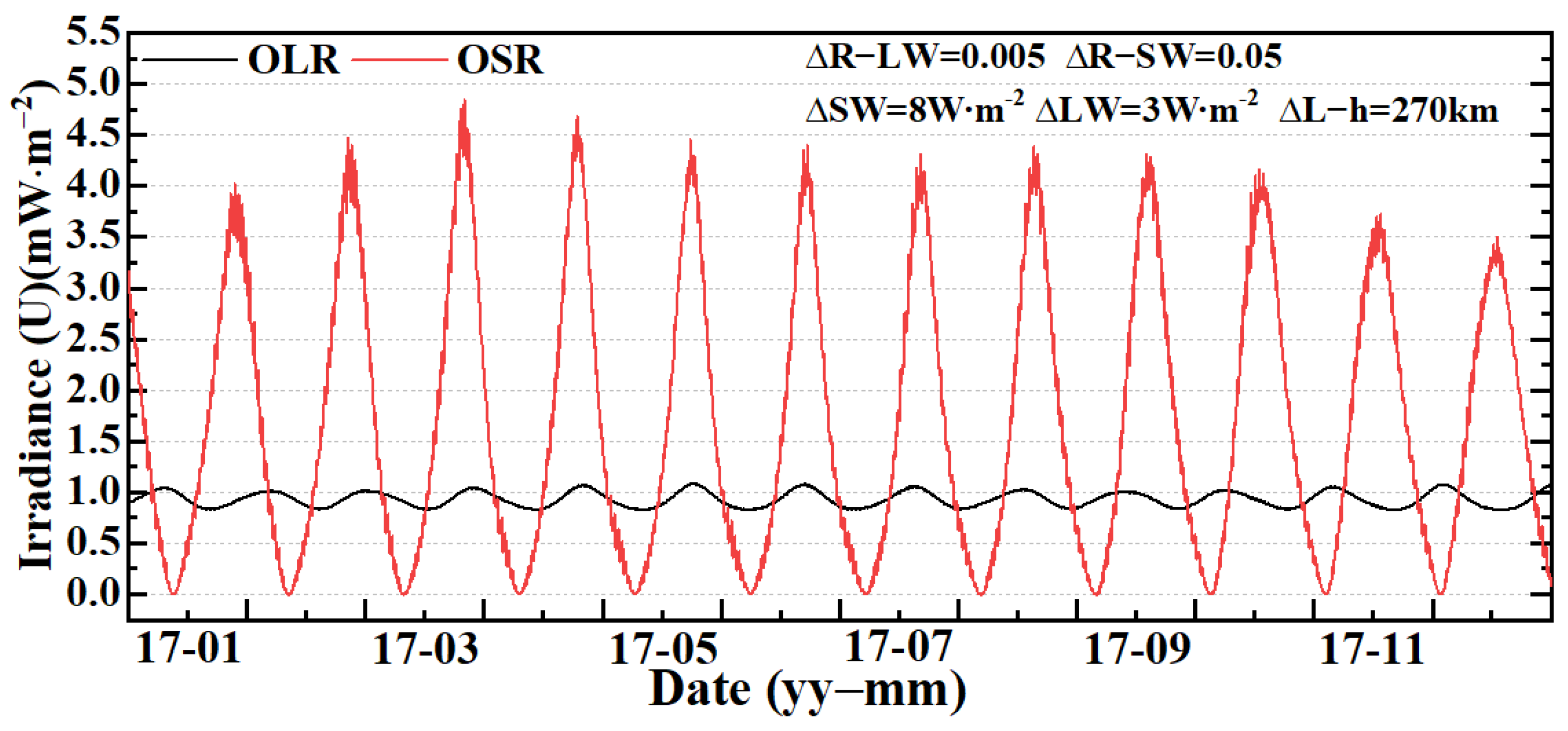
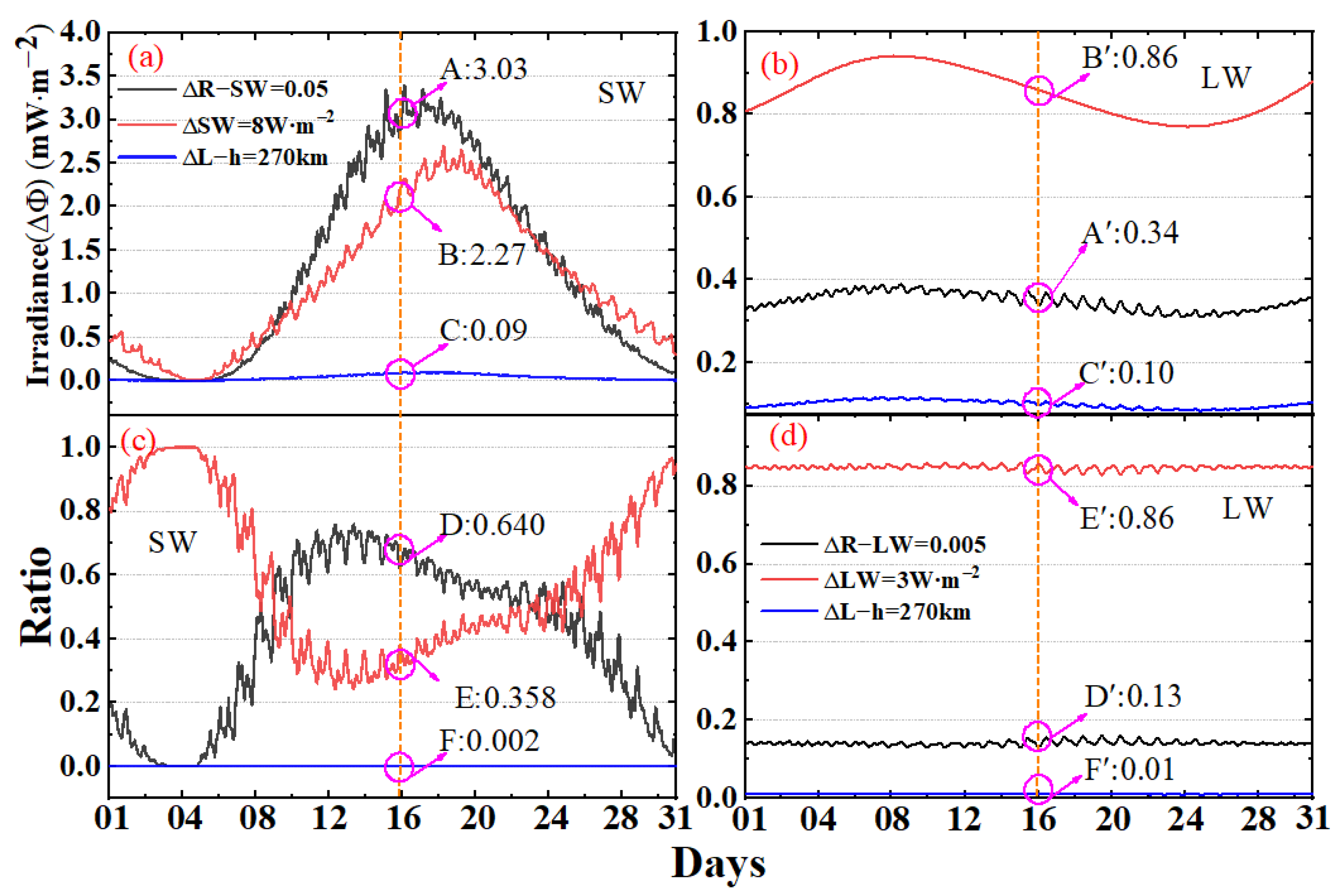
3.5. The Combined Uncertainty
4. Discussion
4.1. The Uncertainty Analysis
4.2. The Potential Applications of Moon-Based Data
4.3. The Dynamic Performance of a Simplified Moon-Based Radiometer
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MERO | Moon-Based Earth Radiation Observation |
| ERB | Earth Radiation Budget |
| EPI | Entrance Pupil Irradiance |
| ADMs | Angular Distribution Models |
| TOA | Top of Earth’s Atmosphere |
| SW | Shortwave |
| LW | Longwave |
| OSR | Outgoing Shortwave Radiation |
| OLR | Outgoing Longwave Radiation |
| ERBE | Earth Radiation Budget Experiment |
| CERES | Clouds and the Earth’s Radiant Energy System |
| GERB | Geostationary Earth Radiation Budget |
| WFOV | Wide Field-of-View |
| NFOV | Narrow Field-of-View |
| DSCOVR | Deep Space Climate Observatory |
| LEO | Low-Earth Orbit |
| GEO | Geostationary Earth Orbit |
| MACR | Moon-based Active Cavity Radiometer |
References
- Loeb, N.G.; Thorsen, T.J.; Norris, J.R.; Wang, H.; Su, W. Changes in Earth’s Energy Budget during and after the “Pause” in Global Warming: An Observational Perspective. Climate 2018, 6, 62. [Google Scholar] [CrossRef]
- Sillmann, J.; Kharin, V.V.; Zwiers, F.; Zhang, X.; Bronaugh, D. Climate extremes indices in the cmip5 multimodel ensemble: Part 2. future climate projections. J. Geophys. Res. Atmos. 2013, 118, 2473–2493. [Google Scholar] [CrossRef]
- Ackerman, S.A.; Platnick, S.; Bhartia, P.K.; Duncan, B.; L’Ecuyer, T.; Heidinger, A.; Skofronick-Jackson, G.; Loeb, N.; Schmit, T.; Smith, N. Satellites See the World’s Atmosphere. Meteorol. Monogr. 2019, 59, 4.1–4.53. [Google Scholar]
- Dewitte, S.; Clerbaux, N. Measurement of the Earth Radiation Budget at the Top of the Atmosphere—A Review. Remote Sens. 2017, 9, 1143. [Google Scholar] [CrossRef]
- Barkstrom, B.R.; Smith, G.L. The Earth Radiation Budget Experiment: Science and implementation. Rev. Geophys. 1986, 24, 379–390. [Google Scholar] [CrossRef]
- Dewitte, S. Editorial for Special Issue “Earth Radiation Budget”. Remote Sens. 2020, 12, 3379. [Google Scholar] [CrossRef]
- Jacobowitz, H.; Soule, H.V.; Kyle, H.L.; House, F.B. The Earth Radiation Budget (ERB) Experiment: An overview. J. Geophys. Res. Atmos. 1984, 89, 5021–5038. [Google Scholar] [CrossRef]
- Smith, G.L.; Green, R.N.; Raschke, E.; Avis, L.M.; Suttles, J.T.; Wielicki, B.A.; Davies, R. Inversion methods for satellite studies of the Earth’s Radiation Budget: Development of algorithms for the ERBE Mission. Rev. Geophys. 1986, 24, 407–421. [Google Scholar] [CrossRef]
- Smith, G.; Priestley, K.; Loeb, N.; Wielicki, B.; Charlock, T.; Minnis, P.; Doelling, D.; Rutan, D. Clouds and Earth Radiant Energy System (CERES), a review: Past, present and future. Adv. Space Res. 2011, 48, 254–263. [Google Scholar] [CrossRef]
- Clerbaux, N.; Dewitte, S.; Bertrand, C.; Caprion, D.; De Paepe, B.; Gonzalez, L.; Ipe, A.; Russell, J.E.; Brindley, H. Unfiltering of the Geostationary Earth Radiation Budget (GERB) Data. Part I: Shortwave Radiation. J. Atmos. Ocean. Technol. 2008, 25, 1087–1105. [Google Scholar] [CrossRef]
- Clerbaux, N.; Dewitte, S.; Bertrand, C.; Caprion, D.; De Paepe, B.; Gonzalez, L.; Ipe, A.; Russell, J.E. Unfiltering of the Geostationary Earth Radiation Budget (GERB) Data. Part II: Longwave Radiation. J. Atmos. Ocean. Technol. 2008, 25, 1106–1117. [Google Scholar] [CrossRef]
- Su, W.; Minnis, P.; Liang, L.; Duda, D.P.; Khlopenkov, K.; Thieman, M.M.; Yu, Y.; Smith, A.; Lorentz, S.; Feldman, D.; et al. Determining the daytime Earth radiative flux from National Institute of Standards and Technology Advanced Radiometer (NISTAR) measurements. Atmos. Meas. Tech. 2020, 13, 429–443. [Google Scholar] [CrossRef]
- Earth Venture Continuity Radiation Budget Science Working Group. Measurement and Instrument Requirement Recommendations for an Earth Venture Continuity Earth Radiation Budget Instrument. 2018. Available online: https://smd-prod.s3.amazonaws.com/science-pink/s3fs-public/atoms/files/ERB_SWG_Rept_Draft_07242018_TAGGED.pdf (accessed on 3 November 2022).
- Guo, H.; Liu, G.; Ding, Y. Moon-based Earth observation: Scientific concept and potential applications. Int. J. Digit. Earth 2017, 11, 546–557. [Google Scholar] [CrossRef]
- Dewitte, S.; Clerbaux, N.; Cornelis, J. Decadal Changes of the Reflected Solar Radiation and the Earth Energy Imbalance. Remote Sens. 2019, 11, 663. [Google Scholar] [CrossRef]
- Ye, H.; Guo, H.; Liu, G.; Ping, J.; Zhang, L.; Zhang, Y. Estimating the Earth’s Outgoing Longwave Radiation Measured from a Moon-Based Platform. Remote Sens. 2021, 13, 2201. [Google Scholar] [CrossRef]
- Zhang, Y.; Bi, S.; Wu, J. The influence of lunar surface position on irradiance of moon-based earth radiation observation. Front. Earth Sci. 2022, 16, 757–773. [Google Scholar] [CrossRef]
- Zhang, Y.; Dewitte, S.; Bi, S. A Model for Estimating the Earth’s Outgoing Radiative Flux from A Moon-Based Radiometer. Remote Sens. 2023, 15, 3773. [Google Scholar] [CrossRef]
- Zhang, G.; Bi, S.; Zhang, Y.; Wu, J.; Meng, X. Systematic scheme and key parameters of moon-based imaging spectrometer. In Infrared, Millimeter-Wave, and Terahertz Technologies V; SPIE: Beijing, China, 2018; Volume 10826, pp. 116–125. [Google Scholar]
- Ye, H.; Guo, H.; Liu, G.; Ren, Y. Observation duration analysis for Earth surface features from a Moon-based platform. Adv. Space Res. 2018, 62, 274–287. [Google Scholar] [CrossRef]
- Zhang, Y.; Bi, S.; Wu, J. Effect of Temporal Sampling Interval on the Irradiance for Moon-Based Wide Field-of-View Radiometer. Sensors 2022, 22, 1581. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Guo, H.; Liu, G.; Shen, G.; Ye, H.; Deng, Y.; Dong, R. Spatio-Temporal Characteristics for Moon-Based Earth Observations. Remote Sens. 2020, 12, 2848. [Google Scholar] [CrossRef]
- Huang, J.; Guo, H.; Liu, G.; Wang, H.; Deng, Y.; Dong, R. Observational angular analysis of Moon-based Earth observations. Int. J. Remote Sens. 2022, 43, 2315–2333. [Google Scholar] [CrossRef]
- Duan, W.; Liu, J.; Yan, Q.; Ruan, H.; Jin, S. The Effect of Spatial Resolution and Temporal Sampling Schemes on the Measurement Error for a Moon-Based Earth Radiation Observatory. Remote Sens. 2021, 13, 4432. [Google Scholar] [CrossRef]
- Chen, G.; Guo, H.; Jiang, H.; Han, C.; Ding, Y.; Wu, K. Analysis of Comprehensive Multi-Factors on Station Selection for Moon-Based Earth Observation. Remote Sens. 2022, 14, 5404. [Google Scholar] [CrossRef]
- Yuan, L.; Liao, J. A Physical-Based Algorithm for Retrieving Land Surface Temperature From Moon-Based Earth Observation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1856–1866. [Google Scholar] [CrossRef]
- Song, Y.; Wang, X.; Bi, S.; Wu, J.; Huang, S. Effects of solar radiation, terrestrial radiation and lunar interior heat flow on surface temperature at the nearside of the Moon: Based on numerical calculation and data analysis. Adv. Space Res. 2017, 60, 938–947. [Google Scholar] [CrossRef]
- Lohmeyer, W.; Cahoy, K. Space weather radiation effects on geostationary satellite solid-state power amplifiers. Space Weather. 2013, 11, 476–488. [Google Scholar] [CrossRef]
- Durante, M.; Cucinotta, F.A. Physical basis of radiation protection in space travel. Rev. Mod. Phys. 2011, 83, 1245–1281. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, H.-N.; He, H.; He, F.; Chen, B.; Feng, J.-Q.; Ping, J.-S.; Shen, C.; Xu, R.-L.; Zhang, X.-X. Analysis of observational data from Extreme Ultra-Violet Camera onboard Chang’E-3 mission. Astrophys. Space Sci. 2016, 361, 1–7. [Google Scholar] [CrossRef]
- Huang, S.; Zhu, P.; Ye, X.; Li, Q.; Shu, L.; Liu, Y.; Fang, W. The Idea of Moon-based Earth Radiation Budget Experiment (MERBE). In Proceedings of the 43rd COSPAR Scientific Assembly, Online, 28 January–4 February 2021; Volume 43, p. 369. [Google Scholar]
- Gristey, J.J.; Su, W.; Loeb, N.G.; Haar, T.H.V.; Tornow, F.; Schmidt, K.S.; Hakuba, M.Z.; Pilewskie, P.; Russell, J.E. Shortwave Radiance to Irradiance Conversion for Earth Radiation Budget Satellite Observations: A Review. Remote Sens. 2021, 13, 2640. [Google Scholar] [CrossRef]
- Su, W.; Corbett, J.; Eitzen, Z.; Liang, L. Next-generation angular distribution models for top-of-atmosphere radiative flux calculation from CERES instruments: Methodology. Atmos. Meas. Tech. 2015, 8, 611–632. [Google Scholar] [CrossRef]
- Loeb, N.G.; Manalo-Smith, N.; Kato, S.; Miller, W.F.; Gupta, S.K.; Minnis, P.; Wielicki, B.A. Angular distribution models for top-of-atmosphere radiative flux estimation from the Clouds and the Earth’s Radiant Energy System instrument on the Tropical Rainfall Measuring Mission satellite. Part I: Methodology. J. Appl. Meteorol. 2003, 42, 240–265. [Google Scholar] [CrossRef]
- Suttles, J.T.; Green, R.N.; Minnis, P.; Smith, G.; Staylor, W.; Wielicki, B.; Walker, I.J.; Young, D.F.; Taylor, V.R.; Stowe, L. Angular Radiation Models for Earth-Atmosphere System; Shortwave Radiation; National Aeronautics and Space Administration: Washington, DC, USA, 1988; Volume 1.
- Suttles, J.T.; Green, R.N.; Smith, G.L.; Wielicki, B.A.; Walker, I.J.; Taylor, V.R.; Stowe, L.L. Angular Radiation Models for Earth Atmosphere System; Longwave Radiation; National Aeronautics and Space Administration: Washington, DC, USA, 1989; Volume 2. [Google Scholar]
- Loeb, N.G.; Doelling, D.R.; Wang, H.; Su, W.; Nguyen, C.; Corbett, J.G.; Liang, L.; Mitrescu, C.; Rose, F.G.; Kato, S. Clouds and the Earth’s Radiant Energy System (CERES) Energy Balanced and Filled (EBAF) Top-of-Atmosphere (TOA) Edition-4.0 Data Product. J. Clim. 2018, 31, 895–918. [Google Scholar] [CrossRef]
- NASA/LARC/SD/ASDC. CERES and GEO-Enhanced TOA, Within-Atmosphere and Surface Fluxes, Clouds and Aerosols 1-Hourly Terra-Aqua Edition4A [Data set]. NASA Langley Atmospheric Science Data Center DAAC. 2017. Available online: https://asdc.larc.nasa.gov/project/CERES/CER_SYN1deg-1Hour_Terra-Aqua-MODIS_Edition4A (accessed on 6 September 2021).
- Jeffreys, H. On the theory of errors and least squares. Proc. R. Soc. London. Ser. A Contain. Pap. A Math. Phys. Character 1932, 138, 48–55. [Google Scholar]
- Park, R.S.; Folkner, W.M.; Williams, J.G.; Boggs, D.H. The JPL planetary and lunar ephemerides DE440 and DE441. Astron. J. 2021, 161, 105. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS- IERS Conventions (2010). International Earth Rotation and Reference Systems Service (IERS) Technical Note. 2016. Available online: https://www.iers.org/IERS/EN/Publications/TechnicalNotes/tn36.html (accessed on 27 January 2020).
- Doelling, D.R.; Loeb, N.G.; Keyes, D.F.; Nordeen, M.L.; Morstad, D.; Nguyen, C.; Wielicki, B.A.; Young, D.F.; Sun, M. Geostationary Enhanced Temporal Interpolation for CERES Flux Products. J. Atmos. Ocean. Technol. 2013, 30, 1072–1090. [Google Scholar] [CrossRef]
- Doelling, D.R.; Sun, M.; Nguyen, L.T.; Nordeen, M.L.; Haney, C.O.; Keyes, D.F.; Mlynczak, P.E. Advances in Geostationary-Derived Longwave Fluxes for the CERES Synoptic (SYN1deg) Product. J. Atmos. Ocean. Technol. 2016, 33, 503–521. [Google Scholar] [CrossRef]
- World Meteorological Organization (WMO). Essential Climate Variables. Available online: https://public.wmo.int/en/programmes/global-climate-observing-system/essentialclimate-variables (accessed on 6 September 2022).
- Schifano, L.; Smeesters, L.; Geernaert, T.; Berghmans, F.; Dewitte, S. Design and Analysis of a Next-Generation Wide Field-of-View Earth Radiation Budget Radiometer. Remote Sens. 2020, 12, 425. [Google Scholar] [CrossRef]
- Zhang, H.; Ye, X.; Zhu, P.; Fang, W.; Wang, Y. Observation System Design and Analysis for a New Staring Earth Radiation Budget Radiometer Based on the Lagrange L1 Point of the Earth–Moon System. Remote Sens. 2022, 14, 1596. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, X.; Feng, J.; Zhu, C.; Cai, Z.; Xu, Y. Application of precision thermal control techniques in Taiji-1 satellite. Chin. J. Space Sci. 2021, 41, 337–341. [Google Scholar] [CrossRef]
- Swartz, W.H.; Lorentz, S.R.; Papadakis, S.J.; Huang, P.M.; Smith, A.W.; Deglau, D.M.; Yu, Y.; Reilly, S.M.; Reilly, N.M.; Anderson, D.E. RAVAN: CubeSat Demonstration for Multi-Point Earth Radiation Budget Measurements. Remote Sens. 2019, 11, 796. [Google Scholar] [CrossRef]
- Li, C.; Wang, C.; Wei, Y.; Lin, Y. China’s present and future lunar exploration program. Science 2019, 365, 238–239. [Google Scholar] [CrossRef] [PubMed]
- Gerstenmaier, W. Progress in Defining the Deep Space Gateway and Transport Plan. In Proceedings of the NASA Advisory Council Human Exploration and Operations Committee Meeting, Washington, DC, USA, 28–29 March 2017. [Google Scholar]
- Zeng, H.; Li, Z.; Xu, R.; Peng, K.; Wang, P. Further Advances for staging orbits of manned lunar exploration mission. Acta Astronaut. 2023, 204, 281–293. [Google Scholar] [CrossRef]
- Saha, D.; Bazmohammadi, N.; Raya-Armenta, J.M.; Bintoudi, A.D.; Lashab, A.; Vasquez, J.C.; Guerrero, J.M. Space Microgrids for Future Manned Lunar Bases: A Review. IEEE Open Access J. Power Energy 2021, 8, 570–583. [Google Scholar] [CrossRef]
- Pei, Z.; Liu, J.; Wang, Q.; Kang, Y.; Zou, Y.; Zhang, H.; Zhang, Y.; He, H.; Wang, Q.; Yang, R.; et al. Overview of lunar exploration and International Lunar Research Station. Chin. Sci. Bull. 2020, 65, 2577–2586. [Google Scholar] [CrossRef]






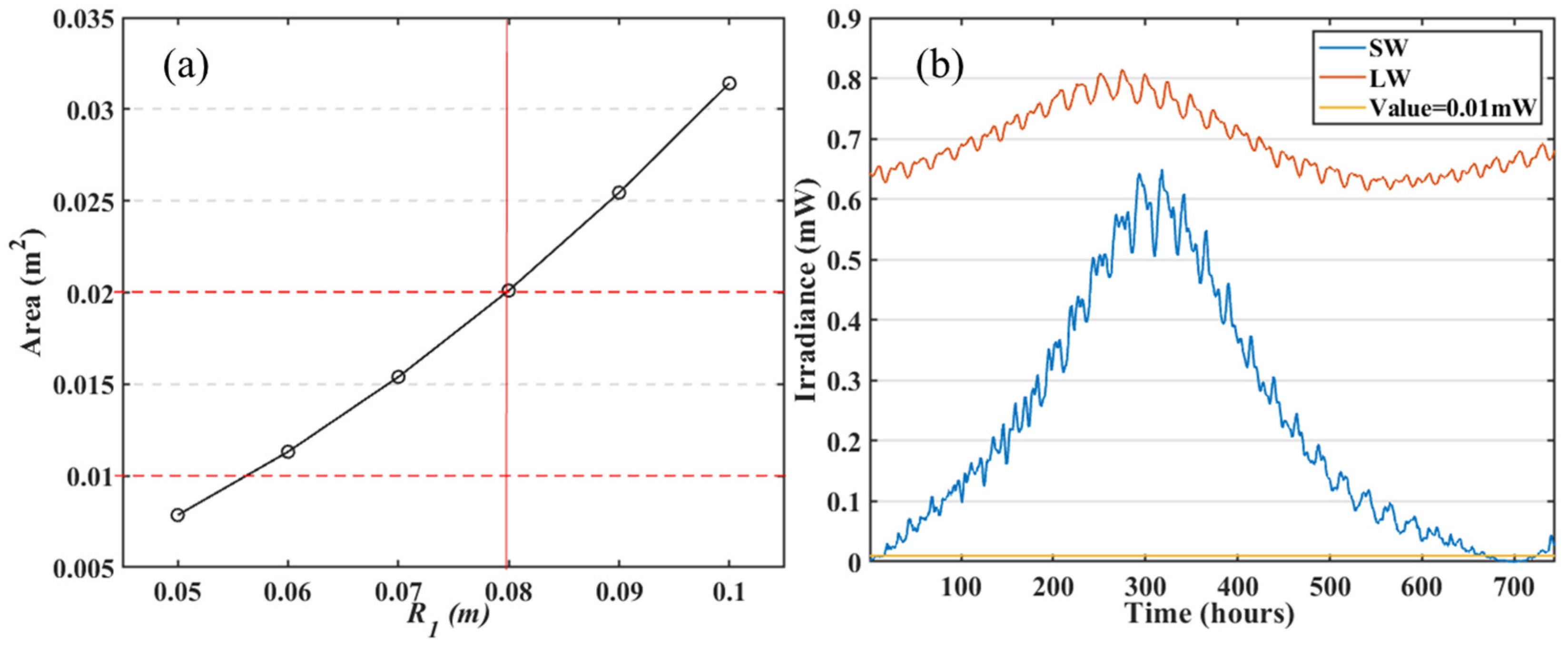
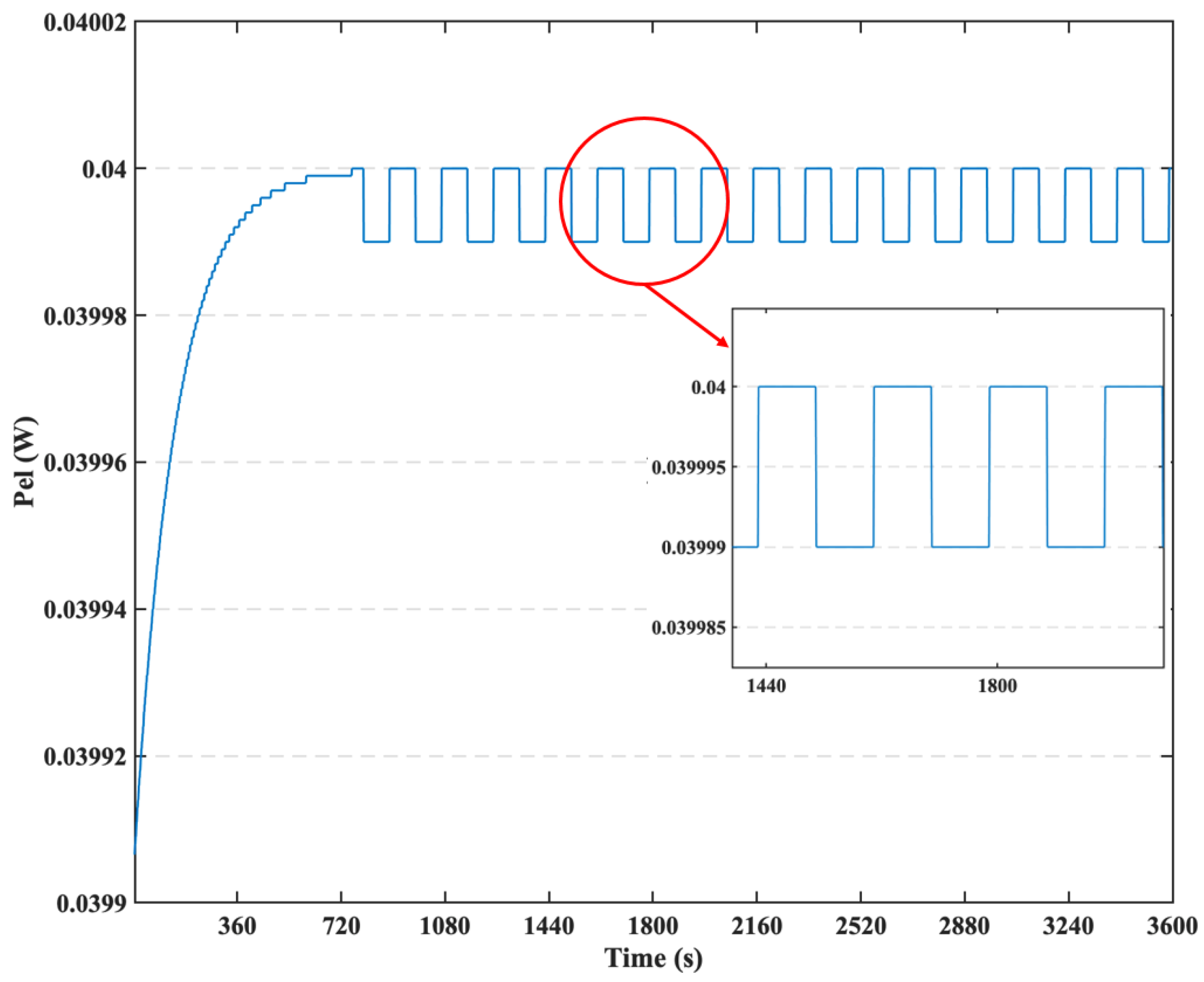
| Band | Range | Ratio (%) | Min | Max | N | |
|---|---|---|---|---|---|---|
| SW (0.2–5 μm) | 0~0.5 | 1.69 | 0.41 | 12.74 | 6720 | |
| 0.5~1.0 | 54.35 | 86.88 | ||||
| 1.0~1.5 | 32.53 | |||||
| 1.5~2.0 | 6.34 | |||||
| >2.0 | 5.09 | |||||
| LW (5–200 μm) | 0.85~0.90 | 7.77 | 0.83 | 1.07 | 9072 | |
| 0.90~0.95 | 16.47 | 88.56% | ||||
| 0.95~1.00 | 18.55 | |||||
| 1.00~1.05 | 53.54 | |||||
| 1.05~1.10 | 3.6 | |||||
| Band | Range (mW∙m−2) | Ratio (%) |
|---|---|---|
| SW (0.2–5 μm) | 0.0~1.0 | 40.35 |
| 1.0~2.0 | 20.19 | |
| 2.0~3.0 | 17.22 | |
| 3.0~4.0 | 17.66 | |
| 4.0~5.2 | 4.58 | |
| LW (5–100 μm) | 0.80~0.90 | 42.48 |
| 0.90~1.00 | 33.52 | |
| 1.00~1.10 | 24.00 |
| CERES OLR | CERES OSR | |
|---|---|---|
| Moon-Based OLR | 1 | −1 |
| Moon-Based OSR | −1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Dewitte, S.; Bi, S. The Uncertainty Analysis of the Entrance Pupil Irradiance for a Moon-Based Earth Radiation Observation Instrument. Remote Sens. 2023, 15, 4132. https://doi.org/10.3390/rs15174132
Zhang Y, Dewitte S, Bi S. The Uncertainty Analysis of the Entrance Pupil Irradiance for a Moon-Based Earth Radiation Observation Instrument. Remote Sensing. 2023; 15(17):4132. https://doi.org/10.3390/rs15174132
Chicago/Turabian StyleZhang, Yuan, Steven Dewitte, and Shengshan Bi. 2023. "The Uncertainty Analysis of the Entrance Pupil Irradiance for a Moon-Based Earth Radiation Observation Instrument" Remote Sensing 15, no. 17: 4132. https://doi.org/10.3390/rs15174132
APA StyleZhang, Y., Dewitte, S., & Bi, S. (2023). The Uncertainty Analysis of the Entrance Pupil Irradiance for a Moon-Based Earth Radiation Observation Instrument. Remote Sensing, 15(17), 4132. https://doi.org/10.3390/rs15174132






