Spatio-Temporal Variation of Critical Relative Humidity Based on Multiple Datasets
Abstract
:1. Introduction
2. Materials and Methods
2.1. CloudSat and CALIPSO Satellite Data
2.2. CALIPSO–GOCCP
2.3. Reanalysis Datasets
2.4. CMIP6 Models
2.5. Methods
3. Results
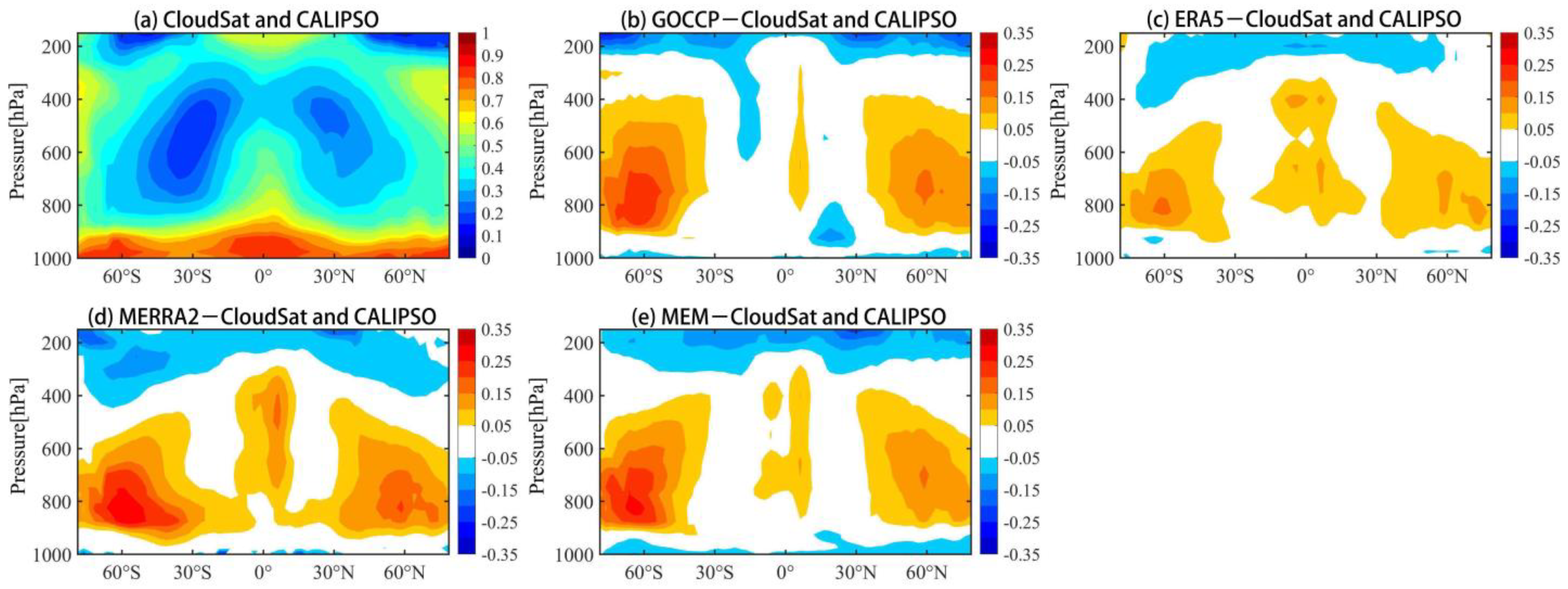
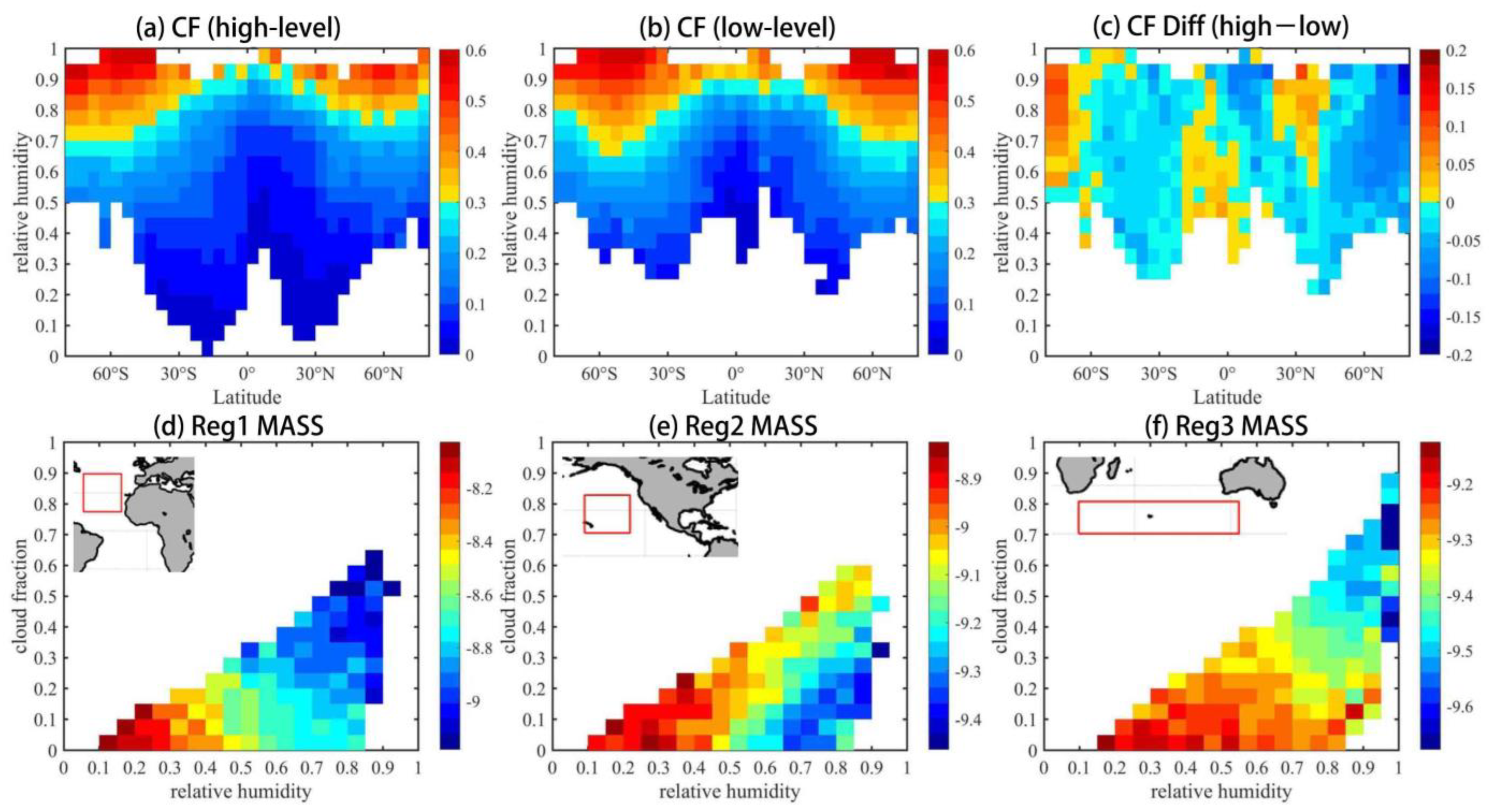
3.1. Spatial Distribution Characteristics of RHc Derived from Different Datasets
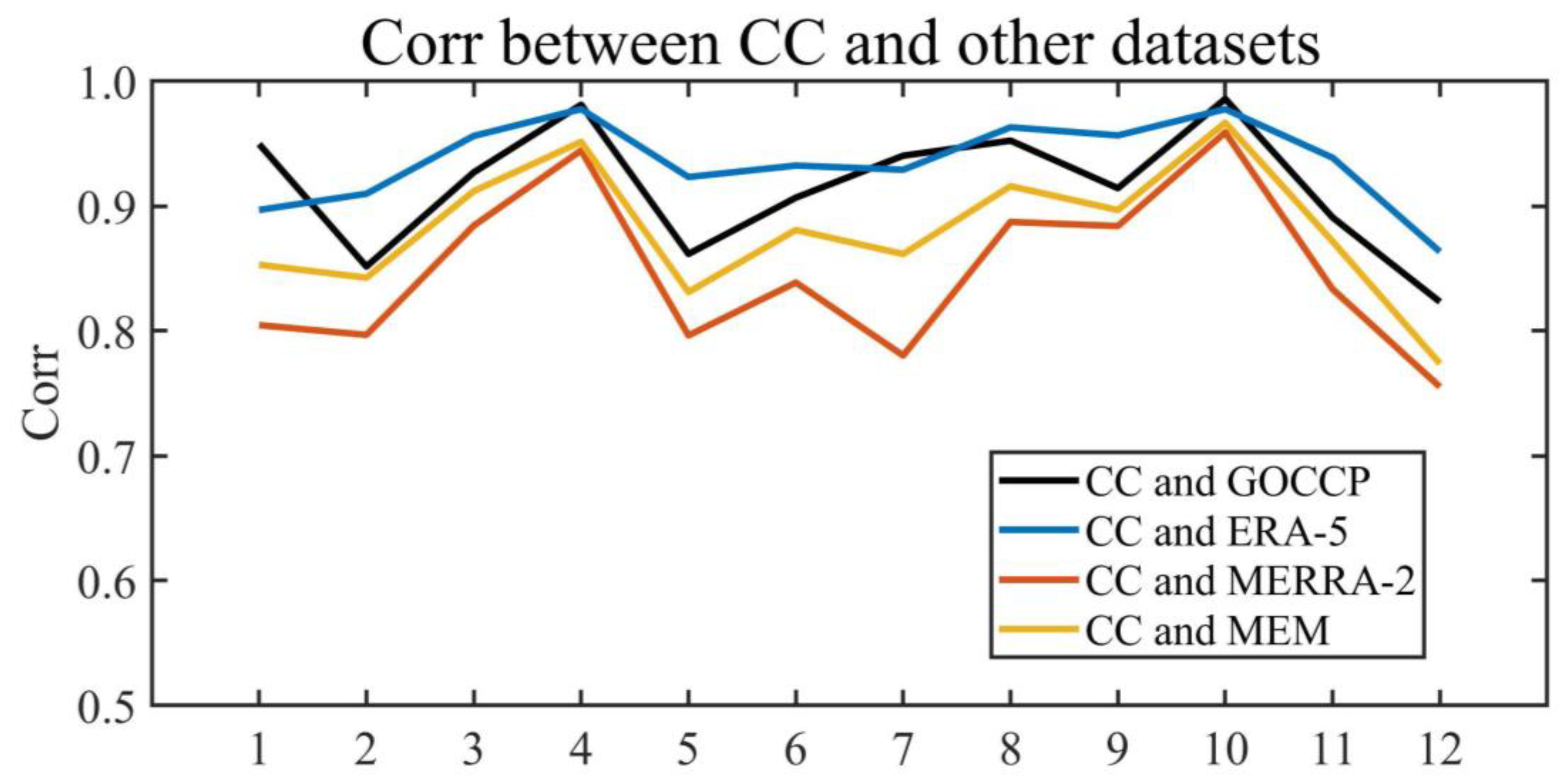
3.2. Temporal Distribution Characteristics of RHc Derived from Different Datasets
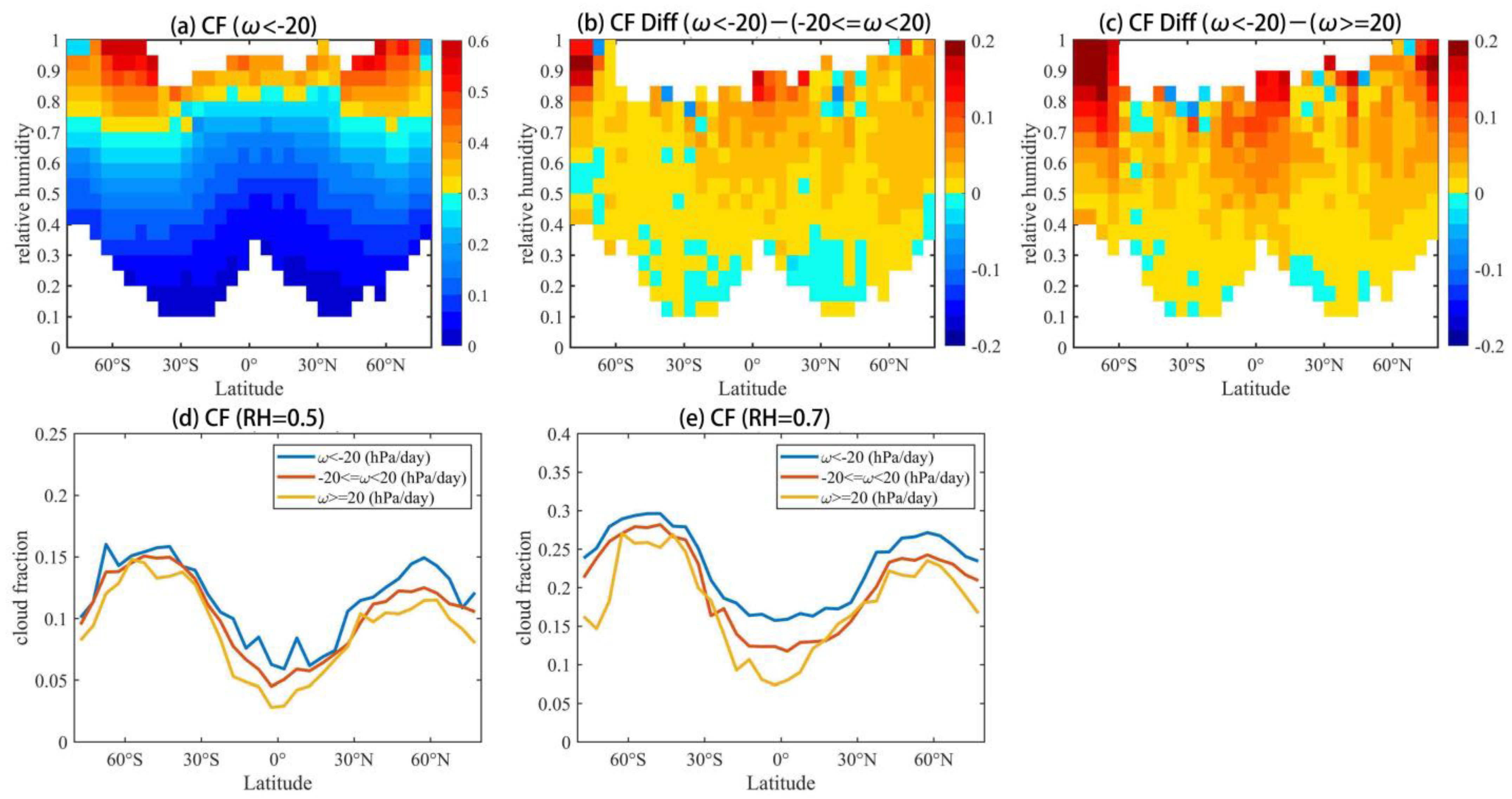
3.3. Effect of Meteorological Conditions and Aerosols on RHc
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ramanathan, V.; Cess, R.D.; Harrison, E.F.; Minnis, P.; Barkstrom, B.R.; Ahmad, E.; Hartmann, D. Cloud-Radiative Forcing and Climate—Results from the Earth Radiation Budget Experiment. Science 1989, 243, 57–63. [Google Scholar] [CrossRef]
- Stephens, G.L. Cloud feedbacks in the climate system: A critical review. J. Clim. 2005, 18, 237–273. [Google Scholar] [CrossRef]
- Tompkins, A.M. A prognostic parameterization for the subgrid-scale variability of water vapor and clouds in large-scale models and its use to diagnose cloud cover. J. Atmos. Sci. 2002, 59, 1917–1942. [Google Scholar] [CrossRef]
- Cheng, A.; Xu, K.-M. Improved Low-Cloud Simulation from the Community Atmosphere Model with an Advanced Third-Order Turbulence Closure. J. Clim. 2015, 28, 5737–5762. [Google Scholar] [CrossRef]
- Qin, Y.; Lin, Y.L.; Xu, S.M.; Ma, H.Y.; Xie, S.C. A Diagnostic PDF Cloud Scheme to Improve Subtropical Low Clouds in NCAR Community Atmosphere Model (CAM5). J. Adv. Model. Earth Syst. 2018, 10, 320–341. [Google Scholar] [CrossRef]
- Lin, Y.; Huang, X.; Liang, Y.; Qin, Y.; Xu, S.; Huang, W.; Xu, F.; Liu, L.; Wang, Y.; Peng, Y.; et al. Community Integrated Earth System Model (CIESM): Description and Evaluation. J. Adv. Model. Earth Syst. 2020, 12, e2019MS002036. [Google Scholar] [CrossRef]
- Andrews, T.; Gregory, J.M.; Webb, M.J.; Taylor, K.E. Forcing, feedbacks and climate sensitivity in CMIP5 coupled atmosphere-ocean climate models. Geophys. Res. Lett. 2012, 39, L09712. [Google Scholar] [CrossRef]
- Seinfeld, J.H.; Bretherton, C.; Carslaw, K.S.; Coe, H.; DeMott, P.J.; Dunlea, E.J.; Feingold, G.; Ghan, S.; Guenther, A.B.; Kahn, R.; et al. Improving our fundamental understanding of the role of aerosol-cloud interactions in the climate system. Proc. Natl. Acad. Sci. USA 2016, 113, 5781–5790. [Google Scholar] [CrossRef]
- Stevens, B.; Sherwood, S.C.; Bony, S.; Webb, M.J. Prospects for narrowing bounds on Earth’s equilibrium climate sensitivity. Earths Future 2016, 4, 512–522. [Google Scholar] [CrossRef]
- Naud, C.M.; Rangwala, I.; Xu, M.; Miller, J.R. A Satellite View of the Radiative Impact of Clouds on Surface Downward Fluxes in the Tibetan Plateau. J. Appl. Meteorol. Climatol. 2015, 54, 479–493. [Google Scholar] [CrossRef]
- Tompkins, A. The parametrization of cloud cover. ECMWF Moist Process. Lect. Note Ser. Tech. Memo 2005, 25, 1–23. [Google Scholar]
- Sundqvist, H.; Berge, E.; Kristjansson, J.E. Condensation and Cloud Parameterization Studies with a Mesoscale Numerical Weather Prediction Model. Mon. Weather Rev. 1989, 117, 1641–1657. [Google Scholar] [CrossRef]
- Quaas, J. Evaluating the “critical relative humidity” as a measure of subgrid-scale variability of humidity in general circulation model cloud cover parameterizations using satellite data. J. Geophys. Res. Atmos. 2012, 117, D09208. [Google Scholar] [CrossRef]
- Chen, G.X.; Wang, W.C.; Yang, S.X.; Wang, Y.X.; Zhang, F.; Wu, K. A Neural Network-Based Scale-Adaptive Cloud-Fraction Scheme for GCMs. J. Adv. Model. Earth Syst. 2023, 15, e2022MS003415. [Google Scholar] [CrossRef]
- Schmidt, G.A.; Ruedy, R.; Hansen, J.E.; Aleinov, I.; Bell, N.; Bauer, M.; Bauer, S.; Cairns, B.; Canuto, V.; Cheng, Y.; et al. Present-day atmospheric simulations using GISS ModelE: Comparison to in situ, satellite, and reanalysis data. J. Clim. 2006, 19, 153–192. [Google Scholar] [CrossRef]
- Scinocca, J.F.; McFarlane, N.A.; Lazare, M.; Li, J.; Plummer, D. Technical Note: The CCCma third generation AGCM and its extension into the middle atmosphere. Atmos. Chem. Phys. 2008, 8, 7055–7074. [Google Scholar] [CrossRef]
- Stevens, B.; Giorgetta, M.; Esch, M.; Mauritsen, T.; Crueger, T.; Rast, S.; Salzmann, M.; Schmidt, H.; Bader, J.; Block, K.; et al. Atmospheric component of the MPI-M Earth System Model: ECHAM6. J. Adv. Model. Earth Syst. 2013, 5, 146–172. [Google Scholar] [CrossRef]
- Wang, X.C.; Liu, Y.M.; Bao, Q.; Wu, G.X. Comparisons of GCM cloud cover parameterizations with cloud-resolving model explicit simulations. Sci. China-Earth Sci. 2015, 58, 604–614. [Google Scholar] [CrossRef]
- Wang, Y.X.; Yang, S.X.; Chen, G.X.; Bao, Q.; Li, J.D. Evaluating two diagnostic schemes of cloud-fraction parameterization using the CloudSat data. Atmos. Res. 2023, 282, 106510. [Google Scholar] [CrossRef]
- Wang, X.C.; Miao, H.; Liu, Y.M.; Bao, Q.; He, B.; Li, J.X.; Zhao, Y.X. The Use of Satellite Data-Based “Critical Relative Humidity” in Cloud Parameterization and Its Role in Modulating Cloud Feedback. J. Adv. Model. Earth Syst. 2022, 14, e2022MS003213. [Google Scholar] [CrossRef]
- Hazra, A.; Chaudhari, H.S.; Rao, S.A.; Goswami, B.N.; Dhakate, A.; Pokhrel, S.; Saha, S.K. Impact of revised cloud microphysical scheme in CFSv2 on the simulation of the Indian summer monsoon. Int. J. Climatol. 2015, 35, 4738–4755. [Google Scholar] [CrossRef]
- De, S.; Hazra, A.; Chaudhari, H.S. Does the modification in “critical relative humidity” of NCEP CFSv2 dictate Indian mean summer monsoon forecast? Evaluation through thermodynamical and dynamical aspects. Clim. Dyn. 2016, 46, 1197–1222. [Google Scholar] [CrossRef]
- Xu, K.M.; Krueger, S.K. Evaluation Of Cloudiness Parameterizations Using a Cumulus Ensemble Model. Mon. Weather Rev. 1991, 119, 342–367. [Google Scholar] [CrossRef]
- Miao, H.; Wang, X.C.; Liu, Y.M.; Wu, G.X. An evaluation of cloud vertical structure in three reanalyses against CloudSat/cloud-aerosol lidar and infrared pathfinder satellite observations. Atmos. Sci. Lett. 2019, 20, e906. [Google Scholar] [CrossRef]
- Vignesh, P.P.; Jiang, J.H.; Pangaluru, K.; Su, H.; Smay, T.; Brighton, N.; Velicogna, I. Assessment of CMIP6 Cloud Fraction and Comparison with Satellite Observations. Earth Space Sci. 2020, 7, e2019EA000975. [Google Scholar] [CrossRef]
- Li, J.D.; Sun, Z.A.; Liu, Y.M.; You, Q.L.; Chen, G.X.; Bao, Q. Top-of-Atmosphere Radiation Budget and Cloud Radiative Effects Over the Tibetan Plateau and Adjacent Monsoon Regions From CMIP6 Simulations. J. Geophys. Res. Atmos. 2021, 126, e2020JD034345. [Google Scholar] [CrossRef]
- Naud, C.M.; Del Genio, A.D.; Bauer, M.; Kovari, W. Cloud Vertical Distribution across Warm and Cold Fronts in CloudSat-CALIPSO Data and a General Circulation Model. J. Clim. 2010, 23, 3397–3415. [Google Scholar] [CrossRef]
- Van Weverberg, K.; Boutle, I.A.; Morcrette, C.J.; Newsom, R.K. Towards retrieving critical relative humidity from ground-based remote-sensing observations. Q. J. R. Meteorol. Soc. 2016, 142, 2867–2881. [Google Scholar] [CrossRef]
- Stephens, G.L.; Vane, D.G.; Tanelli, S.; Im, E.; Durden, S.; Rokey, M.; Reinke, D.; Partain, P.; Mace, G.G.; Austin, R.; et al. CloudSat mission: Performance and early science after the first year of operation. J. Geophys. Res. Atmos. 2008, 113, D00A18. [Google Scholar] [CrossRef]
- Winker, D.M.; Vaughan, M.A.; Omar, A.; Hu, Y.X.; Powell, K.A.; Liu, Z.Y.; Hunt, W.H.; Young, S.A. Overview of the CALIPSO Mission and CALIOP Data Processing Algorithms. J. Atmos. Ocean. Technol. 2009, 26, 2310–2323. [Google Scholar] [CrossRef]
- Mace, G.G.; Zhang, Q.Q.; Vaughan, M.; Marchand, R.; Stephens, G.; Trepte, C.; Winker, D. A description of hydrometeor layer occurrence statistics derived from the first year of merged Cloudsat and CALIPSO data. J. Geophys. Res. Atmos. 2009, 114, D00A26. [Google Scholar] [CrossRef]
- Mace, G.G.; Zhang, Q.Q. The CloudSat radar-lidar geometrical profile product (RL-GeoProf): Updates, improvements, and selected results. J. Geophys. Res. Atmos. 2014, 119, 9441–9462. [Google Scholar] [CrossRef]
- Barker, H.W. Overlap of fractional cloud for radiation calculations in GCMs: A global analysis using CloudSat and CALIPSO data. J. Geophys. Res. Atmos. 2008, 113, D00A01. [Google Scholar] [CrossRef]
- Di Giuseppe, F.; Tompkins, A.M. Generalizing Cloud Overlap Treatment to Include the Effect of Wind Shear. J. Atmos. Sci. 2015, 72, 2865–2876. [Google Scholar] [CrossRef]
- Cesana, G.; Chepfer, H. How well do climate models simulate cloud vertical structure? A comparison between CALIPSO-GOCCP satellite observations and CMIP5 models. Geophys. Res. Lett. 2012, 39, L20803. [Google Scholar] [CrossRef]
- Cesana, G.; Waliser, D.E.; Jiang, X.; Li, J.L.F. Multimodel evaluation of cloud phase transition using satellite and reanalysis data. J. Geophys. Res. Atmos. 2015, 120, 7871–7892. [Google Scholar] [CrossRef]
- Chepfer, H.; Bony, S.; Winker, D.; Chiriaco, M.; Dufresne, J.L.; Seze, G. Use of CALIPSO lidar observations to evaluate the cloudiness simulated by a climate model. Geophys. Res. Lett. 2008, 35, L15704. [Google Scholar] [CrossRef]
- Chepfer, H.; Bony, S.; Winker, D.; Cesana, G.; Dufresne, J.L.; Minnis, P.; Stubenrauch, C.J.; Zeng, S. The GCM-Oriented CALIPSO Cloud Product (CALIPSO-GOCCP). J. Geophys. Res. Atmos. 2010, 115, D00H16. [Google Scholar] [CrossRef]
- Lacour, A.; Chepfer, H.; Shupe, M.D.; Miller, N.B.; Noel, V.; Kay, J.; Turner, D.D.; Guzman, R. Greenland Clouds Observed in CALIPSO-GOCCP: Comparison with Ground-Based Summit Observations. J. Clim. 2017, 30, 6065–6083. [Google Scholar] [CrossRef]
- Cesana, G.; Chepfer, H.; Winker, D.; Getzewich, B.; Cai, X.; Jourdan, O.; Mioche, G.; Okamoto, H.; Hagihara, Y.; Noel, V.; et al. Using in situ airborne measurements to evaluate three cloud phase products derived from CALIPSO. J. Geophys. Res. Atmos. 2016, 121, 5788–5808. [Google Scholar] [CrossRef]
- Wang, F.; Xin, X.G.; Wang, Z.Z.; Cheng, Y.J.; Zhang, J.; Yang, S. Evaluation of cloud vertical structure simulated by recent BCC_AGCM versions through comparison with CALIPSO-GOCCP data. Adv. Atmos. Sci. 2014, 31, 721–733. [Google Scholar] [CrossRef]
- Yin, J.F.; Wang, D.H.; Xu, H.B.; Zhai, G.Q. An investigation into the three-dimensional cloud structure over East Asia from the CALIPSO-GOCCP Data. Sci. China-Earth Sci. 2015, 58, 2236–2248. [Google Scholar] [CrossRef]
- Boudala, F.S.; Milbrandt, J.A.; Isaac, G.A. Evaluation of CanESM Cloudiness, Cloud Type and Cloud Radiative Forcing Climatologies Using the CALIPSO-GOCCP and CERES Datasets. Remote Sens. 2022, 14, 3668. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horanyi, A.; Munoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suarez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef] [PubMed]
- Rotstayn, L.D. Climate sensitivity of the CSIRO GCM: Effect of cloud modeling assumptions. J. Clim. 1999, 12, 334–356. [Google Scholar] [CrossRef]
- Marchand, R.; Mace, G.G.; Ackerman, T.; Stephens, G. Hydrometeor detection using Cloudsat—An earth-orbiting 94-GHz cloud radar. J. Atmos. Ocean. Technol. 2008, 25, 519–533. [Google Scholar] [CrossRef]
- Ham, S.-H.; Kato, S.; Rose, F.G.; Winker, D.; L’Ecuyer, T.; Mace, G.G.; Painemal, D.; Sun-Mack, S.; Chen, Y.; Miller, W.F. Cloud occurrences and cloud radiative effects (CREs) from CERES-CALIPSO-CloudSat-MODIS (CCCM) and CloudSat radar-lidar (RL) products. J. Geophys. Res. Atmos. 2017, 122, 8852–8884. [Google Scholar] [CrossRef]
- Li, J.D.; Mao, J.Y.; Wang, F. Comparative study of five current reanalyses in characterizing total cloud fraction and top-of-the-atmosphere cloud radiative effects over the Asian monsoon region. Int. J. Climatol. 2017, 37, 5047–5067. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, J.; Zhang, L.; Deng, C.; Li, Y.; Jian, B.; Huang, J. Diurnal cycles of cloud cover and its vertical distribution over the Tibetan Plateau revealed by satellite observations, reanalysis datasets, and CMIP6 outputs. Atmos. Chem. Phys. 2023, 23, 743–769. [Google Scholar] [CrossRef]
- Naud, C.M.; Booth, J.F.; Del Genio, A.D. Evaluation of ERA-Interim and MERRA Cloudiness in the Southern Ocean. J. Clim. 2014, 27, 2109–2124. [Google Scholar] [CrossRef]
- Tan, Z.H.; Ma, S.; Wang, X.; Liu, Y.D.; Ai, W.H.; Yan, W. Estimating Layered Cloud Cover from Geostationary Satellite Radiometric Measurements: A Novel Method and Its Application. Remote Sens. 2022, 14, 5693. [Google Scholar] [CrossRef]
- Wu, H.P.; Xu, X.F.; Luo, T.Y.; Yang, Y.D.; Xiong, Z.X.; Wang, Y. Variation and comparison of cloud cover in MODIS and four reanalysis datasets of ERA-interim, ERA5, MERRA-2 and NCEP. Atmos. Res. 2023, 281, 106477. [Google Scholar] [CrossRef]
- Molod, A. Constraints on the Profiles of Total Water PDF in AGCMs from AIRS and a High-Resolution Model. J. Clim. 2012, 25, 8341–8352. [Google Scholar] [CrossRef]
- Yeo, H.; Kim, M.H.; Son, S.W.; Jeong, J.H.; Yoon, J.H.; Kim, B.M.; Kim, S.W. Arctic cloud properties and associated radiative effects in the three newer reanalysis datasets (ERA5, MERRA-2, JRA-55): Discrepancies and possible causes. Atmos. Res. 2022, 270, 106080. [Google Scholar] [CrossRef]
- Tiedtke, M. Representation of Clouds in Large-Scale Models. Mon. Weather Rev. 1993, 121, 3040–3061. [Google Scholar] [CrossRef]
- Binder, H.; Boettcher, M.; Joos, H.; Sprenger, M.; Wernli, H. Vertical cloud structure of warm conveyor belts–a comparison and evaluation of ERA5 reanalysis, CloudSat and CALIPSO data. Weather Clim. Dyn. 2020, 1, 577–595. [Google Scholar] [CrossRef]
- Chen, G.; Wang, W.-C.; Bao, Q.; Li, J. Evaluation of Simulated Cloud Diurnal Variation in CMIP6 Climate Models. J. Geophys. Res. Atmos. 2022, 127, e2021JD036422. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, J.M.; Zhang, W.Y.; Deng, C.; Li, Y.R. Cloud Response Is Significantly Biased by CMIP6 Over the Tibetan Plateau. Geophys. Res. Lett. 2022, 49, e2022GL100903. [Google Scholar] [CrossRef]
- Mahlobo, D.D.; Ndarana, T.; Grab, S.; Engelbrecht, F. Integrated climatology and trends in the subtropical Hadley cell, sunshine duration and cloud cover over South Africa. Int. J. Climatol. 2019, 39, 1805–1821. [Google Scholar] [CrossRef]
- Carrillo, J.; Guerra, J.C.; Cuevas, E.; Barrancos, J. Characterization of the Marine Boundary Layer and the Trade-Wind Inversion over the Sub-tropical North Atlantic. Bound. Layer Meteorol. 2016, 158, 311–330. [Google Scholar] [CrossRef]
- Sherwood, S.C.; Roca, R.; Weckwerth, T.M.; Andronova, N.G. TROPOSPHERIC WATER VAPOR, CONVECTION, AND CLIMATE. Rev. Geophys. 2010, 48, RG2001. [Google Scholar] [CrossRef]
- Zhang, D.M.; Wang, Z.; Liu, D. A global view of midlevel liquid-layer topped stratiform cloud distribution and phase partition from CALIPSO and CloudSat measurements. J. Geophys. Res. Atmos. 2010, 115, D00H13. [Google Scholar] [CrossRef]
- Cesana, G.; Chepfer, H. Evaluation of the cloud thermodynamic phase in a climate model using CALIPSO-GOCCP. J. Geophys. Res. Atmos. 2013, 118, 7922–7937. [Google Scholar] [CrossRef]
- Stengel, M.; Schlundt, C.; Stapelberg, S.; Sus, O.; Eliasson, S.; Willen, U.; Meirink, J.F. Comparing ERA-Interim clouds with satellite observations using a simplified satellite simulator. Atmos. Chem. Phys. 2018, 18, 17601–17614. [Google Scholar] [CrossRef]
- Wright, J.S.; Sun, X.Y.; Konopka, P.; Kruger, K.; Legras, B.; Molod, A.M.; Tegtmeier, S.; Zhang, G.J.; Zhao, X. Differences in tropical high clouds among reanalyses: Origins and radiative impacts. Atmos. Chem. Phys. 2020, 20, 8989–9030. [Google Scholar] [CrossRef]
- Huang, J.; Guan, X.; Ji, F. Enhanced cold-season warming in semi-arid regions. Atmos. Chem. Phys. 2012, 12, 5391–5398. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Noel, V.; Chepfer, H. A global view of horizontally oriented crystals in ice clouds from Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observation (CALIPSO). J. Geophys. Res. Atmos. 2010, 115, D00H23. [Google Scholar] [CrossRef]
- Twomey, S. The nuclei of natural cloud formation part II: The supersaturation in natural clouds and the variation of cloud droplet concentration. Geofis. Pura E Appl. 1959, 43, 243–249. [Google Scholar] [CrossRef]
- Shupe, M.D.; Matrosov, S.Y.; Uttal, T. Arctic mixed-phase cloud properties derived from surface-based sensors at SHEBA. J. Atmos. Sci. 2006, 63, 697–711. [Google Scholar] [CrossRef]
- Reutter, P.; Su, H.; Trentmann, J.; Simmel, M.; Rose, D.; Gunthe, S.S.; Wernli, H.; Andreae, M.O.; Poschl, U. Aerosol- and updraft-limited regimes of cloud droplet formation: Influence of particle number, size and hygroscopicity on the activation of cloud condensation nuclei (CCN). Atmos. Chem. Phys. 2009, 9, 7067–7080. [Google Scholar] [CrossRef]
- Liu, Y.Z.; Huang, J.P.; Wang, T.H.; Li, J.M.; Yan, H.R.; He, Y.L. Aerosol-cloud interactions over the Tibetan Plateau: An overview. Earth-Sci. Rev. 2022, 234, 104216. [Google Scholar] [CrossRef]
- Walcek, C.J. Cloud Cover and Its Relationship to Relative-Humidity during a Springtime Midlatitude Cyclone. Mon. Weather Rev. 1994, 122, 1021–1035. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, C.F.; Dong, X.B.; Fan, G.C.; Zhou, Y.Q.; Wang, Y.; Zhao, L.J.; Lv, F.; Yan, F. Toward understanding the process-level impacts of aerosols on microphysical properties of shallow cumulus cloud using aircraft observations. Atmos. Res. 2019, 221, 27–33. [Google Scholar] [CrossRef]
- Lu, C.S.; Liu, Y.G.; Niu, S.J.; Vogelmann, A.M. Observed impacts of vertical velocity on cloud microphysics and implications for aerosol indirect effects. Geophys. Res. Lett. 2012, 39, L21808. [Google Scholar] [CrossRef]
- Bower, K.N.; Moss, S.J.; Johnson, D.W.; Choularton, T.W.; Latham, J.; Brown, P.R.A.; Blyth, A.M.; Cardwell, J. A parametrization of the ice water content observed in frontal and convective clouds. Q. J. R. Meteorol. Soc. 1996, 122, 1815–1844. [Google Scholar] [CrossRef]
- Li, J.; Lv, Q.; Zhang, M.; Wang, T.; Kawamoto, K.; Chen, S.; Zhang, B. Effects of atmospheric dynamics and aerosols on the fraction of supercooled water clouds. Atmos. Chem. Phys. 2017, 17, 1847–1863. [Google Scholar] [CrossRef]
- Weber, T.; Quaas, J.; Raisanen, P. Evaluation of the statistical cloud scheme in the ECHAM5 model using satellite data. Q. J. R. Meteorol. Soc. 2011, 137, 2079–2091. [Google Scholar] [CrossRef]
- Rotstayn, L.D.; Liu, Y.G. A smaller global estimate of the second indirect aerosol effect. Geophys. Res. Lett. 2005, 32, L05708. [Google Scholar] [CrossRef]
- Lohmann, U.; Stier, P.; Hoose, C.; Ferrachat, S.; Kloster, S.; Roeckner, E.; Zhang, J. Cloud microphysics and aerosol indirect effects in the global climate model ECHAM5-HAM. Atmos. Chem. Phys. 2007, 7, 3425–3446. [Google Scholar] [CrossRef]
- Morrison, H.; Gettelman, A. A new two-moment bulk stratiform cloud microphysics scheme in the community atmosphere model, version 3 (CAM3). Part I: Description and numerical tests. J. Clim. 2008, 21, 3642–3659. [Google Scholar] [CrossRef]
- Li, J.M.; Jian, B.D.; Huang, J.P.; Hu, Y.X.; Zhao, C.F.; Kawamoto, K.; Liao, S.J.; Wu, M. Long-term variation of cloud droplet number concentrations from space-based Lidar. Remote Sens. Environ. 2018, 213, 144–161. [Google Scholar] [CrossRef]
- Jian, B.; Li, J.; Wang, G.; Zhao, Y.; Li, Y.; Wang, J.; Zhang, M.; Huang, J. Evaluation of the CMIP6 marine subtropical stratocumulus cloud albedo and its controlling factors. Atmos. Chem. Phys. 2021, 21, 9809–9828. [Google Scholar] [CrossRef]
- Huang, J.P.; Lin, B.; Minnis, P.; Wang, T.H.; Wang, X.; Hu, Y.X.; Yi, Y.H.; Ayers, J.K. Satellite-based assessment of possible dust aerosols semi-direct effect on cloud water path over East Asia. Geophys. Res. Lett. 2006, 33, L19802. [Google Scholar] [CrossRef]
- Koch, D.; Del Genio, A.D. Black carbon semi-direct effects on cloud cover: Review and synthesis. Atmos. Chem. Phys. 2010, 10, 7685–7696. [Google Scholar] [CrossRef]
- Sakaeda, N.; Wood, R.; Rasch, P.J. Direct and semidirect aerosol effects of southern African biomass burning aerosol. J. Geophys. Res. Atmos. 2011, 116, D12205. [Google Scholar] [CrossRef]
- Menon, S.; Hansen, J.; Nazarenko, L.; Luo, Y.F. Climate effects of black carbon aerosols in China and India. Science 2002, 297, 2250–2253. [Google Scholar] [CrossRef] [PubMed]
- Johnson, B.T.; Shine, K.P.; Forster, P.M. The semi-direct aerosol effect: Impact of absorbing aerosols on marine stratocumulus. Q. J. R. Meteorol. Soc. 2004, 130, 1407–1422. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, R.; Yu, H.B.; Dickinson, R.E.; Juarez, R.N.; Chin, M.; Wang, H. A regional climate model study of how biomass burning aerosol impacts land-atmosphere interactions over the Amazon. J. Geophys. Res. Atmos. 2008, 113, D14S15. [Google Scholar] [CrossRef]
- Fan, J.W.; Rosenfeld, D.; Yang, Y.; Zhao, C.; Leung, L.R.; Li, Z.Q. Substantial contribution of anthropogenic air pollution to catastrophic floods in Southwest China. Geophys. Res. Lett. 2015, 42, 6066–6075. [Google Scholar] [CrossRef]
- Twomey, S. The Influence of Pollution on the Shortwave Albedo of Clouds. J. Atmos. Sci. 1977, 34, 1149–1152. [Google Scholar] [CrossRef]
- Lammel, G.; Novakov, T. Water Nucleation Properties of Carbon-Black and Diesel Soot Particles. Atmos. Environ. 1995, 29, 813–823. [Google Scholar] [CrossRef]
- Odowd, C.D.; Smith, M.H.; Consterdine, I.E.; Lowe, J.A. Marine aerosol, sea-salt, and the marine sulphur cycle: A short review. Atmos. Environ. 1997, 31, 73–80. [Google Scholar] [CrossRef]
- Sun, J.M.; Ariya, P.A. Atmospheric organic and bio-aerosols as cloud condensation nuclei (CCN): A review. Atmos. Environ. 2006, 40, 795–820. [Google Scholar] [CrossRef]
- Ruehl, C.R.; Davies, J.F.; Wilson, K.R. An interfacial mechanism for cloud droplet formation on organic aerosols. Science 2016, 351, 1447–1450. [Google Scholar] [CrossRef] [PubMed]
- Koren, I.; Kaufman, Y.J.; Remer, L.A.; Martins, J.V. Measurement of the effect of Amazon smoke on inhibition of cloud formation. Science 2004, 303, 1342–1345. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Koren, I.; Remer, L.A.; Rosenfeld, D.; Rudich, Y. The effect of smoke, dust, and pollution aerosol on shallow cloud development over the Atlantic Ocean. Proc. Natl. Acad. Sci. USA 2005, 102, 11207–11212. [Google Scholar] [CrossRef]
- Koren, I.; Kaufman, Y.J.; Rosenfeld, D.; Remer, L.A.; Rudich, Y. Aerosol invigoration and restructuring of Atlantic convective clouds. Geophys. Res. Lett. 2005, 32, L14828. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Koren, I. Smoke and pollution aerosol effect on cloud cover. Science 2006, 313, 655–658. [Google Scholar] [CrossRef] [PubMed]
- Myhre, G.; Stordal, F.; Johnsrud, M.; Kaufman, Y.J.; Rosenfeld, D.; Storelvmo, T.; Kristjansson, J.E.; Berntsen, T.K.; Myhre, A.; Isaksen, I.S.A. Aerosol-cloud interaction inferred from MODIS satellite data and global aerosol models. Atmos. Chem. Phys. 2007, 7, 3081–3101. [Google Scholar] [CrossRef]
- Yuan, T.; Remer, L.A.; Yu, H. Microphysical, macrophysical and radiative signatures of volcanic aerosols in trade wind cumulus observed by the A-Train. Atmos. Chem. Phys. 2011, 11, 7119–7132. [Google Scholar] [CrossRef]
- Fan, J.W.; Zhang, R.Y.; Li, G.H.; Tao, W.K. Effects of aerosols and relative humidity on cumulus clouds. J. Geophys. Res. Atmos. 2007, 112, D14204. [Google Scholar] [CrossRef]
- Zhao, C.; Yang, Y.; Chi, Y.; Sun, Y.; Zhao, X.; Letu, H.; Xia, Y. Recent progress in cloud physics and associated radiative effects in China from 2016 to 2022. Atmos. Res. 2023, 293, 106899. [Google Scholar] [CrossRef]
- Fan, J.W.; Wang, Y.; Rosenfeld, D.; Liu, X.H. Review of Aerosol-Cloud Interactions: Mechanisms, Significance, and Challenges. J. Atmos. Sci. 2016, 73, 4221–4252. [Google Scholar] [CrossRef]
- Dusek, U.; Frank, G.P.; Hildebrandt, L.; Curtius, J.; Schneider, J.; Walter, S.; Chand, D.; Drewnick, F.; Hings, S.; Jung, D.; et al. Size matters more than chemistry for cloud-nucleating ability of aerosol particles. Science 2006, 312, 1375–1378. [Google Scholar] [CrossRef]
- Almeida, G.P.; Brito, J.; Morales, C.A.; Andrade, M.F.; Artaxo, P. Measured and modelled cloud condensation nuclei (CCN) concentration in Sao Paulo, Brazil: The importance of aerosol size-resolved chemical composition on CCN concentration prediction. Atmos. Chem. Phys. 2014, 14, 7559–7572. [Google Scholar] [CrossRef]
- Liu, J.J.; Li, Z.Q. Aerosol properties and their influences on low warm clouds during the Two-Column Aerosol Project. Atmos. Chem. Phys. 2019, 19, 9515–9529. [Google Scholar] [CrossRef]
- Zheng, X.J.; Xi, B.K.; Dong, X.Q.; Logan, T.; Wang, Y.; Wu, P. Investigation of aerosol-cloud interactions under different absorptive aerosol regimes using Atmospheric Radiation Measurement (ARM) southern Great Plains (SGP) ground-based measurements. Atmos. Chem. Phys. 2020, 20, 3483–3501. [Google Scholar] [CrossRef]
- Zhao, C.F.; Wang, Y.; Letu, H. New Progress and Challenges in Cloud-Aerosol-Radiation-Precipitation Interactions: Preface for a Special Issue. Adv. Atmos. Sci. 2022, 39, 1983–1985. [Google Scholar] [CrossRef]
- Koren, I.; Martins, J.V.; Remer, L.A.; Afargan, H. Smoke invigoration versus inhibition of clouds over the Amazon. Science 2008, 321, 946–949. [Google Scholar] [CrossRef]
- Guo, J.P.; Su, T.N.; Li, Z.Q.; Miao, Y.C.; Li, J.; Liu, H.; Xu, H.; Cribb, M.; Zhai, P.M. Declining frequency of summertime local-scale precipitation over eastern China from 1970 to 2010 and its potential link to aerosols. Geophys. Res. Lett. 2017, 44, 5700–5708. [Google Scholar] [CrossRef]
- Kahn, B.H.; Teixeira, J. A Global Climatology of Temperature and Water Vapor Variance Scaling from the Atmospheric Infrared Sounder. J. Clim. 2009, 22, 5558–5576. [Google Scholar] [CrossRef]
- Long, C.S.; Fujiwara, M.; Davis, S.; Mitchell, D.M.; Wright, C.J. Climatology and interannual variability of dynamic variables in multiple reanalyses evaluated by the SPARC Reanalysis Intercomparison Project (S-RIP). Atmos. Chem. Phys. 2017, 17, 14593–14629. [Google Scholar] [CrossRef]
- Hersbach, H. Global reanalysis: Goodbye ERA-Interim, hello ERA5. ECMWF Newsl. 2019, 159, 17. [Google Scholar]
- Qian, Y.; Long, C.N.; Wang, H.; Comstock, J.M.; McFarlane, S.A.; Xie, S. Evaluation of cloud fraction and its radiative effect simulated by IPCC AR4 global models against ARM surface observations. Atmos. Chem. Phys. 2012, 12, 1785–1810. [Google Scholar] [CrossRef]
- Lu, J.; Vecchi, G.A.; Reichler, T. Expansion of the Hadley cell under global warming. Geophys. Res. Lett. 2007, 34, L06805. [Google Scholar] [CrossRef]
- Yin, J.H. A consistent poleward shift of the storm tracks in simulations of 21st century climate. Geophys. Res. Lett. 2005, 32, L18701. [Google Scholar] [CrossRef]
- Vecchi, G.A.; Soden, B.J. Global warming and the weakening of the tropical circulation. Bull. Am. Meteorol. Soc. 2007, 88, 1529–1530. [Google Scholar]
- Lei, Y.; Zhang, Q.; He, K.B.; Streets, D.G. Primary anthropogenic aerosol emission trends for China, 1990–2005. Atmos. Chem. Phys. 2011, 11, 931–954. [Google Scholar] [CrossRef]
- Klimont, Z.; Smith, S.J.; Cofala, J. The last decade of global anthropogenic sulfur dioxide: 2000–2011 emissions. Environ. Res. Lett. 2013, 8, 014003. [Google Scholar] [CrossRef]
- Krotkov, N.A.; McLinden, C.A.; Li, C.; Lamsal, L.N.; Celarier, E.A.; Marchenko, S.V.; Swartz, W.H.; Bucsela, E.J.; Joiner, J.; Duncan, B.N.; et al. Aura OMI observations of regional SO2 and NO2 pollution changes from 2005 to 2015. Atmos. Chem. Phys. 2016, 16, 4605–4629. [Google Scholar] [CrossRef]
- Li, J. Pollution Trends in China from 2000 to 2017: A Multi-Sensor View from Space. Remote Sens. 2020, 12, 208. [Google Scholar] [CrossRef]
- Paasonen, P.; Asmi, A.; Petaja, T.; Kajos, M.K.; Aijala, M.; Junninen, H.; Holst, T.; Abbatt, J.P.D.; Arneth, A.; Birmili, W.; et al. Warming-induced increase in aerosol number concentration likely to moderate climate change. Nat. Geosci. 2013, 6, 438–442. [Google Scholar] [CrossRef]
- Touma, D.; Stevenson, S.; Lehner, F.; Coats, S. Human-driven greenhouse gas and aerosol emissions cause distinct regional impacts on extreme fire weather. Nat. Commun. 2021, 12, 212. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Carlson, B.E.; Yung, Y.L.; Lv, D.R.; Hansen, J.; Penner, J.E.; Liao, H.; Ramaswamy, V.; Kahn, R.A.; Zhang, P.; et al. Scattering and absorbing aerosols in the climate system. Nat. Rev. Earth Environ. 2022, 3, 363–379. [Google Scholar] [CrossRef]

| Data | Horizontal Resolution (Latitude × Longitude) | Variables |
|---|---|---|
| CloudSat and CALIPSO | orbital profiles | CF |
| GOCCP | 2° × 2° | CF |
| MERRA-2 | 0.5° × 0.625° | CF; RH; Aerosol Mixing Ratios |
| ERA-5 | 0.25° × 0.25° | CF; RH; W |
| The CMIP-6 model names and their horizontal resolutions | ||
| Source ID | Horizontal Resolution (Latitude × Longitude) | Variables |
| BCC-CSM2-MR | 1.12° × 1.125° | CF |
| GFDL-CM4 | 1° × 1.25° | CF |
| IPSL-CM6A-LR | 1.258° × 2.5° | CF |
| MRI-ESM2-0 | 1.115° × 1.125° | CF |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Li, J.; Xu, S.; Zhao, Y.; Jian, B. Spatio-Temporal Variation of Critical Relative Humidity Based on Multiple Datasets. Remote Sens. 2023, 15, 4187. https://doi.org/10.3390/rs15174187
Zhang W, Li J, Xu S, Zhao Y, Jian B. Spatio-Temporal Variation of Critical Relative Humidity Based on Multiple Datasets. Remote Sensing. 2023; 15(17):4187. https://doi.org/10.3390/rs15174187
Chicago/Turabian StyleZhang, Weiyuan, Jiming Li, Sihang Xu, Yang Zhao, and Bida Jian. 2023. "Spatio-Temporal Variation of Critical Relative Humidity Based on Multiple Datasets" Remote Sensing 15, no. 17: 4187. https://doi.org/10.3390/rs15174187
APA StyleZhang, W., Li, J., Xu, S., Zhao, Y., & Jian, B. (2023). Spatio-Temporal Variation of Critical Relative Humidity Based on Multiple Datasets. Remote Sensing, 15(17), 4187. https://doi.org/10.3390/rs15174187







