Key Factors for Improving the Resolution of Mapped Sea Surface Height from Multi-Satellite Altimeters in the South China Sea
Abstract
:1. Introduction
2. Data and Methods
2.1. Datasets
- New altimetry standards and geophysical corrections were used to improve the accuracy of sea level anomaly (SLA) content. The regional mean sea level (MSL) trend and regional deviation was affected.
- The new ‘internal tide’ correction was used to improve the mesoscale signal mapping.
- The new mean sea level (non-repetitive and recent tasks) or mean profile (repetitive task) was used to improve the accuracy of SLA and regional deviation.
- The new mean dynamic topography (MDT) was used to improve the geostrophic current and regional deviation.
- The mesoscale signal on the L4 products were improved by using the improved mapping parameters.
2.2. A Two-Dimensional Variational Method
3. Results
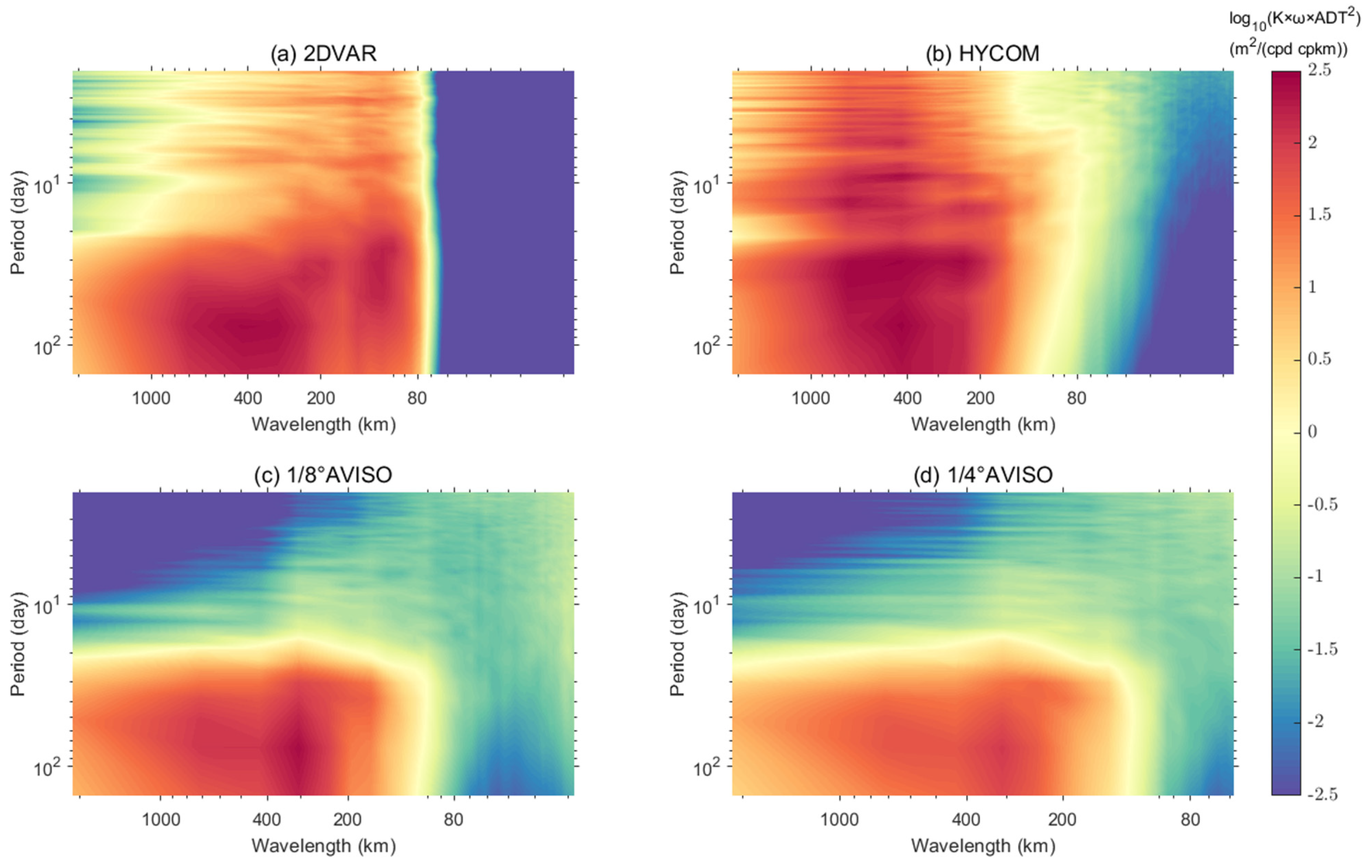
3.1. Signal Proportion of Different Scales in the Background
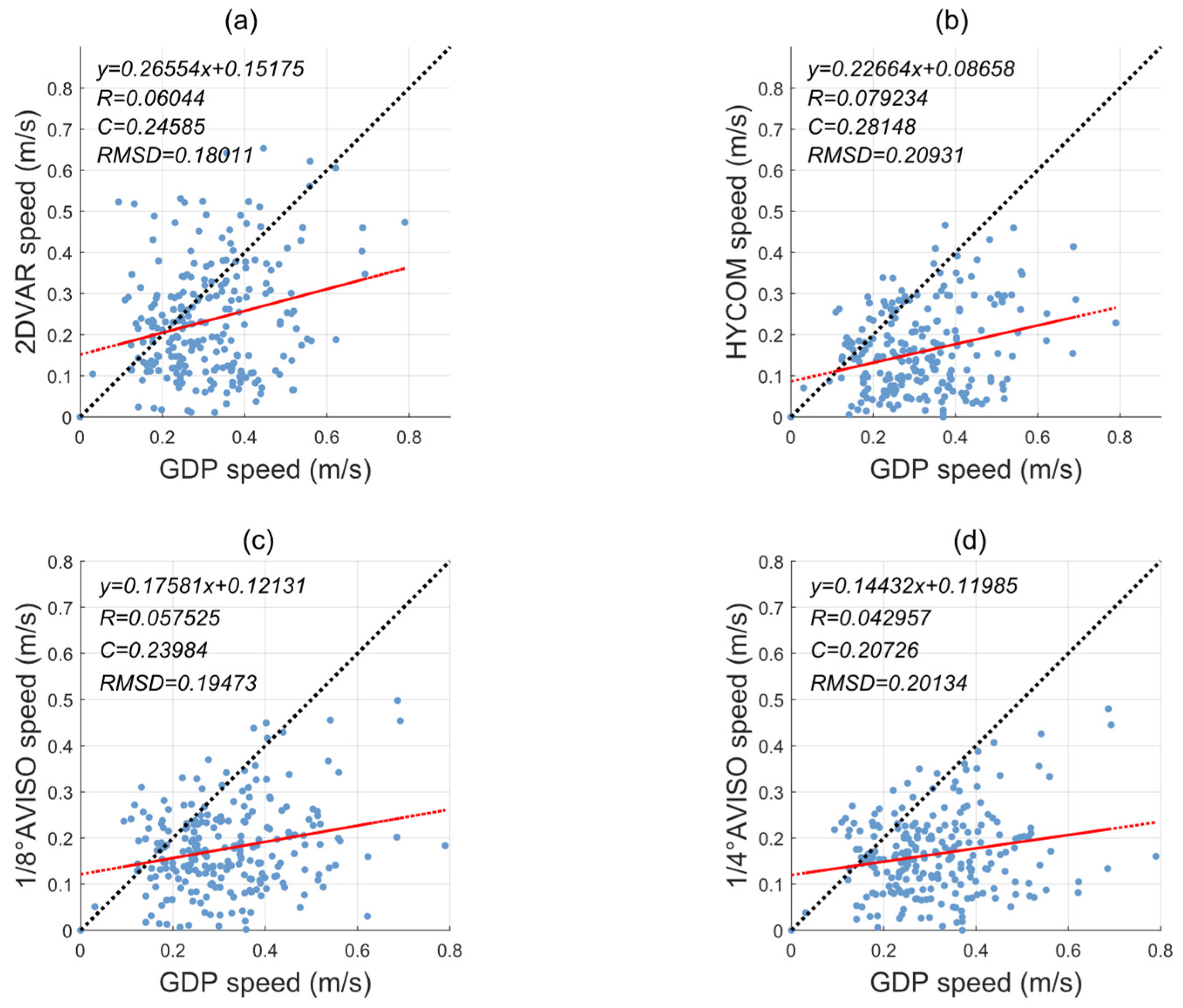
3.2. Evaluation of Accuracy
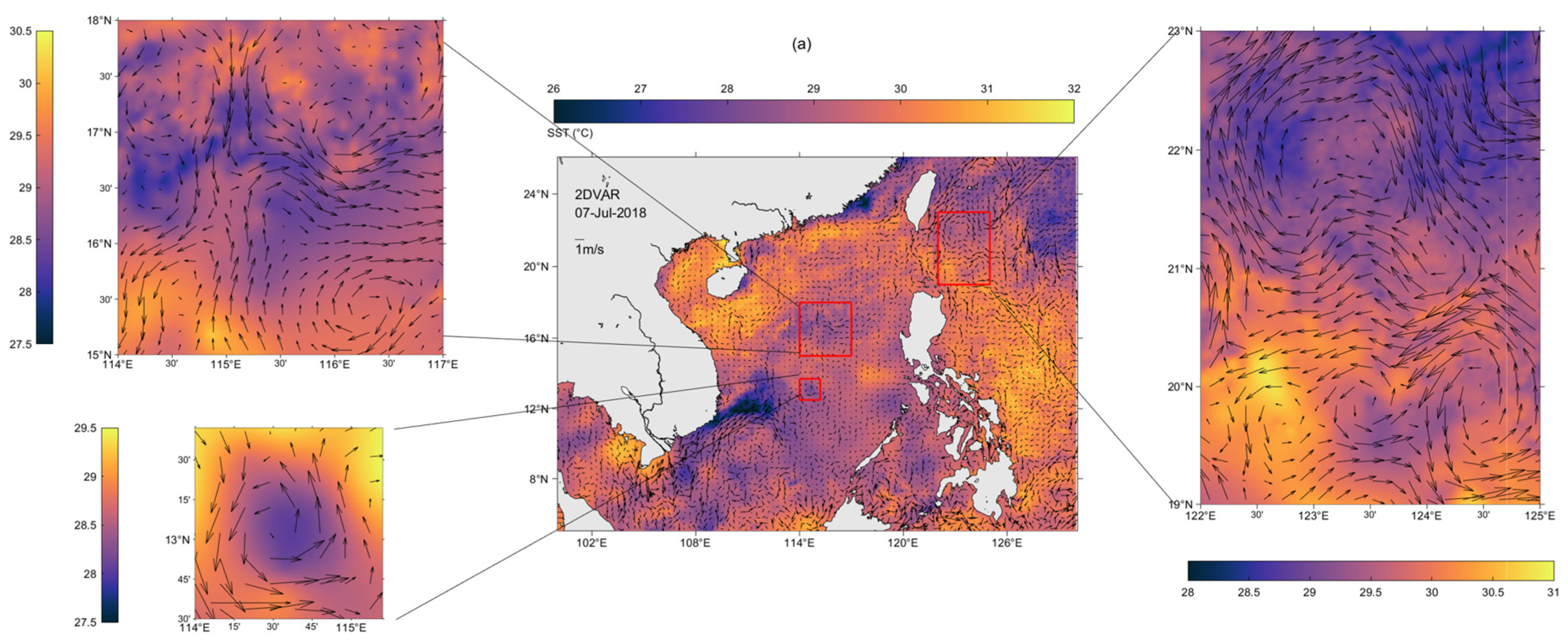
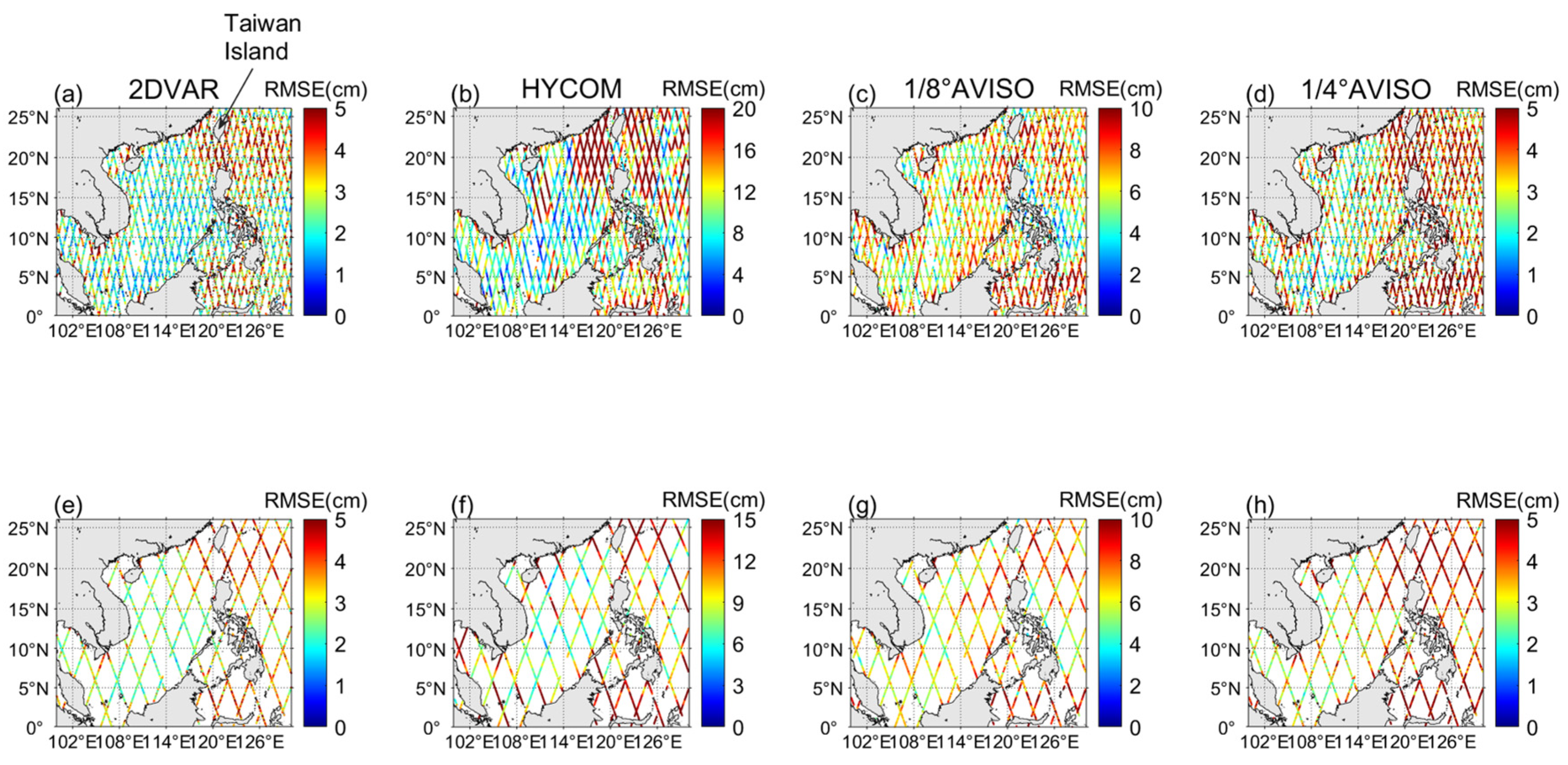
3.2.1. Remote Sensing Evaluation
3.2.2. In Situ Evaluation
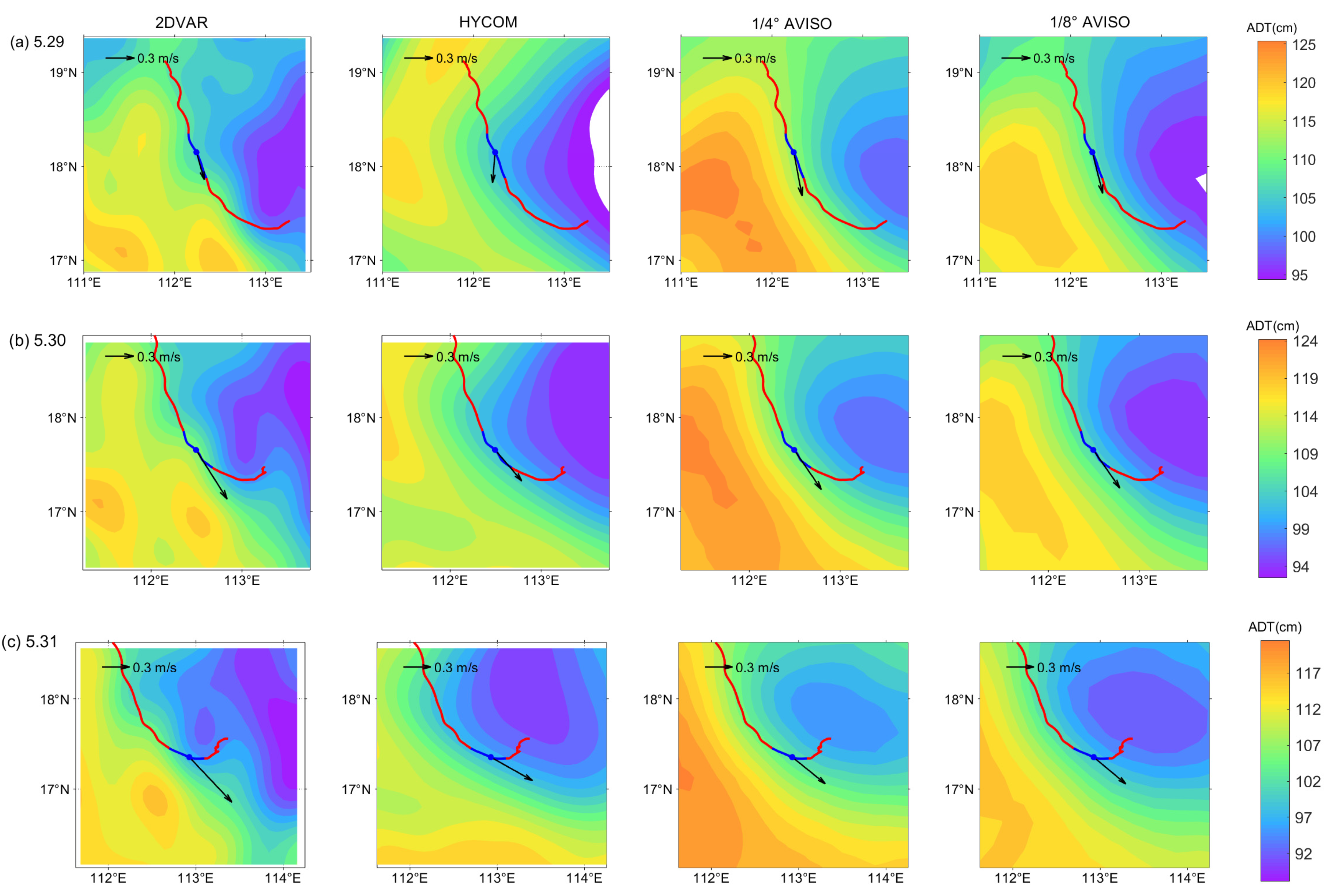
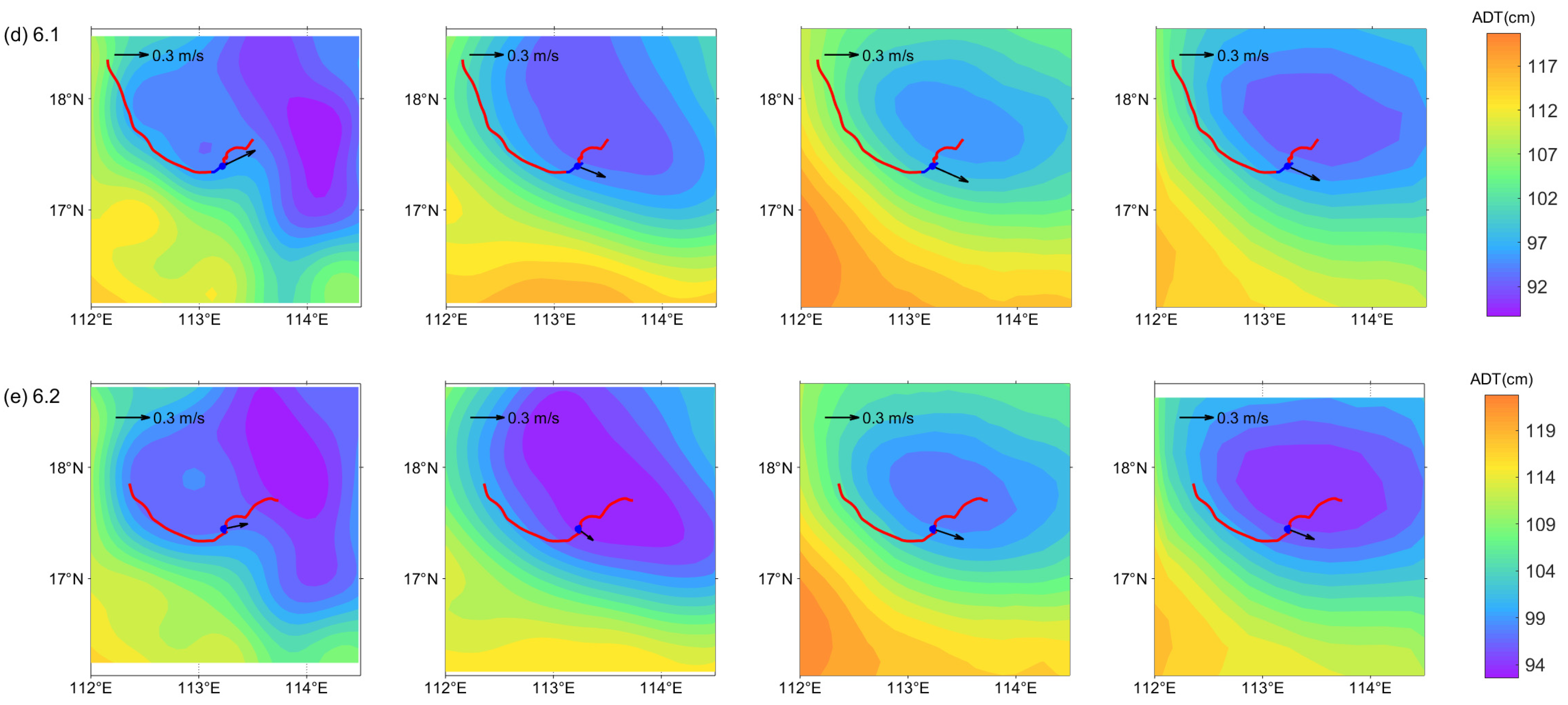
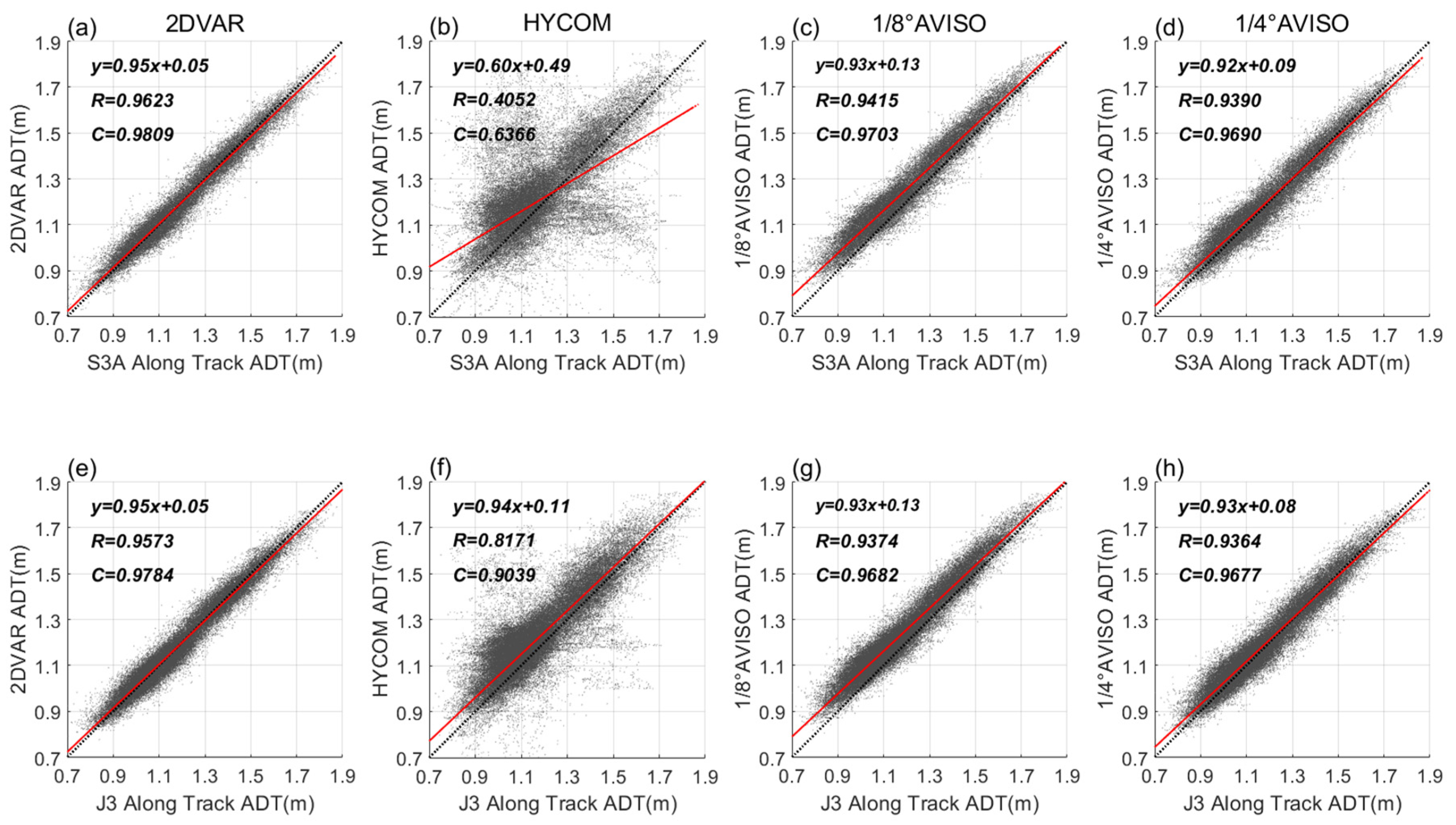
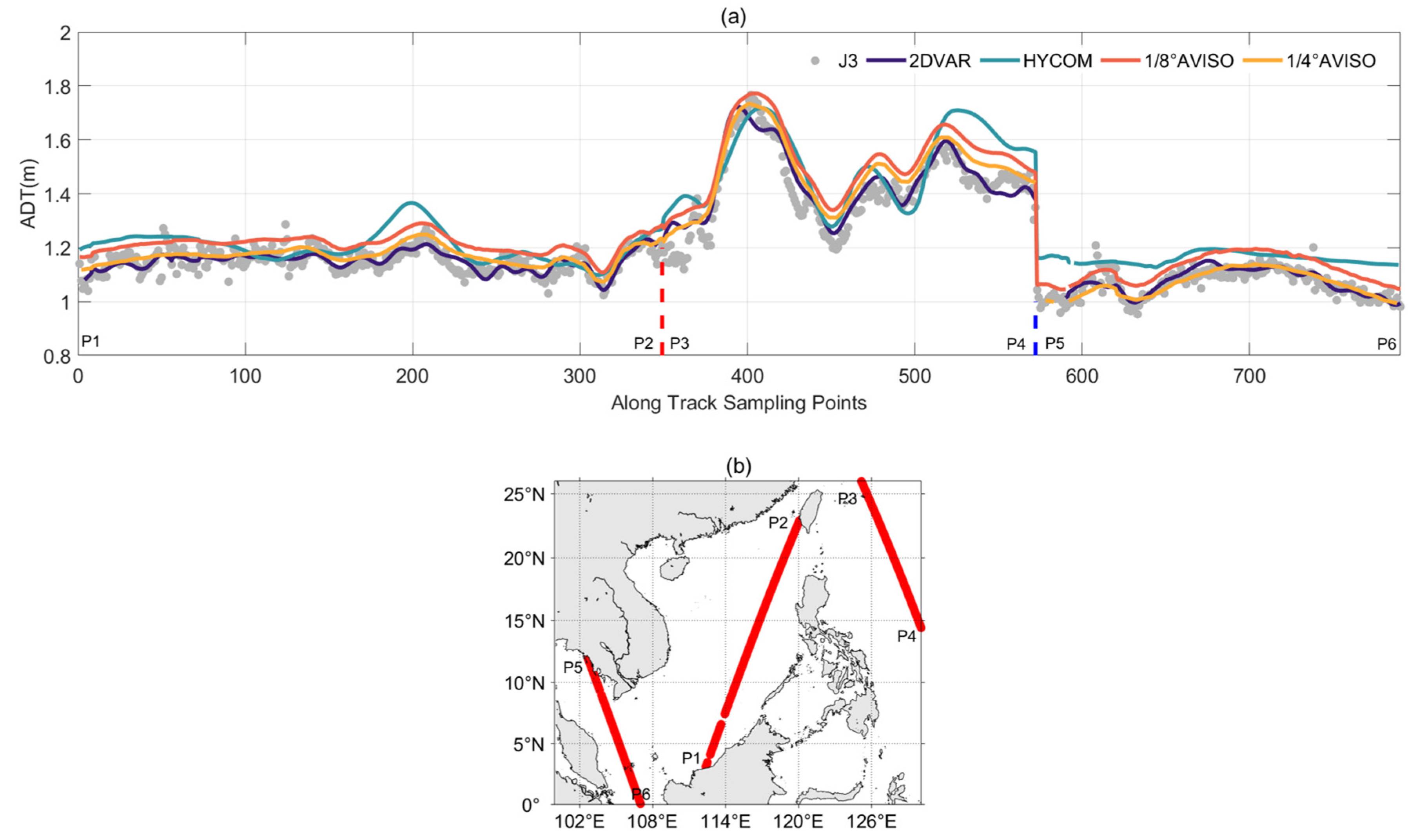
3.2.3. Along-Track Satellite Evaluation
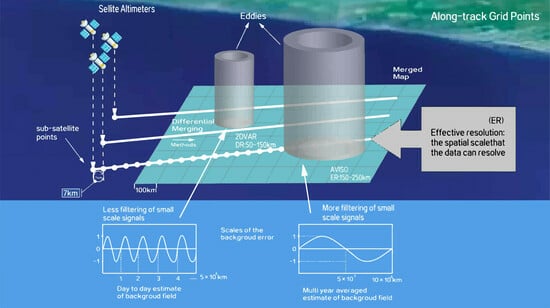
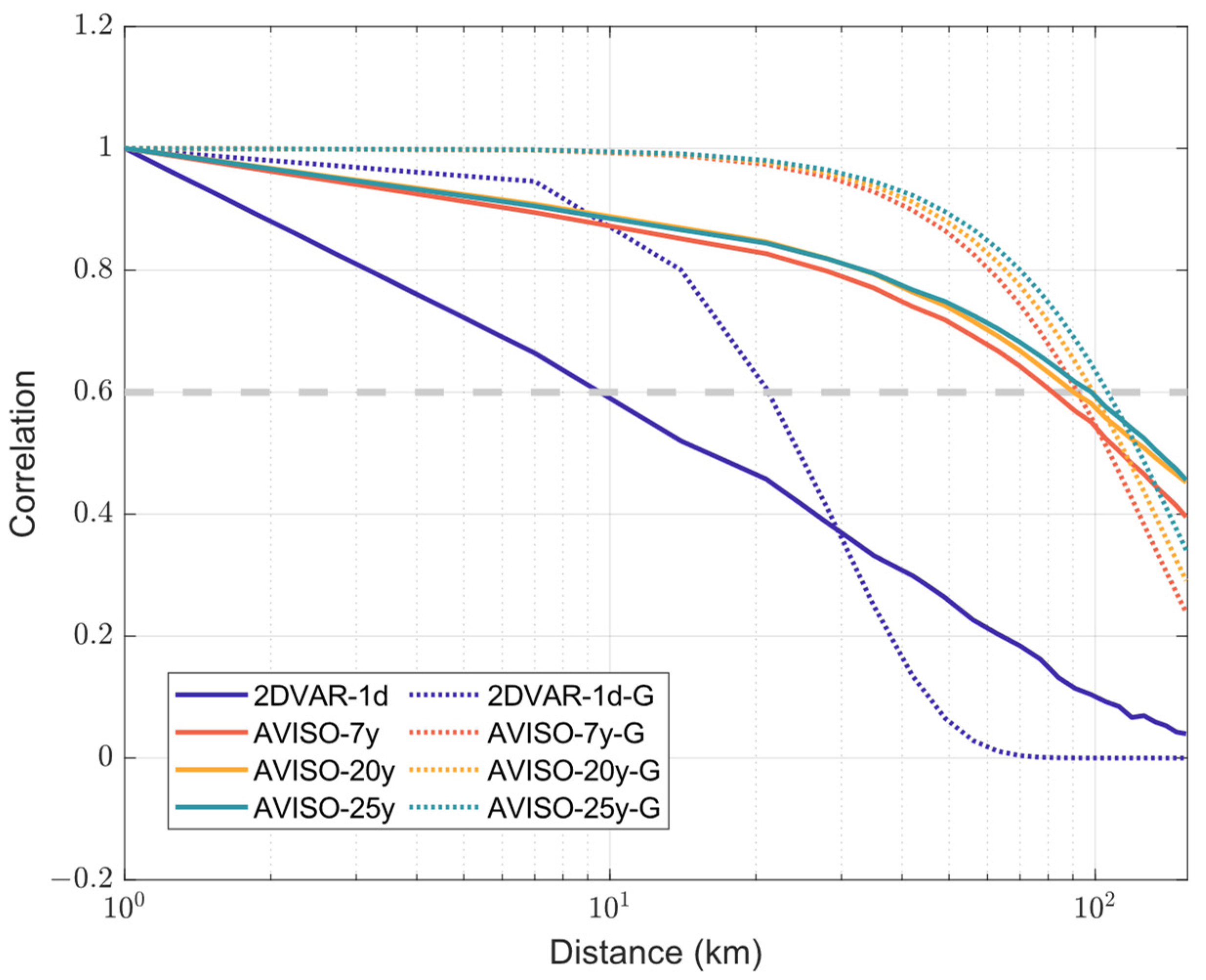
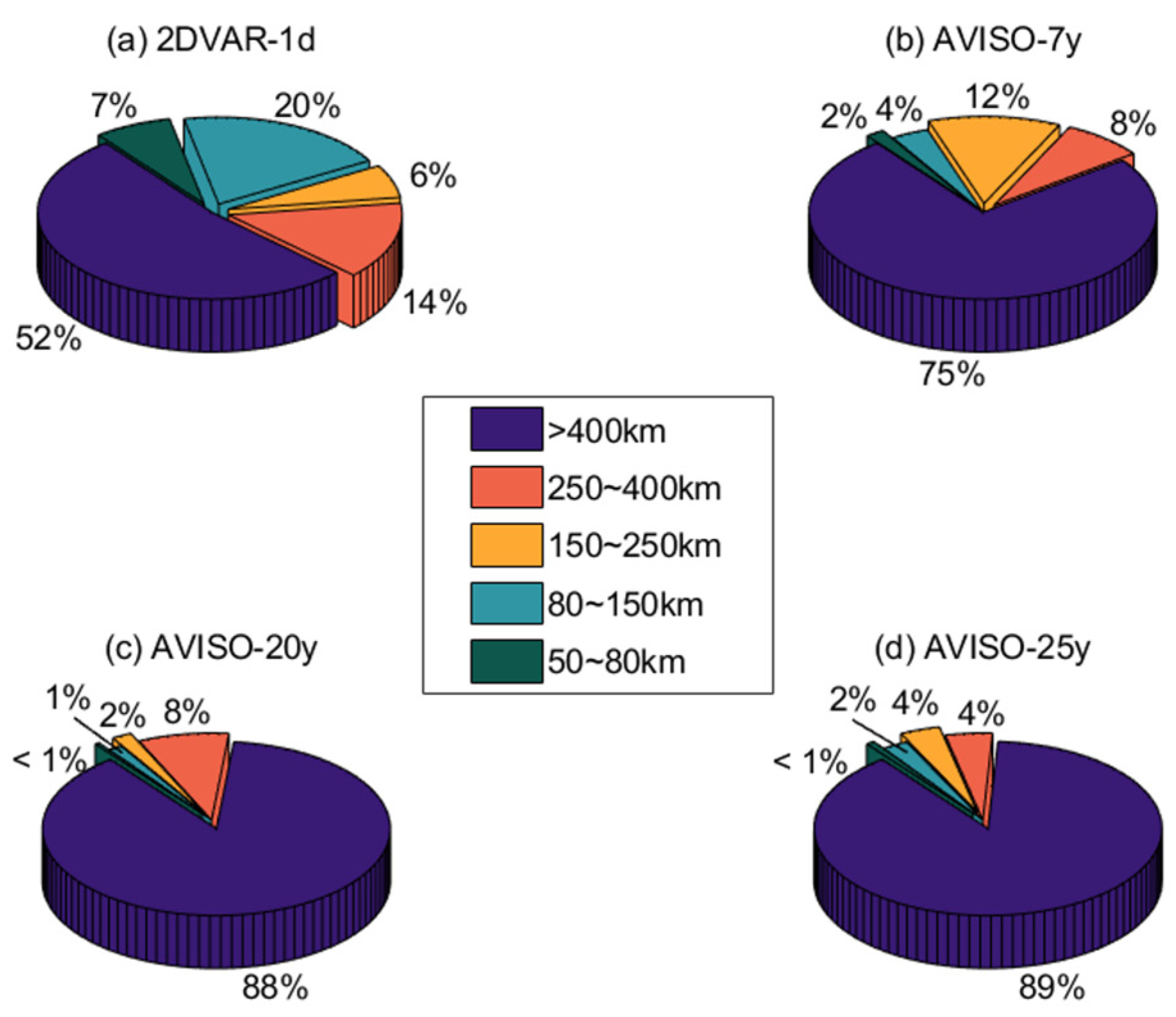
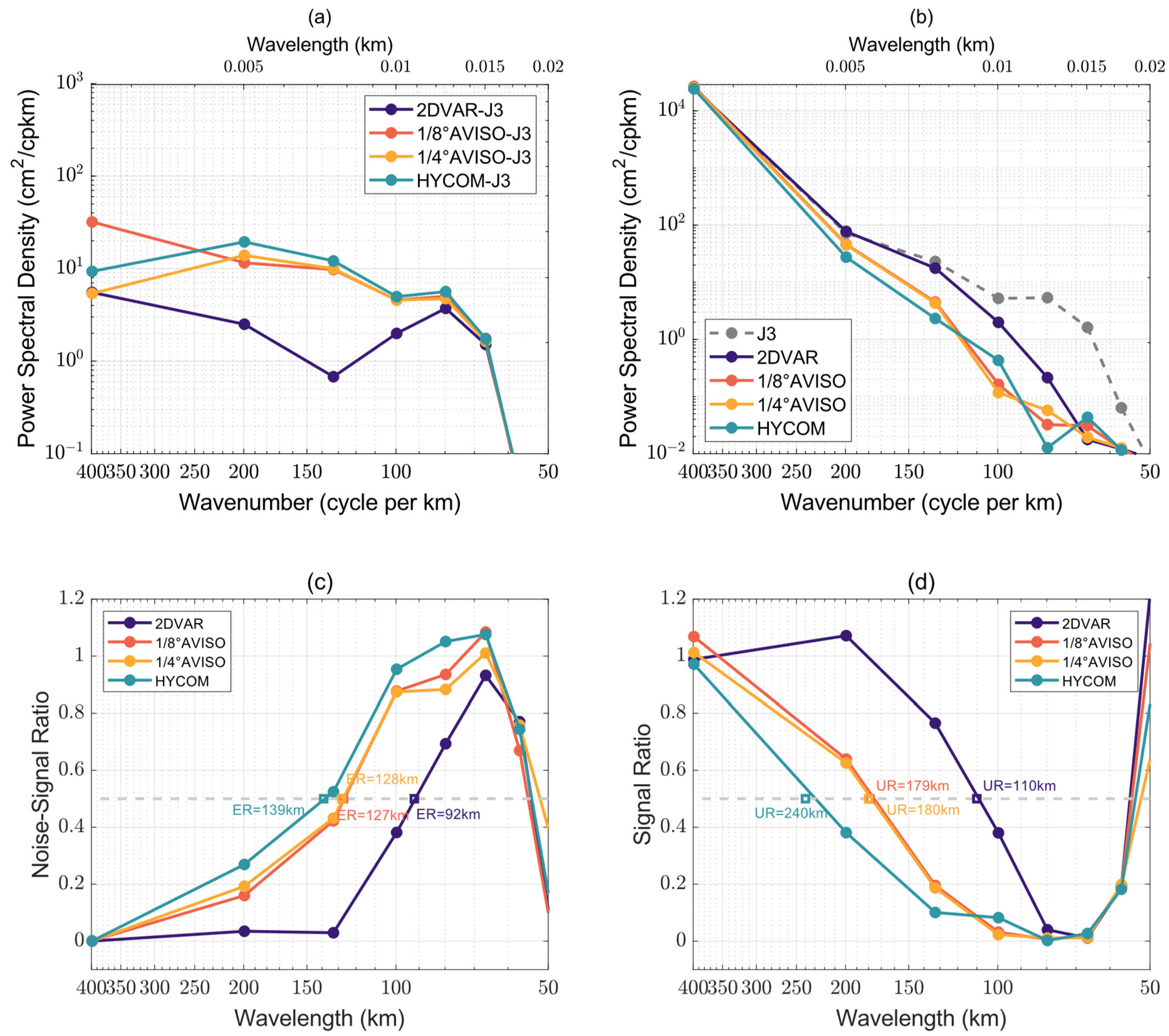
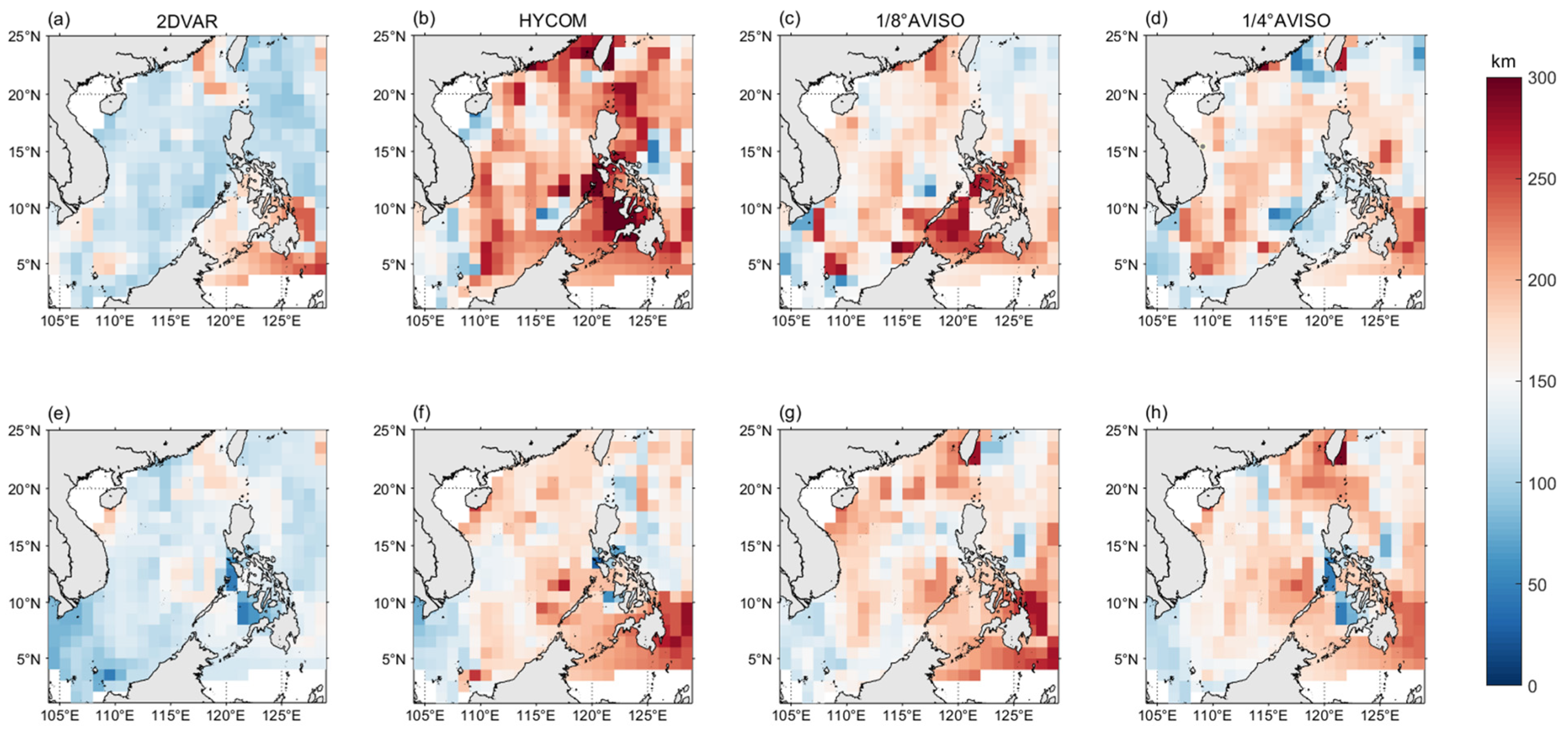
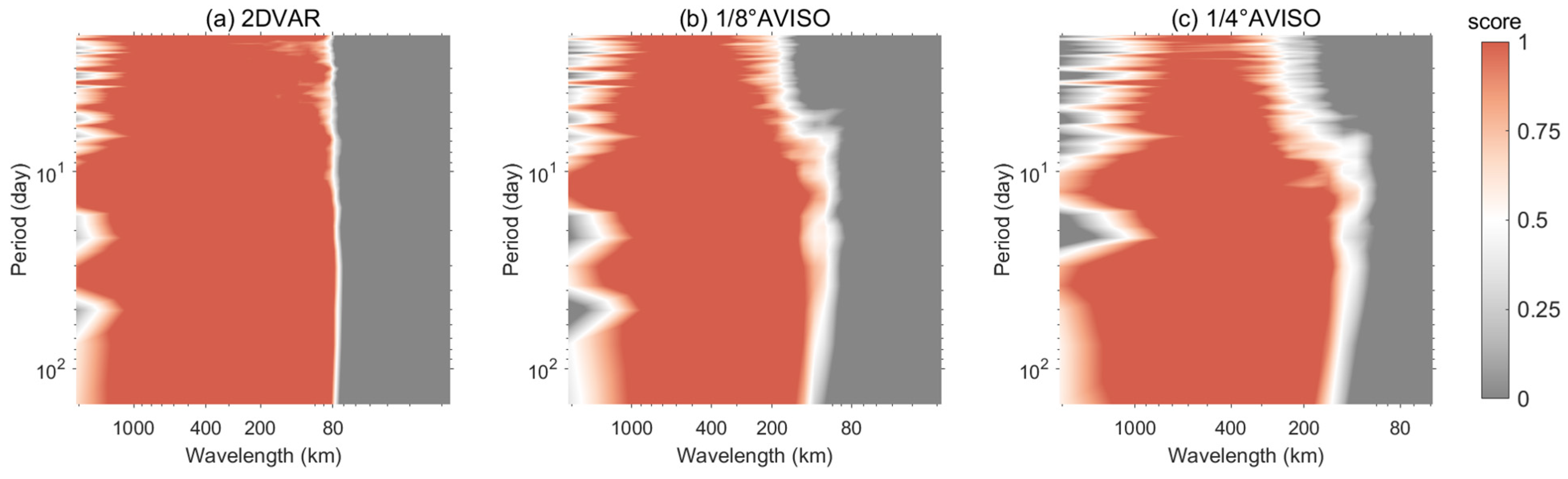
3.3. Evaluation of Effective Resolution
4. Discussion
4.1. Signal Composition in Background Field and Associated Error
4.2. Filtering Effect of Correlation Coefficient Scale in Variational Method
4.3. The Scale of Effective Resolution Compared with Eddy Radius
4.4. The Restriction of HYCOM and the Advantages of 2DVAR
- There is limited historical sampling data, leading to inaccurate assimilation of height field results.
- Non-steric sea surface heights in the altimeter data cannot be assimilated.
- The set of an assimilation thresholds is defined as the noise level of the satellite altimeter (currently set to 4 cm), which restricts the merging of small-scale information.
- The matrix deformation avoids inversion of the background error covariance matrix and can be minimized over the entire grid domain, and is therefore suitable for solving high-resolution problems with a large number of grid points.
- The processing methods of the background error covariance matrix and observation error covariance matrix are more flexible than those of the other models; this flexibility is convenient for simplifying and introducing dynamic constraints.
- Using the observation operator H, it is easy to merge the observation data of different properties.
4.5. Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ubelmann, C.; Dibarboure, G.; Gaultier, L.; Ponte, A.L.S.; Ardhuin, F.; Ballarotta, M.; Faugére, Y. Reconstructing Ocean Surface Current Combining Altimetry and Future Spaceborne Doppler Data. J. Geophys. Res. Ocean. 2021, 126, e2020JC016560. [Google Scholar] [CrossRef]
- Mulet, S.; Rio, M.; Etienne, H.; Artana, C.; Cancet, M.; Dibarboure, G.; Feng, H.; Husson, R.; Picot, N.; Strub, C.P.A.P. The new CNES-CLS18 global mean dynamic topography. Ocean Sci. 2021, 17, 789. [Google Scholar] [CrossRef]
- Elipot, S.; Lumpkin, R.; Perez, R.C.; Lilly, J.M.; Early, J.J.; Sykulski, A.M. A global surface drifter data set at hourly resolution. J. Geophys. Res. Ocean. 2016, 121, 2937–2966. [Google Scholar]
- Abdalla, S.; Kolahchi, A.A.; Ablain, M.; Adusumilli, S.; Bhowmick, S.A.; Alou-Font, E.; Amarouche, L.; Andersen, O.B.; Antich, H.; Aouf, L.; et al. Altimetry for the future: Building on 25 years of progress. Adv. Space Res. 2021, 68, 319–363. [Google Scholar] [CrossRef]
- Wang, G.; Wu, L.; Mei, W.; Xie, S.P. Ocean currents show global intensification of weak tropical cyclones. Nature 2022, 611, 496–500. [Google Scholar] [CrossRef] [PubMed]
- Davis, R.; Talley, L.; Roemmich, D.; Owens, B.; Rudnick, D.; Toole, J.; Weller, R.; McPhaden, M.; Barth, J. 100 Years of Progress in Ocean Observing Systems. Meteorol. Monogr. 2018, 59, 1–46. [Google Scholar] [CrossRef]
- Zilberman, N.; Roemmich, D.; Gille, S.; Gilson, J. Estimating the Velocity and Transport of Western Boundary Current Systems: A Case Study of the East Australian Current near Brisbane. J. Atmos. Ocean. Technol. 2018, 35, 1313–1329. [Google Scholar] [CrossRef]
- Charney, J.; Flierl, G. Oceanic analogues of large scale atmospheric motions. In Evolution of Physical Oceanoaraphy; Warren, B., Wunsch, C., Eds.; MIT Press: Cambridge, MA, USA, 1981; pp. 502–546. [Google Scholar]
- Yu, H.; Li, J.; Wu, K.; Wang, Z.; Yu, H.; Zhang, S.; Hou, Y.; Kelly, R.M. A global high-resolution ocean wave model improved by assimilating the satellite altimeter significant wave height. Int. J. Appl. Earth Obs. Geoinf. 2018, 70, 43–50. [Google Scholar] [CrossRef]
- Detlef, S.; Anny, C. Satellite Altimetry Over Oceans and Land Surfaces. Aeronaut. J. 2019, 123, 1297–1298. [Google Scholar] [CrossRef]
- Archer, M.R.; Li, Z.; Fu, L.L. Increasing the Space–Time Resolution of Mapped Sea Surface Height from Altimetry. J. Geophys. Res. Ocean. 2020, 125, 2019JC015878. [Google Scholar] [CrossRef]
- Liu, L.; Jiang, X.; Fei, J.; Li, Z. Development and evaluation of a new merged sea surface height product from multi-satellite altimeters. Chin. Sci. Bull. 2020, 65, 1888–1897. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- Chelton, D.; Dibarboure, G.; Pujol, M.I.; Taburet, G.; Schlax, M.G. The Spatial Resolution of AVISO Gridded Sea Surface Height Fields; OSTST: Lake Constance, Germany, 2014; pp. 28–31. Available online: https://meetings.aviso.altimetry.fr/fileadmin/user_upload/tx_ausyclsseminar/files/29Red0900-1_OSTST_Chelton.pdf (accessed on 30 March 2022).
- Ubelmann, C.; Klein, P.; Fu, L. Dynamic Interpolation of Sea Surface Height and Potential Applications for Future High-Resolution Altimetry Mapping. J. Atmos. Ocean. Technol. 2015, 32, 177–184. [Google Scholar] [CrossRef]
- Chen, G.; Hou, Y.; Chu, X. Mesoscale eddies in the South China Sea: Mean properties, spatiotemporal variability, and impact on thermohaline structure. J. Geophys. Res. 2011, 116, C06018. [Google Scholar] [CrossRef]
- Wang, G.; Su, J.; Chu, P.C. Mesoscale eddies in the South China Sea observed with altimeter data. Geophys. Res. Lett. 2003, 30, 2121. [Google Scholar] [CrossRef]
- Roberts-Jones, J.; Bovis, K.; Martin, M.J.; McLaren, A. Estimating background error covariance parameters and assessing their impact in the OSTIA system. Remote Sens. Environ. 2016, 176, 117–138. [Google Scholar] [CrossRef]
- Pegliasco, C.; Chaigneau, A.; Morrow, R.; Dumas, F. Detection and tracking of mesoscale eddies in the Mediterranean Sea: A comparison between the Sea Level Anomaly and the Absolute Dynamic Topography fields. Adv. Space Res. 2021, 68, 401–419. [Google Scholar] [CrossRef]
- Jiang, X.; Liu, L.; Li, Z.; Liu, L.; Sian, K.T.C.L.; Dong, C. A Two-Dimensional Variational Scheme for Merging Multiple Satellite Altimetry Data and Eddy Analysis. Remote Sens. 2022, 14, 3026. [Google Scholar] [CrossRef]
- Taburet, G.; Pujol, M.; SL-TAC Team. QUID for Sea Level TAC DUACS Products. Available online: https://catalogue.marine.copernicus.eu/documents/QUID/CMEMS-SL-QUID-008-032-068.pdf (accessed on 5 April 2023).
- Ballarotta, M.; Ubelmann, C.; Pujol, M.I.; Taburet, G.; Fournier, F.; Legeais, J.F.; Faugere, Y.; Delepoulle, A.; Chelton, D.; Dibarboure, G.; et al. On the resolutions of ocean altimetry maps. Ocean Sci. 2019, 15, 1091–1109. [Google Scholar] [CrossRef]
- Lewis, J.M.; Lakshmivarahan, S.; Maryada, S.K.R. Placement of Observations for Variational Data Assimilation: Application to Burgers’ Equation and Seiche Phenomenon. In Data Assimilation for Atmospheric, Oceanic and Hydrologic Applications; Park, S.K., Xu, L., Eds.; Springer: Cham, Switzerland, 2021; Volume IV, pp. 259–275. [Google Scholar] [CrossRef]
- JPL MUR MEaSUREs Project. GHRSST Level 4 MUR Global Foundation Sea Surface Temperature Analysis, Version 4.1; PO.DAAC: Pasadena, CA, USA, 2015. [Google Scholar] [CrossRef]
- Lumpkin, R.; Centurioni, L. Global Drifter Program Quality-Controlled 6-Hour Interpolated Data from Ocean Surface Drifting Buoys. NOAA National Centers for Environmental Information. Dataset. 2019. Available online: https://www.aoml.noaa.gov/phod/gdp/ (accessed on 30 March 2022).
- Pujol, M.; Egrave, F.; Re, Y.; Taburet, G.; Dupuy, S.E.; Phanie; Pelloquin, C.; Ablain, M.; Picot, N. DUACS DT2014: The new multi-mission altimeter data set reprocessed over 20 years. Ocean Sci. 2016, 12, 1067–1090. [Google Scholar] [CrossRef]
- Gaspari, G.; Cohn, S.E. Construction of correlation functions in two and three dimensions. Q. J. R. Meteorol. Soc. 1999, 125, 723–757. [Google Scholar] [CrossRef]
- Li, Z.; Cheng, X.; Gustafson, W.I., Jr.; Vogelmann, A.M. Spectral characteristics of background error covariance and multiscale data assimilation. Int. J. Numer. Methods Fluids 2016, 82, 1035–1048. [Google Scholar] [CrossRef]
- Daley, R. Atmospheric data assimilation. In Cambridge Atmospheric and Space Science Series; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Gaube, P.; Chelton, D.B.; Samelson, R.M.; Schlax, M.G.; O’Neill, L.W. Satellite Observations of mesoscale Eddy-Induced Ekman Pumping. J. Phys. Oceanogr. 2015, 45, 104–132. [Google Scholar] [CrossRef]
- Hausmann, U.; Czaja, A. The observed signature of mesoscale eddies in sea surface temperature and the associated heat transport. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2012, 70, 60–72. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, W.; Tian, J.; Yang, Q.; Qu, T. Spatial structure and temporal variability of the zonal flow in the Luzon Strait (Article). J. Geophys. Res. Ocean. 2015, 120, 759–776. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, F.; Chen, G. Statistical characterization of sea surface temperature over mesoscale eddies in the south China sea. Period. Ocean. Univ. China 2020, 50, 146–156. [Google Scholar] [CrossRef]
- Morrow, R.; Fu, L.; Ardhuin, F.; Benkiran, M.; Chapron, B.; Cosme, E.; D’Ovidio, F.; Farrar, J.T.; Gille, S.; Lapeyre, G.; et al. Global Observations of Fine-Scale Ocean Surface Topography with the Surface Water and Ocean Topography (SWOT) Mission. Front. Mar. Sci. 2019, 6, 232. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J.; Fu, L. An Observing System Simulation Experiment for Ocean State Estimation to Assess the Performance of the SWOT Mission: Part 1—A Twin Experiment. J. Geophys. Res. Ocean. 2019, 124, 4838–4855. [Google Scholar] [CrossRef]
| European Seas | Variance [cm2] | Effective Resolution [km] |
|---|---|---|
| Black Sea | 14.4 (−0.94%) | 100 to 150 (~130) |
| Mediterranean Sea | 15.3 (−4.25%) | 90 to 160 (~130) |
| Experiments/ Models | RMSE [cm] | S | ||
|---|---|---|---|---|
| S3A | J3 | S3A | J3 | |
| 2DVAR | 0.0299 | 0.0340 | / | / |
| HYCOM | 1.5946 | 0.5189 | 0.8987 | 0.9421 |
| 1/8° AVISO | 0.0678 | 0.0688 | 0.6658 | 0.7070 |
| 1/4° AVISO | 0.0396 | 0.0414 | 0.1125 | 0.2313 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Zhang, X.; Fei, J.; Li, Z.; Shi, W.; Wang, H.; Jiang, X.; Zhang, Z.; Lv, X. Key Factors for Improving the Resolution of Mapped Sea Surface Height from Multi-Satellite Altimeters in the South China Sea. Remote Sens. 2023, 15, 4275. https://doi.org/10.3390/rs15174275
Liu L, Zhang X, Fei J, Li Z, Shi W, Wang H, Jiang X, Zhang Z, Lv X. Key Factors for Improving the Resolution of Mapped Sea Surface Height from Multi-Satellite Altimeters in the South China Sea. Remote Sensing. 2023; 15(17):4275. https://doi.org/10.3390/rs15174275
Chicago/Turabian StyleLiu, Lei, Xiaoya Zhang, Jianfang Fei, Zhijin Li, Wenli Shi, Huizan Wang, Xingliang Jiang, Ze Zhang, and Xianyu Lv. 2023. "Key Factors for Improving the Resolution of Mapped Sea Surface Height from Multi-Satellite Altimeters in the South China Sea" Remote Sensing 15, no. 17: 4275. https://doi.org/10.3390/rs15174275
APA StyleLiu, L., Zhang, X., Fei, J., Li, Z., Shi, W., Wang, H., Jiang, X., Zhang, Z., & Lv, X. (2023). Key Factors for Improving the Resolution of Mapped Sea Surface Height from Multi-Satellite Altimeters in the South China Sea. Remote Sensing, 15(17), 4275. https://doi.org/10.3390/rs15174275