Abstract
This study developed a satellite, reanalysis, and gauge data merging model for daily-scale analysis using a random forest algorithm in Sichuan province, characterized by complex terrain. A high-precision daily precipitation merging dataset (MSMP) with a spatial resolution of 0.1° was successfully generated. Through a comprehensive evaluation of the MSMP dataset using various indices across different periods and regions, the following findings were obtained: (1) GPM-IMERG satellite observation data exhibited the highest performance in the region and proved suitable for inclusion as the initial background field in the merging experiment; (2) the merging experiment significantly enhanced dataset accuracy, resulting in a spatiotemporal distribution of precipitation that better aligned with gauge data; (3) topographic factors exerted certain influences on the merging test, with greater accuracy improvements observed in the plain region, while the merging test demonstrated unstable effects in higher elevated areas. The results of this study present a practical approach for merging multi-source precipitation data and provide a novel research perspective to address the challenge of constructing high-precision daily precipitation datasets in regions characterized by complex terrain and limited observational coverage.
1. Introduction
As one of the fundamental meteorological parameters, precipitation plays a crucial role in global water and energy cycles. In recent years, extreme precipitation events have increased due to global warming, posing significant threats to human lives and property and causing substantial economic losses [1,2]. Accurate estimation of precipitation is paramount for weather prediction and meteorological disaster warnings. Surface meteorological stations are a common method used to gather precipitation data. However, due to the uneven distribution of stations and underlying surface complexities, it is challenging to obtain uniformly distributed and continuous precipitation data [3,4]. Meanwhile, the spatial interpolation method used to generate the continuous spatial distribution of precipitation data is characterized by high uncertainty, particularly in regions with complex terrain and limited observations [5,6,7].
In recent years, numerous researchers have conducted extensive research to obtain precipitation data with wide coverage, high precision, and enhanced spatiotemporal resolutions. These efforts have focused on developing multi-source precipitation merging methods that leverage the advantages of various observational data [8,9,10]. Researchers have constructed specific merging models tailored to the characteristics of different study areas. Geographically weighted regression (GWR) [11], optimum interpolation (OI) [12], regression kriging interpolation (RK) [13], Bayesian model averaging (BMA) [14], and other techniques have been employed. Although considerable progress has been made in multi-source precipitation merging, most existing methods primarily concentrate on merging satellite and gauge data with a relatively limited number of data sources involved in the merging process. Moreover, the aforementioned merging methods predominantly involve the numerical merging of the data sources, as both gauge and satellite data only provide direct or indirect precipitation measurements without modeling the physical characteristics of atmospheric changes. Therefore, the obtained multi-source merging data also lack information characteristics in this aspect. In addition, with the increasing demand for spatiotemporal resolutions and accuracy of precipitation datasets, the need to choose precipitation data and parameters from more sources is becoming increasingly urgent, while some traditional data merging methods may not meet such demand. In terms of methods, with the rapid development of machine learning and deep learning, Chiang et al. [8] used recurrent neural networks to integrate hydrological responses from various precipitation sources and forecast flash floods in Taiwan, China. Wu et al. [9] introduced the CNN-LSTM method to conduct a spatiotemporal deep merging scheme for satellite and gauge data in Mainland China. Based on the ANN method, Hong et al. [10] integrated multi-source precipitation data such as satellite, reanalysis, and gauge data to obtain multi-source merging precipitation data with a resolution of 0.1° over the Tibetan Plateau. These studies show that the machine learning method can integrate more information related to precipitation from more sources to a greater extent, and precipitation estimation and precipitation event detection have been significantly improved. However, most machine learning methods are prone to overfitting when training small-batch datasets, and fewer data samples in a local area may eventually affect the accuracy of merged precipitation products.
In the hinterland of southwest China, Sichuan province is located in the upper reaches of the Yangtze River, bordered by Tibet to the west, the Qinling Mountains to the north, and the Yunnan–Guizhou Plateau to the south [11,12]. It contains a variety of landforms, such as plateaus, hills, mountains, plains, and basins. The distribution of stations in Sichuan province is highly uneven. The stations in the plain of eastern Sichuan province are very dense. However, the stations in the western region, especially on the plateau, are sparsely distributed, significantly complicating studying detailed precipitation characteristics in this region. As a key area through which the convective system of the Qinghai–Tibet Plateau moves eastward, Sichuan province often generates local heavy rain and further stimulates or strengthens disastrous processes such as heavy rain and flooding in the middle and lower reaches of the Yangtze River [13]. However, the error of various satellite data for inversion algorithms and the uncertainty of model reanalysis data sources lead to considerable limitations in exploring precipitation characteristics in areas of complex terrain or limited observation [14,15,16]. Therefore, it is vital to explore the distribution characteristics of precipitation in Sichuan province by integrating various precipitation datasets and combining the advantages of multiple precipitation datasets to obtain more accurate grid precipitation datasets. Additionally, this study divides the Sichuan province into three research areas: the plateau region, the basin region, and the transitional zone from the plateau to the basin. The aim is to explore the merging effects in complex terrain and compare the performance between areas with sparse and dense gauge observations, aiming to compensate for the lack of precipitation data in regions with limited or no gauge observations. Ultimately, this research supports theoretical studies of weather system development and high-resolution initial field information for numerical models.
2. Study Area and Data
2.1. Study Area
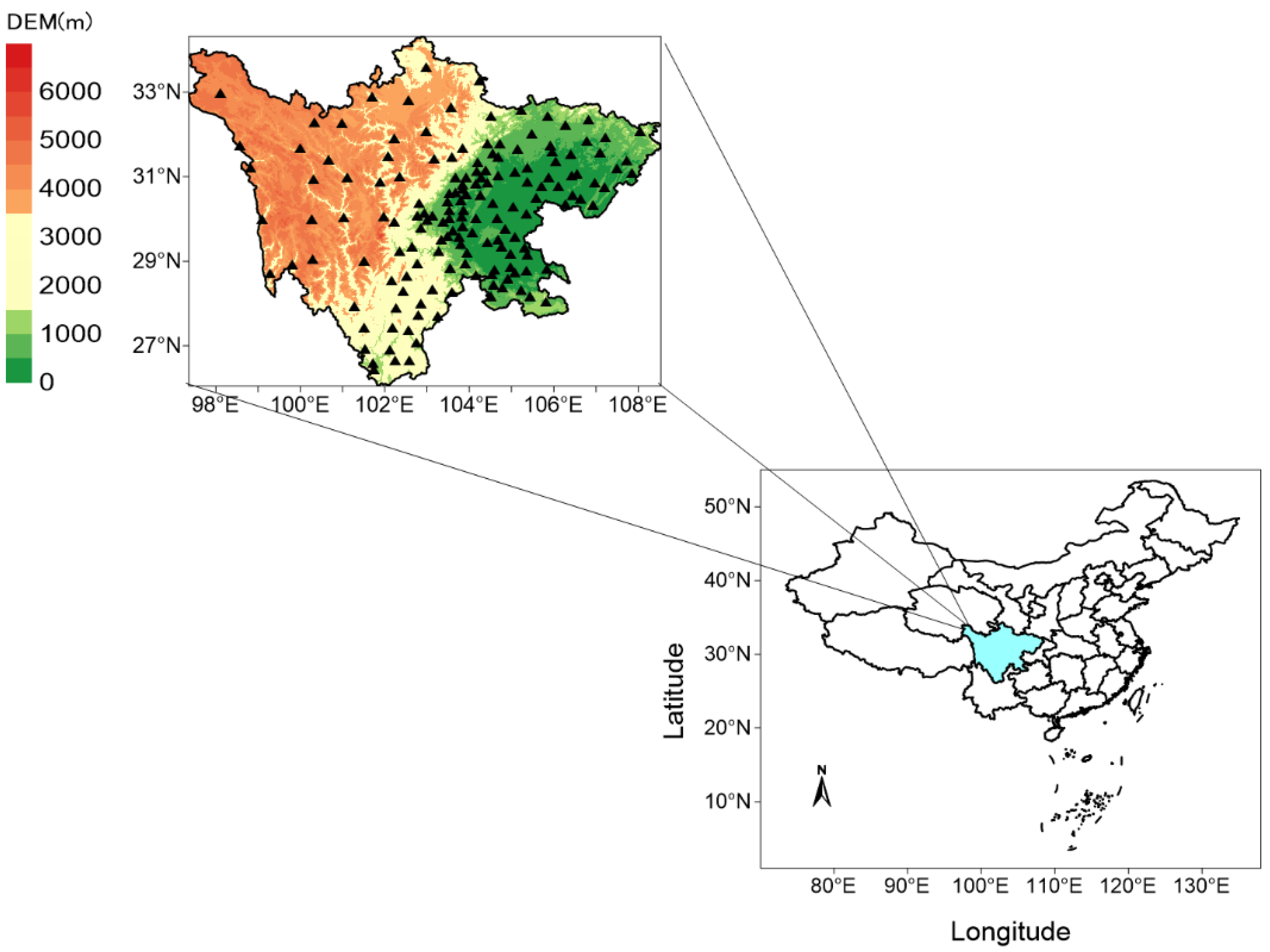
Sichuan province is characterized by complex terrain and significant variations in elevation, with a general trend of higher elevation in the west and lower elevation in the east. The western region mainly consists of plateaus and mountains, with elevations averaging around 4000 m. In contrast, the eastern part is dominated by plains, basins, and hills, with elevations below 1500 m [17]. The dramatic variation in elevation leads to noticeable differences in the spatiotemporal distribution of precipitation in Sichuan province. The eastern region includes the Sichuan Basin and the eastern plain, which have a mild climate and abundant annual precipitation, with most areas receiving over 1000 mm of rainfall. This area belongs to a subtropical humid monsoon climate [13,18]. High plateaus on the Qinghai characterize the northwestern part of Sichuan province–Tibet Plateau’s edge. It has a high altitude and cold climate, with annual precipitation ranging from 500 to 900 mm. Southwestern Sichuan province is primarily mountainous and falls within a subtropical semi-humid climate zone with fewer rainy days and lower rainfall amounts [19,20]. The region’s significant variation in topography and climate makes it an ideal subject for theoretical research and practical applications. In this study, we divide the Sichuan province into three zones based on elevation information: Area I includes the Sichuan Basin, with elevations below 1000 m, Area II includes the hilly areas and the margin of the basin in central and southern Sichuan province, with elevations ranging from 2000 to 3000 m, and Area III represents the high plateaus in western Sichuan province, with elevations above 3000 m. Figure 1 illustrates the elevation information and the distribution of station locations in Sichuan province.
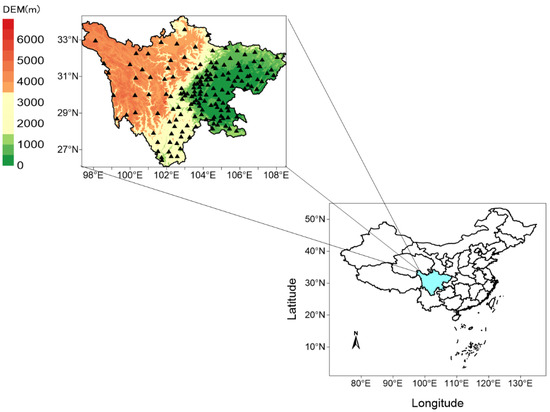
Figure 1.
Location and digital elevation information of Sichuan province. Triangles represent the locations of ordinary national stations.
2.2. Data
Three main types of precipitation data are used in this study: gauge data, satellite remote sensing inversion data, and global model reanalysis data. Gauge data have high precision and are often considered the actual precipitation value to include in a merging experiment. Satellite remote sensing observation data can detect atmospheric characteristics by infrared sensor and estimate precipitation by inversion algorithm and have a wide range of precipitation estimation with high spatiotemporal resolutions and can better reflect the spatiotemporal distribution characteristics of precipitation. Model reanalysis data, through the data assimilation of model data, some satellite data, and gauge data, contain the information description of the physical characteristics of atmospheric change in the model data and can better reflect the physical characteristics of atmospheric change.
The gauge data are obtained from daily precipitation data collected by 4320 automatic weather stations of the Sichuan Meteorological Bureau, and the distance between stations is between 1 and 30 km. This study selects daily precipitation data from stations in Sichuan from 1 January 2018 to 31 December 2020. Since most stations have missing measurements, meteorological stations missing more than ten days a month excluded during the merging model’s evaluation.
The satellite data include GPM-IMERG, CMORPH-BLD, and GSMAP-Gauge precipitation data. The GPM-IMERG precipitation product is a tertiary product derived from the Global Precipitation Measure (GPM), a follow-up project to the Tropical Precipitation Measurement Measure (TRMM). Based on the TRMM, the GPM enhances solid and trace precipitation observation. The CMROPH-BLD precipitation product is a real-time satellite precipitation inversion product developed by NOAA’s Climate Prediction Center (CPC) that uses a “motion vector” approach to estimate precipitation rather than simply using statistical relationships. To a certain extent, it preserves the continuity of the spatiotemporal distribution of precipitation. The Japanese Space Agency is responsible for developing the global precipitation product GSMAP-Gauge. Its precipitation calculation method combines the precipitation inversion methods of TRMM and other pole-orbiting satellites. It uses the geosynchronous orbit (GEO) satellite cloud image to assess high-precision global precipitation in the 60°N to 60°S latitude range. The above satellite data are several mainstream satellite observation products with high accuracy, stability, and long-term series of historical observation data. Many scholars have conducted various evaluations and error analyses on these satellite precipitation products and have evaluated their applicability to China [21,22,23,24].
The data comes from the ERA-5 reanalysis data, the 5th generation of global climate products released by the European Centre for Medium-Range Weather Forecasts (ECMWF), a dataset with a spatiotemporal resolution of 0.25° [25]. Compared to ERA-interim, the ERA-5 reanalysis improved its spatiotemporal resolutions, upgraded its integrated forecast model (IFS) from Cy31r2 to Cy41r2, and integrated ten ensemble members for the first time using the 4D-Varz data assimilation method, assimilating many of the latest instrumental data, including IASI, ASCAT, MWHS-2, TMI, SSMIS, AMSR-2, GMI, etc. Many studies have comprehensively evaluated the ERA-5 reanalysis data. The research results suggest that ERA-5 reanalysis data can better detect precipitation events and reproduce the spatiotemporal distribution characteristics of precipitation [26,27,28].
In addition, the observation accuracy of precipitation by satellites may be affected by terrain and other factors. Additional auxiliary parameters (elevation, slope, latitude, and longitude) are added in this study for the merging experiment to adjust the bias of the precipitation estimation [10,29]. The digital elevation information (DEM) is derived from the Shuttle Radar Topography Mission (SRTM), measured by NASA, with a spatial resolution of 90 m [30]. At the same time, topographic data such as slope, longitude, and latitude are also extracted from DEM elevation data.
Since the spatiotemporal resolutions of the satellite data or reanalysis data are different, to obtain 0.1° daily precipitation datasets in Sichuan province, we need to perform interpolation processing on those data and unify their spatiotemporal resolutions to 0.1° daily. Firstly, the inverse distance-weighted interpolation method is used to interpolate the spatial resolutions of the gridded precipitation data to 0.1°, and the data in a day are aggregated to unify all the precipitation data to the daily scale. In this way, the spatiotemporal characteristics of the original data are retained, and more errors not be introduced to affect the merging experiment [31,32,33,34]. In addition, in order to ensure the validity of the evaluation experiment, we randomly divide the gauge data into two parts according to a ratio of 7:3. One part is used for the correction of the background field and multi-source precipitation merging experiment, and the other part is used for the results evaluation experiment. Table 1 shows the details of the data used in this study.

Table 1.
All data products used in the study.
3. Method
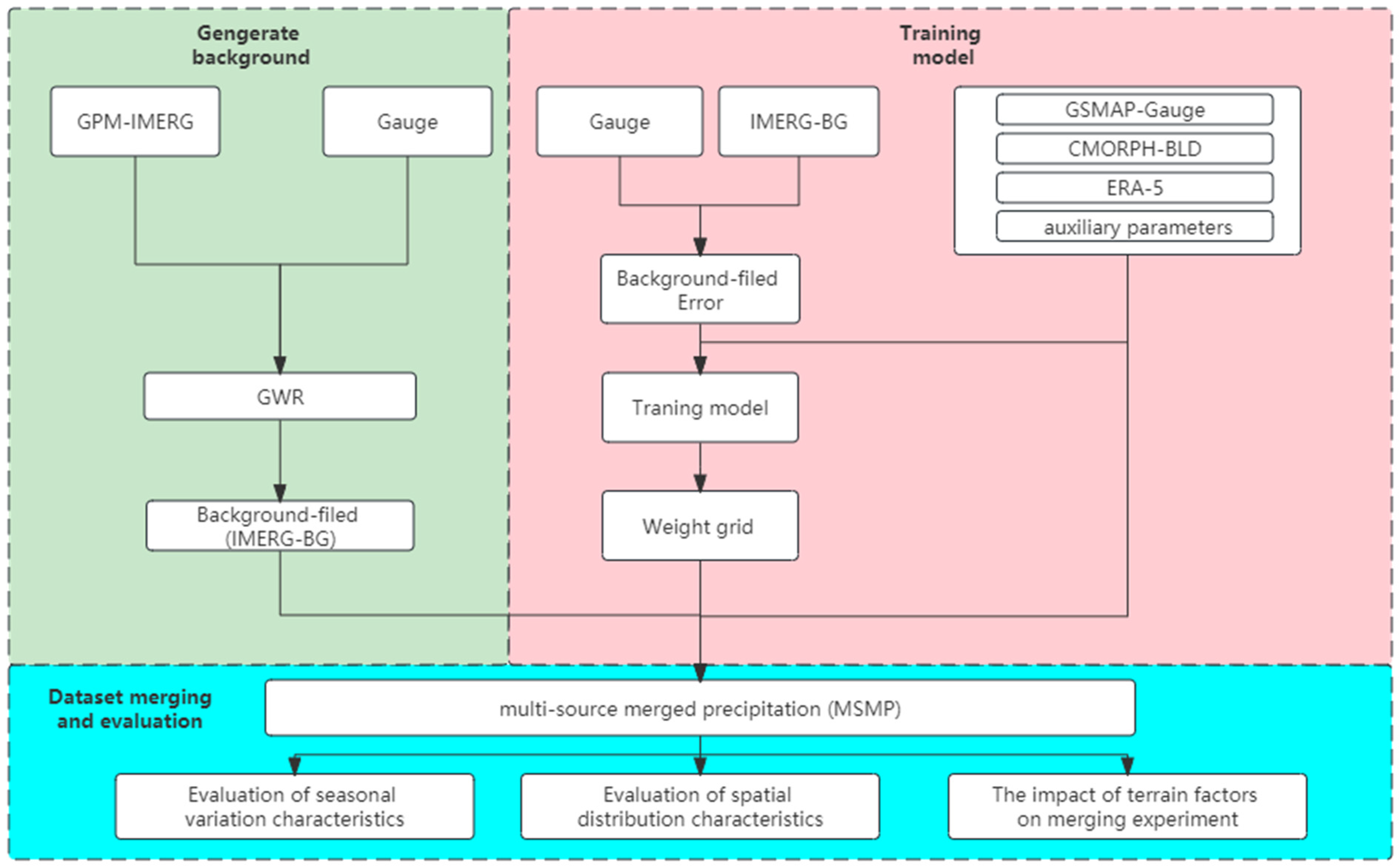
The experimental scheme of this study is mainly divided into three parts: (1) Determining the initial background field. After evaluating the accuracy of the original observation data, this study selects the appropriate precipitation data as the background field, corrects it with the gauge data, and finally obtains the background field with a higher accuracy of 0.1° resolution. (2) Model training. The error between gauge data and the initial background field is the output of a model. The precipitation data of other satellites, reanalysis precipitation data, and auxiliary parameters are input, and the relative weight of each precipitation datum is calculated, predicting the weight matrix in the other grids without a station. (3) Data merging. Combined with the weight matrix obtained by the above method, multi-source precipitation data and auxiliary parameters are used to adjust the initial background field.
3.1. Determination of Background Field
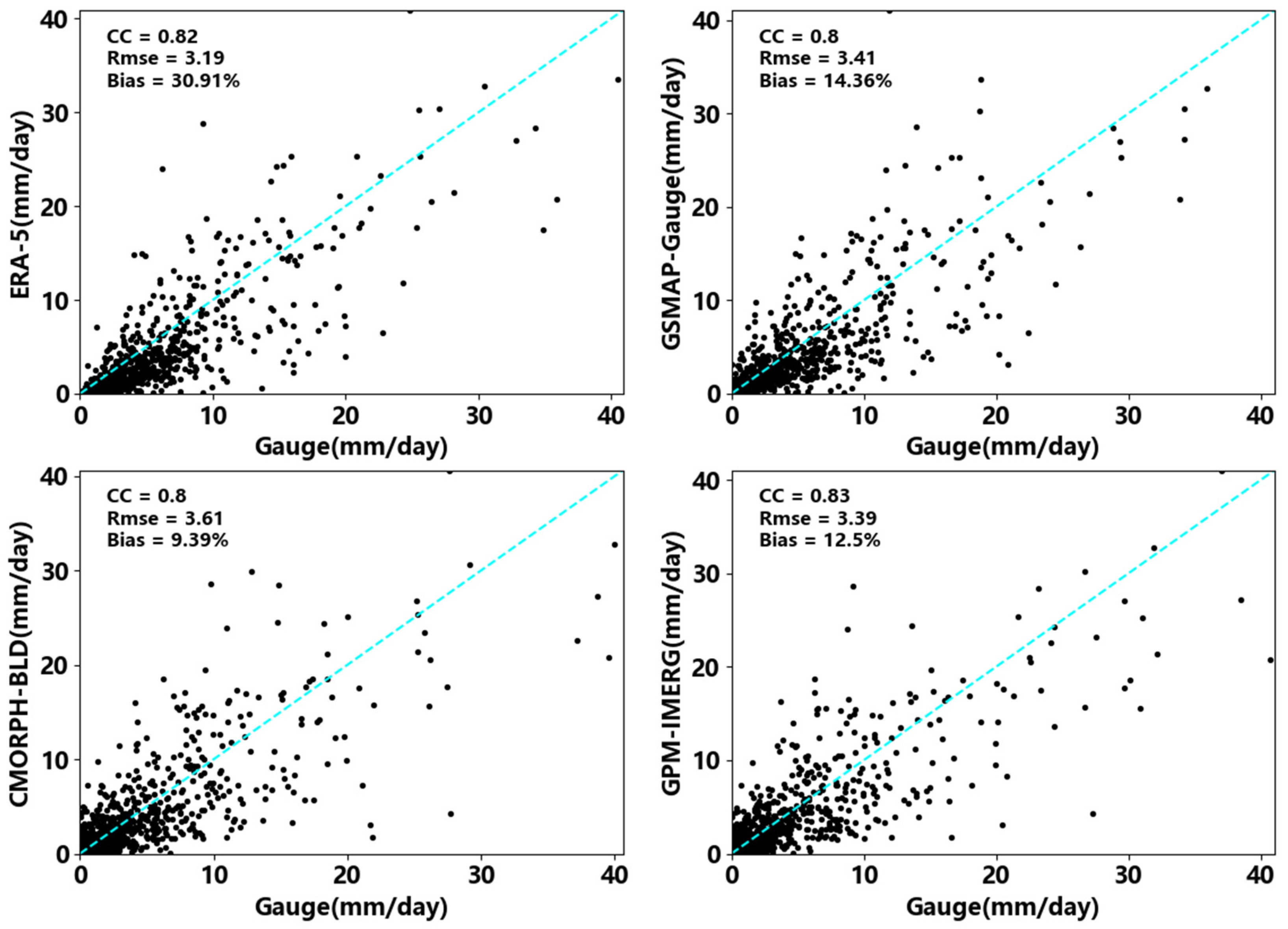
In the merging experiment, the initial background field is the basis of the final merging data, and its spatial distribution characteristics of precipitation and the overall data accuracy greatly affect the effectiveness of the merging experiment. Since the background field information needs to provide the approximate precipitation distribution structure within the observation range, we often use satellite data and reanalysis data with continuous precipitation information as the initial background field [10,35]. We compare the correlation between the satellite data used in this study and the reanalysis data and the gauge data; Figure 2 shows the scatterplot of the daily precipitation of the four precipitation datasets used in this study from 1 February 2018 to 31 December 2020. Each scatterplot represents the daily average precipitation of the four grids of precipitation data and the gauge data in Sichuan province. It can be seen that the ERA-5 precipitation data have the lowest RMSE, but the evaluation index of its bias is too high, and there is an apparent underestimation phenomenon, indicating that there may be more abnormal values in the ERA-5 precipitation data. The CMORPH-BLD precipitation data have the lowest bias evaluation results, but the CC and RMSE evaluation results are the worst, which may not sufficiently reflect the distribution characteristics of actual precipitation. GPM-IMERG precipitation data have the best correlation, and the evaluation results of RMSE and bias are relatively good. Compared with the other three precipitation data, it should be able to reflect the Sichuan region’s precipitation characteristics better. Some researchers have evaluated the applicability of GPM-IMERG precipitation data in Mainland China, and the results showed that GPM-IMERG has quite a good precipitation detection ability and can effectively estimate the spatiotemporal distribution characteristics of precipitation [36,37]. Therefore, this study is based on the GPM-IMERG data, and these are combined with the data of some stations to perform correction experiments to obtain the GPM-IMERG correction data. It is used as the initial background field (IMERG-BG below). The calibration method adopts the GWR method, a spatial regression model based on variable parameters proposed by Fotheringham et al. [38,39]. Compared with traditional spatial interpolation methods, IDW, OK, and other classical methods only use the spatial autocorrelation of precipitation for estimation. The GWR method estimates precipitation by combining gauge observation and geographic information and quantitatively describes the non-stationary relationship between spatial variables based on kernel regression and local smoothing. It can directly describe and explain the quantitative relationship between spatial variables to provide uncertainty estimation of the valuation results and has good computational flexibility so it has obvious advantages over the traditional multiple regression method [40,41]. The basic idea is first to calculate the difference between the actual value and the estimated value around the estimated point, take the spatial distance between the estimated point and the measured point as the dependent variable, use the spatial weight kernel function to calculate the error weight of the estimated point, and obtain the final estimate through the error weight. The formula is shown in Equation (1):
where (u,v) represents the spatial position of the sample point to be measured, x0(u,v) is the constant estimate of the sample point to be measured, xk represents the k-th observation value around the observation point, wk is its corresponding weight, and θ is its random error term.
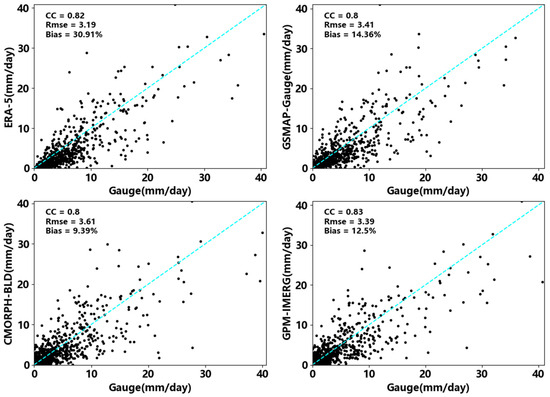
Figure 2.
Evaluation of four precipitation data.
The observation points’ weights are adjusted according to the spatial distance (Euclidean distance) between the observation points and the measured points. In order to determine the appropriate kernel function, three commonly used spatial kernel functions are tested in this study. These include the Gaussian kernel, bi-square kernel, and K-nearest-neighbor kernel functions. By comparing and verifying three calibration experiments using different kernel functions, the results show that the Gaussian kernel function can obtain a better calibration effect, so the Gaussian distance weight method is used to estimate the weight information in this study. Its formula is shown in Equation (2):
where w is the weight of the observation point, d is the Euclidean distance between the observation point and the sample point to be measured, and b is the basic bandwidth of the kernel function.
3.2. Model Training
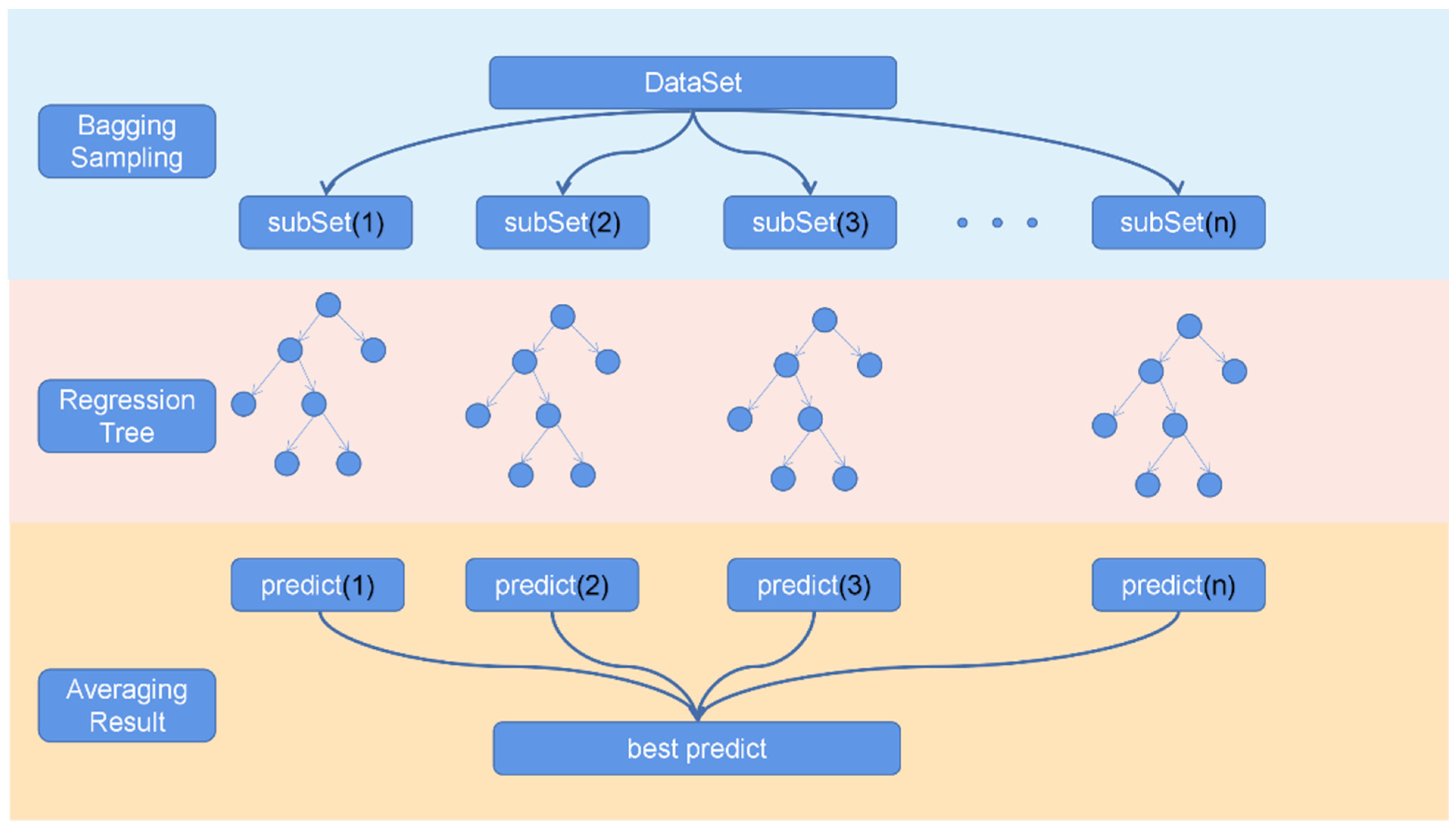
In this study, the weights corresponding to various precipitation information are determined based on the errors between the gauge data and IMERG-BG data, and the other auxiliary parameters are involved in the merging experiment to complete the correction of the IMERG-BG data. The grid with the gauge data is screened out, and the errors between the gauge data and IMERG-BG data are calculated. The grid’s remaining precipitation data and auxiliary parameters are obtained by the nearest proximity method, and a model relationship between satellite data, reanalysis data, and other auxiliary parameters and the errors of IMERG-BG data is built. Random forest (RF) is a classification regression algorithm based on the decision tree model proposed by Breiman [42]. It is an extension of the classification regression tree (CART), which improves the accuracy and stability of the regression model by training multiple classification regression trees and merging the prediction results of multiple trees. Random forest selects the label values of the training data and subsets of the input variables based on the random variables by introducing independent and equally distributed random variables. In addition, in order to improve the accuracy of model prediction, random forest also includes a bagging algorithm [43], which randomly samples multiple training subsets from the training datasets through a random retracting sampling algorithm, and simultaneously trains the obtained multiple training subsets of the decision tree model to generate multiple different weak trainers. Finally, averaging the prediction results of all the models obtains the final predicted value. Random forest is an effective method for classification and regression which can significantly alleviate the overfitting phenomenon. This algorithm integrates the results of classification regression trees with multiple decision trees by the bagging method, cancels part of the random errors, and has a good tolerance for random noise and outliers. Therefore, this study uses a random forest algorithm to fit the model relationship between the three precipitation datasets, auxiliary parameters, and background field errors. Since the model problem in this study is a regression problem in nature, we use the RMSE between the predicted value of the model and the actual error as a loss function to evaluate the quality of the training model, and the final prediction error of the training model is less than 2 mm. Figure 3 is the schematic diagram of random forest.
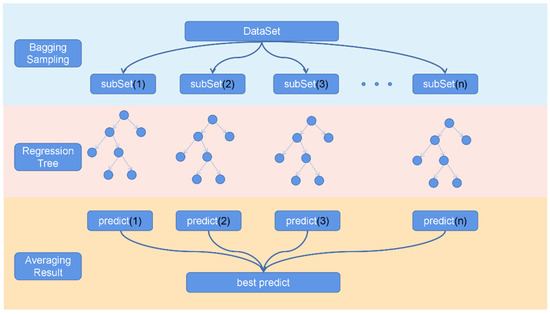
Figure 3.
Schematic diagram of random forest.
3.3. Data Merging
Based on the above research scheme, we use a random forest algorithm to train the weights of precipitation data and auxiliary parameters in the grid with gauge observation to minimize the background field error. Then, in the grid without gauge observation, the error of the background field is directly predicted using the trained model, three precipitation datasets, and the values of the auxiliary parameters. Finally, the error and background field data are added to complete the multi-source precipitation merging experiment. The mathematical description of the whole experiment scheme can beis described by Equation (1), where y is the final merging data, x0 is the IMERG-BG data, m is the number of precipitation products contained in the grid, k is the data of the k-th precipitation data, Wk is its corresponding weight, and θ is the relative deviation obtained according to the other auxiliary parameters.
3.4. Result Evaluation Index
The evaluation indicators used in this study are classified into qualitative and quantitative. Quantitative indicators include the correlation coefficient (CC), bias, mean absolute error (MAE), root-mean-square error (RMSE), and normalized root-mean-square error (NRMSE), which can be used to quantitatively evaluate the correlation and error size between the merging data and the gauge data. Qualitative evaluation measures include the probability of detection (POD), false-positive rate (FAR), and critical success ndex (CSI), which can be used to evaluate the ability of observed data to detect precipitation events. Among them, we define the presence of precipitation events as when the daily precipitation is higher than 0.1 mm. Table 2 shows the calculation formula of the evaluation index.

Table 2.
The calculation formula for the evaluation index.
In the above table, y(i) represents the i-th sample of the precipitation estimation datasets, ytest(i) represents the i-th sample of the validation datasets, m represents the total number of samples, H represents the number of events in which precipitation estimation data can accurately detect precipitation, and F represents the number of events in which precipitation estimation data incorrectly detect precipitation and precipitation does not occur. M represents the number of events in which the precipitation estimation data failed to detect precipitation.
The overall technological route is shown in Figure 4.
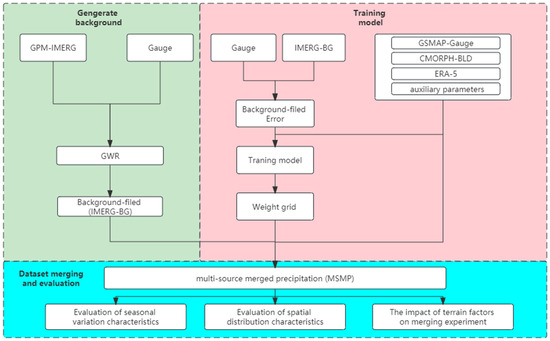
Figure 4.
Technological route of experiment scheme.
4. Analysis and Inspection of Result
4.1. Merging Data Selection
Most current merging experiments are satellite and gauge data two-source precipitation merging experiments [29,44,45,46,47,48]. However, due to the error of the inversion algorithm and sensor observation error, it is often difficult to observe trace precipitation, or it is possible to underestimate heavy precipitation, in satellite data. Therefore, precipitation data from three sources are selected for this study’s merging experiment: measured precipitation data from the gauge, satellite data, and reanalysis data. In order to evaluate the influence of reanalysis data on the merging experiment, this study conducts a two-source merging experiment of satellite and station data successively and a comparative analysis of the three-source merging experiment of satellite data, reanalysis data, and gauge data. The results are shown in Table 3.

Table 3.
Accuracy evaluation of each dataset under the validation dataset.
Table 3 shows the overall accuracy evaluation of each dataset. After analyzing the evaluation results of several original satellite data and reanalysis data, it can be seen that the GPM-IMERG precipitation data have a relatively good evaluation performance, and the correlation and RMSE error between the GPM-IMERG precipitation data and gauge data are better than those of other precipitation observation data. However, the GMAP-Gauge precipitation data perform best in assessing POD and FAR, which shows that the GMAP-Gauge precipitation data have a better ability to detect precipitation events qualitatively. This study focuses on error correction of precipitation data to provide gridded precipitation data with higher accuracy and correlation with the gauge data. In addition, the accuracy of precipitation data is greatly improved after the error correction with the gauge data and the multi-source precipitation merging experiment. The multi-source merging precipitation data’s evaluation performance is the best in qualitative and quantitative evaluation analysis. Secondly, by comparing the evaluation of the two merging experiments, we find that the three-source precipitation merging experiment adding reanalysis data slightly improves in terms of the quantitative evaluation compared with the two-source merging experiment of satellite and station and has better performance in CC, RMSE, and bias. However, the difference between the two merging experiments is insignificant in the qualitative analysis. Generally speaking, merging the experiment with reanalysis data has a better effect. Therefore, in this study, satellite, gauge, and reanalysis data are used as the data source of the merging experiment, and the final merging experiment results are evaluated in many aspects.
4.2. The Effect Evaluation of the Merging Experiment
4.2.1. Evaluation of Seasonal Variation Characteristics
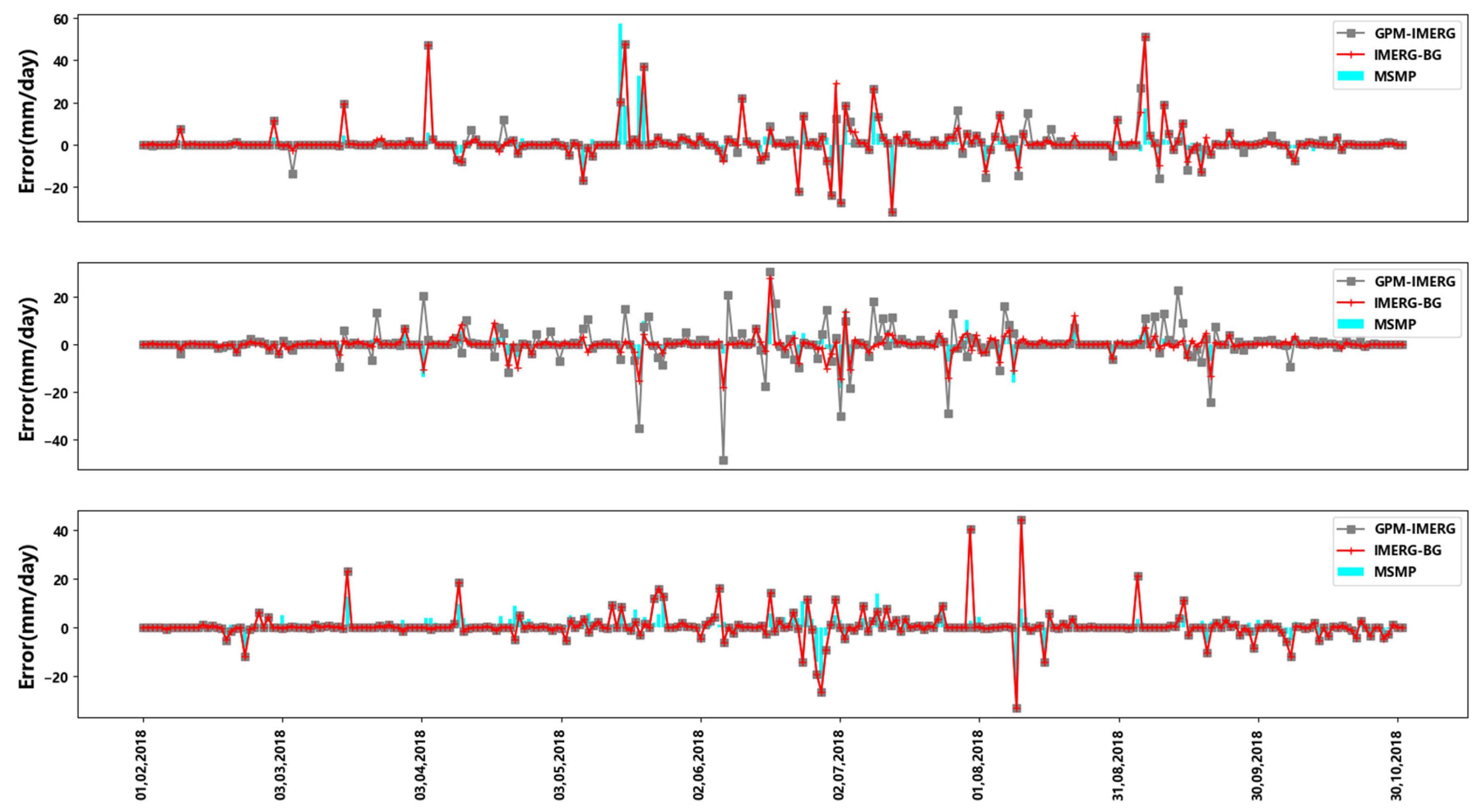
In order to explore the change of actual precipitation with merging precipitation data, this study selects a national meteorological station in each of the three research areas to study the change of precipitation at a single station from 1 February 2018 to 31 October 2018. Figure 5 compares the error changes of the three kinds of precipitation data (GPM-IMERG, IMERG-BG, MSMP) in three national meteorological stations. It can be seen that, after the calibration of the GPM-IMERG satellite data with the gauge data and the multi-source merging experiment, the difference between the satellite precipitation and the gauge precipitation decreases significantly. The variation trend of the difference over time does not change significantly, indicating that the correction of satellite data in this study is only the corresponding error correction of the precipitation value. It makes it closer to the gauge data but does not change the temporal variation characteristics of the original precipitation data.
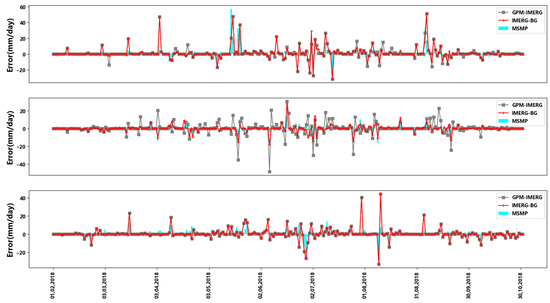
Figure 5.
Precipitation changes of the three stations from 1 February 2018 to 31 October 2018.
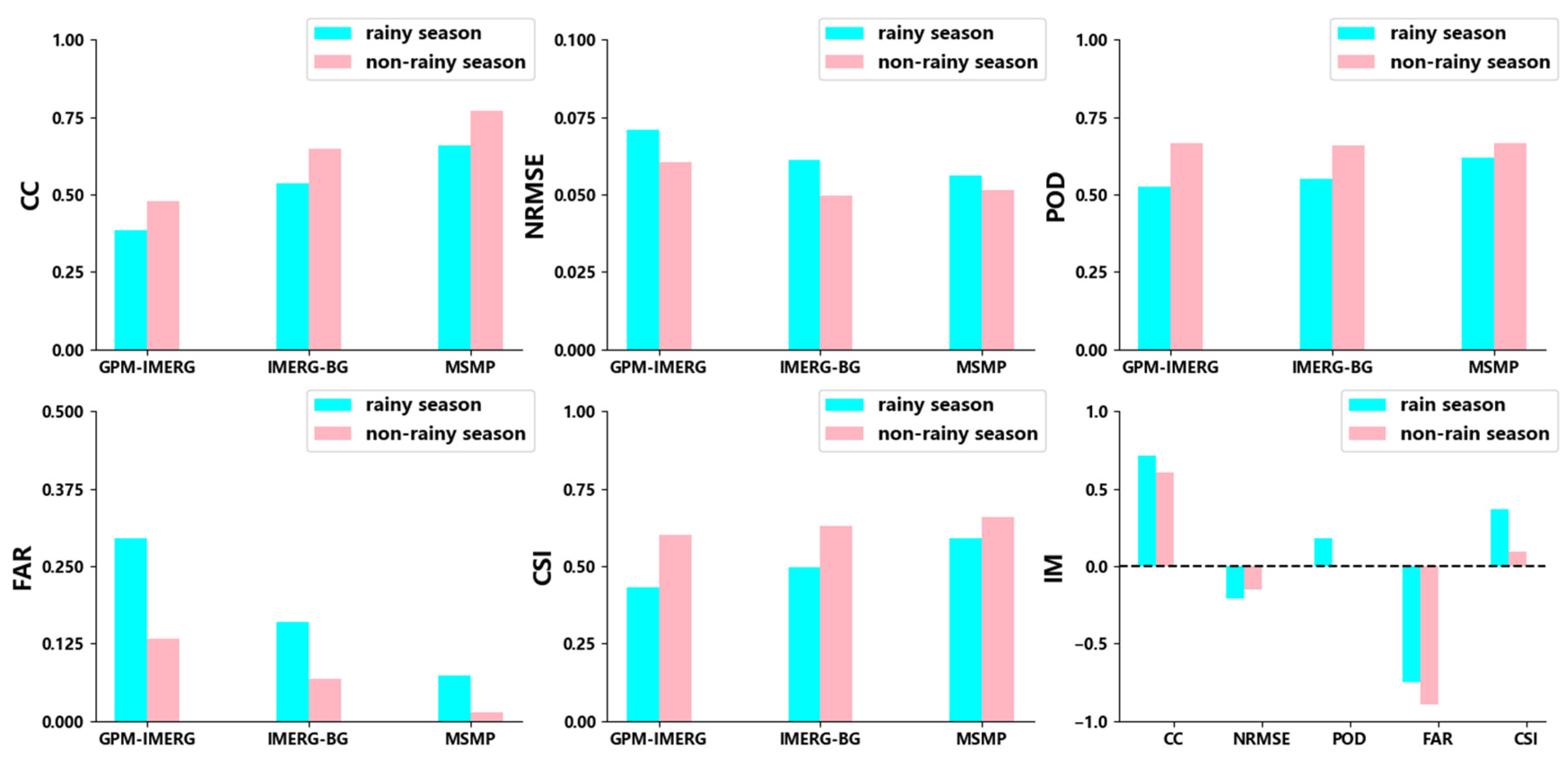
Figure 6 shows the evaluation results of the three kinds of precipitation data in the merging experiment in the rainy season (June to September) and non-rainy season (February to May) of 2018. Among them, the IM index represents the accuracy improvement of the MSMP data in each evaluation index compared with the GPM-IMERG data. It can be seen that, under the quantitative evaluation index, the evaluation performance of satellite data in the rainy season is weaker than in the non-rainy season. After the multi-source merging experiment, the difference in evaluation performance is slightly improved. The multi-source merging experiment has a better effect on improving the accuracy of the satellite observation data during the rainy season. However, on the whole, the multi-source merging precipitation data achieve stronger detection of precipitation information during the non-rainy season.
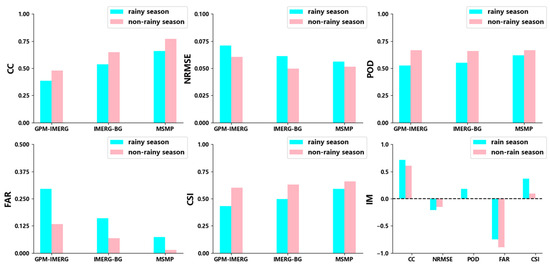
Figure 6.
Evaluation of the GPM-IMERG, IMERG-BG, and MSMP precipitation datasets during the rainy season and non-rainy season in 2018.
Regarding qualitative evaluation indicators, the multi-source merging experiment does not improve the POD index of precipitation events in the non-rainy season. However, it greatly reduces the FAR index of precipitation events, which may be because the precipitation in the non-rainy season is too low, and there is no obvious precipitation phenomenon in many cases [49]. As a result, the training degree of the multi-source precipitation merging model in this period insufficient, so the merging experiment did not improve the POD index of precipitation events. However, on the whole, the MSMP data are better for the detection of precipitation events in non-rainy seasons.
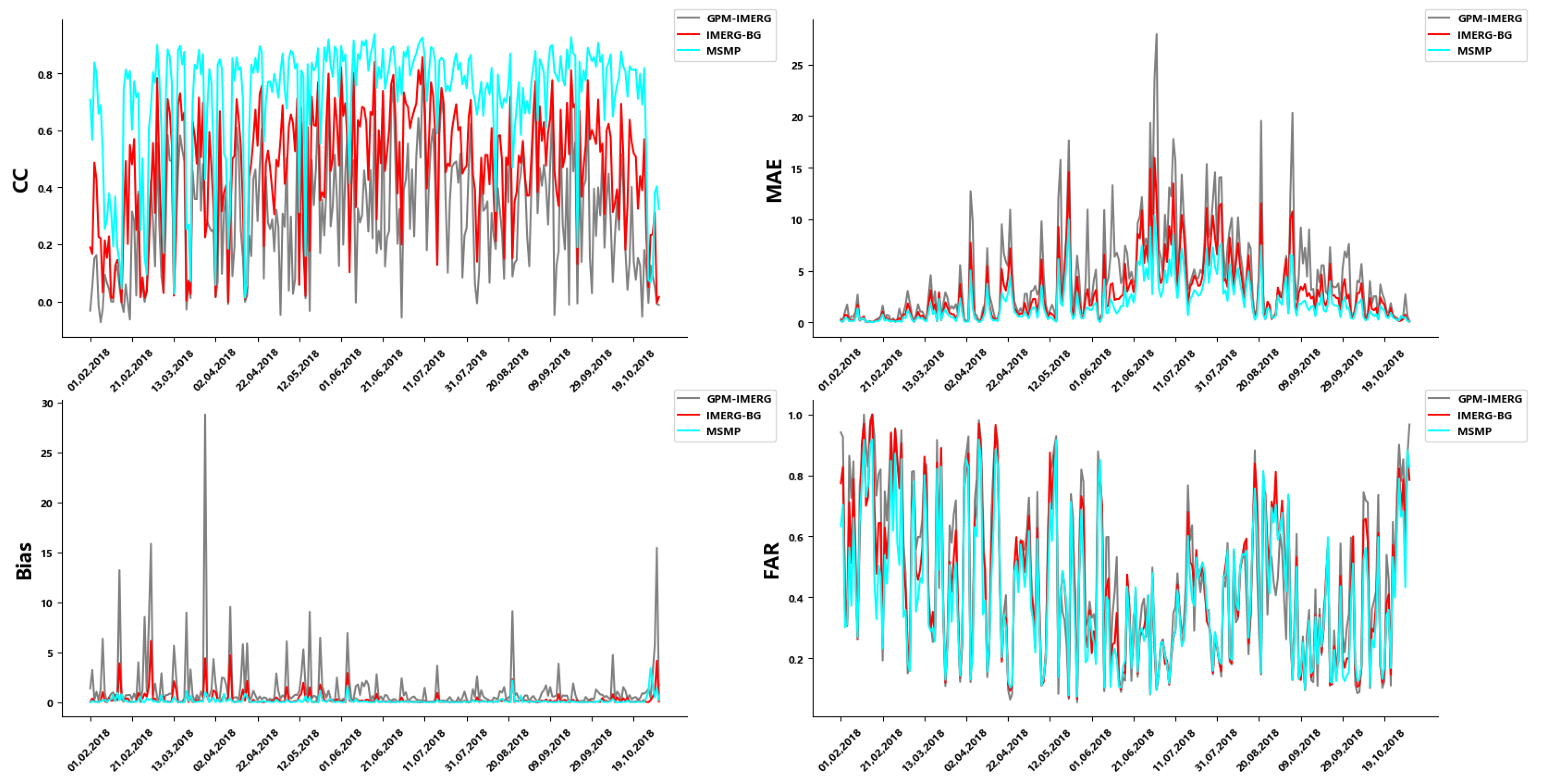
Figure 7 shows the accuracy evaluation of GPM-IMERG, IMERG-BG, and MSMP daily precipitation data. Qualitative and quantitative evaluation indicators show that the original satellite dataset has the lowest accuracy. After calibration with some gauge data, the accuracy of the dataset is improved to some extent, and the accuracy of the dataset is highest after the multi-source merging experiment. In addition, compared with the GPM-IMERG data, the variation trend of the accuracy of the MSMP data does not change much, indicating that the overall experiment scheme not only improves the accuracy of the satellite data but also relatively retains the change of the precipitation sequence of the original satellite data, and only slightly adjusts the numerical value, so that the accuracy of the datasets is greatly improved.
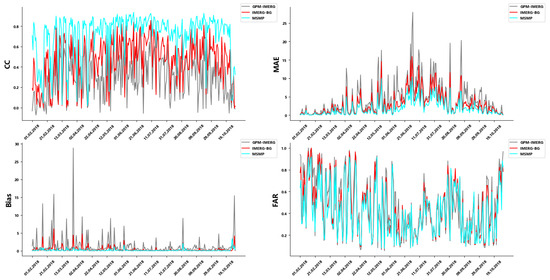
Figure 7.
Variation trend of evolution index of GPM-IMERG, IMERG-BG, and MSMP precipitation datasets.
4.2.2. Evaluation of Spatial Distribution Characteristics
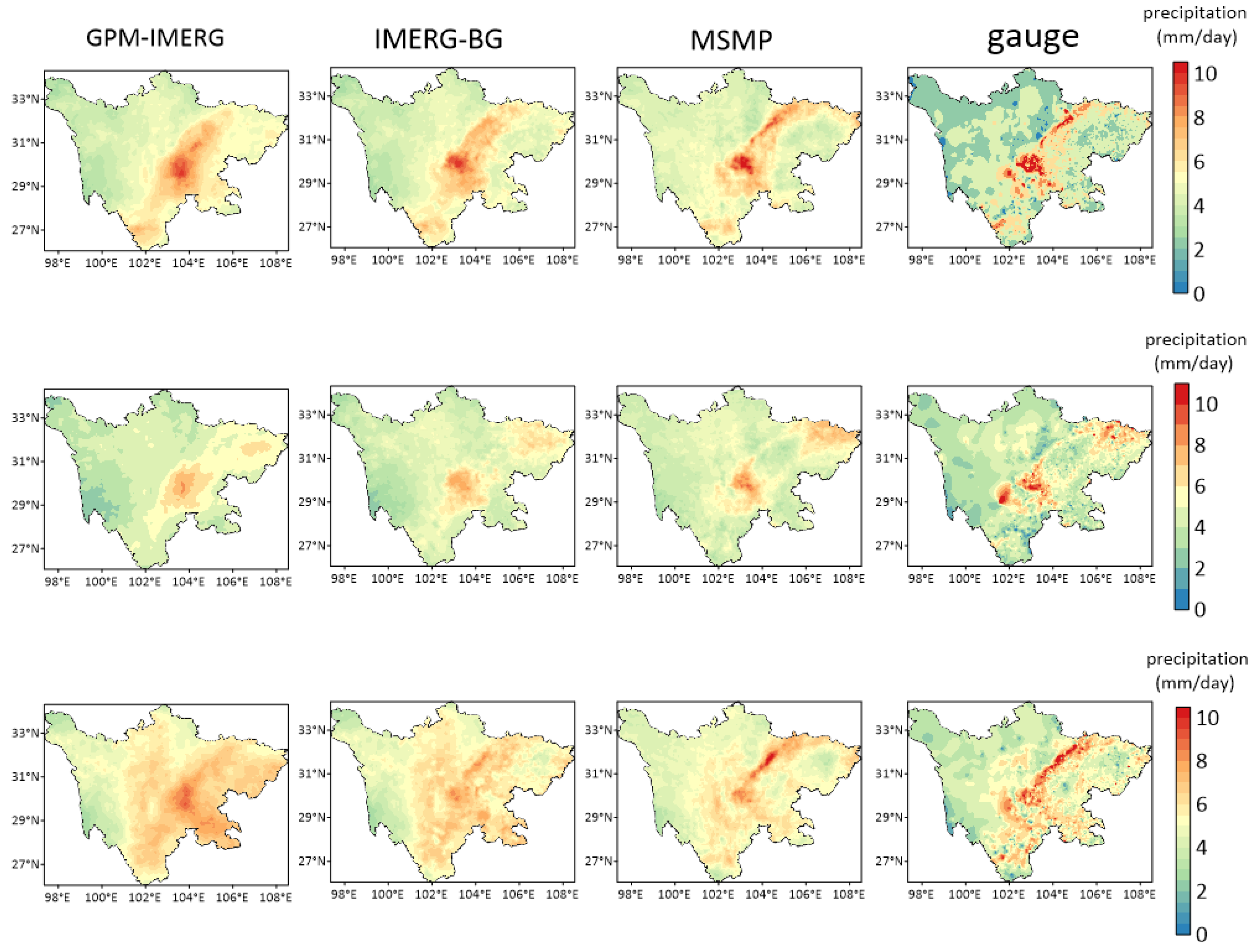
Figure 8 shows the spatial distribution of the average daily precipitation of the GPM-IMEG precipitation data, IMERG-BG precipitation data, MSMP precipitation data, and gauge data during the rainy season from 2018 to 2020. As can be seen from the figure, the overall spatial distribution structure of GPM-IMERG precipitation data is the same as that of the gauge data, but there are still some differences in the local scope. After the error correction experiment and multi-source precipitation merging experiment, the spatial distribution characteristics of satellite precipitation data gradually change and close to the gauge data’s spatial precipitation distribution. The MSMP data show prominent correction compared to the GPM-IMERG data. For example, in terms of precipitation distribution in 2019, the precipitation of the original satellite precipitation data in northeast Sichuan province is low, which is underestimated compared with the gauge data. After a series of correction experiments, the average daily precipitation of the multi-source precipitation merging data in Northeast China increases somewhat, and the spatial distribution is closer to that of the gauge data. In addition, we can see that the precipitation in the plateau and mountain areas of northwest Sichuan province is relatively low, and the daily average precipitation is below 4 mm. Currently, the multi-source precipitation merging experiment presents an overestimation phenomenon. In the south of Sichuan province and the surrounding areas of the Sichuan Basin, there is heavy precipitation, while, in the central area of the basin in the east, the precipitation is relatively reduced. So, in study Area II, there is a north–south heavy precipitation zone, which is more evident in the spatial precipitation distribution in 2018 and 2020. The unique geographical factors and climate of Sichuan province influence this precipitation feature. The Sichuan Basin has a subtropical humid monsoon climate and is surrounded by mountains. In summer, warm and humid air from eastern China cannot easily create rainfall in the basin’s center. The northwestern mountainous area is located on the southeastern edge of the Qinghai–Tibet Plateau. It has relatively little annual precipitation, while, in the southern part of Sichuan province and the edge of the basin, its large altitude difference causes sufficient rainfall [49,50].
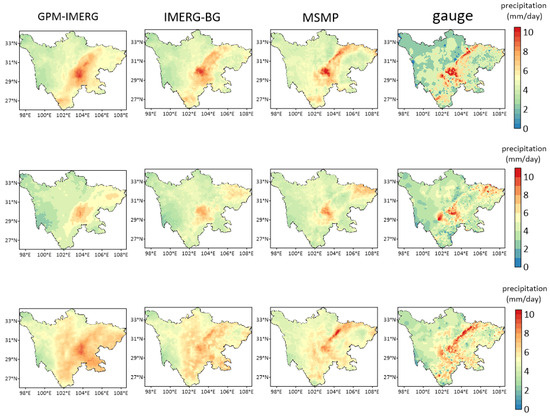
Figure 8.
Spatial distribution characteristics of daily average precipitation of the GPM-IMERG, IMERG-BG, MSMP, and gauge datasets in the rainy seasons of 2018, 2019, and 2020.
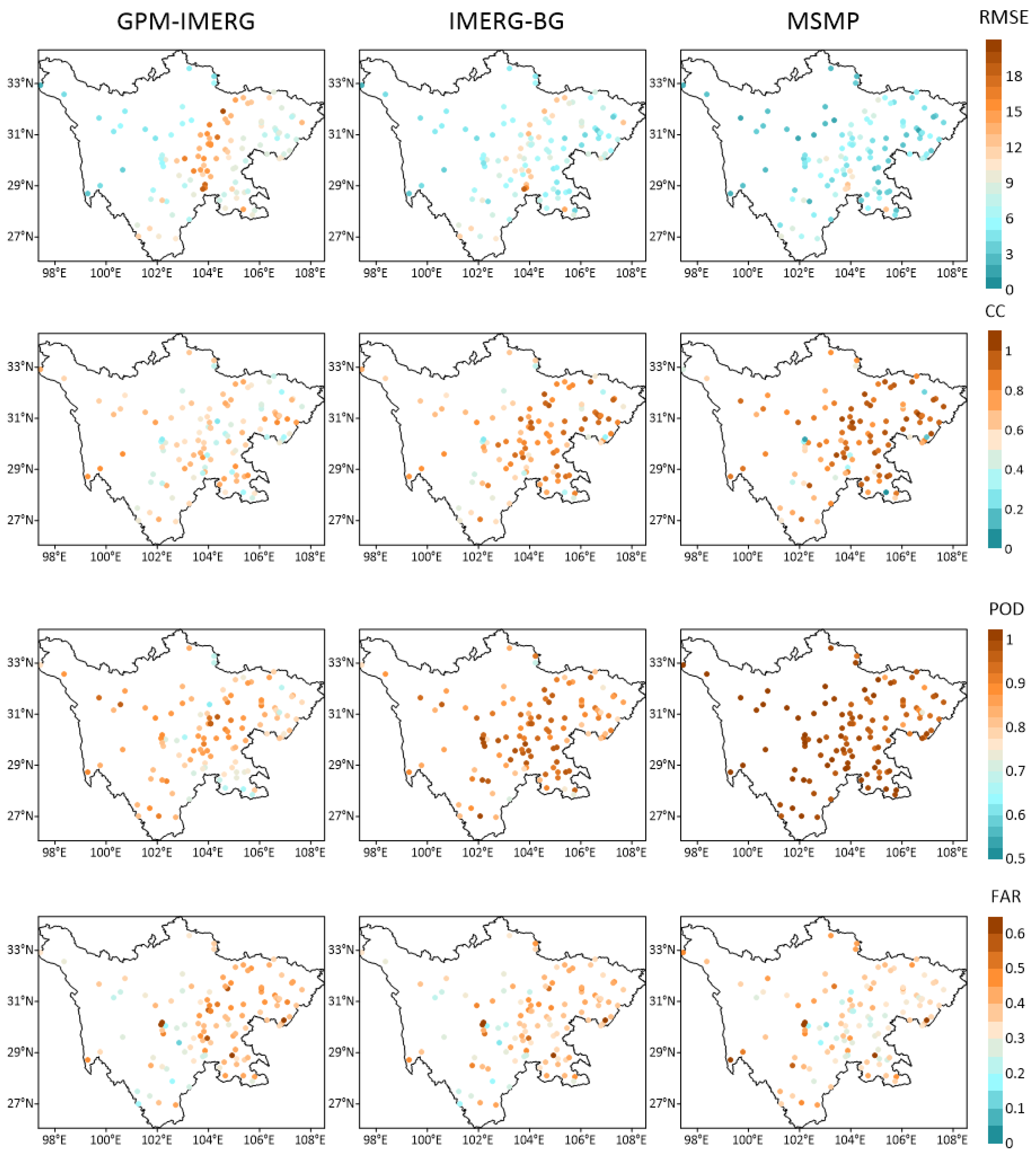
In this study, 130 national meteorological stations are selected to study the improvement effect of the data accuracy of the merging experiments in independent spatial stations. Figure 9 shows the accuracy evaluation of the three kinds of precipitation data from some stations from 1 February 2018 to 31 October 2018. After the merging experiment, in the whole research area, compared with the original satellite data, the accuracy of the multi-source merging precipitation data is improved to a certain extent. Especially in the eastern plain and basin area, the stations are densely distributed, and the effect of the merging experiment is relatively better. Both quantitative and qualitative evaluations perform better. The CC index increases from about 0.5 to 0.8 in most regions, the RMSE index from 15 mm to about 8 mm, the POD index increased from about 0.7 to more than 0.9, and the FAR index decreased from 0.45 to about 0.35.
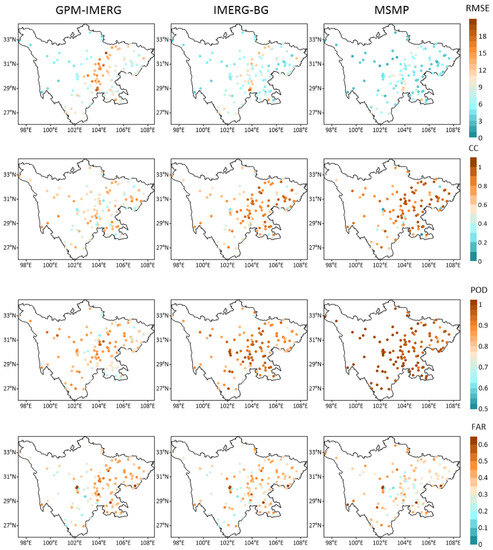
Figure 9.
Accuracy evaluation of the GPM-IMERG, IMERG-BG, and MSMP precipitation datasets at 130 stations.
4.2.3. The Effect of Topographic Factors on Merging Experiments
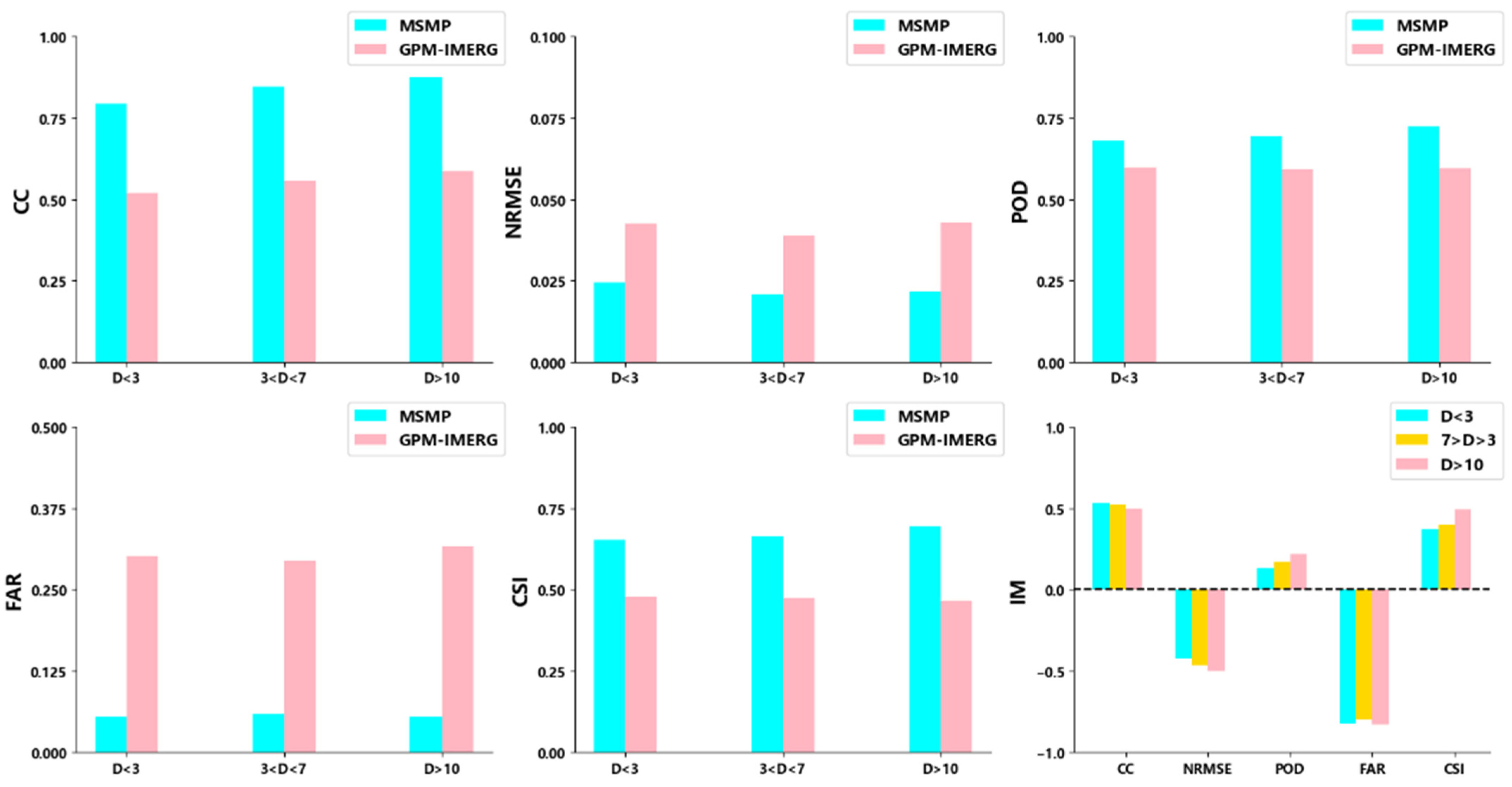
The conventional multi-source merging method is based on multiple regression analysis of gauge data. The effect of the merging experiment often depends on the distribution density of the stations in the study area, and the merging experiment is relatively better in the area with dense stations. In this study, the random forest algorithm is used to conduct the multi-source precipitation merging experiment, and the merging model is built according to the relationship between the precipitation observed by satellites and gauge data, which is relatively less dependent on the station density of the data. In order to verify this phenomenon, in the research area with an elevation of less than 1000 m, the accuracy of the original satellite data and the multiple merging data are evaluated according to the station density D (the number of stations in the 0.1° grid), that is, D < 3, 3 < D < 7, and D > 7. The results are shown in Figure 10, where the IM index of the multi-source merging precipitation data improves compared with the original satellite data under various indicators. It is not difficult to see that, no matter the research area, precipitation data has better performance under various evaluation indicators after the multi-source precipitation merging experiment. It can be seen that there are minor differences in different station density regions, which may be because the MSMP data are obtained based on the initial background field, which is obtained by correcting the original satellite data using the gauge data. The correction effect may be affected by the distribution density of the stations, but the impact is negligible. Therefore, the station density also affects the final experiment effect less.
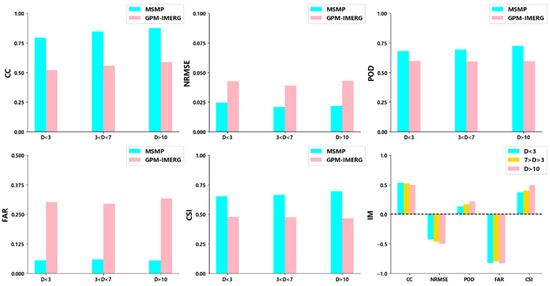
Figure 10.
Accuracy evaluation of GPM-IMERG datasets and MSMP datasets at different station densities.
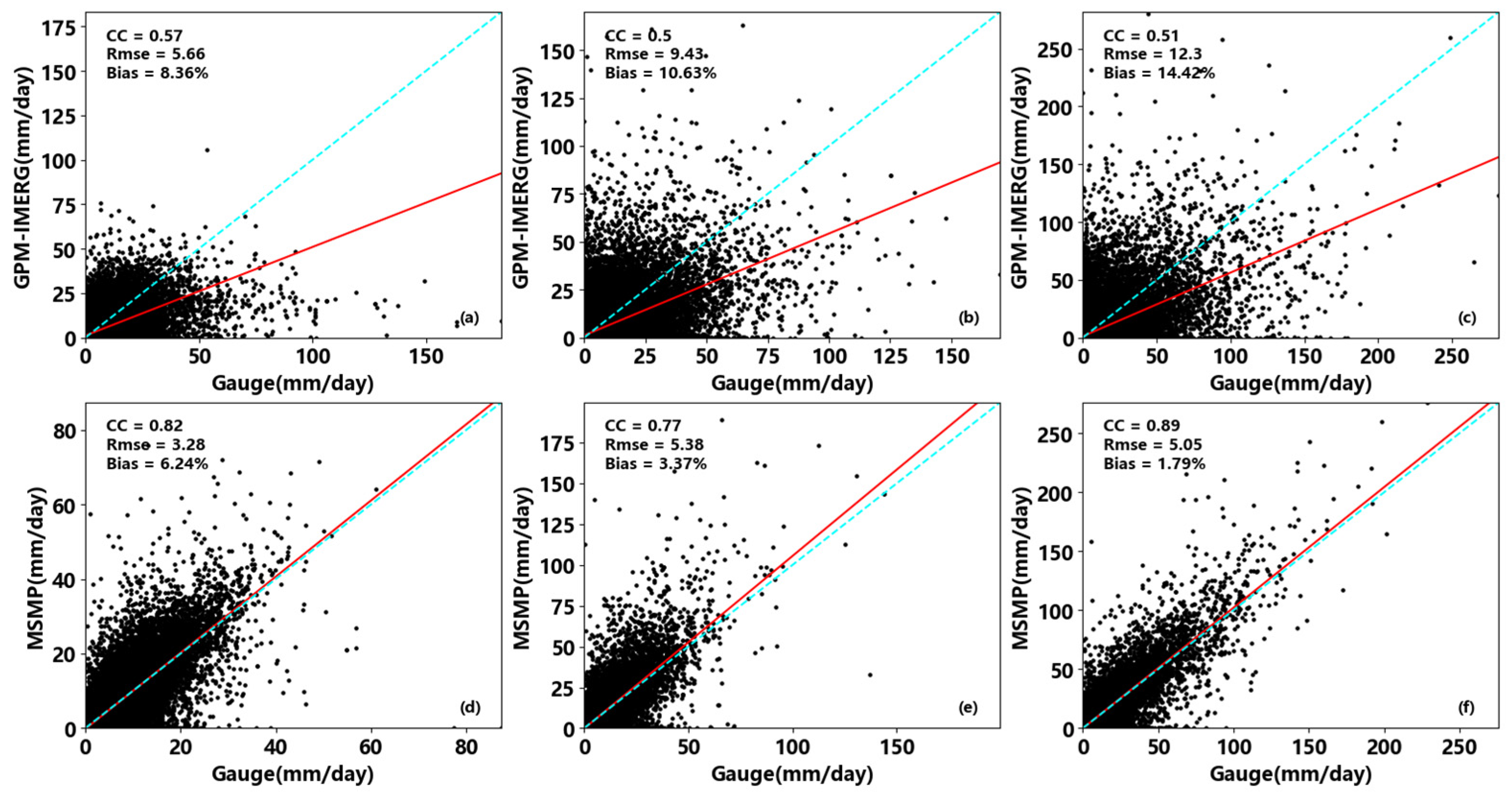
To further investigate the influence of topographic factors on the experiment, the Sichuan province is divided into three study regions based on DEM elevation. Only stations with D < 3 in the three study areas are selected to ensure unbiased evaluation results. The evaluation results are depicted in Figure 11, and all evaluation indices demonstrate a significantly higher accuracy for the MSMP data than for the GPM-IMERG data. Following the merging experiment, the multi-source merging precipitation data exhibit a strong correlation with the gauge data, as supported by the data presented in Table 4. Moreover, through both qualitative and quantitative evaluation metrics, it is observed that the merging experiment conducted in study Area I yields the most favorable outcomes, with all dataset indicators showing the most substantial improvement, which might be attributed to the more stable spatiotemporal distribution of precipitation in the plains and basins, making it easier for the model to capture the consistent features of precipitation distribution.
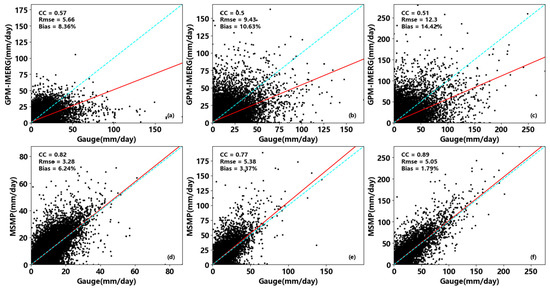
Figure 11.
(a–c) are the regression analysis of GPM-IMERG datasets and gauge data in study area III, II, I; (d–f) are the regression analysis of MSMP datasets and gauge data in study area III, II, I; The blue line represents the ideal regression line, and the red line represents the actual regression line.

Table 4.
Accuracy evaluation of MSMP datasets and GPM-IMERG datasets in the three study areas.
5. Discussion
This study uses satellite and model reanalysis data, including GPM-IMERG, CMORPH-BLD, GSMAP-Gauge, and ERA-5 data. It uses the gauge data as the benchmark to correct and merge the above data. Finally, the multi-source merging precipitation data (0.1°, daily) of the station, satellite, and reanalysis data are obtained. Firstly, the accuracy evaluation and error characteristics analysis of the used satellite data and reanalysis data are carried out. The results show that all the satellite observation data and reanalysis data are more or less overestimated compared with the gauge data, and the overestimation phenomenon is more evident in the ERA reanalysis data. The correlation between the GPM-IMERGE data and the gauge data is the best. Through quantitative and qualitative evaluation of all the observed data, we find that the GPM-IMERG precipitation data perform better in quantitative evaluation, and its CC, RMSE, and bias index are all better. However, its evaluation result is weaker in qualitative evaluation than the GSMAP-Gauge precipitation data. GSMAP-Gauge precipitation products show the best evaluation, with a POD index of 0.63 and a CSI index of 0.58. In general, GPM-IMERG precipitation shows relatively good evaluation. After calibration with the gauge data, all evaluation indexes improve to some extent, meeting our demand for the initial background field of the merging experiment [10,27]. In addition, to verify the influence of the reanalysis data of the addition model on the merging experiment, we compare two merging experiments (Table 3). It can be seen that the three-source merging precipitation data have a better performance in the quantitative evaluation. However, in the qualitative evaluation, the merging experiment effect differs significantly from that of the two-source merging experiment of satellite and station.
The method used in the multi-source merging experiment in this study is a random forest algorithm, and the topographic elements, including slope, elevation, longitude, and latitude, are calculated. Compared with the original satellite data, the evaluation performance of the obtained multi-source merging precipitation data is much better than that of the original satellite data, both in the spatial distribution structure of precipitation and the qualitative and quantitative evaluation of precipitation value, showing the advantages of multi-source merging precipitation data. The random forest algorithm determines the proportion of each precipitation value according to the errors of various precipitation products and auxiliary variables and the gauge data. It determines the weight of precipitation in each grid through the respective precipitation values and auxiliary parameters. The effect of the merging experiment has no significant relationship with the density of stations in a single grid (Figure 9). However, the traditional statistical regression algorithms are more or less dependent on the number of stations in the grid and the area without station observation; the accuracy of the obtained merging precipitation has a significant estimation error [35,51].
In order to evaluate the influence of terrain elements on the merging experiment, the study area is divided into three parts based on elevation, and the accuracy of the three different research areas is evaluated and compared. The results show that terrain elements have a certain influence on the effect of the merging experiment because the detection ability of the original satellite data on surface precipitation is also affected by terrain features, such as altitude and slope. This influence also leads to a certain deviation in the model relationship between the satellite precipitation and gauge data. It has been shown [35] that the precipitation estimation of multi-source precipitation merging products in regions with higher altitudes is highly unstable.
6. Conclusions and Prospects
The following conclusions are obtained through the comprehensive evaluation and analysis of multi-source merging precipitation data:
- (1)
- Through qualitative and quantitative evaluation and analysis of the above grid precipitation data, we find that GPM-IMERG precipitation products perform relatively well under quantitative evaluation indicators and have the best RMSE and CC index;
- (2)
- After the multi-source merging precipitation experiment, satellite data’s accurate evaluation has been greatly improved. In addition, the spatiotemporal distribution changes of precipitation are consistent with the original satellite precipitation data. The correlation with gauge data is also greatly improved. The merging experiment in the non-rainy season improves the accuracy of the satellite data;
- (3)
- Topographic factors have a certain influence on the merging experiment. In the plain and basin area with low elevation and gentle terrain, the merging experiment has a better effect, while, in the plateau and mountain areas with high altitudes, the merging experiment has an unstable effect.
This study focuses on merging multi-source precipitation data, including three global satellite data, reanalysis data, and gauge data. The merging approach incorporates terrain factors as additional parameters and utilizes the random forest algorithm to generate daily precipitation datasets for the Sichuan province from 2018 to 2020 with a spatial resolution of 0.1°. By comparing the merged precipitation data with the original observations, significant improvements are observed in both qualitative and quantitative evaluations. The CC index increases from 0.15 to 0.76, the RMSE index decreases from 10.44 mm to 7.91 mm, the POD index increases from 0.62 to 0.67, and the FAR index decreases from 0.15 to 0.05, demonstrating the feasibility of the proposed merging scheme. Furthermore, future research can incorporate additional multi-source precipitation data, such as weather radar, microwave radiometer, and ground-based GPS-MET data, to further enhance the accuracy of the merged datasets. Efforts should also be made to improve the spatiotemporal resolutions of the multi-source merging data, aiming for sub-hourly or even hourly resolution and a spatial resolution of 1 km or finer. Such advancements in understanding the spatiotemporal characteristics of precipitation in the complex terrain of the Sichuan province hold significant importance.
Author Contributions
Conceptualization, H.W., T.Z., Q.Z. and Z.L. (Zhi Li); methodology, H.W., Z.L. (Zhi Li), J.X., T.Z. and R.Y.; software, H.W. and Z.L. (Zhi Li); formal analysis, H.W., J.X., Q.Z. and Z.L. (Zhihao Liu).; writing—original draft preparation, Z.L. (Zhi Li) and Z.L. (Zhihao Liu); writing—review and editing, H.W., T.Z. and Q.Z.; visualization, H.W., J.X. and R.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was sponsored by the Key R&D Program of Yunnan Provincial Department of Science and Technology (202203AC100006-01), the Project of the Sichuan Department of Science and Technology (2023NSFSC0244), the Open Grants of China Meteorological Administration Radar Meteorology Key Laboratory (2023LRM-A01), the Key Laboratory of Atmospheric Sounding Program of China Meteorological Administration (2022KLAS01Z), the Key Grant Project of Science and Technology Innovation Capacity Improvement Program of CUIT (KYTD202201,KYQN202217), the Opening Foundation of Key Laboratory of Atmosphere Sounding, the China Meteorological Administration, and the CMA Research Centre on Meteorological Observation Engineering Technology (U2021Z01).
Data Availability Statement
Publicly available datasets were used in this study. This data can be found here: (1) GPM-IMERG dataset can be obtained at https://disc.gsfc.nasa.gov/ (accessed on 1 March 2022). (2) GSMAP-Gauge dataset can be obtained at https://sharaku.eorc.jaxa.jp/ (accessed on 1 March 2022). (3) ERA-5 dataset can be obtained at https://cds.climate.copernicus.eu/ (accessed on 1 March 2022). (4) CMORPH-BLD dataset can be obtained at ftp://ftp.cpc.ncep.noaa.gov/ (accessed on 1 March 2022). (5) DEM data can be obtained at https://www.gscloud.cn/ (accessed on 1 March 2022). Gauge data are provided by Sichuan Meteorological Bureau and belong to non-public data. Regarding the datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Acknowledgments
We would like to express our heartfelt gratitude to the Sichuan Meteorological Bureau, National Aeronautics and Space Administration, National Oceanic Atmospheric Administration, European Centre for Medium-Range Weather Forecasts, and Japan Aerospace Exploration Agency for providing the data used in this study. Additionally, we extend our appreciation to the reviewers for their valuable feedback and insightful suggestions, which significantly contributed to enhancing the quality of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yan, Y.; Wang, H.; Li, G.; Xia, J.; Ge, F.; Zeng, Q.; Ren, X.; Tan, L. Projection of Future Extreme Precipitation in China Based on the CMIP6 from a Machine Learning Perspective. Remote. Sens. 2022, 14, 4033. [Google Scholar] [CrossRef]
- Zhang, S.; Gao, H.; Naz, B.S. Monitoring reservoir storage in South Asia from multisatellite remote sensing. Water Resour. Res. 2014, 50, 8927–8943. [Google Scholar] [CrossRef]
- Pereira, P.; Oliva, M.; Misiune, I. Spatial interpolation of precipitation indexes in Sierra Nevada (Spain): Comparing the performance of some interpolation methods. Theor. Appl. Clim. 2015, 126, 683–698. [Google Scholar] [CrossRef]
- Antal, A.; Guerreiro, P.M.P.; Cheval, S. Comparison of spatial interpolation methods for estimating the precipitation distribution in Portugal. Theor. Appl. Climatol. 2021, 145, 1193–1206. [Google Scholar] [CrossRef]
- Tarek, M.; Brissette, F.P.; Arsenault, R. Evaluation of the ERA5 reanalysis as a potential reference dataset for hydrological modelling over North America. Hydrol. Earth Syst. Sci. 2020, 24, 2527–2544. [Google Scholar] [CrossRef]
- Tang, G.; Ma, Y.; Long, D.; Zhong, L.; Hong, Y. Evaluation of GPM Day-1 IMERG and TMPA Version-7 legacy products over Mainland China at multiple spatiotemporal scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D.; Adler, R.F.; Kubota, T.; Ushio, T. Evaluation of GSMaP Precipitation Estimates over the Contiguous United States. J. Hydrometeorol. 2010, 11, 566–574. [Google Scholar] [CrossRef]
- Chiang, Y.-M.; Hsu, K.-L.; Chang, F.-J.; Hong, Y.; Sorooshian, S. Merging multiple precipitation sources for flash flood forecasting. J. Hydrol. 2007, 340, 183–196. [Google Scholar] [CrossRef]
- Wu, H.; Yang, Q.; Liu, J.; Wang, G. A spatiotemporal deep fusion model for merging satellite and gauge precipitation in China. J. Hydrol. 2020, 584, 124664. [Google Scholar] [CrossRef]
- Hong, Z.; Han, Z.; Li, X.; Long, D.; Tang, G.; Wang, J. Generation of an improved precipitation data set from multisource information over the Tibetan Plateau. J. Hydrometeorol. 2021, 22, 1275–1295. [Google Scholar] [CrossRef]
- Wang, H.; Wang, L.; He, J.; Ge, F.; Chen, Q.; Tang, S.; Yao, S. Can the GPM IMERG Hourly Products Replicate the Variation in Precipitation During the Wet Season Over the Sichuan Basin, China? Earth Space Sci. 2020, 7, e2020EA001090. [Google Scholar] [CrossRef]
- Wang, H.; Yan, Y.; Long, K.; Chen, Q.; Fan, X.; Zhang, F.; Tan, L. Relationships Between Rapid Urbanization and Extreme Summer Precipitation Over the Sichuan–Chongqing Area of China. Front. Earth Sci. 2022, 10, 899. [Google Scholar] [CrossRef]
- Wang, H.; Wei, M.; Li, G.; Zhou, S.; Zeng, Q. Analysis of precipitable water vapor from GPS measurements in Chengdu region: Distribution and evolution characteristics in autumn. Adv. Space Res. 2013, 52, 656–667. [Google Scholar] [CrossRef]
- Shen, Y.; Xiong, A.; Wang, Y.; Xie, P. Performance of high-resolution satellite precipitation products over China. J. Geophys. Research. Atmos. 2010, 115, D2. [Google Scholar] [CrossRef]
- Tan, M.L.; Ibrahim, A.L.; Duan, Z.; Cracknell, A.P.; Chaplot, V. Evaluation of Six High-Resolution Satellite and Ground-Based Precipitation Products over Malaysia. Remote. Sens. 2015, 7, 1504–1528. [Google Scholar] [CrossRef]
- Sharifi, E.; Eitzinger, J.; Dorigo, W. Performance of the State-Of-The-Art Gridded Precipitation Products over Mountainous Terrain: A Regional Study over Austria. Remote. Sens. 2019, 11, 2018. [Google Scholar] [CrossRef]
- Chen, C.; Hu, B.; Li, Y. Easy-to-use spatial Random Forest-based downscaling-calibration method for producing high reso-lution and accurate precipitation data. Hydrol. Earth Syst. Sci. 2021, 2021, 1–50. [Google Scholar] [CrossRef]
- Wang, Z.; Zhong, R.; Lai, C.; Chen, J. Evaluation of the GPM IMERG satellite-based precipitation products and the hydrological utility. Atmos. Res. 2017, 196, 151–163. [Google Scholar] [CrossRef]
- Huang, J.; Sun, S.; Xue, Y.; Li, J.; Zhang, J. Spatial and Temporal Variability of Precipitation and Dryness/Wetness During 1961–2008 in Sichuan Province, West China. Water Resour. Manag. 2014, 28, 1655–1670. [Google Scholar] [CrossRef]
- Deng, M.; Lu, R.; Li, C. Contrasts between the Interannual Variations of Extreme Rainfall over Western and Eastern Sichuan in Mid-summer. Adv. Atmos. Sci. 2022, 39, 999–1011. [Google Scholar] [CrossRef]
- Wang, H.; Tan, L.; Zhang, F.; Zheng, J.; Liu, Y.; Zeng, Q.; Yan, Y.; Ren, X.; Xiang, J. Three-Dimensional Structure Analysis and Droplet Spectrum Characteristics of Southwest Vortex Precipitation System Based on GPM-DPR. Remote. Sens. 2022, 14, 4063. [Google Scholar] [CrossRef]
- Lu, C.; Ye, J.; Fang, G.; Huang, X.; Yan, M. Assessment of GPM IMERG Satellite Precipitation Estimation under Complex Climatic and Topographic Conditions. Atmosphere 2021, 12, 780. [Google Scholar] [CrossRef]
- Lu, J.; Jia, L.; Menenti, M.; Yan, Y.; Zheng, C.; Zhou, J. Performance of the Standardized Precipitation Index Based on the TMPA and CMORPH Precipitation Products for Drought Monitoring in China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1387–1396. [Google Scholar] [CrossRef]
- Zhou, Z.; Guo, B.; Xing, W.; Zhou, J.; Xu, F.; Xu, Y. Comprehensive evaluation of latest GPM era IMERG and GSMaP precipitation products over mainland China. Atmos. Res. 2020, 246, 105132. [Google Scholar] [CrossRef]
- Nogueira, M. Inter-comparison of ERA-5, ERA-interim and GPCP rainfall over the last 40 years: Process-based analysis of systematic and random differences. J. Hydrol. 2020, 583, 124632. [Google Scholar] [CrossRef]
- Lei, X.; Xu, W.; Chen, S.; Yu, T.; Hu, Z.; Zhang, M.; Jiang, L.; Bao, R.; Guan, X.; Ma, M.; et al. How Well Does the ERA5 Reanalysis Capture the Extreme Climate Events Over China? Part I: Extreme Precipitation. Front. Environ. Sci. 2022, 10, 921658. [Google Scholar] [CrossRef]
- Zhao, P.; He, Z.; Ma, D.; Wang, W. Evaluation of ERA5-Land reanalysis datasets for extreme temperatures in the Qilian Mountains of China. Front. Ecol. Evol. 2023, 11, 1135895. [Google Scholar] [CrossRef]
- Hersbach, H. The ERA5 Atmospheric Reanalysis. In Proceedings of the AGU Fall Meeting 2016, San Francisco, CA, USA, 12–16 December 2016. [Google Scholar]
- Wang, H.; Li, Z.; Zhang, T.; Chen, Q.; Guo, X.; Zeng, Q.; Xiang, J. Downscaling of GPM satellite precipitation products based on machine learning method in complex terrain and limited observation area. Adv. Space Res. 2023, 72, 2226–2244. [Google Scholar] [CrossRef]
- Capolongo, D.; Gioia, D.; Schiattarella, M. Editorial: Advances in Quantitative Geomorphology: From DEM Analysis to Modeling of Surface Processes. Front. Earth Sci. 2022, 10, 874950. [Google Scholar] [CrossRef]
- Chiang, Y.-M.; Hao, R.-N.; Xu, Y.-P.; Liu, L. Multi-source rainfall merging and reservoir inflow forecasting by ensemble technique and artificial intelligence. J. Hydrol. Reg. Stud. 2022, 44, 101204. [Google Scholar] [CrossRef]
- Pan, Y.; Gu, J.; Yu, J.; Shen, Y.; Shi, C.; Zhou, Z. Test of merging methods for multi-source observed precipitation products at high resolution over China. Acta Meteorol. Sin. 2018, 76, 755–766. [Google Scholar] [CrossRef]
- Nguyen, G.V.; Le, X.-H.; Van, L.N.; Jung, S.; Yeon, M.; Lee, G. Application of Random Forest Algorithm for Merging Multiple Satellite Precipitation Products across South Korea. Remote. Sens. 2021, 13, 4033. [Google Scholar] [CrossRef]
- Nan, T.; Chen, J.; Ding, Z.; Li, W.; Chen, H. Deep learning-based multi-source precipitation merging for the Tibetan Plateau. Sci. China Earth Sci. 2023, 66, 852–870. [Google Scholar] [CrossRef]
- Ma, Y.; Hong, Y.; Chen, Y.; Yang, Y.; Tang, G.; Yao, Y.; Long, D.; Li, C.; Han, Z.; Liu, R. Performance of Optimally Merged Multisatellite Precipitation Products Using the Dynamic Bayesian Model Averaging Scheme Over the Tibetan Plateau. J. Geophys. Res. Atmos. 2018, 123, 814–834. [Google Scholar] [CrossRef]
- Tang, G.; Clark, M.P.; Papalexiou, S.M.; Ma, Z.; Hong, Y. Have satellite precipitation products improved over last two decades? A comprehensive comparison of GPM IMERG with nine satellite and reanalysis datasets. Remote Sens. Environ. 2020, 240, 111697. [Google Scholar] [CrossRef]
- Sui, X.; Li, Z.; Ma, Z.; Xu, J.; Zhu, S.; Liu, H. Ground Validation and Error Sources Identification for GPM IMERG Product over the Southeast Coastal Regions of China. Remote. Sens. 2020, 12, 4154. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; E Charlton, M.; Brunsdon, C. Geographically Weighted Regression: A Natural Evolution of the Expansion Method for Spatial Data Analysis. Environ. Plan. A Econ. Space 1998, 30, 1905–1927. [Google Scholar] [CrossRef]
- Bi, S.; Bi, S.; Chen, D.; Pan, J.; Wang, J. A Double-Smoothing Algorithm for Integrating Satellite Precipitation Products in Areas with Sparsely Distributed In Situ Networks. ISPRS Int. J. Geo-Inf. 2017, 6, 28. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, J.; Sheng, S.; Mansaray, L.R.; Liu, Z.; Wu, H.; Wang, X. A new downscaling-integration framework for high-resolution monthly precipitation estimates: Combining rain gauge observations, satellite-derived precipitation data and geographical ancillary data. Remote. Sens. Environ. 2018, 214, 154–172. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Shen, Y.; Zhao, P.; Pan, Y.; Yu, J. A high spatiotemporal gauge-satellite merged precipitation analysis over China. J. Geophys. Res. Atmos. 2014, 119, 3063–3075. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, Y.; Sun, Z.; Lin, Q.; He, H. Improvement of a combination of TMPA (or IMERG) and ground-based precipitation and application to a typical region of the East China Plain. Sci. Total. Environ. 2018, 640-641, 1165–1175. [Google Scholar] [CrossRef]
- Chao, L.; Zhang, K.; Li, Z.; Zhu, Y.; Wang, J.; Yu, Z. Geographically weighted regression based methods for merging satellite and gauge precipitation. J. Hydrol. 2018, 558, 275–289. [Google Scholar] [CrossRef]
- Pan, Y.; Shen, Y.; Yu, J.J.; Zhao, P. Analysis of the combined gauge-satellite hourly precipitation over China based on the OI technique. Acta Meteorol. Sin. 2012, 70, 1381–1389. [Google Scholar] [CrossRef]
- Yang, P.; Ng, T.L. Fast Bayesian Regression Kriging Method for Real-Time Merging of Radar, Rain Gauge, and Crowdsourced Rainfall Data. Water Resour. Res. 2019, 55, 3194–3214. [Google Scholar] [CrossRef]
- Zhou, C.; Cen, S.; Yueqing, L. Precipitation variation and its impacts in Sichuan in the last 50 years. Acta Geogr. Sin. 2011, 66, 619–630. [Google Scholar] [CrossRef]
- Zeng, S.; Bing, Y. Evaluation of the GPM-based IMERG and GSMaP Precipitation estimates over the Sichuan region. Acta Geogr. Sin. 2019, 74, 1305–1318. [Google Scholar] [CrossRef]
- Xie, P.; Chen, M.; Yang, S.; Yatagai, A.; Hayasaka, T.; Fukushima, Y.; Liu, C. A Gauge-Based Analysis of Daily Precipitation over East Asia. J. Hydrometeorol. 2007, 8, 607–626. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).