Drought-Related Spatiotemporal Cumulative and Time-Lag Effects on Terrestrial Vegetation across China

Abstract

Vegetation is one of the most important indicators of climate change, as it can show regional change in the environment. Vegetation health is affected by various factors, including drought, which has cumulative and time-lag effects on vegetation response. However, the cumulative and time-lag effects of drought on different terrestrial vegetation in China are still unclear. To address this issue, this study examined the cumulative and time-lag effects of drought on vegetation from 2001 to 2020 using the Standardized Precipitation Evapotranspiration Index (SPEI) in the Global SPEI database and the Normalized Difference Vegetation Index (NDVI) in MOD13A3. Based on Sen-Median trend analysis and the Mann–Kendall test, the change trend and significance of the NDVI from 2001 to 2020 were explored. The Pearson correlation coefficient was used to analyze the correlation between the SPEI and NDVI at each cumulative scale and time-lag scale and to further analyze the cumulative and time-lag effects of drought on vegetation. The results show the following: (1) The NDVI value increased at a rate of 0.019/10 years, and the increased area of the NDVI accounted for 80.53% of mainland China, with a spatial trend of low values in the west and high values in the east. (2) The average SPEI cumulative time scale most relevant to the NDVI was 7.3 months, and the cumulative effect demonstrated a high correlation at the scale of 9–12 months and revealed different distributions in different areas. The cumulative effect was widely distributed at the 9-month scale, followed by the 12-month scale. The correlation coefficients of cumulative effects between the SPEI and NDVI for cropland, woodland and grassland peaked at 9 months. (3) The average SPEI time-lag scale for the NDVI was 6.9 months, and the time-lag effect had the highest correlation coefficient at the 7-month scale. The strongest time-lag effect for cropland and grassland was seen at 7 months, while the strongest time-lag effect for woodland was seen at 6 months. Woodland had a lower time-lag effect than grassland at different scales. The research results are significant for their use in aiding the scientific response to drought disasters and making decisions for climate change precautions.

1. Introduction

Drought is a persistent water shortage phenomenon caused by an imbalance between regional water balance or supply and demand [1]. It is a common climatic phenomenon worldwide, affecting a wide range of people, and lasting for a long time, making it one of the most significant meteorological disasters affecting human production and life [2]. Droughts cause huge losses not only to the national economy but also to agricultural production, and lead to many negative environmental problems such as water scarcity, dust storms, and desertification. Therefore, it is necessary to study drought and its mechanism. Drought indices are one of the most effective tools for studying the evolution of drought characteristics, such as the Standardized Precipitation Evapotranspiration Index (SPEI), which is a drought index based on an analysis of the advantages and disadvantages of the Palmer Drought Severity Index (PDSI) and the Standardized Precipitation Index (SPI), objectively characterizing the combined effect of precipitation and evapotranspiration on drought. It is an ideal tool for drought monitoring [3]. The multi-scale SPEI plays an important role in identifying drought. Stefanidis et al. found [4] that SPEI3 and SPEI6 are more efficient in identifying short-term drought, while SPEI12 and SPEI24 are more efficient in identifying long-term drought. Moreover, drought can affect the normal growth of vegetation because of the water shortage, and vegetation growth can also reflect drought conditions at a regional scale. Thus, many studies have explored the correlation between drought and vegetation growth due to the high association between them [5,6,7,8].

For example, Hua et al. (2017) [9] used correlation coefficients to investigate the relationship between the NDVI and SPEI and found that drought plays a key role in vegetation growth during the growing season in Northern China. Vegetation growth is often driven not by current hydrothermal conditions but by earlier drought events [10], so determining the timing of vegetation response to drought is critical for enhancing our understanding of the mechanisms behind vegetation–climate interactions and for developing effective measures to conserve vegetation.

The time-lag effect demonstrates the sensitivity of vegetation to drought by illustrating how a previous drought event affects the current growth of vegetation [10]. The cumulative effect refers to the effect of a water deficit on vegetation growth over time. It relies on time-lag effects, such as the dynamics of climatic conditions (e.g., precipitation and transpiration) over a specific period. This measure can be employed to evaluate vegetation tolerance to drought. Previous authors have extensively studied the cumulative and time-lag effects on vegetation growth [11,12,13]. For instance, Zhan et al. (2022) [8] revealed that 40.4% of vegetation areas in the Yellow River basin were affected by cumulative drought, with the longest accumulation time (eight months) observed in the semi-humid zone, and 91.8% of vegetation areas were affected by lagged drought. Zhao et al. (2020) [14] discovered that vegetation in the arid zone of the Loess Plateau exhibits stronger cumulative and time-lag effects. Wu et al. (2015) [15] reported significant differences in the time-lag effects on vegetation growth on a global scale. Zuo et al. (2021) [16] found a one-month time-lag effect of temperature and precipitation on vegetation in the upstream region of the Yarlung Tsangpo River basin, a one-month time-lag effect of temperature in the midstream region, and no time-lag effect of temperature and precipitation on vegetation in the downstream region. Hu et al. (2020) [17] discovered a one-month time-lag between soil moisture and climate factors in the northwest of the Yangtze River basin. Ji et al. (2003) [18] revealed a three-month time-lag between the growing season of vegetation and precipitation in the Great Plains of the United States. Hua et al. (2019) [5] found that vegetation in Nebraska, USA, has a 30–45-day time-lag after drought. Jiang et al. (2023) [19] found a time-lag effect of drought on vegetation growth, and the average lagged time in karst areas was shorter than that in non-karst areas. Wang et al. (2023) [12] found that 66.41% and 54.57% of vegetation in China has time-lagged and cumulative responses to drought.

Using NDVI and SPEI data on a time scale of 1–12 months from 2001 to 2020, this study employed Sen+MK trend analysis, Pearson correlation analysis, and other statistical analysis methods to explore the cumulative and time-lag effects of drought on regional vegetation growth in China. The spatial and temporal patterns of these effects were examined to provide a scientific foundation for drought monitoring, aiding in the development of appropriate measures to protect the ecological environment and respond to climate change. The findings of this research are significant for their use in aiding the scientific response to drought disasters and contribution to the advancement of scientific knowledge in this area. The objectives of this study were as follows: (1) Are the cumulative and time-lag effects of drought on vegetation consistent across China, and if not, what are the differences? (2) Which is the primary effect of drought on vegetation, the cumulative effect or time-lag effect?

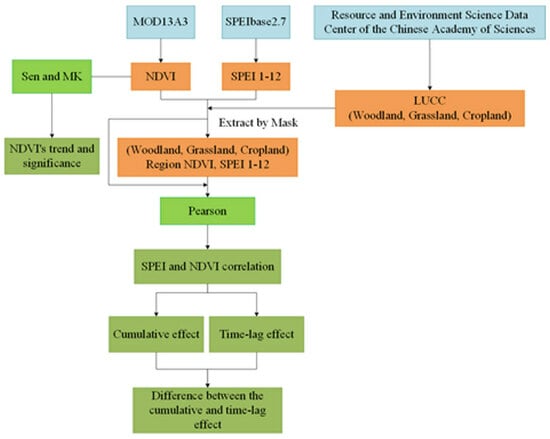
2. Data and Methods

2.1. Data

2.1.1. NDVI Dataset

The NDVI has become the predominant metric used to measure vegetative cover and growth state [20]. The MODIS NDVI complements AVHRR NDVI products, providing continuity for time series applications over this rich historical archive. In this study, we obtained NDVI data from the MOD13A3 dataset made available by NASA, with a spatial resolution of 1 km and a temporal resolution of monthly intervals. This is a gridded Level 3 product of sinusoidal projection. We extracted the NDVI bands and subjected the images to mosaic and cropping procedures over China using the MODIS Reprojection Tool (MRT) downloaded by NASA.

2.1.2. Multi-Scalar SPEI Dataset

The SPEI [21] is commonly employed for drought assessment. Larger SPEI values indicate high humidity, while smaller SPEI values indicate more severe drought. In this study, monthly SPEI data were obtained from the Global SPEI database (version 2.7) of Consejo Superior de Investigaciones Científicas (https://spei.csic.es/spei_database/ (assessed on 13 January 2023)), with a spatial resolution of 0.5° and a time scale ranging from 1 to 48 months. Based on the estimation of potential evapotranspiration according to FAO-56 Penman-Monteith, SPEIbase is able to characterize long-term and robust drought information on a global scale [20]. This study focused on the cumulative and time-lag effects of drought for a 1–12-month period using the SPEI. The Python programming language was used for bilinear resampling of the SPEI data in order to match them with the NDVI data used in this study.

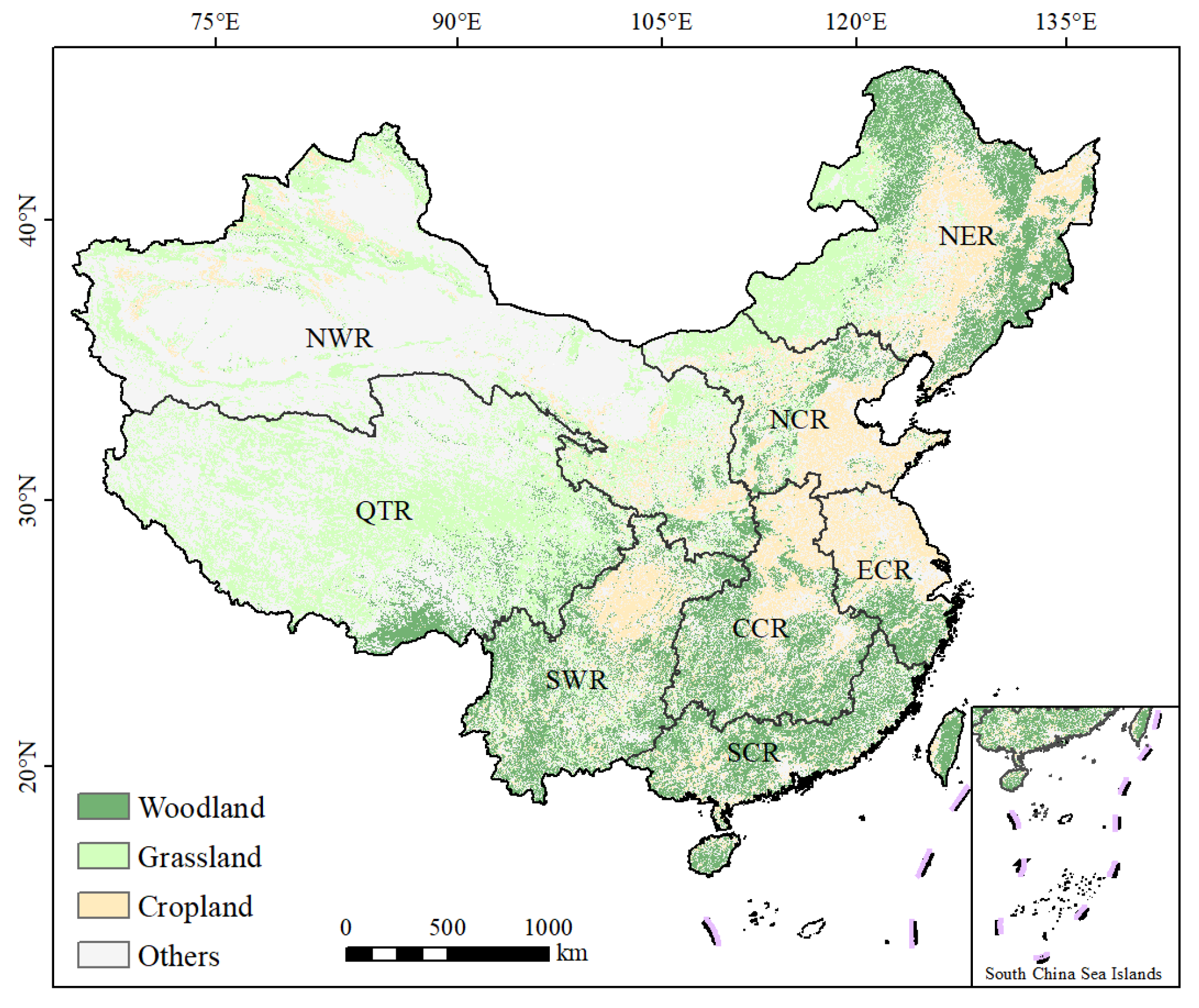
2.1.3. Land Use

The data on land use types were obtained from the Resource and Environment Science Data Center of the Chinese Academy of Sciences (https://www.resdc.cn/ (assessed on 15 January 2023)), with a spatial resolution of 1 km. In this paper, NDVI data on cropland, grassland, and woodland [22] were extracted based on the land use dataset in 2005 and 2020 to explore the cumulative and time-lag effects of drought (Figure 1).

2.2. Methods

2.2.1. Trend Analysis

Sen-Median trend analysis and the Mann–Kendall (MK) test were used to analyze the spatial and temporal evolution patterns of NDVI time series to determine the significance of NDVI trends. Sen’s slope is a nonparametric test in which the steepness of the trend is measured by the median of the slope [23]. The MK test, developed by Mann [24] and Kendall, quantifies trend significance in a time series sample. It does not necessitate adherence to a specific distribution and accommodates missing values [25,26]. The calculation of Sen’s slope (β) can be described by Formula (1), and the Mann–Kendall (Z) test is calculated using Formulas (2)–(5).

$$\beta =median(\frac{x_i-x_j}{i-j}),\forall i<j$$

(1)

where the median is the median function, and x_i and x_j are the NDVI in year i and year j, where i, j = 1, 2, 3,..., n.

$$Z=\left\{\begin{array}{c}\frac{S-1}{\sqrt{var(S)}},S>0\\ 0,S=0\\ \frac{S+1}{\sqrt{var(S)}},S>0\end{array}\right.$$

(2)

$$S={\displaystyle \sum _{i=1}^{n-1}{\displaystyle \sum _{j=i+1}^{n}sign(x_j-x_i)}}$$

(3)

$$var(S)=\frac{n(n-1)(2n+5)}{18}$$

(4)

$$sign(x_j-x_i)=\left\{\begin{array}{l}1,x_j-x_i>0\\ 0,x_j-x_i=0\\ -1,x_j-x_i<0\end{array}\right.$$

(5)

where sign is a symbolic function, x_i and x_j are time series data, and n is the length of the time series data. When the absolute values of Z are greater than 1.64, 1.96, and 2.58, the trend passes the significance test of 90%, 95%, and 99% confidence [27,28].

2.2.2. Cumulative Effect

Pearson correlation analysis [29] can quantify the image-by-image correlation between NDVI time series and the SPEI of different time scales in the study area, i.e., the NDVI and SPEI1, SPEI2,…, SPEI12. In this paper, the maximum correlation coefficient is used to determine the optimal accumulation time between the NDVI and each corresponding SPEI image pixel. This cumulative effect represents the impact of drought on vegetation and is calculated as:

$$r_j=corr(NDVI,SPE{I}_j)1\le j\le 12$$

(6)

$$r_{max-cul}=max(r_j)1\le j\le 12$$

(7)

where r_j is the Pearson correlation coefficient between the NDVI and SPEI, j is the accumulated time from the one- to twelve-month SPEI, and r_max-cul is the maximum value of r_j.

2.2.3. Time-Lag Effect

To explain the time-lag effect of drought on vegetation, Pearson correlation analysis was used to calculate the correlation coefficients between the NDVI and SPEI. The correlation coefficients (r₀, r₁,..., r₁₂) between the NDVI and SPEI1 were calculated at each lag time interval (0 ≤ i ≤ 12). For example, a one-month lag means comparing SPEI1 from November 2000 to November 2020 with the NDVI from January 2001 to December 2020 for correlation analysis. Then, the maximum correlation coefficient r_i of each image element was taken as the optimal correlation, and the number of months for i was considered as the optimal time lag. This calculation was carried out using Formulas (8) and (9):

$$r_i=corr(NDVI,SPE{I}_i)1\le i\le 12$$

(8)

$$r_{max-lag}=max(r_i)0\le i\le 12$$

(9)

where r_i is the Pearson correlation coefficient with a time lag of i months, where i ranges from 0 to 12, NDVI is the NDVI time series from MODIS (2001.1~2020.12), and SPEI is the SPEI1 time series with a time lag of i months (2001.1−i~2020.12−i).

3. Result

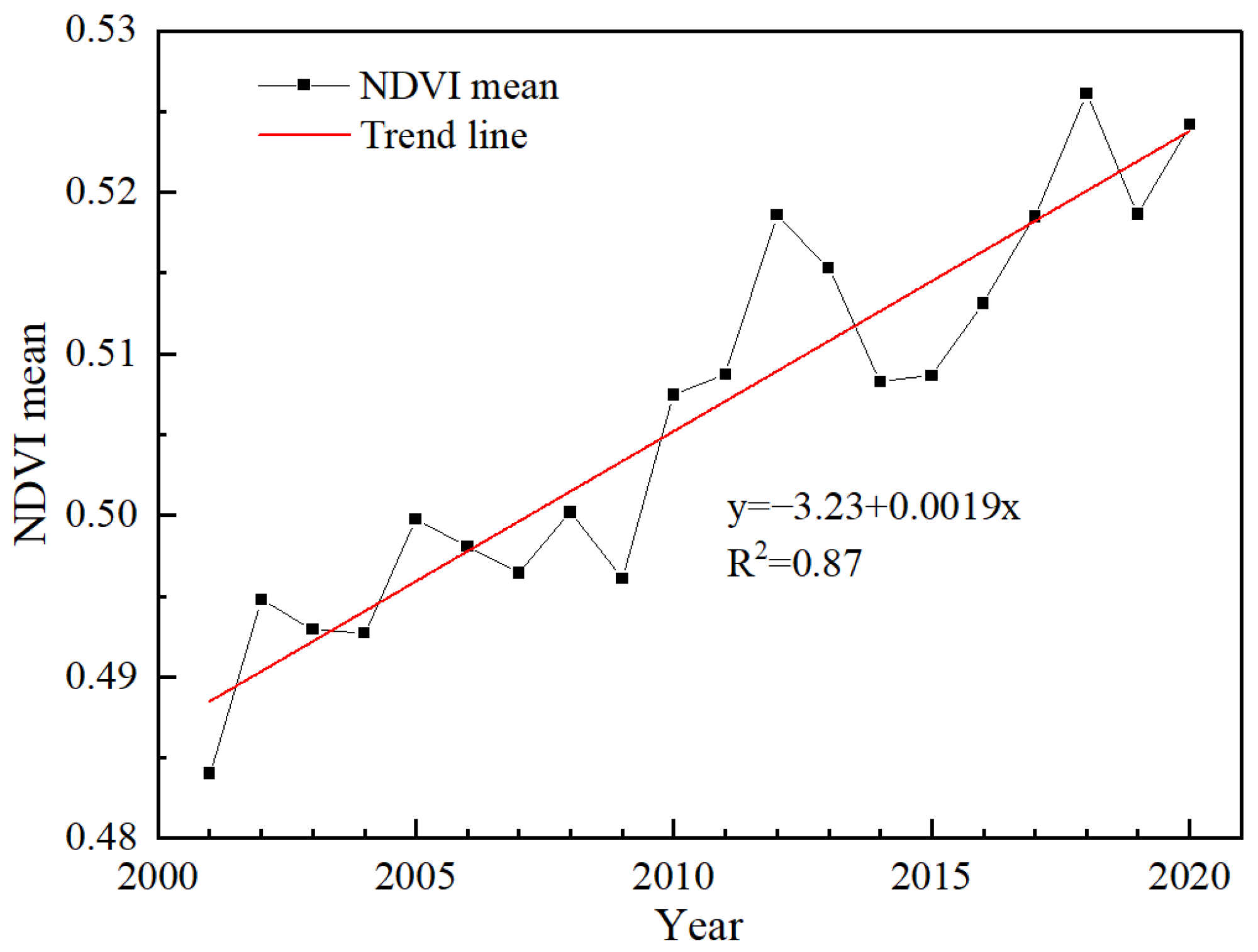
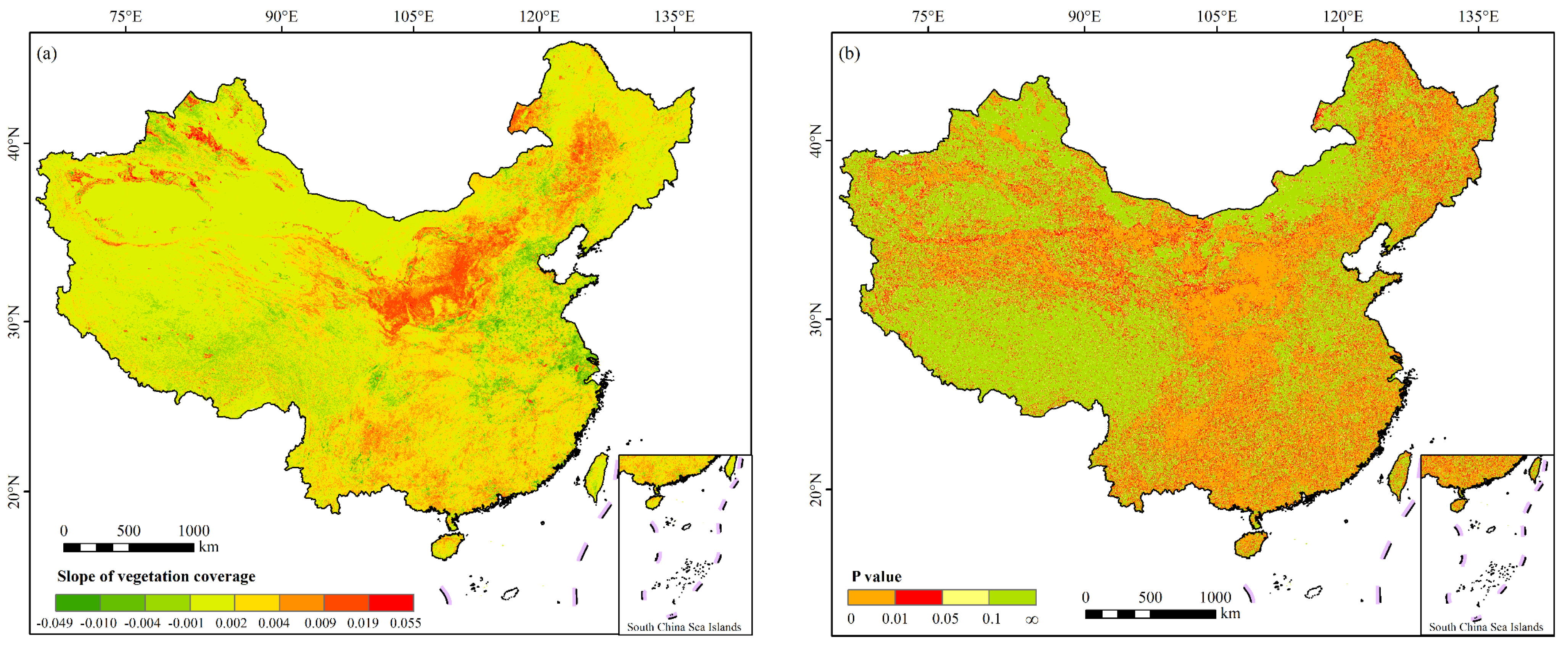
3.1. Spatial and Temporal Trends of NDVI

The interannual variation trend of the NDVI in China from 2001 to 2020 was investigated using linear regression analysis, and the slope of the fitted line indicates the annual growth rate. Figure 2 shows the time series of the annual mean NDVI in China, and the results show that the annual mean NDVI value ranged from 0.484 to 0.526, and the mean NDVI value for 20 years was about 0.506, with a minimum value of 0.484 occurring in 2001 and a maximum value of 0.526 occurring in 2018, and the annual variation in the NDVI showed an improving trend with an interannual growth rate of 0.019/10 years.

The slope of the annual NDVI trend is shown in Figure 3a. The slope changes from −0.049 to 0.055, which indicates a spatial trend of low values in the west and high values in the east, with a weak trend of vegetation recovery in the central region and Northeast, South, and Southwest China, and a downward trend in North China and Qinghai–Tibet. This trend is strongly related to climatic factors such as precipitation [30]. The magnitude of NDVI change from 2001 to 2020 was stable. The NDVI in Northwest China remained constant, with 80.53% of the regions showing an improved NDVI and 41.72% of the regions passing the significance test (p < 0.05) (Figure 3b).

3.2. Cumulative Effect of Drought on Vegetation

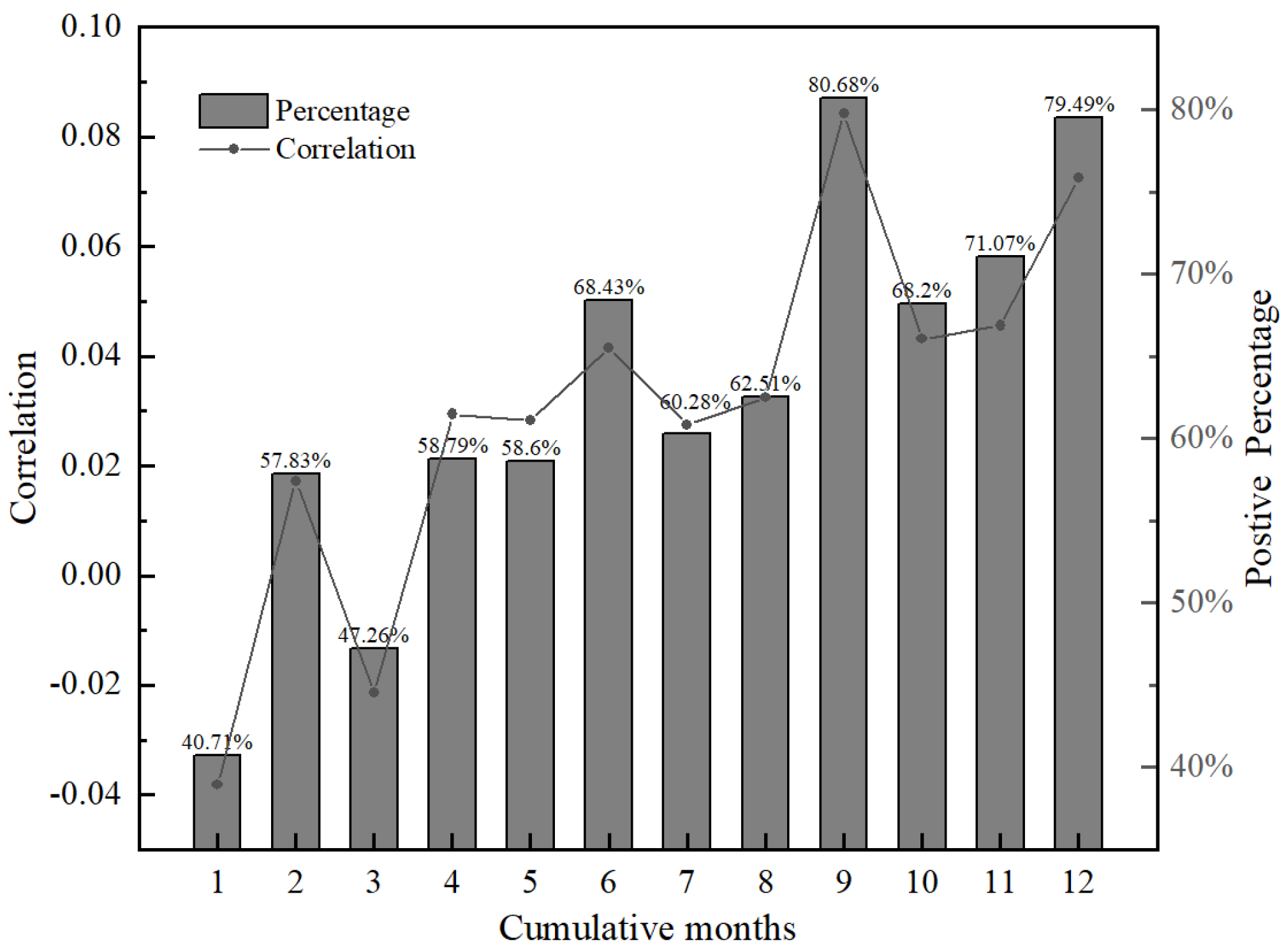
3.2.1. Response of Vegetation to Drought at Different Time Scales

The correlation between the cumulative SPEI and NDVI is shown in Figure 4 and varies considerably at different time scales. The cumulative SPEI and NDVI showed an overall pattern of increasing correlation, with the maximum correlation observed at 9 months (r = 0.084) and the minimum correlation at 1 month (r =−0.038), and a significant association was noted between 9 and 12 months. Additionally, the percentage of area that was positively associated between the cumulative SPEI and the NDVI displayed a similar temporal trend, increasing as the number of cumulative months increased and again peaking at 9 months (80.68%).

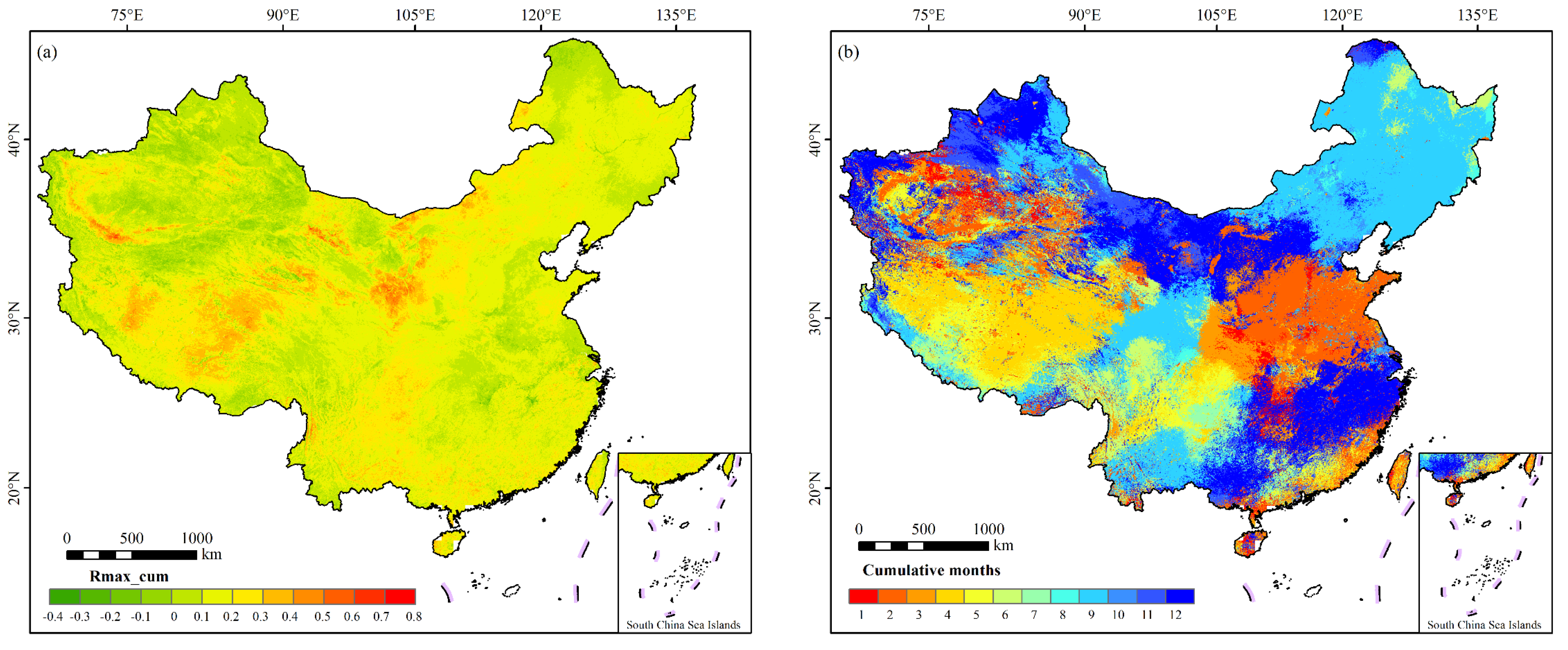
3.2.2. Spatial Distribution of the Cumulative Effect of Drought on Vegetation

The spatial distribution of cumulative effects, which combines two sets of information, is shown in Figure 5. Figure 5a displays the maximum values of the NDVI and SPEI correlation coefficients on a 1–12-month scale, while Figure 5b depicts the corresponding cumulative months. The cumulative effect of drought on the NDVI was positively correlated with the regions that accounted for 94.82% of the area in China, while the significantly correlated and low correlated regions accounted for less land area, mostly including the Qinghai–Tibet Plateau and the Loess Plateau. The optimal cumulative effect showed a clear geographical pattern: a 9-month scale in Northeast China; a 9–12-month scale mainly in Northwest China, with southern Xinjiang and Qinghai–Tibet showing greater variability with a 1–5-month scale and 4–7-month scale, respectively; a roughly 5–9-month scale in Southwest China; a 1–3-month scale in North and Central China; and a 12-month scale in Southern China, except for the southern coastal region, which exhibited a 1–5 month scale. The cumulative effect was most widely distributed across the 9-month scale (24.58%), followed by the 12-month scale (20.05%). Overall, the mean relevant SPEI time scale for the NDVI stood at 7.3 months, showcasing the cumulative effect of drought on vegetation cover.

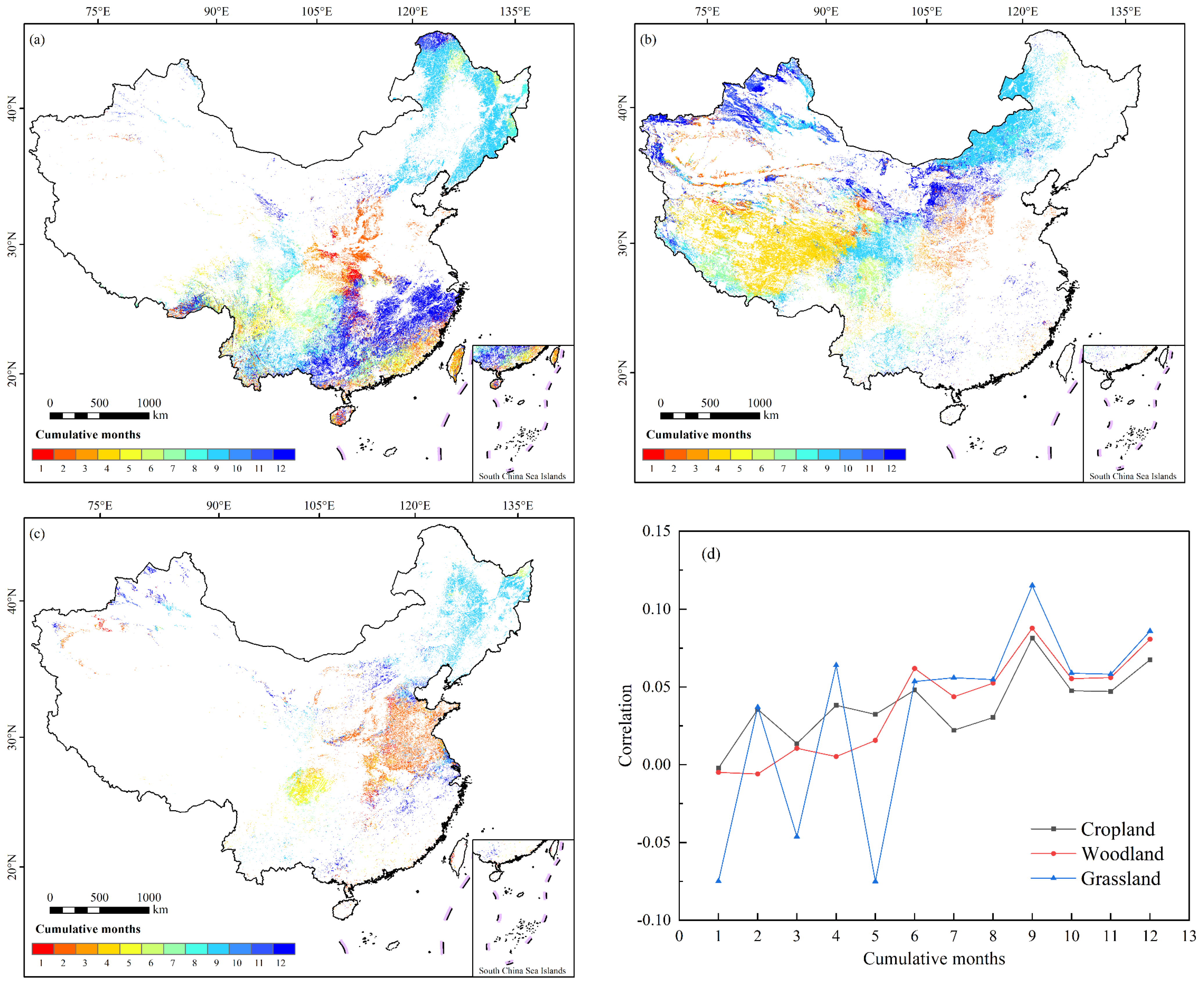
3.2.3. Cumulative Effects of Drought on Different Vegetation Types

Figure 6a–c show the responses of woodland, grassland, and cropland to the cumulative SPEI at each scale, respectively, where the spatial distribution is consistent with the national spatial distribution (Figure 5b). Figure 6d shows that the correlations between different NDVIs and cumulative SPEIs varied widely, and the correlations of cropland and woodland to the SPEI were positive at the 3–12-month cumulative scale. At a cumulative scale of 3–12 months, there was a positive correlation between cropland and woodland and a steady increase in the correlation trend. The correlation between grassland and the SPEI varied significantly from 1 to 6 months of accumulation, and the cumulative scales of 1, 3, and 5 months were all negative. In addition, cropland, woodland, and grassland correlations with the cumulative SPEI peaked at the scale of 9 months (r_cropland = 0.081, r_woodland = 0.088, r_grassland = 0.115), and the cumulative effects from 6 to 12 months followed the order grassland > woodland > cropland. In addition, the average SPEI time scales most relevant to woodland, grassland, and cropland were 8.0, 6.3, and 7.4 months, respectively; that is, the best cumulative time scale followed the order woodland > cropland > grassland. Numerous studies have highlighted the strong connection between vegetation growth and the cumulative impacts of climate factors such as temperature, precipitation, and soil moisture [27,31,32]; such climate factors are the reasons for the correlation coefficient at the 6–12-month cumulative scale and why the optimal cumulative time of grassland was better than that of cropland and woodland.

3.3. Time-Lag Effect of Drought on Vegetation

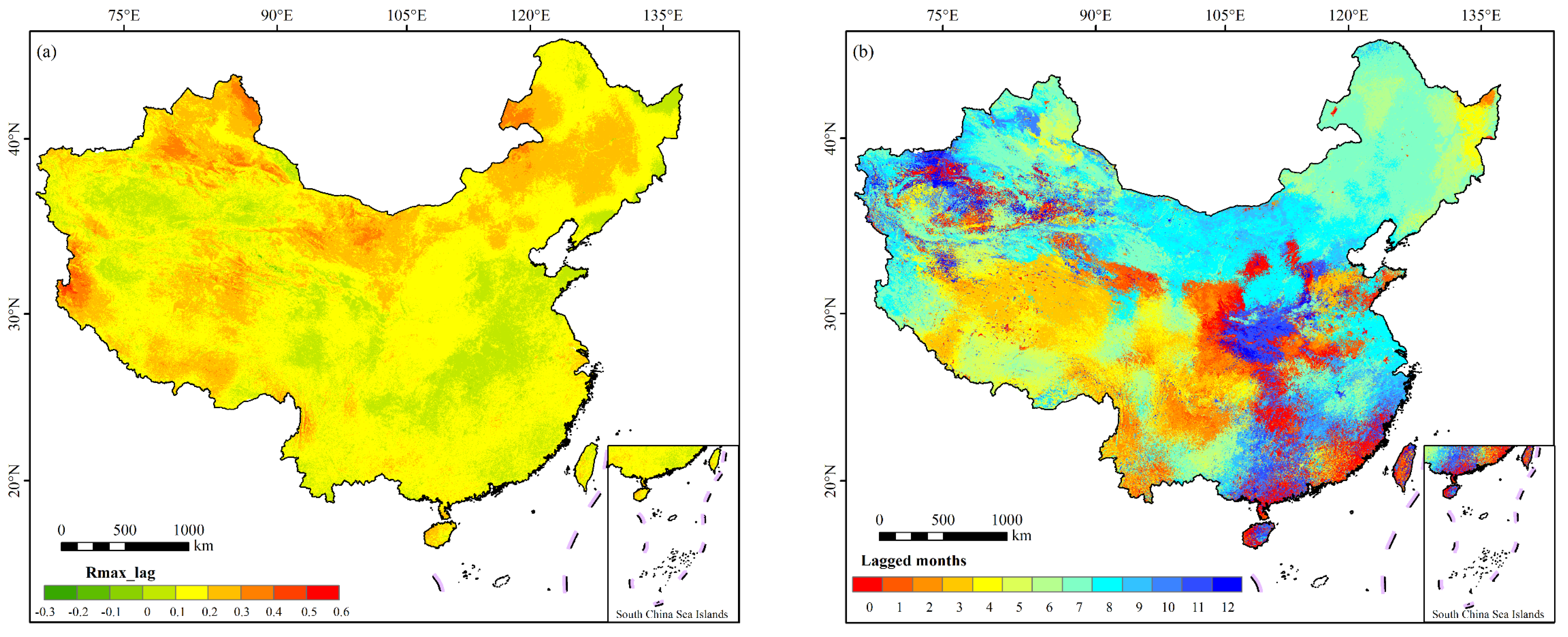
3.3.1. Response of Vegetation to Drought at Different Time Scales

As shown in Figure 7, the correlations between the SPEI and NDVI varied significantly at different time-lag scales, with positive correlations at the 3–10-month scale and negative correlations at the 1, 2, 11, and 12-month scales. The overall trend of the correlation between the NDVI and time-lagged SPEI exhibited an initial increase followed by a decrease, with the strongest correlation occurring at 7 months (r = 0.085) and the weakest at 12 months (r =−0.051). Furthermore, the percentage of area positively correlated with the NDVI and time-lagged SPEI followed the same temporal pattern. The positively correlated area increased and then decreased with the rising number of time-lagged months, reaching a maximum at 7 months (81.33%) and a minimum at 12 months (32.64%).

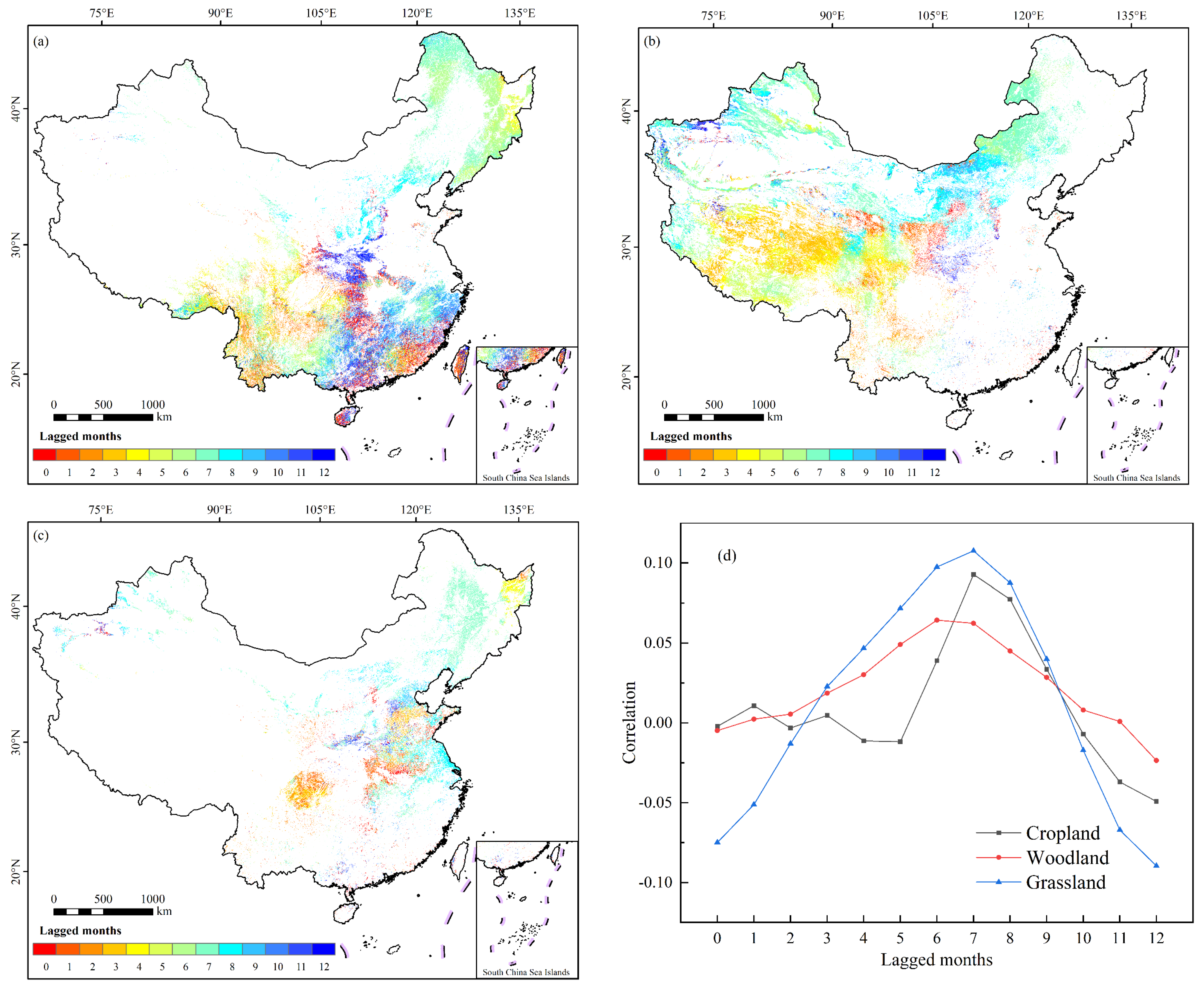
3.3.2. Spatial Distribution of Time-Lagged Effects of Drought on Vegetation

Based on the analysis of the correlation of the NDVI with the SPEI at a 1-month time scale, the time-lag effect of drought on vegetation generated with the time-lag month with the largest correlation is shown in Figure 8. Figure 8a reveals that 99.05% of the regions showed a positive time-lag effect, while very few showed a significant and low correlation, and 96.15% showed a weak positive correlation. Figure 8b shows that the optimal time-lag had strong spatial geographic variations: 6–8 months in the northeast; 7–9 months in the Loess Plateau region; 5–7 months in northern Xinjiang, with large differences in the time-lag in southern Xinjiang; 3–6 months in Qinghai–Tibet; 2–6 months in Southwest China; 8–12 months in Central China; 8 months in Northern China; and 9–11 months in Southern China. The time-lag interval was mainly 6–8 months (44.85%). In general, the average SPEI time scale for the NDVI was 6.9 months, which proves that drought has a time-lag effect on the NDVI.

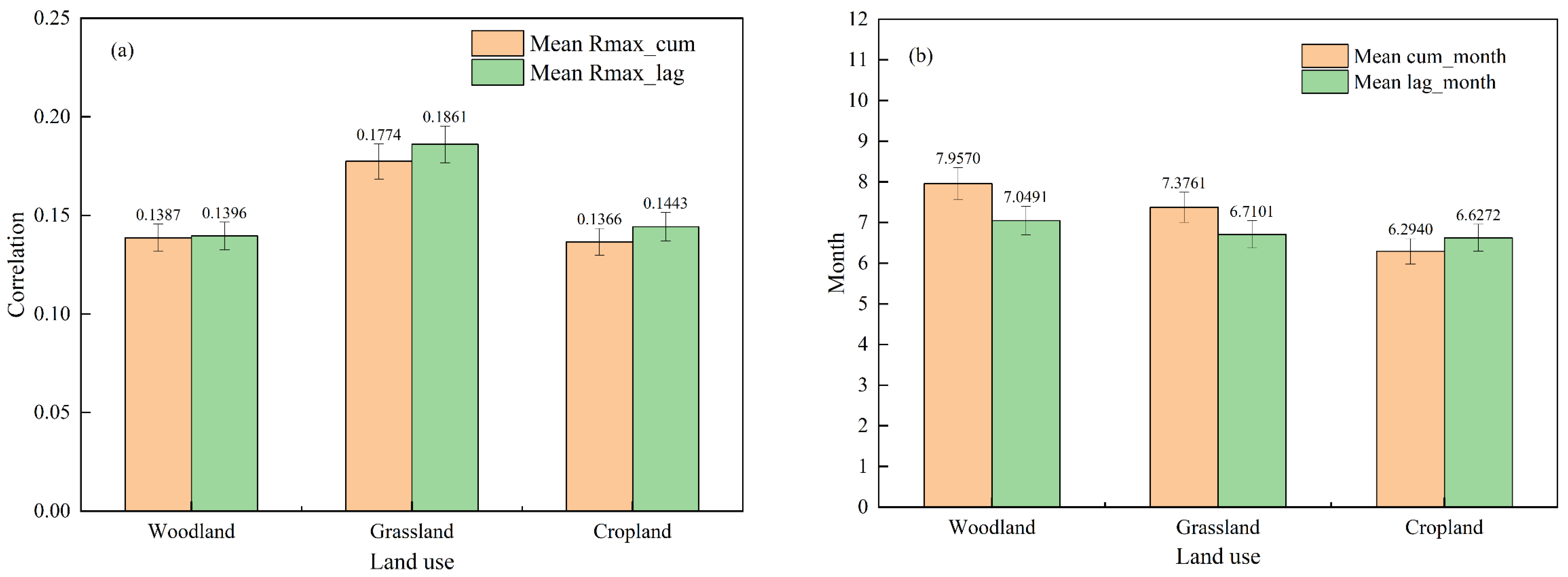
3.3.3. Time-Lag Effect of Drought on Different Vegetation Types

The time-lag effects of different vegetation types, shown in Figure 9a–c, are similar to the nationwide spatial distribution (Figure 8b). Figure 9d shows the correlation between different vegetation indices and the SPEI. The correlation between the SPEI and NDVI exhibited significant variability across various time scales in grassland. Notably, at a time-lag of 4–9 months, a positive correlation emerged between the NDVI and SPEI, with the strongest time-lag effect observed at 7 months (r_grassland = 0.072). The response amplitude of woodland to the SPEI at each time-lag time was lower than that of grassland, and the correlation between the NDVI and SPEI at a time-lag of 2–11 months was positive, and the strongest time-lag effect was observed at 6 months (r_woodland = 0.064). The response of cropland to the SPEI at each time-lag time fluctuated greatly, and the response of the NDVI to the SPEI was positively correlated at 6–9 months and peaked at 7 months (r_cropland = 0.093). In addition, the average SPEI time scales for woodland, grassland, and cropland were 7.0, 6.7, and 6.6 months, respectively.

4. Discussion

4.1. The Effects of Drought on Different Vegetation Types

To deeply understand the difference between cumulative and time-lagged effects, the extreme value phase difference method (ΔRmax = Rmax_cum − Rmax_lag) was used to explore the difference. As shown in Figure 10a, the regions where the time-lag effect was greater than the cumulative effect were mainly distributed in northern Xinjiang and Northeast China. The cumulative effect was stronger than the time-lag effect in the Qinghai–Tibet Plateau, Southwest Region, and some eastern regions. Figure 10b shows the statistical rule of the difference between the cumulative effect and time-lag effect. It was found that the cumulative effect of drought had a higher time-lag effect in 52.15% of the area. ΔRmax fell between −0.10–0 (33.77%) and 0–0.1 (36.36%), followed by −0.2–−0.1 (13.89%) and 0.1–0.2 (10.45%).

Further research was carried out on the dominance of time-lag and cumulative effects of drought on the three vegetation types: cropland, grassland, and woodland. Figure 11a demonstrates that in grassland, as opposed to cropland and woodland, there was a stronger correlation between cumulative and time-lag effects. All three vegetation types also had a stronger time-lag effect than cumulative effect. Figure 11b reveals that the cumulative mean number of months was larger than the mean number of time-lag months for grassland and woodland, while the cumulative mean number of months was smaller than the mean number of time-lag months for cropland. Additionally, the cumulative and time-lag mean number of months was also larger for woodland than for cropland and grassland.

4.2. Reliability of the Framework

At present, the relationship between climate and vegetation is the research object of various scholars in different fields. Many different methods have been used to explore the cumulative effects of drought on vegetation, for example, the SPI, PDSI, and temperature vegetation drought index (TVDI). The SPI collects and standardizes data from meteorological observation sites for hydrological drought monitoring. The PDSI is a meteorological drought index derived from the water balance principle, which takes into account prior precipitation, moisture supply, and potential emanation [33]. The TVDI is an index used for soil moisture inversion in vegetation regions that relies on optical and thermal infrared remote sensing channel data. However, the PDSI and TVDI have fixed time scales and do not take into account the characteristics of multi-scale drought [34,35]. The SPEI is primarily used to monitor meteorological drought [8,14], while the SPI is primarily used to monitor agricultural drought [36]. The SPEI considers both precipitation and the sensitivity of the PDSI to potential evapotranspiration changes, integrating multiple time scales of the SPI [7].

The NDVI and EVI are commonly used to monitor vegetation growth. Matsushita et al. (2007) [37] showed that the ratio characteristic of the NDVI could eliminate the influence of atmospheric conditions such as solar angle, terrain, clouds, etc., but supersaturation would occur in high-value regions [38]. Compared with the NDVI, the EVI eliminates this effect, but the EVI does not consider the noise generated by terrain as an important factor affecting the calibration of a vegetation index. Combined with China’s complex geomorphic units, the NDVI, which has a reduced topographic impact, is more suitable for large-scale vegetation monitoring, and comprehensive consideration of the NDVI can better characterize vegetation growth. The indices used in this paper, the NDVI and SPEI, have been confirmed by previous studies [8,14].

In addition to remote sensing products, satellite datasets are also important for obtaining the NDVI. The existing AVHRR, the Himawari-8 and Sentinel-2 datasets, are widely used. However, the earlier time range of AVHR-NDVI and the shorter time range of Himawari-8 would have limited the research. In addition, the high spatial resolution of Sentinel-2 leads to too much uncertainty in resampling SPEI data to the same resolution. Therefore, MODIS products were selected in this paper.

4.3. Uncertainty and Future Improvements

The spatial distribution characteristics of the maximum correlation coefficients and their corresponding time scales in most of China are generally consistent with regional results, such as those for Loess Plateau grassland [14] and the Yellow River basin [8], indicating that this study accurately reflects the spatial correlation between the NDVI and SPEI at different time scales. However, there are some disadvantages, such as the simple correlation analysis and low spatial resolution because of the complex relationships between vegetation and the environment and regional differences. The relationship between vegetation growth and drought is nonlinear and complex, and the use of correlation coefficient analysis oversimplifies the cumulative and time-lag effects [39]. The SPEI dataset has low resolution, leading to uncertainties when resampling to match the resolution of the NDVI. In addition, the influence of climate and soil moisture on vegetation growth has been demonstrated [16,40,41,42], but this paper only considers the influence of the SPEI on vegetation, ignoring the influence of other factors on vegetation growth, which unavoidably affected the results. Further research is necessary to investigate the impact of additional factors on vegetation growth, aiming to enhance clarity and reliability in terms of accuracy.

5. Conclusions

This paper analyzed the spatial and temporal changes in the NDVI and the correlation between the NDVI and SPEI at various time scales to summarize the cumulative and time-lag effects of drought on woodland, grassland, and cropland from 2001 to 2020 and drew the following conclusions:

• The NDVI increased at a rate of 0.019/10 years, demonstrating the spatial variation trend of low values in the west and high values in the east, with an increase in the NDVI seen in 80.53% of areas.
• The average SPEI cumulative time scale most relevant to the NDVI was 7.3 months, and the cumulative effect of drought on vegetation showed a strong correlation at 9–12 months. There were significant regional differences in the cumulative effect’s spatial distribution, with the cumulative scale being most widely distributed at 9 months and then 12 months, primarily in the northeast and northwest. The cumulative effects of drought on cropland, woodland, and grassland all showed the maximum correlation and the strongest cumulative effect at 9 months, and the correlation coefficients were ranked as grassland > woodland > cropland from 6 to 12 months of accumulation, and the average SPEI time scales most relevant to woodland, grassland, and cropland were 8.0, 6.3, and 7.4 months, respectively; that is, the best cumulative time followed the order woodland > cropland > grassland.
• The average SPEI time-lag scale related to the NDVI was 6.9 months, and the time-lag effect of drought on vegetation showed a maximum correlation at 7 months. The spatial distribution of the time-lag effect also had obvious territoriality, and the lag time interval was primarily 6–8 months, with cropland and grassland having the strongest time-lag effect at 7 months and woodland having the strongest time-lag effect at 6 months, and the time-lag effect of woodland on all scales was lower than that of grassland, and the average SPEI time scales related to woodland, grassland, and cropland were 7.0, 6.7, and 6.6 months, respectively.