Robust Multiplexing Waveform Design for Integrated OFDM Radar and Communication via Complex Weight Optimization
Abstract
:1. Introduction
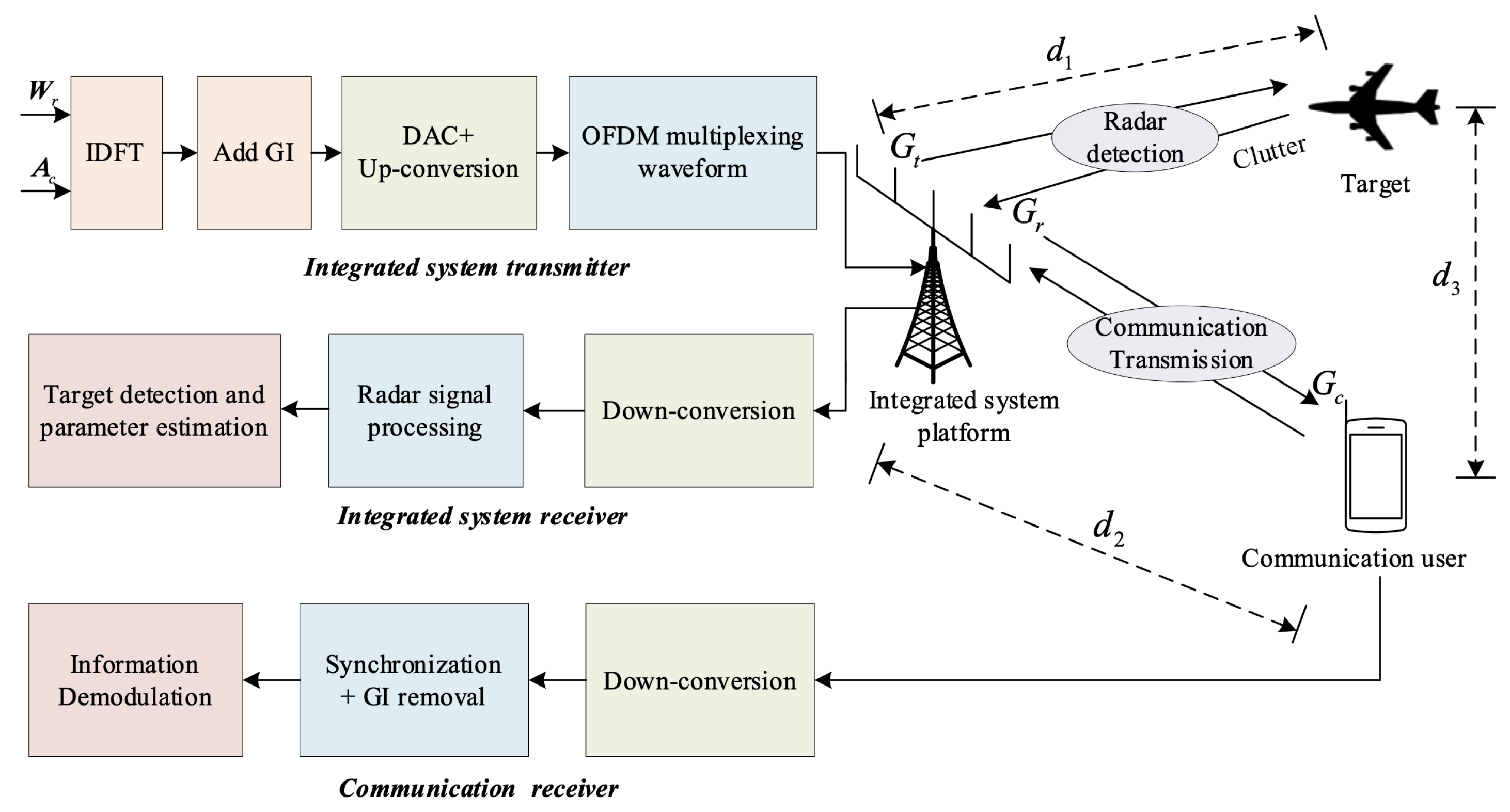
2. System Model and Problem Description
3. Robust OFDM Multiplexing Waveform Design
3.1. Constraint Relaxation-Based Robust OFDM Waveform (ROW-CR) Design
3.2. Parameter Hierarchical Optimization-Based Robust OFDM Waveform (ROW-PHO) Design
4. Numerical Simulation
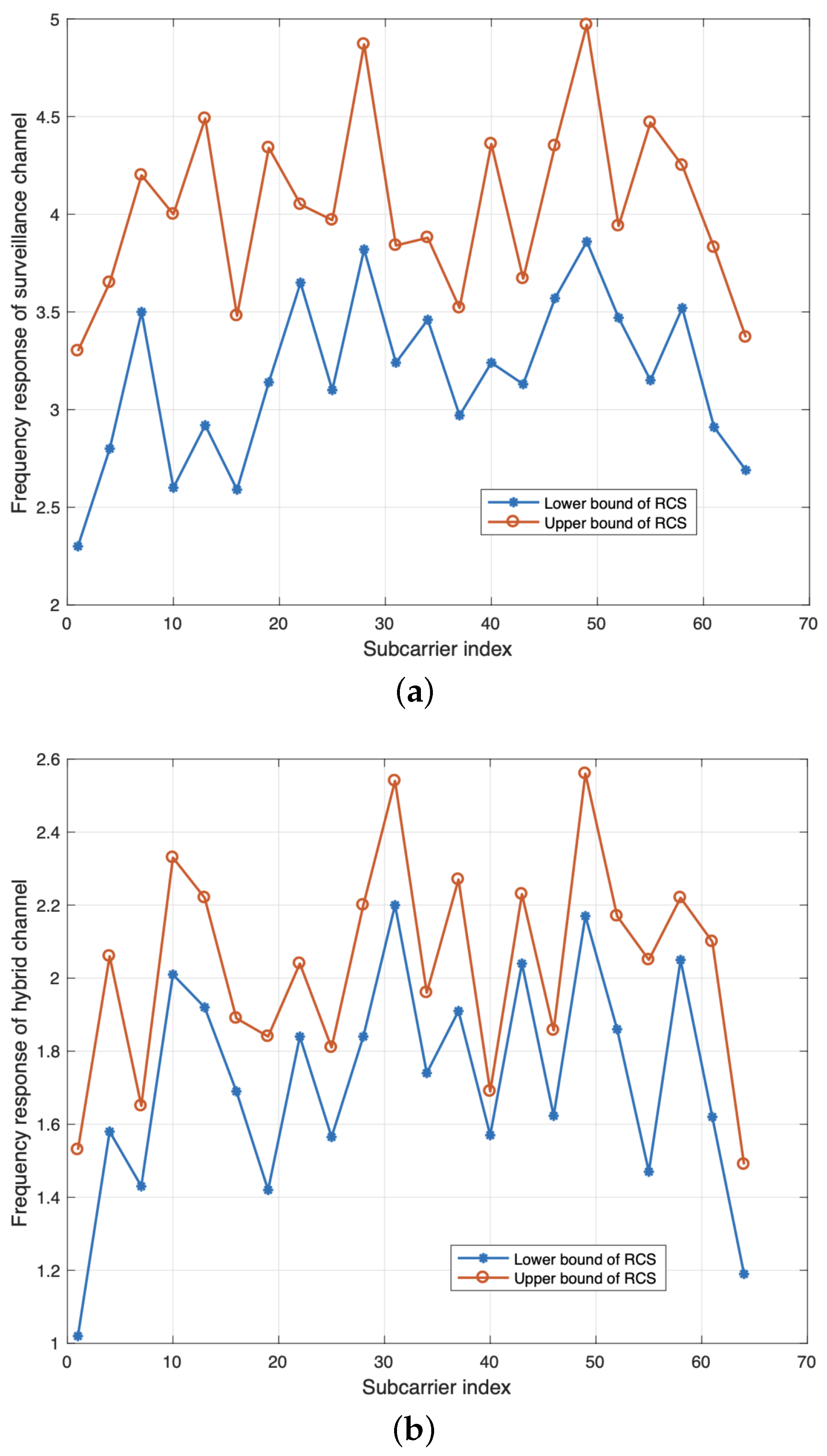
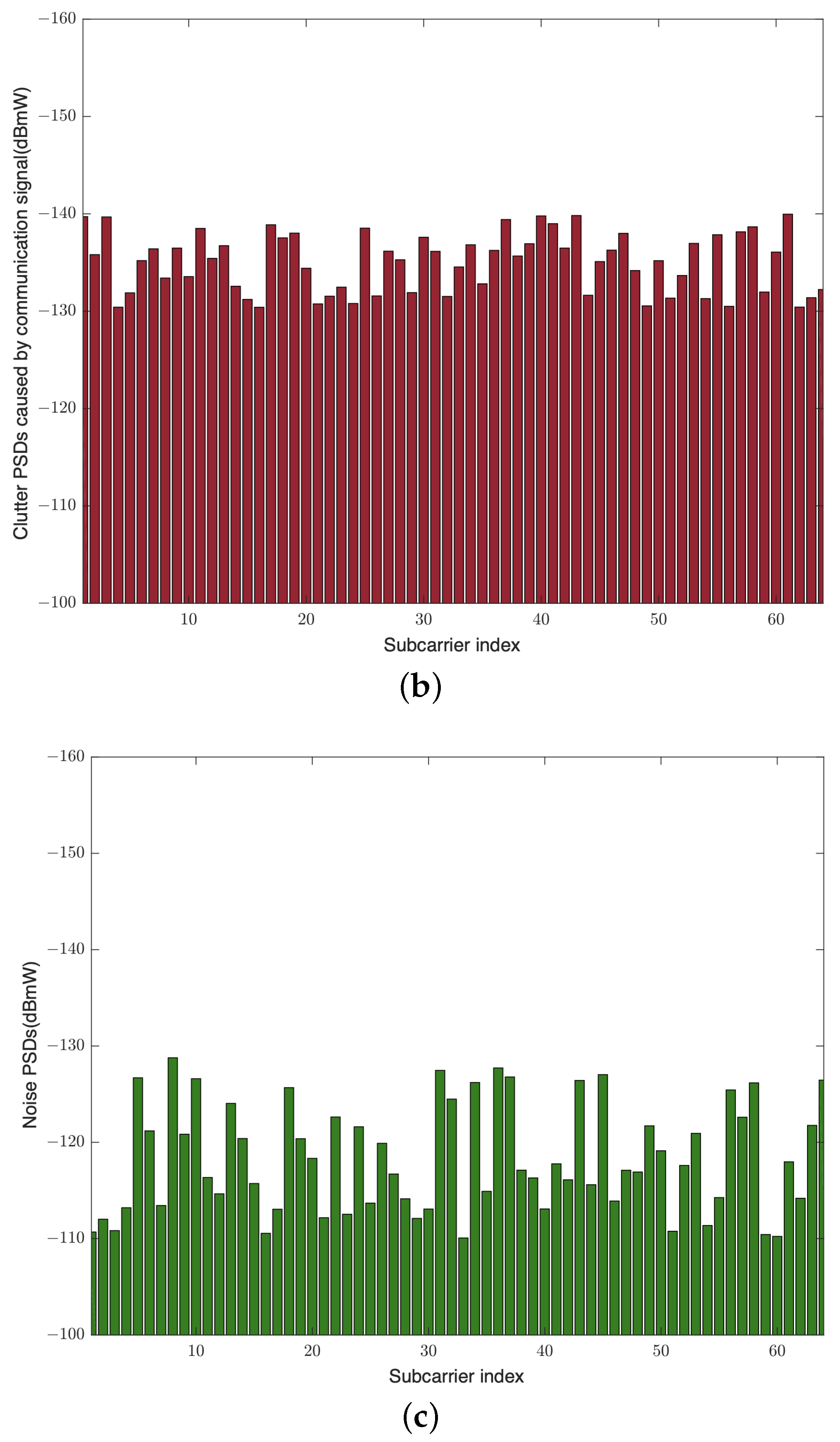
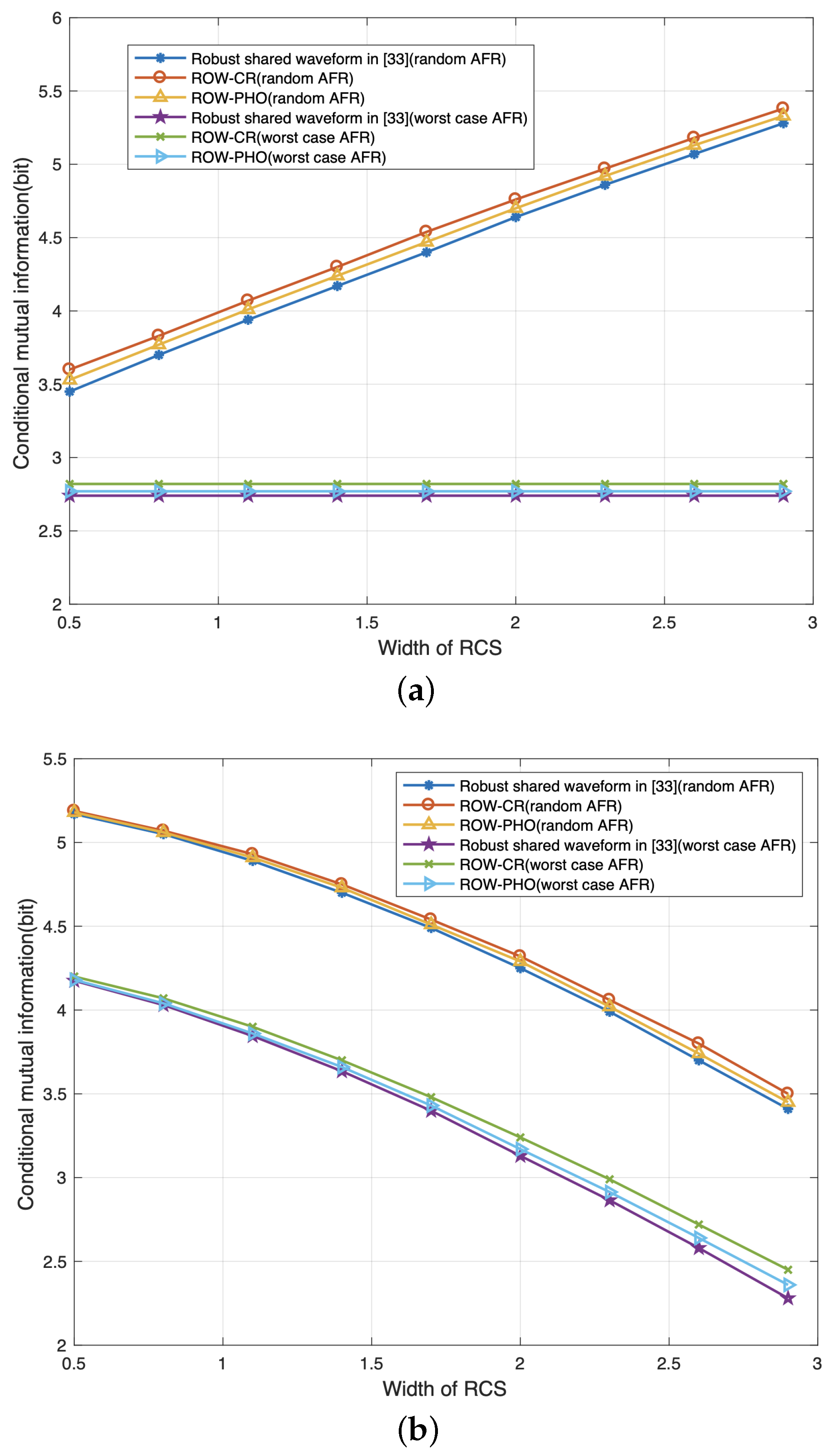
4.1. Radar Performance
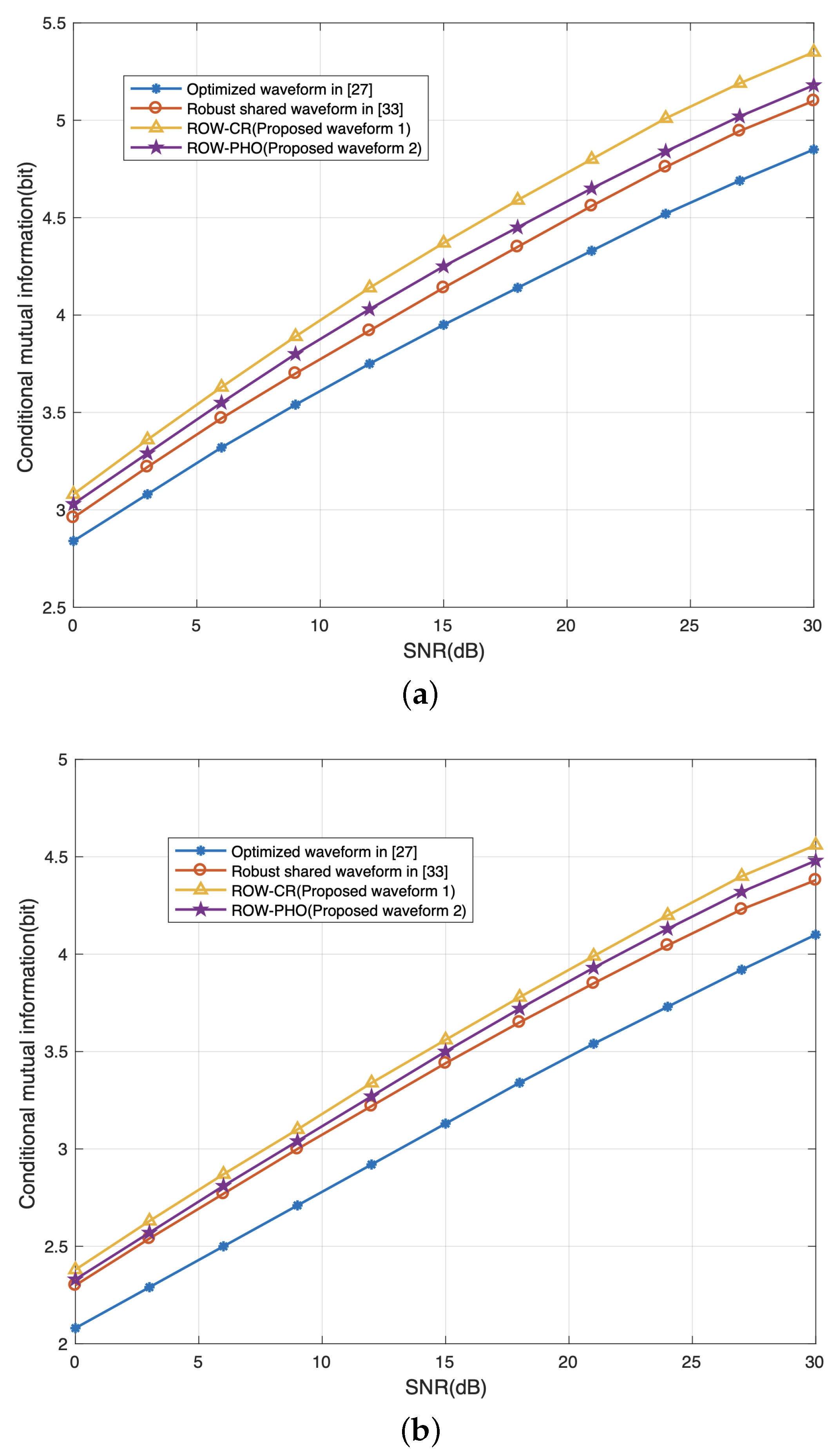
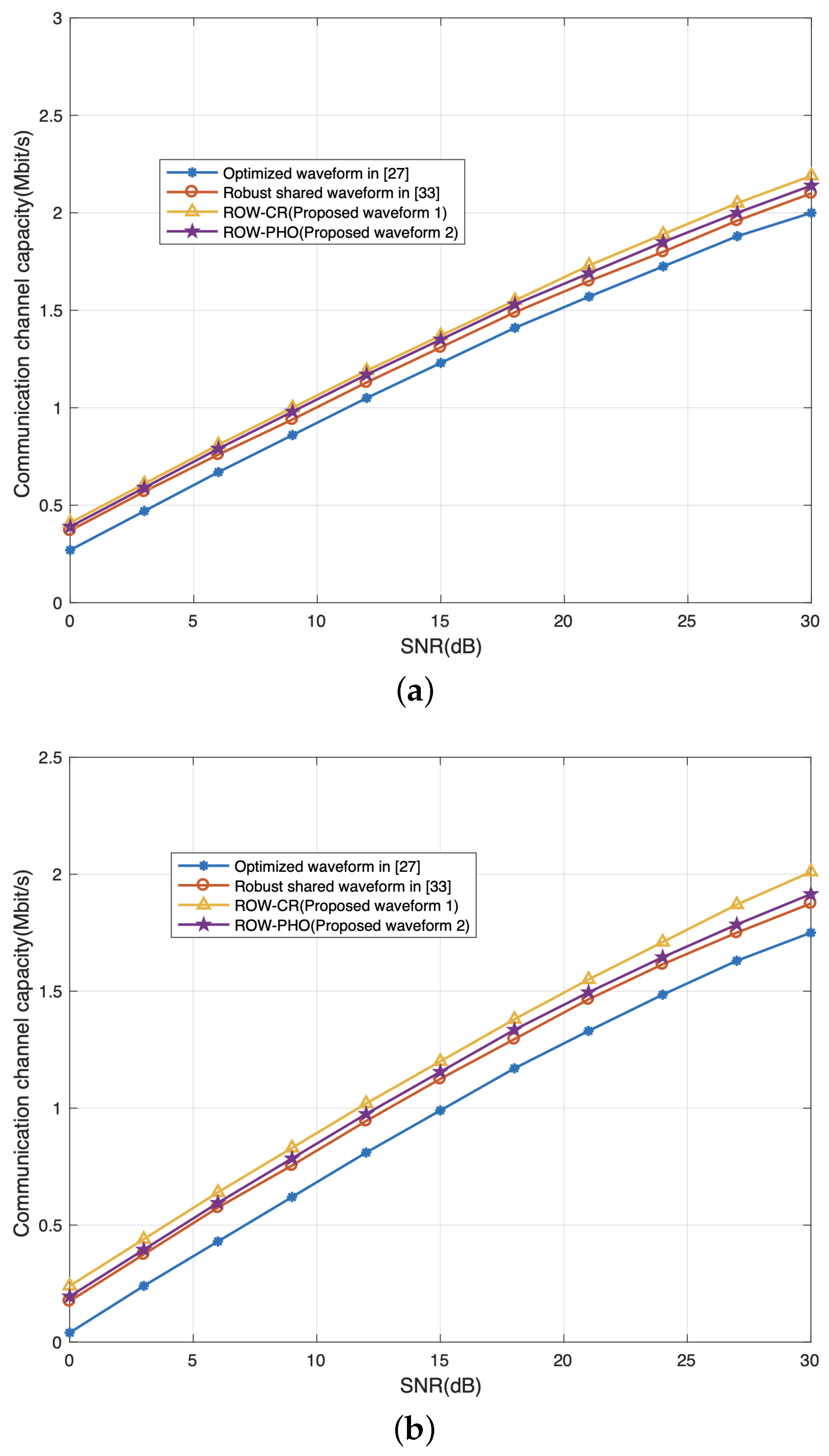
4.2. Communication Performance
4.3. Comparison of Computational Complexity
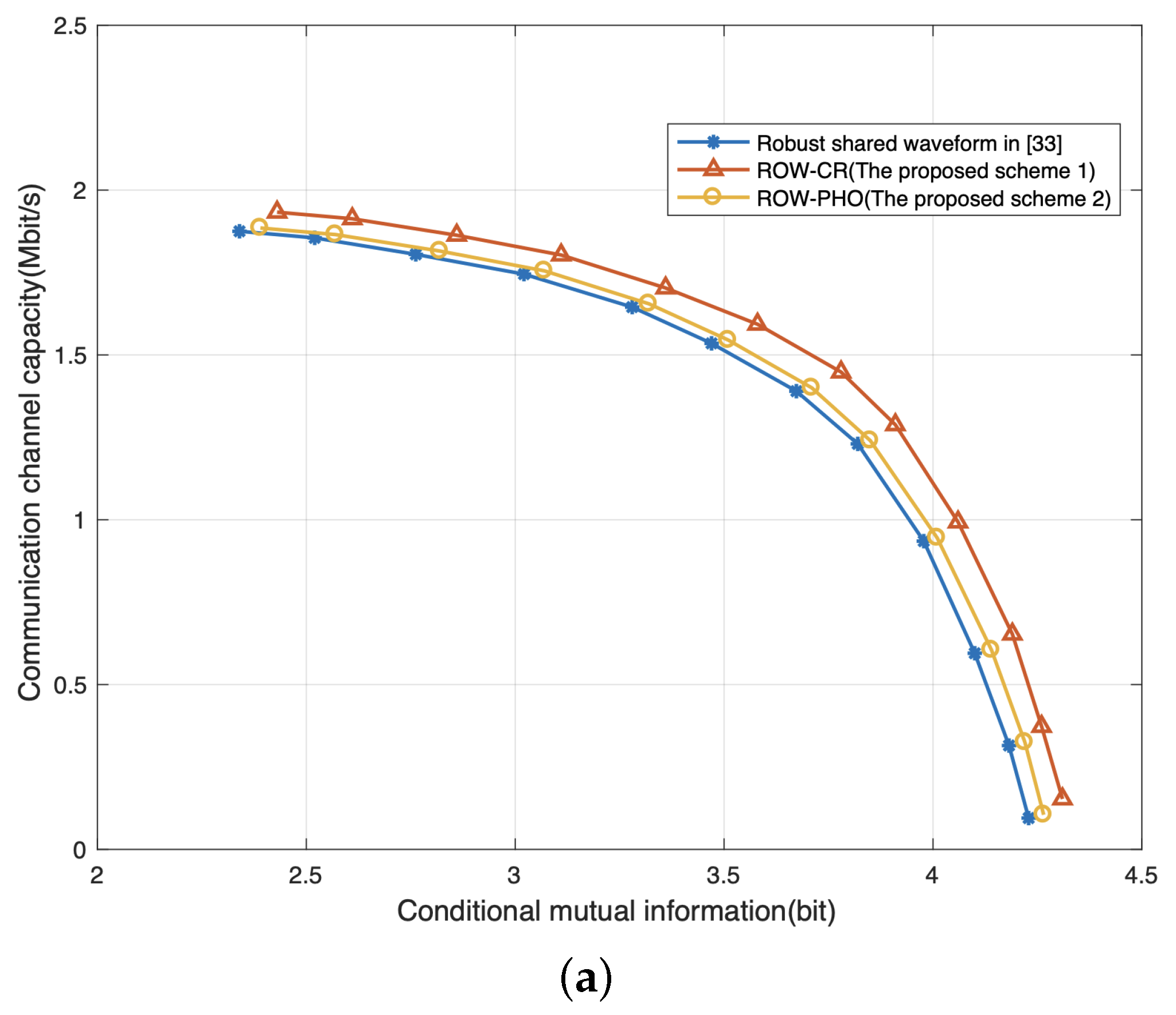
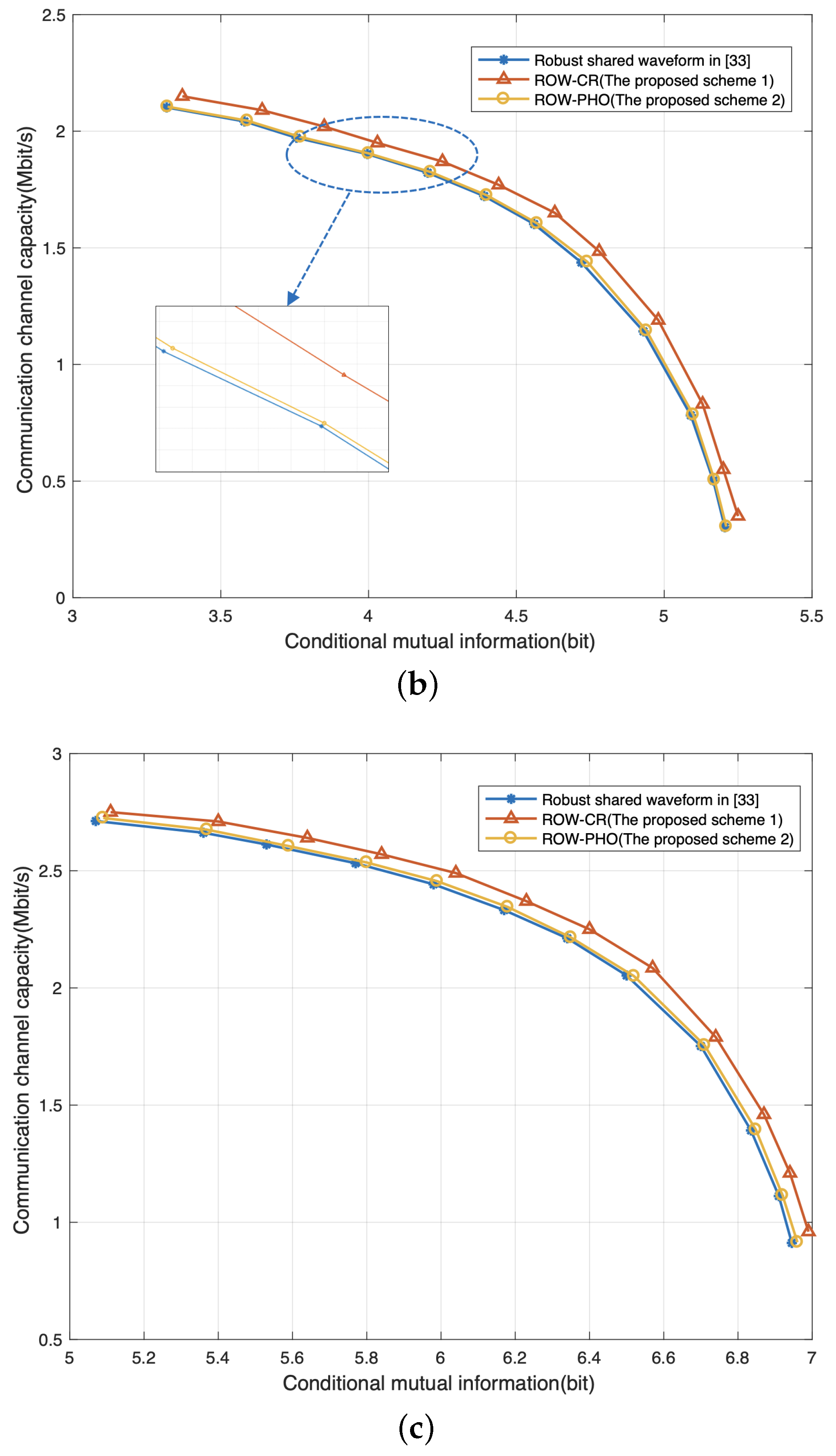
4.4. Radar–Communication Trade-Off
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| OFDM | orthogonal frequency division multiplexing |
| UAV | unmanned aerial vehicle |
| RCS | restricted closed sets |
| IDFT | inverse discrete Fourier transform |
| ISI | inter-symbol interference |
| CP | cyclic prefix |
| GI | guard interval |
| DAC | digital-to-analog conversion |
| AWGN | additive white Gaussian noise |
| ROW-CR | robust OFDM waveform based on constraint relaxation |
| ROW-PHO | robust OFDM waveform based on parameter hierarchical optimization |
| PSD | power spectral density |
| SNR | signal-to-noise ratio |
References
- Cheng, Z.; Liao, B.; He, Z.; Li, Y.; Li, J. Spectrally compatible waveform design for MIMO radar in the presence of multiple targets. IEEE Trans. Signal Process. 2018, 66, 3543–3555. [Google Scholar] [CrossRef]
- Yu, Q.; Lin, H.; Chen, H. Intelligent radio for next generation wireless communications: An overview. IEEE Wireless Commun. 2019, 26, 94–101. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, F.; Masouros, C.; Heath, R.; Feng, Z.; Zheng, L.; Petropulu, A. An overview of signal processing techniques for joint communication and radar sensing. IEEE J. Sel. Top. Signal Process. 2021, 15, 1295–1315. [Google Scholar] [CrossRef]
- Liu, F.; Zhou, L.; Masouros, C.; Li, A.; Luo, W.; Petropulu, A. Toward Dual-functional Radar-Communication Systems: Optimal Waveform Design. IEEE Trans. Signal Process. 2018, 66, 4264–4279. [Google Scholar] [CrossRef]
- Zheng, L.; Lops, M.; Eldar, Y.C.; Wang, X. Radar and Communication Coexistence: An Overview: A Review of Recent Methods. IEEE Signal Process. Mag. 2019, 36, 85–99. [Google Scholar] [CrossRef]
- Qian, J.; Lops, M.; Zheng, L.; Wang, X.; He, Z. Joint System Design for Coexistence of MIMO Radar and MIMO Communication. IEEE Trans. Signal Process. 2018, 66, 3504–3519. [Google Scholar] [CrossRef]
- Zhang, J.; Rahman, M.L.; Huang, X.; Guo, Y.; Chen, S.; Heath, R.W. Perceptive mobile network: Cellular networks with radio vision via joint communication and radar sensing. IEEE Veh. Technol. Mag. 2021, 16, 20–30. [Google Scholar] [CrossRef]
- Liu, F.; Masouros, C.; Petropulu, A.P.; Griffiths, H.; Hanzo, L. Joint Radar and Communication Design: Applications, State-of-the-Art, and the Road Ahead. IEEE Trans. Commun. 2020, 68, 3834–3862. [Google Scholar] [CrossRef]
- Liu, F.; Masouros, C. A tutorial on joint radar and communication transmission for vehicular networks—Part I: Background and fundamentals. IEEE Commun. Lett. 2021, 25, 322–326. [Google Scholar] [CrossRef]
- Lashkari, A.H.; Parhizkar, B.; Ngan, M.N.A. WiFi-based indoor positioning system. In Proceeding of the 2010 Second International Conference on Computer and Network Technology, Bangkok, Thailand, 23–25 April 2010; pp. 76–78. [Google Scholar]
- Xiao, Z.; Zeng, Y. Waveform design and performance analysis for full-duplex integrated sensing and communication. IEEE J. Sel. Areas Commun. 2022, 40, 1823–1837. [Google Scholar] [CrossRef]
- Keskin, M.F.; Koivunen, V.; Wymeersch, H. Limited feedforward waveform design for OFDM dual-functional radar-communications. IEEE Trans. Signal Process. 2021, 69, 2955–2970. [Google Scholar] [CrossRef]
- Liu, Y.; Liao, G.; Chen, Y.; Xu, J.; Yin, Y. Super-resolution range and velocity estimations with OFDM integrated radar and communications waveform. IEEE Trans. Veh. Technol. 2020, 69, 11659–11672. [Google Scholar] [CrossRef]
- Zhu, S.; Yang, R.; Li, X.; Zuo, J.; Li, D.; Ding, Y. An optimizing method of OFDM radar communication and jamming shared waveform based on improved greedy algorithm. IEEE Access. 2020, 8, 186462–186473. [Google Scholar] [CrossRef]
- Ma, D.; Shlezinger, N.; Huang, T.; Liu, Y.; Eldar, Y.C. Joint radar-communication strategies for autonomous vehicles: Combining two key automotive technologies. IEEE Signal Process. Mag. 2020, 37, 85–97. [Google Scholar] [CrossRef]
- Temiz, M.; Alsusa, E.; Baidas, M.W. Optimized precoders for massive MIMO OFDM dual radar-communication systems. IEEE Trans. Commun. 2021, 69, 4781–4794. [Google Scholar] [CrossRef]
- Yu, X.; Yao, X.; Yang, J.; Zhang, L.; Kong, L.; Cui, G. Integrated waveform design for MIMO radar and communication via spatio-spectral modulation. IEEE Trans. Signal Process. 2022, 70, 2293–2305. [Google Scholar] [CrossRef]
- Wang, X.; Zhai, W.; Zhang, X.; Wang, X.; Amin, M.G. Enhanced Automotive Sensing Assisted by Joint Communication and Cognitive Sparse MIMO Radar. IEEE Trans. Aerosp. Electron. Syst. 2023. [Google Scholar] [CrossRef]
- Xu, C.; Clerckx, B.; Chen, S.; Mao, Y.; Zhang, J. Rate-splitting multiple access for multi-antenna joint radar and communications. IEEE J. Sel. Top. Signal Process. 2021, 15, 1332–1347. [Google Scholar] [CrossRef]
- Rong, J.; Liu, F.; Miao, Y. High-Efficiency Optimization Algorithm of PMEPR for OFDM Integrated Radar and Communication Waveform Based on Conjugate Gradient. Remote Sens. 2022, 14, 1715. [Google Scholar] [CrossRef]
- Xu, R.; Peng, L.; Zhao, W.; Mi, Z. Radar mutual information and communication channel capacity of integrated radar-communication system using MIMO. ICT Exp. 2015, 1, 102–105. [Google Scholar] [CrossRef]
- Setlur, P.; Rangaswamy, M. Waveform design for radar STAP in signal dependent interference. IEEE Trans. Signal Process. 2016, 64, 19–34. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, H.; Wang, J. Robust multiple-input multiple- output radar waveform design in the presence of clutter. Iet Radar Sonar Navig. 2016, 10, 1249–1259. [Google Scholar] [CrossRef]
- Zhao, Z.; Wan, X.; Zhang, D.; Cheng, F. An experimental study of HF passive bistatic radar via hybrid sky-surface wave mode. IEEE Trans. Antennas Propag. 2013, 61, 415–424. [Google Scholar] [CrossRef]
- Grossi, E.; Lops, M.; Venturino, L. Joint Design of Surveillance Radar and MIMO Communication in Cluttered Environments. IEEE Trans. Signal Process. 2020, 68, 1544–1557. [Google Scholar] [CrossRef]
- Shi, C.; Wang, F.; Sellathurai, M.; Zhou, J.; Salous, S. Power minimization-based robust OFDM radar waveform design for radar and communication systems in coexistence. IEEE Trans. Signal Process. 2018, 66, 1316–1330. [Google Scholar] [CrossRef]
- Shi, C.; Wang, F.; Salous, S.; Zhou, J. Joint subcarrier assignment and power allocation strategy for integrated radar and communications system based on power minimization. IEEE Sens. J. 2019, 19, 11167–11179. [Google Scholar] [CrossRef]
- Liu, Y.; Liao, G.; Xu, J.; Yang, Z.; Huang, L.; Zhang, Y. Transmit power adaptation for orthogonal frequency division multiplexing integrated radar and communication systems. J. Appl. Remote Sens. 2017, 11, 035017. [Google Scholar] [CrossRef]
- Liu, Y.; Liao, G.; Yang, Z.; Xu, J. Multiobjective optimal waveform design for OFDM integrated radar and communication systems. Signal Process. 2017, 141, 331–342. [Google Scholar] [CrossRef]
- Ahmed, A.; Zhang, Y.D.; Hassanien, A. Joint Radar-Communications Exploiting Optimized OFDM Waveforms. Remote Sens. 2021, 13, 4376. [Google Scholar] [CrossRef]
- Chiriyath, A.R.; Paul, B.; Bliss, D.W. Radar-communications convergence: Coexistence, cooperation, and co-design. IEEE Trans. Cognit. Commun. Netw. 2017, 3, 1–12. [Google Scholar] [CrossRef]
- Chiriyath, A.R.; Paul, B.; Jacyna, G.M.; Bliss, D.W. Inner bounds on performance of radar and communications co-existence. IEEE Trans. Signal Process. 2015, 53, 464–474. [Google Scholar] [CrossRef]
- Liu, Y.; Liao, G.; Yang, Z. Robust OFDM integrated radar and communications waveform design based on information theory. Signal Process. 2019, 162, 317–329. [Google Scholar] [CrossRef]
- Hsu, H.W.; Lee, M.C.; Gu, M.; Lin, Y.; Lee, T.S. Analysis and Design for Pilot Power Allocation and Placement in OFDM Based Integrated Radar and Communication in Automobile Systems. IEEE Trans. Veh. Technol. 2022, 71, 1519–1535. [Google Scholar] [CrossRef]
- Hwang, S.; Seo, J.; Park, J.; Kim, H.; Jeong, B.J. Compressive Sensing-Based Radar Imaging and Subcarrier Allocation for Joint MIMO OFDM Radar and Communication System. Sensors 2021, 21, 2382. [Google Scholar] [CrossRef]
- Shi, C.G.; Salous, S.; Wang, F.; Zhou, J.J. Low probability of intercept based adaptive radar waveform optimization in signal dependent clutter for joint radar and cellular communication systems. EURASIP J. Adv. Signal Process. 2016, 2016, 111. [Google Scholar] [CrossRef]
- Bica, M.; Koivunen, V. Generalized multicarrier radar: Models and performance. IEEE Trans. Signal Process. 2016, 64, 4389–4402. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, Y.; Yeo, T.-S.; Han, J.; Peng, Z. Joint Sequence Optimization-Based OFDM Waveform Design for Integrated Radar and Communication Systems. IEEE Trans. Veh. Technol. 2022, 71, 12734–12748. [Google Scholar] [CrossRef]
- Bell, M.R. Information theory and radar waveform design. IEEE Trans. Inf. Theory 1993, 39, 1578–1597. [Google Scholar] [CrossRef]
- Turlapaty, A.; Jin, Y.W. A joint design of transmit waveforms for radar and communications systems in coexistence. In Proceeding of the 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 315–319. [Google Scholar]
- Yan, S.; He, B.; Zhou, X.; Cong, Y.; Swindlehurst, A.L. Delay-intolerant covert communications with either fixed or random transmit power. IEEE Trans. Inf. Forensics Secur. 2019, 14, 129–140. [Google Scholar] [CrossRef]
- Yang, Y.; Blum, R.S. Minimax robust MIMO radar waveform design. IEEE J. Sel. Top. Signal Process. 2007, 1, 147–155. [Google Scholar] [CrossRef]
- Liu, Y.; Liao, G.; Xu, J.; Yang, Z.; Zhang, Y. Adaptive OFDM integrated radar and communications waveform design based on information theory. IEEE Commun. Lett. 2017, 21, 2174–2177. [Google Scholar] [CrossRef]
- Zheng, L.; Kan, H.; Li, Y.; Peng, J.; Tang, D. Constructing New APN Functions Through Relative Trace Functions. IEEE Trans. Inf. Theory 2022, 68, 7528–7537. [Google Scholar] [CrossRef]
- Li, M. Generalized Lagrange Multiplier Method and KKT Conditions With an Application to Distributed Optimization. IEEE Trans. Circuits Syst. II 2019, 66, 252–256. [Google Scholar] [CrossRef]
- Liu, H.; Yu, W. Discrete-Time Algorithm for Distributed Unconstrained Optimization Problem With Finite-Time Computations. IEEE Trans. Circuits Syst. II 2021, 68, 351–355. [Google Scholar] [CrossRef]
- Wijewardhana, U.L.; Codreanu, M.; Latva-aho, M. An Interior-Point Method for Modified Total Variation Exploiting Transform-Domain Sparsity. IEEE Signal Process. Lett. 2017, 24, 56–60. [Google Scholar] [CrossRef]
- Malyuta, D.; Reynolds, T.P.; Szmuk, M.; Lew, T.; Bonalli, R.; Pavone, M.; Acikmese, B. Convex Optimization for Trajectory Generation: A Tutorial on Generating Dynamically Feasible Trajectories Reliably and Efficiently. IEEE Control Syst. Mag. 2022, 42, 40–113. [Google Scholar] [CrossRef]



| Parameters | Value |
|---|---|
| Subcarrier spacing | 0.25 MHz |
| Carrier frequency | 5 GHz |
| Number of subcarriers | 64 |
| Number of antennas | 8 |
| / | 25 dB |
| 2 dB | |
| // | 10 km |
| Methods | Running Time under the Same Hardware Conditions (s) | |||
|---|---|---|---|---|
| Optimized waveform design in [27] | 0.91 | 1.63 | 2.93 | 7.74 |
| Robust waveform design in [33] | 1.98 | 2.81 | 5.66 | 15.21 |
| ROW-CR (Proposed scheme 1) | 2.04 | 2.75 | 5.52 | 14.34 |
| ROW-PHO (Proposed scheme 2) | 1.05 | 1.56 | 2.74 | 6.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Cao, Y.; Yeo, T.-S.; Cheng, Y.; Fu, J. Robust Multiplexing Waveform Design for Integrated OFDM Radar and Communication via Complex Weight Optimization. Remote Sens. 2023, 15, 4438. https://doi.org/10.3390/rs15184438
Wang Y, Cao Y, Yeo T-S, Cheng Y, Fu J. Robust Multiplexing Waveform Design for Integrated OFDM Radar and Communication via Complex Weight Optimization. Remote Sensing. 2023; 15(18):4438. https://doi.org/10.3390/rs15184438
Chicago/Turabian StyleWang, Yang, Yunhe Cao, Tat-Soon Yeo, Yuanhao Cheng, and Jie Fu. 2023. "Robust Multiplexing Waveform Design for Integrated OFDM Radar and Communication via Complex Weight Optimization" Remote Sensing 15, no. 18: 4438. https://doi.org/10.3390/rs15184438
APA StyleWang, Y., Cao, Y., Yeo, T.-S., Cheng, Y., & Fu, J. (2023). Robust Multiplexing Waveform Design for Integrated OFDM Radar and Communication via Complex Weight Optimization. Remote Sensing, 15(18), 4438. https://doi.org/10.3390/rs15184438







