Improving the Transferability of Deep Learning Models for Crop Yield Prediction: A Partial Domain Adaptation Approach
Abstract
:1. Introduction
2. Materials
2.1. Experimental Site and Crop Yield Records
2.2. Satellite-Derived Vegetation Indices and Meteorological Variables
2.3. Data Preprocessing
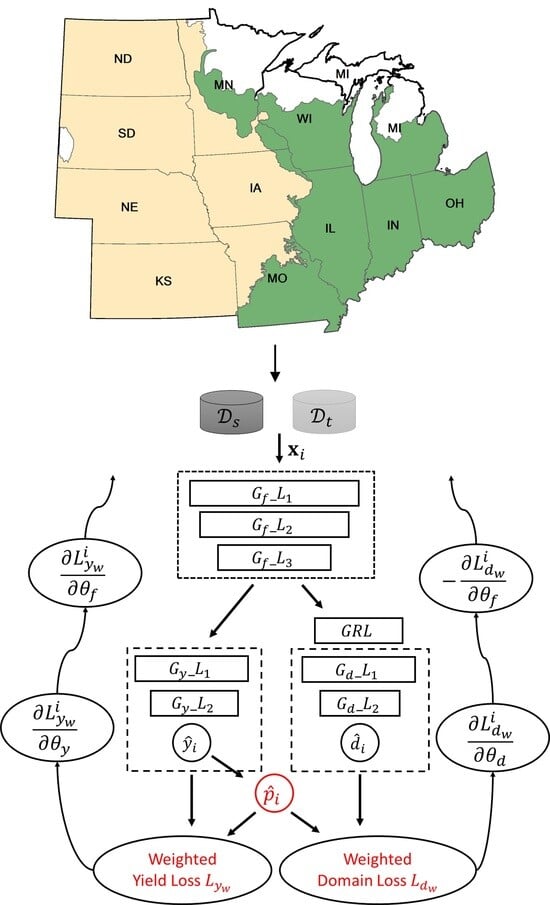
3. Methodology
4. Experiments and Results
4.1. Experiment Setup
4.2. Evaluation Results
5. Discussion
5.1. Weighting Mechanism Analysis
5.2. t-SNE Visualization
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kluger, D.M.; Owen, A.B.; Lobell, D.B. Combining randomized field experiments with observational satellite data to assess the benefits of crop rotations on yields. Environ. Res. Lett. 2022, 17, 044066. [Google Scholar] [CrossRef]
- Dado, W.T.; Deines, J.M.; Patel, R.; Liang, S.-Z.; Lobell, D.B. High-Resolution Soybean Yield Mapping Across the US Midwest Using Subfield Harvester Data. Remote Sens. 2020, 12, 3471. [Google Scholar] [CrossRef]
- Gao, F.; Anderson, M.; Daughtry, C.; Johnson, D. Assessing the Variability of Corn and Soybean Yields in Central Iowa Using High Spatiotemporal Resolution Multi-Satellite Imagery. Remote Sens. 2018, 10, 1489. [Google Scholar] [CrossRef]
- Lobell, D.B.; Hammer, G.L.; McLean, G.; Messina, C.; Roberts, M.J.; Schlenker, W. The critical role of extreme heat for maize production in the United States. Nat. Clim. Chang. 2013, 3, 497–501. [Google Scholar] [CrossRef]
- Zhou, W.; Guan, K.; Peng, B.; Tang, J.; Jin, Z.; Jiang, C.; Grant, R.; Mezbahuddin, S. Quantifying carbon budget, crop yields and their responses to environmental variability using the ecosys model for U.S. Midwestern agroecosystems. Agric. For. Meteorol. 2021, 307, 108521. [Google Scholar] [CrossRef]
- Lv, Z.; Huang, H.; Li, X.; Zhao, M.; Benediktsson, J.A.; Sun, W.; Falco, N. Land Cover Change Detection with Heterogeneous Remote Sensing Images: Review, Progress, and Perspective. Proc. IEEE 2022, 110, 1976–1991. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Feng, L.; Ma, Y.; Du, Q. A new attention-based CNN approach for crop mapping using time series Sentinel-2 images. Comput. Electron. Agric. 2021, 184, 106090. [Google Scholar] [CrossRef]
- Kang, Y.; Ozdogan, M.; Zhu, X.; Ye, Z.; Hain, C.R.; Anderson, M.C. Comparative assessment of environmental variables and machine learning algorithms for maize yield prediction in the US Midwest. Environ. Res. Lett. 2020, 15, 064005. [Google Scholar] [CrossRef]
- Johnson, D.M. An assessment of pre- and within-season remotely sensed variables for forecasting corn and soybean yields in the United States. Remote Sens. Environ. 2014, 141, 116–128. [Google Scholar] [CrossRef]
- Kamir, E.; Waldner, F.; Hochman, Z. Estimating wheat yields in Australia using climate records, satellite image time series and machine learning methods. ISPRS J. Photogramm. Remote Sens. 2019, 160, 124–135. [Google Scholar] [CrossRef]
- Marshall, M.; Belgiu, M.; Boschetti, M.; Pepe, M.; Stein, A.; Nelson, A. Field-level crop yield estimation with PRISMA and Sentinel-2. ISPRS J. Photogramm. Remote Sens. 2022, 187, 191–210. [Google Scholar] [CrossRef]
- Chen, S.; Liu, W.; Feng, P.; Ye, T.; Ma, Y.; Zhang, Z. Improving Spatial Disaggregation of Crop Yield by Incorporating Machine Learning with Multisource Data: A Case Study of Chinese Maize Yield. Remote Sens. 2022, 14, 2340. [Google Scholar] [CrossRef]
- Sun, J.; Di, L.; Sun, Z.; Shen, Y.; Lai, Z. County-Level Soybean Yield Prediction Using Deep CNN-LSTM Model. Sensors 2019, 19, 4363. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Z.; Luo, Y.; Cao, J.; Xie, R.; Li, S. Integrating satellite-derived climatic and vegetation indices to predict smallholder maize yield using deep learning. Agric. For. Meteorol. 2021, 311, 108666. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Z.; Kang, Y.; Özdoğan, M. Corn yield prediction and uncertainty analysis based on remotely sensed variables using a Bayesian neural network approach. Remote Sens. Environ. 2021, 259, 112408. [Google Scholar] [CrossRef]
- Hunt, M.L.; Blackburn, G.A.; Carrasco, L.; Redhead, J.W.; Rowland, C.S. High resolution wheat yield mapping using Sentinel-2. Remote Sens. Environ. 2019, 233, 111410. [Google Scholar] [CrossRef]
- Nguyen, L.H.; Robinson, S.; Galpern, P. Medium-resolution multispectral satellite imagery in precision agriculture: Mapping precision canola (Brassica napus L.) yield using Sentinel-2 time series. Precis. Agric. 2022, 23, 1051–1071. [Google Scholar] [CrossRef]
- Lv, Z.; Zhang, P.; Sun, W.; Benediktsson, J.A.; Li, J.; Wang, W. Novel Adaptive Region Spectral–Spatial Features for Land Cover Classification With High Spatial Resolution Remotely Sensed Imagery. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5609412. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Feng, L.; Du, Q.; Runge, T. Combining Multi-Source Data and Machine Learning Approaches to Predict Winter Wheat Yield in the Conterminous United States. Remote Sens. 2020, 12, 1232. [Google Scholar] [CrossRef]
- Kouw, W.M.; Loog, M. An Introduction to Domain Adaptation and Transfer Learning. 2018. Available online: http://arxiv.org/abs/1812.11806 (accessed on 15 September 2023).
- Tuia, D.; Persello, C.; Bruzzone, L. Domain Adaptation for the Classification of Remote Sensing Data: An Overview of Recent Advances. IEEE Geosci. Remote Sens. Mag. 2016, 4, 41–57. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Z. A Bayesian Domain Adversarial Neural Network for Corn Yield Prediction. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5513705. [Google Scholar] [CrossRef]
- Chew, R.; Rineer, J.; Beach, R.; O’neil, M.; Ujeneza, N.; Lapidus, D.; Miano, T.; Hegarty-Craver, M.; Polly, J.; Temple, D.S. Deep Neural Networks and Transfer Learning for Food Crop Identification in UAV Images. Drones 2020, 4, 7. [Google Scholar] [CrossRef]
- Wang, A.X.; Tran, C.; Desai, N.; Lobell, D.; Ermon, S. Deep Transfer Learning for Crop Yield Prediction with Remote Sensing Data. In Proceedings of the 1st ACM SIGCAS Conference on Computing and Sustainable Societies, San Jose, CA, USA, 20–22 June 2018. [Google Scholar] [CrossRef]
- Khaki, S.; Pham, H.; Wang, L. Simultaneous corn and soybean yield prediction from remote sensing data using deep transfer learning. Sci. Rep. 2021, 11, 11132. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Han, S.; Meng, Y.; Feng, H.; Li, Z.; Chen, J.; Song, X.; Zhu, Y.; Yang, G. Transfer-Learning-Based Approach for Yield Prediction of Winter Wheat from Planet Data and SAFY Model. Remote Sens. 2022, 14, 5474. [Google Scholar] [CrossRef]
- Schwalbert, R.A.; Amado, T.; Corassa, G.; Pott, L.P.; Prasad, P.; Ciampitti, I.A. Satellite-based soybean yield forecast: Integrating machine learning and weather data for improving crop yield prediction in southern Brazil. Agric. For. Meteorol. 2020, 284, 107886. [Google Scholar] [CrossRef]
- Zhao, S.; Yue, X.; Zhang, S.; Li, B.; Zhao, H.; Wu, B.; Krishna, R.; Gonzalez, J.E.; Sangiovanni-Vincentelli, A.L.; Seshia, S.A.; et al. A Review of Single-Source Deep Unsupervised Visual Domain Adaptation. IEEE Trans. Neural Netw. Learn. Syst. 2020, 33, 473–493. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Rao, W.; Sun, S.; Xie, L.; Chng, E.S.; Li, H. Unsupervised Domain Adaptation via Domain Adversarial Training for Speaker Recognition. ICASSP IEEE Int. Conf. Acoust. Speech Signal Process. Proc. 2018, 2018, 4889–4893. [Google Scholar] [CrossRef]
- Han, T.; Liu, C.; Yang, W.; Jiang, D. A novel adversarial learning framework in deep convolutional neural network for intelligent diagnosis of mechanical faults. Knowl.-Based Syst. 2019, 165, 474–487. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Z.; Yang, H.L.; Yang, Z. An adaptive adversarial domain adaptation approach for corn yield prediction. Comput. Electron. Agric. 2021, 187, 106314. [Google Scholar] [CrossRef]
- Ye, C.; Yang, J.; Ding, H. High-accuracy prediction and compensation of industrial robot stiffness deformation. Int. J. Mech. Sci. 2022, 233, 107638. [Google Scholar] [CrossRef]
- Ma, Y.; Yang, Z.; Zhang, Z. Multi-source Maximum Predictor Discrepancy for Unsupervised Domain Adaptation on Corn Yield Prediction. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4401315. [Google Scholar] [CrossRef]
- Gu, X.; Yu, X.; Yang, Y.; Sun, J.; Xu, Z. Adversarial Reweighting for Partial Domain Adaptation. Adv. Neural Inf. Process. Syst. 2021, 18, 14860–14872. [Google Scholar]
- Zhang, J.; Ding, Z.; Li, W.; Ogunbona, P. Importance Weighted Adversarial Nets for Partial Domain Adaptation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8156–8164. [Google Scholar] [CrossRef]
- Cao, Z.; Ma, L.; Long, M.; Wang, J. Partial Adversarial Domain Adaptation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; 11212, pp. 139–155. [Google Scholar] [CrossRef]
- Cao, Z.; Long, M.; Wang, J.; Jordan, M.I. Partial Transfer Learning with Selective Adversarial Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2724–2732. [Google Scholar] [CrossRef]
- Russello, H. Convolutional Neural Networks for Crop Yield Prediction using Satellite Images. M.S. Thesis. IBM Cent. Adv. Stud.. 2018. Available online: https://www.semanticscholar.org/paper/Convolutional-Neural-Networks-for-Crop-Yield-using-Russello-Shang/b49aa569ff63d045b7c0ce66d77e1345d4f9745c (accessed on 15 September 2023).
- Omernik, J.M.; Griffith, G.E. Ecoregions of the Conterminous United States: Evolution of a Hierarchical Spatial Framework. Environ. Manag. 2014, 54, 1249–1266. [Google Scholar] [CrossRef] [PubMed]
- Bolton, D.K.; Friedl, M.A. Forecasting crop yield using remotely sensed vegetation indices and crop phenology metrics. Agric. For. Meteorol. 2013, 173, 74–84. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Ciganda, V.; Rundquist, D.C.; Arkebauer, T.J. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32, L08403. [Google Scholar] [CrossRef]
- Gao, B.-C. Naval Research Laboratory, 4555 Overlook Ave. Remote Sens. Environ. 1996, 7212, 257–266. [Google Scholar] [CrossRef]
- Park, S.; Feddema, J.J.; Egbert, S.L. MODIS land surface temperature composite data and their relationships with climatic water budget factors in the central Great Plains. Int. J. Remote Sens. 2005, 26, 1127–1144. [Google Scholar] [CrossRef]
- Thornton, M.M.; Shrestha, R.; Wei, Y.; Thornton, P.E.; Kao, S.; Wilson, B.E. Daymet: Monthly Climate Summaries on a 1-km Grid for North America, Version 4 R1; ORNL DAAC: Oak Ridge, TN, USA, 2022. [Google Scholar]
- Jin, Y.; Chen, B.; Lampinen, B.D.; Brown, P.H. Advancing Agricultural Production with Machine Learning Analytics: Yield Determinants for California’s Almond Orchards. Front. Plant Sci. 2020, 11, 290. [Google Scholar] [CrossRef]
- Han, W.; Yang, Z.; Di, L.; Mueller, R. CropScape: A Web service based application for exploring and disseminating US conterminous geospatial cropland data products for decision support. Comput. Electron. Agric. 2012, 84, 111–123. [Google Scholar] [CrossRef]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; Marchand, M.; Lempitsky, V. Domain-Adversarial Training of Neural Networks. J. Mach. Learn. Res. 2017, 17, 1–35. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, UK, 2016. [Google Scholar]
- Sun, C.; Zhou, J.; Ma, Y.; Xu, Y.; Pan, B.; Zhang, Z. A review of remote sensing for potato traits characterization in precision agriculture. Front. Plant Sci. 2022, 13, 871859. [Google Scholar] [CrossRef] [PubMed]
- Deines, J.M.; Patel, R.; Liang, S.-Z.; Dado, W.; Lobell, D.B. A million kernels of truth: Insights into scalable satellite maize yield mapping and yield gap analysis from an extensive ground dataset in the US Corn Belt. Remote Sens. Environ. 2021, 253, 112174. [Google Scholar] [CrossRef]
- Sun, C.; Feng, L.; Zhang, Z.; Ma, Y.; Crosby, T.; Naber, M.; Wang, Y. Prediction of End-Of-Season Tuber Yield and Tuber Set in Potatoes Using In-Season UAV-Based Hyperspectral Imagery and Machine Learning. Sensors 2020, 20, 5293. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32, 8026–8037. [Google Scholar]
- van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]










| Domain | Environment and Climate | # Samples | Land Cover Layer | Variables |
|---|---|---|---|---|
| Eastern Temperate Forests (ETFs) | Largely covered by closed-canopy deciduous forests with a humid and temperate climate. | Corn: 5650 Soybean: 5658 | USDA-NASS Cropland Data Layer (CDL) |
|
| Great Plains (GPs) | Comparatively low biodiversity with a hot summer and low rainfall. | Corn: 5599 Soybean: 5229 |
| Year | Experiment | RF | DNN | ADANN | PDANN | ||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | ||
| 2019 | GP → ETF | 0.33 | 1.13 | 0.37 | 1.09 | 0.53 | 0.94 | 0.56 | 0.91 |
| ETF → GP | 0.70 | 1.28 | 0.68 | 1.31 | 0.73 | 1.20 | 0.78 | 1.10 | |
| 2020 | GP → ETF | 0.52 | 1.06 | 0.59 | 1.28 | 0.67 | 0.89 | 0.71 | 0.83 |
| ETF → GP | 0.54 | 1.67 | 0.64 | 1.46 | 0.75 | 1.22 | 0.77 | 1.18 | |
| 2021 | GP → ETF | 0.53 | 1.08 | 0.49 | 1.17 | 0.59 | 1.01 | 0.65 | 0.94 |
| ETF → GP | 0.75 | 1.67 | 0.71 | 1.80 | 0.74 | 1.70 | 0.75 | 1.67 | |
| Year | Experiment | RF | DNN | ADANN | PDANN | ||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | ||
| 2019 | GP → ETF | 0.01 | 0.46 | 0.31 | 0.39 | 0.50 | 0.33 | 0.53 | 0.31 |
| ETF → GP | 0.69 | 0.35 | 0.65 | 0.39 | 0.74 | 0.34 | 0.74 | 0.34 | |
| 2020 | GP → ETF | 0.27 | 0.20 | 0.50 | 0.33 | 0.56 | 0.31 | 0.65 | 0.28 |
| ETF → GP | 0.67 | 0.44 | 0.62 | 0.47 | 0.68 | 0.43 | 0.72 | 0.40 | |
| 2021 | GP → ETF | 0.42 | 0.42 | 0.53 | 0.39 | 0.56 | 0.37 | 0.60 | 0.35 |
| ETF → GP | 0.75 | 0.53 | 0.64 | 0.64 | 0.74 | 0.54 | 0.79 | 0.49 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Yang, Z.; Huang, Q.; Zhang, Z. Improving the Transferability of Deep Learning Models for Crop Yield Prediction: A Partial Domain Adaptation Approach. Remote Sens. 2023, 15, 4562. https://doi.org/10.3390/rs15184562
Ma Y, Yang Z, Huang Q, Zhang Z. Improving the Transferability of Deep Learning Models for Crop Yield Prediction: A Partial Domain Adaptation Approach. Remote Sensing. 2023; 15(18):4562. https://doi.org/10.3390/rs15184562
Chicago/Turabian StyleMa, Yuchi, Zhengwei Yang, Qunying Huang, and Zhou Zhang. 2023. "Improving the Transferability of Deep Learning Models for Crop Yield Prediction: A Partial Domain Adaptation Approach" Remote Sensing 15, no. 18: 4562. https://doi.org/10.3390/rs15184562
APA StyleMa, Y., Yang, Z., Huang, Q., & Zhang, Z. (2023). Improving the Transferability of Deep Learning Models for Crop Yield Prediction: A Partial Domain Adaptation Approach. Remote Sensing, 15(18), 4562. https://doi.org/10.3390/rs15184562