Background Reconstruction via 3D-Transformer Network for Hyperspectral Anomaly Detection
Abstract
:1. Introduction
- (1)
- A 3DTR network is proposed for hyperspectral anomaly detection that aims to reconstruct the background precisely by reflecting the multi-dimensional similarity in HSIs. Specifically, the TR module is utilized to handle the similarity among pixels, which is beneficial for the reconstruction of background compared to AE-based anomaly detectors that handle each pixel separately. Moreover, by fully considering the high spectral resolution of HSIs and the high spectral similarity among single-band images, a novel spectral TR network is proposed to reconstruct each band by other bands. To our knowledge, this is the first time that spectral similarity has been characterized among hundreds of single-band images by a TR module for hyperspectral anomaly detection;
- (2)
- In view of the potential contamination of anomalies in the reconstruction results of the background, a pre-detection procedure for anomalies is executed so that the potential anomalies can be removed in the training process of the 3DTR. Existing patch-generating methods simply set a single window around the tested pixel and regard all pixels in this window as a patch, which may include a number of irrelevant pixels and affect the precision of the background reconstruction. To solve this problem, a novel patch-generation method is proposed to select the most similar pixels around the center pixel in each patch, so that contamination from weakly relevant and irrelevant pixels in the background reconstruction are significantly reduced.
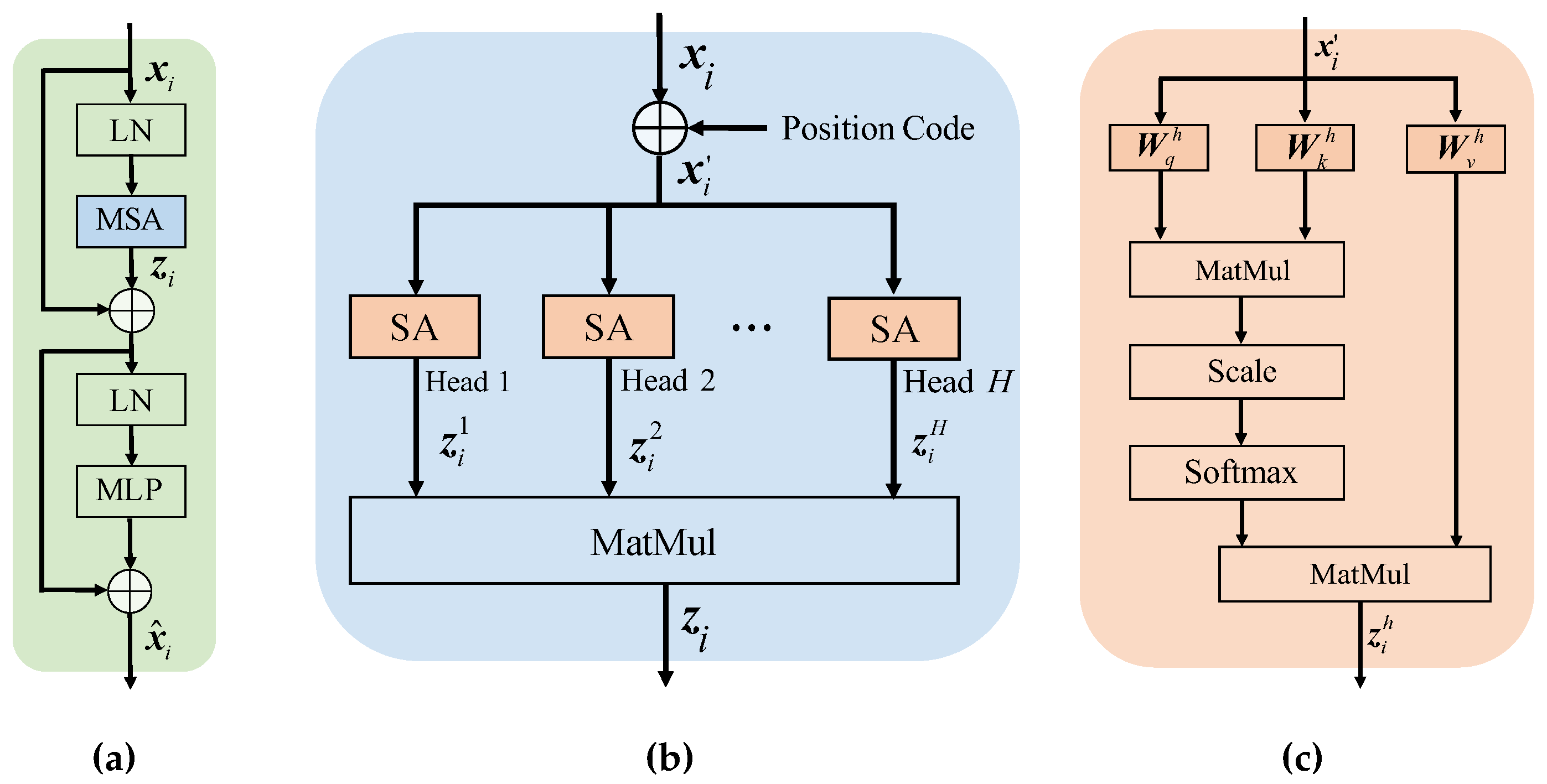
2. Related Works
- Step 1:
- the input is an arbitrary sequence with L elements, which is processed from a pixel or a patch of the tested image. To avoid the shortcoming where the position information is missed by the self-attention mechanism, an artificial or random position code is added to the original input: .
- Step 2:
- each input is multiplied by three pre-set transformation matrices , , and , respectively. Three corresponding vectors are obtained, i.e., query , key , and value .
- Step 3:
- the attention score is calculated between the input and other arbitrary input by the above transformed vectors, i.e., .
- Step 4:
- The softmax activation layer is operated on the attention score .
- Step 5:
- the attention output is computed .
3. Proposed Method
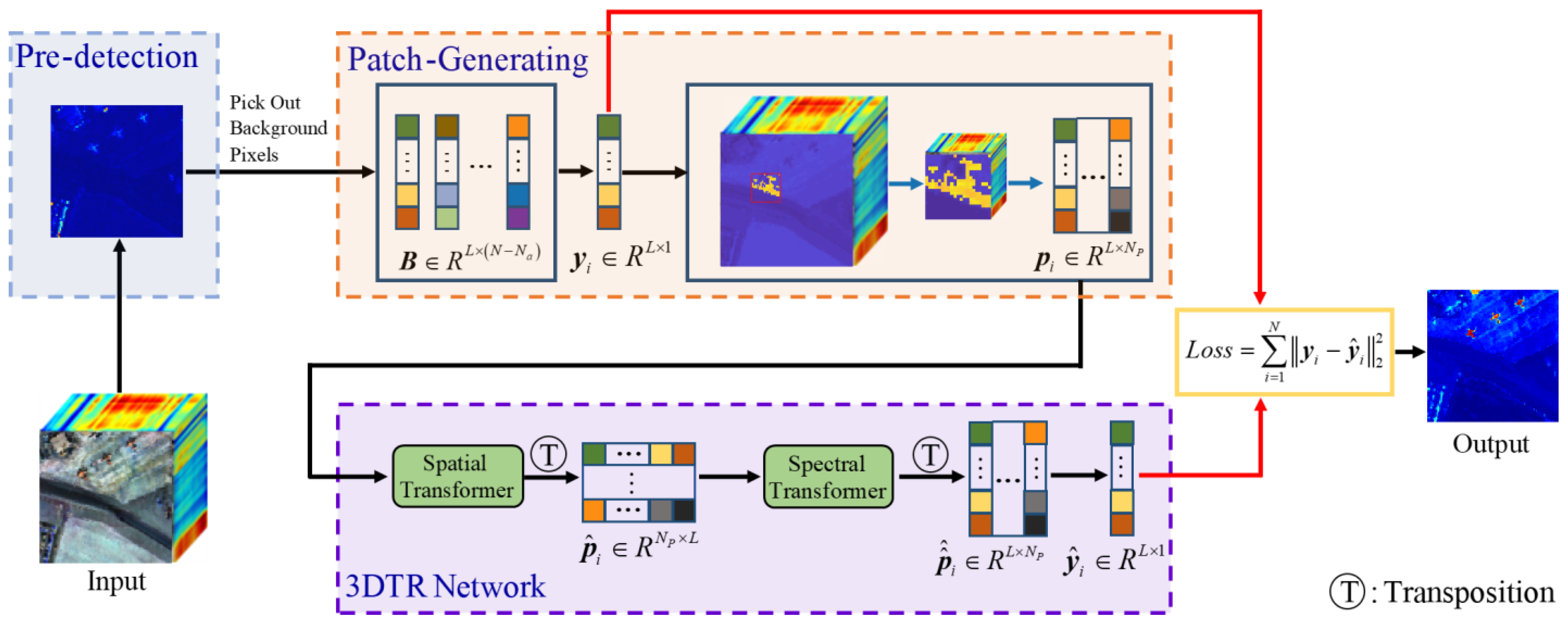
3.1. 3DTR Network for Anomaly Detection
- Step 1:
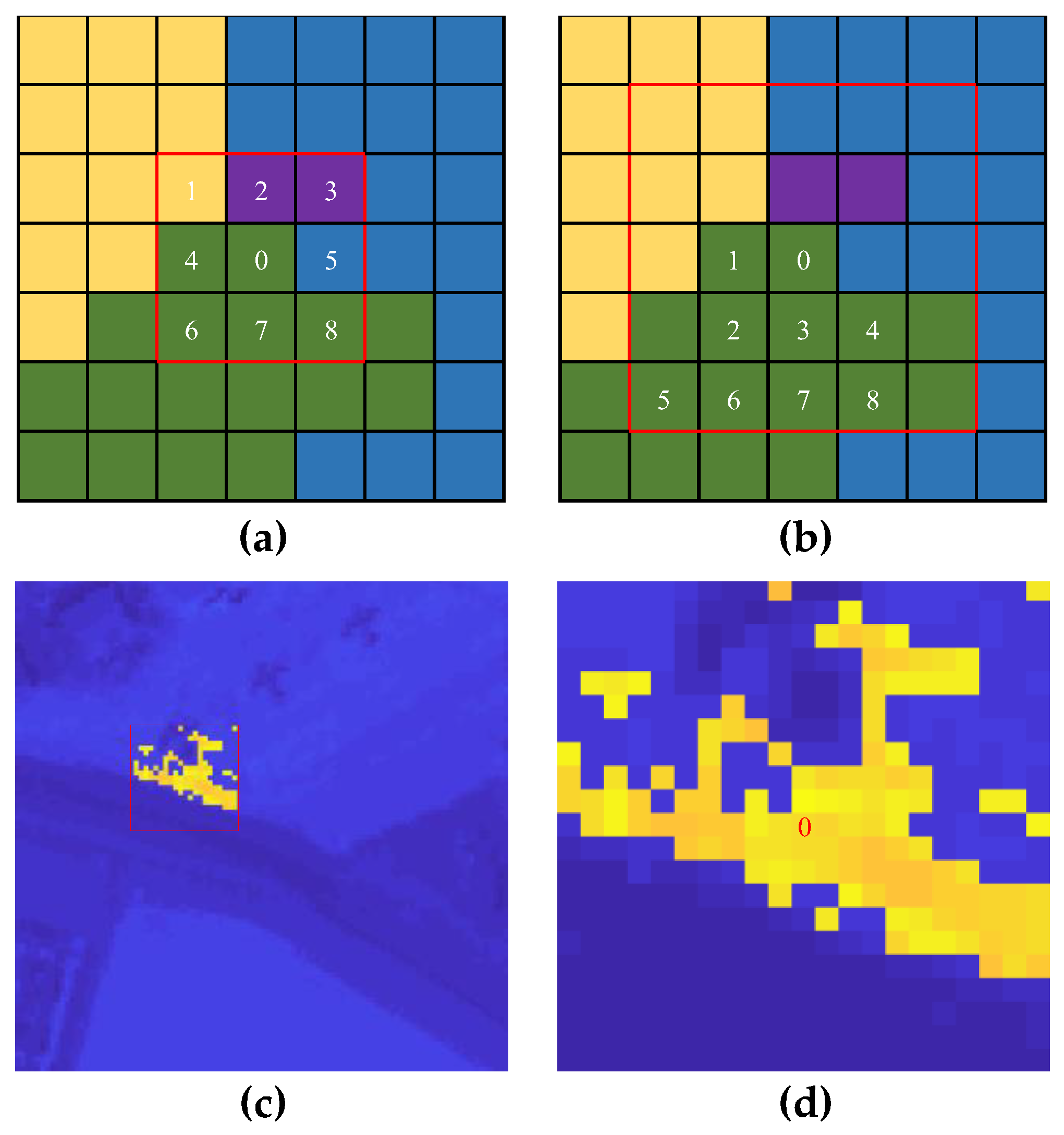
- By considering that the neighboring region of is more important in the reconstruction process compared to the whole HSIs, this paper uses a patch rather than the whole HSI to generate the reconstructed pixel . Moreover, to avoid contamination by uncorrelated pixels, the proposed patch-generating method generates a one-to-one corresponding patch by selecting highly correlated pixels around , in which comes first in .
- Step 2:
- Input to the -head TR module, in which each pixel of is considered as an input sequence. By considering the interrelations among pixels, the patch is reconstructed by this spatial TR module.
- Step 3:
- To characterize the spectral similarity among spectral bands of HSIs, the transposed patch is fed into the -head TR module, in which each band of is considered as an input sequence. By considering the interrelations among spectral bands, the transposed patch is reconstructed by this spectral TR module.
- Step 4:
- Then, the first column of the reconstructed patch is the reconstructed pixel .
3.2. Removing Potential Anomalies
3.3. Patch-Generating
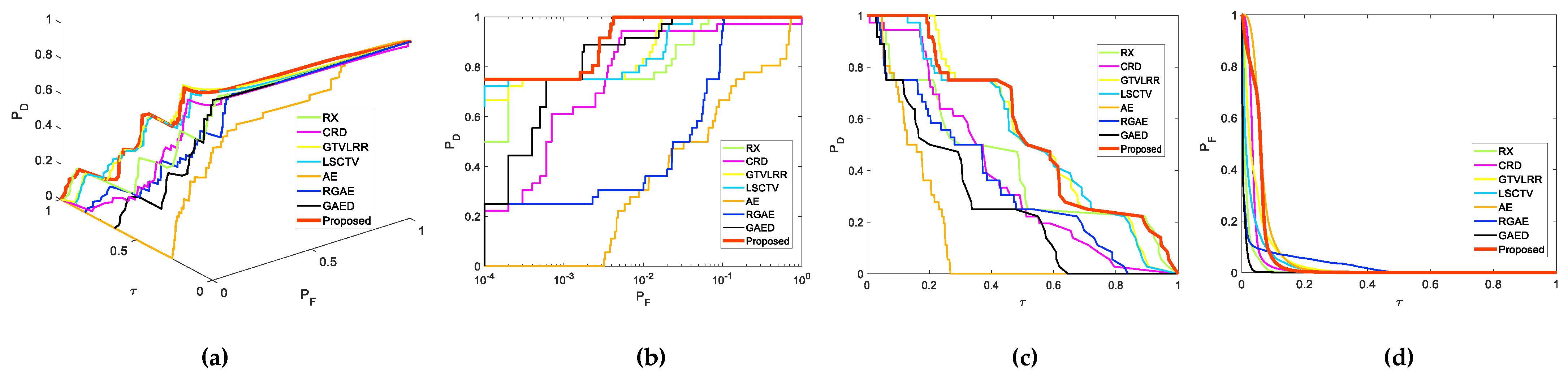
4. Experimental Results and Analysis
4.1. Synthetic Data Experiments
4.1.1. Experiments on the First Synthetic Dataset
4.1.2. Experiments on the Second Synthetic Dataset
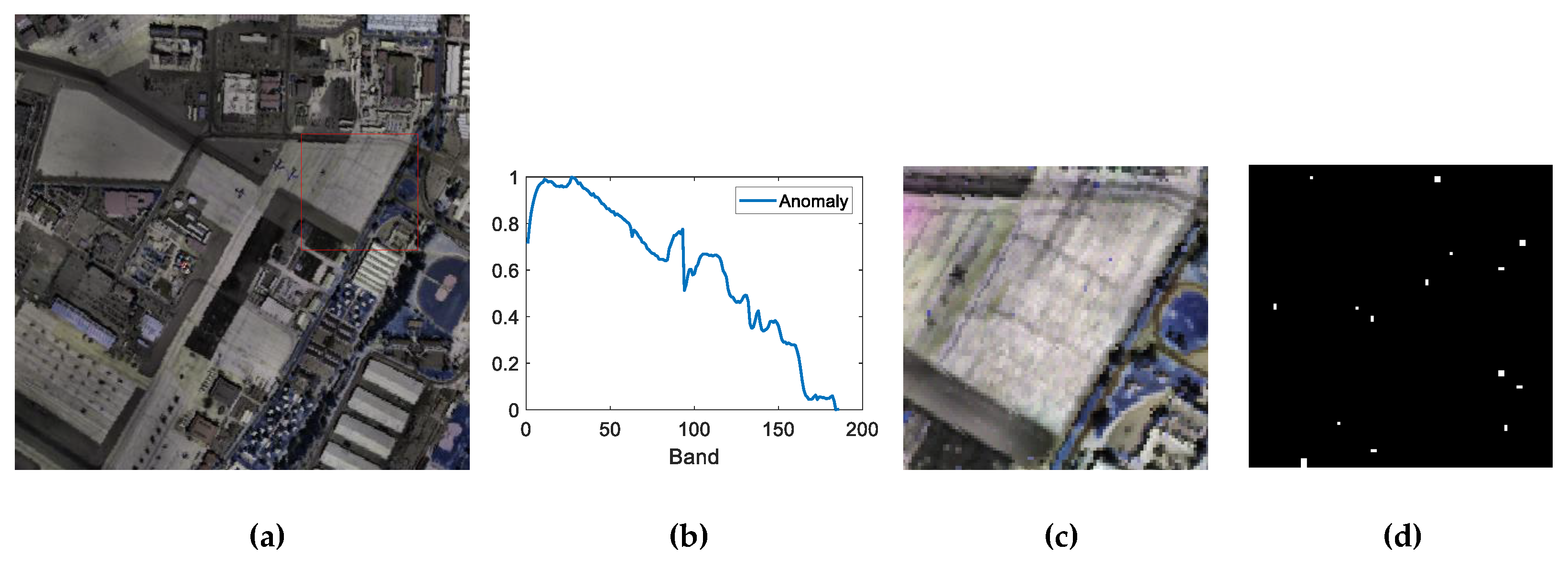
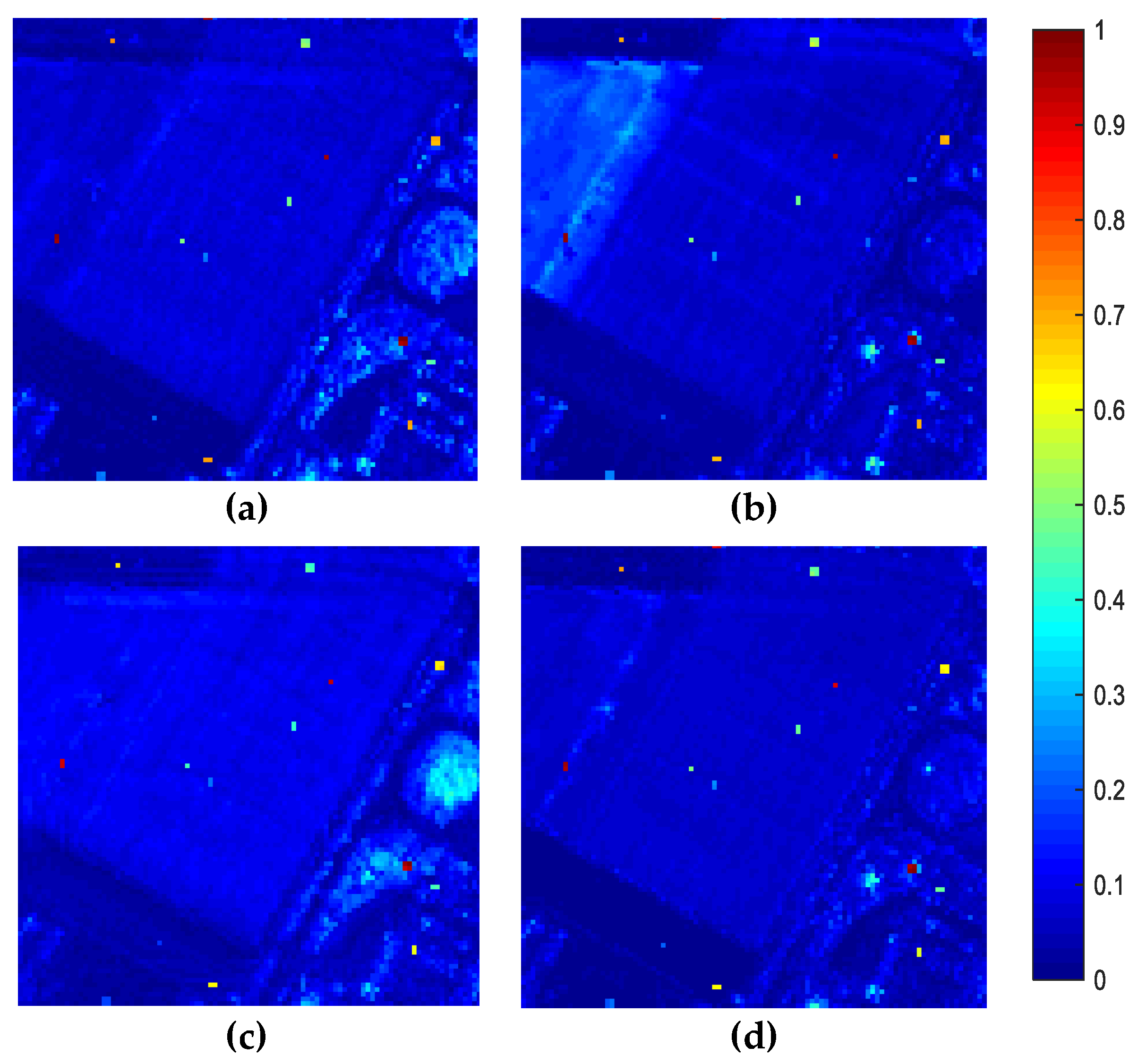
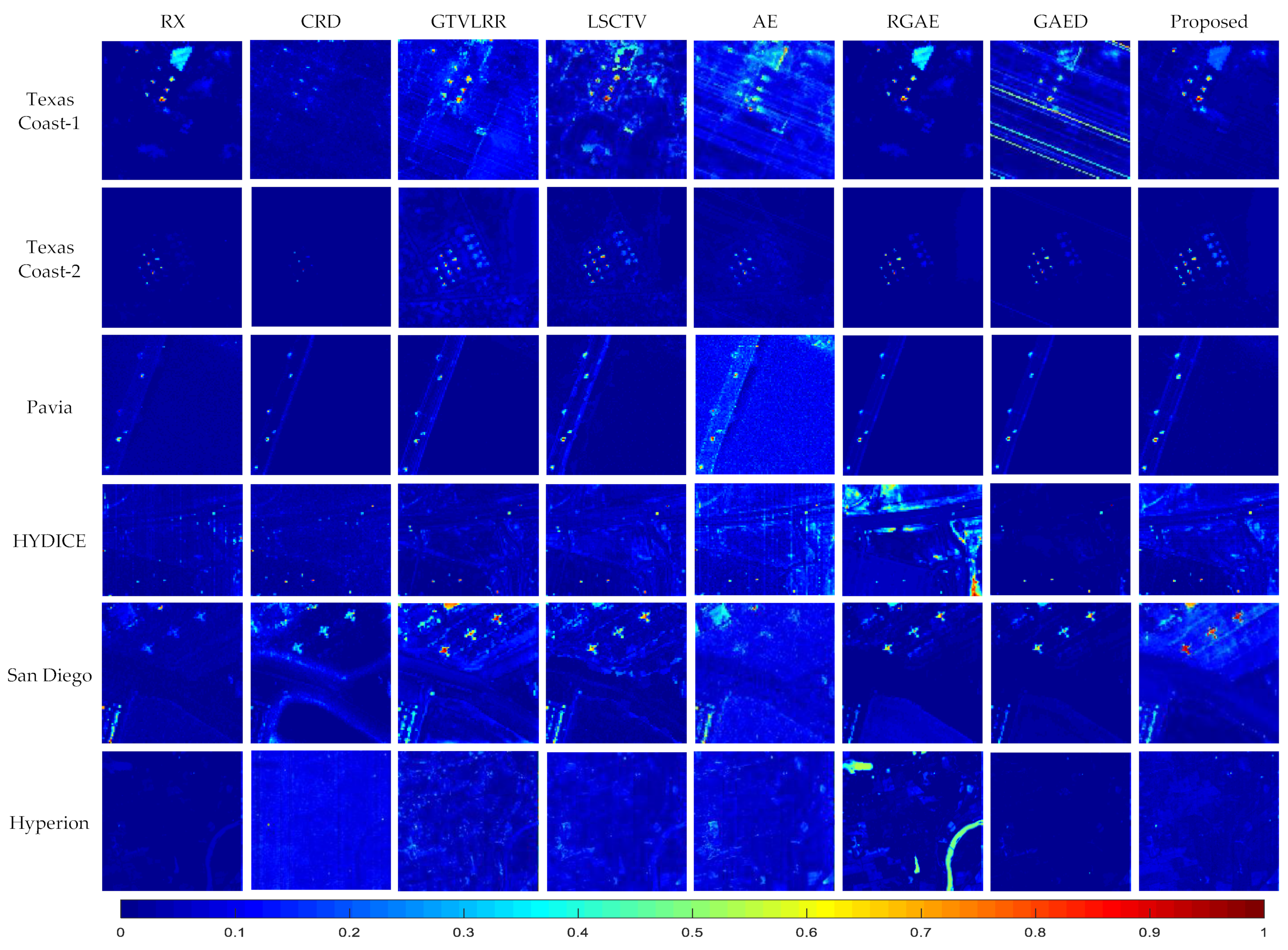
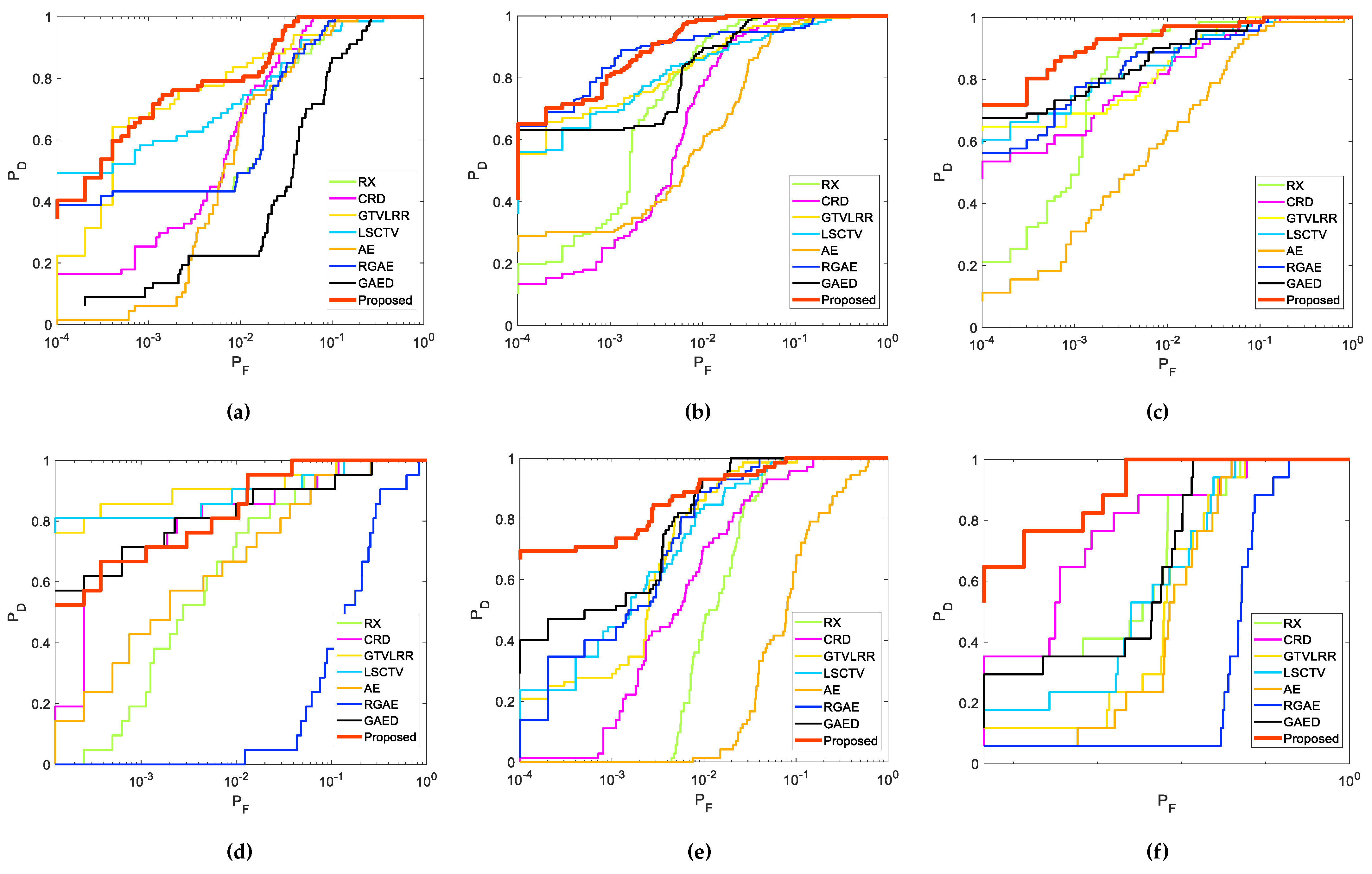
4.2. Real Data Experiments
4.3. Summary
- (1)
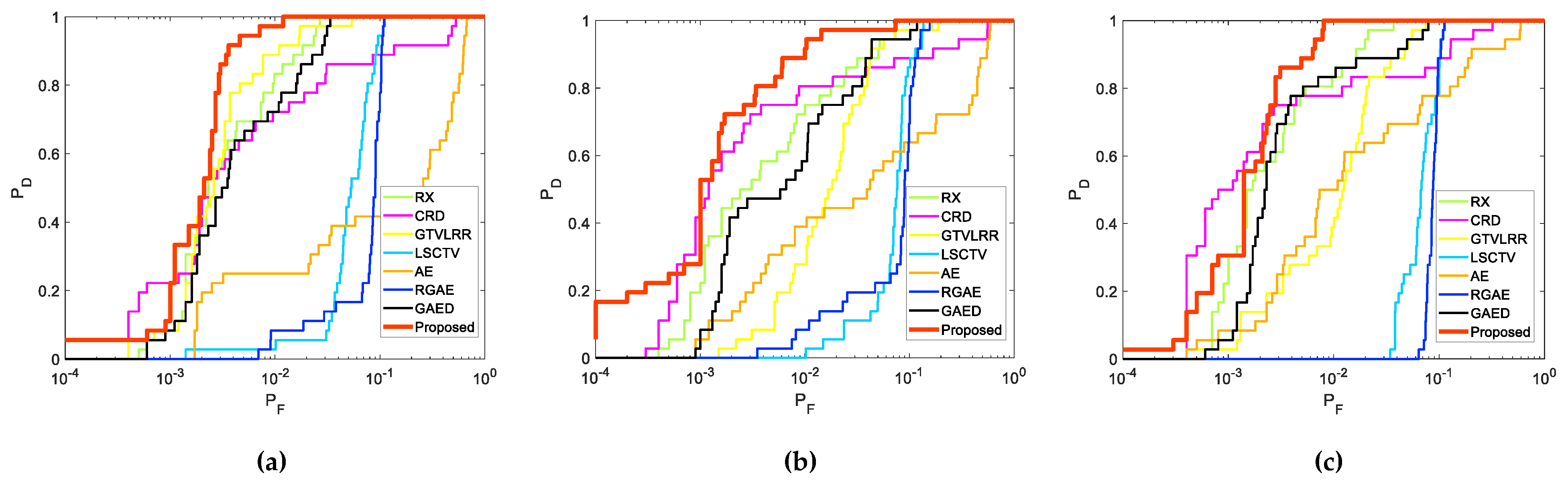
- Effectiveness: Owing to the unique long-range self-attention mechanism of TR, the spatial similarity among pixels and the spectral similarity among bands are characterized precisely by the 3DTR network. This strategy is more effective for reconstructing a background than AE-based detectors when considering spatial properties. To obtain a better reconstruction result for a background, coarse pre-detection is executed to avoid the contamination of anomalies. In addition, the proposed patch-generation method alleviates the contamination of weakly relevant pixels in the reconstruction procedure. The experimental results demonstrated that the proposed method is able to identify all anomalies effectively;
- (2)
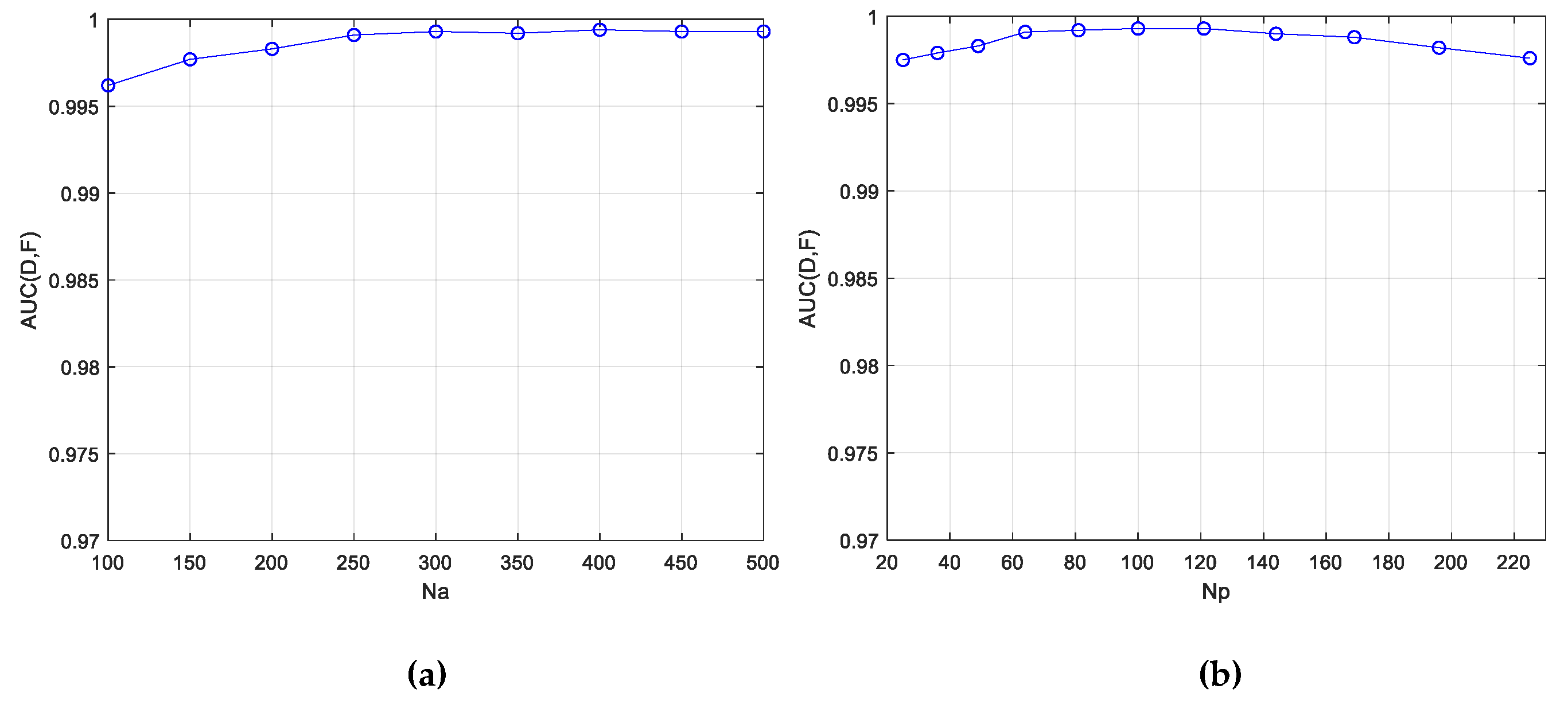
- Convenience in Parameter Settings: There is only one loss item in the loss function, and thus no trade-off parameters need to be set. In addition, an analysis of the parameter settings indicates that the detection accuracies of the proposed method are insensitive to changes in the pre-detection parameter and the patch-generation parameter over a relatively wide range. Moreover, and are fixed throughout all the experiments, and satisfactory anomaly detection results are still achieved;
- (3)
- Robustness to Noise: For a full consideration of the spatial similarity among pixels and the spectral similarity among bands by the proposed method, random noise is effectively eliminated by characterizing the spatial properties. Specifically, the experimental results on two group synthetic datasets with different anomalous abundances and different levels of noise demonstrate that the proposed method is robust.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral remote sensing data analysis and future challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef]
- Ghamisi, P.; Yokoya, N.; Li, J.; Liao, W.; Liu, S.; Plaza, J.; Rasti, B.; Plaza, A. Advances in hyperspectral image and signal processing: A comprehensive overview of the state of the art. IEEE Geosci. Remote Sens. Mag. 2017, 5, 37–78. [Google Scholar] [CrossRef]
- Liu, L.; Wang, Y.; Peng, J.; Zhang, L.; Zhang, B.; Cao, Y. Latent relationship guided stacked sparse autoencoder for hyperspectral imagery classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3711–3725. [Google Scholar] [CrossRef]
- Wang, X.; Tan, K.; Du, Q.; Chen, Y.; Du, P. CVA2E: A conditional variational autoencoder with an adversarial training process for hyperspectral imagery classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5676–5692. [Google Scholar] [CrossRef]
- Sun, L.; Wu, F.; Zhan, T.; Liu, W.; Wang, J.; Jeon, B. Weighted nonlocal low-rank tensor decomposition method for sparse unmixing of hyperspectral images. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 1174–1188. [Google Scholar] [CrossRef]
- Nasrabadi, N.M. Hyperspectral target detection: An overview of current and future challenges. IEEE Signal Process. Mag. 2014, 31, 34–44. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, L.; Du, B.; Zhang, L. Hyperspectral anomaly detection based on machine learning: An overview. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2022, 15, 3351–3364. [Google Scholar] [CrossRef]
- He, C.; Sun, L.; Huang, W.; Zhang, J.; Zheng, Y.; Jeon, B. TSLRLN: Tensor subspace low-rank learning with non-local prior for hyperspectral image mixed denoising. Signal Process. 2021, 184, 108060. [Google Scholar] [CrossRef]
- Sun, L.; He, C.; Zheng, Y.; Tang, S. SLRL4D: Joint restoration of subspace low-rank learning and non-local 4-D transform filtering for hyperspectral image. Remote Sens. 2020, 12, 2979. [Google Scholar] [CrossRef]
- Dao, M.; Kwan, C.; Ayhan, B.; Tran, T.D. Burn scar detection using cloudy MODIS images via low-rank and sparsity-based models. In Proceedings of the 2016 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Washington, DC, USA, 7–9 December 2016; pp. 177–181. [Google Scholar]
- Huang, Z.; Li, S. From difference to similarity: A manifold ranking based hyperspectral anomaly detection framework. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8118–8130. [Google Scholar] [CrossRef]
- Gagnon, M.-A.; Tremblay, P.; Savary, S.; Lagueux, P.; Chamberland, M. Standoff thermal hyperspectral imaging for flare and smokestack characterization in industrial environments. In Proceedings of the 2013 5th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Gainesville, FL, USA, 26–28 June 2013; pp. 1–4. [Google Scholar]
- Kruse, F.A.; Boardman, J.W.; Huntington, J.F. Comparison of airborne hyperspectral data and EO-1 Hyperion for mineral mapping. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1388–1400. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Tong, Q.; Sun, X. The spectral crust project—Research on new mineral exploration technology. In Proceedings of the 2012 4th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Shanghai, China, 4–7 June 2012; pp. 1–4. [Google Scholar]
- Eismann, M.T.; Stocker, A.D.; Nasrabadi, N.M. Automated hyperspectral cueing for civilian search and rescue. Proc. IEEE 2009, 97, 1031–1055. [Google Scholar] [CrossRef]
- Antson, L.; Vandenhoeke, A.; Shimoni, M.; Hamesse, C.; Luong, H. Detection and tracking of search and rescue personnel under hindered light conditions using hyperspectral imaging. In Proceedings of the 2022 12th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Rome, Italy, 13–16 September 2022; pp. 1–6. [Google Scholar]
- Ardouin, J.-P.; Lévesque, J.; Rea, T.A. A demonstration of hyperspectral image exploitation for military applications. In Proceedings of the 2007 10th International Conference on Information Fusion, Quebec, QC, Canada, 9–12 July 2007; pp. 1–8. [Google Scholar]
- Racek, F.; Barta, V. Spectrally based method of target detection in acquisition system of general fire control system. In Proceedings of the 2017 International Conference on Military Technologies (ICMT), Brno, Czech Republic, 31 May–2 June 2017; pp. 22–26. [Google Scholar]
- Reed, I.S.; Yu, X. Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1760–1770. [Google Scholar] [CrossRef]
- Li, W.; Du, Q. Collaborative representation for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1463–1474. [Google Scholar] [CrossRef]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM 2011, 58, 11. [Google Scholar] [CrossRef]
- Wang, W.; Li, S.; Qi, H.; Ayhan, B.; Kwan, C.; Vance, S. Identify anomaly component by sparsity and low rank. In Proceedings of the 2015 7th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Tokyo, Japan, 2–5 June 2015; pp. 1–4. [Google Scholar]
- Liu, G.; Lin, Z.; Yan, S.; Sun, J.; Yu, Y.; Ma, Y. Robust recovery of subspace structures by low-rank representation. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 171–184. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Z.; Li, J.; Plaza, A.; Wei, Z. Anomaly detection in hyperspectral images based on low-rank and sparse representation. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1990–2000. [Google Scholar] [CrossRef]
- Cheng, T.; Wang, B. Graph and total variation regularized lowrank representation for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 391–406. [Google Scholar] [CrossRef]
- Feng, R.; Li, H.; Wang, L.; Zhong, Y.; Zhang, L.; Zeng, T. Local spatial constraint and total variation for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Hinton, G.E.; Zemel, R.S. Autoencoders, minimum description length and Helmholtz free energy. Adv. Neural Inf. Process. Syst. 1994, 6, 3–10. [Google Scholar]
- Jiang, T.; Li, Y.; Xie, W.; Du, Q. Discriminative Reconstruction Constrained Generative Adversarial Network for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4666–4679. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 2672–2680. [Google Scholar] [CrossRef]
- Fan, G.; Ma, Y.; Mei, X.; Fan, F.; Huang, J.; Ma, J. Hyperspectral anomaly detection with robust graph autoencoders. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Jiang, K.; Xie, W.; Li, Y.; Lei, J.; He, G.; Du, Q. Semisupervised spectral learning with generative adversarial network for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5224–5236. [Google Scholar] [CrossRef]
- Xiang, P.; Ali, S.; Jung, S.K.; Zhou, H. Hyperspectral anomaly detection with guided autoencoder. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Sun, L.; Zhao, G.; Zheng, Y.; Wu, Z. Spectral–spatial feature tokenization transformer for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Hu, X.; Yang, W.; Wen, H.; Liu, Y.; Peng, Y. A lightweight 1-D convolution augmented transformer with metric learning for hyperspectral image classification. Sensors 2021, 21, 1751. [Google Scholar] [CrossRef]
- He, X.; Chen, Y.; Lin, Z. Spatial-spectral transformer for hyperspectral image classification. Remote Sens. 2021, 13, 498. [Google Scholar] [CrossRef]
- Wang, Y.; Hong, D.; Sha, J.; Gao, L.; Liu, L.; Zhang, Y.; Rong, X. Spectral–spatial–temporal transformers for hyperspectral image change detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Xiao, S.; Zhang, T.; Xu, Z.; Qu, J.; Hou, S.; Dong, W. Anomaly detection of hyperspectral images based on transformer with spatial–spectral dual-window mask. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2023, 16, 1414–1426. [Google Scholar]
- Li, K.; Wang, S.; Zhang, X.; Xu, Y.; Xu, W.; Tu, Z. Pose recognition with cascade transformers. CVPR 2021, 1944–1953. [Google Scholar] [CrossRef]
- Zheng, S.; Lu, J.; Zhao, H.; Zhu, X.; Luo, Z.; Wang, Y.; Fu, Y.; Feng, J.; Xiang, T.; Torr, P.; et al. Rethinking semantic segmentation from a sequence-to-sequence perspective with transformers. CVPR 2021, 6877–6886. [Google Scholar] [CrossRef]
- He, X.; Zhou, Y.; Zhao, J.; Zhang, D.; Yao, R.; Xue, Y. Swin transformer embedding UNet for remote sensing image semantic segmentation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Dai, X.; Chen, Y.; Yang, J.; Zhang, P.; Yuan, L.; Zhang, L. Dynamic DETR: End-to-end object detection with dynamic attention. ICCV 2021, 2968–2977. [Google Scholar] [CrossRef]
- Rao, W.; Gao, L.; Qu, Y.; Sun, X.; Zhang, B.; Chanussot, J. Siamese transformer network for hyperspectral image target detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–19. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, Y.; Ma, L.; Li, J.; Zheng, W. Spectral–spatial transformer network for hyperspectral image classification: A factorized architecture search framework. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Chang, C.-I. An effective evaluation tool for hyperspectral target detection: 3D receiver operating characteristic curve analysis. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5131–5153. [Google Scholar] [CrossRef]
- Schweizer, S.M.; Moura, J.M.F. Efficient detection in hyperspectral imagery. IEEE Trans. Image Process. 2001, 10, 584–597. [Google Scholar]





| Network | Parameter | Value | |
|---|---|---|---|
| Spatial Transformer | MSA | Head | 5 |
| MLP | Input Channel | L | |
| Hidden Channel | 10 | ||
| Spectral Transformer | MSA | Head | 5 |
| MLP | Input Channel | 121 | |
| Hidden Channel | 10 | ||
| Algorithm | AUC(D, F)↑ | AUC(D, τ)↑ | AUC(F, τ)↓ | AUCTD↑ | AUCBS↑ | AUCSNPR↑ | AUCTDBS↑ | AUCOD↑ | Training Time (s) | Test Time (s) |
|---|---|---|---|---|---|---|---|---|---|---|
| RX | 0.9912 | 0.4263 | 0.0153 | 1.4176 | 0.9760 | 27.9235 | 0.4111 | 1.4023 | — | 0.2168 |
| CRD | 0.9686 | 0.3841 | 0.0375 | 1.3527 | 0.9311 | 10.2562 | 0.3466 | 1.3152 | — | 3.2920 |
| GTVLRR | 0.9969 | 0.5496 | 0.0446 | 1.5465 | 0.9523 | 12.3336 | 0.5051 | 1.5020 | — | 101.5662 |
| LSC-TV | 0.9954 | 0.5355 | 0.0300 | 1.5309 | 0.9654 | 17.8493 | 0.5055 | 1.5009 | — | 405.3491 |
| AE | 0.8286 | 0.1543 | 0.0680 | 0.9829 | 0.7606 | 2.2688 | 0.0863 | 0.9149 | 8.5587 | 0.0865 |
| RGAE | 0.9588 | 0.3507 | 0.0282 | 1.3095 | 0.9307 | 12.4451 | 0.3225 | 1.2813 | 81.5106 | 0.0679 |
| GAED | 0.9978 | 0.2707 | 0.0066 | 1.2686 | 0.9912 | 41.0101 | 0.2641 | 1.2620 | 18.8871 | 0.0630 |
| Proposed | 0.9993 | 0.5574 | 0.0510 | 1.5566 | 0.9433 | 9.9541 | 0.5064 | 1.5056 | 159.1680 | 9.7920 |
| Algorithm | RX | CRD | GTVLRR | LSCTV | AE | RGAE | GAED | Proposed |
|---|---|---|---|---|---|---|---|---|
| 30 dB | 0.9908 ± 0.0017 | 0.9628 ± 0.0250 | 0.9952 ± 0.0029 | 0.9868 ± 0.0031 | 0.8744 ± 0.0435 | 0.9578 ± 0.0028 | 0.9957 ± 0.0022 | 0.9987 ± 0.0005 |
| 25 dB | 0.9810 ± 0.0035 | 0.9450 ± 0.0314 | 0.9949 ± 0.0030 | 0.9814 ± 0.0043 | 0.8623 ± 0.0443 | 0.9564 ± 0.0040 | 0.9954 ± 0.0026 | 0.9975 ± 0.0016 |
| 20 dB | 0.9569 ± 0.0269 | 0.9348 ± 0.0340 | 0.9932 ± 0.0042 | 0.9762 ± 0.0091 | 0.8534 ± 0.0494 | 0.9546 ± 0.0082 | 0.9930 ± 0.0045 | 0.9944 ± 0.0039 |
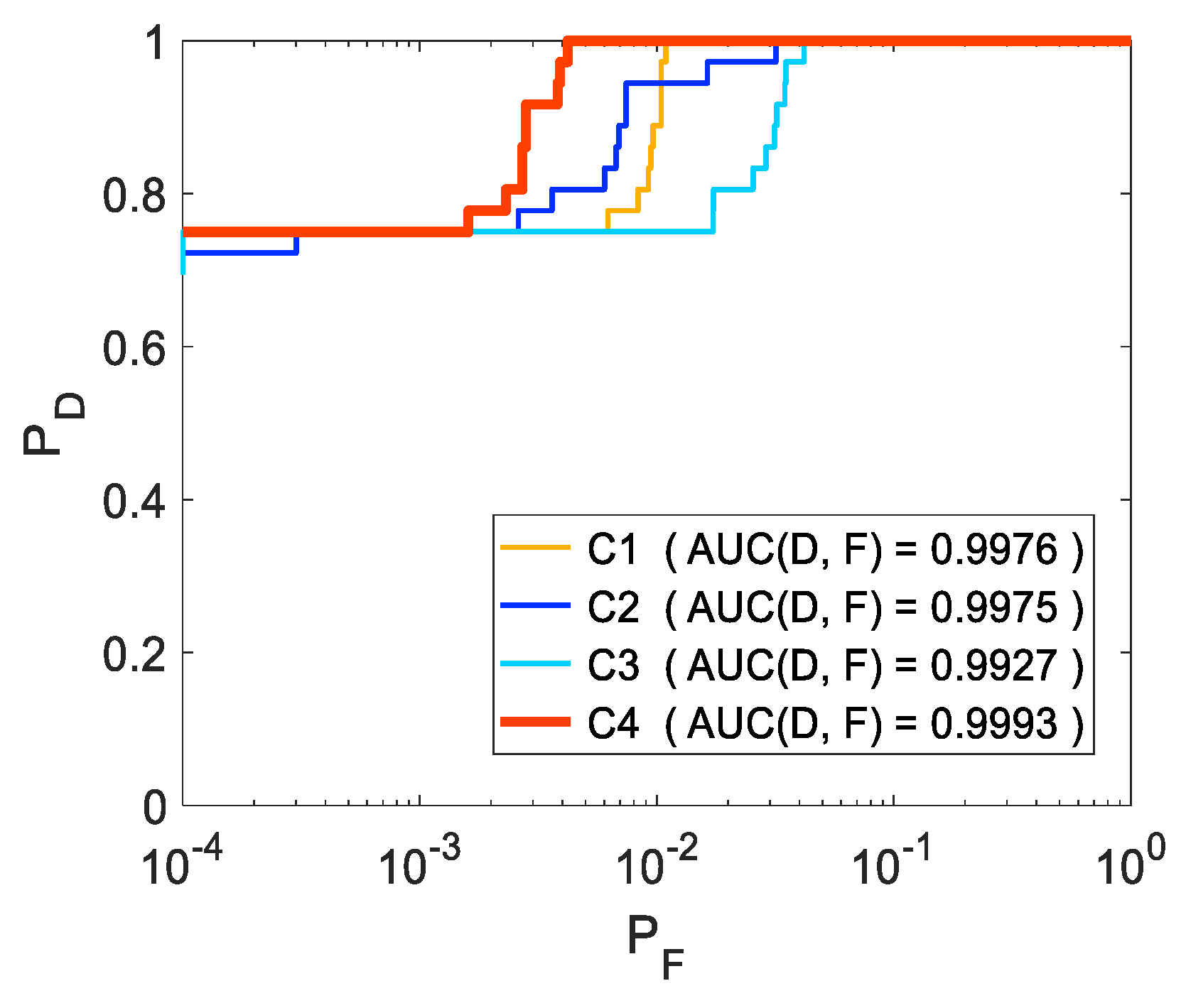
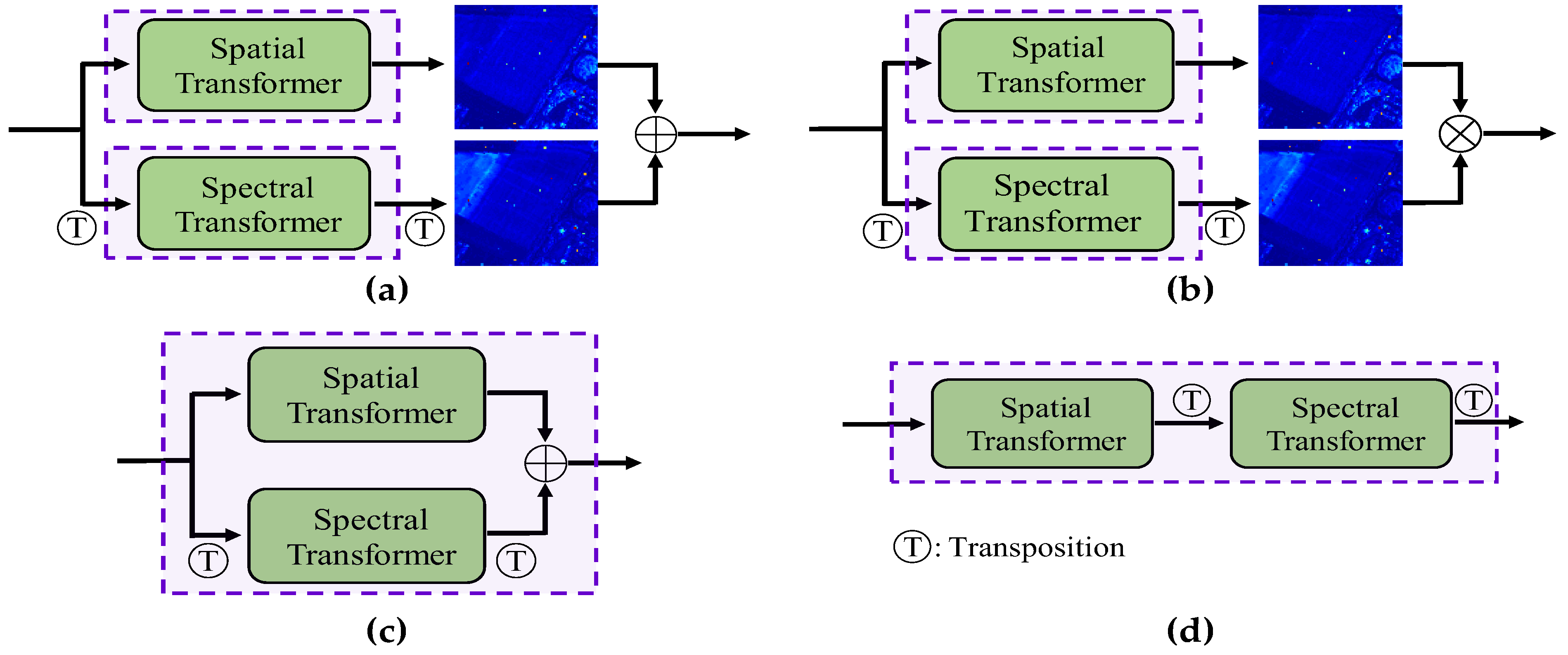
| Ablation Cases | Details | |
|---|---|---|
| Ablation on Different Components | C1 | Only spatial TR module with the proposed patch-generating method |
| C2 | Only spectral TR module with the proposed patch-generating method | |
| C3 | The proposed 3DTR network with a single window to generate patches | |
| C4 | The proposed 3DTR network with the proposed patch-generating method | |
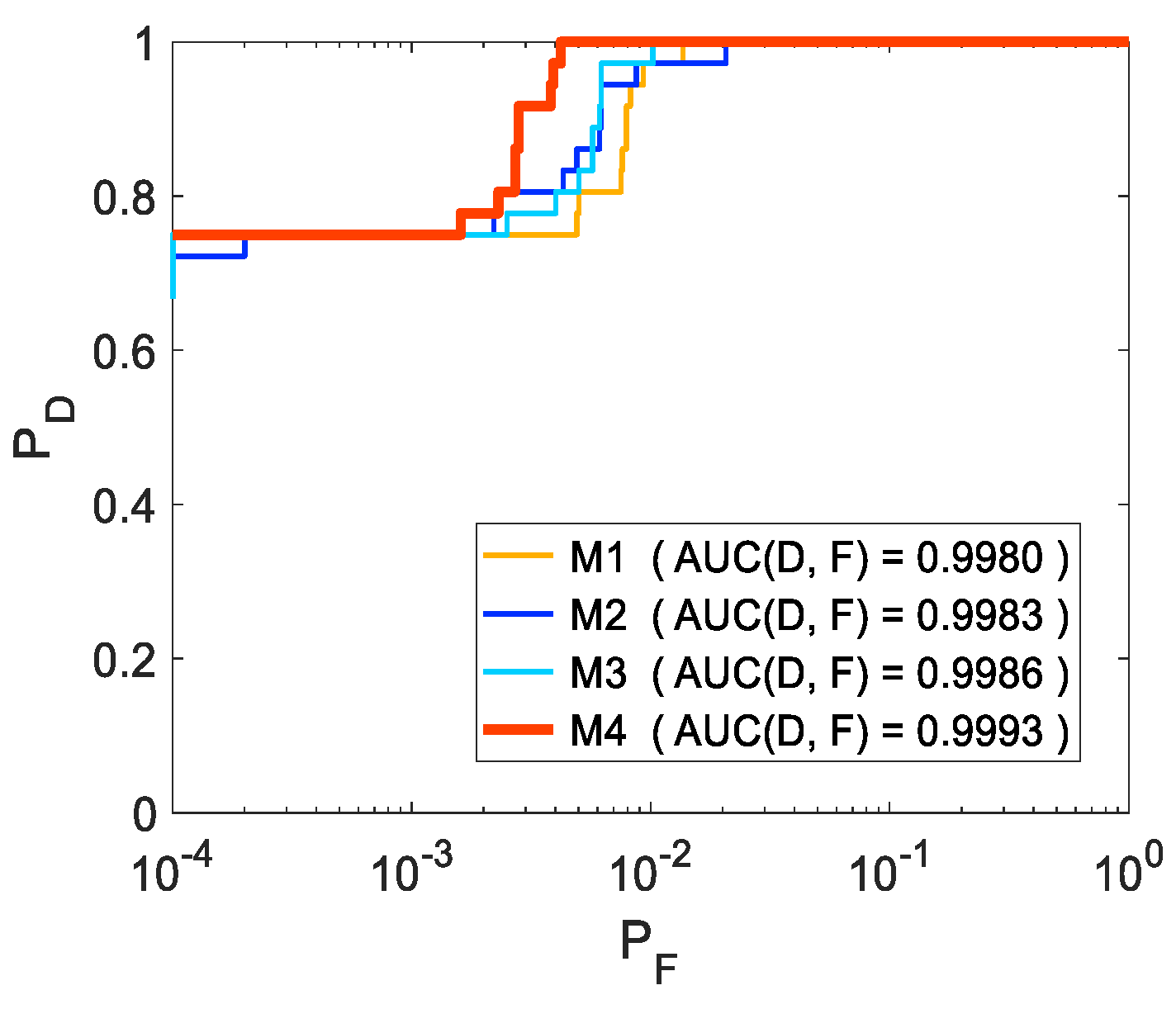
| Ablation on Different Combination Modes | M1 | Add the respective detection results of two TR modules |
| M2 | Multiply the respective detection results of two TR modules | |
| M3 | Combine two TR modules in parallel anatomically | |
| M4 | Combine two TR modules in series anatomically, namely the proposed 3DTR network | |
| Algorithm | RX | CRD | GTVLRR | LSCTV | AE | RGAE | GAED | Proposed |
|---|---|---|---|---|---|---|---|---|
| 30 dB | 0.9846 ± 0.0041 | 0.9409 ± 0.0338 | 0.9931 ± 0.0035 | 0.9408 ± 0.0082 | 0.8318 ± 0.0571 | 0.9133 ± 0.0054 | 0.9875 ± 0.0043 | 0.9946 ± 0.0019 |
| 25 dB | 0.9760 ± 0.0073 | 0.9291 ± 0.0370 | 0.9835 ± 0.0086 | 0.9317 ± 0.0092 | 0.8205 ± 0.0588 | 0.9102 ± 0.0058 | 0.9823 ± 0.0078 | 0.9939 ± 0.0038 |
| 20 dB | 0.9464 ± 0.0281 | 0.9199 ± 0.0507 | 0.9710 ± 0.0112 | 0.9309 ± 0.0125 | 0.7946 ± 0.0869 | 0.9072 ± 0.0068 | 0.9792 ± 0.0082 | 0.9912 ± 0.0066 |
| Datasets | Size | Bands | Number of Anomalies | Anomaly Types | Window Sizes of CRD |
|---|---|---|---|---|---|
| Texas Coast-1 | 100 × 100 | 204 | 67 (0.67%) | Buildings | (3, 7) |
| Texas Coast-2 | 100 × 100 | 207 | 155 (1.55%) | Buildings | (3, 15) |
| Pavia | 100 × 100 | 102 | 71 (0.71%) | Vehicles | (3, 13) |
| HYDICE | 80 × 100 | 174 | 21 (0.26%) | Buildings and Vehicles | (3, 9) |
| San Diego | 100 × 100 | 186 | 72 (0.72%) | Airplanes | (3, 7) |
| Hyperion | 150 × 150 | 155 | 17 (0.08%) | Storage Silo | (3, 11) |
| Algorithm | RX | CRD | GTVLRR | LSC-TV | AE | RGAE | GAED | Proposed |
|---|---|---|---|---|---|---|---|---|
| Texas Coast-1 | 0.9810 | 0.9883 | 0.9905 | 0.9818 | 0.9809 | 0.9821 | 0.9909 | 0.9946 |
| Texas Coast-2 | 0.9964 | 0.9918 | 0.9927 | 0.9887 | 0.9819 | 0.9926 | 0.9959 | 0.9991 |
| Pavia | 0.9913 | 0.9917 | 0.9948 | 0.9937 | 0.9712 | 0.9927 | 0.9948 | 0.9972 |
| HYDICE | 0.9860 | 0.9892 | 0.9930 | 0.9906 | 0.9762 | 0.7949 | 0.9808 | 0.9959 |
| San Diego | 0.9827 | 0.9833 | 0.9945 | 0.9929 | 0.8755 | 0.9940 | 0.9951 | 0.9958 |
| Hyperion | 0.9925 | 0.9944 | 0.9889 | 0.9908 | 0.9880 | 0.9408 | 0.9949 | 0.9996 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Wang, B. Background Reconstruction via 3D-Transformer Network for Hyperspectral Anomaly Detection. Remote Sens. 2023, 15, 4592. https://doi.org/10.3390/rs15184592
Wu Z, Wang B. Background Reconstruction via 3D-Transformer Network for Hyperspectral Anomaly Detection. Remote Sensing. 2023; 15(18):4592. https://doi.org/10.3390/rs15184592
Chicago/Turabian StyleWu, Ziyu, and Bin Wang. 2023. "Background Reconstruction via 3D-Transformer Network for Hyperspectral Anomaly Detection" Remote Sensing 15, no. 18: 4592. https://doi.org/10.3390/rs15184592
APA StyleWu, Z., & Wang, B. (2023). Background Reconstruction via 3D-Transformer Network for Hyperspectral Anomaly Detection. Remote Sensing, 15(18), 4592. https://doi.org/10.3390/rs15184592







