Using Film-Mulched Drip Irrigation to Improve the Irrigation Water Productivity of Cotton in the Tarim River Basin, Central Asia
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data
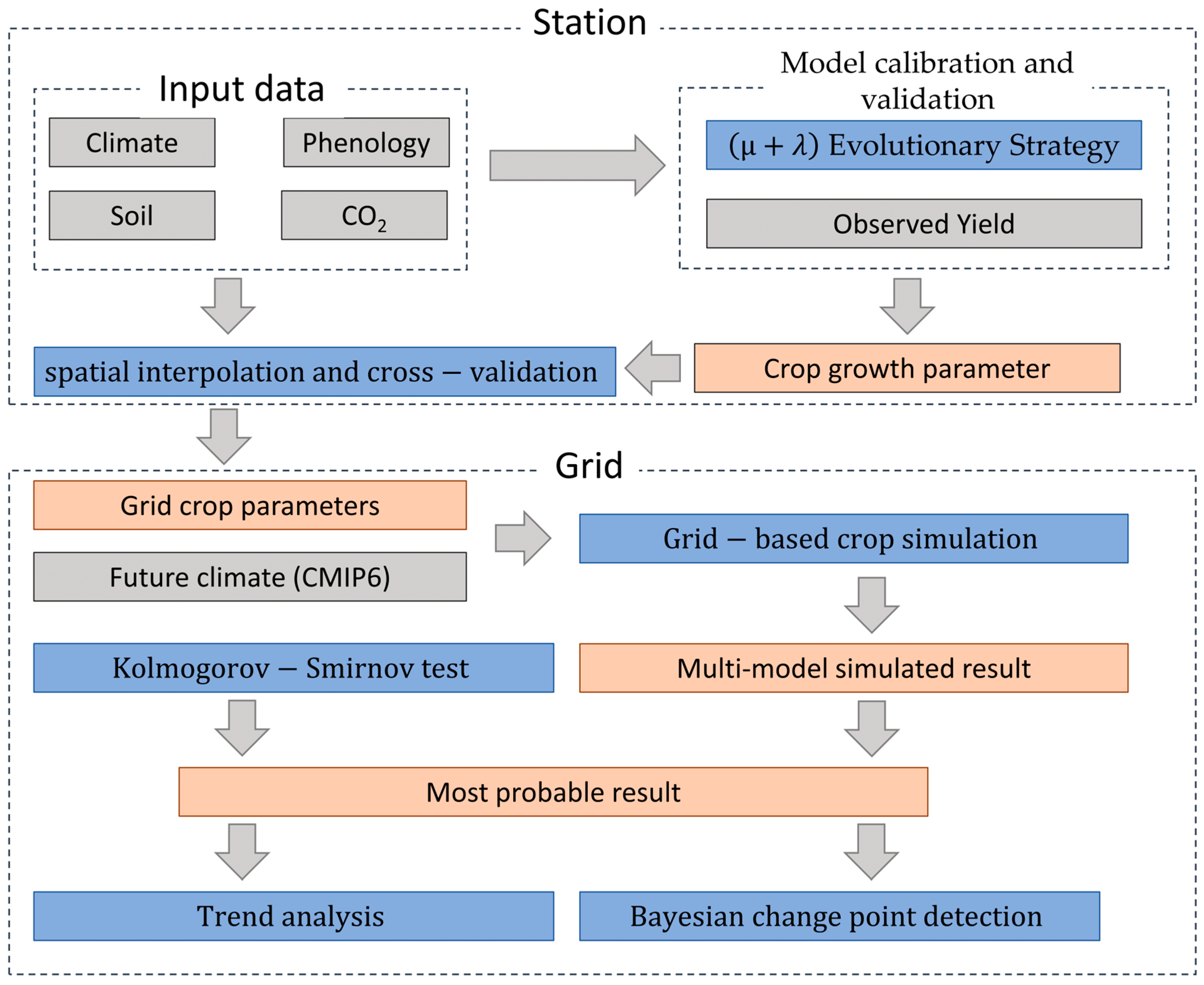
2.3. Methods
2.3.1. AquaCrop Model
2.3.2. Model Calibration and Validation
2.3.3. Grid-Based Crop Simulation
2.3.4. Irrigation Water Productivity (WPI)
2.3.5. Multi-Model Ensemble and the Kolmogorov–Smirnov Test
2.3.6. Trend Analysis and Bayesian Change-Point Detection
3. Results
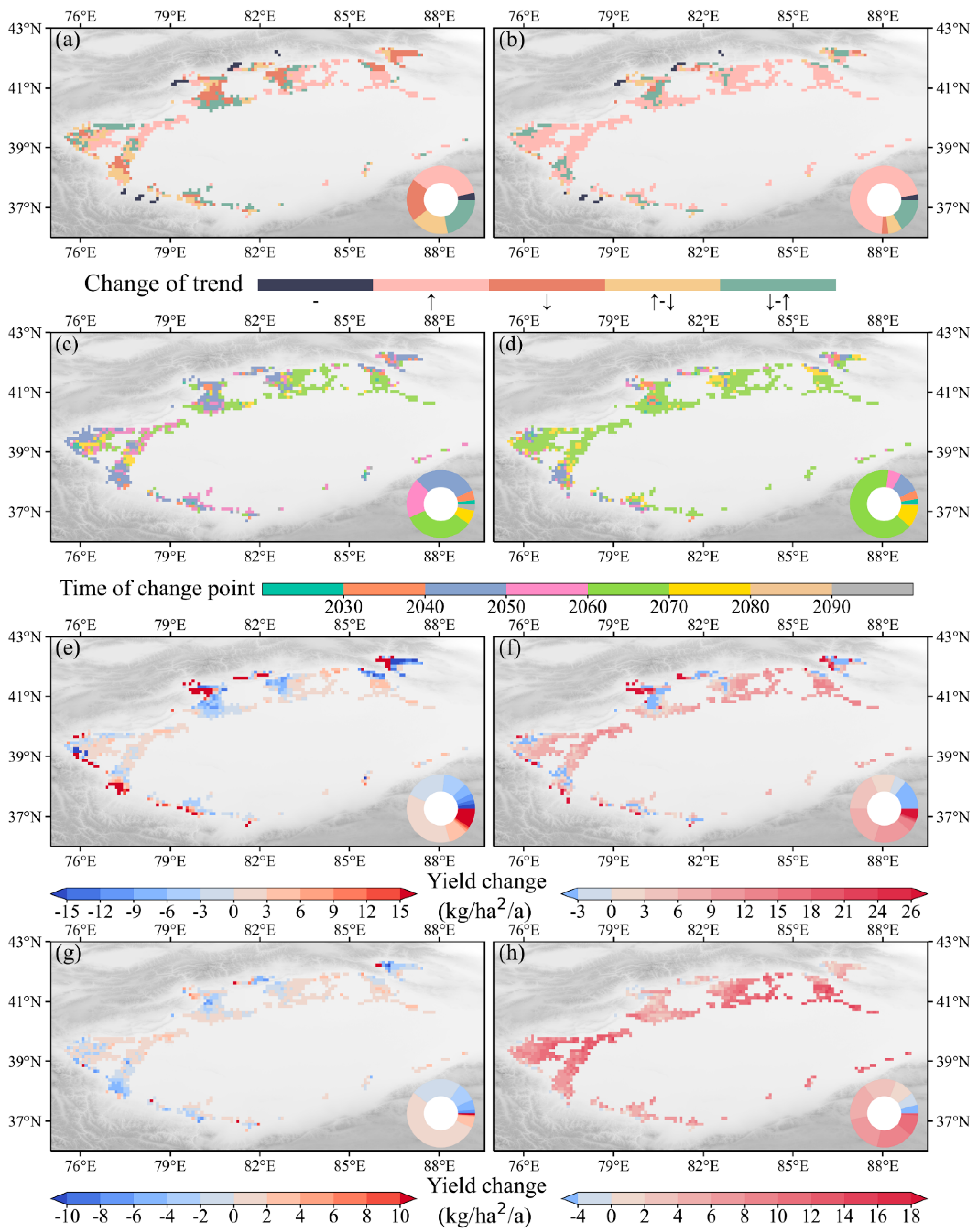
3.1. Spatial–Temporal Variations of Future Cotton Yield in the TRB
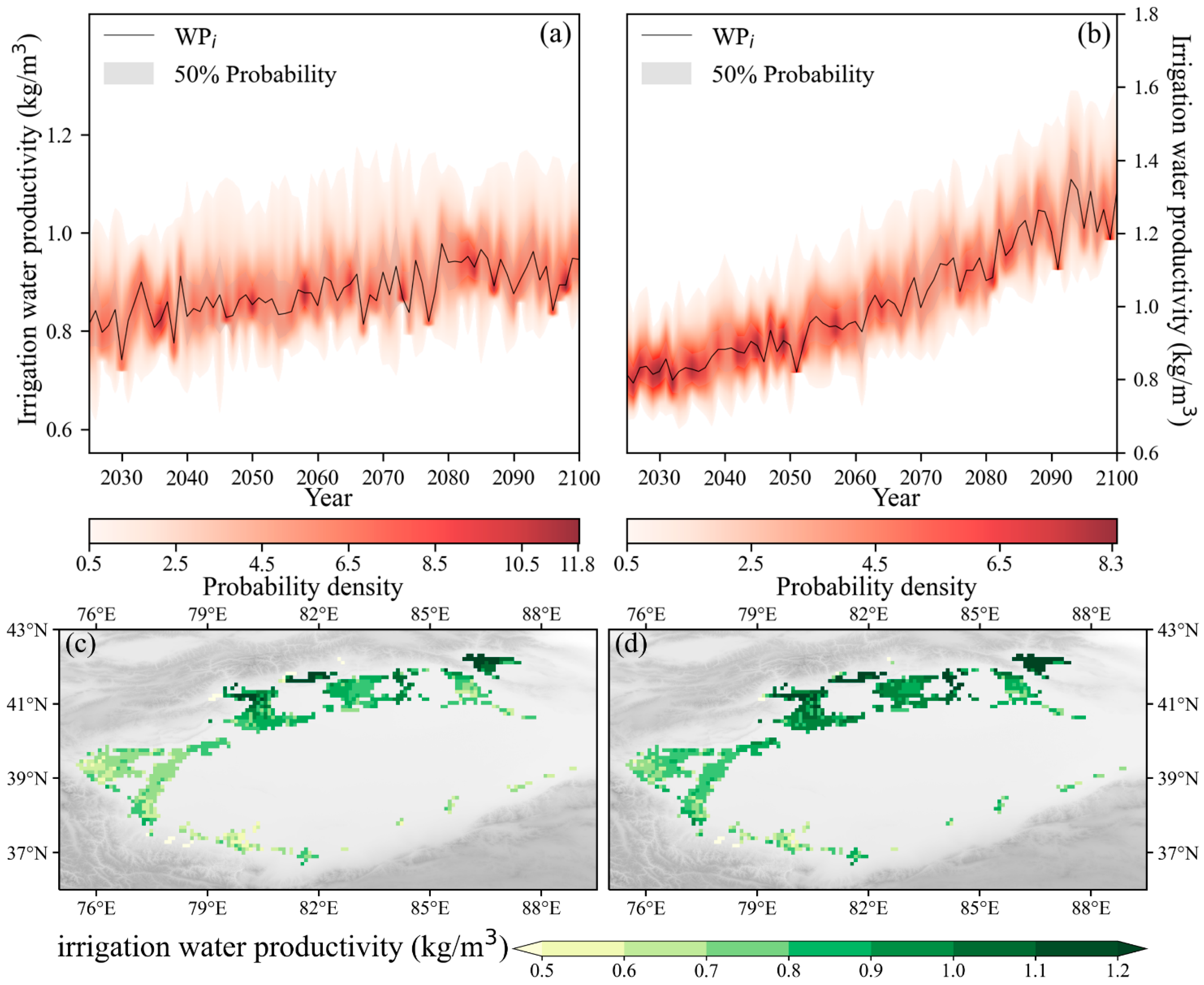
3.2. Spatial-Temporal Variations of Future Cotton WPI in the TRB
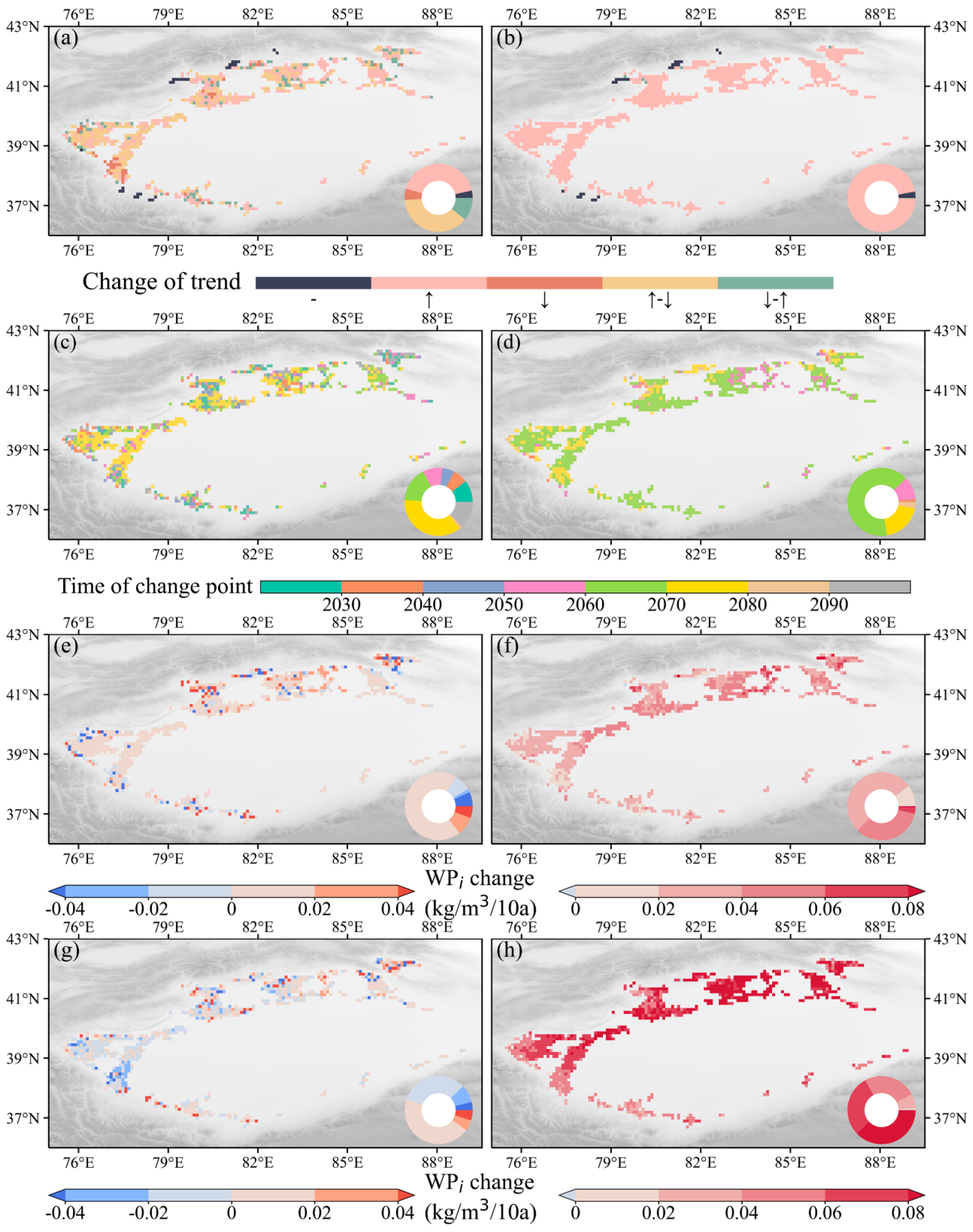
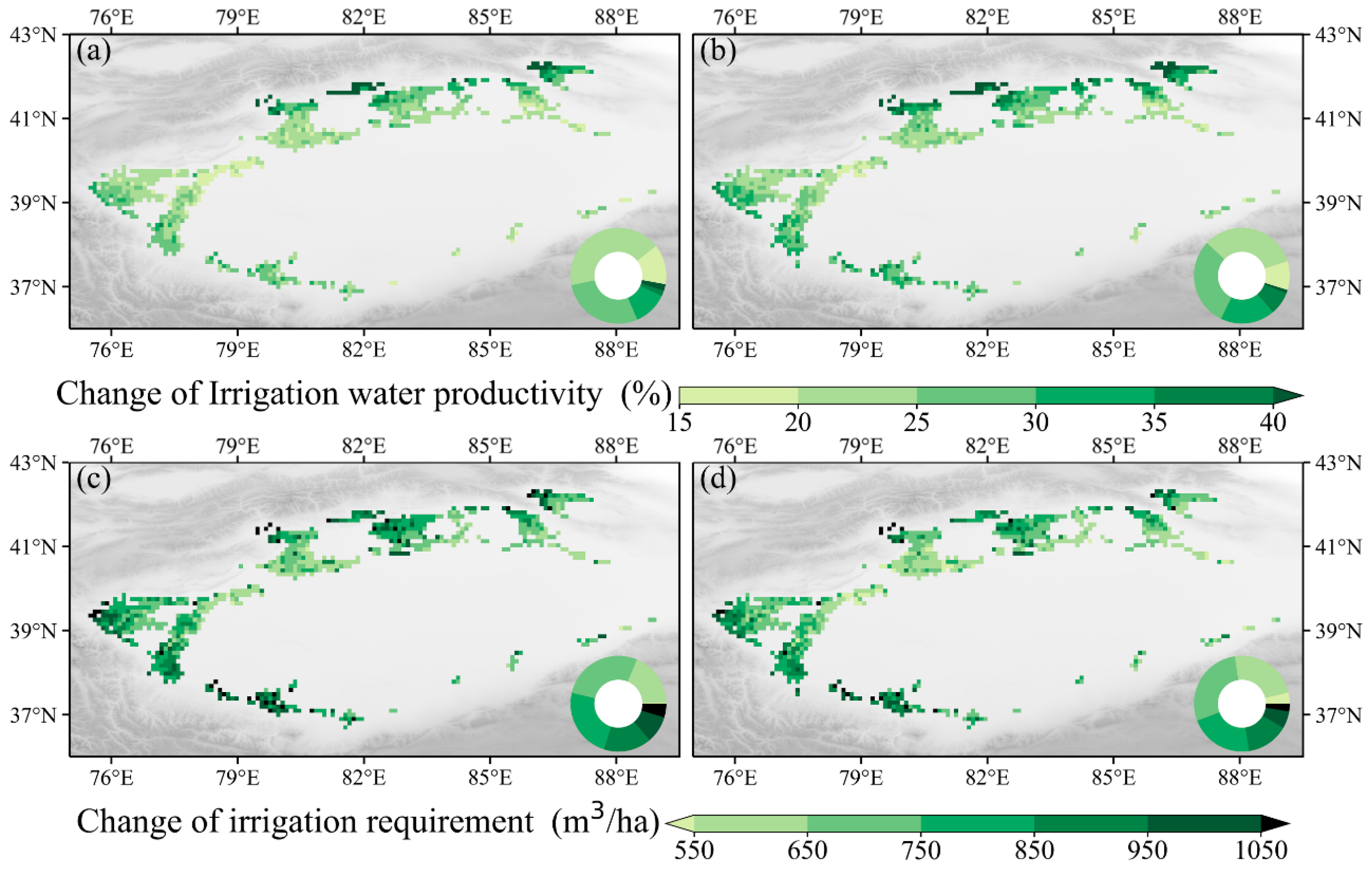
3.3. FMDI’s Ability to Improve Future Cotton WPI in the TRB
4. Discussion
4.1. Evaluation of the Simulation Results and Changes in the Cotton Yield and WPI
4.2. Influencing Factors of the FMDI’s Water-Saving Capacities
4.3. Shortcomings of AquaCrop and the Study Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- IPCC. Climate Change 2021: The Physical Science Basis. In Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Jägermeyr, J.; Müller, C.; Ruane, A.C.; Elliott, J.; Balkovic, J.; Castillo, O.; Faye, B.; Foster, I.; Folberth, C.; Franke, J.A.; et al. Climate impacts on global agriculture emerge earlier in new generation of climate and crop models. Nat. Food 2021, 2, 873–885. [Google Scholar] [CrossRef] [PubMed]
- Hasegawa, T.; Fujimori, S.; Havlík, P.; Valin, H.; Bodirsky, B.L.; Doelman, J.C.; Fellmann, T.; Kyle, P.; Koopman, J.F.L.; Lotze-Campen, H.; et al. Risk of increased food insecurity under stringent global climate change mitigation policy. Nat. Clim. Chang. 2018, 8, 699–703. [Google Scholar] [CrossRef]
- Guan, X.; Ma, J.; Huang, J.; Huang, R.; Zhang, L.; Ma, Z. Impact of oceans on climate change in drylands. Sci. China Earth Sci. 2019, 62, 891–908. [Google Scholar] [CrossRef]
- Lian, X.; Piao, S.; Chen, A.; Huntingford, C.; Fu, B.; Li, L.Z.X.; Huang, J.; Sheffield, J.; Berg, A.M.; Keenan, T.F.; et al. Multifaceted characteristics of dryland aridity changes in a warming world. Nat. Rev. Earth Environ. 2021, 2, 232–250. [Google Scholar] [CrossRef]
- Putnam, A.E.; Broecker, W.S. Human-induced changes in the distribution of rainfall. Sci. Adv. 2017, 3, e1600871. [Google Scholar] [CrossRef]
- Wang, J.; Song, C.; Reager, J.T.; Yao, F.; Famiglietti, J.S.; Sheng, Y.; MacDonald, G.M.; Brun, F.; Schmied, H.M.; Marston, R.A.; et al. Recent global decline in endorheic basin water storages. Nat. Geosci. 2018, 11, 926–932. [Google Scholar] [CrossRef]
- Qin, Y.; Abatzoglou, J.T.; Siebert, S.; Huning, L.S.; AghaKouchak, A.; Mankin, J.S.; Hong, C.; Tong, D.; Davis, S.J.; Mueller, N.D. Agricultural risks from changing snowmelt. Nat. Clim. Chang. 2020, 10, 459–465. [Google Scholar] [CrossRef]
- Yao, J.; Chen, Y.; Guan, X.; Zhao, Y.; Chen, J.; Mao, W. Recent climate and hydrological changes in a mountain–basin system in Xinjiang, China. Earth Sci. Rev. 2022, 226, 103957. [Google Scholar] [CrossRef]
- Koudahe, K.; Sheshukov, A.Y.; Aguilar, J.; Djaman, K. Irrigation-Water Management and Productivity of Cotton: A Review. Sustainability 2021, 13, 10070. [Google Scholar] [CrossRef]
- Fu, J.; Wang, W.; Zaitchik, B.; Nie, W.; Fei, E.X.; Miller, S.M.; Harman, C.J. Critical Role of Irrigation Efficiency for Cropland Expansion in Western China Arid Agroecosystems. Earth’s Future 2022, 10, e2022EF002955. [Google Scholar] [CrossRef]
- Zou, M.; Kang, S. Closing the irrigation water productivity gap to alleviate water shortage in an endorheic basin. Sci. Total Environ. 2022, 853, 158449. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Mei, X.; Wang, J.; Huang, F.; Hao, W.; Li, B. Drip fertigation significantly increased crop yield, water productivity and nitrogen use efficiency with respect to traditional irrigation and fertilization practices: A meta-analysis in China. Agric. Water Manag. 2021, 244, 106534. [Google Scholar] [CrossRef]
- Ding, Z.; Ali, E.F.; Elmahdy, A.M.; Ragab, K.E.; Seleiman, M.F.; Kheir, A.M.S. Modeling the combined impacts of deficit irrigation, rising temperature and compost application on wheat yield and water productivity. Agric. Water Manag. 2021, 244, 106626. [Google Scholar] [CrossRef]
- Feng, Y.; Hao, W.; Gao, L.; Li, H.; Gong, D.; Cui, N. Comparison of maize water consumption at different scales between mulched and non-mulched croplands. Agric. Water Manag. 2019, 216, 315–324. [Google Scholar] [CrossRef]
- Cheng, M.; Wang, H.; Fan, J.; Zhang, S.; Wang, Y.; Li, Y.; Sun, X.; Yang, L.; Zhang, F. Water productivity and seed cotton yield in response to deficit irrigation: A global meta-analysis. Agric. Water Manag. 2021, 255, 107027. [Google Scholar] [CrossRef]
- Zheng, J.; Fan, J.; Zhang, F.; Zhuang, Q. Evapotranspiration partitioning and water productivity of rainfed maize under contrasting mulching conditions in Northwest China. Agric. Water Manag. 2021, 243, 106473. [Google Scholar] [CrossRef]
- Kader, M.A.; Senge, M.; Mojid, M.A.; Ito, K. Recent advances in mulching materials and methods for modifying soil environment. Soil Tillage Res. 2017, 168, 155–166. [Google Scholar] [CrossRef]
- Mo, F.; Li, X.Y.; Niu, F.J.; Zhang, C.R.; Li, S.K.; Zhang, L.; Xiong, Y.C. Alternating small and large ridges with full film mulching increase linseed (Linum usitatissimum L.) productivity and economic benefit in a rainfed semiarid environment. Field Crops Res. 2018, 219, 120–130. [Google Scholar] [CrossRef]
- Zhou, L.-M.; Li, F.-M.; Jin, S.-L.; Song, Y. How two ridges and the furrow mulched with plastic film affect soil water, soil temperature and yield of maize on the semiarid Loess Plateau of China. Field Crops Res. 2009, 113, 41–47. [Google Scholar] [CrossRef]
- Zhang, M.; Dong, B.; Qiao, Y.; Yang, H.; Wang, Y.; Liu, M. Effects of sub-soil plastic film mulch on soil water and salt content and water utilization by winter wheat under different soil salinities. Field Crops Res. 2018, 225, 130–140. [Google Scholar] [CrossRef]
- Chen, N.; Li, X.; Šimůnek, J.; Zhang, Y.; Shi, H.; Hu, Q.; Xin, M. Evaluating soil salts dynamics under biodegradable film mulching with different disintegration rates in an arid region with shallow and saline groundwater: Experimental and modeling study. Geoderma 2022, 423, 115969. [Google Scholar] [CrossRef]
- Tan, S. Performance of AquaCrop model for cotton growth simulation under film-mulched drip irrigation in southern Xinjiang, China. Agric. Water Manag. 2018, 196, 99–113. [Google Scholar] [CrossRef]
- Ngwira, A.R.; Aune, J.B.; Thierfelder, C. DSSAT modelling of conservation agriculture maize response to climate change in Malawi. Soil Tillage Res. 2014, 143, 85–94. [Google Scholar] [CrossRef]
- Feng, P.; Wang, B.; Macadam, I.; Taschetto, A.S.; Abram, N.J.; Luo, J.-J.; King, A.D.; Chen, Y.; Li, Y.; Liu, D.L.; et al. Increasing dominance of Indian Ocean variability impacts Australian wheat yields. Nat. Food 2022, 3, 862–870. [Google Scholar] [CrossRef] [PubMed]
- Raes, D.; Steduto, P.; Hsiao, T.C.; Fereres, E. AquaCrop—The FAO Crop Model to Simulate Yield Response to Water: II. Main Algorithms and Software Description. Agron. J. 2009, 101, 438–447. [Google Scholar] [CrossRef]
- Liu, B.; Asseng, S.; Müller, C.; Ewert, F.; Elliott, J.; Lobell, D.B.; Martre, P.; Ruane, A.C.; Wallach, D.; Jones, J.W.; et al. Similar estimates of temperature impacts on global wheat yield by three independent methods. Nat. Clim. Chang. 2016, 6, 1130–1136. [Google Scholar] [CrossRef]
- Zhao, C.; Liu, B.; Piao, S.; Wang, X.; Lobell, D.B.; Huang, Y.; Huang, M.; Yao, Y.; Bassu, S.; Ciais, P.; et al. Temperature increase reduces global yields of major crops in four independent estimates. Proc. Natl. Acad. Sci. USA 2017, 114, 9326–9331. [Google Scholar] [CrossRef]
- Zheng, H.; Wei, X.; Tada, R.; Clift, P.D.; Wang, B.; Jourdan, F.; Wang, P.; He, M. Late Oligocene-early Miocene birth of the Taklimakan Desert. Proc. Natl. Acad. Sci. USA 2015, 112, 7662–7667. [Google Scholar] [CrossRef]
- Li, Z.; Liu, T.; Huang, Y.; Peng, J.; Ling, Y. Evaluation of the CMIP6 Precipitation Simulations Over Global Land. Earth’s Future 2022, 10, e2021EF002500. [Google Scholar] [CrossRef]
- Lange, S. Trend-preserving bias adjustment and statistical downscaling with ISIMIP3BASD (v1.0). Geosci. Model Dev. 2019, 12, 3055–3070. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56. Available online: https://www.fao.org/3/X0490E/X0490E00.htm (accessed on 10 September 2020).
- FAO; IIASA; ISRIC; ISSCAS; JRC. Harmonized World Soil Database (Version 1.2). Available online: http://webarchive.iiasa.ac.at/Research/LUC/External-World-soil-database/HTML/ (accessed on 10 September 2020).
- Committee, X.S.Y. Xinjiang Statistical Yearbook. Available online: https://tjj.xinjiang.gov.cn/tjj/zhhvgh/list_nj1.shtml (accessed on 10 September 2020).
- Xu, X.; Liu, J.; Zhang, S.; Li, R.; Yan, C.; Wu, S. Remote sensing data set of multi-period land use monitoring in China(CNLUCC). In Resource and Environmental Science Data Registration and Publication System; Resource and Environment Science and Data Center: Beijing, China, 2018. [Google Scholar] [CrossRef]
- Jiang, T.; Sun, S.; Li, Z.; Li, Q.; Lu, Y.; Li, C.; Wang, Y.; Wu, P. Vulnerability of crop water footprint in rain-fed and irrigation agricultural production system under future climate scenarios. Agric. For. Meteorol. 2022, 326, 109164. [Google Scholar] [CrossRef]
- Iqbal, M.A.; Shen, Y.; Stricevic, R.; Pei, H.; Sun, H.; Amiri, E.; Penas, A.; del Rio, S. Evaluation of the FAO AquaCrop model for winter wheat on the North China Plain under deficit irrigation from field experiment to regional yield simulation. Agric. Water Manag. 2014, 135, 61–72. [Google Scholar] [CrossRef]
- Voloudakis, D. Prediction of climate change impacts on cotton yields in Greece under eight climatic models using the AquaCrop crop simulation model and discriminant function analysis. Agric. Water Manag. 2015, 147, 116–128. [Google Scholar] [CrossRef]
- Kelly, T.D.; Foster, T. AquaCrop-OSPy: Bridging the gap between research and practice in crop-water modeling. Agric. Water Manag. 2021, 254, 106976. [Google Scholar] [CrossRef]
- Dirk, R.; Steduto, P.; Hsiao, T.C.; Fereres, A.E. FAO Crop-Water Productivity Model to Simulate Yield Response to Water. Available online: https://www.fao.org/aquacrop/resources/referencemanuals/en/ (accessed on 10 September 2020).
- Li, S.X.; Wang, Z.H.; Li, S.Q.; Gao, Y.J.; Tian, X.H. Effect of plastic sheet mulch, wheat straw mulch, and maize growth on water loss by evaporation in dryland areas of China. Agric. Water Manag. 2013, 116, 39–49. [Google Scholar] [CrossRef]
- Guo, D.; Olesen, J.E.; Pullens, J.W.M.; Guo, C.; Ma, X. Calibrating AquaCrop model using genetic algorithm with multi-objective functions applying different weight factors. Agron. J. 2021, 113, 1420–1438. [Google Scholar] [CrossRef]
- Zhu, A.X.; Lu, G.N.; Liu, J.; Qin, C.Z.; Zhou, C.H. Spatial prediction based on Third Law of Geography. Ann. GIS 2018, 24, 225–240. [Google Scholar] [CrossRef]
- Zhu, A.; Lv, G.; Zhou, C.; Qin, C. Geographic Similarity: Third Law of Geography? J. Geo-Inf. Sci. 2020, 22, 673–679. [Google Scholar] [CrossRef]
- Choudhury, M.R.; Mellor, V.; Das, S.; Christopher, J.; Apan, A.; Menzies, N.W.; Chapman, S.; Dang, Y.P. Improving estimation of in-season crop water use and health of wheat genotypes on sodic soils using spatial interpolation techniques and multi-component metrics. Agric. Water Manag. 2021, 255, 107007. [Google Scholar] [CrossRef]
- Wu, Y.-H.; Hung, M.-C.; Patton, J. Assessment and visualization of spatial interpolation of soil pH values in farmland. Precis. Agric. 2013, 14, 565–585. [Google Scholar] [CrossRef]
- Rodrigues, G.C.; Pereira, L.S. Assessing economic impacts of deficit irrigation as related to water productivity and water costs. Biosyst. Eng. 2009, 103, 536–551. [Google Scholar] [CrossRef]
- Pereira, L.S.; Cordery, I.; Iacovides, I. Improved indicators of water use performance and productivity for sustainable water conservation and saving. Agric. Water Manag. 2012, 108, 39–51. [Google Scholar] [CrossRef]
- Fernández, J.E.; Alcon, F.; Diaz-Espejo, A.; Hernandez-Santana, V.; Cuevas, M.V. Water use indicators and economic analysis for on-farm irrigation decision: A case study of a super high density olive tree orchard. Agric. Water Manag. 2020, 237, 106074. [Google Scholar] [CrossRef]
- Massey, F.J. The kolmogorov-smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Vlček, O.; Huth, R. Is daily precipitation Gamma-distributed? Atmos. Res. 2009, 93, 759–766. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, P.; Chen, X.; Jiang, T. Hydrological extremes in the Poyang Lake basin, China: Changing properties, causes and impacts. Hydrol. Process. 2011, 25, 3121–3130. [Google Scholar] [CrossRef]
- Birnbaum, Z.W. Numerical Tabulation of the Distribution of Kolmogorov’s Statistic for Finite Sample Size. J. Am. Stat. Assoc. 1952, 47, 425–441. [Google Scholar] [CrossRef]
- Lilliefors, H.W. On kolmogorov-smirnov test for normality with mean and variance unknown. J. Am. Stat. Assoc. 1967, 62, 399–402. [Google Scholar] [CrossRef]
- Zhao, K.; Wulder, M.A.; Hu, T.; Bright, R.; Wu, Q.; Qin, H.; Li, Y.; Toman, E.; Mallick, B.; Zhang, X.; et al. Detecting change-point, trend, and seasonality in satellite time series data to track abrupt changes and nonlinear dynamics: A Bayesian ensemble algorithm. Remote Sens. Environ. 2019, 232, 111181. [Google Scholar] [CrossRef]
- Erdman, C.; Emerson, J.W. bcp: An R package for performing a Bayesian analysis of change point problems. J. Stat. Softw. 2007, 23, 1–13. [Google Scholar] [CrossRef]
- Ji, X.; Cobourn, K.M. Weather Fluctuations, Expectation Formation, and Short-Run Behavioral Responses to Climate Change. Environ. Resour. Econ. 2020, 78, 77–119. [Google Scholar] [CrossRef]
- Qiao, P.; Lei, M.; Yang, S.; Yang, J.; Guo, G.; Zhou, X. Comparing ordinary kriging and inverse distance weighting for soil as pollution in Beijing. Env. Sci. Pollut. Res. Int. 2018, 25, 15597–15608. [Google Scholar] [CrossRef] [PubMed]
- Meng, Q.; Liu, Z.; Borders, B.E. Assessment of regression kriging for spatial interpolation—Comparisons of seven GIS interpolation methods. Cartogr. Geogr. Inf. Sci. 2013, 40, 28–39. [Google Scholar] [CrossRef]
- Berndt, C.; Haberlandt, U. Spatial interpolation of climate variables in Northern Germany—Influence of temporal resolution and network density. J. Hydrol. Reg. Stud. 2018, 15, 184–202. [Google Scholar] [CrossRef]
- Sekulić, A.; Kilibarda, M.; Heuvelink, G.B.M.; Nikolić, M.; Bajat, B. Random Forest Spatial Interpolation. Remote Sens. 2020, 12, 1687. [Google Scholar] [CrossRef]
- Gamage, D.; Thompson, M.; Sutherland, M.; Hirotsu, N.; Makino, A.; Seneweera, S. New insights into the cellular mechanisms of plant growth at elevated atmospheric carbon dioxide concentrations. Plant Cell Env. 2018, 41, 1233–1246. [Google Scholar] [CrossRef]
- Allen, L.H.; Kimball, B.A.; Bunce, J.A.; Yoshimoto, M.; Harazono, Y.; Baker, J.T.; Boote, K.J.; White, J.W. Fluctuations of CO2 in Free-Air CO2 Enrichment (FACE) depress plant photosynthesis, growth, and yield. Agric. For. Meteorol. 2020, 284, 107899. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Chiang, F.; Huning, L.S.; Love, C.A.; Mallakpour, I.; Mazdiyasni, O.; Moftakhari, H.; Papalexiou, S.M.; Ragno, E.; Sadegh, M. Climate Extremes and Compound Hazards in a Warming World. Annu. Rev. Earth Planet. Sci. 2020, 48, 519–548. [Google Scholar] [CrossRef]
- Hasegawa, T.; Sakurai, G.; Fujimori, S.; Takahashi, K.; Hijioka, Y.; Masui, T. Extreme climate events increase risk of global food insecurity and adaptation needs. Nat. Food 2021, 2, 587–595. [Google Scholar] [CrossRef]
- Bennett, D.R.; Harms, T.E. Crop Yield and Water Requirement Relationships for Major Irrigated Crops in Southern Alberta. Can. Water Resour. J. 2011, 36, 159–170. [Google Scholar] [CrossRef]
- Nistor, M.-M.; Cheval, S.; Gualtieri, A.F.; Dumitrescu, A.; Boţan, V.E.; Berni, A.; Hognogi, G.; Irimuş, I.A.; Porumb-Ghiurco, C.G. Crop evapotranspiration assessment under climate change in the Pannonian basin during 1991–2050. Meteorol. Appl. 2017, 24, 84–91. [Google Scholar] [CrossRef]
- Zabel, F.; Muller, C.; Elliott, J.; Minoli, S.; Jagermeyr, J.; Schneider, J.M.; Franke, J.A.; Moyer, E.; Dury, M.; Francois, L.; et al. Large potential for crop production adaptation depends on available future varieties. Glob. Chang. Biol. 2021, 27, 3870–3882. [Google Scholar] [CrossRef] [PubMed]
- He, L.; Asseng, S.; Zhao, G.; Wu, D.; Yang, X.; Zhuang, W.; Jin, N.; Yu, Q. Impacts of recent climate warming, cultivar changes, and crop management on winter wheat phenology across the Loess Plateau of China. Agric. For. Meteorol. 2015, 200, 135–143. [Google Scholar] [CrossRef]
- Minoli, S.; Jagermeyr, J.; Asseng, S.; Urfels, A.; Muller, C. Global crop yields can be lifted by timely adaptation of growing periods to climate change. Nat. Commun. 2022, 13, 7079. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Li, Y.; Lin, H.; Feng, H.; Dyck, M. Effects of different mulching technologies on evapotranspiration and summer maize growth. Agric. Water Manag. 2018, 201, 309–318. [Google Scholar] [CrossRef]




| RMSE | ||
|---|---|---|
| Calibration | 122.47 kg/ha | 0.95 |
| Validation | 131.91 kg/ha | 0.92 |
| Crop Parameter | Optimal Interpolation Method | Interpolation Main Parameter | RMSE | ||
|---|---|---|---|---|---|
| Main Parameter | Parameter Values | ||||
| Planting | UK | Semivariogram Props | Quadratic drift | 39.46% | 0.60 |
| Emergence | SP | Spline Type | Regularized | 39.91% | 0.56 |
| HI_Start | SP | Spline Type | Tension | 22.16% | 0.38 |
| Flowering | SP | Spline Type | Tension | 11.46% | 0.47 |
| Senescence | GPI | Power | 1 | 8.26% | 0.51 |
| Maturity | GPI | Power | 1 | 8.46% | 0.55 |
| Plant Density | GPI | Power | 3 | 30.84% | 0.52 |
| CCX | GPI | Power | 3 | 5.5% | 0.78 |
| CDC | UK | Semivariogram Props | Quadratic drift | 17.1% | 0.63 |
| CGC | SP | Spline Type | Regularized | 18.2% | 0.27 |
| HI0 | GPI | Power | 1 | 11.59% | 0.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Chen, Y.; Li, Z.; Duan, W.; Fang, G.; Wang, C.; He, G.; Wei, W. Using Film-Mulched Drip Irrigation to Improve the Irrigation Water Productivity of Cotton in the Tarim River Basin, Central Asia. Remote Sens. 2023, 15, 4615. https://doi.org/10.3390/rs15184615
Zhu J, Chen Y, Li Z, Duan W, Fang G, Wang C, He G, Wei W. Using Film-Mulched Drip Irrigation to Improve the Irrigation Water Productivity of Cotton in the Tarim River Basin, Central Asia. Remote Sensing. 2023; 15(18):4615. https://doi.org/10.3390/rs15184615
Chicago/Turabian StyleZhu, Jianyu, Yaning Chen, Zhi Li, Weili Duan, Gonghuan Fang, Chuan Wang, Ganchang He, and Wei Wei. 2023. "Using Film-Mulched Drip Irrigation to Improve the Irrigation Water Productivity of Cotton in the Tarim River Basin, Central Asia" Remote Sensing 15, no. 18: 4615. https://doi.org/10.3390/rs15184615
APA StyleZhu, J., Chen, Y., Li, Z., Duan, W., Fang, G., Wang, C., He, G., & Wei, W. (2023). Using Film-Mulched Drip Irrigation to Improve the Irrigation Water Productivity of Cotton in the Tarim River Basin, Central Asia. Remote Sensing, 15(18), 4615. https://doi.org/10.3390/rs15184615










