InfoLa-SLAM: Efficient Lidar-Based Lightweight Simultaneous Localization and Mapping with Information-Based Keyframe Selection and Landmarks Assisted Relocalization
Abstract
:1. Introduction
2. Related Work
2.1. Keyframe Selection
2.2. Relocalization
3. Methodology
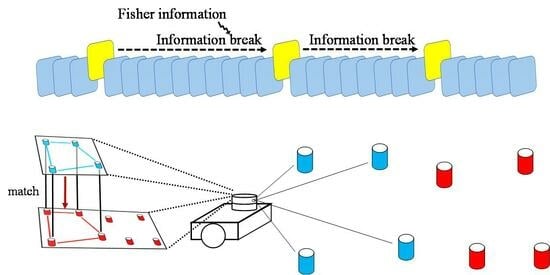
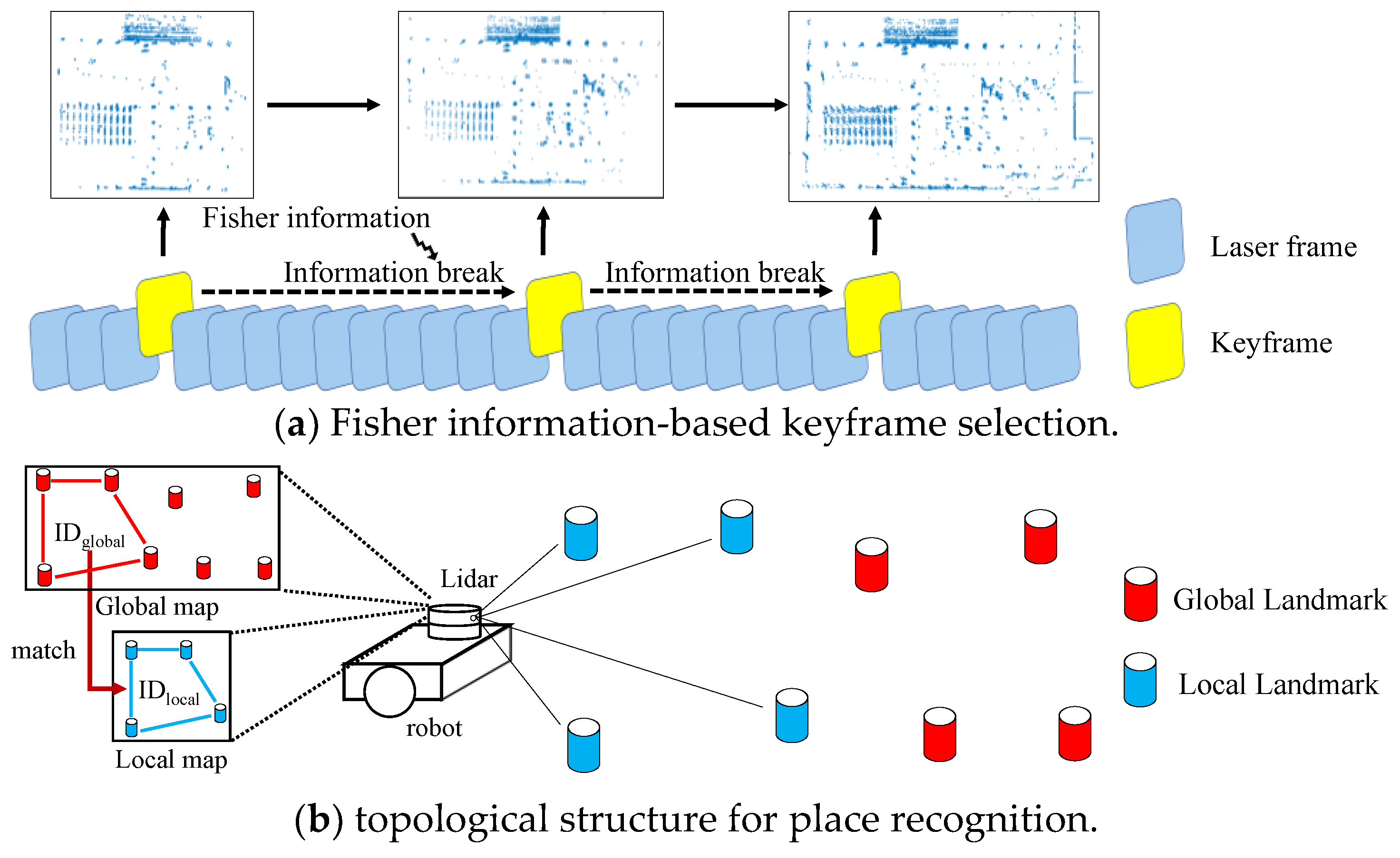
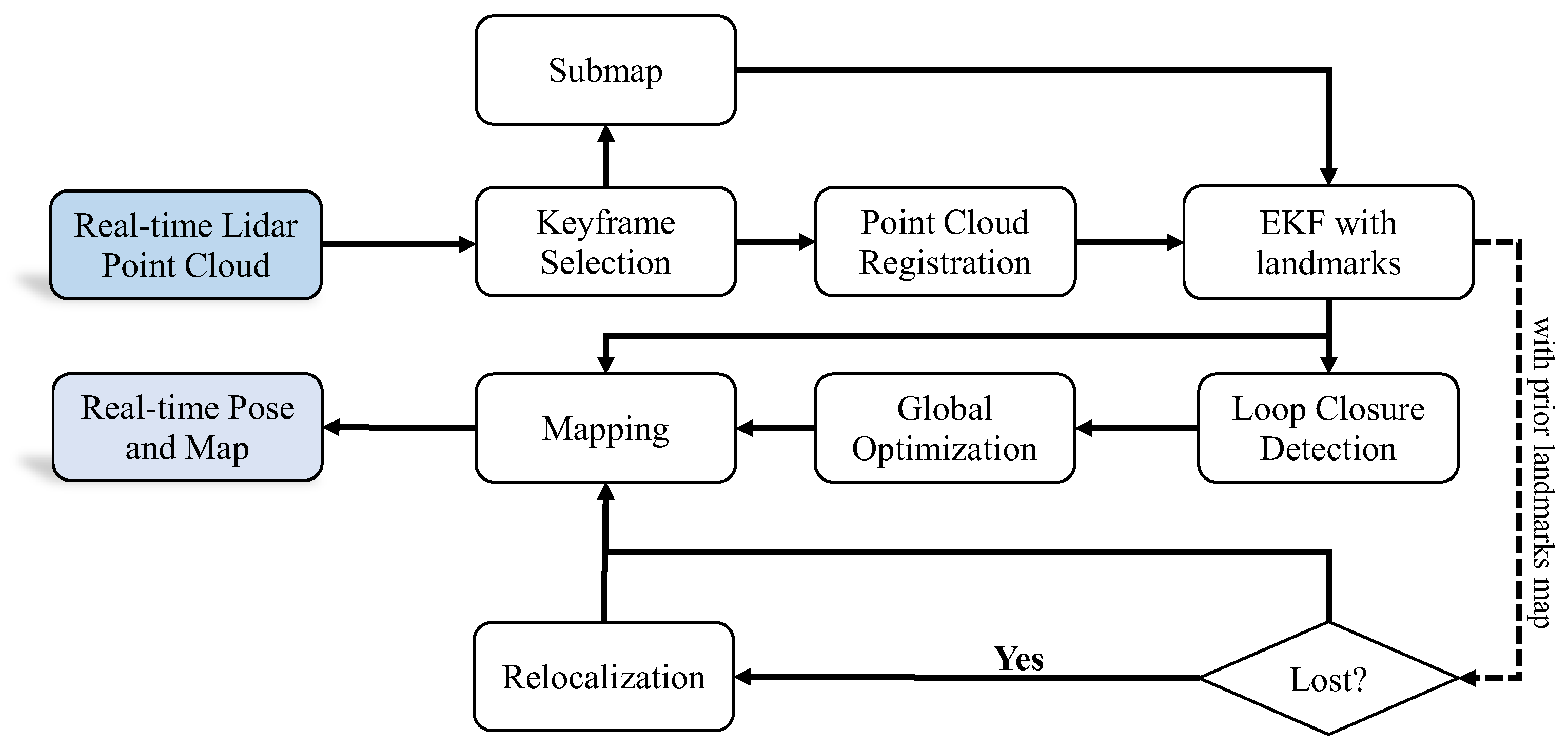
3.1. System Overview
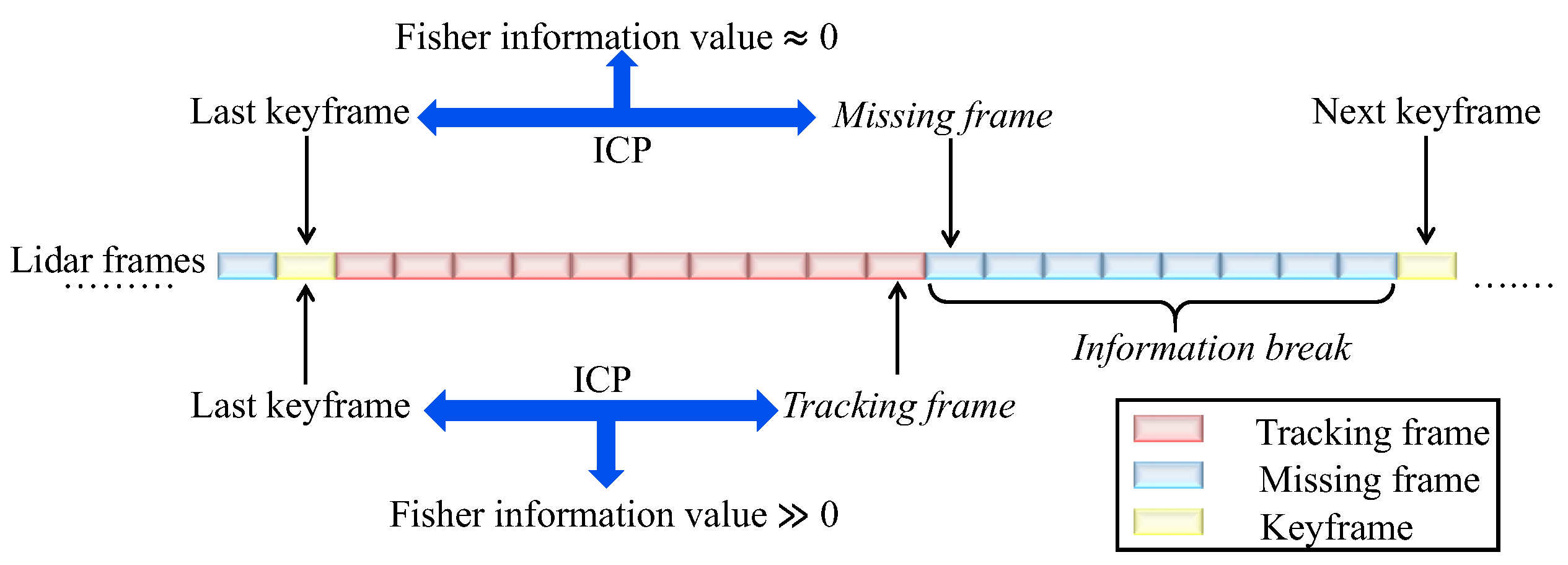
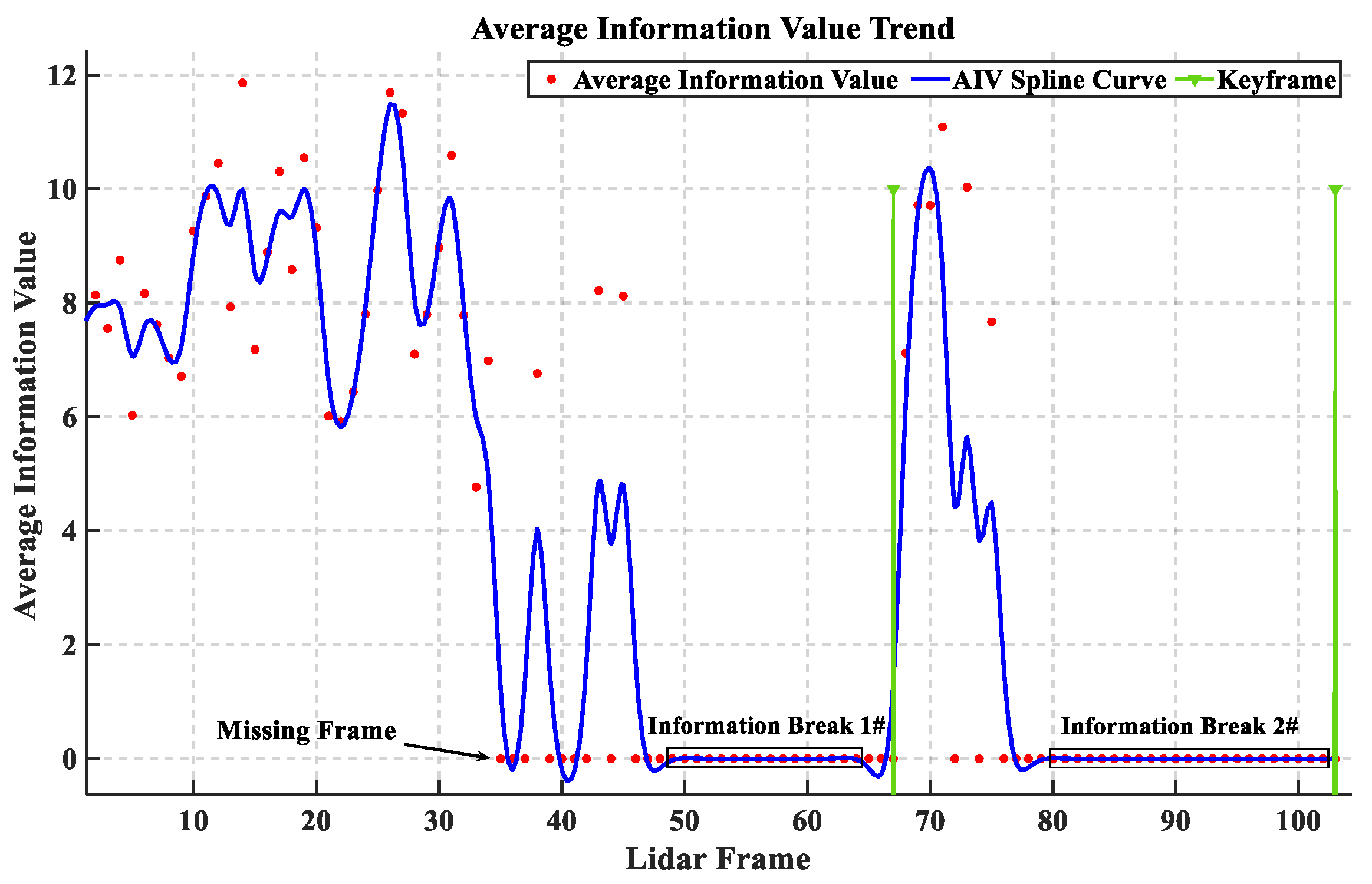
3.2. Keyframe Selection Strategy
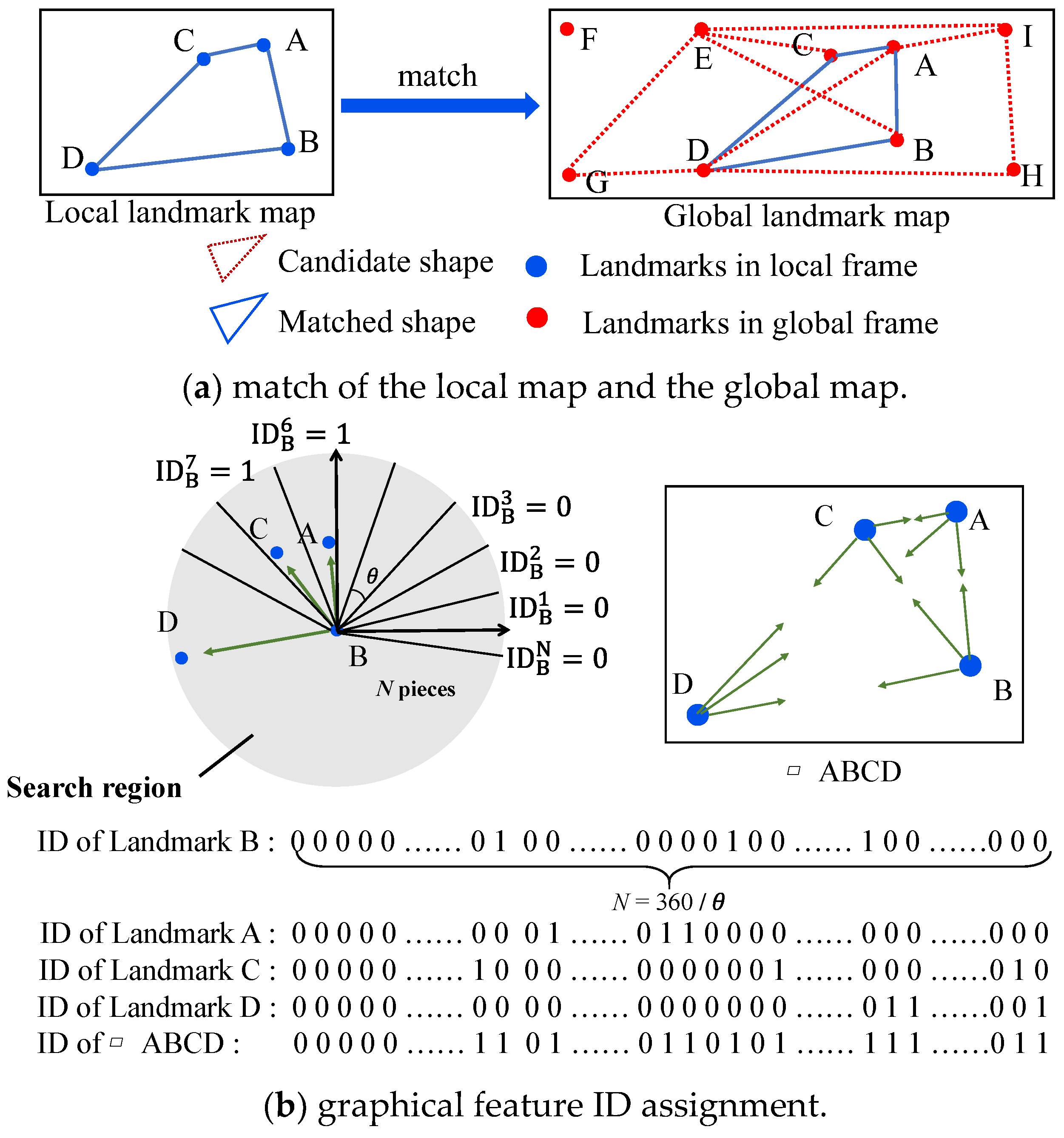
3.3. Adaptive Relocalization
4. Experiments
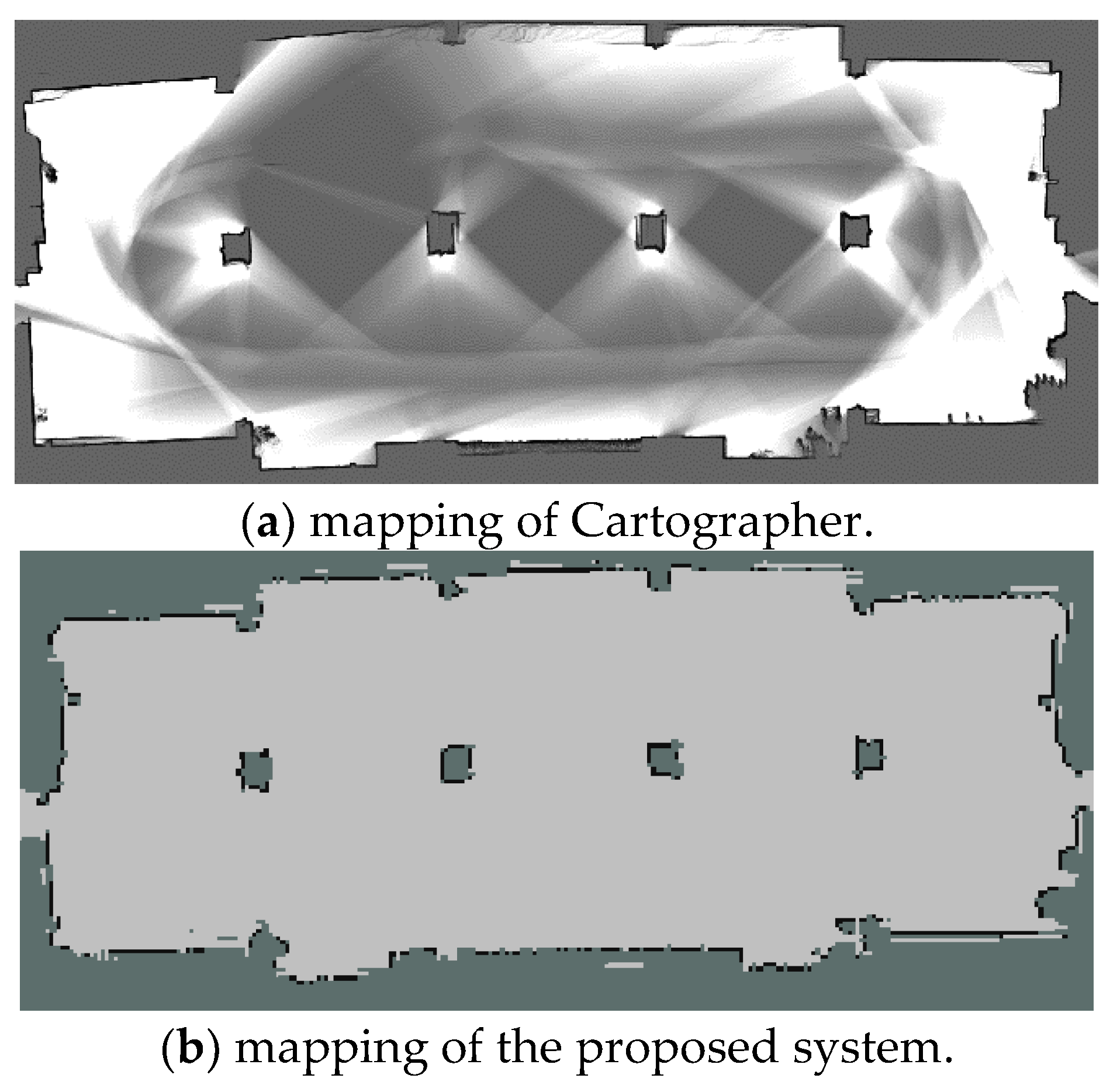
4.1. Keyframe Selection
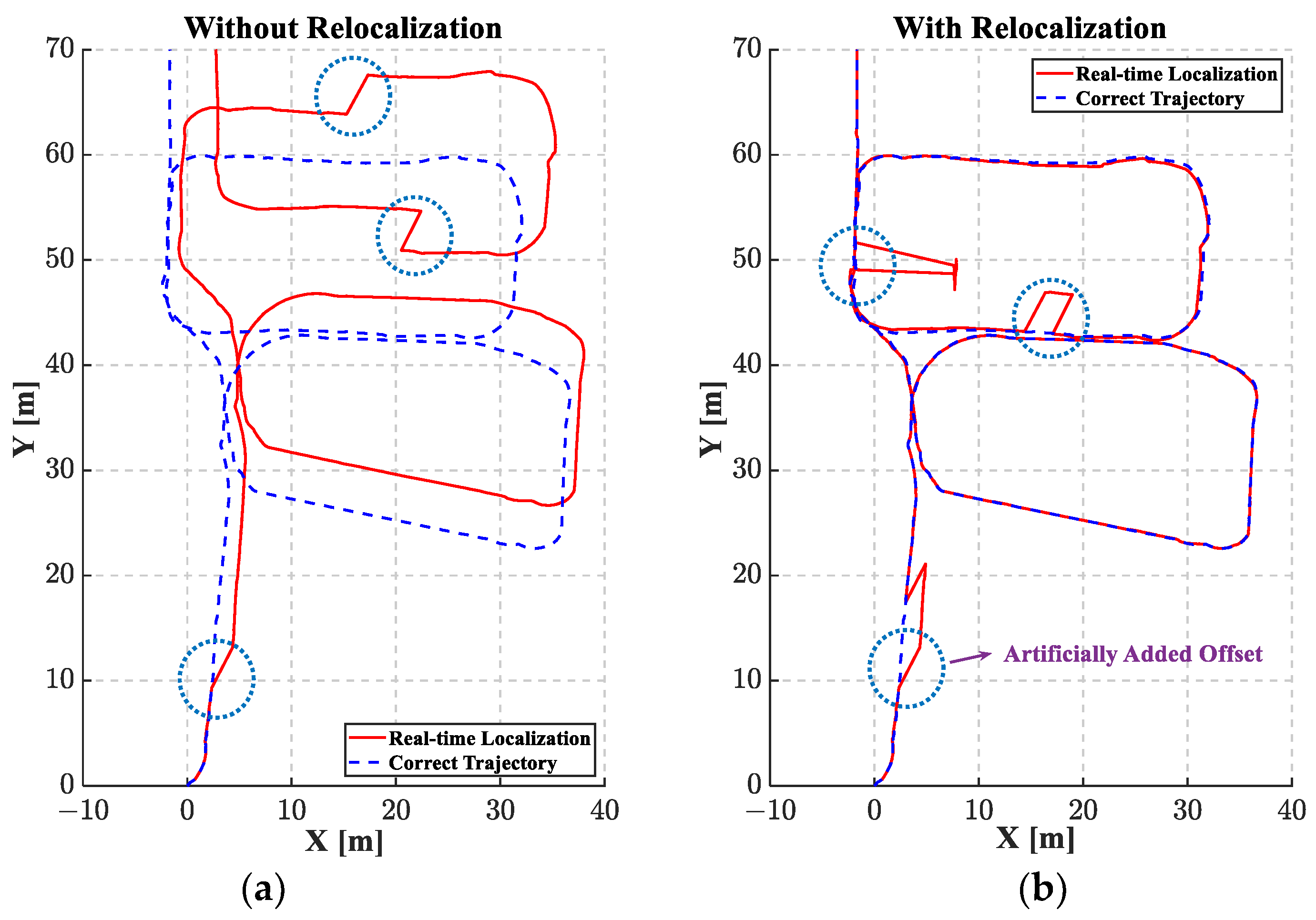
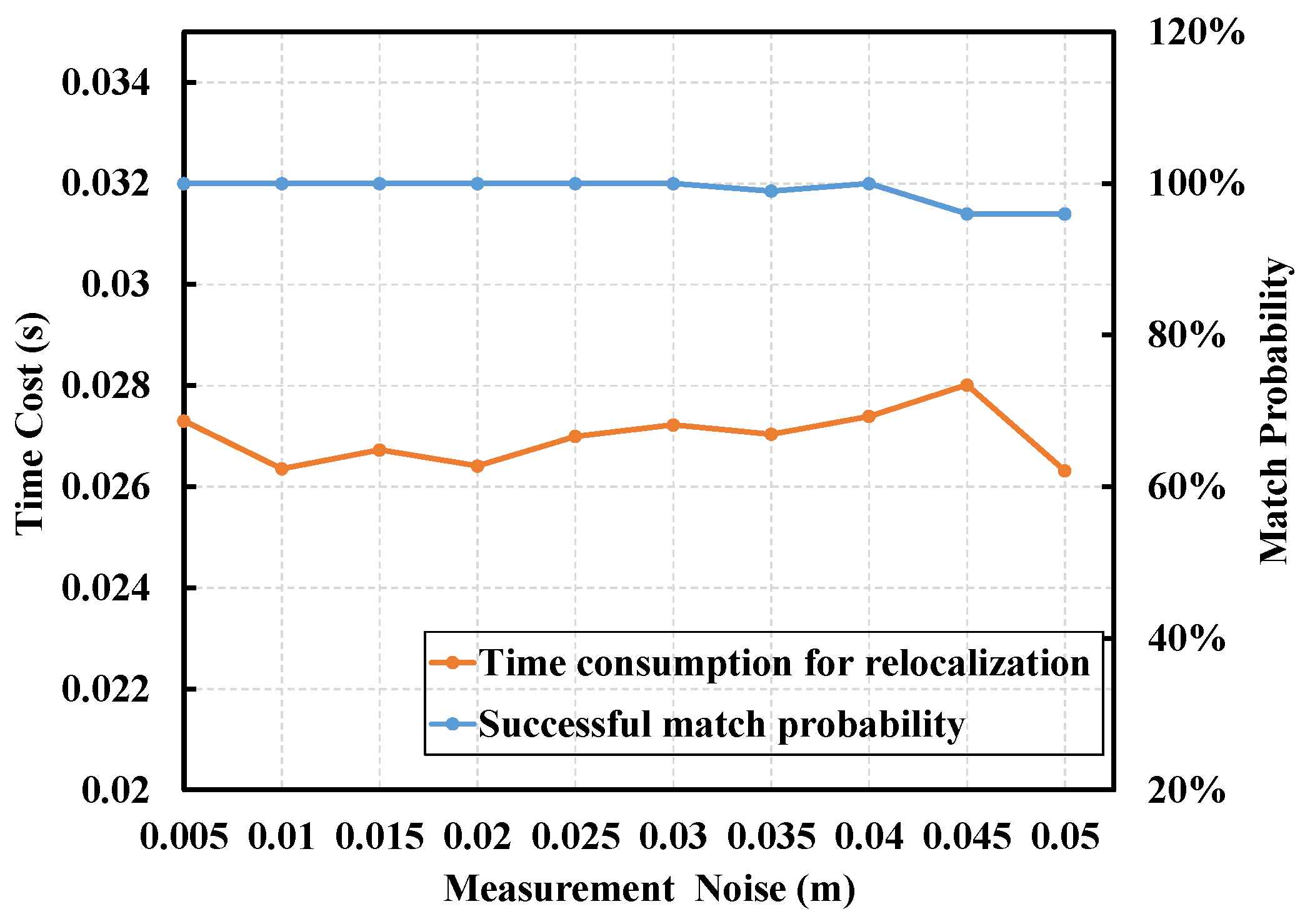
4.2. Relocalization
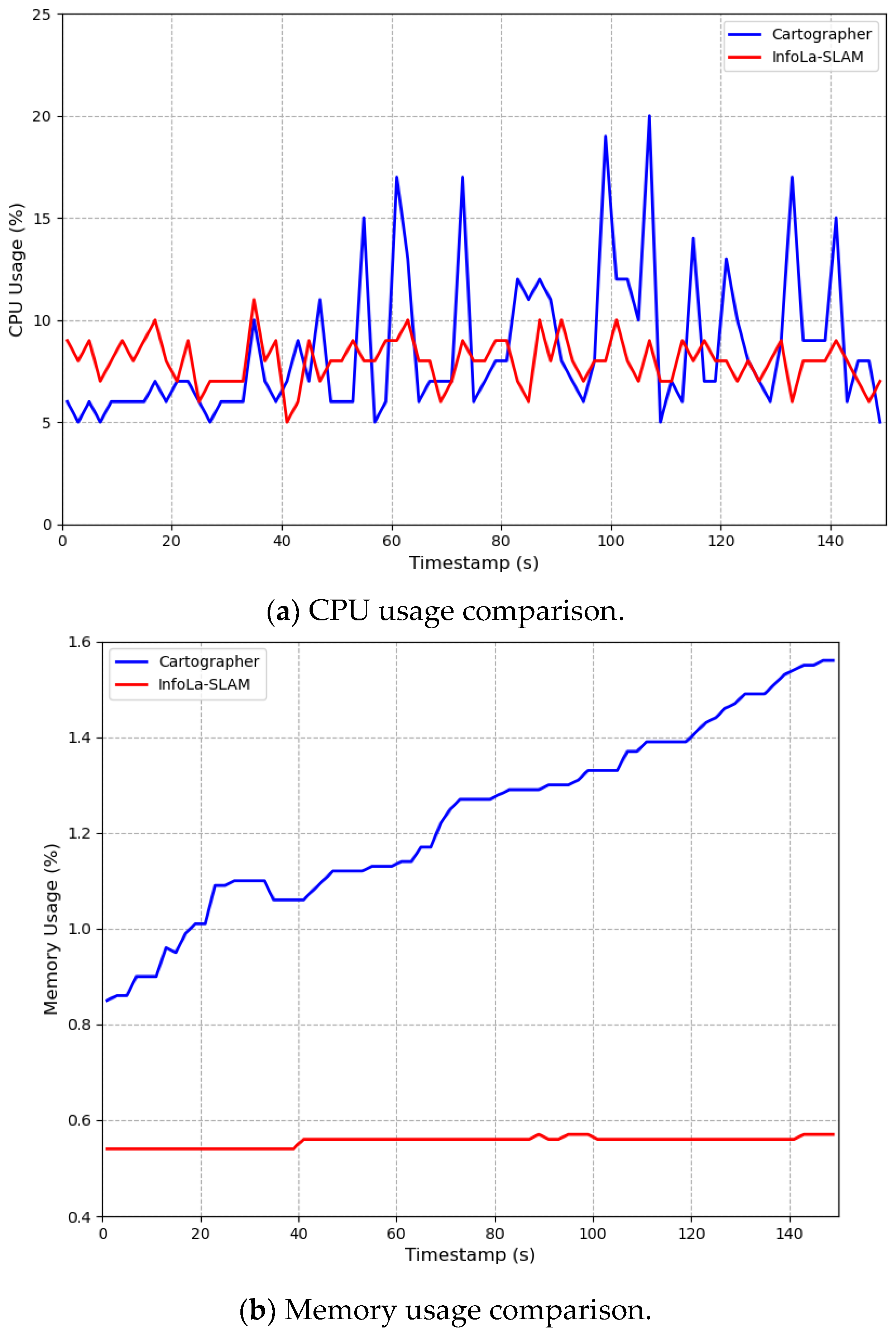
4.3. Lightweight Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- Proof of
- 2.
- Proof of
References
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; Leonard, J.J. Past, Present, and Future of Simultaneous Localization and Mapping: Toward the Robust-Perception Age. IEEE Trans. Robot. 2016, 32, 1309–1332. [Google Scholar] [CrossRef]
- Hess, W.; Kohler, D.; Rapp, H.; Andor, D. Real-time loop closure in 2D LIDAR SLAM. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016. [Google Scholar]
- Ali, A.J.B.; Kouroshli, M.; Semenova, S.; Hashemifar, Z.S.; Ko, S.Y.; Dantu, K. Edge-SLAM: Edge-Assisted Visual Simultaneous Localization and Mapping. ACM Trans. Embed. Comput. Syst. 2022, 22, 18. [Google Scholar] [CrossRef]
- Kuo, J.; Muglikar, M.; Zhang, Z.; Scaramuzza, D. Redesigning SLAM for Arbitrary Multi-Camera Systems. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020. [Google Scholar]
- Lin, Y.; Hongwei, M.; Yan, W.; Jing, X.; Chuanwei, W. A Tightly Coupled LiDAR-Inertial SLAM for Perceptually Degraded Scenes. Sensors 2022, 22, 3063. [Google Scholar]
- Shan, T.; Englot, B.; Meyers, D.; Wang, W.; Ratti, C.; Rus, D. Lio-sam: Tightly-coupled lidar inertial odometry via smoothing and mapping. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 5135–5142. [Google Scholar]
- Forster, C.; Zhang, Z.; Gassner, M.; Werlberger, M.; Scaramuzza, D. SVO: Semidirect Visual Odometry for Monocular and Multicamera Systems. IEEE Trans. Robot. 2017, 33, 249–265. [Google Scholar] [CrossRef]
- Engel, J.; Koltun, V.; Cremers, D. Direct Sparse Odometry. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 611–625. [Google Scholar] [CrossRef] [PubMed]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A Versatile and Accurate Monocular SLAM System. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Qin, T.; Li, P.; Shen, S. Vins-mono: A robust and versatile monocular visual-inertial state estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Harmat, A.; Sharf, I.; Trentini, M. Parallel Tracking and Mapping with Multiple Cameras on an Unmanned Aerial Vehicle; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Xie, P.; Su, W.; Li, B.; Jian, R.; Huang, R.; Zhang, S.; Wei, J. Modified Keyframe Selection Algorithm and Map Visualization Based on ORB-SLAM2. In Proceedings of the 2020 4th International Conference on Robotics and Automation Sciences (ICRAS), Chengdu, China, 6–8 June 2020; pp. 142–147. [Google Scholar]
- Das, A.; Waslander, S.L. Entropy based keyframe selection for Multi-Camera Visual SLAM. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September—3 October 2015. [Google Scholar]
- Jiao, J.; Ye, H.; Zhu, Y.; Liu, M. Robust Odometry and Mapping for Multi-LiDAR Systems with Online Extrinsic Calibration. IEEE Trans. Robot. 2020, 38, 351–371. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. LOAM: Lidar odometry and mapping in real-time. In Proceedings of the Robotics: Science and Systems, Berkeley, CA, USA, 12–16 July 2014; pp. 1–9. [Google Scholar]
- Piao, J.-C.; Kim, S.-D. Real-Time Visual–Inertial SLAM Based on Adaptive Keyframe Selection for Mobile AR Applications. IEEE Trans. Multimed. 2019, 21, 2827–2836. [Google Scholar] [CrossRef]
- Tang, X.; Fu, W.; Jiang, M.; Peng, G.; Wu, Z.; Yue, Y.; Wang, D. Place recognition using line-junction-lines in urban environments. In Proceedings of the 2019 IEEE International Conference on Cybernetics and Intelligent Systems (CIS) and IEEE Conference on Robotics, Automation and Mechatronics (RAM), Bangkok, Thailand, 18–20 November 2019; pp. 530–535. [Google Scholar]
- Arandjelovic, R.; Gronat, P.; Torii, A.; Pajdla, T.; Sivic, J. NetVLAD: CNN architecture for weakly supervised place recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5297–5307. [Google Scholar]
- Peng, G.; Zhang, J.; Li, H.; Wang, D. Attentional pyramid pooling of salient visual residuals for place recognition. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 885–894. [Google Scholar]
- Peng, G.; Huang, Y.; Li, H.; Wu, Z.; Wang, D. LSDNet: A Lightweight Self-Attentional Distillation Network for Visual Place Recognition. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 6608–6613. [Google Scholar]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. BRIEF: Binary Robust Independent Elementary Features. In Proceedings of the European Conference on Computer Vision, Crete, Greece, 5–11 September 2010. [Google Scholar]
- Jin, S.; Wu, Z.; Zhao, C.; Zhang, J.; Peng, G.; Wang, D. SectionKey: 3-D Semantic Point Cloud Descriptor for Place Recognition. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 9905–9910. [Google Scholar]
- Fan, Y.; He, Y.; Tan, U.X. Seed: A Segmentation-Based Egocentric 3D Point Cloud Descriptor for Loop Closure Detection. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020. [Google Scholar]
- Wang, H.; Wang, C.; Xie, L. Intensity Scan Context: Coding Intensity and Geometry Relations for Loop Closure Detection. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020. [Google Scholar]
- Wang, Y.; Sun, Z.; Xu, C.-Z.; Sarma, S.E.; Yang, J.; Kong, H. Lidar iris for loop-closure detection. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 5769–5775. [Google Scholar]
- He, L.; Wang, X.; Zhang, H. M2DP: A novel 3D point cloud descriptor and its application in loop closure detection. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016. [Google Scholar]
- Kim, G.; Kim, A. Scan Context: Egocentric Spatial Descriptor for Place Recognition within 3D Point Cloud Map. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018. [Google Scholar]
- Chen, X.; Läbe, T.; Milioto, A.; Röhling, T.; Vysotska, O.; Haag, A.; Behley, J.; Stachniss, C. OverlapNet: Loop Closing for LiDAR-based SLAM. In Proceedings of the Robotics: Science and Systems XVI, Virtual Event, 12–16 July 2021. [Google Scholar]
- Scovanner, P.; Ali, S.; Shah, M. A 3-dimensional sift descriptor and its application to action recognition. In Proceedings of the 15th ACM International Conference on Multimedia, Augsburg, Germany, 25–29 September 2007. [Google Scholar]
- Sipiran, I.; Bustos, B. A Robust 3D Interest Points Detector Based on Harris Operator. In Proceedings of the Eurographics Workshop on 3D Object Retrieval, Norrköping, Sweden, 2 May 2010. [Google Scholar]
- Tsourounis, D.; Kastaniotis, D.; Theoharatos, C.; Kazantzidis, A.; Economou, G. SIFT-CNN: When Convolutional Neural Networks Meet Dense SIFT Descriptors for Image and Sequence Classification. J. Imaging 2022, 8, 256. [Google Scholar] [CrossRef] [PubMed]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Censi, A. On achievable accuracy for range-finder localization. In Proceedings of the Robotics and Automation, Roma, Italy, 10–14 April 2007. [Google Scholar]
- Casella, G.; Berger, R.L. Statistical Inference; Cengage Learning: Boston, MA, USA, 2021. [Google Scholar]
- Censi, A. On achievable accuracy for pose tracking. In Proceedings of the Robotics and Automation, Kobe, Japan, 12–17 May 2009. [Google Scholar]





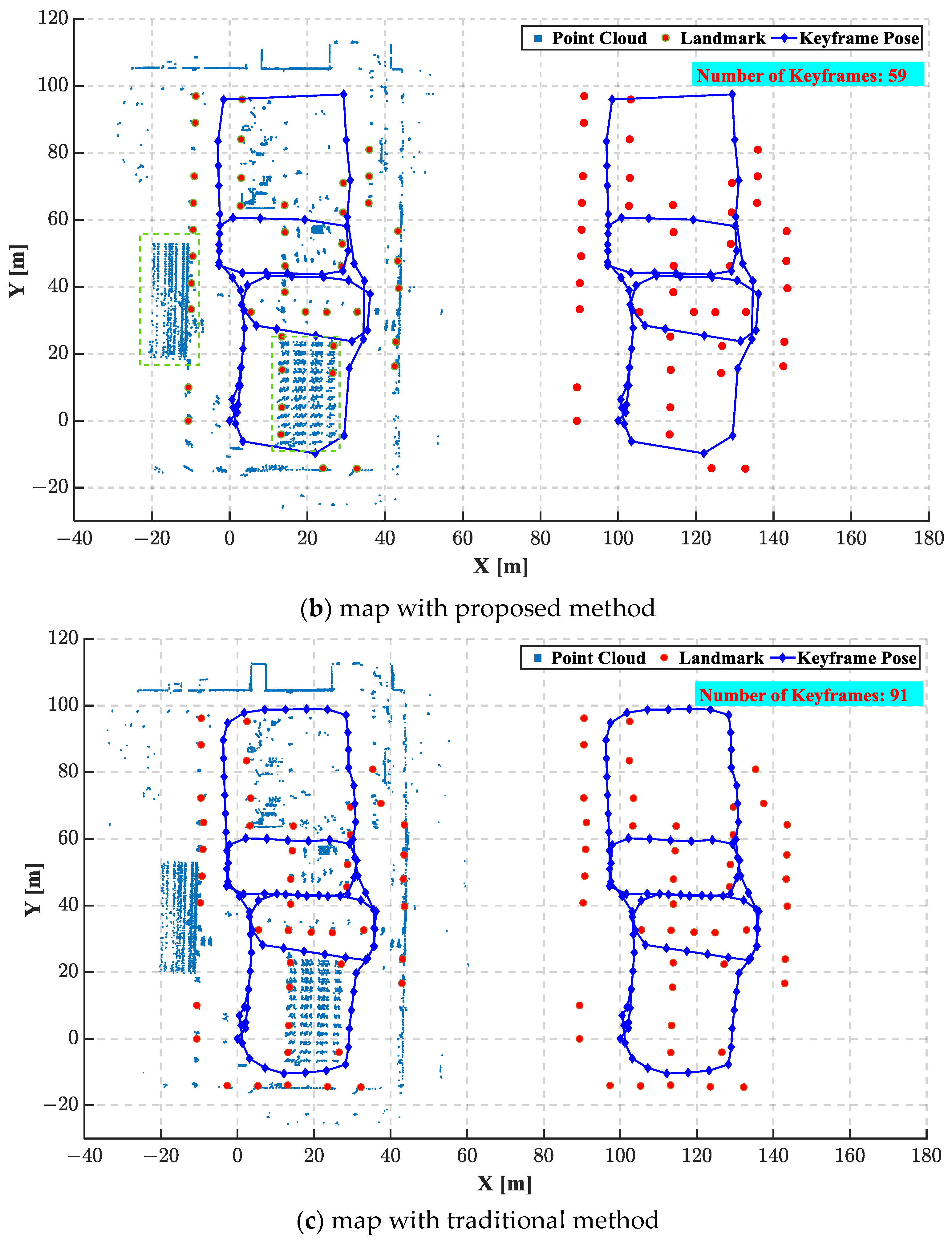
| Method | Area Error (Relative) | Point Error (Relative) | RMSE |
|---|---|---|---|
| InfoLa-SLAM | 6.44% | 1.97% | 0.31 |
| Traditional method | 9.97% | 6.34% | 0.51 |
| Metric | InfoLa-SLAM | Cartographer |
|---|---|---|
| Area error (relative to GT) | 2.9% | 5.5% |
| RMSE | 0.39 | 0.49 |
| Metric | InfoLa-SLAM | Cartographer |
|---|---|---|
| CPU load (mean) | 7.98% | 8.52% |
| CPU load (variance) | 1.29 | 12.5 |
| CPU load (peak) | 11.0% | 20.0% |
| Memory usage (mean) | 0.55% | 1.23% |
| Memory usage (variance) | 0.0001 | 0.037 |
| Memory usage (peak) | 0.57% | 1.56% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.; Dong, H.; Ye, W.; Dong, X.; Xu, S. InfoLa-SLAM: Efficient Lidar-Based Lightweight Simultaneous Localization and Mapping with Information-Based Keyframe Selection and Landmarks Assisted Relocalization. Remote Sens. 2023, 15, 4627. https://doi.org/10.3390/rs15184627
Lin Y, Dong H, Ye W, Dong X, Xu S. InfoLa-SLAM: Efficient Lidar-Based Lightweight Simultaneous Localization and Mapping with Information-Based Keyframe Selection and Landmarks Assisted Relocalization. Remote Sensing. 2023; 15(18):4627. https://doi.org/10.3390/rs15184627
Chicago/Turabian StyleLin, Yuan, Haiqing Dong, Wentao Ye, Xue Dong, and Shuogui Xu. 2023. "InfoLa-SLAM: Efficient Lidar-Based Lightweight Simultaneous Localization and Mapping with Information-Based Keyframe Selection and Landmarks Assisted Relocalization" Remote Sensing 15, no. 18: 4627. https://doi.org/10.3390/rs15184627
APA StyleLin, Y., Dong, H., Ye, W., Dong, X., & Xu, S. (2023). InfoLa-SLAM: Efficient Lidar-Based Lightweight Simultaneous Localization and Mapping with Information-Based Keyframe Selection and Landmarks Assisted Relocalization. Remote Sensing, 15(18), 4627. https://doi.org/10.3390/rs15184627