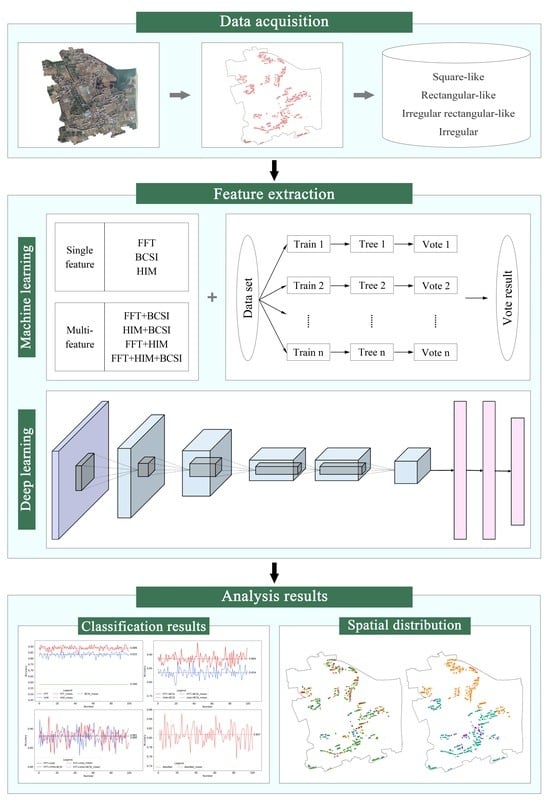
Research on the Shape Classification Method of Rural Homesteads Based on Parcel Scale—Taking Yangdun Village as an Example
Abstract
:1. Introduction
- (1)
- We introduced mature methods from other fields into homestead classification and demonstrated an effective approach for classifying homestead shapes through experimentation, including the determination of key parameters for FFT and the random forest (RF) method.
- (2)
- We conducted a numerical comparison to reveal the practicality of common shape classification methods for homesteads, encompassing four method categories and eight scenarios, including both machine learning and deep learning.
- (3)
- We conducted a comparative analysis of multiple feature extraction methods with a single classification algorithm, departing from the common practice of comparing multiple classification methods with a single feature extraction method. This approach offers insights for future research.
- (4)
- Utilizing Yangdun Village as a case study, we elucidated the spatiotemporal variation patterns in rural homestead shapes in the context of the “homesteads reform”.
2. Materials and Methods
2.1. Study Area
2.2. Data Source
- (1)
- Spatial distribution data of homesteads: This dataset includes vector data for the years 2010, 2015, and 2020. The 2010 and 2015 data were meticulously compiled parcel by parcel, utilizing Google Earth satellite imagery and on-site surveys. The 2020 vector data were obtained from the Deqing County Agriculture and Rural Bureau.
- (2)
- Remote sensing data: Our dataset includes Google Earth satellite images from 2010 and 2015, accessible at https://earth.google.com (accessed on 20 December 2021).
- (3)
- Field survey data: Field visits were conducted to determine the locations of homesteads within the study area and to document the reasons for any changes.
2.3. Construction of Homestead Patch Classification Scheme
2.3.1. Classification Scheme
2.3.2. Classification Criteria
2.4. Feature Extraction Methods and Scenario Design
2.4.1. Fast Fourier Transform Algorithms
2.4.2. Hu Invariant Moments Algorithm
2.4.3. Boyce–Clark (BC) Shape Index
2.4.4. Characteristic Scenario Design
2.5. Classification Model Construction
2.5.1. Random Forest Method
2.5.2. AlexNet Method
2.6. Accuracy Evaluation
3. Results
3.1. Effect of Different Interval Degrees of BCSI
3.2. Comparison of Classification Accuracy of Different Feature Extraction Technologies
3.2.1. Overall Accuracy
3.2.2. Between-Category Accuracy
3.3. Shape Spatiotemporal Evolution Characteristics of Homesteads in Yangdun Village
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, Z.; Zhuo, Y.; Li, G.; Bennett, R.M.; Liao, R.; Wu, C.; Wu, Y. An LADM-based model to facilitate land tenure reform of rural homesteads in China. Land Use Policy 2022, 120, 106271. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, S.; Zhao, Z.; Li, B.; Fan, B.; Zhou, G. Spatio-Temporal Features and Influencing Factors of Homesteads Expansion at Village Scale. Land 2022, 11, 1706. [Google Scholar] [CrossRef]
- Ren, Y.; Wang, Y.; Li, Z.; Zhao, Z. Spatial and temporal distribution and utilization characteristics of rural homestead resources in China. J. China Agric. Univ. 2020, 25, 175–186. [Google Scholar]
- Lin, C. Comparison and reference of rural homestead management system between China and Vietnam. World Agric. 2018, 107–113. [Google Scholar] [CrossRef]
- Xiao, W.; Gao, L. Main practices and enlightenment of high-quality management of rural houses in typical foreign countries. J. Hunan Inst. Social. 2020, 21, 78–82. [Google Scholar] [CrossRef]
- Li, J.; Zhang, J. A morphing method for smooth area features based on Fourier transform. Geomat. Inf. Sci. Wuhan Univ. 2017, 42, 1104–1109. [Google Scholar] [CrossRef]
- Sui, K.; Kim, H.-G. Research on application of multimedia image processing technology based on wavelet transform. Eurasip J. Image Video Process. 2019, 2019, 24. [Google Scholar] [CrossRef]
- Liu, Y.K.; Žalik, B. An efficient chain code with Huffman coding. Pattern Recognit. 2004, 38, 553–557. [Google Scholar] [CrossRef]
- Shen, W.; Du, C.; Jiang, Y.; Zeng, D.; Zhang, Z. Bag of Shape Features with a learned pooling function for shape recognition. Pattern Recognit. Lett. 2018, 106, 33–40. [Google Scholar] [CrossRef]
- Yu, Y.; He, K.; Wu, F. Graph convolution neural network method for shape classification of areal settlements. Acta Geod. Et Cartogr. Sin. 2022, 51, 2390–2402. [Google Scholar] [CrossRef]
- Liu, L.; Zou, Y.; Chen, B. Review on Research Progress of 2D Shape Description and Classification. Comput. Eng. Appl. 2021, 57, 39–47. [Google Scholar] [CrossRef]
- Li, Y.; Lu, X.; Yan, H.; Wang, W.; Li, P. A Skeleton-Line-Based Graph Convolutional Neural Network for Areal Settlements’ Shape Classification. Appl. Sci. 2022, 12, 10001. [Google Scholar] [CrossRef]
- Xiong, H.; Zheng, B.; Jia, L. Urban Space Expansion in China under the Interaction between the Driving Force and the Restriction. Econ. Geogr. 2016, 36, 82–88. [Google Scholar] [CrossRef]
- Licciardi, G.A.; Villa, A.; Mura, M.D.; Bruzzone, L.; Chanussot, J.; Benediktsson, J.A. Retrieval of the Height of Buildings From WorldView-2 Multi-Angular Imagery Using Attribute Filters and Geometric Invariant Moments. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 71–79. [Google Scholar] [CrossRef]
- Yan, X.; Ai, T.; Yang, M. A simplification of residential feature by the shape cognition and template matching method. Acta Geod. Et Cartogr. Sin. 2016, 45, 874. [Google Scholar] [CrossRef]
- Yan, X.; Ai, T.; Zhang, X. Template matching and simplification method for building features based on shape cognition. ISPRS Int. J. Geo-Inf. 2017, 6, 250. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, Y.; Nie, G.; Cheng, H.; Yang, X.; Chen, X.; Gross, L. Building Extraction and Floor Area Estimation at the Village Level in Rural China Via a Comprehensive Method Integrating UAV Photogrammetry and the Novel EDSANet. Remote Sens. 2022, 14, 5175. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Abdel-Hamid, O.; Mohamed, A.-r.; Jiang, H.; Deng, L.; Penn, G.; Yu, D. Convolutional neural networks for speech recognition. IEEE/ACM Trans. Audio Speech Lang. Process. (TASLP) 2014, 22, 1533–1545. [Google Scholar] [CrossRef]
- Yan, X.; Ai, T.; Yang, M.; Yin, H. A graph convolutional neural network for classification of building patterns using spatial vector data. ISPRS J. Photogramm. Remote Sens. 2019, 150, 259–273. [Google Scholar] [CrossRef]
- Yang, M.; Kong, B.; Dang, R.; Yan, X. Classifying urban functional regions by integrating buildings and points-of-interest using a stacking ensemble method. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102753. [Google Scholar] [CrossRef]
- Meng, C.; Song, Y.; Ji, J.; Jia, Z.; Zhou, Z.; Gao, P.; Liu, S. Automatic classification of rural building characteristics using deep learning methods on oblique photography. In Building Simulation; Tsinghua University Press: Beijing, China, 2022; pp. 1161–1174. [Google Scholar]
- Yan, X.; Ai, T.; Yang, M.; Tong, X. Graph convolutional autoencoder model for the shape coding and cognition of buildings in maps. Int. J. Geogr. Inf. Sci. 2021, 35, 490–512. [Google Scholar] [CrossRef]
- Jiao, Y.Y.; Liu, P.Z.; Liu, A.; Liu, S. Map building shape classification method based on Alexne. J. Geo-Inf. Sci. 2022, 24, 2333–2341. [Google Scholar] [CrossRef]
- Yang, B. The Reformer Deqing②|Createdmultiple “National Firsts” Land Reform Brought about Great Changes in the Mountains and Villages. 2019. Available online: https://zj.zjol.com.cn/news.html?id=1281250 (accessed on 15 November 2021).
- Bhargava, A.; Bansal, A. Fruits and vegetables quality evaluation using computer vision: A review. J. King Saud Univ.-Comput. Inf. Sci. 2021, 33, 243–257. [Google Scholar] [CrossRef]
- Khoje, S.; Bodhe, S. Performance comparison of Fourier transform and its derivatives as shape descriptors for mango grading. Int. J. Comput. Appl. 2012, 53, 17–22. [Google Scholar] [CrossRef]
- Hu, M.K. Visual pattern recognition by moment invariants. IRE Trans. Inf. Theory 1962, 8, 179–187. [Google Scholar] [CrossRef]
- Flusser, J.; Suk, T. Pattern recognition by affine moment invariants. Pattern Recognit. 1993, 26, 167–174. [Google Scholar] [CrossRef]
- Boyce, R.R.; Clark, W.A. The concept of shape in geography. Geogr. Rev. 1964, 54, 561–572. [Google Scholar] [CrossRef]
- Wang, X.; Liu, J.; Zhuang, D.; Jiang, Y.; Zhang, H.; Yu, R. Spatial-temporal changes of the shapes of Chinese cities. Resour. Sci 2005, 27, 20–25. [Google Scholar] [CrossRef]
- Wang, T.; Hui, Y.; Rui, P.; Ying, S. Morphological types division and its formation of dispersed rural settlements based on Alpha Shape: A case of Long Town, Mizhi County. Arid Land Geogr. 2022, 45, 946–954. [Google Scholar]
- Zhang, P.; Hu, S. Fine crop classification by remote sensing in complex planting areas based on field parcel. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2019, 35, 125–134. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Li, G.; Li, H.; Wan, H.; Li, L. Research on determinants of species richness in xinjiang based on random forest appraoch. China Environ. Sci. 2021, 41, 941–950. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.C., Jr.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef] [PubMed]
- Hu, Q. Research on Crop Remote Sensing Recognition Method Based on Time Series MODIS Images. Ph.D. Thesis, Chinese Academy of Agricultural Sciences, Beijing, China, 2018. [Google Scholar]
- Lin, Z.; Yao, J.; Su, X. Extracting planting information of early rice using MODIS index and random forest in Jiangxi Province, China. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2022, 38, 197–205. [Google Scholar]
- Wang, Q.; Song, G. Changes of cultivated land pattern and its spatial driving factors in the typical regions of Lower Liaohe Plain. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2021, 37, 275–283. [Google Scholar] [CrossRef]
- Huang, J.; Liu, H.; Ning, J.; Ouyang, X.; Zang, H. Study of Adaptability of the Primary Afforestation Species in Chongyi County, Jiangxi Province Based on Random Forest. For. Resour. Manag. 2022, 117–125. [Google Scholar] [CrossRef]
- Qing, J. Remote Sensing Evaluation of Rice Planting System in Jiangxi Province. Master’s Thesis, Jiangxi Normal University, Nanchang, China, 2020. [Google Scholar]
- Yang, B.; Chen, S.; Yu, H.; Qin, A. Remote sensing estimation of rice yied based on random forest regression method. J. China Agric. Univ. 2020, 25, 26–34. [Google Scholar] [CrossRef]
- Xue, J.; Zong, Y.; Yang, Z. Gesture recognition based on improved YCBCR space and multi-feature integration. Comput. Appl. Softw. 2016, 33, 151–155. [Google Scholar] [CrossRef]
- Chen, B.; Rao, H.; Liu, M. Shape feature recognition of camellia fruit basd on Fourier descriptors and Hu invariant moments. Zhejiang Agric. Sci. 2020, 61, 1876–1880. [Google Scholar] [CrossRef]
- Lo, C. Changes in the shapes of Chinese Cities, 1934–1974. Prof. Geogr. 2005, 32, 173–183. [Google Scholar] [CrossRef]
- Pan, J.; Dai, W. Spatial-Temporal Characteristics in Urban Morphology of Majior Cities in China during 1990–2010. Econ. Geogr. 2015, 35, 44–52. [Google Scholar] [CrossRef]
- Wu, C.; Wang, Z.; Hu, S.; Lepine, J.; Na, X.; Ainalis, D.; Stettler, M. An Automated Machine-Learning Approach for Road Pothole Detection Using Smartphone Sensor Data. Sensors 2020, 20, 5564. [Google Scholar] [CrossRef]
- Chauhan, N.K.; Singh, K. Performance Assessment of Machine Learning Classifiers Using Selective Feature Approaches for Cervical Cancer Detection. Wirel. Pers. Commun. 2022, 124, 2335–2366. [Google Scholar] [CrossRef]
- Sedik, A.; Marey, M.; Mostafa, H. WFT-Fati-Dec: Enhanced Fatigue Detection AI System Based on Wavelet Denoising and Fourier Transform. Appl. Sci. 2023, 13, 2785. [Google Scholar] [CrossRef]
- Yang, K.; Zhang, H.; Wang, F.; Lai, R. Extraction of Broad-Leaved Tree Crown Based on UAV Visible Images and OBIA-RF Model: A Case Study for Chinese Olive Trees. Remote Sens. 2022, 14, 2469. [Google Scholar] [CrossRef]











| Serial Number | ϕ1 | ϕ2 | ϕ3 | ϕ4 | ϕ5 | ϕ6 | ϕ7 |
|---|---|---|---|---|---|---|---|
| 1 | 2.838 | 5.780 | 11.959 | 12.404 | 24.587 | 15.316 | 25.799 |
| 2 | 2.845 | 5.871 | 10.072 | 10.568 | 21.053 | 14.794 | 21.026 |
| 3 | 2.747 | 5.560 | 10.102 | 10.303 | 20.506 | 13.094 | 21.696 |
| 4 | 3.114 | 6.828 | 10.819 | 11.853 | 23.374 | 15.518 | 23.309 |
| 5 | 3.107 | 6.810 | 10.695 | 11.603 | 22.807 | 15.089 | 23.072 |
| 6 | 2.758 | 5.601 | 10.256 | 10.359 | 20.668 | 13.228 | 21.638 |
| 7 | 3.135 | 7.018 | 10.976 | 12.625 | 24.806 | 16.533 | 24.466 |
| 8 | 3.172 | 8.412 | 13.285 | 14.154 | 27.882 | 18.661 | 28.578 |
| 9 | 3.031 | 6.394 | 10.753 | 11.509 | 22.810 | 15.314 | 22.773 |
| 10 | 2.961 | 6.137 | 10.674 | 11.207 | 22.153 | 14.286 | 22.933 |
| Feature Category | Feature Scenarios | Feature Variable | Feature Size |
|---|---|---|---|
| FFT | FS1 | The first 40 descriptors of the FFT | 40 |
| HIM | FS2 | Seven moments of HIM | 7 |
| BCSI | FS3 | Value of BCSI | 1 |
| FFT + BCSI | FS4 | The first 40 descriptors of the FFT, value of BCSI | 41 |
| HIM + BCSI | FS5 | Seven moments of HIM, value of BCSI | 8 |
| FFT + HIM | FS6 | The first 40 descriptors of the FFT, seven moments of HIM | 47 |
| FFT + HIM + BCSI | FS7 | The first 40 descriptors of the FFT, seven moments of HIM, value of BCSI | 48 |
| Homestead Shape Category | Classification Accuracy | Category 1 | Category 2 | Category 3 | Category 4 |
|---|---|---|---|---|---|
| FFT | Accuracy (%) | 84.6 | 91.3 | 83.5 | 89.3 |
| Recall (%) | 84.9 | 90.7 | 83.9 | 91.4 | |
| HIM | Accuracy (%) | 79.5 | 87.7 | 73.4 | 79.7 |
| Recall (%) | 84.7 | 90 | 65.9 | 73.6 | |
| BCSI | Accuracy (%) | 75 | 58.2 | 48.1 | 47.2 |
| Recall (%) | 66.7 | 79.4 | 33 | 31.2 | |
| FFT + BCSI | Accuracy (%) | 85.4 | 91.7 | 82.2 | 87 |
| Recall (%) | 86 | 90.7 | 83.4 | 88.5 | |
| HIM + BCSI | Accuracy (%) | 80.6 | 87.8 | 73.1 | 79.6 |
| Recall (%) | 84.9 | 90 | 66.1 | 74.4 | |
| FFT + HIM | Accuracy (%) | 85.4 | 91.5 | 81.7 | 85.9 |
| Recall (%) | 85.7 | 90.8 | 82.4 | 87.9 | |
| FFT + HIM + BCSI | Accuracy (%) | 84.6 | 91.7 | 80.6 | 86.8 |
| Recall (%) | 86.9 | 90.5 | 82.5 | 85.7 | |
| AlexNet | Accuracy (%) | 77.6 | 91.5 | 60.0 | 61.2 |
| Recall (%) | 76.0 | 84.0 | 74.9 | 70.6 |
| Shape Category | Number of Homesteads | ||
|---|---|---|---|
| Year 2010 | Year 2015 | Year 2020 | |
| Square-like | 144 | 145 | 48 |
| Rectangular-like | 490 | 472 | 316 |
| Irregular rectangular-like | 154 | 160 | 152 |
| Irregular | 89 | 94 | 73 |
| Total number | 877 | 871 | 589 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Fan, B.; Li, H.; Liu, Y.; Wei, R.; Liu, S. Research on the Shape Classification Method of Rural Homesteads Based on Parcel Scale—Taking Yangdun Village as an Example. Remote Sens. 2023, 15, 4763. https://doi.org/10.3390/rs15194763
Zhang J, Fan B, Li H, Liu Y, Wei R, Liu S. Research on the Shape Classification Method of Rural Homesteads Based on Parcel Scale—Taking Yangdun Village as an Example. Remote Sensing. 2023; 15(19):4763. https://doi.org/10.3390/rs15194763
Chicago/Turabian StyleZhang, Jie, Beilei Fan, Hao Li, Yunfei Liu, Ren Wei, and Shengping Liu. 2023. "Research on the Shape Classification Method of Rural Homesteads Based on Parcel Scale—Taking Yangdun Village as an Example" Remote Sensing 15, no. 19: 4763. https://doi.org/10.3390/rs15194763
APA StyleZhang, J., Fan, B., Li, H., Liu, Y., Wei, R., & Liu, S. (2023). Research on the Shape Classification Method of Rural Homesteads Based on Parcel Scale—Taking Yangdun Village as an Example. Remote Sensing, 15(19), 4763. https://doi.org/10.3390/rs15194763