Close-Range Transmission Line Inspection Method for Low-Cost UAV: Design and Implementation
Abstract
:1. Introduction
- A novel low-cost transmission line close-range inspection method using a GNSS receiver, RGB camera, and mm-wave radar is proposed. Line identification provides the relative distance and heading deviation of the UAV to the transmission line. The relative distance is further processed with the UAV states to improve robustness to identification failures. The mm-wave radar provides the relative horizontal distance. The relative information ensures that the UAV can fly along the transmission line within close range;
- Heading correction and two correction modules, waypoint correction and auxiliary controller, are proposed to ensure that the UAV can always maintain its position above the line. The waypoint correction solves the problem of the deviation between the planned mission and actual line position, caused by the low GNSS receiver accuracy. The auxiliary controller copes with the unknown disturbances during inspection, ensuring that the transmission line is always within the capture area;
- Based on the developed UAV, the proposed method was finally verified in actual flight in a 10 kV energized transmission line environment; the verification process can be found at https://www.youtube.com/watch?v=jwAD2eolVRI (accessed on 5 October 2023). The UAV could fly along the transmission line during the experiment and capture HD images. Hence, the proposed low-cost method can be practically applied to transmission line inspection tasks.
2. Problem Statement and System Overview
2.1. Problem Statement
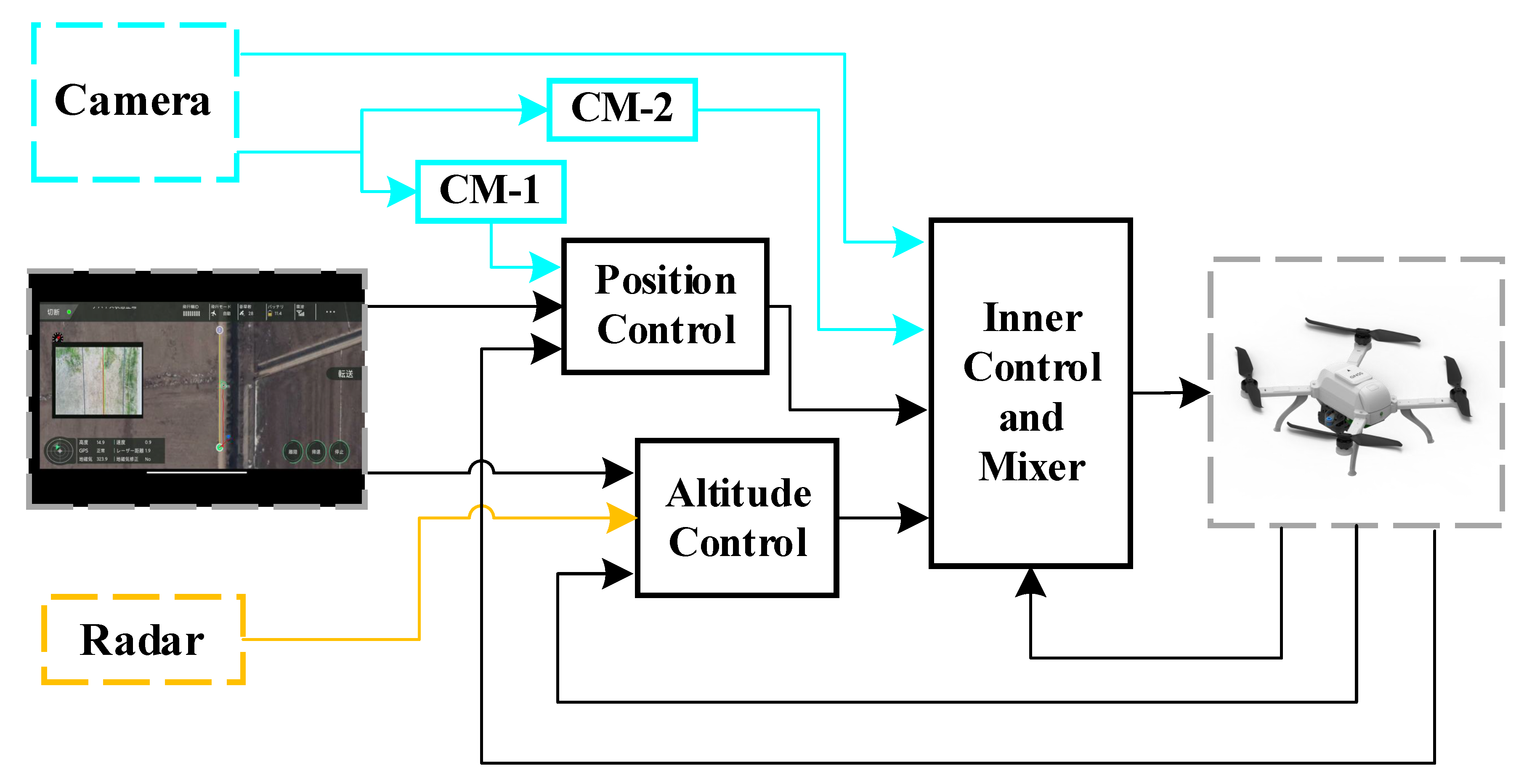
2.2. System Overview
3. Transmission Line Position Estimation
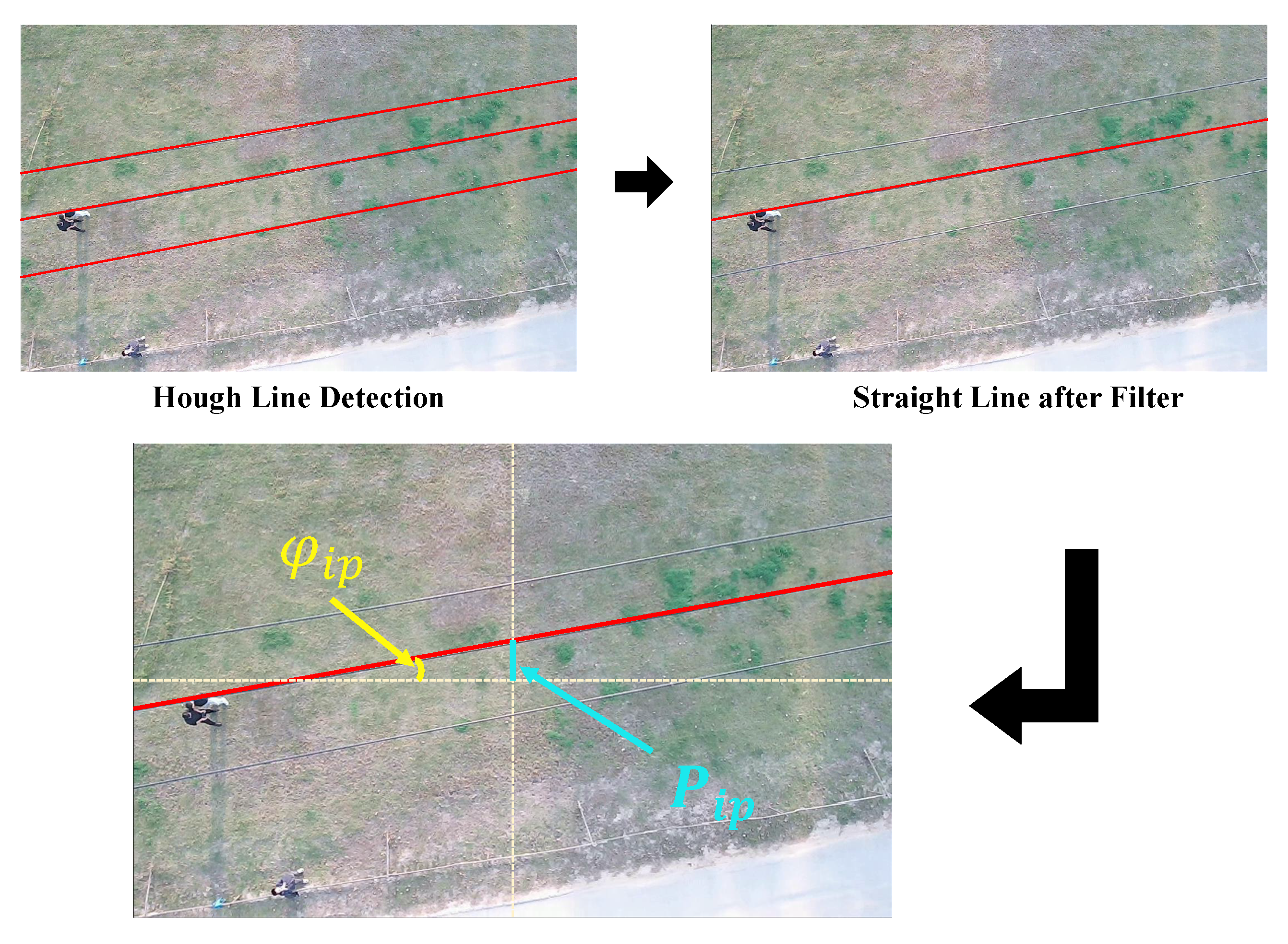
3.1. Transmission Line Identification
- The transmission lines from the same tower are made of the same material and have similar characteristics.
- The UAV’s heading should be consistent with the direction of the line; the transmission lines are parallel and share the same direction. In cases of significant direction changes in the transmission line, additional waypoints can be included. This involves dividing the line into multiple directions of unchanged segments for sequential inspection.
- In unique situations, such as tilted cameras, the transmission line may coincide and intersect.
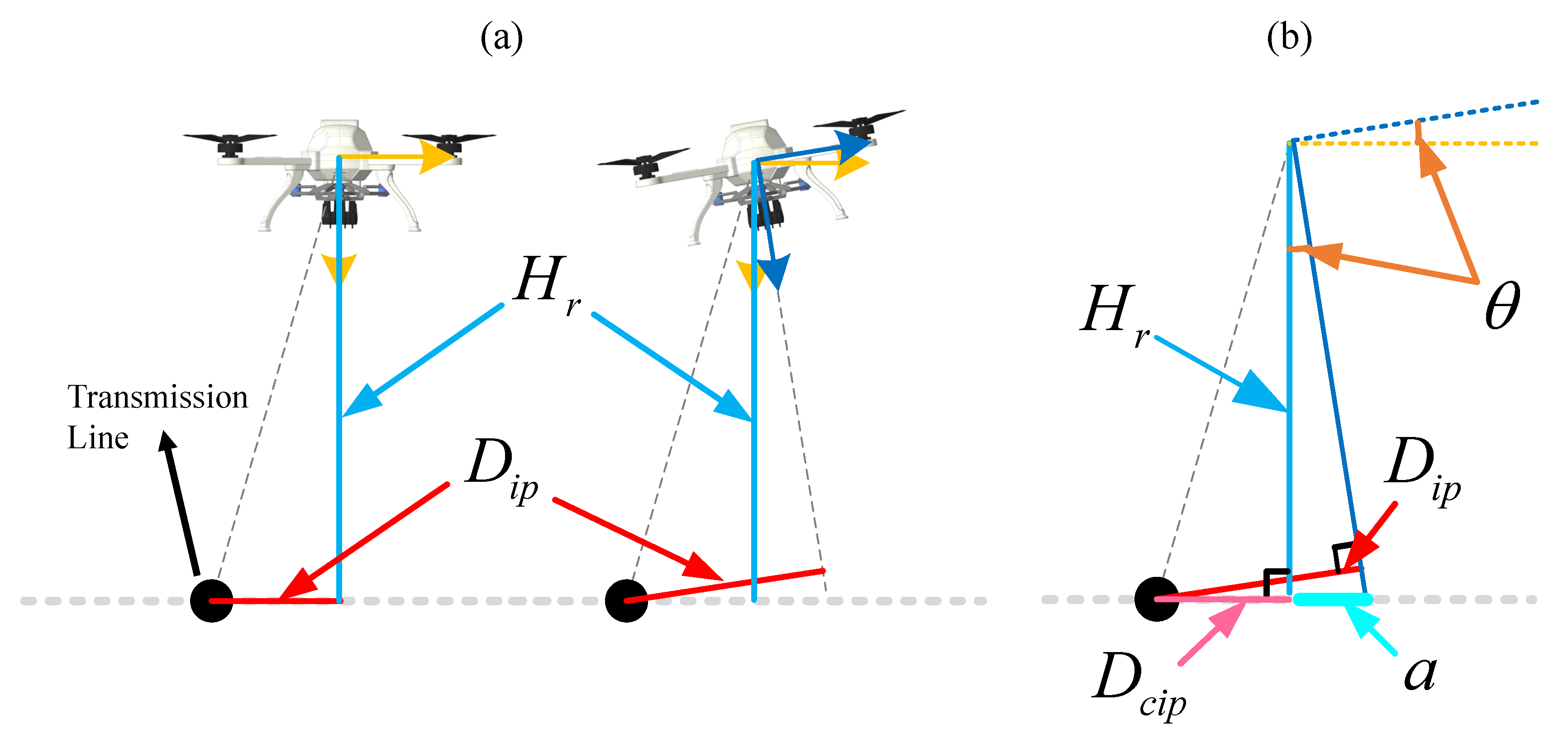
3.2. Transmission Line Distance Conversion
3.3. Transmission Line Position Estimation
4. Transmission Line Inspection System
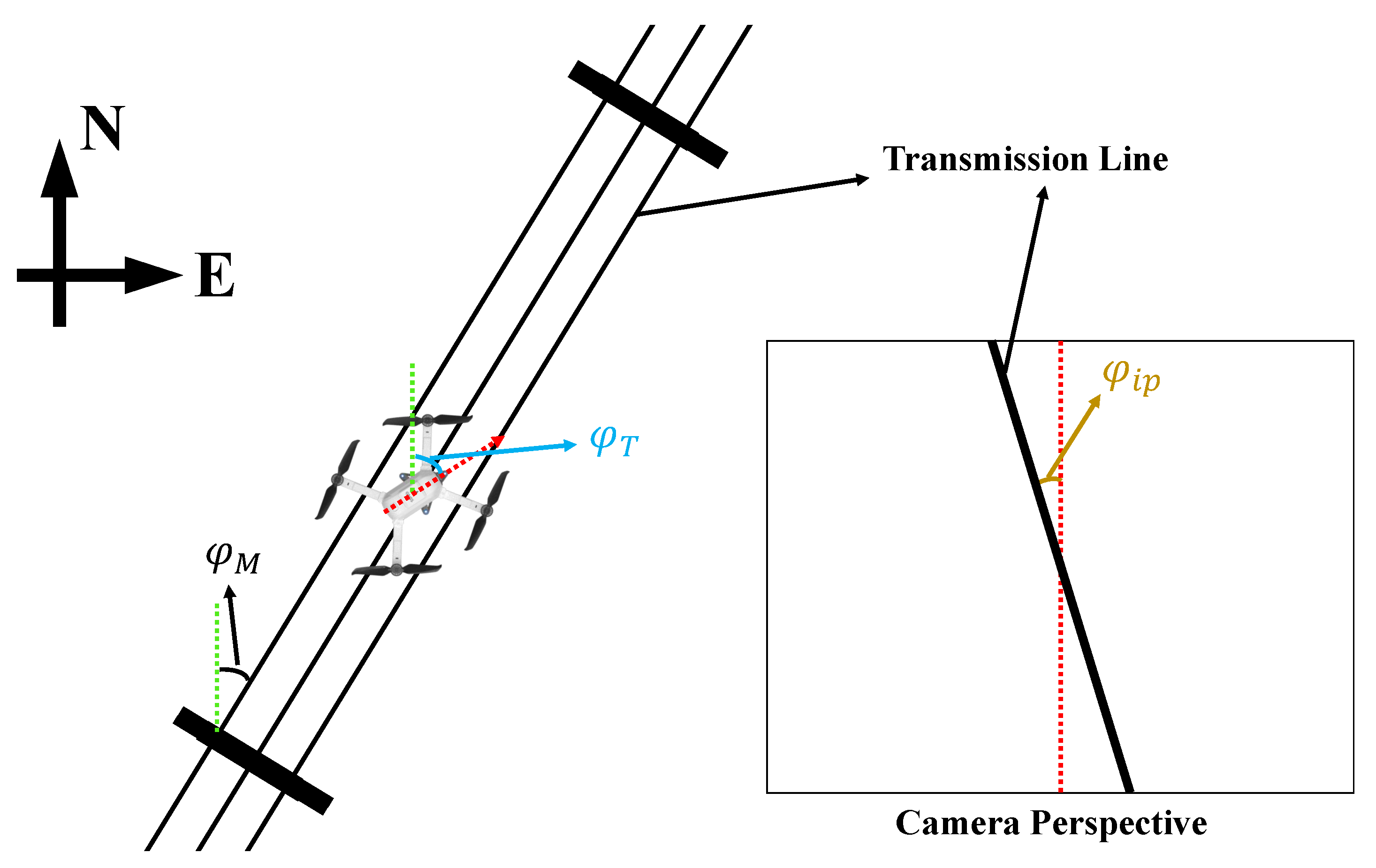
4.1. Heading Correction
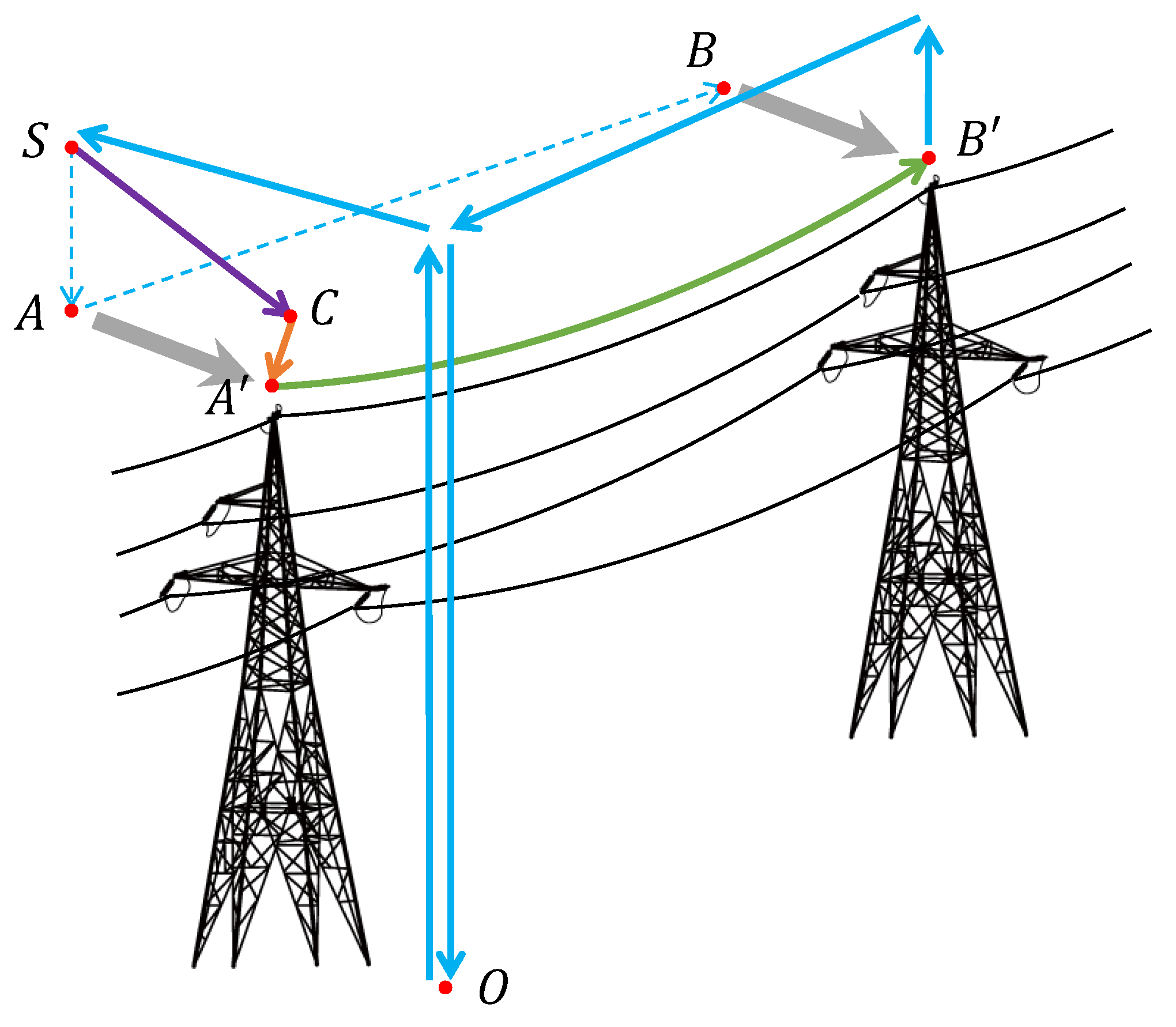
4.2. Correction Module 1: Waypoint Correction
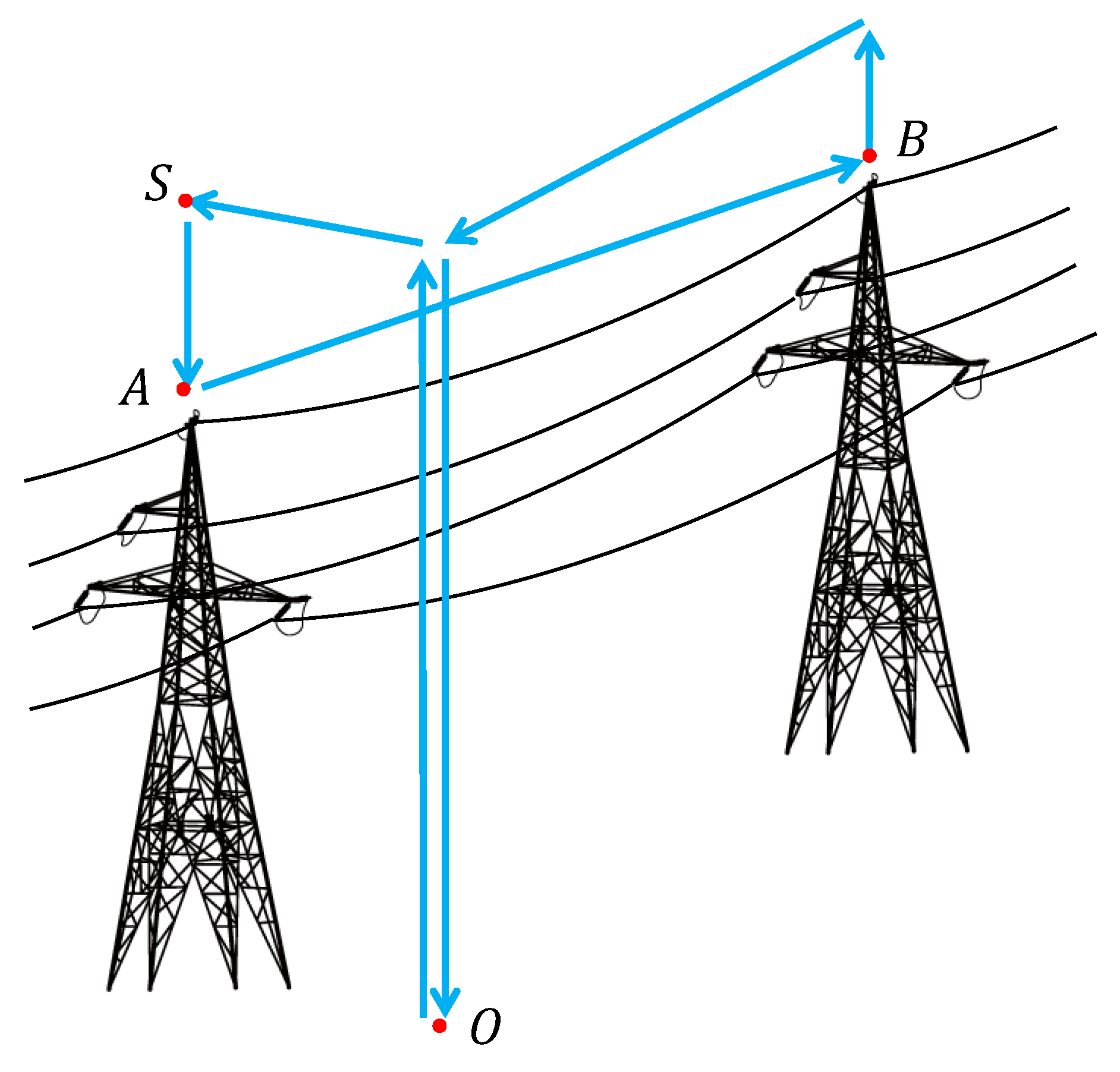
- Case 1: The planned mission trajectory does not match the actual line position. This situation will be further aggravated by the positioning deviation of the UAV’s sensors and the measurement deviation of the start and endpoints of the transmission line.
- Case 2: The UAV flies from A to B without considering external interferences; if the UAV deviates from the trajectory due to wind interference, line information will be lost, leading to incomplete inspection results.
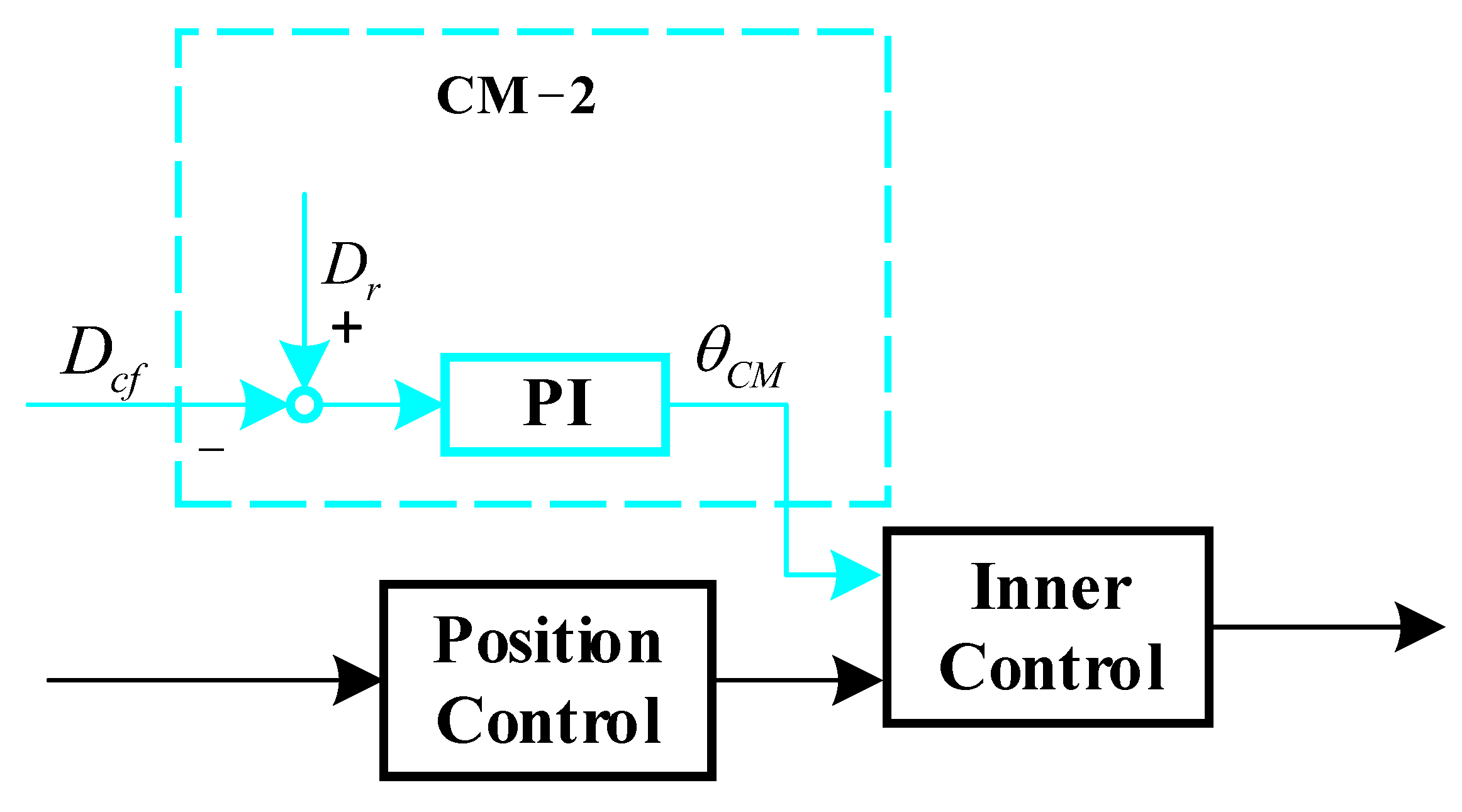
4.3. Correction Module 2: Auxiliary Controller
5. Experiment and Verification
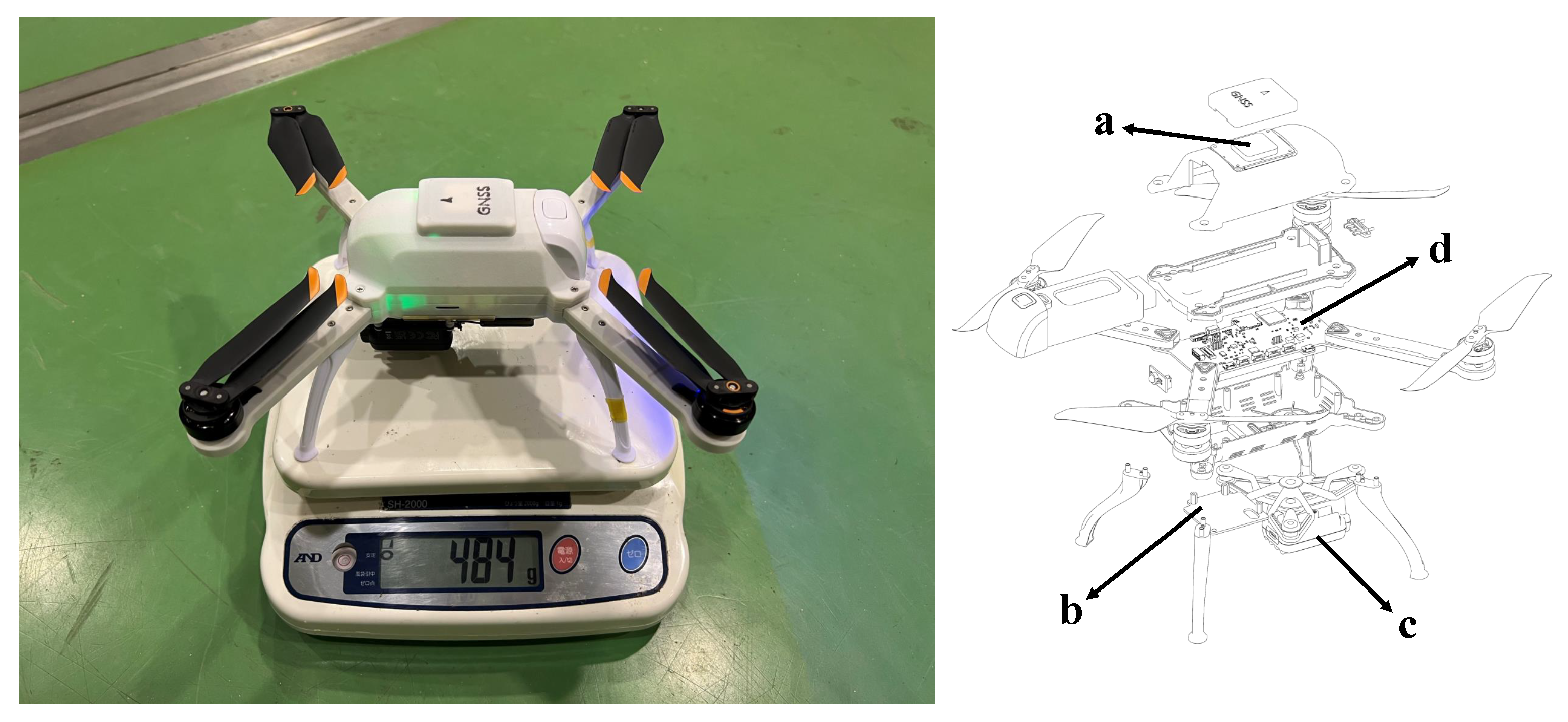
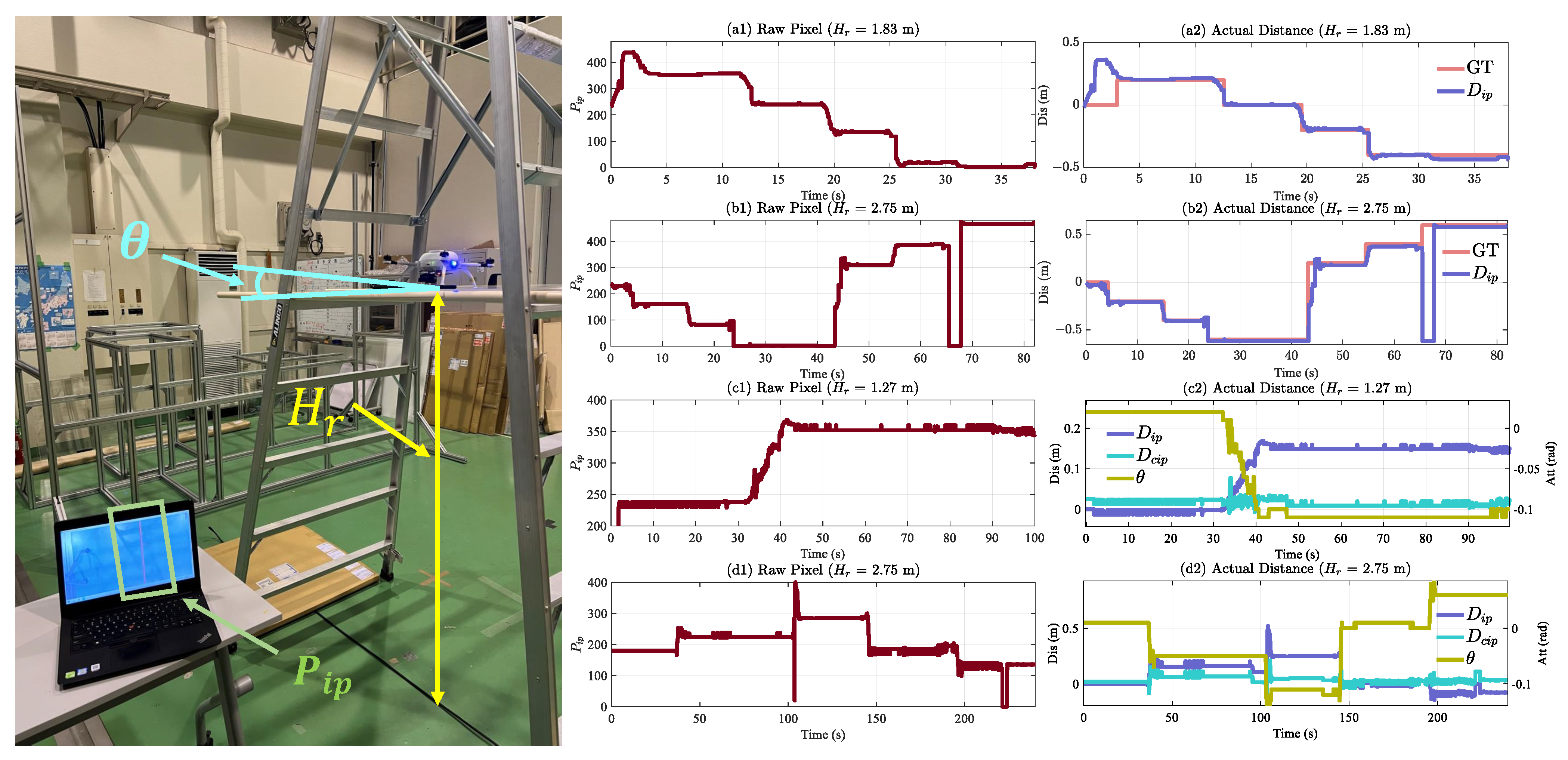
5.1. Validation Platform
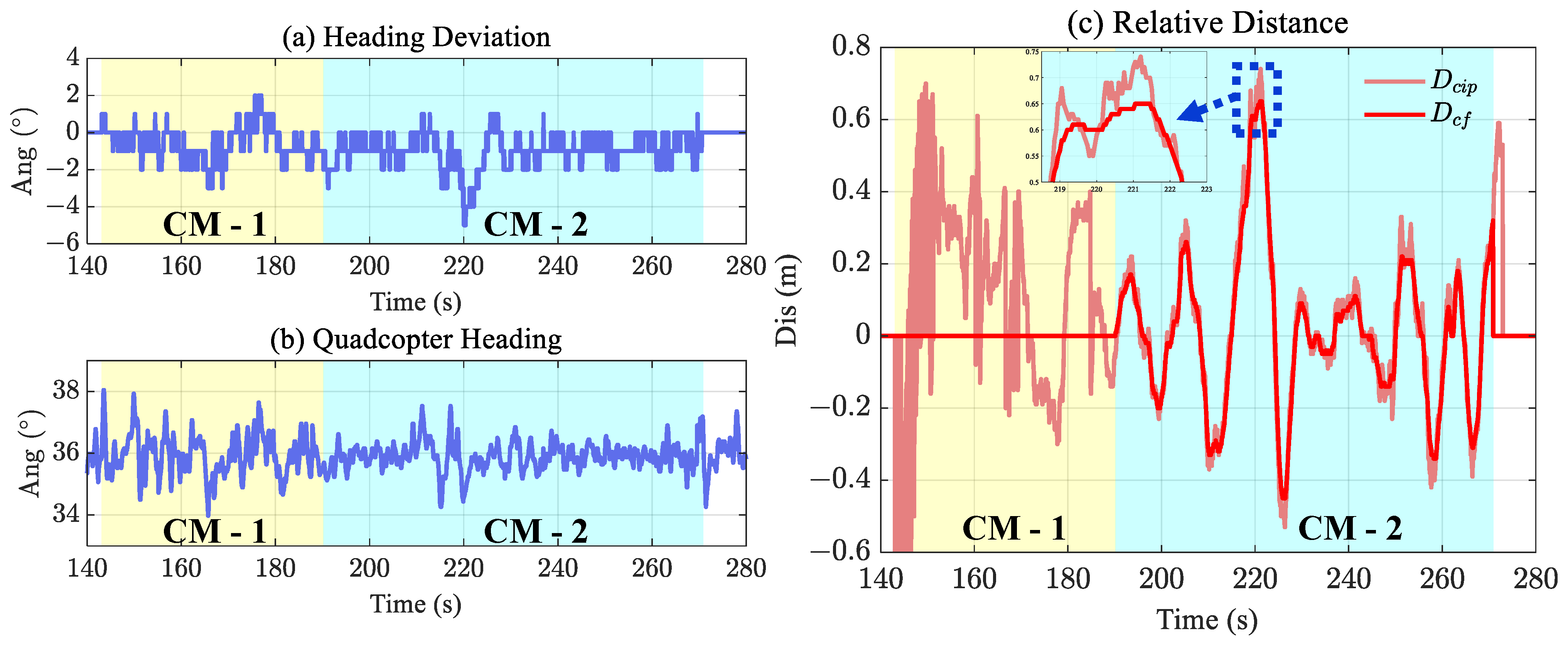
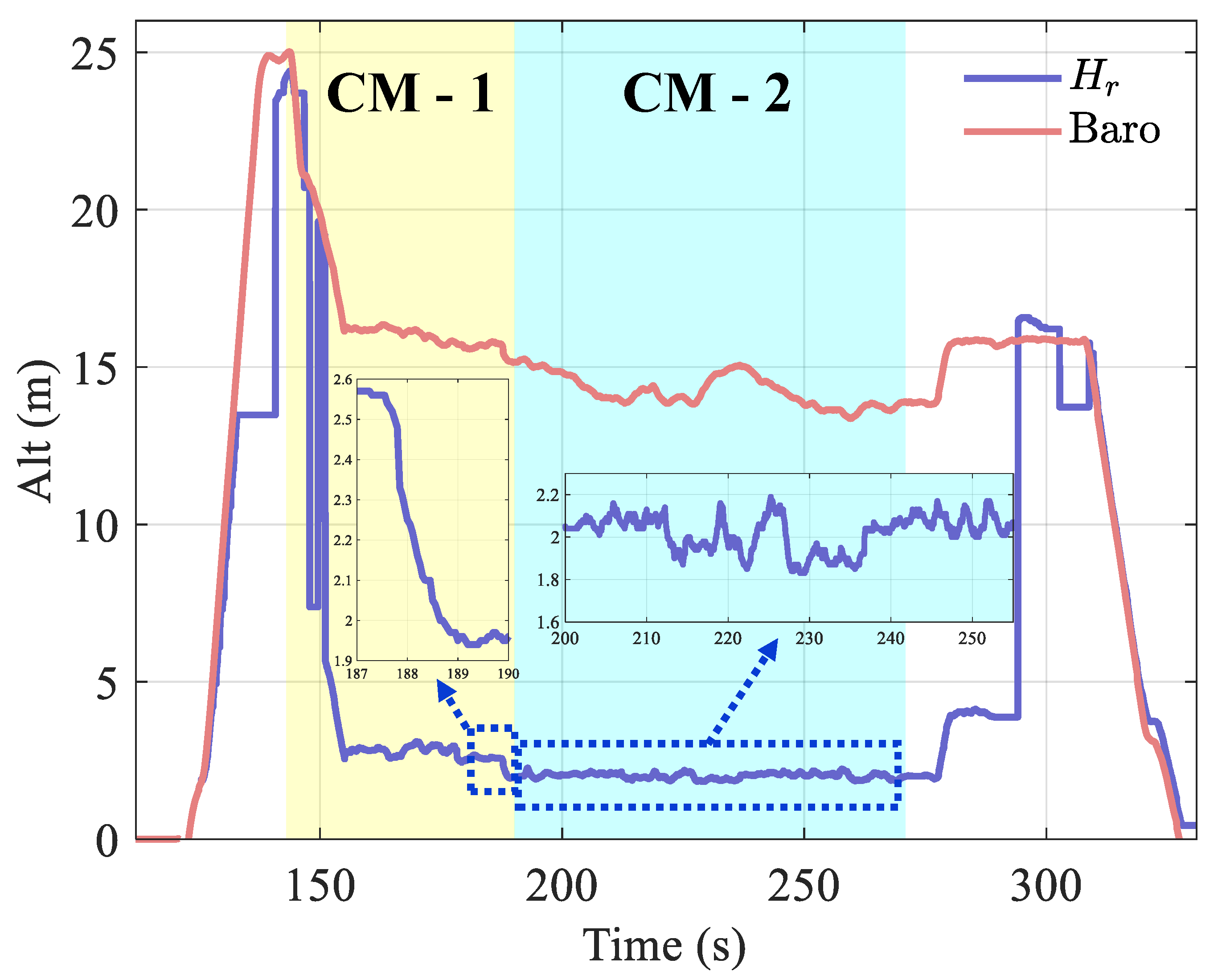
5.2. Relative Distance Verification
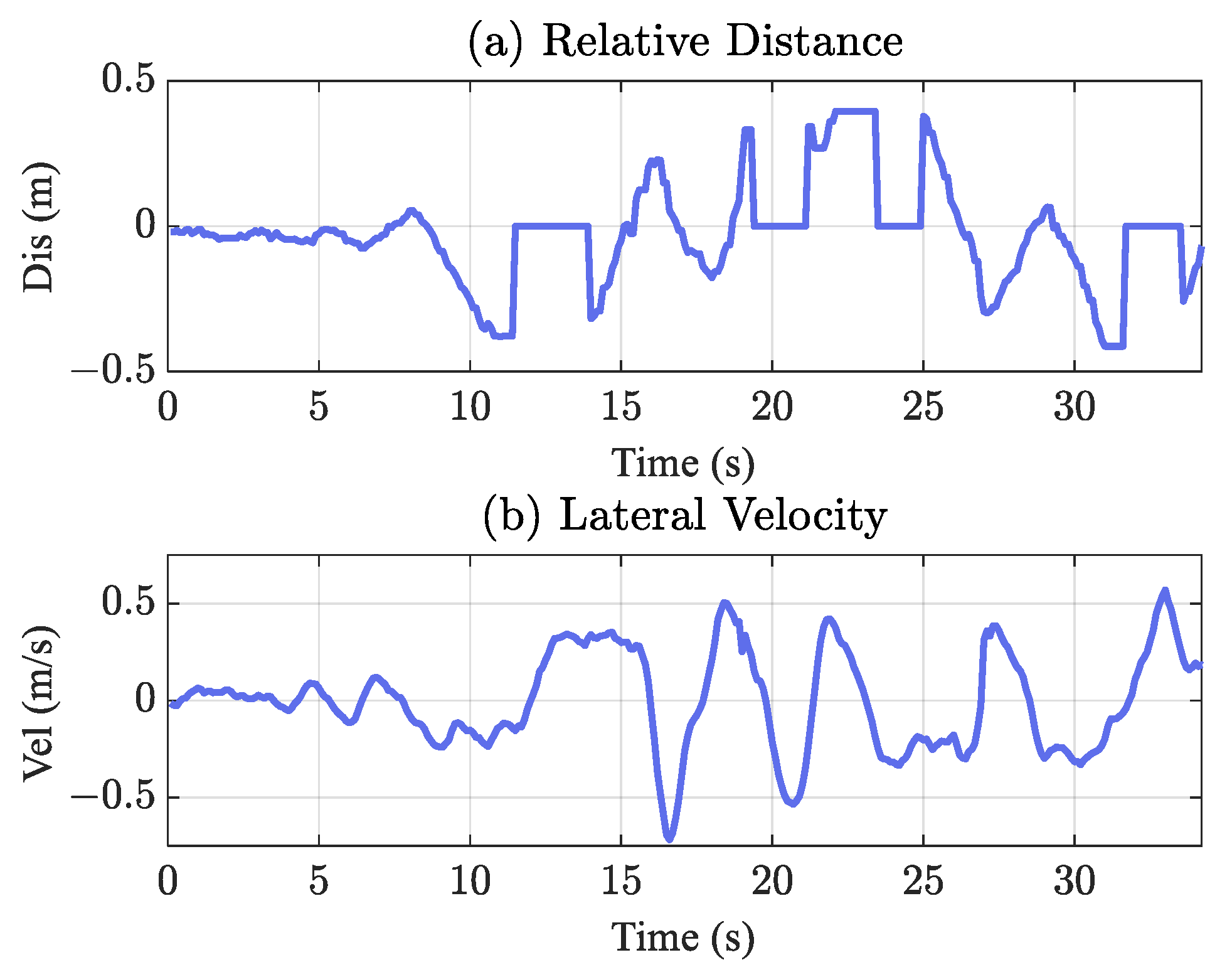
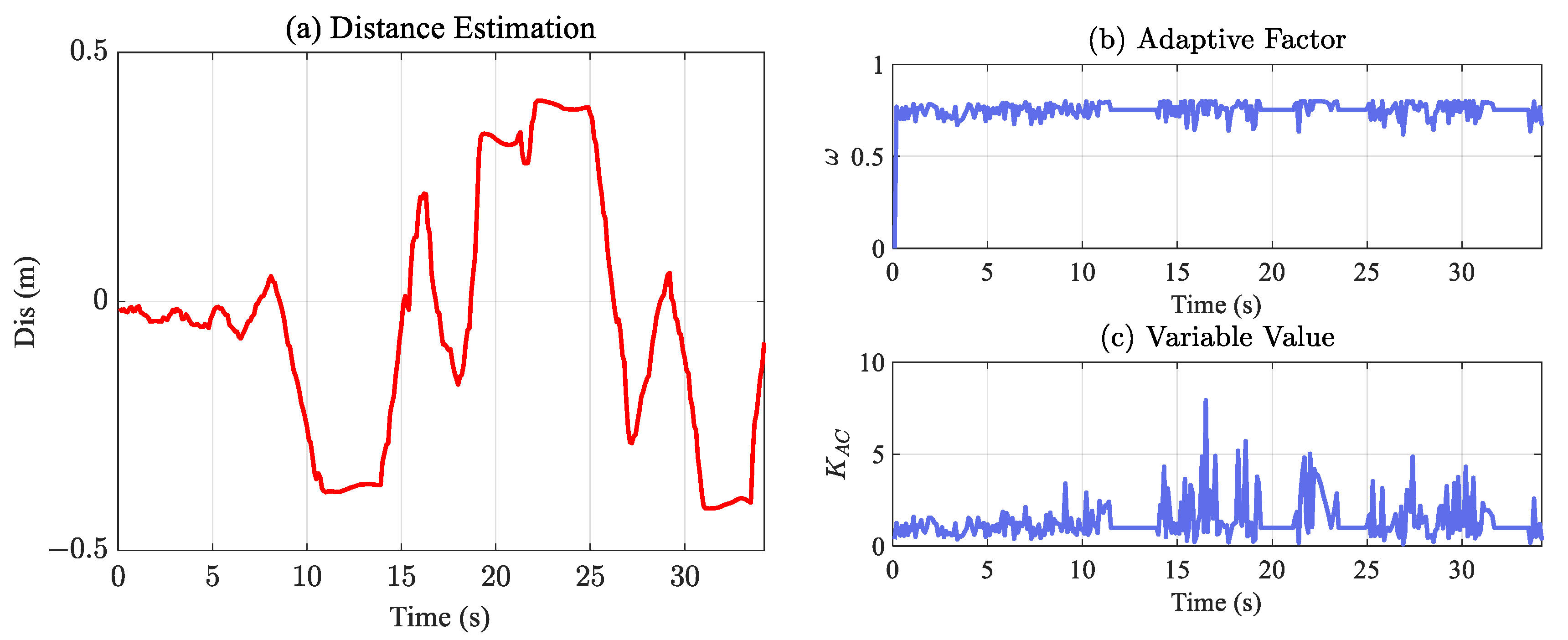
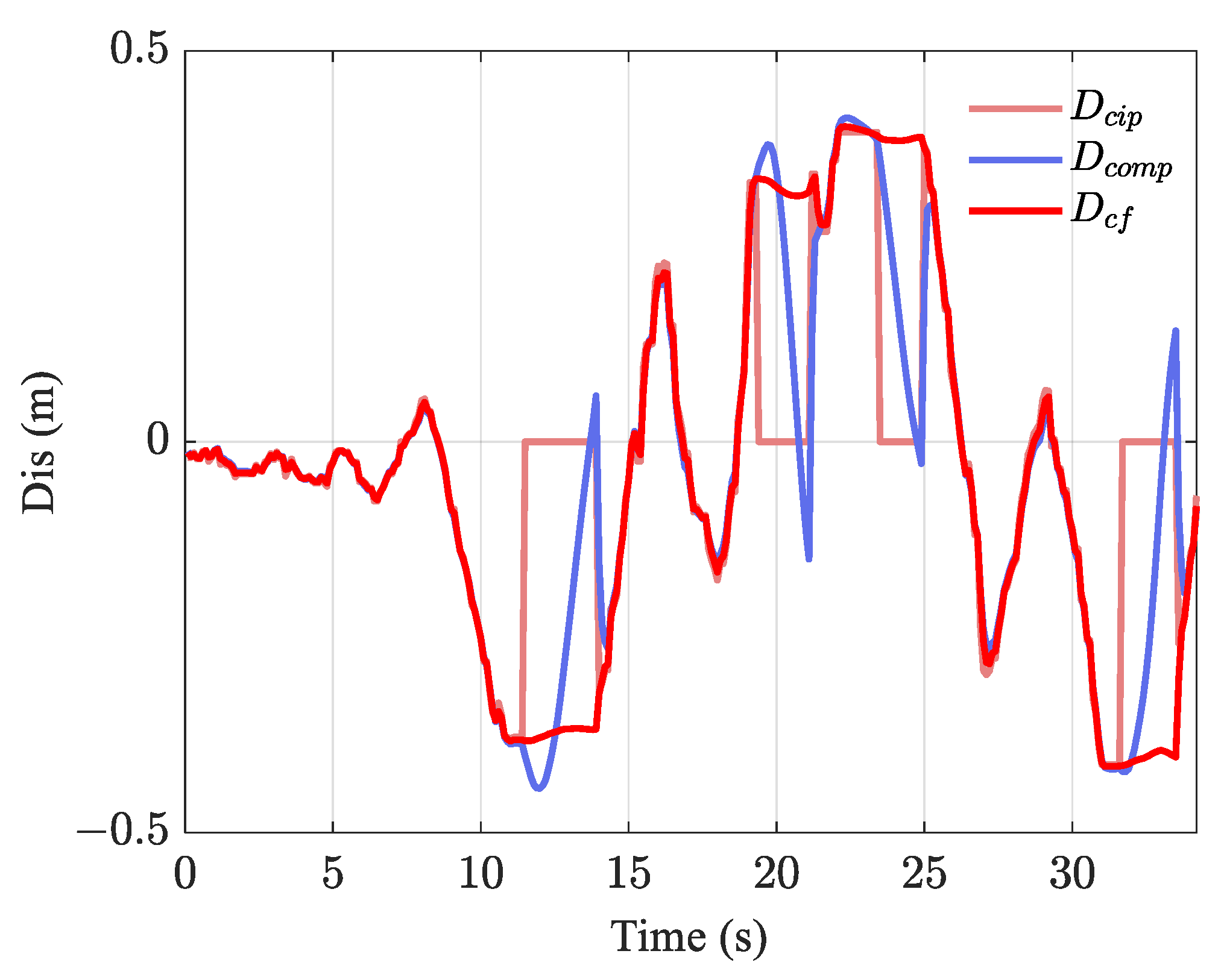
5.3. Adaptive Complementary Filter Verification
5.4. Heading Correction Verification
5.5. Transmission Line Inspection Application
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Katrasnik, J.; Pernus, F.; Likar, B. A survey of mobile robots for distribution power line inspection. IEEE Trans. Power Deliv. 2009, 25, 485–493. [Google Scholar] [CrossRef]
- Takaya, K.; Ohta, H.; Kroumov, V.; Shibayama, K.; Nakamura, M. Development of UAV system for autonomous power line inspection. In Proceedings of the 2019 23rd International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 9–11 October 2019; pp. 762–767. [Google Scholar]
- Savva, A.; Zacharia, A.; Makrigiorgis, R.; Anastasiou, A.; Kyrkou, C.; Kolios, P.; Panayiotou, C.; Theocharides, T. ICARUS: Automatic autonomous power infrastructure inspection with UAVs. In Proceedings of the 2021 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 15–18 June 2021; pp. 918–926. [Google Scholar]
- Luque-Vega, L.F.; Castillo-Toledo, B.; Loukianov, A.; Gonzalez-Jimenez, L.E. Power line inspection via an unmanned aerial system based on the quadrotor helicopter. In Proceedings of the MELECON 2014—2014 17th IEEE Mediterranean Electrotechnical Conference, Beirut, Lebanon, 13–16 April 2014; pp. 393–397. [Google Scholar]
- Jiang, S.; Jiang, W.; Huang, W.; Yang, L. UAV-based oblique photogrammetry for outdoor data acquisition and offsite visual inspection of transmission line. Remote Sens. 2017, 9, 278. [Google Scholar] [CrossRef]
- Katrasnik, J.; Pernus, F.; Likar, B. New robot for power line inspection. In Proceedings of the 2008 IEEE Conference on Robotics, Automation and Mechatronics, Chengdu, China, 21–24 September 2008; pp. 1195–1200. [Google Scholar]
- Lopez Lopez, R.; Batista Sanchez, M.J.; Perez Jimenez, M.; Arrue, B.C.; Ollero, A. Autonomous uav system for cleaning insulators in power line inspection and maintenance. Sensors 2021, 21, 8488. [Google Scholar] [CrossRef] [PubMed]
- Jenssen, R.; Roverso, D. Automatic autonomous vision-based power line inspection: A review of current status and the potential role of deep learning. Int. J. Electr. Power Energy Syst. 2018, 99, 107–120. [Google Scholar]
- Yang, L.; Fan, J.; Liu, Y.; Li, E.; Peng, J.; Liang, Z. A review on state-of-the-art power line inspection techniques. IEEE Trans. Instrum. Meas. 2020, 69, 9350–9365. [Google Scholar] [CrossRef]
- Zhou, R.; Jiang, W.; Jiang, S. A novel method for high-voltage bundle conductor reconstruction from airborne LiDAR data. Remote Sens. 2018, 10, 2051. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, X.; Fang, Y.; Chen, S. UAV low altitude photogrammetry for power line inspection. ISPRS Int. J. Geo-Inf. 2017, 6, 14. [Google Scholar] [CrossRef]
- He, T.; Zeng, Y.; Hu, Z. Research of multi-rotor UAVs detailed autonomous inspection technology of transmission lines based on route planning. IEEE Access 2019, 7, 114955–114965. [Google Scholar] [CrossRef]
- Fang, S.; Haiyang, C.; Sheng, L.; Xiaoyu, W. A framework of power pylon detection for UAV-based power line inspection. In Proceedings of the 2020 IEEE 5th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 12–14 June 2020; pp. 350–357. [Google Scholar]
- Li, H.; Dong, Y.; Liu, Y.; Ai, J. Design and Implementation of UAVs for Bird’s Nest Inspection on Transmission Lines Based on Deep Learning. Drones 2022, 6, 252. [Google Scholar] [CrossRef]
- Yang, T.W.; Yin, H.; Ruan, Q.Q.; Da Han, J.; Qi, J.T.; Yong, Q.; Wang, Z.T.; Sun, Z.Q. Overhead power line detection from UAV video images. In Proceedings of the 2012 19th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Auckland, New Zealand, 28–30 November 2012; pp. 74–79. [Google Scholar]
- Ballard, D.H. Generalizing the Hough transform to detect arbitrary shapes. Pattern Recognit. 1981, 13, 111–122. [Google Scholar] [CrossRef]
- Zormpas, A.; Moirogiorgou, K.; Kalaitzakis, K.; Plokamakis, G.A.; Partsinevelos, P.; Giakos, G.; Zervakis, M. Power transmission lines inspection using properly equipped unmanned aerial vehicle (UAV). In Proceedings of the 2018 IEEE International Conference on Imaging Systems and Techniques (IST), Krakow, Poland, 16–18 October 2018; pp. 1–5. [Google Scholar]
- Li, Z.; Liu, Y.; Hayward, R.; Zhang, J.; Cai, J. Knowledge-based power line detection for UAV surveillance and inspection systems. In Proceedings of the 2008 23rd International Conference Image and Vision Computing New Zealand, Christchurch, New Zealand, 26–28 November 2008; pp. 1–6. [Google Scholar]
- Tian, F.; Wang, Y.; Zhu, L. Power line recognition and tracking method for UAVs inspection. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015; pp. 2136–2141. [Google Scholar]
- Zhang, H.; Yang, W.; Yu, H.; Zhang, H.; Xia, G.S. Detecting power lines in UAV images with convolutional features and structured constraints. Remote Sens. 2019, 11, 1342. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, L.; Wang, B.; Chen, X.; Wang, Q.; Zheng, T. High speed automatic power line detection and tracking for a UAV-based inspection. In Proceedings of the 2012 International Conference on Industrial Control and Electronics Engineering, Xi’an, China, 23–25 August 2012; pp. 266–269. [Google Scholar]
- Dietsche, A.; Cioffi, G.; Hidalgo-Carrió, J.; Scaramuzza, D. Powerline tracking with event cameras. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27–30 September 2021. [Google Scholar]
- Kim, S.; Kim, D.; Jeong, S.; Ham, J.W.; Lee, J.K.; Oh, K.Y. Fault diagnosis of power transmission lines using a UAV-mounted smart inspection system. IEEE Access 2020, 8, 149999–150009. [Google Scholar] [CrossRef]
- Cerón, A.; Mondragón, I.; Prieto, F. Onboard visual-based navigation system for power line following with UAV. Int. J. Adv. Robot. Syst. 2018, 13. [Google Scholar] [CrossRef]
- Deng, C.; Liu, J.Y.; Liu, Y.B.; Tan, Y.Y. Real time autonomous transmission line following system for quadrotor helicopters. In Proceedings of the 2016 International Conference on Smart Grid and Clean Energy Technologies (ICSGCE), Chengdu, China, 19–22 October 2016; pp. 61–64. [Google Scholar]
- Mirallès, F.; Hamelin, P.; Lambert, G.; Lavoie, S.; Pouliot, N.; Montfrond, M.; Montambault, S. LineDrone Technology: Landing an unmanned aerial vehicle on a power line. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 6545–6552. [Google Scholar]
- Schofield, O.B.; Iversen, N.; Ebeid, E. Autonomous power line detection and tracking system using UAVs. Microprocess. Microsyst. 2022, 94, 104609. [Google Scholar] [CrossRef]
- Malle, N.H.; Nyboe, F.F.; Ebeid, E.S.M. Onboard Powerline Perception System for UAVs Using mmWave Radar and FPGA-Accelerated Vision. IEEE Access 2022, 10, 113543–113559. [Google Scholar] [CrossRef]
- Peng, X.Y.; Qing, Z.; Rao, Z.Q. Intelligent diagnosis technology for corona discharge defects of transmission lines based on UAV-based UV detection. High Volt. Technol. 2014, 40, 2292–2298. [Google Scholar]
- Guan, H.; Sun, X.; Su, Y.; Hu, T.; Wang, H.; Wang, H.; Guo, Q. UAV-lidar aids automatic intelligent powerline inspection. Int. J. Electr. Power Energy Syst. 2021, 130, 106987. [Google Scholar] [CrossRef]
- Ishino, R.; Tsutsumi, F. Detection system of damaged cables using video obtained from an aerial inspection of transmission lines. In Proceedings of the IEEE Power Engineering Society General Meeting, Denver, CO, USA, 6–10 June 2004; pp. 1857–1862. [Google Scholar]
- Yan, Y.; Zhao, J.; Wang, Z.; Yan, Y. An novel variable step size LMS adaptive filtering algorithm based on hyperbolic tangent function. In Proceedings of the 2010 International Conference on Computer Application and System Modeling (ICCASM 2010), Taiyuan, China, 22–24 October 2010; p. 233. [Google Scholar]
- PLK–LC2001l. 2020. Available online: http://www.plcomp.com/Home/detail.html/3011 (accessed on 21 September 2023).
- OAK–1. 2020. Available online: https://shop.luxonis.com/products/oak-1?variant=42664380334303 (accessed on 21 September 2023).
- IAR. Available online: https://www.iar.com/ (accessed on 21 September 2023).







| Platform | Weight | Primary Sensors | Inspection Method | |
|---|---|---|---|---|
| [3] | DJI Matrice 300 | >6.3 kg | RTK, RGB Camera, Thermal Camera; | Long-Range; |
| [23] | DJI M600 Pro | 8.7 kg | GNSS, UV Camera; | Long-Range; |
| [24] | DJI 550 | >1.3 kg | GNSS, RGB Camera; | Long-Range; |
| [25] | TQuad1000 | >2.0 kg | Double Antenna GNSS, 3D LiDAR; | Long-Range, Line-Tracking; |
| [26] | Commercial UAV (1.12 × 1.12 × 0.63 m) | 14.0 kg | GNSS, Camera, LiDAR; | Close-Range, Line-Tracking; |
| [28] | Holybro QAV250 | 0.61 kg (No Battery) | GNSS, RGB Camera, mm-Wave Radar; | Close-Range; |
| [30] | DJI Matrice 210 | >3.8 kg | RTK, RGB Camera, 3D LiDAR; | Long-Range; |
| Proposed | Self Developed | 0.48 kg | GNSS, RGB Camera, mm-Wave Radar; | Close-range, Line-Tracking |
| Characteristic | Parameters |
|---|---|
| Navigation System | GNSS + Compass |
| Size | 0.24 × 0.24 × 0.15 m |
| Total Weight | 484 g |
| Components Weight (Camera) | 53.1 g |
| Components Weight (Radar, Battery) | 12 g |
| Components Weight (Battery) | 118.3 g |
| Endurance | 15 min |
| Maximum Wind Resistance | 5 m/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Wang, W.; Li, Z.; Namiki, A.; Suzuki, S. Close-Range Transmission Line Inspection Method for Low-Cost UAV: Design and Implementation. Remote Sens. 2023, 15, 4841. https://doi.org/10.3390/rs15194841
Wang Q, Wang W, Li Z, Namiki A, Suzuki S. Close-Range Transmission Line Inspection Method for Low-Cost UAV: Design and Implementation. Remote Sensing. 2023; 15(19):4841. https://doi.org/10.3390/rs15194841
Chicago/Turabian StyleWang, Qi, Wei Wang, Ziran Li, Akio Namiki, and Satoshi Suzuki. 2023. "Close-Range Transmission Line Inspection Method for Low-Cost UAV: Design and Implementation" Remote Sensing 15, no. 19: 4841. https://doi.org/10.3390/rs15194841





