Estimations of the Ground-Level NO2 Concentrations Based on the Sentinel-5P NO2 Tropospheric Column Number Density Product
Abstract
1. Introduction
- How much does the accuracy of surface NO2 modeling improve if the S-5P TCVD NO2 product is assimilated into a model?
- What are the impacts of the meteorological conditions and anthropogenic factors on the NO2 modeling results?
- What are the impacts of the temporal averaging of NO2 retrievals and in situ measurements on the overall accuracy?
- Which machine learning models provide the most accurate NO2 estimations?
- What was the accuracy of the latest S-5P TROPOMI TCVD NO2 product version 2.3.1 released on 16 December 2021 [38]?
2. Materials and Methods
2.1. Study Area
2.2. Materials
2.2.1. NO2 Tropospheric Vertical Column Density (NO2 TVCD) Product Retrieved from Sentinel-5P Satellite TROPOMI Measurements
- The NO2 slant column densities are retrieved from the measured radiance and irradiance spectra using the differential optical absorption spectroscopy (DOAS) method;
- The separation of tropospheric and stratospheric columns, i.e., their conversion to tropospheric and stratospheric slant columns;
2.2.2. In Situ Air Quality Measurements
2.2.3. Meteorological Data
2.2.4. Ancillary Data
2.3. Methods
2.3.1. Modeling of Surface NO2 Mass Concentration
- Linear regression with one independent variable (LM)—NO2 TVCD;
- Multiple linear regression with several independent variables (MLM)—NO2 TVCD, T, P, RAD, WS, PBLH, NIGHTLIGHT, POPULATION, ROADS DENSITY, and ELEVATION;
- Random forests with several independent variables (RF)—NO2 TVCD, T, P, RAD, WS, PBLH, NIGHTLIGHT, POPULATION, ROADS DENSITY, ELEVATION, and CT;
- Radial kernel support vector machine with several independent variables (SVM)—NO2 TVCD, T, P, RAD, WS, PBLH, NIGHTLIGHT, POPULATION, ROADS DENSITY, ELEVATION, and CT.
- Stations measuring surface NO2 closer than 100 m from the road (2 stations; 1024 observations; 2% of all observations).
2.3.2. Validation methodology
- R-squared (R2):
- Mean squared error (MSE):
- Root mean squared error (RMSE):
- Bias:
- Mean absolute error (MAE):
- Mean percentage absolute error (MAPE):
2.3.3. Ranking the Modeling Skills of the Selected Predictors
- Compute the model’s MSE;
- For each variable in the model:
- (a)
- Permute the variable;
- (b)
- Calculate the new model MSE according to the variable permutation;
- (c)
- Take the difference between the model MSE and new model MSE;
- 3.
- Collect the results in a list;
- 4.
- Rank the variables’ importance according to the %IncMSE values, whereby the greater the value, the more important the variable [83].
2.3.4. Determining the Variability of the NO2 TVCD and Surface NO2 with Respect to the Meteorological Conditions and Anthropogenic Factors
- 2 °C for T;
- 250 m above ground for PBLH;
- 2 m/s for WS;
- N, S, E, W, SE, SW, NW, and NE for WD;
- 27 types of atmospheric circulations;
- 20 nW/cm2/sr for NIGHTLIGHT;
- People/km for POPULATION.
3. Results
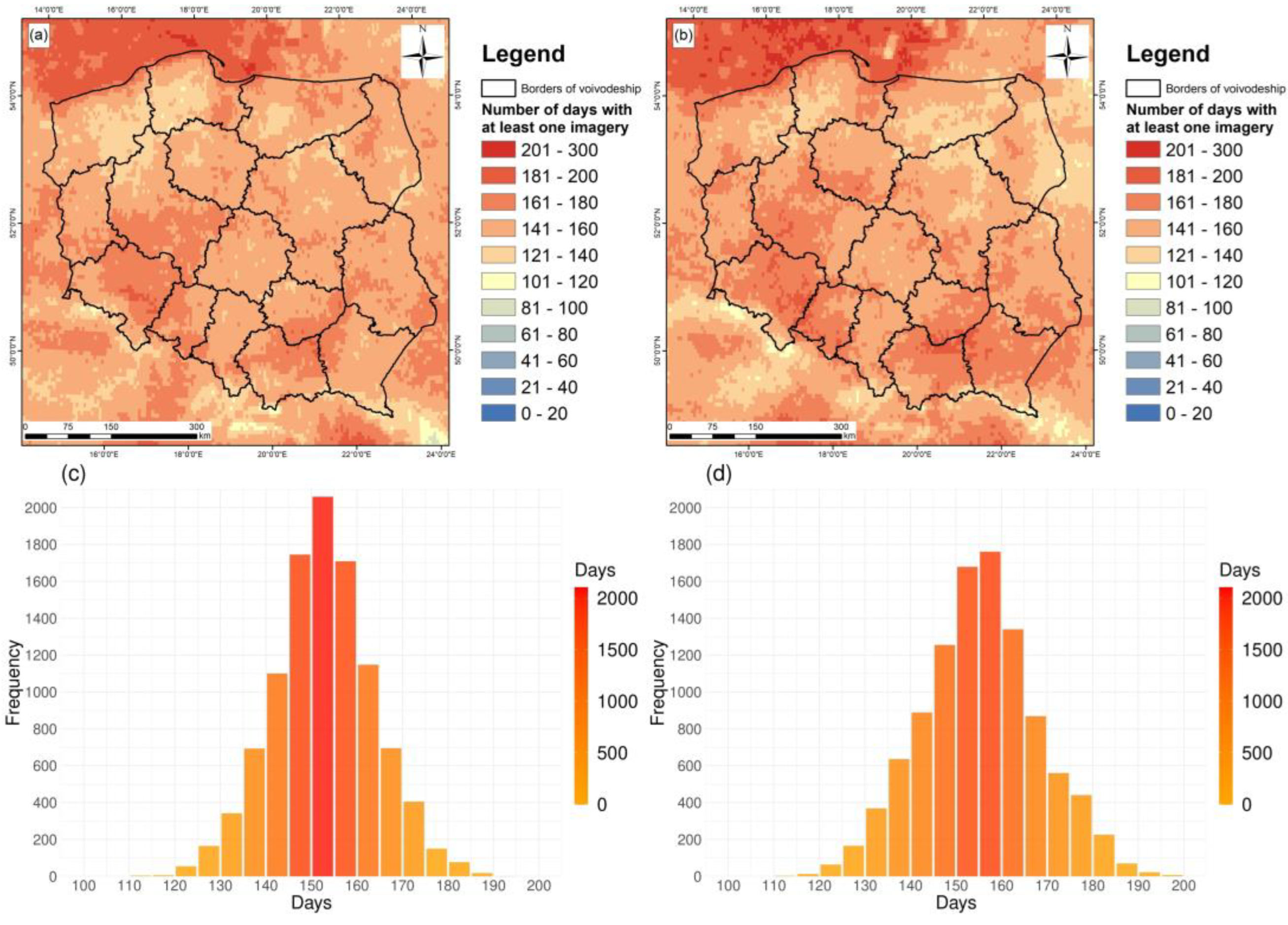
3.1. Numbers of Observations
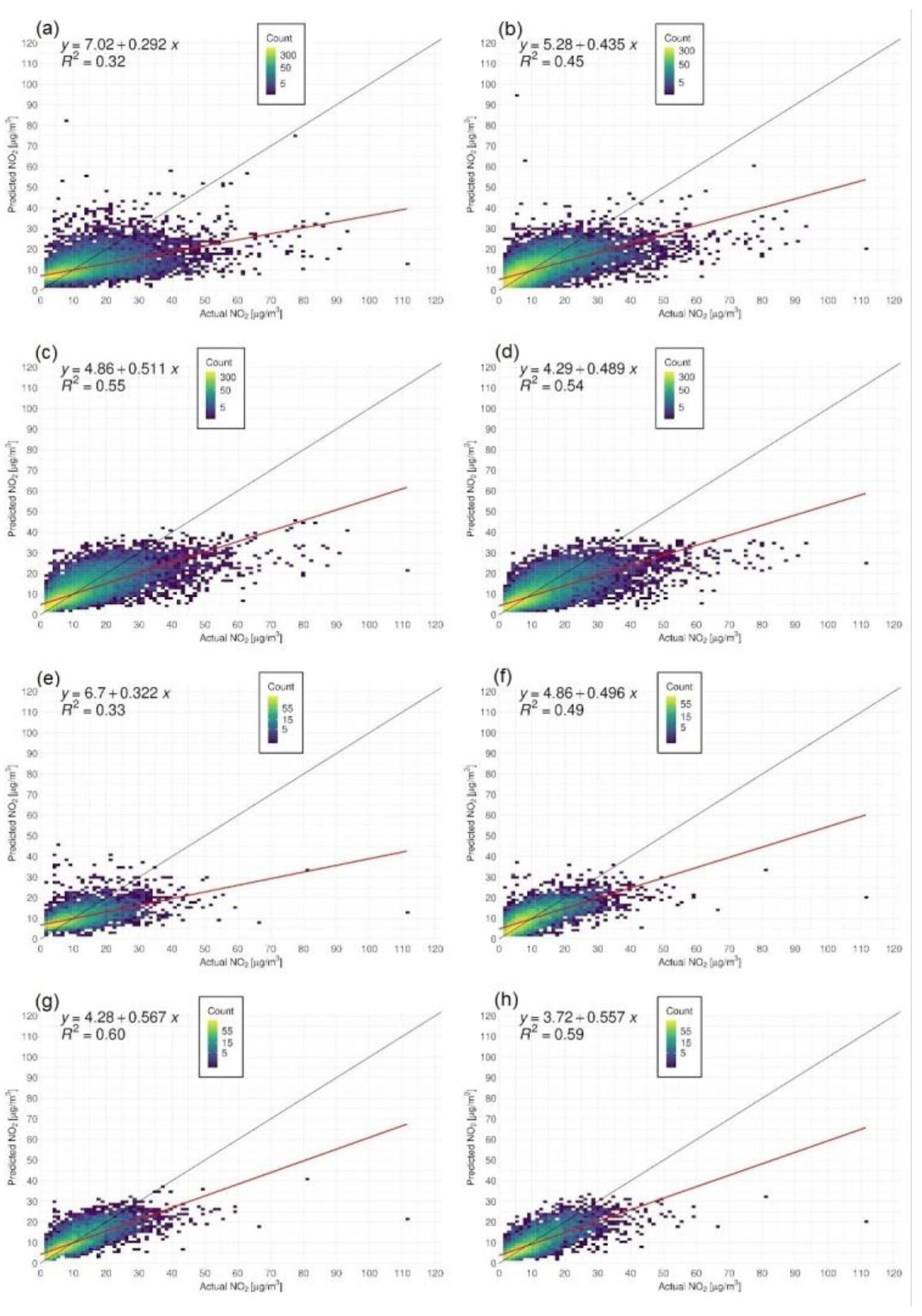
3.2. Modeling of Surface NO2 Mass Concentration
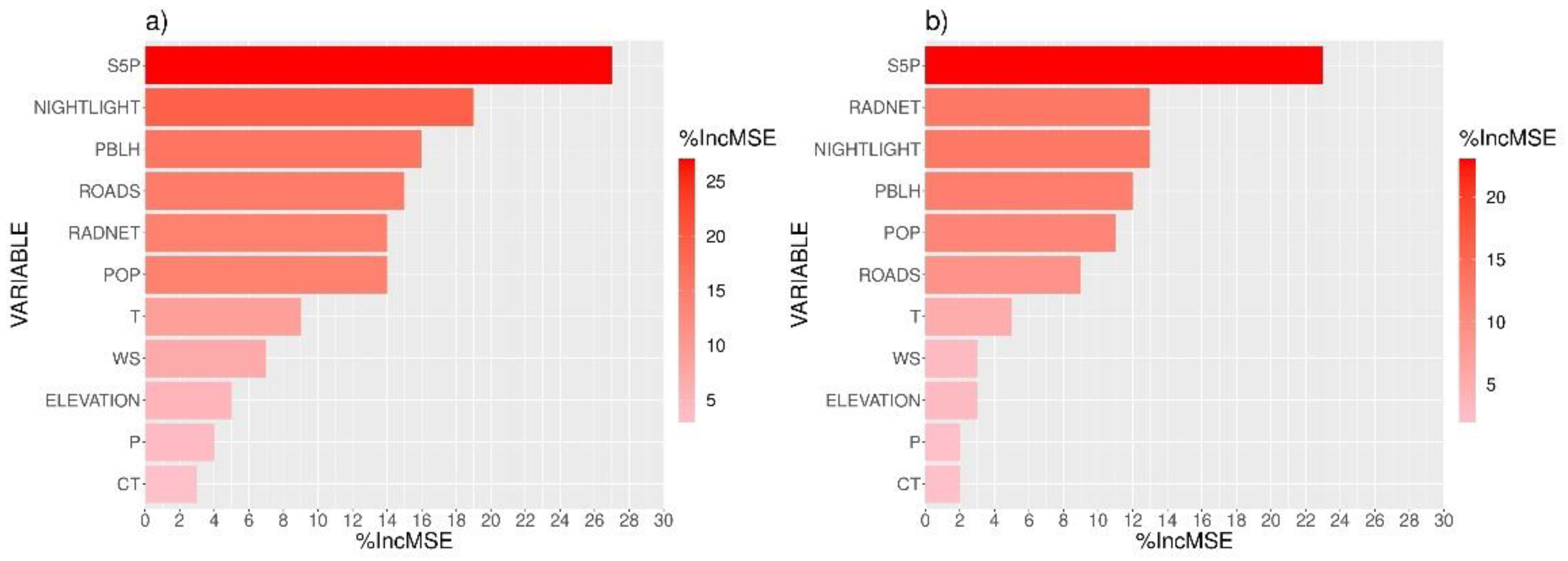
3.3. Variables’ Importance
- Those with an impact higher than or equal to 10% on the changes in MSE: S5P, NIGHTLIGHT, PBLH, ROADS, RAD, and POP;
- Those with an impact lower than 10% on the changes in MSE: T, P, WS, ELEVATION, and CT.
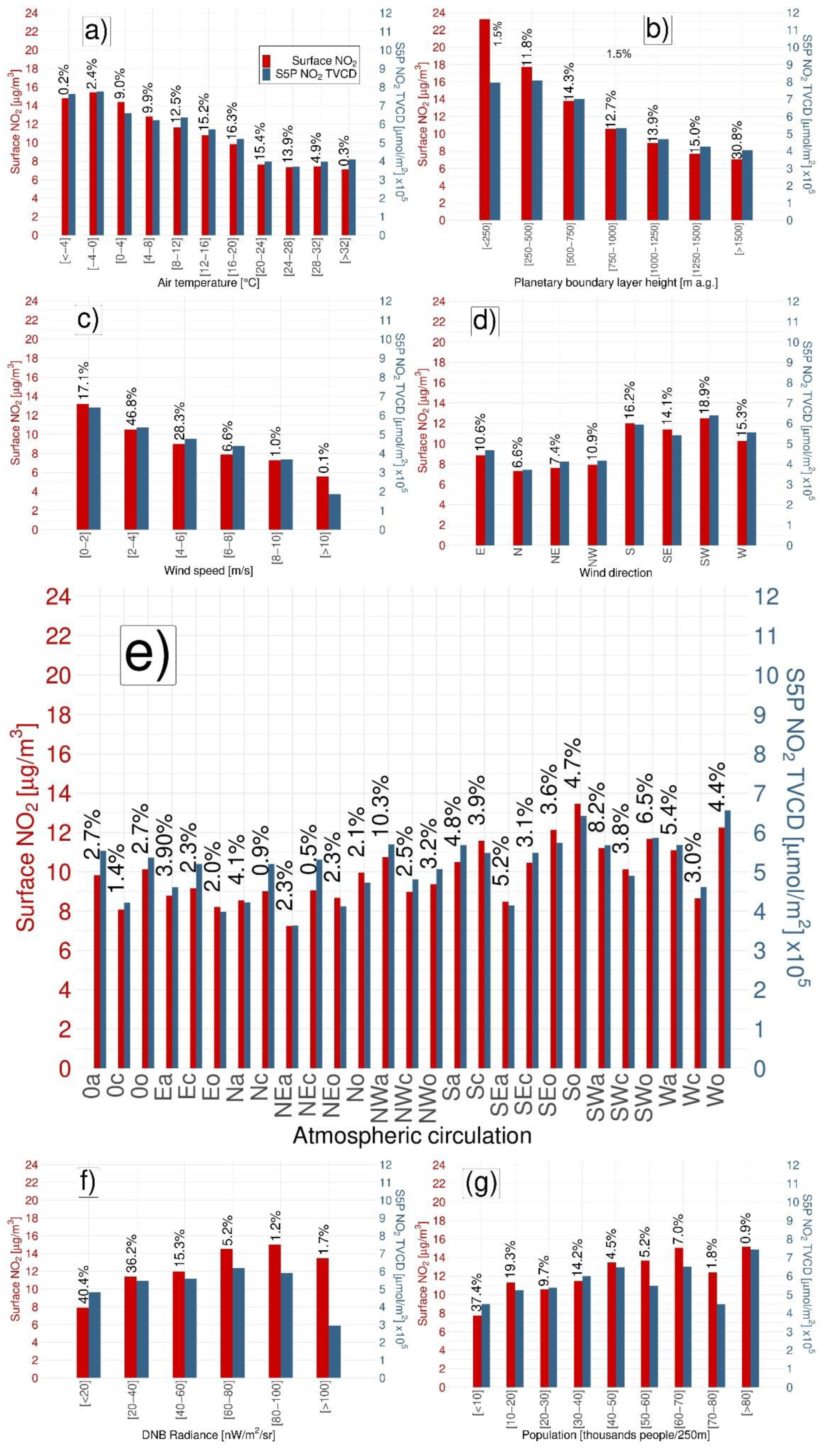
3.4. Changes in NO2 TVCD and Surface NO2 Mass Concentration in Respect to Meteorological Conditions and Other Factors
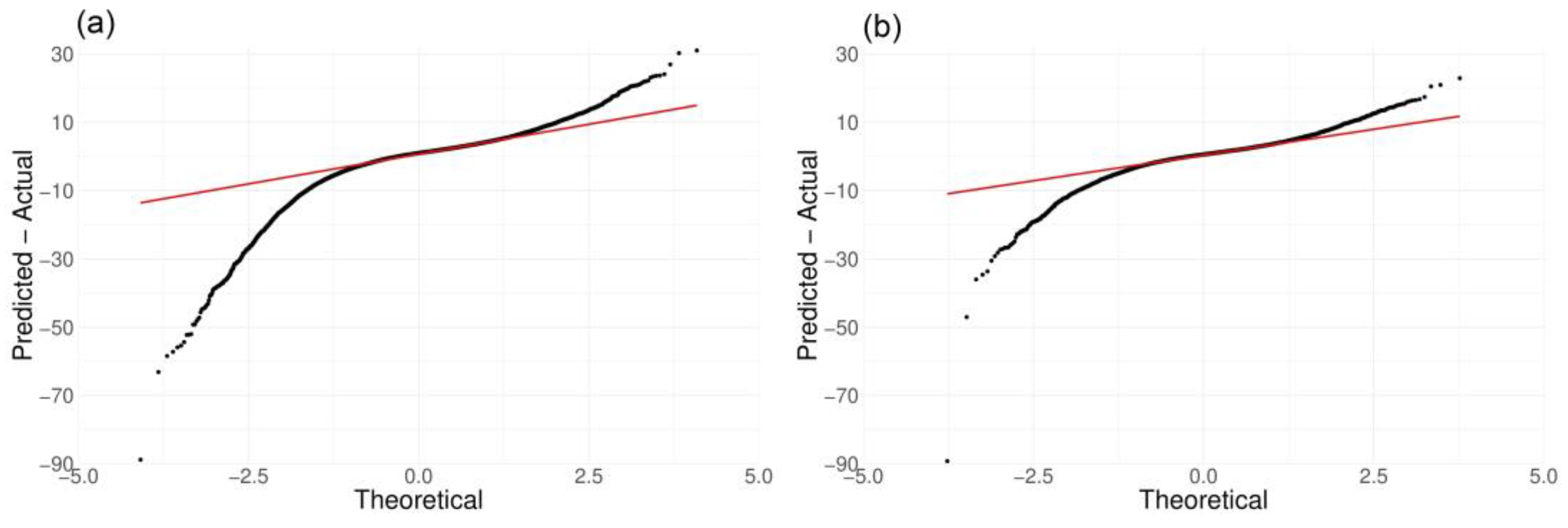
4. Discussion
5. Conclusions
- There were at least 120 days per year when it was possible to perform model calculations for Poland using TROPOMI observations;
- The results revealed that the machine learning methods (RF and SVM) gave ca. 63% accuracy for hourly estimations of NO2 and 69% accuracy for weekly averages;
- The implementation of meteorological and anthropogenic variables improved the quality of the models. The MLM approach gave 6% (hourly) and 7% (weekly) lower MAPE values than the LM-S5P approach, while the RF and SVM approaches gave 11% (hourly) and 12% (weekly) lower MAPE values than the LM-S5P approach;
- The planetary boundary layer height, solar radiation, nightlights, roads density, and population influenced the estimations the most;
- The air temperature, wind speed, surface pressure, elevation, and type of atmospheric circulation influenced the estimations the least;
- The trends for the surface NO2 and TVCD of NO2 were negative for increases in air temperature, PBLH, and wind speed, while they were positive for increases in population and nightlights;
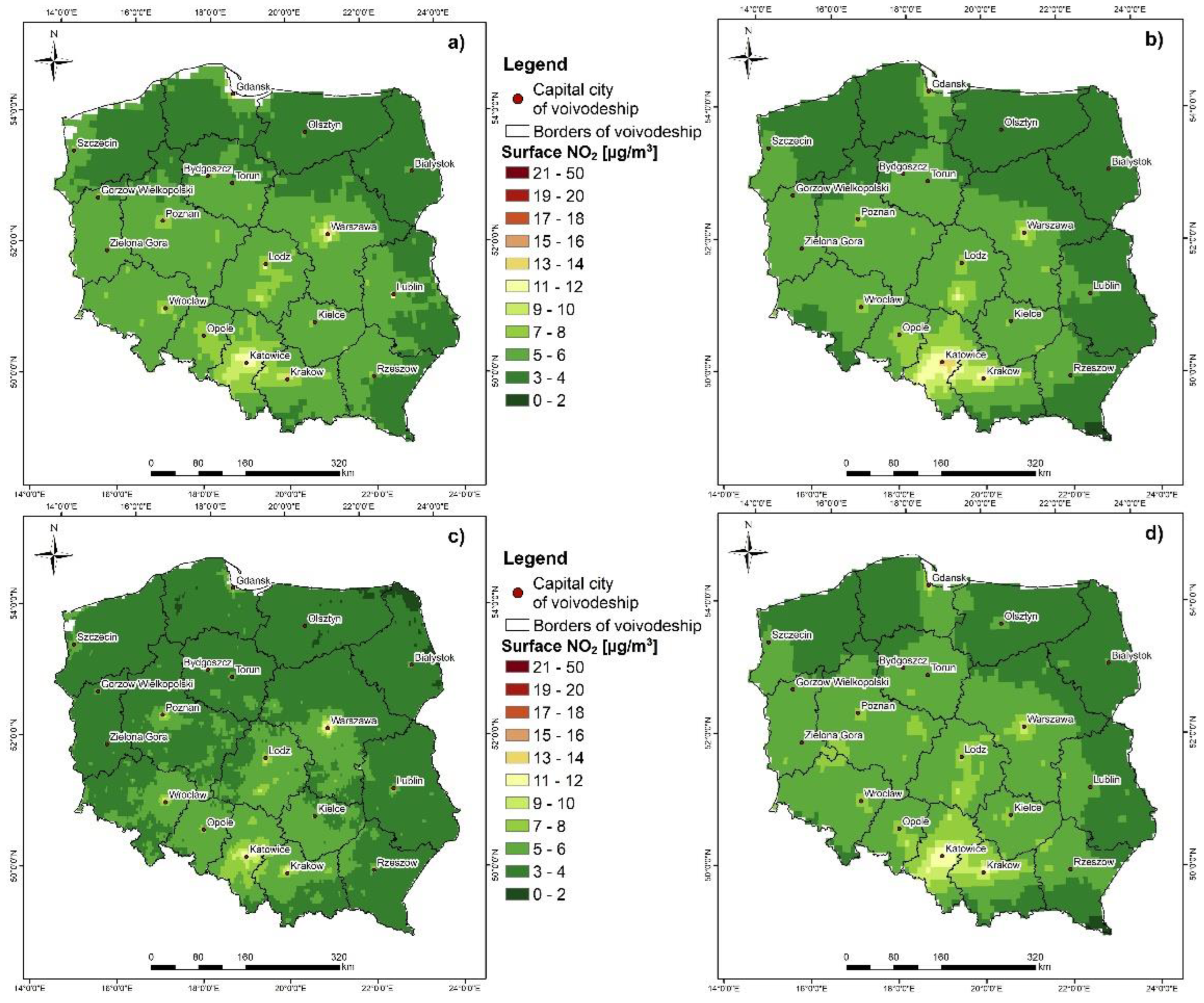
- The RF model created within the study was better fitted to the actual values than the CAMS ensemble median model.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sroczyński, J. The Impact of Atmos. In Air Pollution on Human Health; PAN: Wrocław, Poland, 1988. (In Polish) [Google Scholar]
- World Health Origination. WHO Air Quality Guidelines for Particulate Matter, Ozone, Nitrogen Dioxide and Sulfur Dioxide. Available online: https://apps.who.int/iris/handle/10665/345329 (accessed on 10 October 2021).
- European Environment Agency. Air Quality in Europe—2020. Report. EEA Report No 9/2020. Available online: https://www.eea.europa.eu/publications/air-quality-in-europe-2020-report (accessed on 10 October 2021).
- Duprè, C.; Stevens, C.J.; Ranke, T.; Bleeker, A.; Peppler-Lisbach, C.O.R.D.; Gowing, D.J.; Dise, N.D.; Dorland, E.; Bobbkink, R.; Diekmann, M. Changes in species richness and composition in European acidic grasslands over the past 70 years: The contribution of cumulative atmospheric nitrogen deposition. Glob. Chang. Biol. 2010, 16, 344–357. [Google Scholar] [CrossRef]
- Schoeberl, M.R.; Douglass, A.R.; Hilsenrath, E.; Bhartia, P.K.; Beer, R.; Waters, J.W.; Gunson, M.R.; Fridevaiux, L.; Gille, J.C.; Barnett, J.J.; et al. Overview of the EOS Aura mission. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1066–1074. [Google Scholar] [CrossRef]
- National Aeronautics and Space Administration-OMI Science Team. OMI/Aura Level 2 Nitrogen Dioxide (NO2) Trace Gas Column Data 1-Orbit subset Swath along CloudSat track 1-Orbit Swath 13x24 km, Edited by GES DISC, NASA Goddard Space Flight Center, Goddard Earth Sciences Data and Information Services Center (GES DISC). 2012. Available online: https://disc.gsfc.nasa.gov/datasets/OMNO2_CPR_003/summary (accessed on 20 October 2022).
- Jamali, S.; Klingmyr, D.; Tagesson, T. Global-scale patterns and trends in tropospheric NO2 concentrations, 2005–2018. Remote Sens. 2020, 12, 3526. [Google Scholar] [CrossRef]
- Krotkov, N.A.; McLinden, C.A.; Li, C.; Lamsal, L.N.; Celarier, E.A.; Marchenko, S.V.; Swartz, W.H.; Bucsela, W.J.; Joiner, J.; Duncan, W.N.; et al. Aura OMI observations of regional SO 2 and NO 2 pollution changes from 2005 to 2015. Atmos. Chem. Phys. 2016, 16, 4605–4629. [Google Scholar] [CrossRef]
- Paraschiv, S.; Constantin, D.E.; Paraschiv, S.L.; Voiculescu, M. OMI and ground-based in-situ tropospheric nitrogen dioxide observations over several important European cities during 2005–2014. Int. J. Environ. Res. Public Health 2017, 14, 1415. [Google Scholar] [CrossRef]
- Georgoulias, A.K.; van der A, R.J.; Stammes, P.; Boersma, K.F.; Eskes, H.J. Trends and trend reversal detection in 2 decades of tropospheric NO2 satellite observations. Atmos. Chem. Phys. 2019, 19, 6269–6294. [Google Scholar] [CrossRef]
- Veefkind, J.; Aben, I.; McMullan, K.; Förster, H.; de Vries, J.; Otter, G.; Claas, J.; Eskes, H.; de Haan, J.; Kleipool, Q. TROPOMI on the ESA Sentinel-5 Precursor: A GMES mission for global observations of the Atmos. composition for climate, air quality and ozone layer applications. Remote Sens. Environ. 2012, 120, 70–83. [Google Scholar] [CrossRef]
- Bauwens, M.; Compernolle, S.; Stavrakou, T.; Müller, J.; Van Gent, J.; Eskes, H.; Levelt, P.F.; van der A, R.; Veefkind, J.P.; Vlietinck, J.; et al. Impact of Coronavirus Outbreak on NO2 Pollution Assessed Using TROPOMI and OMI Observations. Geophys. Res. Lett. 2020, 47, e2020GL087978. [Google Scholar] [CrossRef]
- Qin, K.; Rao, L.; Xu, J.; Bai, Y.; Zou, J.; Hao, N.; Li, S.; Yu, C. Estimating ground level NO2 concentrations over Central-Eastern China using a satellite-based geographically and temporally weighted regression model. Remote Sens. 2017, 9, 950. [Google Scholar] [CrossRef]
- Ialongo, I.; Virta, H.; Eskes, H.; Hovila, J.; Douros, J. Comparison of TROPOMI/Sentinel-5 Precursor NO2 observations with ground-based measurements in Helsinki. Atmos. Meas. Tech. 2020, 13, 205–218. [Google Scholar] [CrossRef]
- Kang, Y.; Choi, H.; Im, J.; Park, S.; Shin, M.; Song, C.K.; Kim, S. Estimation of surface-level NO2 and O3 concentrations using TROPOMI data and machine learning over East Asia. Environ. Pollut. 2021, 288, 117711. [Google Scholar] [CrossRef] [PubMed]
- Griffin, D.; Zhao, X.; McLinden, C.A.; Boersma, F.; Bourassa, A.; Dammers, E.; Degenstein, D.; Eskes, H.; Fehr, L.; Fioletov, V.; et al. High resolution mapping of nitrogen dioxide with TROPOMI: First results and validation over the Canadian oil sands. Geophys. Res. Lett. 2019, 46, 1049–1060. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Z.; Yang, Z.; Wu, Z.; Marinello, F. Spatial variation of NO2 and its impact factors in China: An application of sentinel-5P products. Remote Sens. 2021, 11, 1939. [Google Scholar] [CrossRef]
- Cersosimo, A.; Serio, C.; Masiello, G. TROPOMI NO2 tropospheric column data: Regridding to 1 km grid-resolution and assessment of their consistency with in situ surface observations. Remote Sens. 2020, 12, 2212. [Google Scholar] [CrossRef]
- Jeong, U.; Hong, H. Assessment of tropospheric concentrations of NO2 from the TROPOMI/Sentinel-5 Precursor for the estimation of long-term exposure to surface NO2 over South Korea. Remote Sens. 2021, 13, 1877. [Google Scholar] [CrossRef]
- Plaisance, H.; Piechocki-Minguy, A.; Garcia-Fouque, S.; Galloo, J.C. Influence of meteorological factors on the NO2 measurements by passive diffusion tube. Atmos. Environ. 2004, 38, 573–580. [Google Scholar] [CrossRef]
- Zhou, Y.; Brunner, D.; Hueglin, C.; Henne, S.; Staehelin, J. Changes in OMI tropospheric NO2 columns over Europe from 2004 to 2009 and the influence of meteorological variability. Atmos. Environ. 2012, 46, 482–495. [Google Scholar] [CrossRef]
- Kamińska, J.A. A random forest partition model for predicting NO2 concentrations from traffic flow and meteorological conditions. Sci. Total Environ. 2019, 651, 475–483. [Google Scholar] [CrossRef]
- Kang, H.; Zhu, B.; Zhu, C.; de Leeuw, G.; Hou, X.; Gao, J. Natural and anthropogenic contributions to long-term variations of SO2, NO2, CO, and AOD over East China. Atmos. Res. 2019, 215, 284–293. [Google Scholar] [CrossRef]
- Voiculescu, M.; Constantin, D.E.; Condurache-Bota, S.; Călmuc, V.; Roșu, A.; Dragomir Bălănică, C.M. Role of meteorological parameters in the diurnal and seasonal variation of NO2 in a Romanian urban environment. Int. J. Environ. Res. Public Health 2020, 17, 6228. [Google Scholar] [CrossRef]
- Beirle, S.; Platt, U.; Wenig, M.; Wagner, T. Weekly cycle of NO 2 by GOME measurements: A signature of anthropogenic sources. Atmos. Chem. Phys. 2003, 3, 2225–2232. [Google Scholar] [CrossRef]
- Van Der A, R.J.; Peters, D.H.M.U.; Eskes, H.; Boersma, K.F.; Van Roozendael, M.; De Smedt, I.; Kelder, H.M. Detection of the trend and seasonal variation in tropospheric NO2 over China. J. Geophys. Res. Atmos. 2006, 111, D12317. [Google Scholar] [CrossRef]
- Lamsal, L.N.; Martin, R.V.; Padmanabhan, A.; Van Donkelaar, A.; Zhang, Q.; Sioris, C.E.; Chance, K.; Kurosu, T.P.; Newchurch, M.J. Application of satellite observations for timely updates to global anthropogenic NOx emission inventories. Geophys. Res. Lett. 2011, 38, L05810. [Google Scholar] [CrossRef]
- Grzybowski, P.T.; Markowicz, K.M.; Musiał, J.P. Reduction of air pollution in Poland in spring 2020 during the lockdown caused by the COVID-19 pandemic. Remote Sens. 2021, 13, 3784. [Google Scholar] [CrossRef]
- Kim, M.; Brunner, D.; Kuhlmann, G. Importance of satellite observations for high-resolution mapping of near-surface NO2 by machine learning. Remote Sens. Environ. 2021, 264, 112573. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Wang, C.; Wang, T.; Wang, P.; Rakitin, V. Comparison and Validation of TROPOMI and OMI NO2 Observations over China. Atmosphere 2020, 11, 636. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. Lightgbm: A highly efficient gradient boosting decision tree. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2017; p. 30. [Google Scholar]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; Volume 1, pp. 278–282. [Google Scholar]
- Shen, F.; Chao, J.; Zhao, J. Forecasting exchange rate using deep belief networks and conjugate gradient method. Neurocomputing 2015, 167, 243–253. [Google Scholar] [CrossRef]
- Karsoliya, S. Approximating number of hidden layer neurons in multiple hidden layer BPNN architecture. Int. J. Eng. Trends Technol. 2012, 3, 714–717. [Google Scholar]
- Chan, K.L.; Khorsandi, E.; Liu, S.; Baier, F.; Valks, P. Estimation of surface NO2 concentrations over Germany from TROPOMI satellite observations using a machine learning method. Remote Sens. 2021, 13, 969. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Eskes, H.; van Geffen, J.; Sneep, M.; Veefkind, P.; Niemeijer, S.; Zehner, C. S5P Nitrogen Dioxide v02.03.01 Intermediate Reprocessing on the S5P-PAL System: Readme File. Available online: https://data-portal.s5p-pal.com/ (accessed on 2 January 2022).
- Meteomodel.pl. Available online: https://meteomodel.pl/ (accessed on 10 January 2022).
- Chief Inspectorate of Environmental Protection. Available online: http://www.gios.gov.pl/pl (accessed on 10 January 2022).
- Boersma, K.F.; Eskes, H.J.; Veefkind, J.P.; Brinksma, E.J.; van der A, R.J.; Sneep, M.; Van Den Oord, G.H.J.; Levelt, P.F.; Stammes, P.; Gleason, J.F.; et al. Near-real time retrieval of tropospheric NO2 from OMI. Atmos. Chem. Phys. Discuss. 2007, 7, 2103–2118. [Google Scholar] [CrossRef]
- Boersma, K.F.; Eskes, H.J.; Dirksen, R.J.; van der A, R.J.; Veefkind, J.P.; Stammes, P.; Huijnen, V.; Kleipool, Q.L.; Sneep, M.; Claas, J.; et al. An improved tropospheric NO2 column retrieval algorithm for the Ozone Monitoring Instrument. Atmos. Meas. Tech. 2011, 4, 1905–1928. [Google Scholar] [CrossRef]
- Boersma, K.F.; Eskes, H.J.; Richter, A.; De Smedt, I.; Lorente, A.; Beirle, S.; van Geffen, J.H.G.M.; Zara, M.; Peters, E.; Van Roozendael, M.; et al. Improving algorithms and uncertainty estimates for satellite NO2 retrievals: Results from the quality assurance for the essential climate variables (QA4ECV) project. Atmos. Meas. Tech. 2018, 11, 6651–6678. [Google Scholar] [CrossRef]
- van Geffen, J.H.G.M.; Boersma, K.F.; Van Roozendael, M.; Hendrick, F.; Mahieu, E.; De Smedt, I.; Sneep, M.; Veefkind, J.P. Improved spectral fitting of nitrogen dioxide from OMI in the 405–465 nm window. Atmos. Meas. Tech. 2015, 8, 1685–1699. [Google Scholar] [CrossRef]
- Williams, J.E.; Boersma, K.F.; Le Sager, P.; Verstraeten, W.W. The high-resolution version of TM5-MP for optimized satellite retrievals: Description and validation. Geosci. Model Dev. 2017, 10, 721–750. [Google Scholar] [CrossRef]
- Loyola, D.; Lutz, R.; Argyrouli, A.; Spurr, R. S5P/TROPOMI ATBD Cloud Products. German Aerospace Center 2020. Available online: https://sentinel.esa.int/documents/247904/2476257/Sentinel-5P-TROPOMI-ATBD-Clouds (accessed on 15 October 2022).
- Kaspar, F.; Schulzweida, U.; Müller, R. Climate data operators” as a user-friendly processing tool for CM SAF’s satellite-derived climate monitoring products. In Proceedings of the EUMETSAT Meteorological Satellite Conference, Cordoba, Spain, 20–24 September 2010; pp. 20–24. [Google Scholar]
- Hijmans, R.J.; Van Etten, J.; Mattiuzzi, M.; Sumner, M.; Greenberg, J.A.; Lamigueiro, O.P.; Shortridge, A. Raster Package in R. Version. 2013. Available online: https://mirrors.sjtug.sjtu.edu.cn/cran/web/packages/raster/ (accessed on 1 October 2022).
- Pierce, D.; Pierce, M.D. Package ‘ncdf4’. 2019. Available online: https://www.vps.fmvz.usp.br/CRAN/web/packages/ncdf4/ncdf4.pdf (accessed on 1 October 2022).
- Bivand, R.; Keitt, T.; Rowlingson, B.; Pebesma, E.; Sumner, M.; Hijmans, R.; Bivand, M.R. Package ‘rgdal’. Bindings for the Geospatial Data Abstraction Library. 2015. Available online: https://cran.r-project.org/web/packages/rgdal/index.html (accessed on 1 October 2022).
- Verhoelst, T.; Compernolle, S.; Pinardi, G.; Lambert, J.-C.; Eskes, H.J.; Eichmann, K.-U.; Fjæraa, A.M.; Granville, J.; Niemeijer, S.; Cede, A.; et al. Ground-based validation of the Copernicus Sentinel-5P TROPOMI NO2 measurements with the NDACC ZSL-DOAS, MAX-DOAS and Pandonia global networks. Atmos. Meas. Tech. 2021, 14, 481–510. [Google Scholar] [CrossRef]
- Pattinson, W.; Longley, I.; Kingham, S. Using mobile monitoring to visualise diurnal variation of traffic pollutants across two near-highway neighbourhoods. Atmos. Environ. 2014, 94, 782–792. [Google Scholar] [CrossRef]
- Targino, A.C.; Gibson, M.D.; Krecl, P.; Rodrigues, M.V.C.; dos Santos, M.M.; de Paula Correa, M. Hotspots of black carbon and PM2.5 in an urban area and relationships to traffic characteristics. Environ. Pollut. 2016, 218, 475–486. [Google Scholar] [CrossRef]
- Flemming, J.; Stern, R.; Yamartino, R. A new air quality regime classification scheme for O3, NO2, SO2 and PM10 observations sites. Atmos. Environ. 2005, 39, 6121–6129. [Google Scholar] [CrossRef]
- Kamińska, J.A.; Chalfen, M.; Szczucka-Lasota, B. Influence of car traffic and meteorological conditions on the care of nitrogen oxides. Autobusy Tech. Eksploat. Syst. Transp. 2017, 18, 93–99. (In Polish) [Google Scholar]
- Muñoz-Sabater, J. ERA5-Land Hourly Data from 1981 to Present, Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2019. [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Hufkens, K.; Stauffer, R.; Campitelli, E. The Ecwmfr Package: An Interface to ECMWF API Endpoints. 2019. [CrossRef]
- Gribbon, K.T.; Bailey, D.G. A novel approach to real-time bilinear interpolation. In Proceedings of the DELTA 2004 Second IEEE International Workshop on Electronic Design, Test and Applications, Perth, Australia, 28–30 January 2004; pp. 126–131. [Google Scholar] [CrossRef]
- Mastyło, M. Bilinear interpolation theorems and applications. J. Funct. Anal. 2013, 265, 185–207. [Google Scholar] [CrossRef]
- Han, D. Comparison of commonly used image interpolation methods. In Proceedings of the 2nd International Conference on Computer Science and Electronics Engineering (ICCSEE 2013), Hangzhou, China, 22–23 March 2013; Atlantis Press: Amsterdam, The Netherlands, 2013; pp. 1556–1559. [Google Scholar] [CrossRef]
- Lityński, J. A Numerical Classification of Circulation and Weather Types for Poland; Prace PIHM State Hydrological and Meteorological Institute: Saint Petersburg, Russia, 1968; Volume 97, pp. 3–14, Warszawa. (In Polish, Summaries in English and Russian). [Google Scholar]
- Lityński, J. Classifi cation numérique des types de circulation et des types de temps en Pologne. Cah. Geogr. Que. 1971, 14, 329–338. [Google Scholar]
- Lityński, J. Numerical classification of types of atmospheric circulation and types of weather in Poland. Prace i Studia IG UW, 11, Klimatologia. 1973, 6, 19–29, (In Polish, Summaries in English and Russian). [Google Scholar]
- Pianko-Kluczynska, K. A new calendar of atmospheric circulation types according to J. Litynski. Wiadomości Meteorol. Hydrol. Gospod. Wodnej 2007, 1, 65–85. (In Polish) [Google Scholar]
- Nowosad, M. Variability of meridional circulation over Poland according to the Lityński classification formula. Pr. I Studia Geogr. 2011, 47, 41–48. (in Polish). [Google Scholar]
- Kulesza, K. A new look at the classification of the types of atmospheric circulation by J. Lityński. Pr. Geogr. 2017, 150, 79–94. [Google Scholar] [CrossRef]
- Ghude, S.D.; Beig, G.; Fadnavis, S.; Polade, S.D. Satellite derived trends in NO2 over the major global hotspot regions during the past decade and their inter-comparison. Environ. Pollut. 2009, 157, 1873–1878. [Google Scholar] [CrossRef]
- Marinello, S.; Butturi, M.A.; Gamberini, R. How changes in human activities during the lockdown impacted air quality parameters: A review. Environ. Prog. Sustain. Energy 2021, 40, e13672. [Google Scholar] [CrossRef]
- European Commission, Joint Research Centre (JRC); Columbia University, Center for International Earth Science Information Network—CIESIN (2015): GHS Population Grid, Derived from GPW4, Multitemporal (1975, 1990, 2000, 2015). European Commission, Joint Research Centre (JRC). Available online: https://data.jrc.ec.europa.eu/dataset/jrc-ghsl-ghs_pop_gpw4_globe_r2015a (accessed on 28 February 2022).
- Xie, Y.; Weng, Q.; Weng, A. A comparative study of NPP-VIIRS and DMSP-OLS nighttime light imagery for derivation of urban demographic metrics. In Proceedings of the 2014 Third International Workshop on Earth Observation and Remote Sensing Applications (EORSA), Changsha, China, 11–14 June 2014; pp. 335–339. [Google Scholar] [CrossRef]
- Bennett, M.M.; Smith, L.C. Advances in using multitemporal night-time lights satellite imagery to detect, estimate, and monitor socioeconomic dynamics. Remote Sens. Environ. 2017, 192, 176–197. [Google Scholar] [CrossRef]
- Stathakis, D.; Baltas, P. Seasonal population estimates based on night-time lights. Comput. Environ. Urban Syst. 2018, 68, 133–141. [Google Scholar] [CrossRef]
- Small, C.; Elvidge, C.D.; Baugh, K. Mapping urban structure and spatial connectivity with VIIRS and OLS night light imagery. In Proceedings of the Joint Urban Remote Sensing Event 2013, Sao Paulo, Brazil, 21–23 April 2013; pp. 230–233. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Baugh, K.; Zhizhin, M.; Hsu, F.C.; Ghosh, T. VIIRS night-time lights. Int. J. Remote Sens. 2017, 38, 5860–5879. [Google Scholar] [CrossRef]
- OpenStreetMap. Available online: https://wiki.openstreetmap.org/wiki/Main_Page (accessed on 20 December 2021).
- Jarvis, A.H.I.; Reuter, A.; Nelson, E.; Guevara. Hole-Filled SRTM for the Globe Version 4, Available from the CGIAR-CSI SRTM 90m. Available online: https://srtm.csi.cgiar.org (accessed on 20 December 2021).
- Varga-Balogh, A.; Leelőssy, Á.; Lagzi, I.; Mészáros, R. Time-dependent downscaling of PM2. 5 predictions from CAMS air quality models to urban monitoring sites in Budapest. Atmosphere 2020, 11, 669. [Google Scholar] [CrossRef]
- Copernicus Atmosphere Monitoring Service—CAMS. The CAMS European Air Quality Ensemble Forecasts Welcomes Two New State-of-the-Art Models. Available online: https://atmosphere.copernicus.eu/cams-european-air-quality-ensemble-forecasts-welcomes-two-new-state-art-models (accessed on 14 January 2022).
- Copernicus Atmosphere Monitoring Service—CAMS. CAMS Regional: European Air Quality Analysis and Forecast Data Documentation. Available online: https://confluence.ecmwf.int/display/CKB/CAMS+Regional%3A+European+air+quality+analysis+and+forecast+data+documentation (accessed on 14 January 2022).
- van Zoest, V.M.; Stein, A.; Hoek, G. Outlier Detection in Urban Air Quality Sensor Networks. Water, Air, Soil Pollut. 2016, 229, 111. [Google Scholar] [CrossRef] [PubMed]
- Bring, J. How to standardize regression coefficients. Am. Stat. 1994, 48, 209–213. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Genuer, R.; Poggi, J.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Oliveira, S.; Oehler, F.; San-Miguel-Ayanz, J.; Camia, A.; Pereira, J.M. Modeling spatial patterns of fire occurrence in Mediterranean Europe using Multiple Regression and Random Forest. For. Ecol. Manag. 2012, 275, 117–129. [Google Scholar] [CrossRef]
- Goldberg, D.L.; Anenberg, S.C.; Kerr, G.H.; Mohegh, A.; Lu, Z.; Streets, D.G. TROPOMI NO 2 in the United States: A Detailed Look at the Annual Averages, Weekly Cycles, Effects of Temperature, and Correlation With Surface NO2 Concentrations. Earth’s Future 2021, 9, e2020EF001665. [Google Scholar] [CrossRef]
- Kawka, M.; Struzewska, J.; Kaminski, J. Spatial and Temporal Variation of NO2 Vertical Column Densities (VCDs) over Poland: Comparison of the Sentinel-5P TROPOMI Observations and the GEM-AQ Model Simulations. Atmosphere 2021, 12, 896. [Google Scholar] [CrossRef]
- Kaminski, J.W.; Neary, L.; Struzewska, J.; McConnell, J.C.; Lupu, A.; Jarosz, J.; Toyota, K.; Gong, S.L.; Côté, J.; Liu, X.; et al. GEM-AQ, an on-line global multiscale chemical weather modelling system: Model description and evaluation of gas phase chemistry processes. Atmos. Chem. Phys. 2008, 8, 3255–3281. [Google Scholar] [CrossRef]
- Kamińska, J.A.; Turek, T. Explicit and implicit description of the factors impact on the NO2 concentration in the traffic corridor. Archiv. Environ. Prot. 2020, 46, 93–99. [Google Scholar]
- Marecal, V.; Peuch, V.-H.; Andersson, C.; Andersson, S.; Arteta, J.; Beekmann, M.; Benedictow, A.; Bergstrom, R.W.; Bessagnet, B.; Cansado, A.; et al. A regional air quality forecasting system over Europe: The MACC-II daily ensemble production. Geosci. Model Dev. 2015, 8, 2777–2813. [Google Scholar] [CrossRef]
- Meteo-France. Quarterly Report on ENSEMBLE NRT Productions (Daily Analyses and Forecasts) and Their Verification, at the Surface and Above Surface. Available online: https://atmosphere.copernicus.eu/sites/default/files/custom-uploads/EQC-regional/CAMS50_2018SC2_D5.2-3.1.ENSEMBLE-SON2020_202102_NRTProduction_Report_v1.pdf (accessed on 1 March 2022).
- van Geffen, J.; Eskes, H.; Compernolle, S.; Pinardi, G.; Verhoelst, T.; Lambert, J.-C.; Sneep, M.; ter Linden, M.; Ludewig, A.; Boersma, K.F.; et al. Sentinel-5P TROPOMI NO2 retrieval: Impact of version v2.2 improvements and comparisons with OMI and ground-based data. Atmospheric Meas. Tech. 2022, 15, 2037–2060. [Google Scholar] [CrossRef]
- Liu, S.; Valks, P.; Beirle, S.; Loyola, D.G. Nitrogen dioxide decline and rebound observed by GOME-2 and TROPOMI during COVID-19 pandemic. Air Qual. Atmos. Health 2021, 14, 1737–1755. [Google Scholar] [CrossRef] [PubMed]
- Celarier, E.A.; Brinksma, E.J.; Gleason, J.F.; Veefkind, J.P.; Cede, A.; Herman, J.; Ionov, D.; Goutail, F.; Pommereau, J.-P.; Lambert, J.-C.; et al. Validation of Ozone Monitoring Instrument nitrogen dioxide columns. J. Geophys. Res. Atmos. 2008, 113, D10S15. [Google Scholar] [CrossRef]
- Herman, J.; Abuhassan, N.; Kim, J.; Kim, J.; Dubey, M.; Raponi, M.; Tzortziou, M. Underestimation of column NO 2 amounts from the OMI satellite compared to diurnally varying ground-based retrievals from multiple PANDORA spectrometer instruments. Atmos. Meas. Tech. 2019, 12, 5593–5612. [Google Scholar] [CrossRef]
- Goldberg, D.L.; Saide, P.E.; Lamsal, L.N.; de Foy, B.; Lu, Z.; Woo, J.H.; Kim, Y.; Kim, J.; Gao, M.; Carmichael, G.; et al. A top-down assessment using OMI NO 2 suggests an underestimate in the NO x emissions inventory in Seoul, South Korea, during KORUS-AQ. Atmos. Chem. Phys. 2019, 19, 1801–1818. [Google Scholar] [CrossRef]
- Schaub, D.; Boersma, K.F.; Kaiser, J.W.; Weiss, A.K.; Folini, D.; Eskes, H.J.; Buchmann, B. Comparison of GOME tropospheric NO2 columns with NO2 profiles deduced from ground-based in situ measurements. Atmos. Meas. Tech. 2006, 6, 3211–3229. [Google Scholar] [CrossRef]
- Judd, L.M.; Al-Saadi, J.A.; Szykman, J.J.; Valin, L.C.; Janz, S.J.; Kowalewski, M.G.; Eskes, H.J.; Veefkind, J.P.; Cede, A.; Mueller, M.; et al. Evaluating Sentinel-5P TROPOMI tropospheric NO2 column densities with airborne and Pandora spectrometers near New York City and Long Island Sound. Atmos. Meas. Tech. 2020, 13, 6113–6140. [Google Scholar] [CrossRef]

| Surface NO2 Mass Concentration Estimations [µg/m3] | ||||||||
|---|---|---|---|---|---|---|---|---|
| MEAN | MIN | MAX | SD | 1st Q | 3rd Q | |||
| Testing dataset (n = 27,241) | 10.1 | <0.1 | 111.4 | 8.9 | 4.4 | 13.1 | ||
| Training dataset (n = 22,678) | 10.4 | <0.1 | 100.6 | 8.6 | 4.4 | 12.9 | ||
| METHOD | R2 | MSE | RMSE [µg/m3] | Bias [µg/m3] | MAE [µg/m3] | MAPE [%] | ||
| Hourly measurements | LM-S5P | 0.32 | 53.2 | 7.3 | 0.1 | 4.9 | 48.4 | |
| MLM | 0.45 | 43.1 | 6.6 | 0.4 | 4.2 | 42.1 | ||
| RF | 0.53 | 34.8 | 5.9 | <0.1 | 3.7 | 37.2 | ||
| SVM | 0.54 | 37.7 | 6.1 | 1.0 | 3.7 | 36.9 | ||
| METHOD | R2 | MSE | RMSE [µg/m3] | Bias [µg/m3] | MAE [µg/m3] | MAPE [%] | ||
| Weekly averages | LM-S5P | 0.33 | 38.1 | 6.2 | 0.1 | 4.3 | 42.4 | |
| MLM | 0.49 | 29.0 | 5.4 | 0.2 | 3.6 | 35.5 | ||
| RF | 0.60 | 23.1 | 4.8 | −0.1 | 3.1 | 30.8 | ||
| SVM | 0.59 | 24.3 | 4.9 | 0.8 | 3.2 | 31.2 | ||
| 1st Q | 2–3rd Q | 4th Q | |
|---|---|---|---|
| Hourly measurements | 2.5 | 1.7 | −5.1 |
| Weekly averages | 2.2 | 1.3 | −4.0 |
| Variable | S5P | T | P | RAD | WS | PBLH | NIGHTLIGHT | POP | ROADS | ELEVATION | INTERCEPT |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Coefficient hourly | 0.62 (57%) | −0.01 (1%) | −0.03 (3%) | −0.06% (6%) | −0.07 (6%) | −0.08 (7%) | 0.05 (5%) | 0.03 (3%) | 0.06 (6%) | 0.01 (1%) | 0.07 (6%) |
| Coefficient weekly | 0.69 (53%) | −0.04 (3%) | −0.04 (3%) | −0.06 (5%) | −0.07 (5%) | −0.10 (8%) | 0.06 (5%) | 0.04 (3%) | 0.08 (6%) | 0.01 (1%) | 0.10 (8%) |
| R2 | MAE [μg/m3] | MAPE [%] | |
|---|---|---|---|
| RF MODEL | 0.54 | 3.9 | 40.0 |
| CAMS | 0.46 | 5.4 | 52.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grzybowski, P.T.; Markowicz, K.M.; Musiał, J.P. Estimations of the Ground-Level NO2 Concentrations Based on the Sentinel-5P NO2 Tropospheric Column Number Density Product. Remote Sens. 2023, 15, 378. https://doi.org/10.3390/rs15020378
Grzybowski PT, Markowicz KM, Musiał JP. Estimations of the Ground-Level NO2 Concentrations Based on the Sentinel-5P NO2 Tropospheric Column Number Density Product. Remote Sensing. 2023; 15(2):378. https://doi.org/10.3390/rs15020378
Chicago/Turabian StyleGrzybowski, Patryk Tadeusz, Krzysztof Mirosław Markowicz, and Jan Paweł Musiał. 2023. "Estimations of the Ground-Level NO2 Concentrations Based on the Sentinel-5P NO2 Tropospheric Column Number Density Product" Remote Sensing 15, no. 2: 378. https://doi.org/10.3390/rs15020378
APA StyleGrzybowski, P. T., Markowicz, K. M., & Musiał, J. P. (2023). Estimations of the Ground-Level NO2 Concentrations Based on the Sentinel-5P NO2 Tropospheric Column Number Density Product. Remote Sensing, 15(2), 378. https://doi.org/10.3390/rs15020378






