Lithospheric Stress Due to Mantle Convection and Mantle Plume over East Africa from GOCE and Seismic Data
Abstract
:1. Introduction
2. Theory
3. Study Area and Data
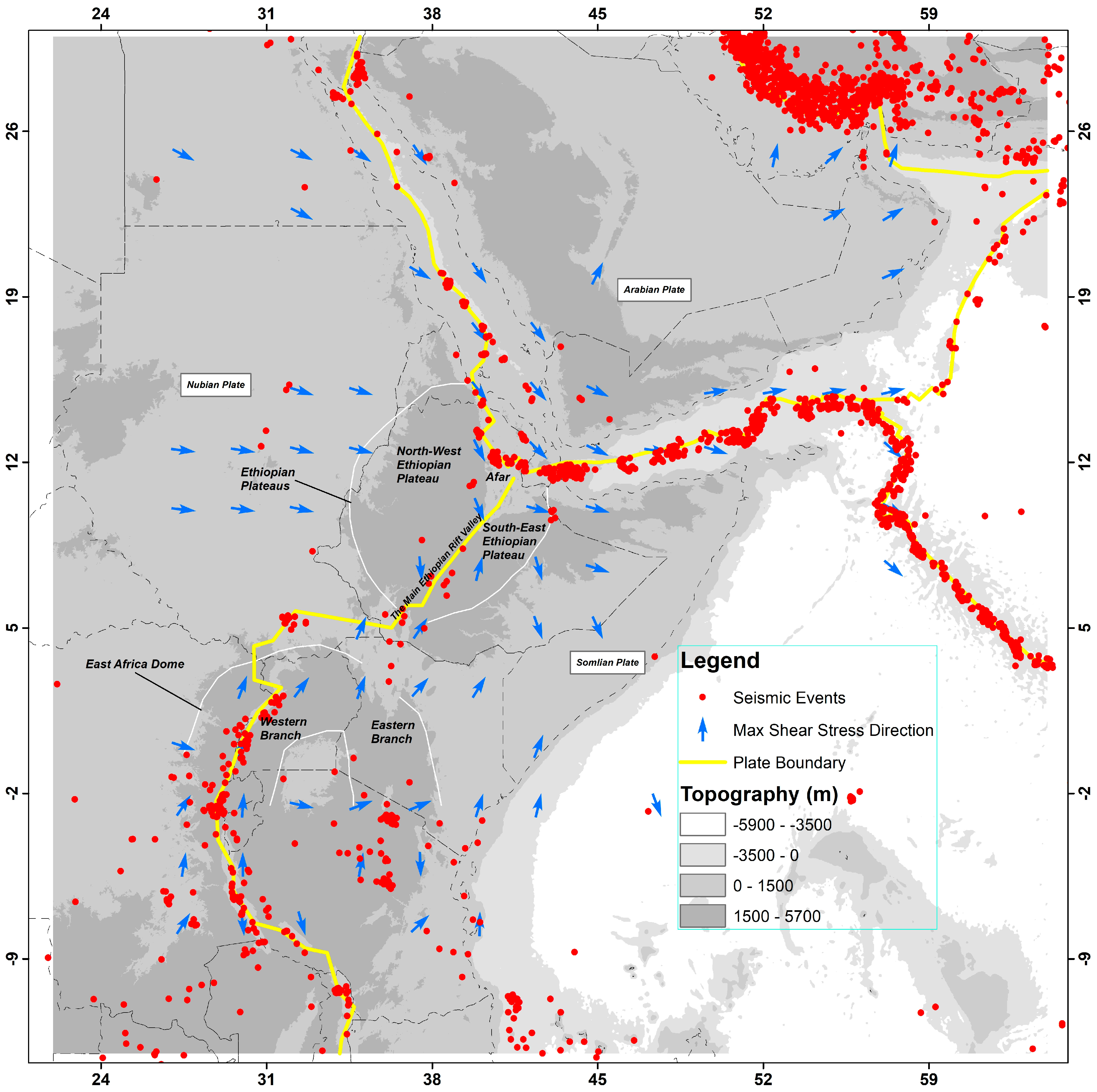
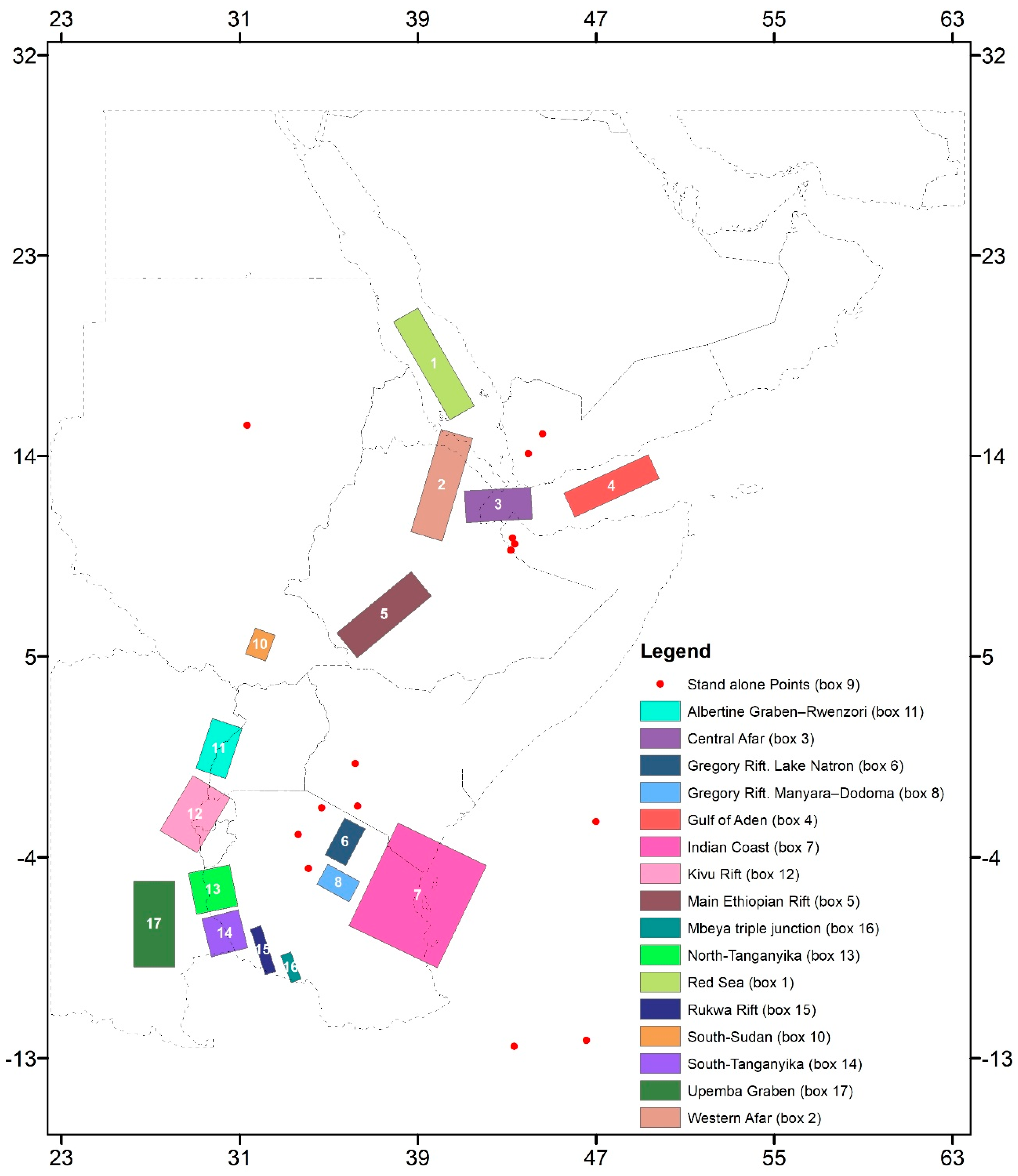
3.1. Study Area
3.2. Data
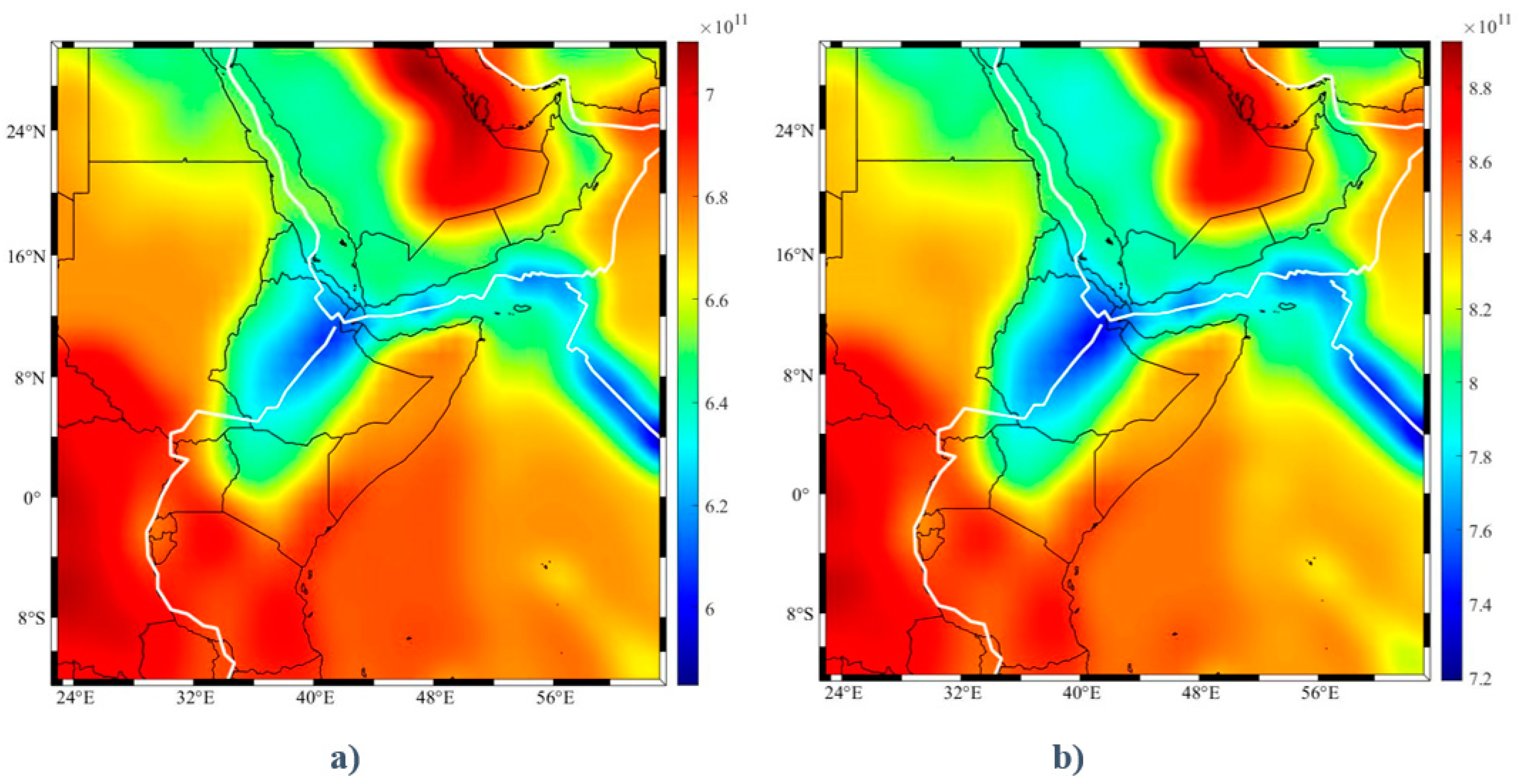
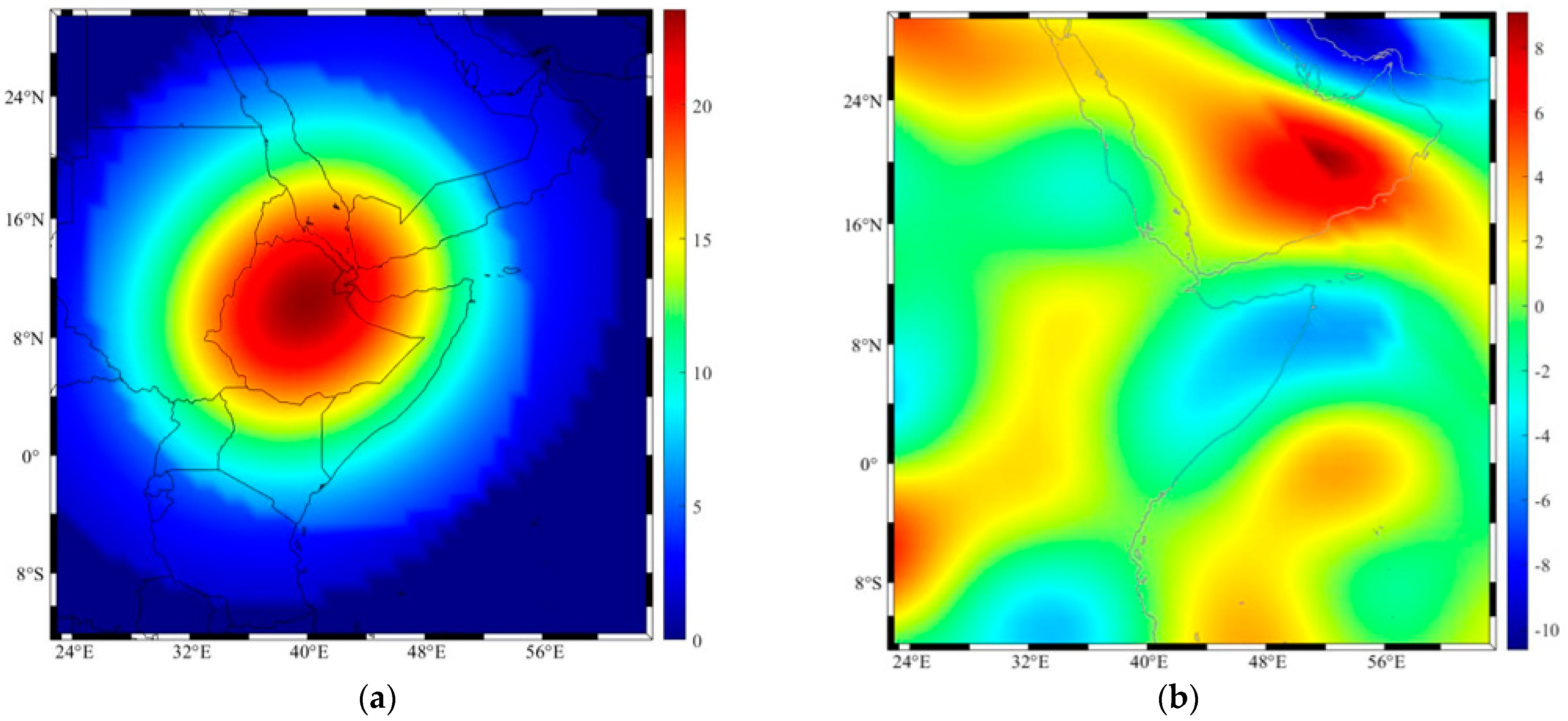
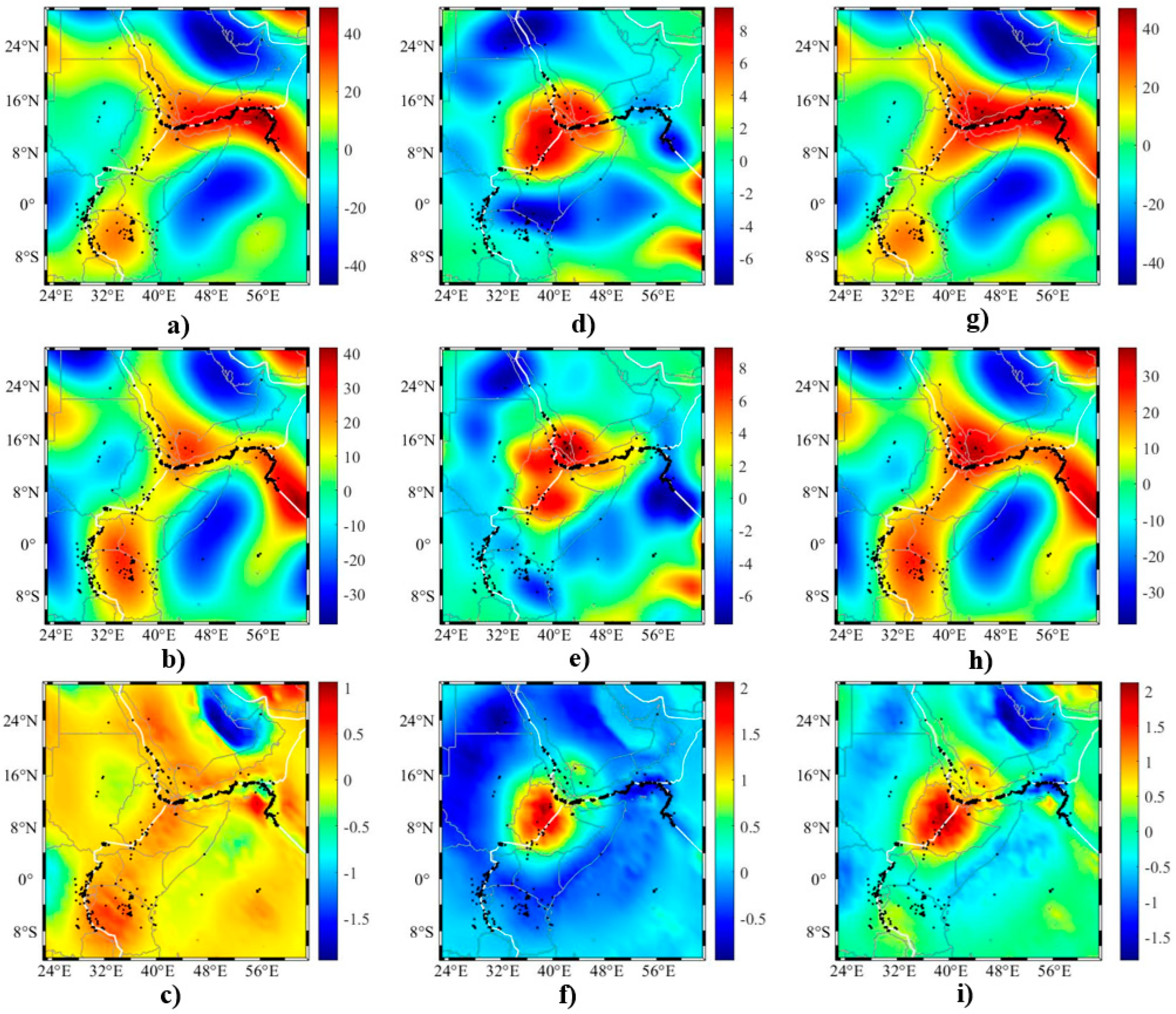
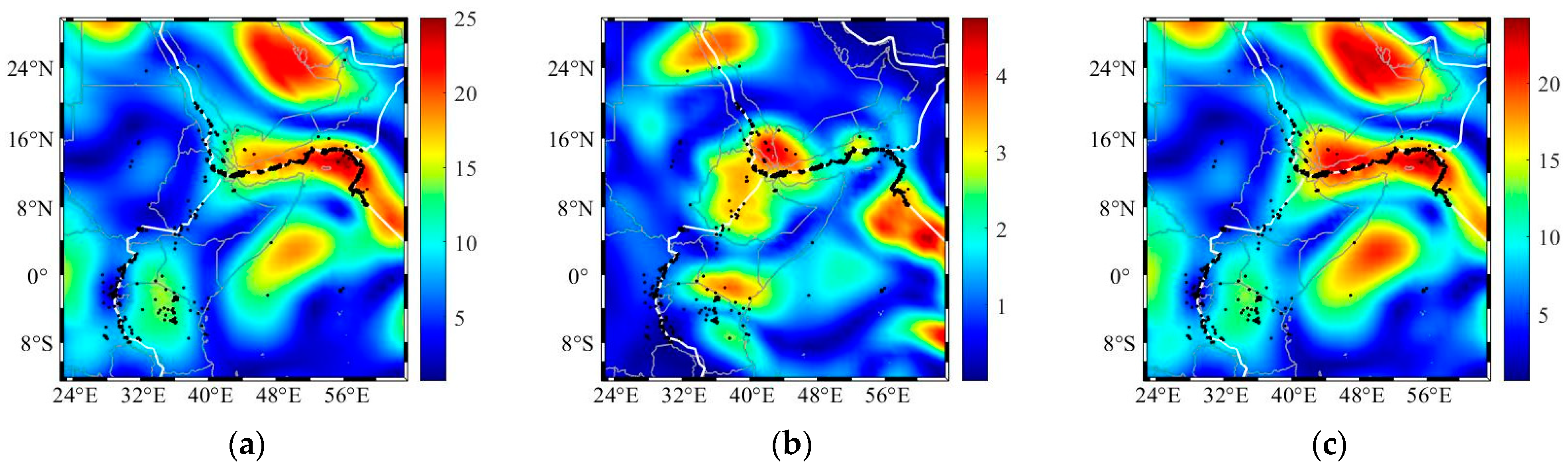
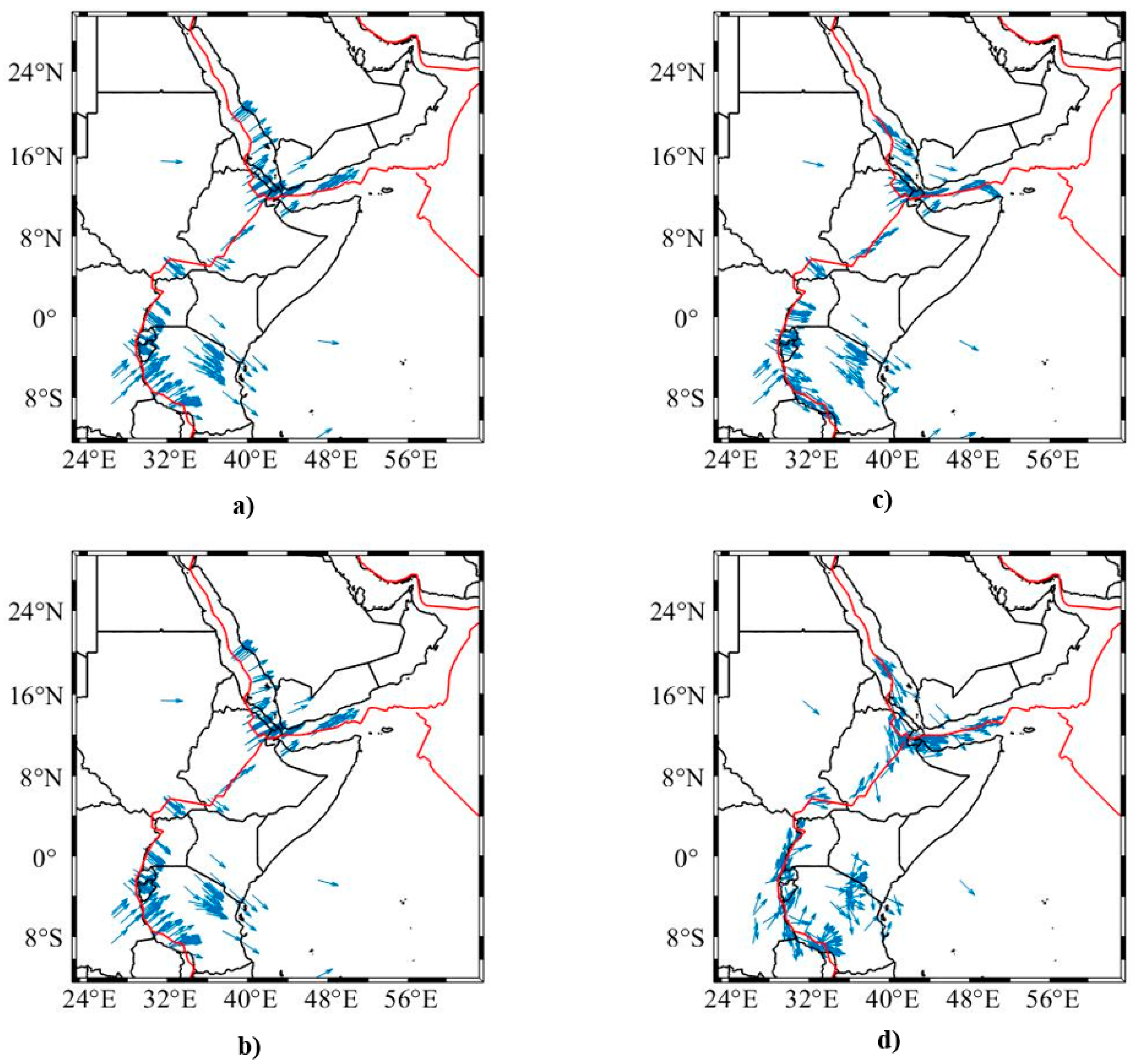
4. Lithospheric Stress Using Mantle Convection and Mantle Plume
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Teisseyre, R.; Czechowski, L.; Leliwa-Kopystyński, J.B.T.-D. (Eds.) 5—The Evolving Earth and its Lithospheric Stresses. In Physics and Evolution of the Earth’s Interior; Elsevier: Amsterdam, The Netherlands, 1993; pp. 272–347. ISBN 09269606. [Google Scholar]
- Aldaajani, T.Z.; Almalki, K.A.; Betts, P.G. Plume Versus Slab-Pull: Example from the Arabian Plate. Front. Earth Sci. 2021, 9, 494. [Google Scholar] [CrossRef]
- Liu, H.-S. Convection pattern and stress system under the African plate. Phys. Earth Planet. Inter. 1977, 15, 60–68. [Google Scholar] [CrossRef]
- Runcorn, S.K. Flow in the Mantle Inferred from the Low Degree Harmonics of the Geopotential. Geophys. J. Int. 1967, 14, 375–384. [Google Scholar] [CrossRef]
- McKenzie, D.P. Some remarks on heat flow and gravity anomalies. J. Geophys. Res. 1967, 72, 6261–6273. [Google Scholar] [CrossRef]
- Marsh, B.; Marsh, J. On global gravity anomalies and two-scale mantle convection. J. Geophys. Res. 1976, 81, 5267–5280. [Google Scholar] [CrossRef]
- Hager, B.H.; O’Connell, R.J. A simple global model of plate dynamics and mantle convection. J. Geophys. Res. Solid Earth 1981, 86, 4843–4867. [Google Scholar] [CrossRef]
- Liu, H.-S. Mantle convection pattern and subcrustal stress field under Asia. Phys. Earth Planet. Inter. 1978, 16, 247–256. [Google Scholar] [CrossRef]
- Pei-Hua, H.; Rong-Shan, F. The mantle convection pattern and force source mechanism of recent tectonic movement in China. Phys. Earth Planet. Inter. 1982, 28, 261–268. [Google Scholar] [CrossRef]
- Fu, R.; Huang, P. The global stress field in the lithosphere obtained from the satellite gravitational harmonics. Phys. Earth Planet. Inter. 1983, 31, 269–276. [Google Scholar] [CrossRef]
- Liu, H.-S. A dynamical basis for crustal deformation and seismotectonic block movements in central Europe. Phys. Earth Planet. Inter. 1983, 32, 146–159. [Google Scholar] [CrossRef]
- Rong-Shan, F. Plate Motions, Earth’S Geoid Anomalies, and Mantle Convection. Slow Deform. Transm. Stress Earth 1989, 49, 47–54. [Google Scholar] [CrossRef]
- Fu, R.; Huang, J. Global stress pattern constrained on deep mantle flow and tectonic features. Phys. Earth Planet. Inter. 1990, 60, 314–323. [Google Scholar] [CrossRef]
- ESA. Gravity Field and Steady-State Ocean Circulation Mission, ESA SP-1233(1), Report for Mission Selection of the Four Candidate Earth Explorer Missions; ESA Publications Division: Noordwijk, The Netherlands, 1999. [Google Scholar]
- Eshagh, M. From Satellite Gradiometry Data to Subcrustal Stress Due to Mantle Convection. Pure Appl. Geophys. 2014, 171, 2391–2406. [Google Scholar] [CrossRef]
- Eshagh, M. Local recovery of lithospheric stress tensor from GOCE gravitational tensor. Geophys. J. Int. 2017, 209, 317–333. [Google Scholar] [CrossRef]
- Eshagh, M.; Fatolazadeh, F.; Tenzer, R. Lithospheric stress, strain and displacement changes from GRACE-FO time-variable gravity: Case study for Sar-e-Pol Zahab Earthquake 2018. Geophys. J. Int. 2020, 223, 379–397. [Google Scholar] [CrossRef]
- Kornfeld, R.P.; Arnold, B.W.; Gross, M.A.; Dahya, N.T.; Klipstein, W.M.; Gath, P.F.; Bettadpur, S. GRACE-FO: The Gravity Recovery and Climate Experiment Follow-On Mission. J. Spacecr. Rockets 2019, 56, 931–951. [Google Scholar] [CrossRef]
- Eshagh, M. Satellite Gravimetry and the Solid Earth: Mathematical Foundations; Elsevier: Amsterdam, The Netherlands, 2020; ISBN 9780128169360. [Google Scholar]
- Morgan, W.J. Gravity anomalies and convection currents: 1. A sphere and cylinder sinking beneath the surface of a viscous fluid. J. Geophys. Res. 1965, 70, 6175–6187. [Google Scholar] [CrossRef]
- Sembroni, A.; Faccenna, C.; Becker, T.W.; Molin, P.; Abebe, B. Long-term, deep-mantle support of the Ethiopia-Yemen Plateau. Tectonics 2016, 35, 469–488. [Google Scholar] [CrossRef] [Green Version]
- Gvirtzman, Z.; Faccenna, C.; Becker, T.W. Isostasy, flexure, and dynamic topography. Tectonophysics 2016, 683, 255–271. [Google Scholar] [CrossRef] [Green Version]
- Heidbach, O.; Rajabi, M.; Cui, X.; Fuchs, K.; Müller, B.; Reinecker, J.; Reiter, K.; Tingay, M.; Wenzel, F.; Xie, F.; et al. The World Stress Map database release 2016: Crustal stress pattern across scales. Tectonophysics 2018, 744, 484–498. [Google Scholar] [CrossRef]
- Molnar, P.; England, P.C.; Jones, C.H. Mantle dynamics, isostasy, and the support of high terrain. J. Geophys. Res. Solid Earth 2015, 120, 1932–1957. [Google Scholar] [CrossRef]
- Gedamu, A.A.; Eshagh, M.; Bedada, T.B. Effects of mantle dynamics on estimating effective elastic thickness of the lithosphere. J. African Earth Sci. 2021, 183, 104318. [Google Scholar] [CrossRef]
- Bird, P. An updated digital model of plate boundaries. Geochem. Geophys. Geosystems 2003, 4, 60–68. [Google Scholar] [CrossRef]
- Varet, J. Geology of Afar (East Africa); Springer: Cham, Switzerland, 2017. [Google Scholar]
- Hayes, G.P.; Jones, E.S.; Stadler, T.J.; Barnhart, W.D.; McNamara, D.E.; Benz, H.M.; Furlong, K.P.; Villaseñor, A. Seismicity of the Earth 1900-2013 East African Rift; US Geological Survey: Reston, VA, USA, 2014.
- Eshagh, M.; Pitoňák, M. Elastic Thickness Determination from on-orbit GOCE Data and CRUST1.0. Pure Appl. Geophys. 2019, 176, 685–696. [Google Scholar] [CrossRef] [Green Version]
- Laske, G.; Masters, G.; Ma, Z.; Pasyanos, M. Update on CRUST1.0-A 1-degree Global Model of Earth’s Crust. In EGU General Assembly Conference Abstracts; AA (SIO, UCSD, IGPP-0225, La Jolla, United States (GLASKE@UCSD.EDU, 001 858-534 5332)), AB(SIO, UCSD, IGPP-0225, La Jolla, United States (GLASKE@UCSD.EDU, 001 858-534 5332)), AC(SIO, UCSD, IGPP-0225, La Jolla, United States (GLASKE@UCSD.EDU, 001 858-534 53)); La Jolla, CA, USA, 2013; p. EGU2013-2658. Available online: https://ui.adsabs.harvard.edu/abs/2013EGUGA..15.2658L (accessed on 11 December 2022).
- Gedamu, A.A.; Eshagh, M.; Bedada, T.B. Moho determination from GOCE gradiometry data over Ethiopia. J. African Earth Sci. 2020, 163, 103741. [Google Scholar] [CrossRef]
- Brockmann, J.M.; Schubert, T.; Schuh, W.-D. An Improved Model of the Earth’s Static Gravity Field Solely Derived from Reprocessed GOCE Data. Surv. Geophys. 2021, 42, 277–316. [Google Scholar] [CrossRef]
- Panet, I.; Pajot-Métivier, G.; Greff-Lefftz, M.; Métivier, L.; Diament, M.; Mandea, M. Mapping the mass distribution of Earth’s mantle using satellite-derived gravity gradients. Nat. Geosci. 2014, 7, 131–135. [Google Scholar] [CrossRef]
- Runcorn, S. Satellite Gravity Measurements and a Laminar Viscous Flow Model of the Earth’s Mantle. J. Geophys. Res. 1964, 69, 4389–4394. [Google Scholar] [CrossRef]
- Rouby, H.; Greff-Lefftz, M.; Besse, J. Mantle dynamics, geoid, inertia and TPW since 120Myr. Earth Planet. Sci. Lett. 2010, 292, 301–311. [Google Scholar] [CrossRef]
- Conrad, C.P.; Lithgow-Bertelloni, C. Influence of continental roots and asthenosphere on plate-mantle coupling. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef] [Green Version]
- Schubert, G.; Turcotte, D.L.; Olson, P. Mantle Convection in the Earth and Planets; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Phillips, R.J.; Lambeck, K. Gravity fields of the terrestrial planets: Long-wavelength anomalies and tectonics. Rev. Geophys. 1980, 18, 27–76. [Google Scholar] [CrossRef]
- Tenzer, R.; Eshagh, M.; Jin, S. Martian sub-crustal stress from gravity and topographic models. Earth Planet. Sci. Lett. 2015, 425, 84–92. [Google Scholar] [CrossRef]
- Al-Dabbagh, M.E. The Arabian Plate: Unique fit of the earth’s surface jig saw puzzle. Arab. J. Geosci. 2014, 7, 3297–3307. [Google Scholar] [CrossRef]
- Delvaux, D.; Barth, A. African stress pattern from formal inversion of focal mechanism data. Tectonophysics 2010, 482, 105–128. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gedamu, A.A.; Eshagh, M.; Bedada, T.B. Lithospheric Stress Due to Mantle Convection and Mantle Plume over East Africa from GOCE and Seismic Data. Remote Sens. 2023, 15, 462. https://doi.org/10.3390/rs15020462
Gedamu AA, Eshagh M, Bedada TB. Lithospheric Stress Due to Mantle Convection and Mantle Plume over East Africa from GOCE and Seismic Data. Remote Sensing. 2023; 15(2):462. https://doi.org/10.3390/rs15020462
Chicago/Turabian StyleGedamu, Andenet A., Mehdi Eshagh, and Tulu B. Bedada. 2023. "Lithospheric Stress Due to Mantle Convection and Mantle Plume over East Africa from GOCE and Seismic Data" Remote Sensing 15, no. 2: 462. https://doi.org/10.3390/rs15020462
APA StyleGedamu, A. A., Eshagh, M., & Bedada, T. B. (2023). Lithospheric Stress Due to Mantle Convection and Mantle Plume over East Africa from GOCE and Seismic Data. Remote Sensing, 15(2), 462. https://doi.org/10.3390/rs15020462






