HDM-RRT: A Fast HD-Map-Guided Motion Planning Algorithm for Autonomous Driving in the Campus Environment
Abstract
1. Introduction
- (1)
- We propose a CR-Map layer to quantify the collision risk coefficient on the road, greatly expanding the prior information of the HD-Map to guide motion planning. The CR-Map is combined with Gaussian distribution for sampling, which significantly improves the efficiency of motion planning algorithms in campus scenes.
- (2)
- The node optimization strategy of the sampling-based algorithm is deeply optimized through the prior information of the CR-Map, which greatly improves the convergence rate, reduces the number of iterations and solves the problem of poor stability in campus environments.
- (3)
- The proposed HDM-RRT algorithm achieves optimal real-time performance and high-quality trajectories for autonomous driving in campus scenes. It is of great significance for applications such as self-driving buses, last-mile delivery logistics and unmanned patrol vehicles in campus and residential environments.
2. Related Work
3. Fundamentals of Algorithms
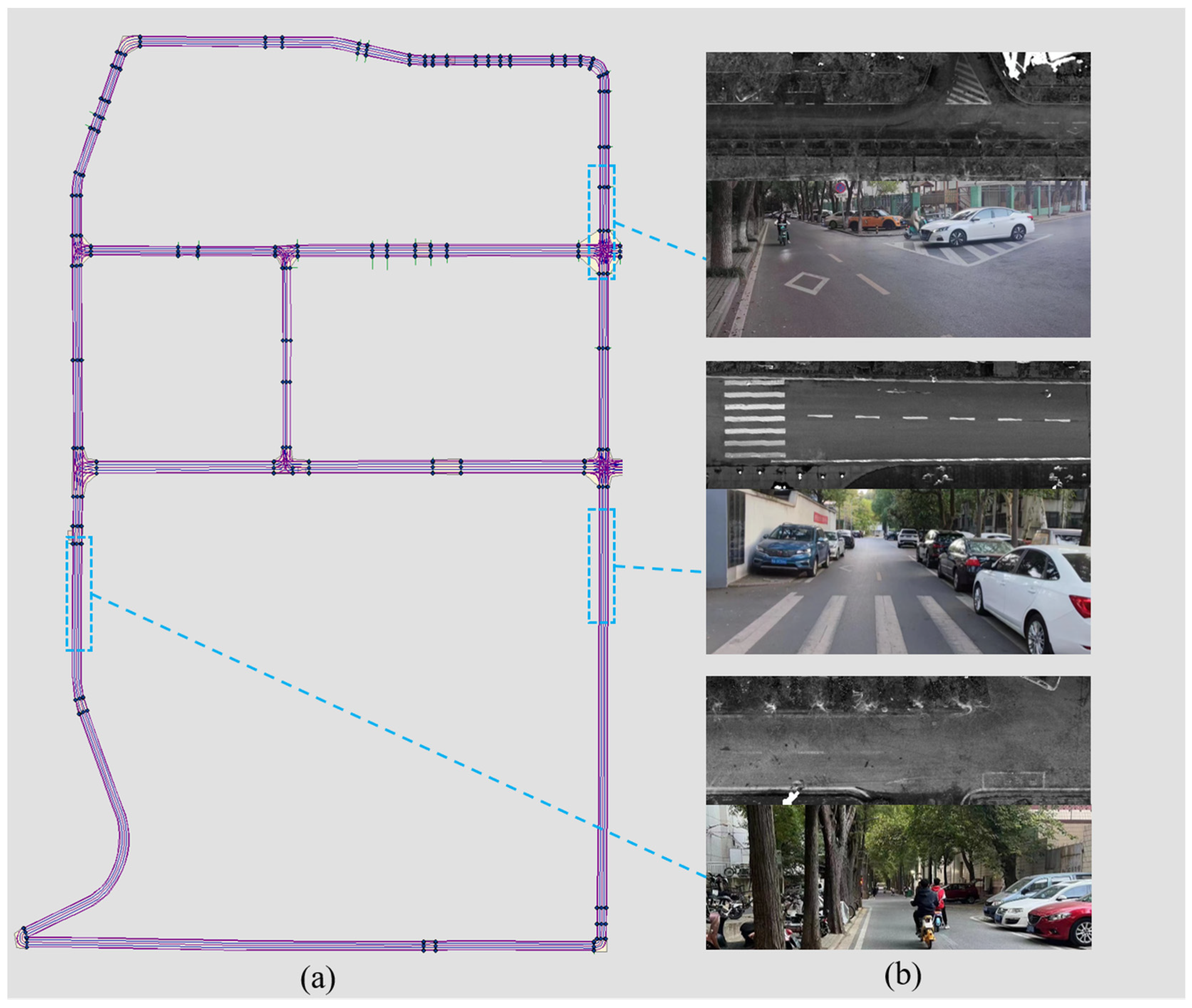
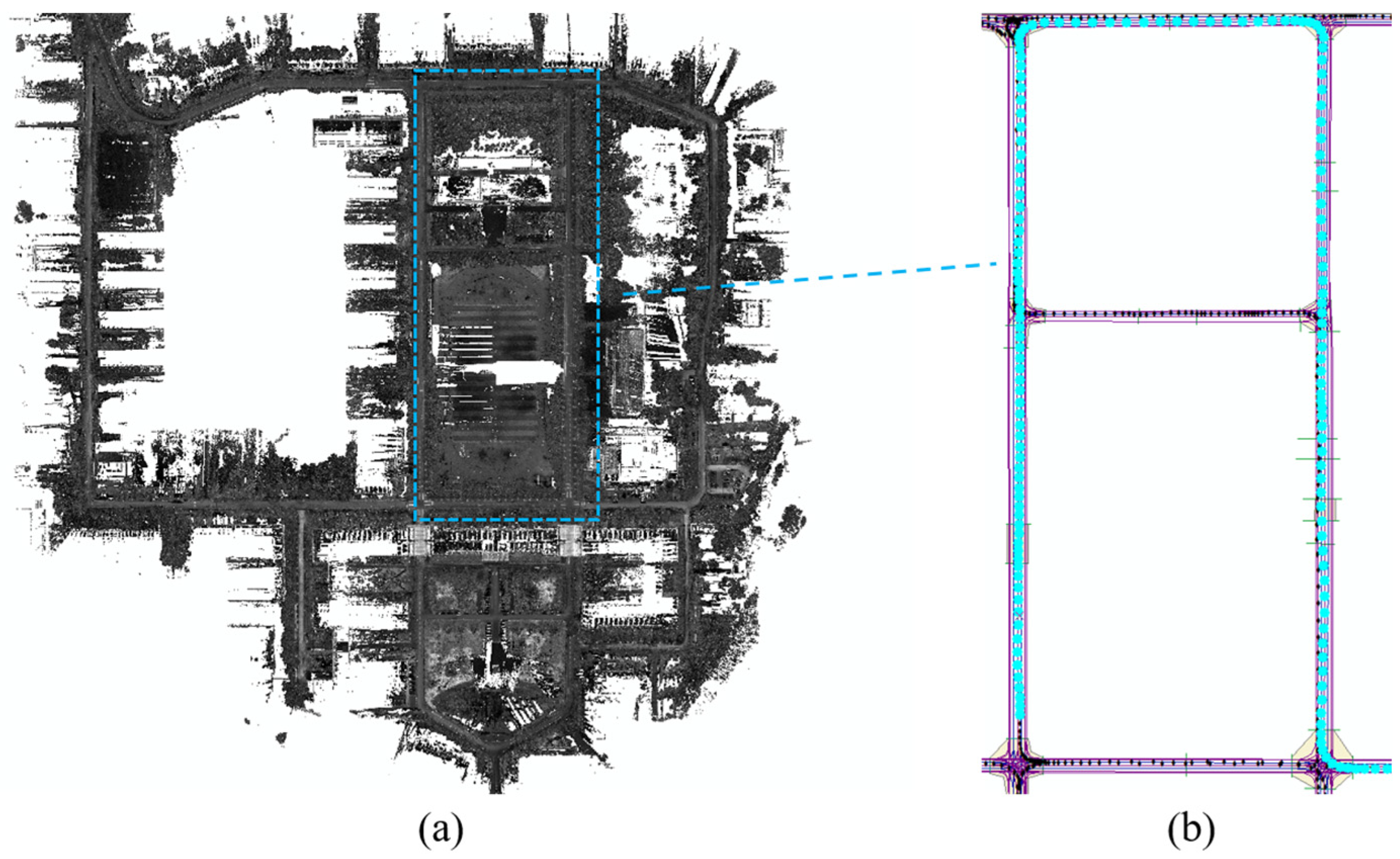
3.1. HD-Map of Wuhan University
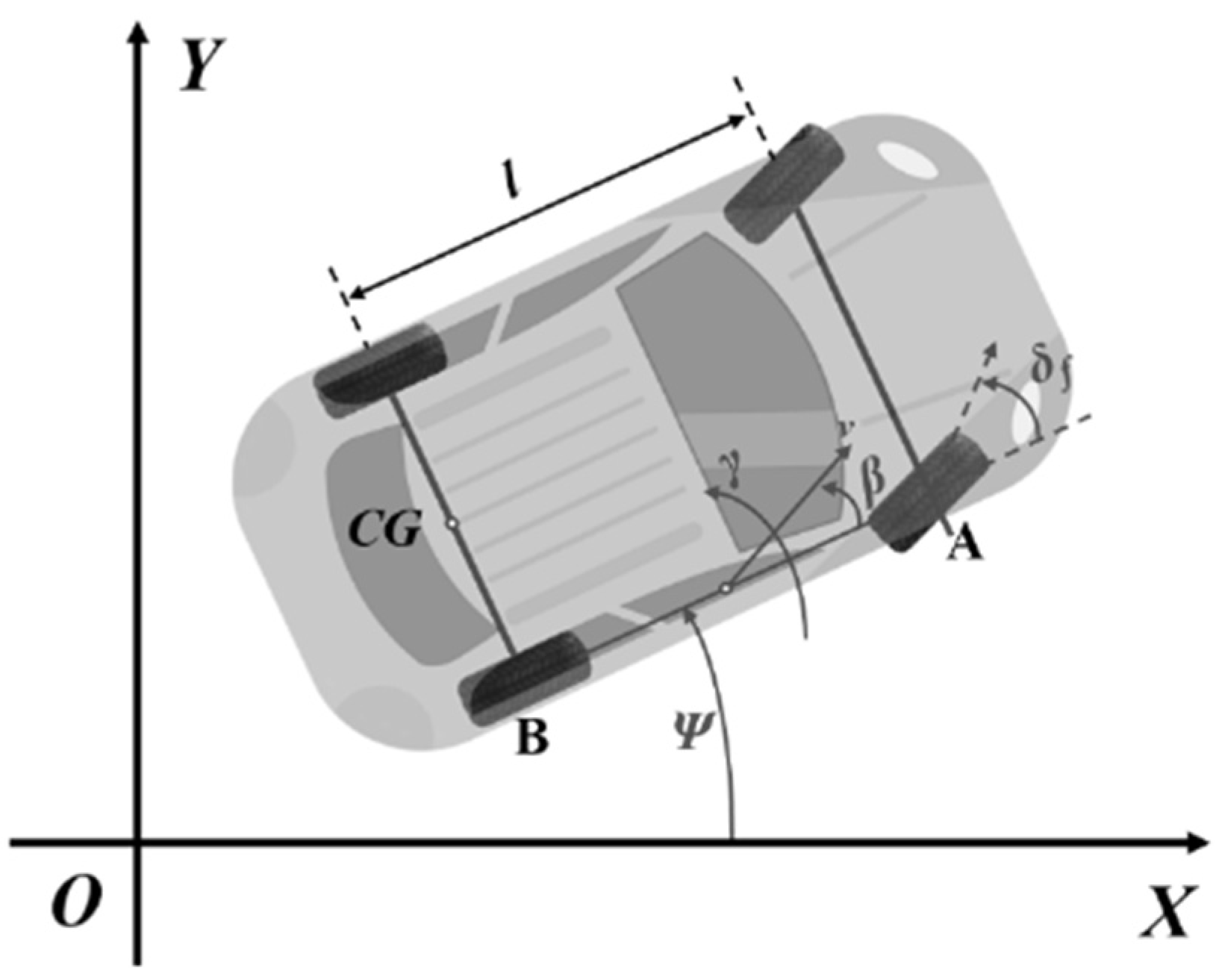
3.2. Vehicle Kinematic Model and Steering
- (1)
- : checks the obstacle collision; if the is feasible, it returns true.
- (2)
- : returns a random sample point without collision.
- (3)
- : returns the nodeclosest to pointin the tree.
- (4)
- : returns the set of nodes near the node in the tree.
- (5)
- : propagates a local pathfrom pointto point.
3.3. Sampling-Based Algorithms: RRT and RRT*
| Algorithm 1: RRT* |
| 1: Tree (V ← xinit E ←Ø); |
| 2: while Flag_stop do |
| 3: xrand ← SampleFree; |
| 4: xnearest ← Nearest(T = (V,E), xrand); |
| 5: xnew ← Steer(xnearest, xrand); |
| 6: costmin ←∞; |
| 7: if Collision_free(xnearest, xnew) then |
| 8: Xnearnodes ← NearNodes(T = (V,E), xnew); |
| 9: foreach xnear in Xnearnodes do |
| 10: Rewire (xnear, xnew, costmin); |
| 11: end |
| 12: V ←V ∪ {xnew}; |
| 13: E ← E ∪ {(xnearest, xnew)}; |
| 14: foreach xnear in Xnearnodes do |
| 15: if Rewire (xnew, xnear, costmin) then |
| 16: xparent ← Parent(xnear); |
| 17: E ← E{(xparent, xnear)}∪{(xnew, xnear)}; |
| 18: end |
| 19: end |
| 20: end |
| 21: end |
| Algorithm 2: Rewire (x1, x2, costmin) |
| 1: if cost(x1) + cost(Line(x1, x2)) < costmin then |
| 2: costmin ← cost(x1) + cost(Line(x1, x2)); |
| 3: Return true |
| 4: end |
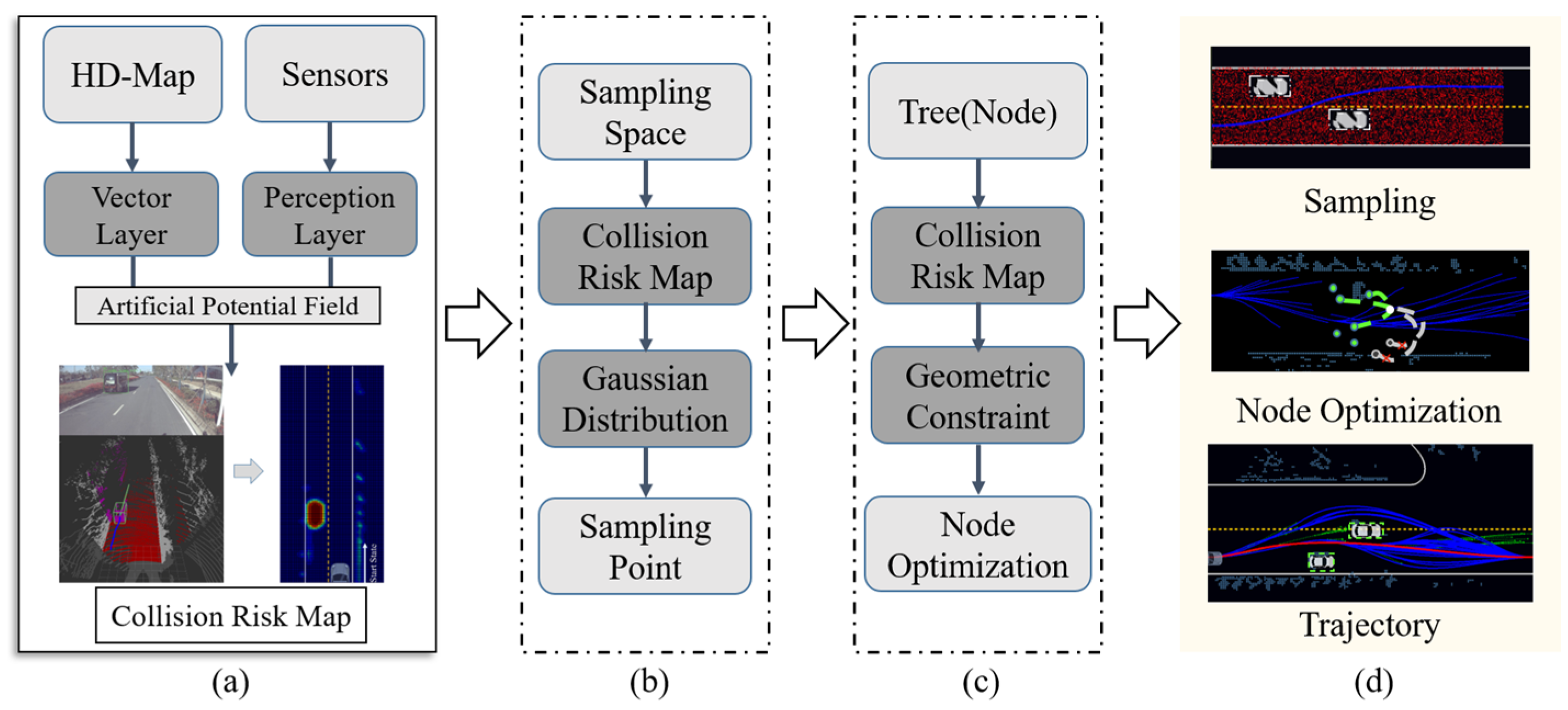
4. The Proposed HDM-RRT Algorithm
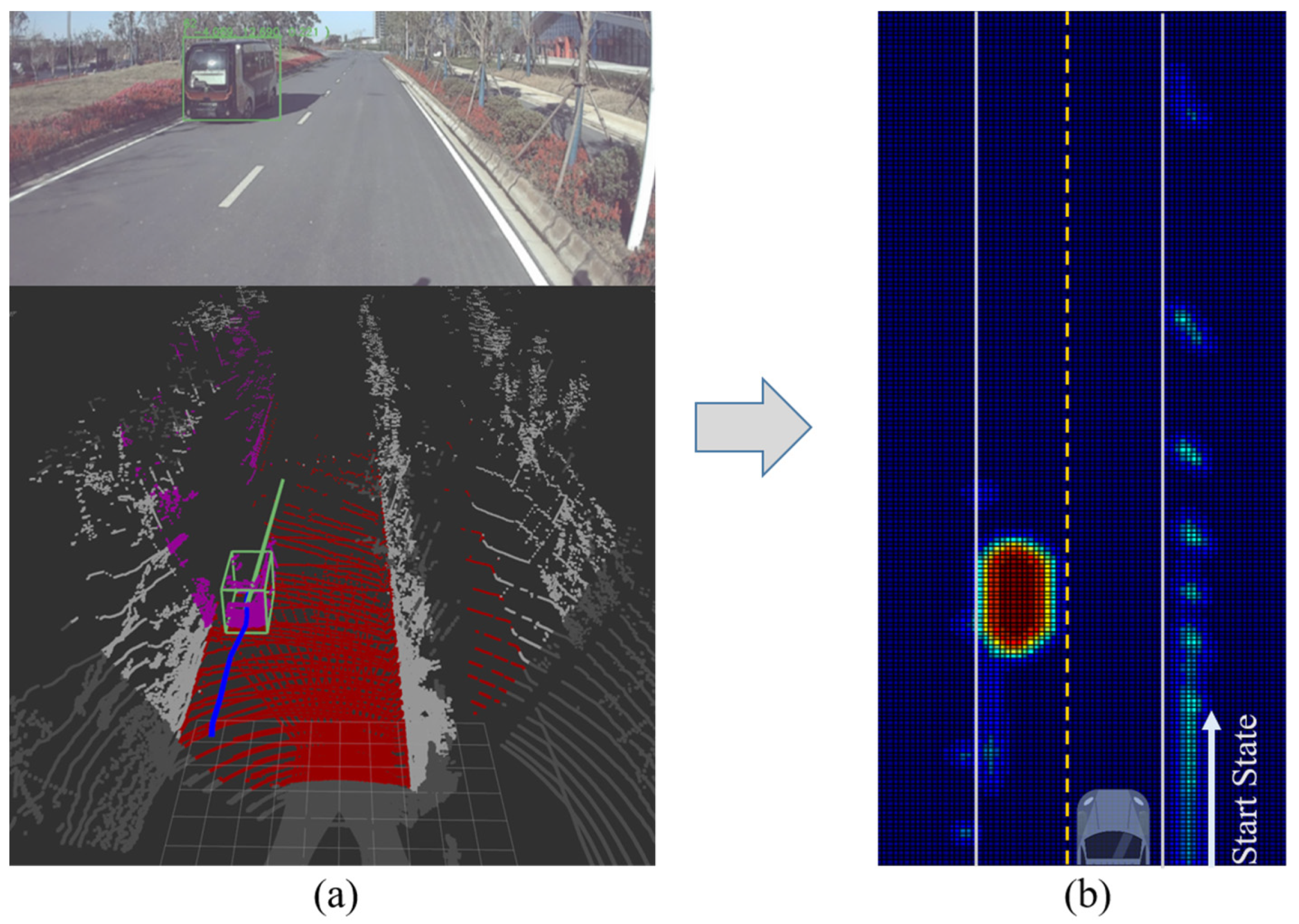
4.1. Collision Risk Map (CR-Map)
4.2. Structure of the Proposed HDM-RRT Algorithm
| Algorithm 3: HDM_RRT* |
| 1: Tree (V ← xinit E ←Ø); |
| 2: xrand ← CR_GussianSampling; |
| 3: xnearnodes ← Nearest(T = (V, E), xrand); |
| 4: foreach xnear in xnearnodes sort() do |
| 5: xnew = Steer(xrand, xnearnodes); |
| 6: if constrains_check() then |
| 7: xtemp = xnear; |
| 8: Break; |
| 9: end |
| 10: end |
| 11: xnearnodes ← Nearest(T = (V,E), xnew); |
| 12: foreach xnear in xnearnodes do |
| 13: if cost(xnew) < costmin && constrains_check() then |
| 14: costmin ← cost(xnew) |
| 15: xtemparent = xnear; |
| 16: end |
| 17: end |
| 18: xtemp = xtemparent; |
| 19: while xtemp!= xinit do |
| 20: xtemp = xtemp.getparent(); |
| 21: if cost(xtemp) + cost(xtemp, xnew) < costmin && constrains_check() then |
| 22: Costmin ← cost(xtemp) + cost(xtemp, xnew); |
| 23: xfinalparent = xtemp; |
| 24: end |
| 25: end |
| 26: V ← V ∪{xnew}; E ← E ∪{(xfinalparent, xnew)}; |
| 27: Flag_add = true; |
4.2.1. Sampling Strategy
| Algorithm 4: CR_GussianSampling |
| 1: x0, y0, θ0 = GetReferencepoint(); |
| 2: do |
| 3: Radiusrandom, θrandom = BoxMuller(); |
| 4: Radius = σradius * abs(Radiusrandom); |
| 5: θ = σθ * θrandom + θ0; |
| 6: RandomPoint.x = x0 + Radius * cos(θ); |
| 7: RandomPoint.y = y0 + Radius * sin(θ); |
| 8: while (rand(max_risk) < CRcoefficient(RandomPoint)); |
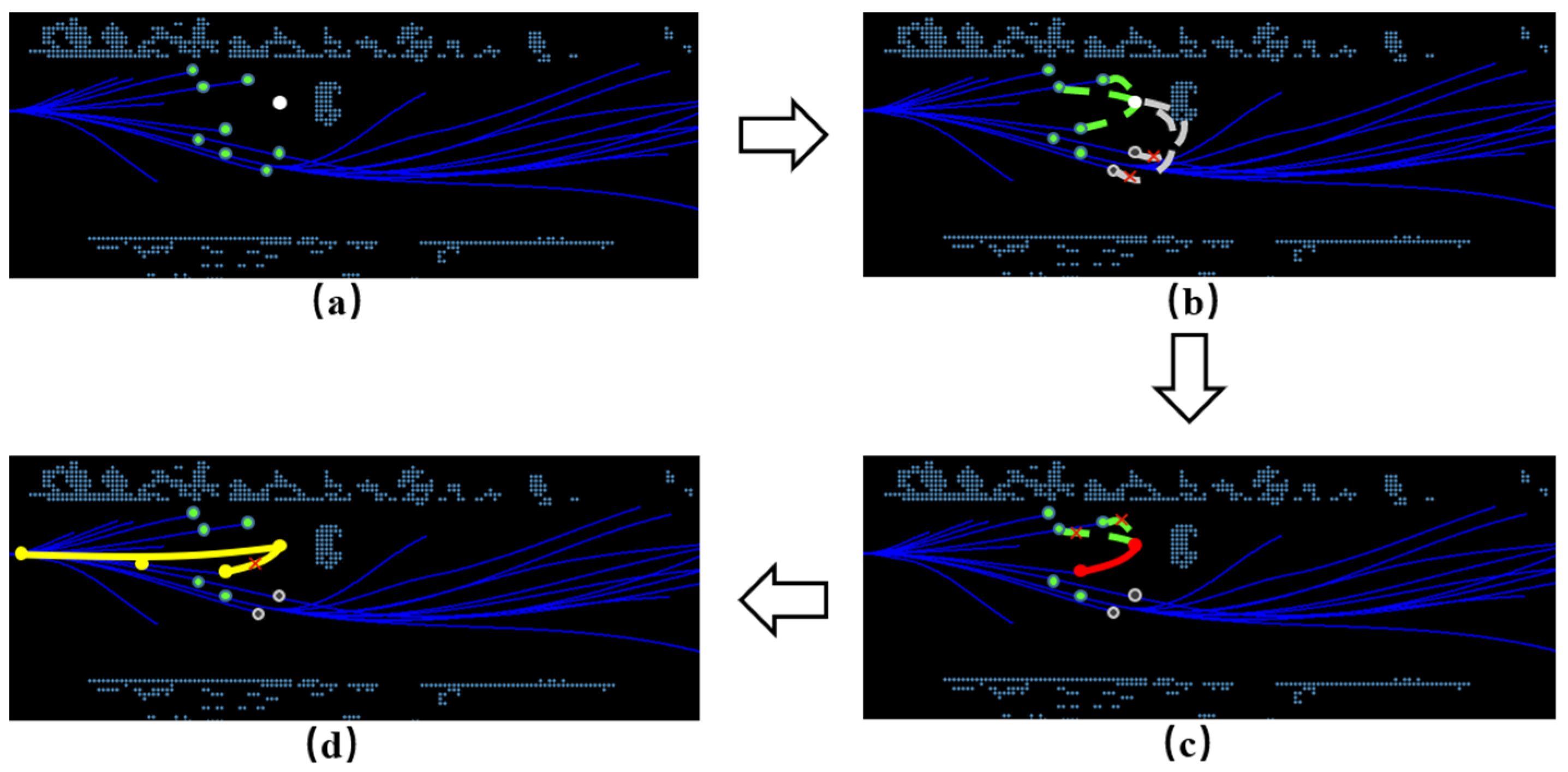
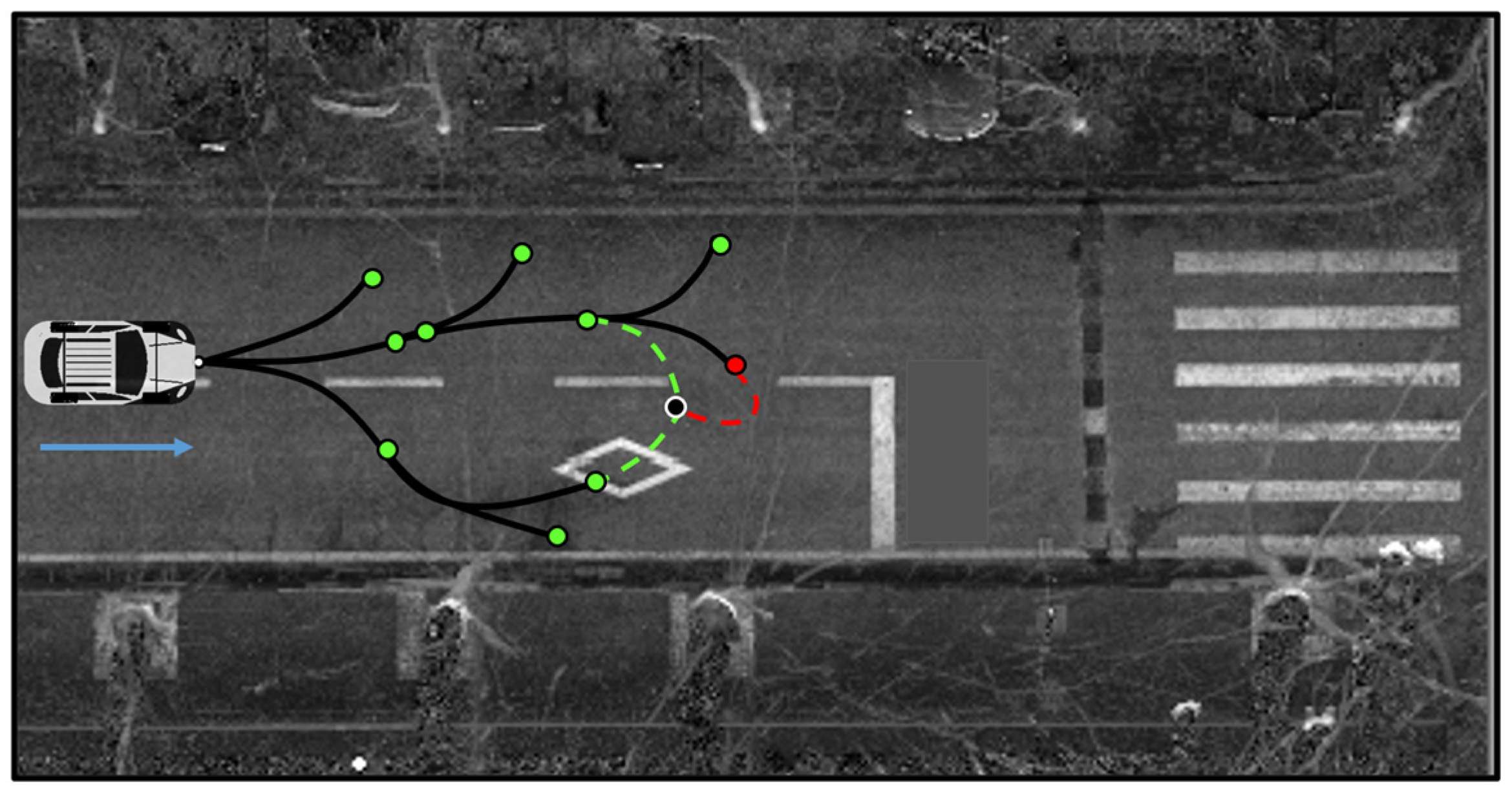
4.2.2. Node Optimization Strategy
4.2.3. Constraints and Filters
- (1)
- Curvature constraint: The Dubins curve is one of the most widely used trajectory methods in autonomous driving, but its curvature is not continuous, which is not conducive to the stability of AVs. The clothoid curve is employed to generate the trajectory from state A to state B. As discussed in Section 3.2, the clothoid curve is a G1 continuous curve generated using the Fresnel integral. Unlike the curvature discontinuities of the Dubins curve, the curvature of the clothoid curve varies linearly with the arc. Studies have shown that the clothoid curve is highly consistent with vehicle driving [45]. In calculating the clothoid curve, it is easy to obtain the curvature of the starting point and goal point, and the curvature rate. By limiting the curve curvature, the trajectory quality can be controlled effectively and fit the vehicle steering model.
- (2)
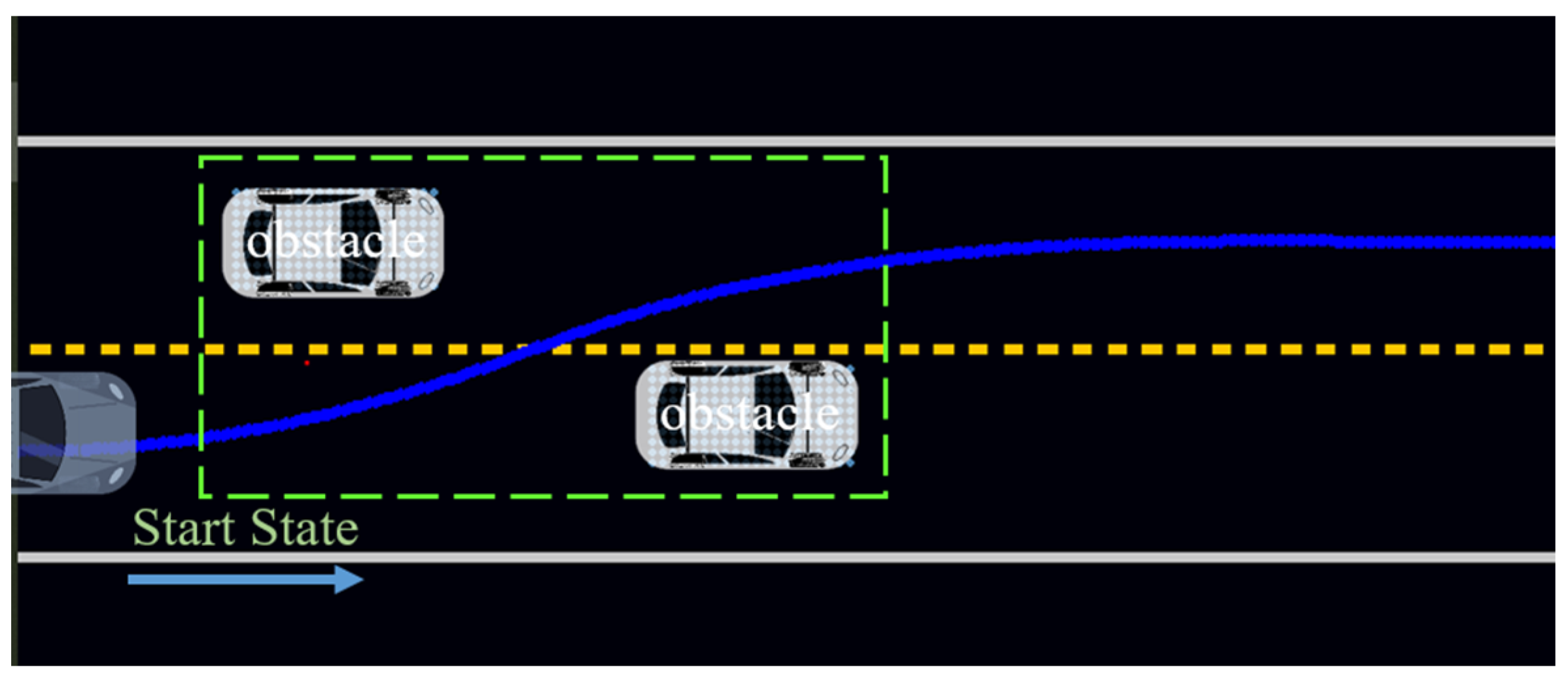
- Detour constraint: In actual traffic scenes, roads are directional. When driving a vehicle on the road, it must comply with the traffic rules’ constraints and cannot be turned around at will. Therefore, we added a circuitous constraint here. It is required that the sampling point should not select a node whose relative direction is opposite to the road direction. The schematic diagram is shown in Figure 11.
- (3)
- Turning radius constraint: The trajectory needs to meet the kinodynamic constraints of the vehicle when driving, and each vehicle has its turning radius. Therefore, it is necessary to add the constraint of the vehicle’s turning radius to the curve so that the vehicle can pursue the planned trajectory better, as shown in Equation (7):
5. Experiments and Analysis
5.1. Experimental Design
5.1.1. Experimental Purpose
5.1.2. Experimental Environment
5.1.3. Experimental Platform
5.1.4. Experimental Steps
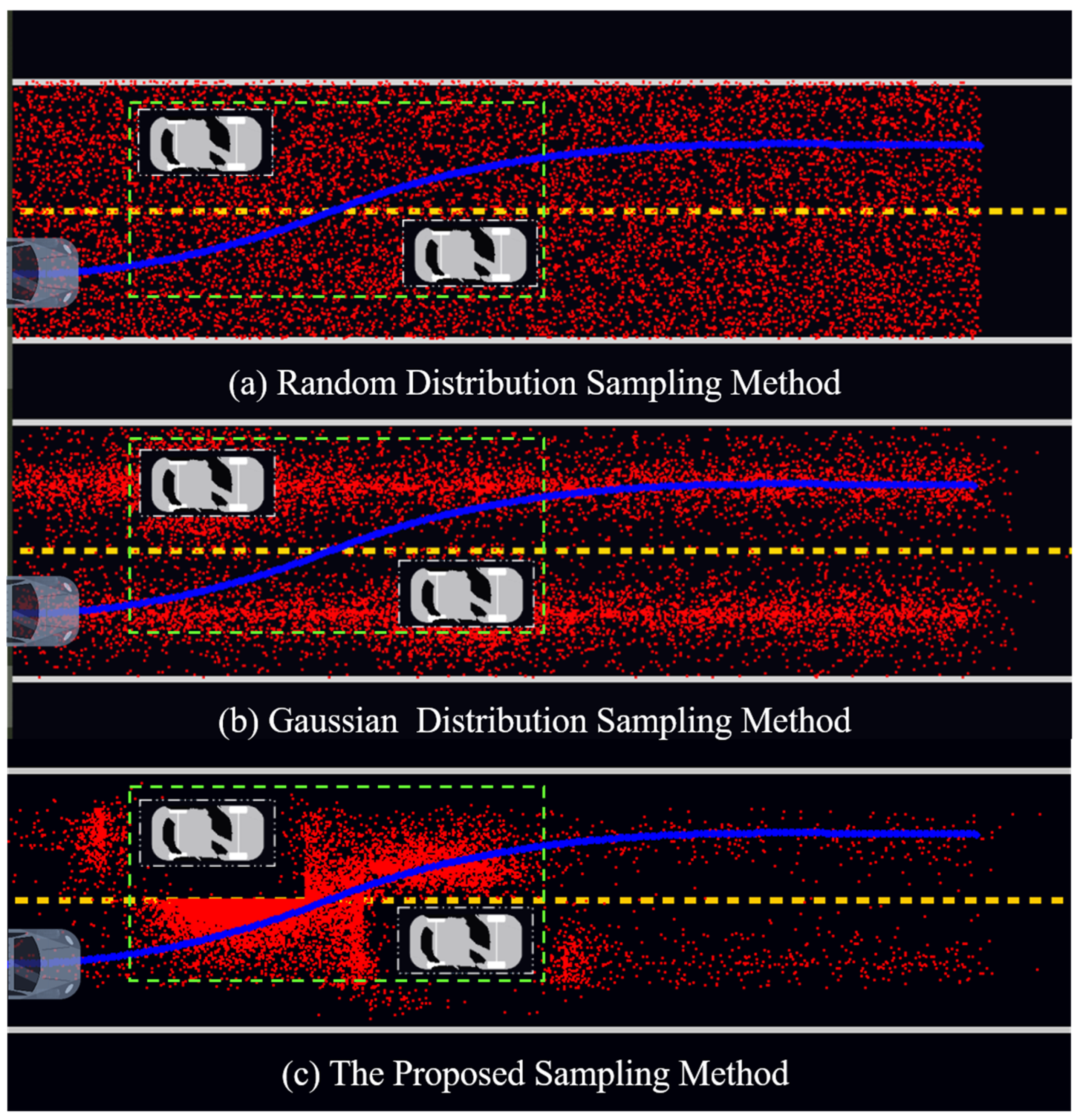
5.2. Sampling Efficiency Analysis
5.3. Node Optimization Analysis
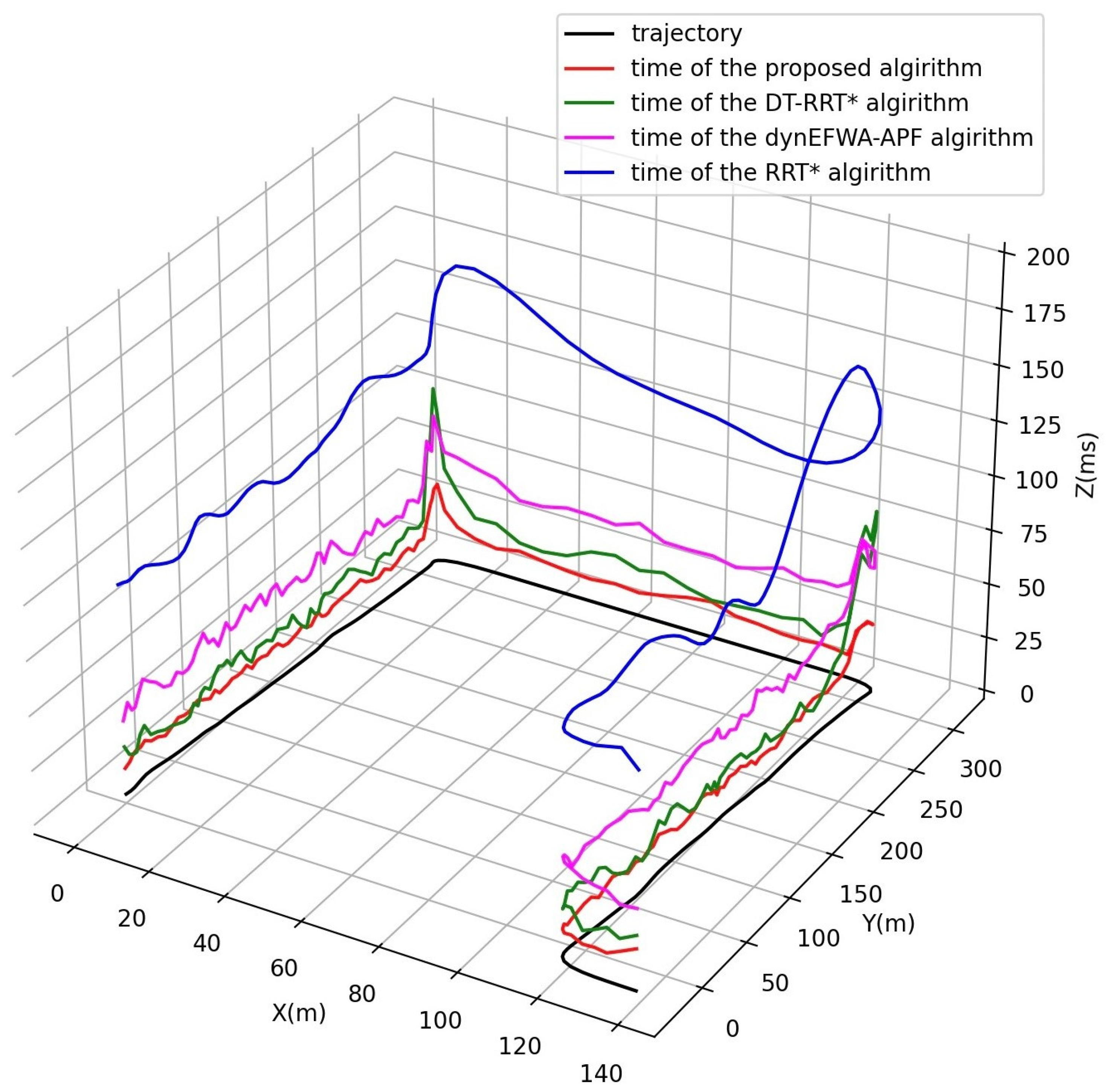
5.4. Algorithm Efficiency Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schwarting, W.; Alonso-Mora, J.; Rus, D. Planning and decision-making for autonomous vehicles. Annu. Rev. Control. Robot. Auton. Syst. 2018, 1, 187–210. [Google Scholar] [CrossRef]
- Pei, S.; Kretzschmar, H.; Dotiwalla, X.; Chouard, A.; Patnaik, V.; Tsui, P.; Guo, J.; Zhou, Y.; Chai, Y.; Caine, B.; et al. Scalability in perception for autonomous driving: Waymo open dataset. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 10 December 2019; pp. 2443–2451. [Google Scholar]
- Levinson, J.; Askeland, J.; Becker, J.; Dolson, J.; Held, D.; Kammel, S.; Kolter, J.Z.; Langer, D.; Pink, O.; Pratt, V.; et al. Towards fully autonomous driving: Systems and algorithms. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), New York, NY, USA, 5–9 June 2011; pp. 163–168. [Google Scholar]
- Zhou, J.; Guo, Y.; Bian, Y.; Huang, Y.; Li, B. Lane Information Extraction for High Definition Maps Using Crowdsourced Data. IEEE Trans. Intell. Transp. Syst. 2022, 1–11. [Google Scholar] [CrossRef]
- Aldibaja, M.; Suganuma, N.; Yanase, R. 2.5D Layered Sub-Image LIDAR Maps for Autonomous Driving in Multilevel Environments. Remote Sensing 2022, 14, 5847. [Google Scholar] [CrossRef]
- Xiao, J.; Guo, H.; Yao, Y.; Zhang, S.; Zhou, J.; Jiang, Z. Multi-Scale Object Detection with the Pixel Attention Mechanism in a Complex Background. Remote Sens. 2022, 14, 3969. [Google Scholar] [CrossRef]
- Zhang, H.; Li, W.; Qian, C.; Li, B. A real time localization system for vehicles using terrain-based time series subsequence matching. Remote Sens. 2020, 12, 2607. [Google Scholar] [CrossRef]
- Kang, M.-S.; Ahn, J.-H.; Im, J.-U.; Won, J.-H. Lidar- and V2X-Based Cooperative Localization Technique for Autonomous Driving in a GNSS-Denied Environment. Remote Sens. 2022, 14, 5881. [Google Scholar] [CrossRef]
- Shan, Y.; Zheng, B.; Chen, L.; Chen, L.; Chen, D. A reinforcement learning-based adaptive path tracking approach for autonomous driving. IEEE Trans. Veh. Technol. 2020, 69, 10581–10595. [Google Scholar] [CrossRef]
- Feng, G.; Han, Y.; Li, S.E.; Shaobing, X.; Dongfang, D. Accurate Pseudospectral Optimization of Nonlinear Model Predictive Control for High-performance Motion Planning. IEEE Trans. Intell. Veh. 2022, 1. [Google Scholar] [CrossRef]
- Latombe, J.C. Motion planning: A journey of robots, molecules, digital actors, and other artifacts. Int. J. Robot. Res. 1999, 18, 1119–1128. [Google Scholar] [CrossRef]
- Li, B.; Liu, S.; Tang, J.; Gaudiot, J.L.; Zhang, L.; Kong, Q. Autonomous last-mile delivery vehicles in complex traffic environments. Computer 2020, 53, 26–35. [Google Scholar] [CrossRef]
- Wu, Y.; Ding, Y.; Ding, S.; Savaria, Y.; Li, M. Autonomous Last-Mile Delivery Based on the Cooperation of Multiple Heterogeneous Unmanned Ground Vehicles. Math. Probl. Eng. 2021, 2021, 5546581. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, L.; Kong, Q.; Zhu, W.; Zheng, J.; Zhuang, L.; Xu, X. Motion planning in complex urban environments: An industrial application on autonomous last-mile delivery vehicles. J. Field Robot. 2022, 39, 1258–1285. [Google Scholar] [CrossRef]
- Dolgov, D.; Thrun, S.; Montemerlo, M.; Diebel, J. Path planning for autonomous vehicles in unknown semi-structured environments. Int. J. Robot. Res. 2010, 29, 485–501. [Google Scholar] [CrossRef]
- Karur, K.; Sharma, N.; Dharmatti, C.; Siegel, J.E. A survey of path planning algorithms for mobile robots. Vehicles 2021, 3, 448–468. [Google Scholar] [CrossRef]
- Paden, B.; Čáp, M.; Yong, S.Z.; Yershov, D.; Frazzoli, E. A survey of motion planning and control techniques for self-driving urban vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–55. [Google Scholar] [CrossRef]
- LaValle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning; TR 98-11; Department of Computer Science, Iowa State University: Ames, IA, USA, 1998. [Google Scholar]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Wang, J.; Li, B.; Meng, M.Q.H. Kinematic Constrained Bi-directional RRT with Efficient Branch Pruning for robot path planning. Expert Syst. Appl. 2021, 170, 114541. [Google Scholar] [CrossRef]
- Chen, L.; Shan, Y.; Tian, W.; Li, B.; Cao, D. A fast and efficient double-tree RRT-like sampling-based planner applying on mobile robotic systems. IEEE/ASME Trans. Mechatron. 2018, 23, 2568–2578. [Google Scholar] [CrossRef]
- Zheng, L.; Song, H.; Li, B.; Zhang, H. Generation of lane-level road networks based on a trajectory-similarity-join pruning strategy. ISPRS Int. J. Geo.-Inf. 2019, 8, 416. [Google Scholar] [CrossRef]
- Zuo, X.; Zhou, J.; Yang, F.; Su, F.; Zhu, H.; Li, L. Real-time Global Action Planning for Unmanned Ground Vehicle Exploration in Three-dimensional Spaces. Expert Syst. Appl. 2022, 215, 119264. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Kathib, O. Real-time obstacle avoidance for manipulators and mobile robots. Int. J. Robot. Res. 1986, 5, 490–496. [Google Scholar]
- Min, H.; Xiong, X.; Wang, P.; Yu, Y. Autonomous driving path planning algorithm based on improved A algorithm in unstructured environment. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 513–526. [Google Scholar] [CrossRef]
- Tang, G.; Tang, C.; Claramunt, C.; Hu, X.; Zhou, P. Geometric A-star algorithm. An improved A-star algorithm for AGV path planning in a port environment. IEEE Access 2021, 9, 59196–59210. [Google Scholar] [CrossRef]
- Dolgov, D.; Thrun, S.; Montemerlo, M.; Diebel, J. Practical search techniques in path planning for autonomous driving. Ann. Arbor. 2008, 1001, 18–80. [Google Scholar]
- Koren, Y.; Borenstein, J. Potential field methods and their inherent limitations for mobile robot navigation. Icra 1991, 1398–1404. [Google Scholar]
- Xinyu, W.; Xiaojuan, L.; Yong, G.; Jiadong, S.; Rui, W. Bidirectional potential guided rrt for motion planning. IEEE Access 2019, 7, 95046–95057. [Google Scholar] [CrossRef]
- Wang, P.; Gao, S.; Li, L.; Sun, B.; Cheng, S. Obstacle avoidance path planning design for autonomous driving vehicles based on an improved artificial potential field algorithm. Energies 2019, 12, 2342. [Google Scholar] [CrossRef]
- Li, H.; Liu, W.; Yang, C.; Wang, W.; Qie, T.; Xiang, T. An Optimization-based Path Planning Approach for Autonomous Vehicles using dynEFWA-Artificial Potential Field. IEEE Trans. Intell. Veh. 2021, 7, 263–272. [Google Scholar] [CrossRef]
- LaValle, S.M.; Kuffner Jr, J.J. Randomized kinodynamic planning. Int. J. Robot. Res. 2001, 20, 378–400. [Google Scholar] [CrossRef]
- Kuwata, Y.; Teo, J.; Fiore, G.; Karaman, S.; Frazzoli, E.; How, J.P. Real-time motion planning with applications to autonomous urban driving. IEEE Trans. Control Syst. Technol. 2009, 17, 1105–1118. [Google Scholar] [CrossRef]
- Jaillet, L.; Hoffman, J.; Van den Berg, J.; Abbeel, P.; Porta, J.M.; Goldberg, K. EG-RRT: Environment-guided random trees for kinodynamic motion planning with uncertainty and obstacles. In Proceedings of the International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 2646–2652. [Google Scholar]
- Perez, A.; Platt, R.; Konidaris, G.; Kaelbling, L.; Lozano-Perez, T. LQR-RRT: Optimal sampling-based motion planning with automatically derived extension heuristics. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St Paul, MN, USA, 14–18 May 2012; pp. 2537–2542. [Google Scholar]
- Karaman, S.; Frazzoli, E. Incremental sampling-based algorithms for optimal motion planning. Robot. Sci. Syst. VI 2010, 104. [Google Scholar] [CrossRef]
- Gammell, J.D.; Strub, M.P. Asymptotically optimal sampling-based motion planning methods. Annu. Rev. Control. Robot. Auton. Syst. 2021, 4, 295–318. [Google Scholar] [CrossRef]
- Salzman, O.; Halperin, D. Asymptotically near-optimal RRT for fast, high-quality motion planning. IEEE Trans. Robot. 2016, 32, 473–483. [Google Scholar] [CrossRef]
- Littlefield, Z.; Bekris, K.E. Informed asymptotically near-optimal planning for field robots with dynamics. In Field and Service Robotics; Springer: Cham, Switzerland, 2018; pp. 449–463. [Google Scholar]
- Pareekutty, N.; James, F.; Ravindran, B.; Shah, S.V. qRRT: Quality-Biased Incremental RRT for Optimal Motion Planning in Non-Holonomic Systems. arXiv 2021, arXiv:2101.02635, 2021. [Google Scholar]
- Gan, Y.; Zhang, B.; Ke, C.; Zhu, X.; He, W.; Ihara, T. Research on Robot Motion Planning Based on RRT Algorithm with Nonholonomic Constraints. Neural Process. Lett. 2021, 53, 3011–3029. [Google Scholar] [CrossRef]
- Yuncheng, L.; Jie, S. A revised Gaussian distribution sampling scheme based on RRT algorithms in robot motion planning. In Proceedings of the 2017 3rd International Conference on Control, Automation and Robotics (ICCAR), Nagoya, Japan, 24–26 April 2017; pp. 22–26. [Google Scholar]
- Xi, H. Obstacle avoidance trajectory planning of redundant robots based on improved Bi-RRT. Int. J. Syst. Assur. Eng. Manag. 2021, 1–10. [Google Scholar] [CrossRef]
- Ge, Q.; Li, A.; Li, S.; Du, H.; Huang, X.; Niu, C. Improved Bidirectional RRT Path Planning Method for Smart Vehicle. Math. Probl. Eng. 2021, 2021, 6669728. [Google Scholar] [CrossRef]
- Qureshi, A.H.; Iqbal, K.F.; Qamar, S.M.; Islam, F.; Ayaz, Y.; Muhammad, N. Potential guided directional-RRT for accelerated motion planning in cluttered environments. In Proceedings of the 2013 IEEE International Conference on Mechatronics and Automation, Takamatsu, Japan, 4–7 August 2013; pp. 519–524. [Google Scholar]
- Tang, X.; Chen, F. Robot path planning algorithm based on bi-rrt and potential field. In Proceedings of the 2020 IEEE International Conference on Mechatronics and Automation (ICMA), Beijing, China, 13–16 October 2020; pp. 1251–1256. [Google Scholar]
- An, H.; Hu, J.; Lou, P. Obstacle Avoidance Path Planning Based on Improved APF and RRT. In Proceedings of the 2021 4th International Conference on Advanced Electronic Materials, Computers and Software Engineering (AEMCSE), Changsha, China, 26–28 March 2021; pp. 1028–1032. [Google Scholar]
- Polack, P.; Altché, F.; d’Andréa-Novel, B.; de La Fortelle, A. The kinematic bicycle model: A consistent model for planning feasible trajectories for autonomous vehicles? In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 812–818. [Google Scholar]
- Bertolazzi, E.; Frego, M. Fast and accurate clothoid fitting. arXiv 2012, arXiv:1209.0910. [Google Scholar]
- Shan, Y.; Yang, W.; Chen, C.; Zhou, J.; Zheng, L.; Li, B. CF-pursuit: A pursuit method with a clothoid fitting and a fuzzy controller for autonomous vehicles. Int. J. Adv. Robot. Syst. 2015, 12, 134. [Google Scholar] [CrossRef]









| Algorithms | Contributions | Limitations |
|---|---|---|
| RRT [18] | Fast and effective in complex problems | RRT always converges to a suboptimal solution |
| RRT* [19] | Asymptotically optimal | Slow convergence rate to the optimum results in low efficiency of RRT* |
| DT-RRT* [21] | Fast convergence rate and optimal trajectory | The performance of DT-RRT* depends on the quality of reference RRT-path |
| dynEFWA-APF [33] | Safe, smooth and dynamically feasible path | Algorithm applications are limited by the complexity of the environment |
| Proposed HDM-RRT Algorithm Improvements | ||
| Improving the efficiency and stability while ensuring the trajectory quality in challenging campus environment | ||
| Full Form | Abbreviations |
|---|---|
| High-definition map | HD-Map |
| HD-Map-guided rapidly-exploring random tree | HDM-RRT |
| Collision risk map | CR-Map |
| Autonomous vehicle | AV |
| Artificial potential field | APF |
| Rapidly-exploring random tree | RRT |
| Area of interest | AOI |
| Symbols | Meanings |
|---|---|
| represents the vehicle coordinates, represents the intersection Angle between the head direction and coordinate axis | |
| Velocity of vehicle | |
| Acceleration of vehicle | |
| Front-wheel angle of vehicle | |
| Angular velocity of front wheel | |
| The wheelbase length | |
| The obstacle-free space | |
| The obstacle space | |
| The control space | |
| Initial condition of vehicle | |
| Goal region of vehicle | |
| Feasible trajectory | |
| A tree containing nodes and edges | |
| Repulsive force field | |
| Distance between the grid point and obstacle | |
| Influence radius of obstacles | |
| Maximum value of the repulsive force |
| Item | Attributes |
|---|---|
| Number of lanes | 2 |
| Lane width | 2.3–3 m |
| Speed | <30 km/h |
| Intersections | 2 |
| T-junctions | 6 |
| Sensors | Attributes |
|---|---|
| Vehicle parameters | 4.3 m long, 1.7 m wide and 2.2 m high (including sensors) |
| Navigation system | Integrated IMU, Beidou and wheel speedometer |
| LIDAR | 32-Line LIDAR |
| Radar | Two millimeter-wave radars |
| Camera | Four cameras, including a depth camera |
| Experiments | Programming Languages | Platforms | Visualizations |
|---|---|---|---|
| Experiment 1 | Python | Pycharm | Pygame Library |
| Experiment 2 | Python | Pycharm | Pygame Library |
| Experiment 3 | C++ | ROS | Matplotlib Library |
| Item (10,000 Samples) | Probability (Points in AOI) | Probability (Points Near the Trajectory (<0.5 m)) |
|---|---|---|
| Random distribution sampling | 1522/10,000 | 935/10,000 |
| Gaussian distribution sampling | 2038/10,000 | 2852/10,000 |
| The proposed sampling | 8013/10,000 | 3648/10,000 |
| Item | Scene | RRT* [19] | DT-RRT* [21] | Proposed Algorithm |
|---|---|---|---|---|
| Iterations of the first trajectory (number of times) | Scene 1 | 52 | 41 | 9 |
| Scene 2 | 259 | 108 | 24 | |
| Scene 3 | 55 | 13 | 11 | |
| Iterations of the optimal trajectory (number of times) | Scene 1 | 245 | 134 | 81 |
| Scene 2 | 358 | 198 | 114 | |
| Scene 3 | 469 | 132 | 120 | |
| Frequency of failures (in 1000 iterations) | Scene 1 | 0 | 0 | 0 |
| Scene 2 | 11/100 | 0 | 0 | |
| Scene 3 | 0 | 0 | 0 | |
| Length of the optimal trajectory (m) | Scene 1 | 40.36 | 40.36 | 40.38 |
| Scene 2 | 40.76 | 40.71 | 40.60 | |
| Scene 3 | 40.78 | 42.65 | 40.61 |
| Item | RRT* [19] | DT-RRT* [21] | dynEFWA-APF [33] | Proposed Algorithm |
|---|---|---|---|---|
| Failed times (manual intervention times) | 4 | 0 | 1 | 0 |
| Average iterations of first trajectory | 169 | 54 | / | 18 |
| Average iterations of optimal trajectory | 421 | 142 | / | 111 |
| Average number of trajectories | 35 | 51 | 1 | 78 |
| Average computation time of first trajectory (ms) | 104.79 | 24.10 | 42.24 | 15.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Cao, Y.; Zhou, J.; Huang, Y.; Li, B. HDM-RRT: A Fast HD-Map-Guided Motion Planning Algorithm for Autonomous Driving in the Campus Environment. Remote Sens. 2023, 15, 487. https://doi.org/10.3390/rs15020487
Guo X, Cao Y, Zhou J, Huang Y, Li B. HDM-RRT: A Fast HD-Map-Guided Motion Planning Algorithm for Autonomous Driving in the Campus Environment. Remote Sensing. 2023; 15(2):487. https://doi.org/10.3390/rs15020487
Chicago/Turabian StyleGuo, Xiaomin, Yongxing Cao, Jian Zhou, Yuanxian Huang, and Bijun Li. 2023. "HDM-RRT: A Fast HD-Map-Guided Motion Planning Algorithm for Autonomous Driving in the Campus Environment" Remote Sensing 15, no. 2: 487. https://doi.org/10.3390/rs15020487
APA StyleGuo, X., Cao, Y., Zhou, J., Huang, Y., & Li, B. (2023). HDM-RRT: A Fast HD-Map-Guided Motion Planning Algorithm for Autonomous Driving in the Campus Environment. Remote Sensing, 15(2), 487. https://doi.org/10.3390/rs15020487









