Inversion of Regional Groundwater Storage Changes Based on the Fusion of GNSS and GRACE Data: A Case Study of Shaanxi–Gansu–Ningxia
Abstract
:1. Introduction
2. Data and Fusion Method
2.1. Data
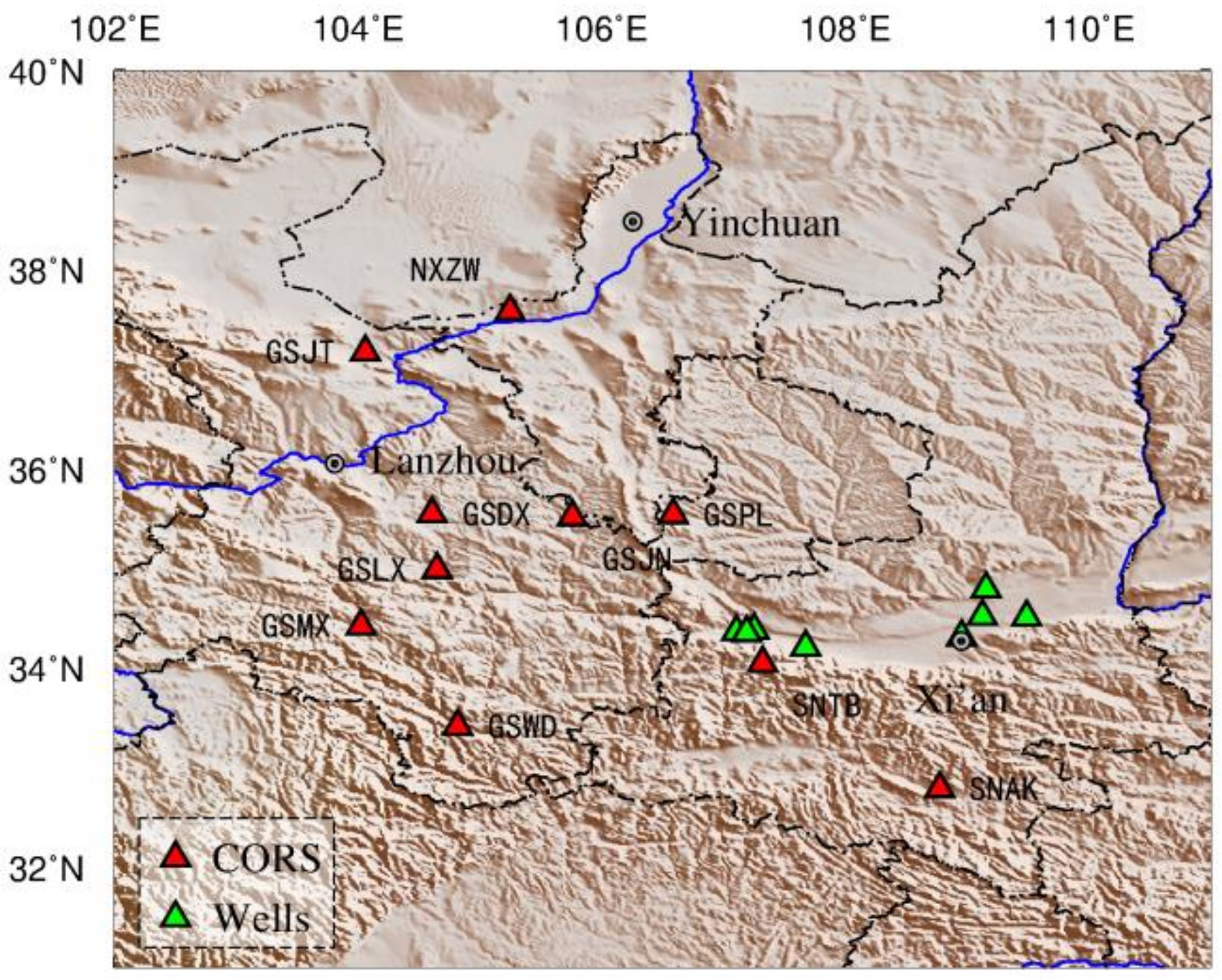
2.1.1. GNSS Data
2.1.2. GRACE Data and Post-Processing
2.1.3. Atmospheric Pressure Data
2.1.4. MSLA Data
2.1.5. GLDAS Noah Hydrological Model
2.1.6. WGHM Hydrological Model
2.1.7. In Situ Data of Groundwater Level
2.2. Fusion Method
2.2.1. The Inversion from GNSS Data
2.2.2. The Estimation from GRACE Data
2.2.3. Fusion Method Based on GNSS and GRACE Data
3. Fusion Results and Analysis
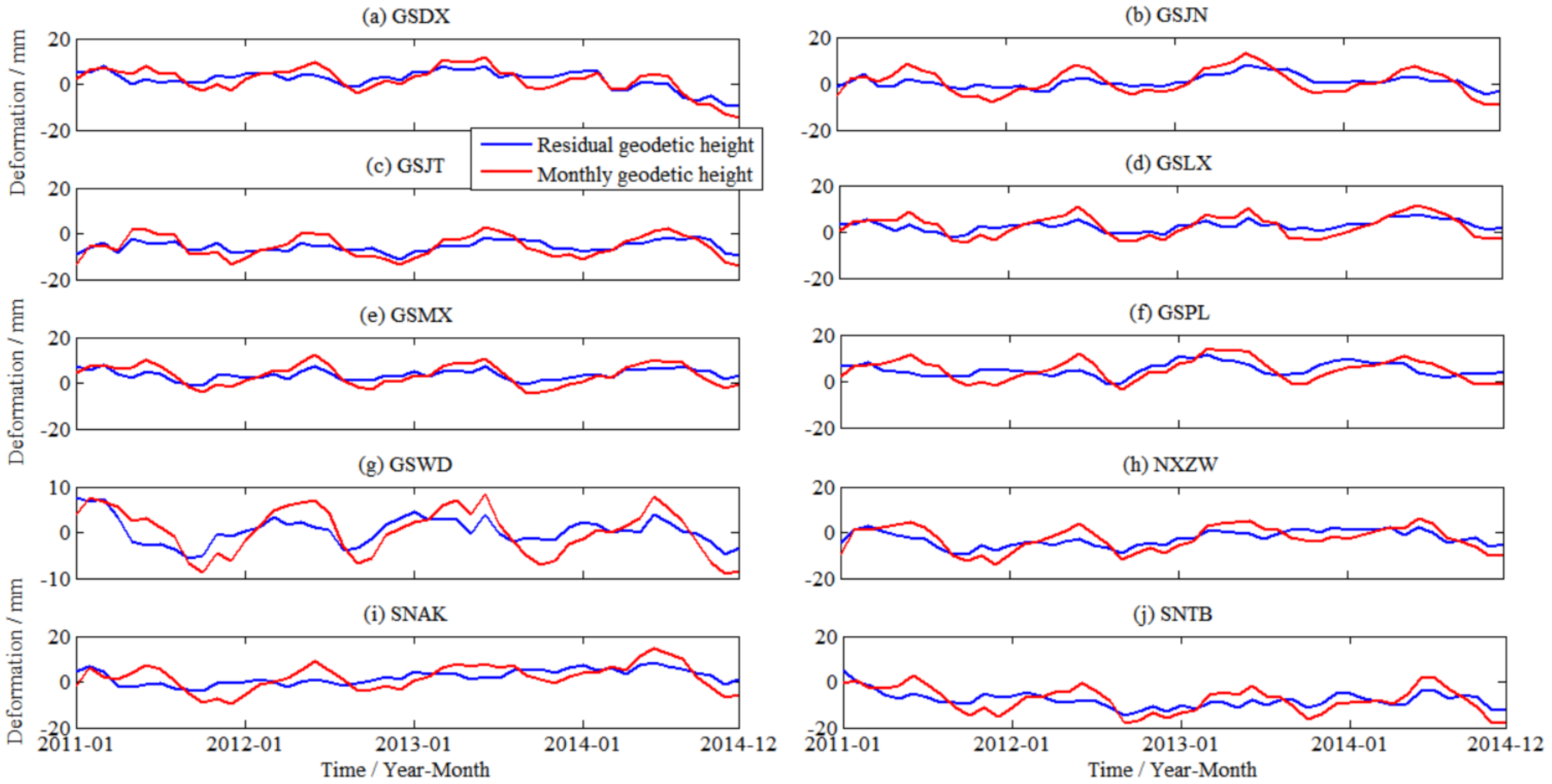
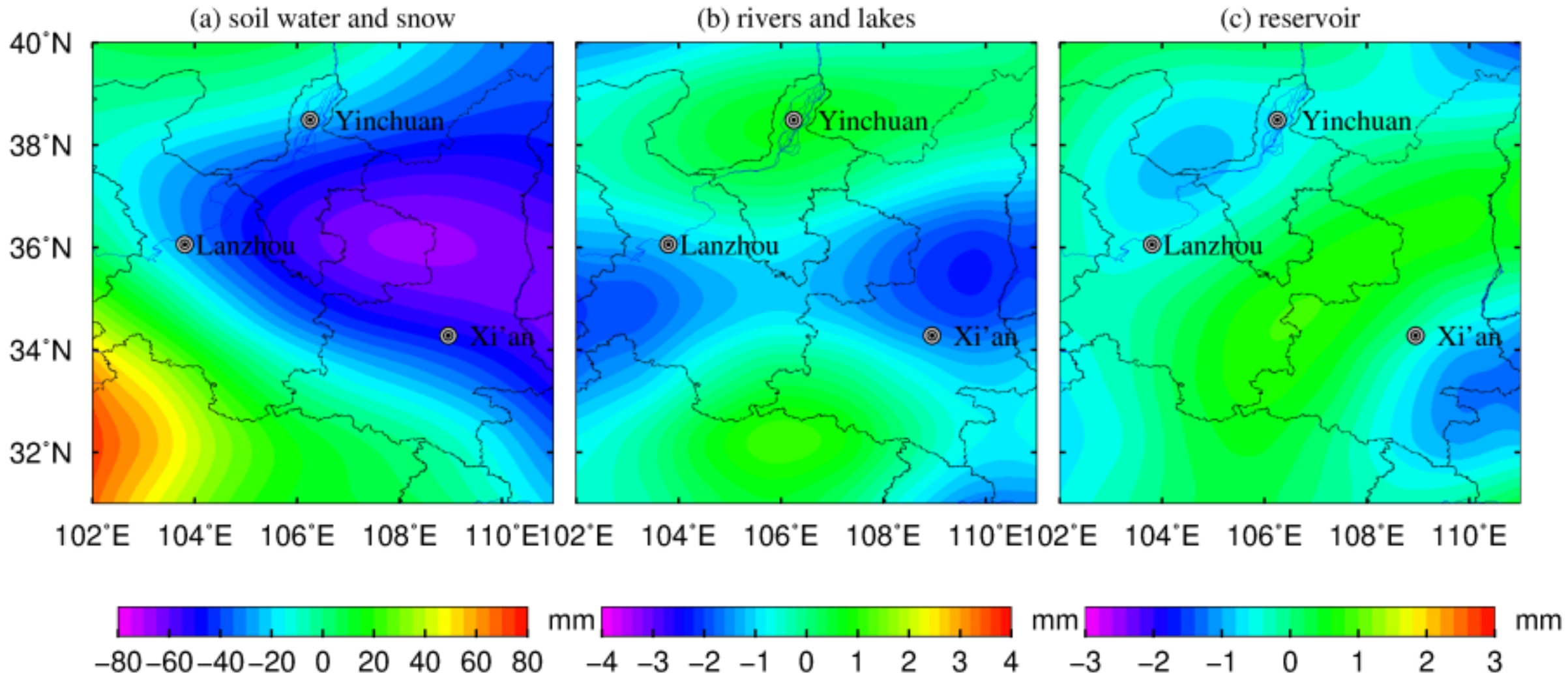
3.1. GNSS Data Extraction and Environmental Loading Deformation Calculation
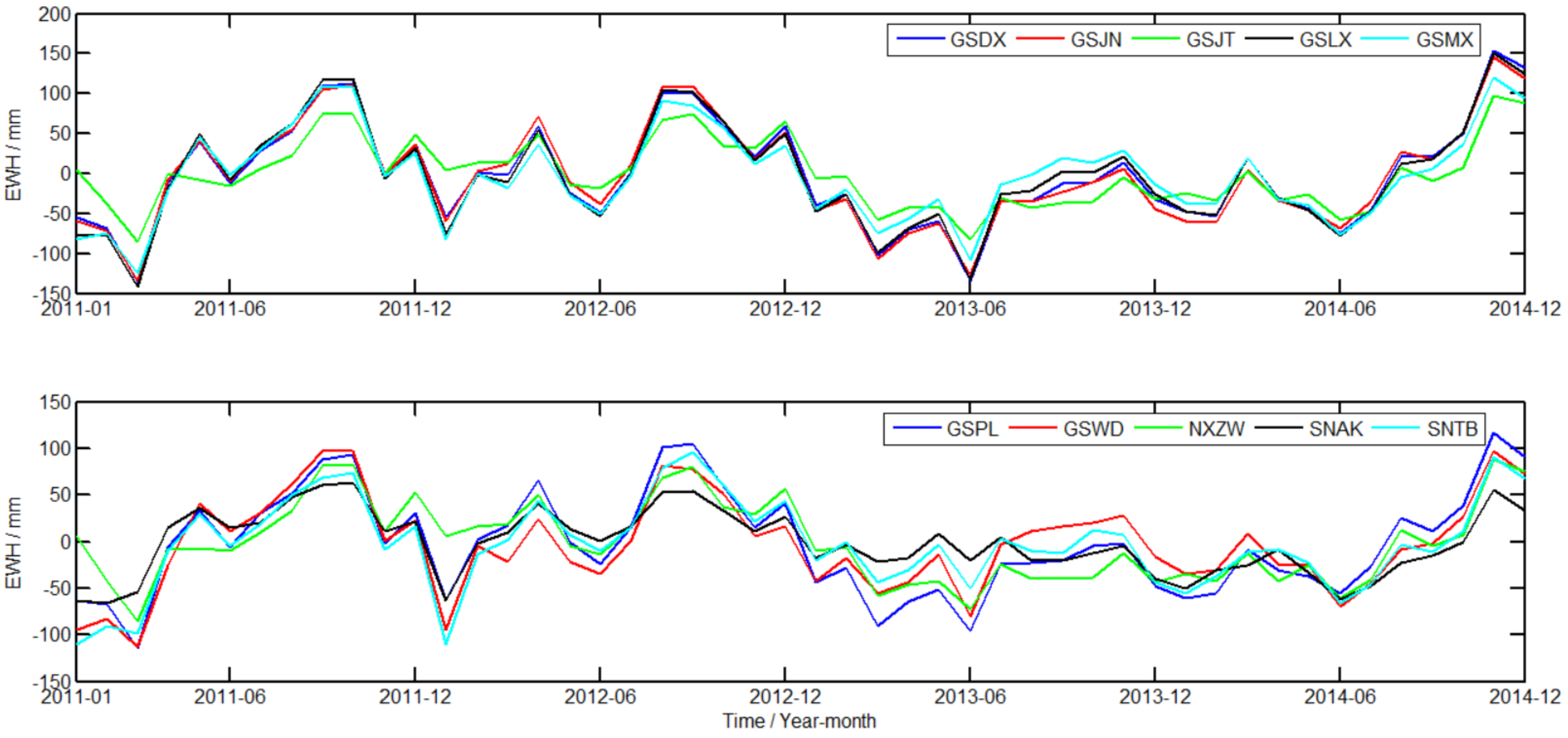
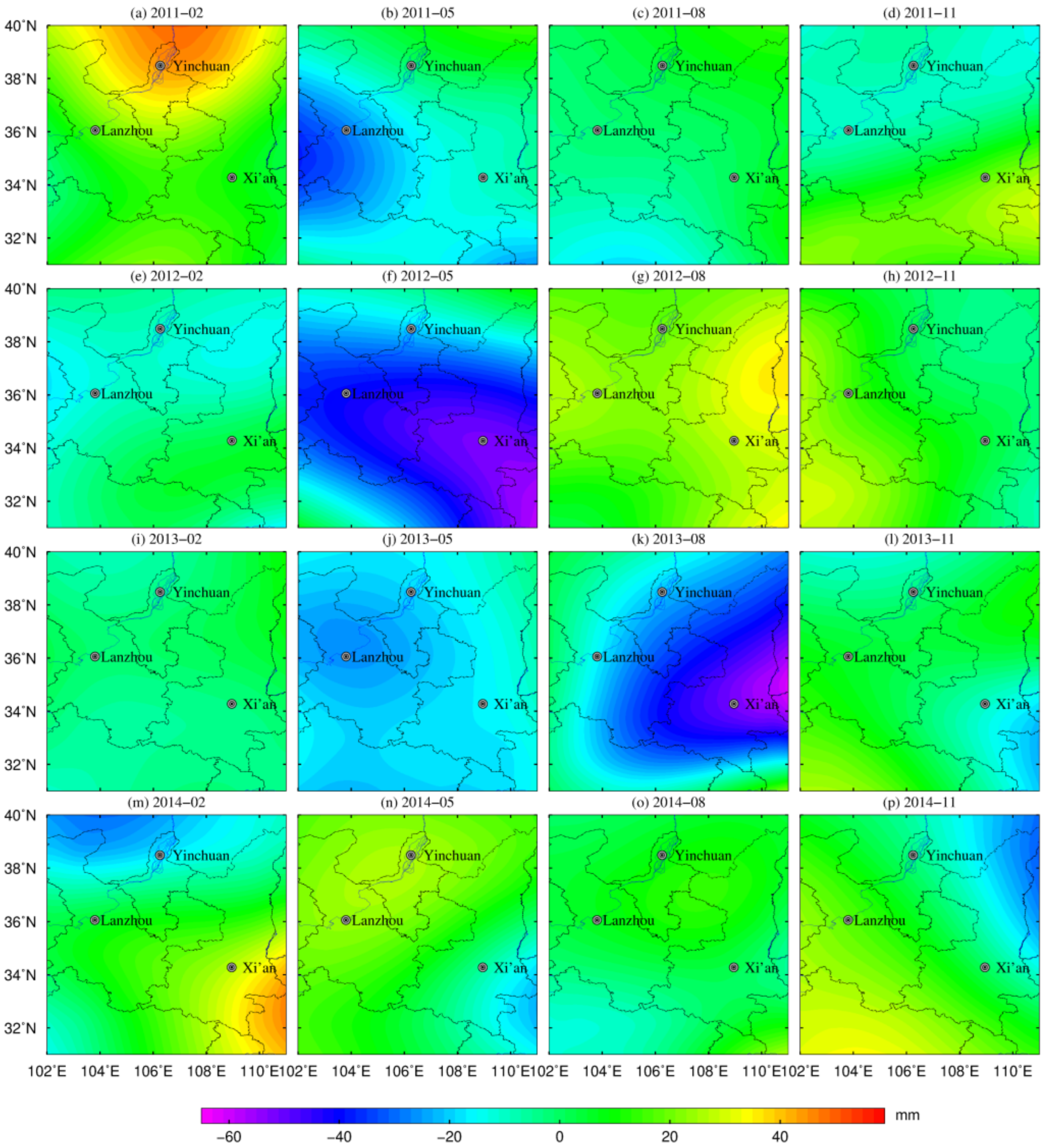
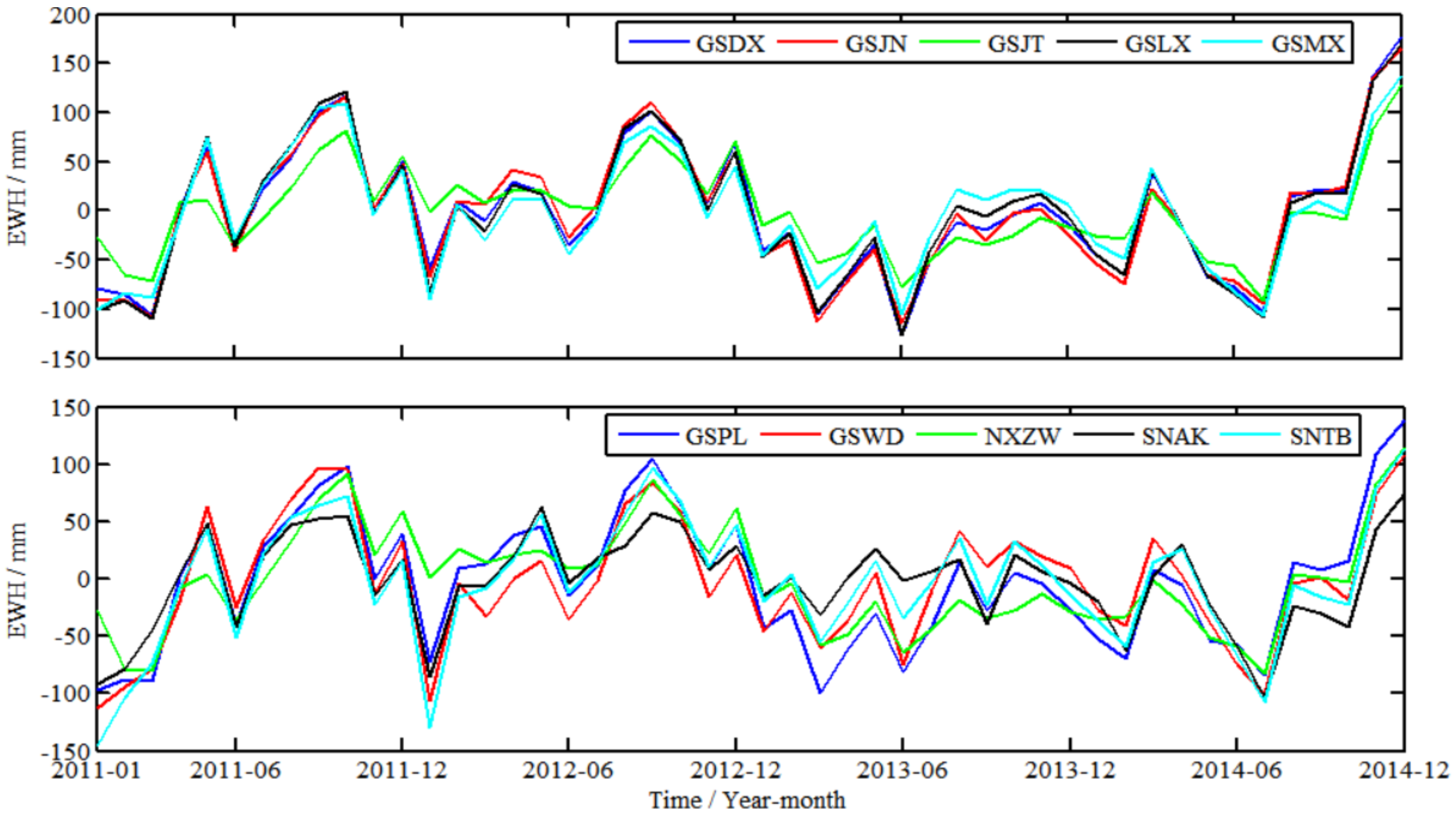
3.2. Regional GWS Variation Derived from GNSS
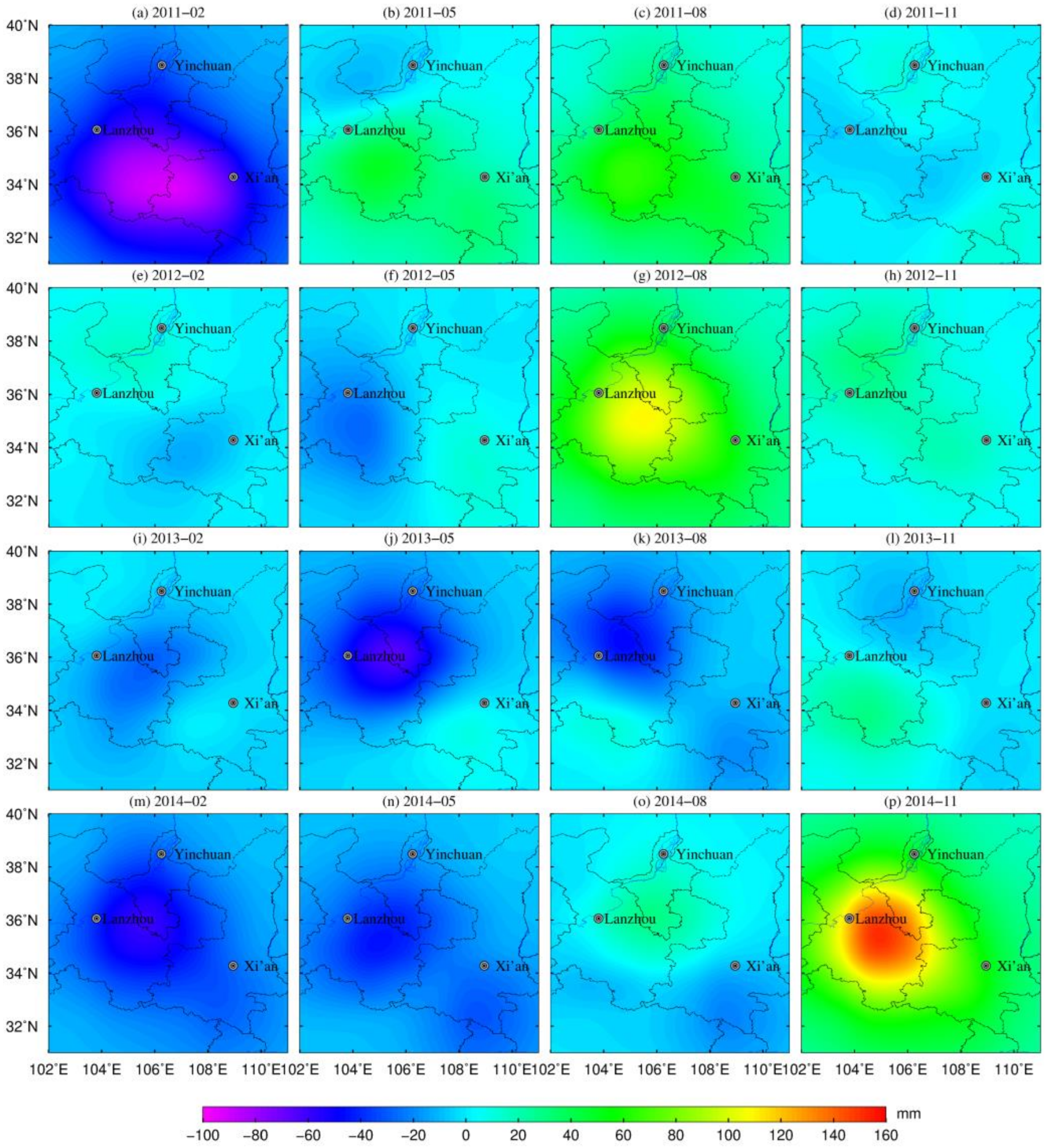
3.3. Regional GWS Changes Derived from GRACE
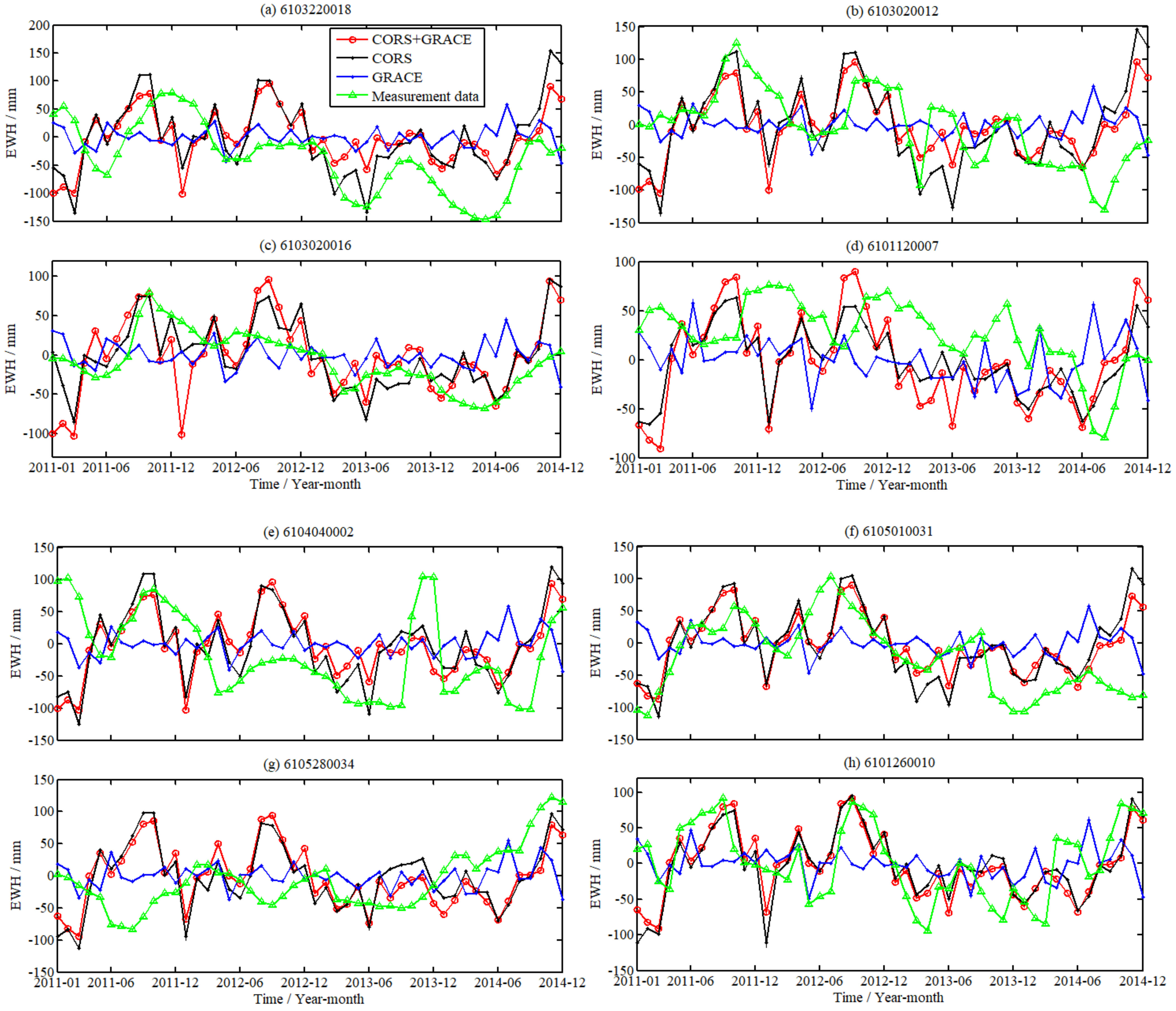
3.4. Regional GWS Changes Based on the Fusion Method
4. Discussions on the Fusion Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhong, M.; Duan, J.; Xu, H.; Peng, P.; Yan, H.; Zhu, Y. Trend of China land water storage redistribution at medi- and large-spatial scales in recent five years by satellite gravity observations. Chin. Sci. Bull. 2009, 54, 816–821. [Google Scholar] [CrossRef] [Green Version]
- Yin, W.; Han, S.C.; Zheng, W.; Yeo, I.Y.; Hu, L.; Tangdamrongsub, N.; Ghobadi-Far, K. Improved water storage estimates within the North China Plain by assimilating GRACE data into the CABLE model. J. Hydrol. 2020, 590, 125348. [Google Scholar] [CrossRef]
- Feng, W.; Wang, C.Q.; Mu, D.P.; Zhong, M.; Zhong, Y.L.; Xu, H.Z. Groundwater storage variations in the North China plain from GRACE with spatial constraints. Chin. J. Geophys. 2017, 60, 1630–1642. [Google Scholar]
- Xu, C.; Gong, Z. Review of the Post-processing methods on GRACE time varied gravity data. Geomat. Inf. Sci. Wuhan Univ. 2016, 41, 503–510. [Google Scholar]
- Cheng, P.; Wen, H.; Liu, H.; Dong, J. Research situation and future development of satellite geodesy. Geomat. Inf. Sci. Wuhan Univ. 2019, 44, 48–54. [Google Scholar]
- Kornfeld, R.P.; Arnold, B.W.; Gross, M.A.; Dahya, N.T.; Klipstein, W.M.; Gath, P.F.; Bettadpur, S. GRACE-FO: The Gravity Recovery and Climate Experiment Follow-On mission. J. Spacecr. Rocket. 2019, 56, 931–951. [Google Scholar] [CrossRef]
- Li, F.; Kusche, J.; Rietbroek, R.; Wang, Z.; Forootan, E.; Schulze, K.; Lück, C. Comparison of data-driven techniques to reconstruct (1992–2002) and predict (2017–2018) GRACE-like gridded total water storage changes using climate inputs. Water Resour. Res. 2020, 56, e2019WR026551. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Z.; Hsu, Y.J.; Yuan, L.; Huang, D. Monitoring time-varying terrestrial water storage changes using daily GNSS measurements in Yunnan, southwest China. Remote Sens. Environ. 2021, 254, 112249. [Google Scholar] [CrossRef]
- Adusumilli, S.; Borsa, A.A.; Fish, M.A.; McMillan, H.K.; Silverii1et, F. A decade of water storage changes across the contiguous United States from GPS and satellite gravity. Geophys. Res. Lett. 2019, 46, 13006–13015. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Lo, M.; Ho, S.L.; Bethune, J.; Anderson, K.J.; Syed, T.H.; Rodell, M. Satellites measure recent rates of groundwater depletion in California’s Central Valley. Geophys. Res. Lett. 2011, 38, L03403–L03406. [Google Scholar]
- Tiwari, V.M.; Wahr, J.; Swenson, S. Dwindling groundwater resources in northern India, from satellite gravity observations. Geophys. Res. Lett. 2009, 36, 184–201. [Google Scholar] [CrossRef] [Green Version]
- Hsieh, W. Nonlinear multichannel and time series analysis by neural network methods. Rev. Geophys. 2004, 42, 1003–1027. [Google Scholar] [CrossRef] [Green Version]
- Jiang, W.; Wang, K.; Li, Z.; Zhou, X.; Ma, Y.; Ma, J. Prospect and Theory of GNSS Coordinate Time Series Analysis. Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 2112–2123. [Google Scholar]
- Liu, R.; Zou, R.; Li, J.; Zhang, C.; Zhao, B.; Zhang, Y. Vertical displacements driven by groundwater storage changes in the North China Plain detected by GPS observations. Remote Sens. 2018, 10, 259. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.; Argus, D.F.; Freymueller, J.T.; Heflin, M.B. Horizontal motion in elastic response to seasonal loading of rain water in the Amazon Basin and monsoon water in Southeast Asia observed by GPS and inferred from GRACE. Geophys. Res. Lett. 2013, 40, 6048–6053. [Google Scholar] [CrossRef]
- Wang, L.; Chen, C.; Zou, R.; Du, J. Surface gravity and deformation effects of water storage changes in China’s Three Gorges Reservoir constrained by modeled results and in situ measurements. J. Appl. Geophys. 2014, 108, 25–34. [Google Scholar] [CrossRef]
- Jin, S.; Zhang, T. Terrestrial water storage anomalies associated with drought in southwestern USA from GPS observations. Surv. Geophys. 2016, 37, 1139–1156. [Google Scholar] [CrossRef]
- Chanard, K.; Fleitout, L.; Calais, E.; Rebischung, P.; Avouac, J.P. Toward a global horizontal and vertical elastic loading deformation model derived from GRACE and GNSS station position time series. J. Geophys. Res. Solid Earth 2018, 123, 3225–3237. [Google Scholar] [CrossRef] [Green Version]
- Rajner, M.; Liwosz, T. Analysis of seasonal position variation for selected GNSS sites in Poland using loading modelling and GRACE data. Geod. Geodyn. 2017, 8, 253–259. [Google Scholar] [CrossRef]
- Sarkar, T.; Kannaujiya, S.; Taloor, A.K.; Ray, P.K.C.; Chauhan, P. Integrated study of GRACE data derived interannual groundwater storage variability over water stressed Indian regions. Groundw. Sustain. Dev. 2020, 10, 100376–100395. [Google Scholar] [CrossRef]
- Liu, R.; Zhong, B.; Li, X.; Zheng, K.; Liang, H.; Cao, J.; Lyu, H. Analysis of groundwater changes (2003–2020) in the North China Plain using geodetic measurements. J. Hydrol. Reg. Stud. 2022, 41, 101085. [Google Scholar] [CrossRef]
- Wang, H.; Xiang, L.; Steffen, H.; Wu, P.; Jiang, L.; Shen, Q.; Hayashi, M. GRACE-based estimates of groundwater variations over North America from 2002 to 2017. Geod. Geodyn. 2022, 13, 11–23. [Google Scholar] [CrossRef]
- Li, X.; Zhong, B.; Li, J.; Liu, R. Analysis of terrestrial water storage changes in the Shaan-Gan-Ning Region using GPS and GRACE/GFO. Geod. Geodyn. 2022, 11, 179–188. [Google Scholar] [CrossRef]
- Herring, T.A.; King, R.W.; Floyd, M.A.; McClusky, S.C. Introduction to GAMIT/GLOBK. Available online: http://geoweb.mit.edu/gg/Intro_GG.pdf (accessed on 2 June 2018).
- Wang, L.; Chen, C.; Thomas, M.; Kaban, M.K.; Güntner, A.; Du, J. Increased water storage of Lake Qinghai during 2004–2012 from GRACE data, hydrological models, radar altimetry and in situ measurements. Geophys. J. Int. 2018, 212, 679–693. [Google Scholar] [CrossRef]
- Li, W.; Wang, W.; Zhang, C.; Wen, H.; Zhong, Y.; Zhu, Y.; Li, Z. Bridging terrestrial water storage anomaly during GRACE/GRACE-FO gap using SSA method: A case study in China. Sensors 2019, 19, 4144. [Google Scholar] [CrossRef]
- Li, W.; Dong, J.; Wang, W.; Wen, H.; Liu, H.; Guo, Q.; Zhang, C. Regional Crustal Vertical Deformation Driven by Terrestrial Water Load Depending on CORS Network and Environmental Loading Data: A Case Study of Southeast Zhejiang. Sensors 2021, 21, 7699. [Google Scholar] [CrossRef]
- Shi, T.; Guo, J.; Yan, H.; Chang, X.; Ji, B.; Liu, X. Assessing Height Variations in Qinghai-Tibet Plateau from Time-Varying Gravity Data and Hydrological Model. Remote Sens. 2022, 14, 4707. [Google Scholar] [CrossRef]
- Lenczuk, A.; Leszczuk, G.; Klos, A.; Kosek, W.; Bogusz, J. Study on the inter-annual hydrology-induced displacements in Europe using GRACE and hydrological models. J. Appl. Geod. 2020, 14, 393–403. [Google Scholar] [CrossRef]
- Li, J.; Chen, J.L.; Wilson, C.R. Topographic effects on coseismic gravity change for the 2011 Tohoku-Oki earthquake and comparison with GRACE. J. Geophys. Res. Solid Earth 2016, 121, 5509–5537. [Google Scholar] [CrossRef]
- Matsuo, K.; Heki, K. Coseismic and postseismic gravity changes of the 2011 Tohoku-Oki Earthquake from satellite gravimetry. AGU Fall Meet. Abstr. 2011, 38, 131010149. [Google Scholar]
- Swenson, S.; Chambers, D.; Whar, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. 2008, 113, B8. [Google Scholar] [CrossRef] [Green Version]
- Loomis, B.D.; Rachlin, K.E.; Luthcke, S.B. Improved Earth oblateness rate reveals increased ice sheet losses and mass-driven sea level rise. Geophys. Res. Lett. 2019, 46, 6910–6917. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhong, M.; Feng, W.; Zhang, Z.; Shen, Y.; Wu, D. Groundwater Depletion in the West Liaohe River Basin, China and its implications revealed by GRACE and in situ measurements. Remote Sens. 2018, 10, 493. [Google Scholar] [CrossRef] [Green Version]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Vitart, F. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Save, H. GRACE RL06 Reprocessing and Results from CSR[R]; EGU General Assembly: Vienna, Austria, 2018. [Google Scholar]
- Sheng, C. Characteristics of non-tectonic crustal deformation from surface loads around Chinese mainland and correction model. Recent Dev. World Seismol. 2014, 11, 45–48. [Google Scholar]
- Hussain, D.; Khan, A.A.; Hassan SN, U.; Naqvi SA, A.; Jamil, A. A time series assessment of terrestrial water storage and its relationship with hydro-meteorological factors in Gilgit-Baltistan region using GRACE observation and GLDAS-Noah model. SN Appl. Sci. 2021, 3, 1–11. [Google Scholar] [CrossRef]
- Döll, P.; Müller Schmied, H.; Schuh, C.; Portmann, F.T.; Eicker, A. Global-scale assessment of groundwater depletion and related groundwater abstractions: Combining hydrological modeling with information from well observations and GRACE satellites. Water Resour. Res. 2014, 50, 5698–5720. [Google Scholar] [CrossRef]
- Zhou, M.; Liu, X.; Yuan, J.; Jin, X.; Niu, Y.; Guo, J.; Gao, H. Seasonal variation of GPS-derived the principal ocean tidal constituents’ loading displacement parameters based on moving harmonic analysis in Hong Kong. Remote Sens. 2021, 13, 279. [Google Scholar] [CrossRef]
- Müller Schmied, H.; Cáceres, D.; Eisner, S.; Flörke, M.; Herbert, C.; Niemann, C.; Döll, P. The global water resources and use model WaterGAP v2.2d: Model description and evaluation. Geosci. Model Dev. 2021, 14, 1037–1079. [Google Scholar] [CrossRef]
- Jiang, Z.; Hsu, Y.J.; Yuan, L.; Yang, X.; Ding, Y.; Tang, M.; Chen, C. Characterizing spatiotemporal patterns of terrestrial water storage variations using GNSS vertical data in Sichuan, China. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022398. [Google Scholar] [CrossRef]
- Jiang, Z.; Hsu, Y.J.; Yuan, L.; Cheng, S.; Feng, W.; Tang, M.; Yang, X. Insights into hydrological drought characteristics using GNSS-inferred large-scale terrestrial water storage deficits. Earth Planet. Sci. Lett. 2022, 578, 117294. [Google Scholar] [CrossRef]
- Guo, J.; Wang, G.; Guo, H.; Lin, M.; Peng, H.; Chang, X.; Jiang, Y. Validating precise orbit determination from satellite-borne GPS data of Haiyang-2D. Remote Sens. 2022, 14, 2477. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhong, M.; Mao, Y.; Ji, B. Evaluation of evapotranspiration for exorheic catchments of China during the GRACE era: From a water balance perspective. Remote Sens. 2020, 12, 511. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Xiang, L.; Jia, L.; Jiang, L.; Wang, Z.; Hu, B.; Gao, P. Load Love numbers and Green’s functions for elastic Earth models PREM, iasp91, ak135, and modified models with refined crustal structure from Crust 2.0. Comput. Geosci. 2012, 49, 190–199. [Google Scholar] [CrossRef]
- Paulson, A.; Zhong, S.; Wahr, J. Inference of Mantle Viscosity from GRACE and Relative Sea Level Data. Geophys. J. R. Astron. Soc. 2007, 171, 497–508. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Dong, J.; Wang, W.; Zhong, Y.; Zhang, C.; Wen, H.; Yao, G. The Crustal Vertical Deformation Driven by Terrestrial Water Load from 2010 to 2014 in Shaanxi–Gansu–Ningxia Region Based on GRACE and GNSS. Water 2022, 14, 964. [Google Scholar] [CrossRef]
- Shi, T.; Liu, X.; Mu, D.; Li, C.; Guo, J.; Xing, Y. Reconstructing gap data between GRACE and GRACE-FO based on multi-layer perceptron and analyzing terrestrial water storage changes in the Yellow River basin. Chin. J. Geophys. 2022, 65, 2448–2463. (In Chinese) [Google Scholar]
- Zhang, L.; Tang, H.; Sun, W. Comparison of GRACE and GNSS seasonal load displacements considering regional averages and discrete points. J. Geophys. Res. Solid Earth 2021, 126, e2021JB021775. [Google Scholar] [CrossRef]







| Parameter | Processing Mode |
|---|---|
| Tropospheric model | Saastamoinen + GPT2w + estimation |
| Ionosphere delay model | LC_AUTCLN |
| Ambiguity resolution | LAMBDA method |
| Satellite cut-off elevation angle (°) | 10 |
| Sampling interval data | 15 s |
| Solid tide model | IERS2010 |
| Ocean tide model | FES2004 (otl_FES2004.grid) |
| Atmospheric mapping function | VMF1 |
| Solar radiation pressure model | ECOMC model |
| PCO/PCV | IGS14 atx |
| Framework of prior coordinates | ITRF2014 |
| Inertial framework | J2000 |
| IDS of Water Level Monitoring Station | Correlation Coefficients (GNSS/GRACE/Fusion) | IDS of Water Level Monitoring Station | Correlation Coefficients (GNSS/GRACE/Fusion) |
|---|---|---|---|
| 6103220018 | 0.35/−0.02/0.20 | 6103020012 | 0.30/−0.18/0.32 |
| 6103020016 | 0.60/−0.06/0.40 | 6101120007 | 0.17/−0.06/0.07 |
| 6104040002 | 0.21/−0.11/0.05 | 6105010031 | 0.41/−0.02/0.53 |
| 6105280034 | −0.06/0.15/−0.04 | 6101260010 | 0.49/0.21/0.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Zhang, C.; Wang, W.; Guo, J.; Shen, Y.; Wang, Z.; Bi, J.; Guo, Q.; Zhong, Y.; Li, W.; et al. Inversion of Regional Groundwater Storage Changes Based on the Fusion of GNSS and GRACE Data: A Case Study of Shaanxi–Gansu–Ningxia. Remote Sens. 2023, 15, 520. https://doi.org/10.3390/rs15020520
Li W, Zhang C, Wang W, Guo J, Shen Y, Wang Z, Bi J, Guo Q, Zhong Y, Li W, et al. Inversion of Regional Groundwater Storage Changes Based on the Fusion of GNSS and GRACE Data: A Case Study of Shaanxi–Gansu–Ningxia. Remote Sensing. 2023; 15(2):520. https://doi.org/10.3390/rs15020520
Chicago/Turabian StyleLi, Wanqiu, Chuanyin Zhang, Wei Wang, Jinyun Guo, Yingchun Shen, Zhiwei Wang, Jingxue Bi, Qiuying Guo, Yulong Zhong, Wei Li, and et al. 2023. "Inversion of Regional Groundwater Storage Changes Based on the Fusion of GNSS and GRACE Data: A Case Study of Shaanxi–Gansu–Ningxia" Remote Sensing 15, no. 2: 520. https://doi.org/10.3390/rs15020520
APA StyleLi, W., Zhang, C., Wang, W., Guo, J., Shen, Y., Wang, Z., Bi, J., Guo, Q., Zhong, Y., Li, W., Zhu, C., & Xu, P. (2023). Inversion of Regional Groundwater Storage Changes Based on the Fusion of GNSS and GRACE Data: A Case Study of Shaanxi–Gansu–Ningxia. Remote Sensing, 15(2), 520. https://doi.org/10.3390/rs15020520









