Target Detection Method Based on Adaptive Step-Size SAMP Combining Off-Grid Correction for Coherent Frequency-Agile Radar
Abstract
:1. Introduction
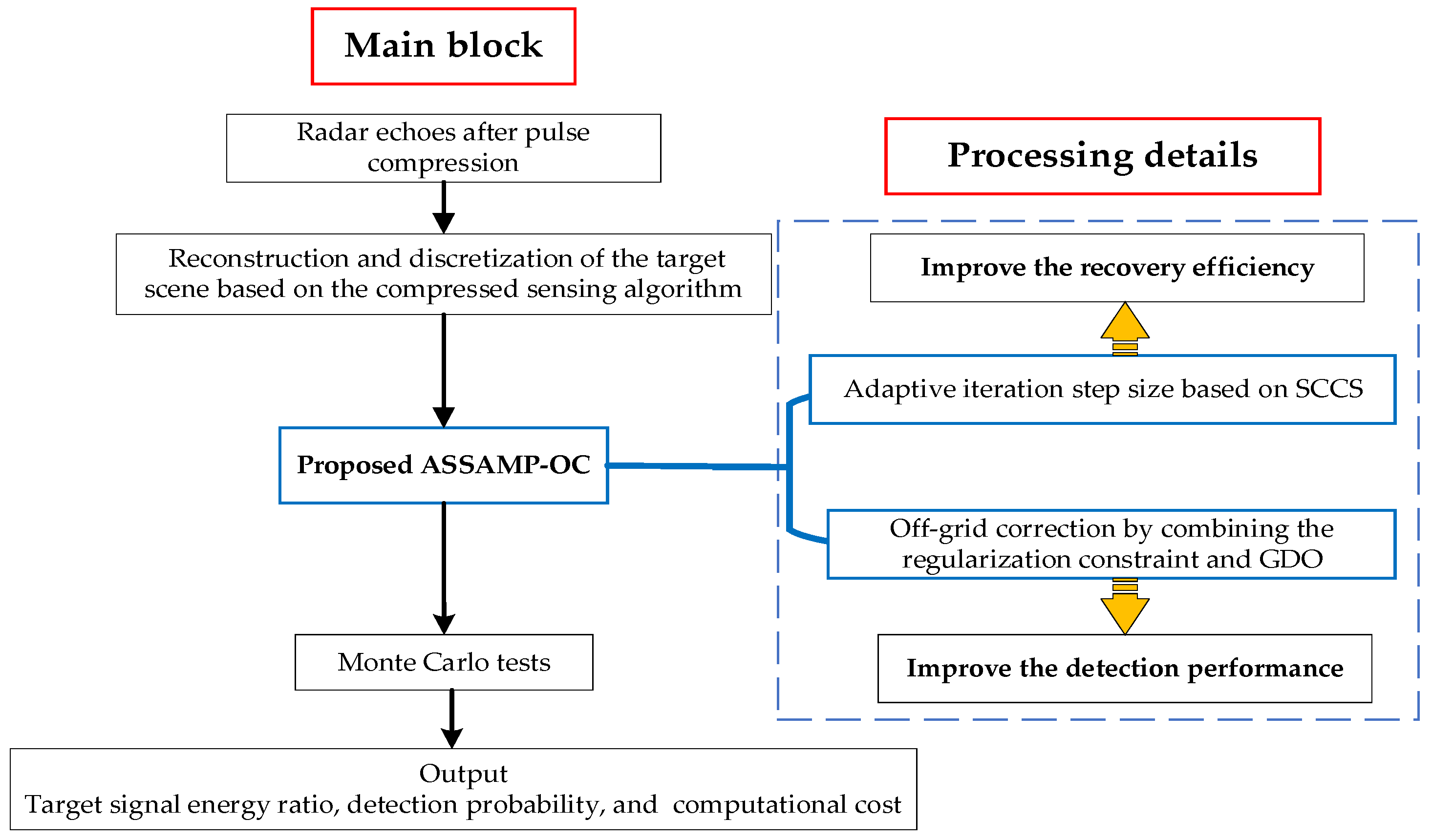
- Improving the signal recovery efficiency: An adaptive step-size method based on Spearman correlation coefficients (SCCS) is proposed to solve the problem of a large number of iterations in the traditional SAMP method. In addition, a convergence criterion based on polynomial fitting error is introduced, which is beneficial to further speed up the algorithm.
- Improving the target detection performance: The BSSE can be suppressed effectively by using off-grid correction by combining the regularization theory and gradient descent optimization (GDO), which can improve the signal recovery quality and reduce the CI gain loss without the prior information of the sparse lever.
2. Echo Signal Model and Sparse Representation
3. Proposed Method
3.1. Analysis of the SAMP Algorithm
3.2. Analysis of the ASSAMP-OC Algorithm
3.2.1. Adaptive Step Size Design
3.2.2. Off-Grid Correction
- Regularized Constraint
- Acquisition of Mismatch Coefficient
| Algorithm 1: Target Detection Method Based on Adaptive Step-Size SAMP combining Off-Grid Correction for Coherent Frequency-Agile Radar. |
| Input: Sensing matrix , Observation signal , Initial step size Output: Recovery signal 1: Initialization: {Initial residual} {Support set} {Index set size} {Initial iteration step size} {Iteration number} {Threshold of correlation coefficient} = 1 × 10 −3 {Convergence threshold of Polynomial fitting error} {Maximum number of iterations} 2: Repeat:
|
4. Simulation and Experimental Results
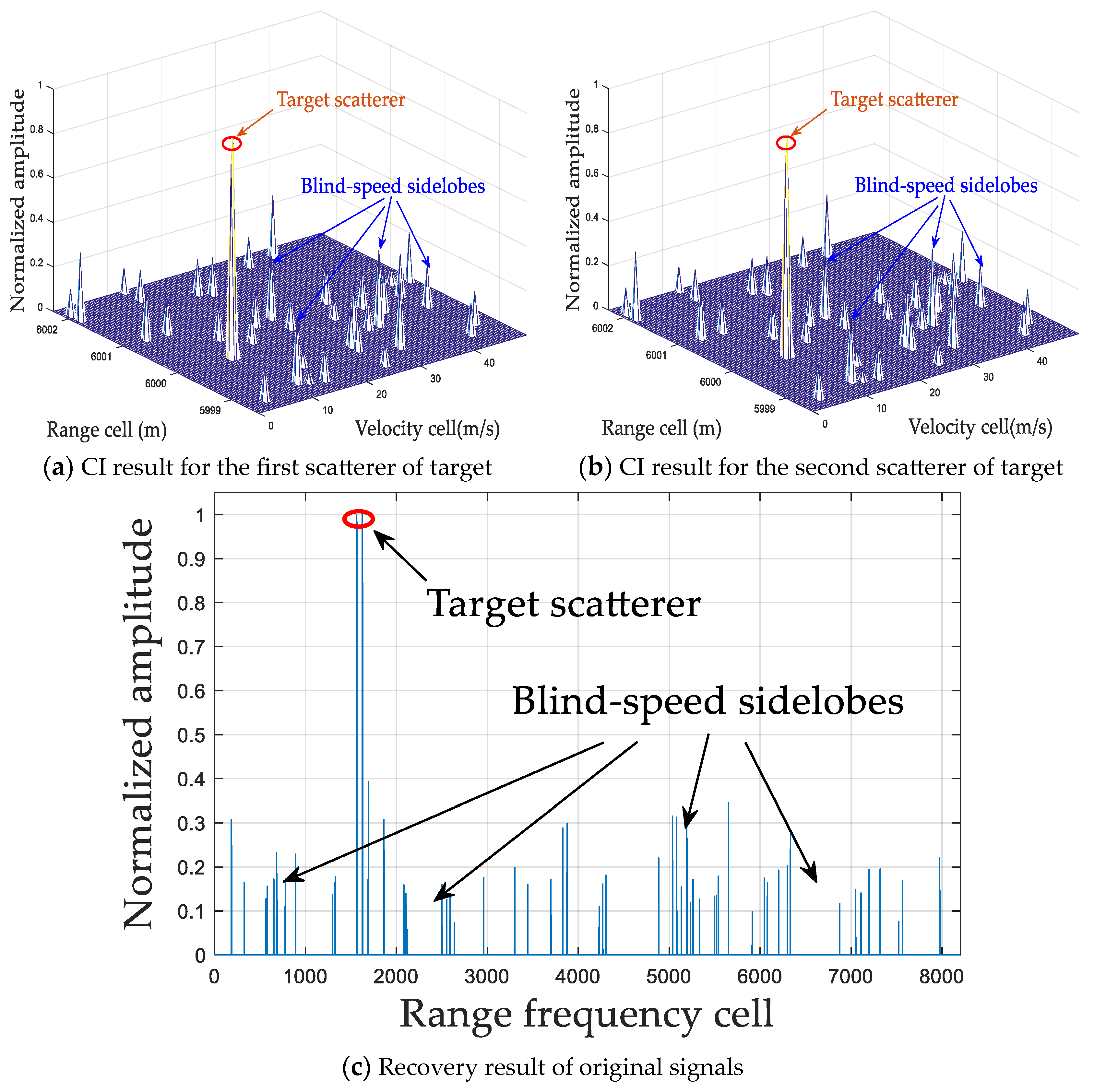
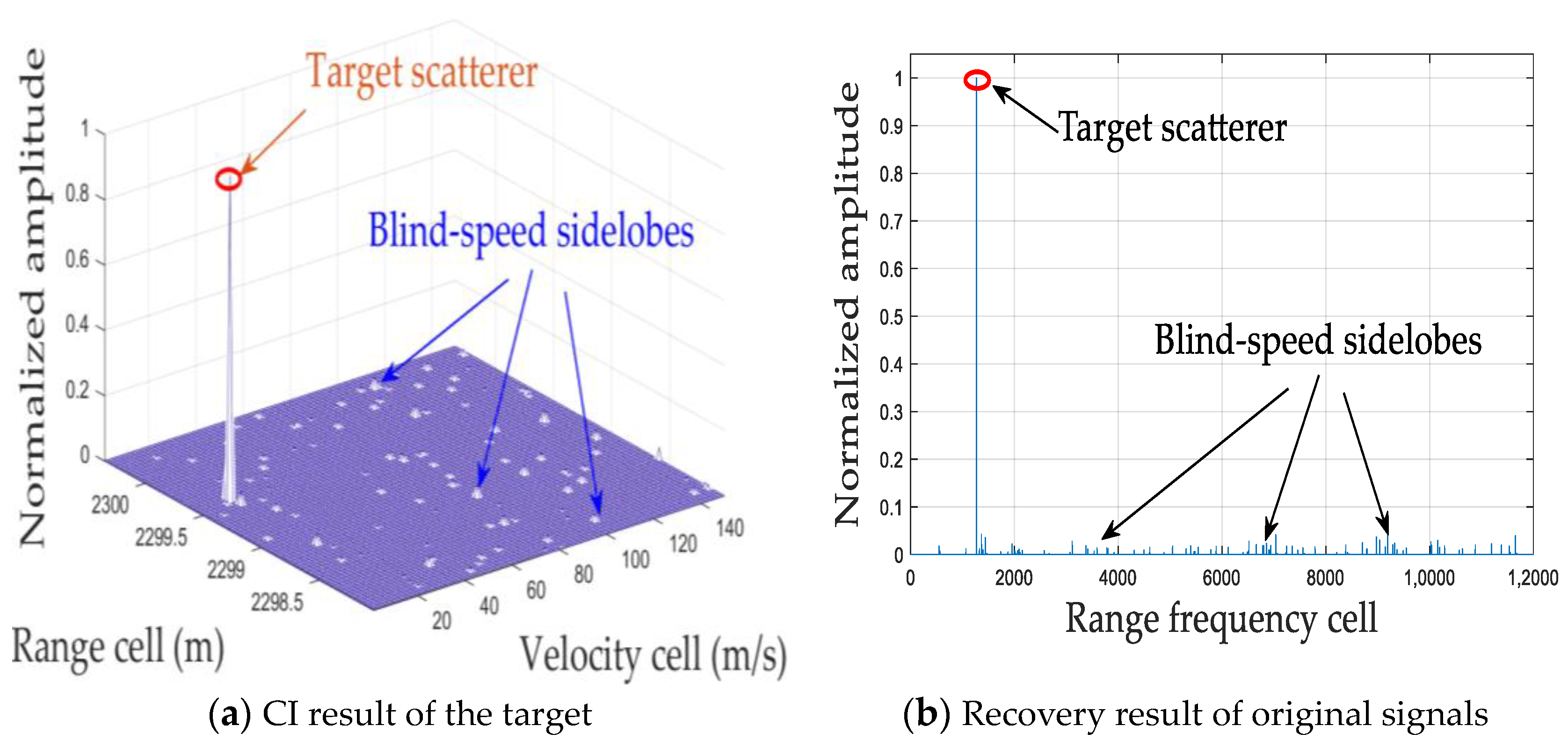
4.1. Simulation Results
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bao, M.; Jia, B.; Li, Y.; Guo, L.; Xing, M. Coherent integration for maneuvering target detection at low SNR based on Radon-general linear chirplet transform. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Ma, J.; Huang, P.; Yu, J.; Liang, G.; Liao, G. An efficient coherent integration method for maneuvering target detection with nonuniform pulse sampling based on filterbank framework. IEEE Geosci. Remote Sens. Lett. 2020, 17, 2045–2049. [Google Scholar] [CrossRef]
- Zhen, D.; Zhang, Z.; Yu, W. An adaptive OFDM detection strategy for range and Doppler spread targets in non-Gaussian clutter. IEEE Access 2018, 6, 61223–61231. [Google Scholar]
- Wang, Z.; He, Z.; He, Q.; Cheng, Z. Persymmetric range-spread targets detection in compound Gaussian sea clutter with inverse Gaussian texture. IEEE Geosci. Remote Sens. Lett. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Li, Y.; Huang, T.; Xu, X.; Liu, Y.; Eldar, Y.C. Phase transition in frequency agile radar using compressed sensing. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020. [Google Scholar]
- Liu, S.; Cao, Y.; Yeo, T.S.; Wu, W.; Liu, Y. Adaptive clutter suppression in randomized stepped-frequency radar. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1317–1333. [Google Scholar] [CrossRef]
- Li, Y.H.; Huang, T.Y.; Xu, X.Y. Phase transitions in frequency agile radar using compressed sensing. IEEE Trans. Signal Process. 2021, 69, 4801–4818. [Google Scholar] [CrossRef]
- Zhao, Y.N.; Zhao, Z.Q.; Tong, F.Q.; Sun, P. Joint design of transmitting waveform and receiving filter via novel riemannian idea for DFRC system. Remote Sens. 2023, 15, 3548. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, X.; Cao, R. Novel approach for ISAR cross-range scaling based on the multidelay discrete polynomial-phase transform combined with Keystone transform. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1221–1231. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Kong, L.; Yi, W. Fast non-searching method for maneuvering target detection and motion parameters estimation. IEEE Trans. Signal Process. 2016, 64, 2232–2244. [Google Scholar] [CrossRef]
- Chen, X.L.; Guan, J.; Huang, Y.; He, Y. Space-range-Doppler focus-based low-observable moving target detection using frequency diverse array MIMO radar. IEEE Access 2018, 6, 43892–43904. [Google Scholar] [CrossRef]
- Huang, T.; Liu, Y.; Li, G. Randomized stepped frequency ISAR imaging. In Proceedings of the 2012 IEEE Radar Conference (RADAR), Atlanta, GA, USA, 7–11 May 2012. [Google Scholar]
- Wehner, D. High-Resolution Radar; Radar Library, Artech House, Incorporated: Norwood, MA, USA, 1995. [Google Scholar]
- Maric, S.; Titlebaum, E.L. A class of frequency hop codes with nearly ideal characteristics for use in multiple-access spread-spectrum communications and radar and sonar systems. IEEE Trans. Commun. 1992, 40, 1442–1447. [Google Scholar] [CrossRef]
- Yu, J.; Xu, J.; Peng, Y.N.; Xia, X.G. Radon-Fourier transform for radar target detection (III): Optimality and fast implementations. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 991–1004. [Google Scholar] [CrossRef]
- Qian, L.C.; Xu, J.; Xia, X.G.; Sun, W.F.; Long, T.; Peng, Y.N. Fast implementation of generalized Radon-Fourier transform for maneuvering radar target detection. Electron. Lett. 2012, 48, 1427–1428. [Google Scholar] [CrossRef]
- Yan, L.; Zhou, X.; Long, T.; Xia, X.G.; Wang, Y.L.; Farina, A. Adaptive Radon–Fourier transform for weak radar target detection. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1641–1663. [Google Scholar]
- Lang, P.; Fu, X.J.; Dong, J.; Yang, J. An efficient radon Fourier transform-based coherent integration method for target detection. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Lin, S.; Zhang, M.; Cheng, X.; Zhou, K.X.; Zhao, S.B.; Wang, H. Hyperspectral anomaly detection via sparse representation and collaborative representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 946–961. [Google Scholar] [CrossRef]
- Xu, W.W.; Zhou, Y.H.; Wang, X.K.; Chen, W.C. MoG-based robust sparse representation for seismic erratic noise suppression. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Ma, L. Radio map crowdsourcing update method using sparse representation and low rank matrix recovery for WLAN indoor positioning system. IEEE Trans. Wirel. Commun. Lett. 2021, 10, 1188–1191. [Google Scholar] [CrossRef]
- Huang, T.; Liu, Y.; Meng, H.; Wang, X. Cognitive random stepped frequency radar with sparse recovery. IEEE Trans. Aerosp. Electron. Syst. 2013, 50, 858–870. [Google Scholar] [CrossRef]
- Yu, Y.; Petropulu, A.; Poor, H. CSSF MIMO RADAR: Compressive-sensing and step-frequency based MIMO radar. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 1490–1505. [Google Scholar] [CrossRef]
- Dong, J.Y.; Lyu, W.T.; Zhou, D.; Xu, W.Q. Variational Bayesian and generalized approximate message passing-based sparse Bayesian learning model for image recovery. IEEE Signal Process. Lett. 2022, 29, 2328–2332. [Google Scholar] [CrossRef]
- Pan, T.H.; Wu, C.; Chen, Q. Sparse recovery using block sparse bayesian learning with fast marginalized likelihood maximization for near-infrared spectroscopy. IEEE Trans. Instrum. Meas. 2022, 71, 1–10. [Google Scholar]
- Guo, Y.J.; Wen, W.K.; Wu, P.R.; Xia, M.H. A sparsity adaptive algorithm to recover NB-IoT signal from legacy LTE interference. IEEE Trans. Wirel. Commun. Lett. 2021, 10, 2703–2707. [Google Scholar] [CrossRef]
- Hu, Y.F.; Zhao, L.Q. A fuzzy selection compressive sampling matching pursuit algorithm for its practical application. IEEE Access 2019, 7, 144101–144124. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Lee, B.; Ko, K.; Hong, J.; Ku, B.; Ko, H. Information bottleneck measurement for compressed sensing image recovery. IEEE Signal Process. Lett. 2022, 29, 1943–1947. [Google Scholar] [CrossRef]
- Li, J.; Sacchi, M.D. An lp-space matching pursuit algorithm and its application to robust seismic data denoising via time-domain radon transform. Geophysics 2021, 86, 171–183. [Google Scholar] [CrossRef]
- Zong, Z.Y.; Fu, T.; Yin, X.Y. High-dimensional generalized orthogonal matching pursuit with singular value decomposition. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Nguyen, N.; Needell, D.; Woolf, T. Linear convergence of stochastic iterative greedy algorithms with sparse constraints. IEEE Trans. Inf. Theory 2017, 63, 6869–6895. [Google Scholar] [CrossRef]
- Pei, L.; Jiang, H.; Li, M. Weighted double-backtracking matching pursuit for block-sparse recovery. IET Signal Process. 2016, 10, 930–935. [Google Scholar] [CrossRef]
- Li, Y.J.; Chen, W.D. A correlation coefficient sparsity adaptive matching pursuit algorithm. IEEE Signal Process. Lett. 2023, 30, 190–194. [Google Scholar] [CrossRef]
- Do, T.T.; Gan, L.; Nguyen, N.; Tran, T.D. Sparsity adaptive matching pursuit algorithm for practical compressed sensing. In Proceedings of the 2008 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 26–29 October 2008. [Google Scholar]
- Tang, C. Sparsity adaptive matching pursuit algorithm with variable proportion. Commun. Technol. 2019, 52, 1620–1625. [Google Scholar]
- Yu, M.; Yu, X.; Zeng, S.; Yang, Q. Equal sinusoidal division of array manifold matrix based on direction-of-arrival estimation for dual-functional radar-communication. In Proceedings of the Journal of Physics: Conference Series, Kunming, China, 4–6 June 2021. [Google Scholar]
- Wang, R.; Zhang, J.; Ren, S.; Li, Q. A reducing iteration orthogonal matching pursuit algorithm for compressive sensing. Tsinghua Sci. Technol. 2021, 1, 71–79. [Google Scholar] [CrossRef]
- Yu, Z. Variable step-size compressed sensing-based sparsity adaptive matching pursuit algorithm for speech recovery. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; pp. 7344–7349. [Google Scholar]
- Zhang, X.; Liu, Y.; Wang, X. A sparsity pre-estimated adaptive matching pursuit algorithm. J. Elect. Comput. Eng. 2021, 2021, 5598180. [Google Scholar]
- Fu, Y.; Liu, S.; Ren, C. Adaptive step-size matching pursuit algorithm for practical sparse recovery. Circuits Syst. Signal Process. 2017, 36, 2275–2291. [Google Scholar] [CrossRef]
- Candes, E.; Tao, T. Near-optimal signal recovery from random projections: Universal encoding strategies. IEEE Trans. Inform. Theory 2006, 52, 5406–5425. [Google Scholar] [CrossRef]

















| Parameters | Value |
|---|---|
| Carrier frequency | 10 GHz |
| Signal bandwidth | 100 MHz |
| Pulse width | 50 μs |
| Sampling frequency | 2.5 GHz |
| Pulse repetition time | 300 μs |
| Radar system loss | 4 dB |
| Carrier frequency step interval | 30 MHz |
| Pulse number of CPI | 128 |
| Methods | /s | ||
|---|---|---|---|
| SAMP | 0.66 | 0.99 | 0.22 |
| CCSAMP | 0.68 | 1 | 0.068 |
| SAMP-OC | 0.98 | 1 | 0.5 |
| RFT-WOA | 0.99 | 1 | 9.01 |
| ROMP with the prior information of spare lever | 1 | 1 | 0.0047 |
| Proposed method | 1 | 1 | 0.38 |
| SCR/dB | 9.8 | 10.44 | 12.87 | 14.12 |
|---|---|---|---|---|
| SAMP | 0.43 | 0.61 | 0.87 | 0.91 |
| CCSAMP | 0.47 | 0.73 | 0.93 | 0.96 |
| SAMP-OC | 0.55 | 0.85 | 1 | 1 |
| RFT-WOA | 0.47 | 0.86 | 0.99 | 1 |
| ROMP with the prior information of sparse lever | 0.55 | 0.86 | 1 | 1 |
| Proposed method | 0.55 | 0.86 | 1 | 1 |
| SCR/dB | 9.8 | 10.44 | 12.87 | 14.12 |
|---|---|---|---|---|
| SAMP | 0.34 | 0.5 | 0.61 | 0.61 |
| CCSAMP | 0.34 | 0.52 | 0.62 | 0.63 |
| SAMP-OC | 0.54 | 0.82 | 0.98 | 1 |
| RFT-WOA | 0.37 | 0.83 | 0.99 | 1 |
| ROMP with the prior information of sparse lever | 0.55 | 0.83 | 1 | 1 |
| Proposed method | 0.55 | 0.83 | 1 | 1 |
| Methods | Time/s |
|---|---|
| SAMP | 0.21 |
| CCSAMP | 0.1 |
| SAMP-OC | 0.48 |
| RFT-WOA | 0.93 |
| ROMP with the prior information of sparse lever | 0.007 |
| Proposed method | 0.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, J.; Fu, X.; Zhan, K.; Zhao, X.; Dong, J.; Wu, J. Target Detection Method Based on Adaptive Step-Size SAMP Combining Off-Grid Correction for Coherent Frequency-Agile Radar. Remote Sens. 2023, 15, 4921. https://doi.org/10.3390/rs15204921
Chang J, Fu X, Zhan K, Zhao X, Dong J, Wu J. Target Detection Method Based on Adaptive Step-Size SAMP Combining Off-Grid Correction for Coherent Frequency-Agile Radar. Remote Sensing. 2023; 15(20):4921. https://doi.org/10.3390/rs15204921
Chicago/Turabian StyleChang, Jiayun, Xiongjun Fu, Kai Zhan, Xuezhou Zhao, Jian Dong, and Junqiang Wu. 2023. "Target Detection Method Based on Adaptive Step-Size SAMP Combining Off-Grid Correction for Coherent Frequency-Agile Radar" Remote Sensing 15, no. 20: 4921. https://doi.org/10.3390/rs15204921
APA StyleChang, J., Fu, X., Zhan, K., Zhao, X., Dong, J., & Wu, J. (2023). Target Detection Method Based on Adaptive Step-Size SAMP Combining Off-Grid Correction for Coherent Frequency-Agile Radar. Remote Sensing, 15(20), 4921. https://doi.org/10.3390/rs15204921





