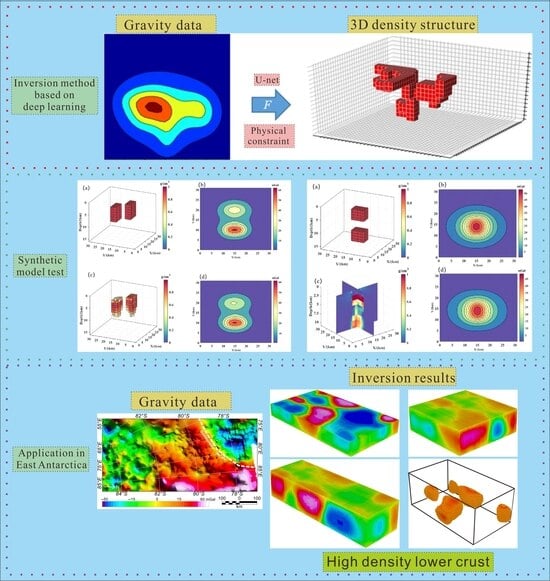
Improved Gravity Inversion Method Based on Deep Learning with Physical Constraint and Its Application to the Airborne Gravity Data in East Antarctica
Abstract
:1. Introduction
2. Forward Modeling of Gravity Anomalies
3. Gravity Inversion Based on U-net Network
3.1. Introduction to U-net Network
3.2. Improvement of Loss Function
3.3. Establishment of Sample Datasets
3.4. Inversion Calculation Process
3.5. Inversion Results of the Synthetic Model Data
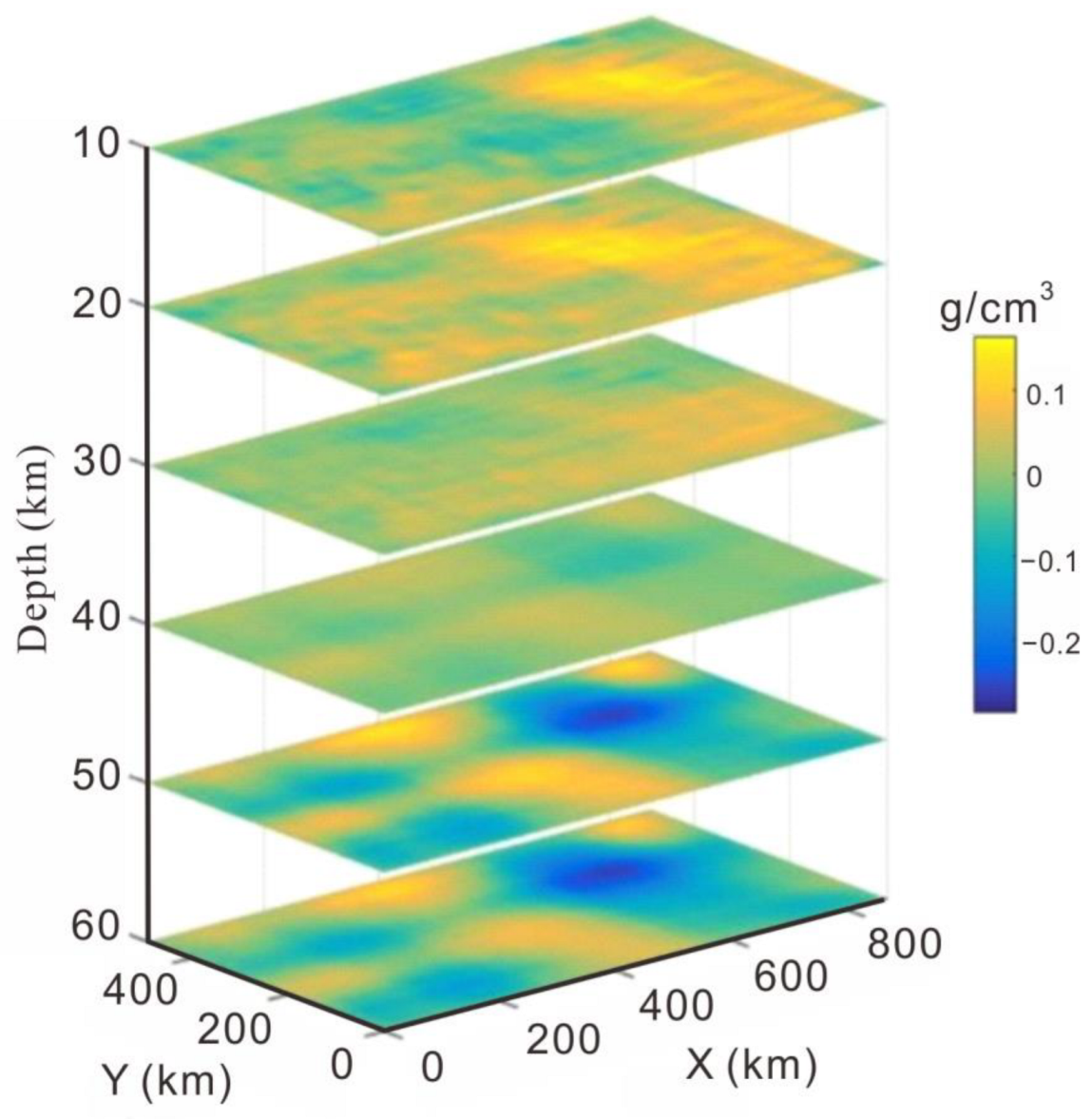
4. Application in East Antarctica
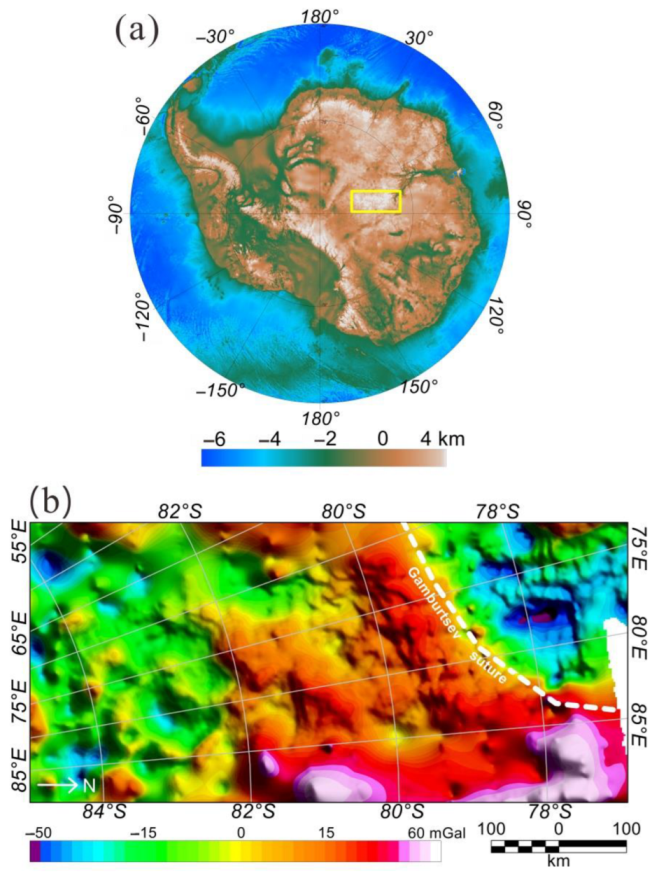
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Y.; Oldenburg, D.W. 3-D inversion of gravity data. Geophysics 1998, 63, 109–119. [Google Scholar] [CrossRef]
- Nabighian, M.N.; Ander, M.E.; Grauch, V.J.S.; Hansen, R.O.; LaFehr, T.R.; Li, Y.; Pearson, W.C.; Peirce, J.W.; Phillips, J.D.; Ruder, M.E. Historical development of the gravity method in exploration. Geophysics 2005, 70, 63ND–89ND. [Google Scholar] [CrossRef]
- Oldenburg, D.W. The Inversion and interpretation of gravity anomalies. Geophysics 1974, 39, 526–536. [Google Scholar] [CrossRef]
- Silva, J.B.C.; Costa, D.C.L.; Barbosa, V.C.F. Gravity inversion of basement relief and estimation of density contrast variation with depth. Geophysics 2006, 71, J51–J58. [Google Scholar] [CrossRef]
- Tikhonov, A.N.; Goncharsky, A.V.; Stepanov, V.V.; Yagola, A.G. Numerical methods for the approximate solution of ill-posed problems on compact sets. In Numerical Methods for the Solution of Ill-Posed Problems; Springer: Dordrecht, The Netherlands, 1995; pp. 65–79. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. 3-D inversion of magnetic data. Geophysics 1996, 61, 394–408. [Google Scholar] [CrossRef]
- Last, B.J. Compact gravity inversion. Geophysics 2012, 48, 713–721. [Google Scholar] [CrossRef]
- Portniaguine, O.; Zhdanov, M.S. Focusing geophysical inversion images. Geophysics 1999, 64, 874–887. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, Y.; Yan, J.; Wang, H.; Qiu, Y. 3D inversion of full gravity gradient tensor data in spherical coordinate system using local north-oriented frame. Earth Planets Space 2018, 70, 58. [Google Scholar] [CrossRef]
- Portniaguine, O.; Zhdanov, M.S. 3-D magnetic inversion with data compression and image focusing. Geophysics 2002, 67, 1532–1541. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. Fast inversion of large-scale magnetic data using wavelet transforms and a logarithmic barrier method. Geophys. J. Int. 2003, 152, 251–265. [Google Scholar] [CrossRef]
- Foks, N.L.; Krahenbuhl, R.; Li, Y. Adaptive sampling of potential-field data: A direct approach to compressive inversion. Geophysics 2014, 79, IM1–IM9. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, G.; Liu, Y.; Fan, Z. Deep Learning for 3-D Inversion of Gravity Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5905918. [Google Scholar] [CrossRef]
- Guo, R.; Yao, H.M.; Li, M.; Ng, M.K.P.; Abubakar, A. Joint Inversion of Audio-Magnetotelluric and Seismic Travel Time Data With Deep Learning Constraint. IEEE Trans. Geosci. Remote Sens. 2020, 59, 7982–7995. [Google Scholar] [CrossRef]
- Kim, Y.; Nakata, N. Geophysical inversion versus machine learning in inverse problems. Lead. Edge 2018, 37, 894–901. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Beroza, G.C. Deep-learning seismology. Science 2022, 377, eabm4470. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.; Yin, C.; Ren, X.; Su, Y. Fast imaging of time-domain airborne EM data using deep learning technology. Geophysics 2020, 85, E163–E170. [Google Scholar] [CrossRef]
- Puzyrev, V. Deep learning electromagnetic inversion with convolutional neural networks. Geophys. J. Int. 2019, 218, 817–832. [Google Scholar] [CrossRef]
- Qi, S.; Wang, Y.; Li, Y.; Wu, X.; Ren, Q.; Ren, Y. Two-Dimensional Electromagnetic Solver Based on Deep Learning Technique. IEEE J. Multiscale Multiphysics Comput. Tech. 2020, 5, 83–88. [Google Scholar] [CrossRef]
- Guo, J.; Li, Y.; Jessell, M.W.; Giraud, J.; Li, C.; Wu, L.; Li, F.; Liu, S. 3D geological structure inversion from Noddy-generated magnetic data using deep learning methods. Comput. Geosci. 2021, 149, 104701. [Google Scholar] [CrossRef]
- Khan, A.; Ghorbanian, V.; Lowther, D. Deep Learning for Magnetic Field Estimation. IEEE Trans. Magn. 2019, 55, 7202304. [Google Scholar] [CrossRef]
- Pollok, S.; Bjørk, R.; Jørgensen, P.S. Inverse Design of Magnetic Fields Using Deep Learning. IEEE Trans. Magn. 2021, 57, 2101604. [Google Scholar] [CrossRef]
- Yang, Q.; Hu, X.; Liu, S.; Jie, Q.; Wang, H.; Chen, Q. 3-D Gravity Inversion Based on Deep Convolution Neural Networks. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3001305. [Google Scholar] [CrossRef]
- Zhang, S.; Yin, C.; Cao, X.; Sun, S.; Liu, Y.; Ren, X. DecNet: Decomposition network for 3D gravity inversion. Geophysics 2022, 87, G103–G114. [Google Scholar] [CrossRef]
- Huang, R.; Liu, S.; Qi, R.; Zhang, Y. Deep Learning 3D Sparse Inversion of Gravity Data. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022476. [Google Scholar] [CrossRef]
- Wang, Y.-F.; Zhang, Y.-J.; Fu, L.-H.; Li, H.-W. Three-dimensional gravity inversion based on 3D U-Net++. Appl. Geophys. 2021, 18, 451–460. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, Z. The Identification of Impact Craters from GRAIL-Acquired Gravity Data by U-Net Architecture. Remote Sens. 2022, 14, 2783. [Google Scholar] [CrossRef]
- Boulanger, O.; Chouteau, M. Constraints in 3D gravity inversion. Geophys. Prospect. 2001, 49, 265–280. [Google Scholar] [CrossRef]
- Li, X.; Chouteau, M. Three-Dimensional Gravity Modeling In All Space. Surv. Geophys. 1998, 19, 339–368. [Google Scholar] [CrossRef]
- Nagy, D.; Papp, G.; Benedek, J. The gravitational potential and its derivatives for the prism. J. Geod. 2000, 74, 552–560. [Google Scholar] [CrossRef]
- Bell, R.E.; Ferraccioli, F.; Creyts, T.T.; Braaten, D.; Corr, H.; Das, I.; Damaske, D.; Frearson, N.; Jordan, T.; Rose, K.; et al. Widespread Persistent Thickening of the East Antarctic Ice Sheet by Freezing from the Base. Science 2011, 331, 1592–1595. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Ferraccioli, F.; Zhou, W.; Yuan, Y.; Gao, J.; Tian, G. Tectonic Implications for the Gamburtsev Subglacial Mountains, East Antarctica, from Airborne Gravity and Magnetic Data. Remote Sens. 2023, 15, 306. [Google Scholar] [CrossRef]
- Ferraccioli, F.; Finn, C.A.; Jordan, T.A.; Bell, R.E.; Anderson, L.M.; Damaske, D. East Antarctic rifting triggers uplift of the Gamburtsev Mountains. Nature 2011, 479, 388–392. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Tian, G.; Bangbing, W.; Ferraccioli, F.; Seddon, S.; Finn, C.; Bell, R. Crustal structure of the Gamburtsev Province, East Antarctica, from airborne geophysics. In Proceedings of the 2017 SEG International Exposition and Annual Meeting, Houston, TX, USA, 24–29 September 2017. [Google Scholar]
- Bo, S.; Siegert, M.J.; Mudd, S.M.; Sugden, D.; Fujita, S.; Xiangbin, C.; Yunyun, J.; Xueyuan, T.; Yuansheng, L. The Gamburtsev mountains and the origin and early evolution of the Antarctic Ice Sheet. Nature 2009, 459, 690–693. [Google Scholar] [CrossRef] [PubMed]
- An, M.; Wiens, D.A.; Zhao, Y.; Feng, M.; Nyblade, A.A.; Kanao, M.; Li, Y.; Maggi, A.; Lévêque, J.-J. S-velocity model and inferred Moho topography beneath the Antarctic Plate from Rayleigh waves. J. Geophys. Res. Solid Earth 2015, 120, 359–383. [Google Scholar] [CrossRef]
- Fretwell, P.; Pritchard, H.D.; Vaughan, D.G.; Bamber, J.L.; Barrand, N.E.; Bell, R.; Bianchi, C.; Bingham, R.G.; Blankenship, D.D.; Casassa, G. Bedmap2: Improved ice bed, surface and thickness datasets for Antarctica. Cryosphere Discuss. 2013, 7, 375–393. [Google Scholar] [CrossRef]












| Model | ||
|---|---|---|
| Model I | 11.0988 | 21.0992 |
| Model I (without data fitting) | 11.0823 | 60.2477 |
| Model II | 13.8248 | 20.9244 |
| Model II (without data fitting) | 14.3762 | 73.0496 |
| Model III | 14.9442 | 25.7893 |
| Model III (without data fitting) | 15.0122 | 69.4803 |
| Model IV | 13.9615 | 17.7656 |
| Model IV (without data fitting) | 13.7121 | 67.6317 |
| Comparing Objects | Density Ranges in g/cm3 | X-Axis Ranges in km | Depth Ranges in km |
|---|---|---|---|
| This study | 0.02–0.16 | 245–560 | 40–68 |
| 0.04–0.16 | 260–550 | 40–67 | |
| 0.06–0.16 | 300–520 | 40–60 | |
| Ferraccioli et al., 2011 [33] | - | 250–680 | 46–58 |
| Wu et al., 2023 [32] | - | 245–670 | 40–58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, G.; Wei, Y.; Dong, S.; Zhang, T.; Yang, C.; Qin, L.; Guan, Q. Improved Gravity Inversion Method Based on Deep Learning with Physical Constraint and Its Application to the Airborne Gravity Data in East Antarctica. Remote Sens. 2023, 15, 4933. https://doi.org/10.3390/rs15204933
Wu G, Wei Y, Dong S, Zhang T, Yang C, Qin L, Guan Q. Improved Gravity Inversion Method Based on Deep Learning with Physical Constraint and Its Application to the Airborne Gravity Data in East Antarctica. Remote Sensing. 2023; 15(20):4933. https://doi.org/10.3390/rs15204933
Chicago/Turabian StyleWu, Guochao, Yue Wei, Siyuan Dong, Tao Zhang, Chunguo Yang, Linjiang Qin, and Qingsheng Guan. 2023. "Improved Gravity Inversion Method Based on Deep Learning with Physical Constraint and Its Application to the Airborne Gravity Data in East Antarctica" Remote Sensing 15, no. 20: 4933. https://doi.org/10.3390/rs15204933
APA StyleWu, G., Wei, Y., Dong, S., Zhang, T., Yang, C., Qin, L., & Guan, Q. (2023). Improved Gravity Inversion Method Based on Deep Learning with Physical Constraint and Its Application to the Airborne Gravity Data in East Antarctica. Remote Sensing, 15(20), 4933. https://doi.org/10.3390/rs15204933