A Probabilistic Method-Based Smartphone GNSS Fault Detection and Exclusion System Utilizing PDR Step Length
Abstract
:1. Introduction
- (1)
- The introduction of an intelligent evolutionary algorithm-optimized particle filter for integrating GNSS and PDR. By incorporating a Krill Herd (KH) algorithm with the particle filter, we address the issue of particle degeneracy, effectively enhancing position accuracy.
- (2)
- We present a probabilistic GNSS fault detection method. This method utilizes the estimated step length derived from accelerometer measurements to construct a probabilistic model for detecting GNSS faults.
2. PDR and KF-PDR/GNSS Integration
2.1. PDR Mechanism
2.2. PDR/GNSS Integration
3. PDR and KF-PDR/GNSS Integration
3.1. Particle Filter
3.2. Krill Herd (KH) Algorithm
- (1)
- Induced movement: the movement of krill individuals is affected by the other individuals in the group;
- (2)
- Foraging behavior of krill individuals;
- (3)
- Random diffusion motion of krill individuals.
3.3. KHA-PF PDR/GNSS
4. Fault Detection
- (1)
- False alarm: the detector decides for , but actually is true.
- (2)
- Miss, the detector decides for , but is true.
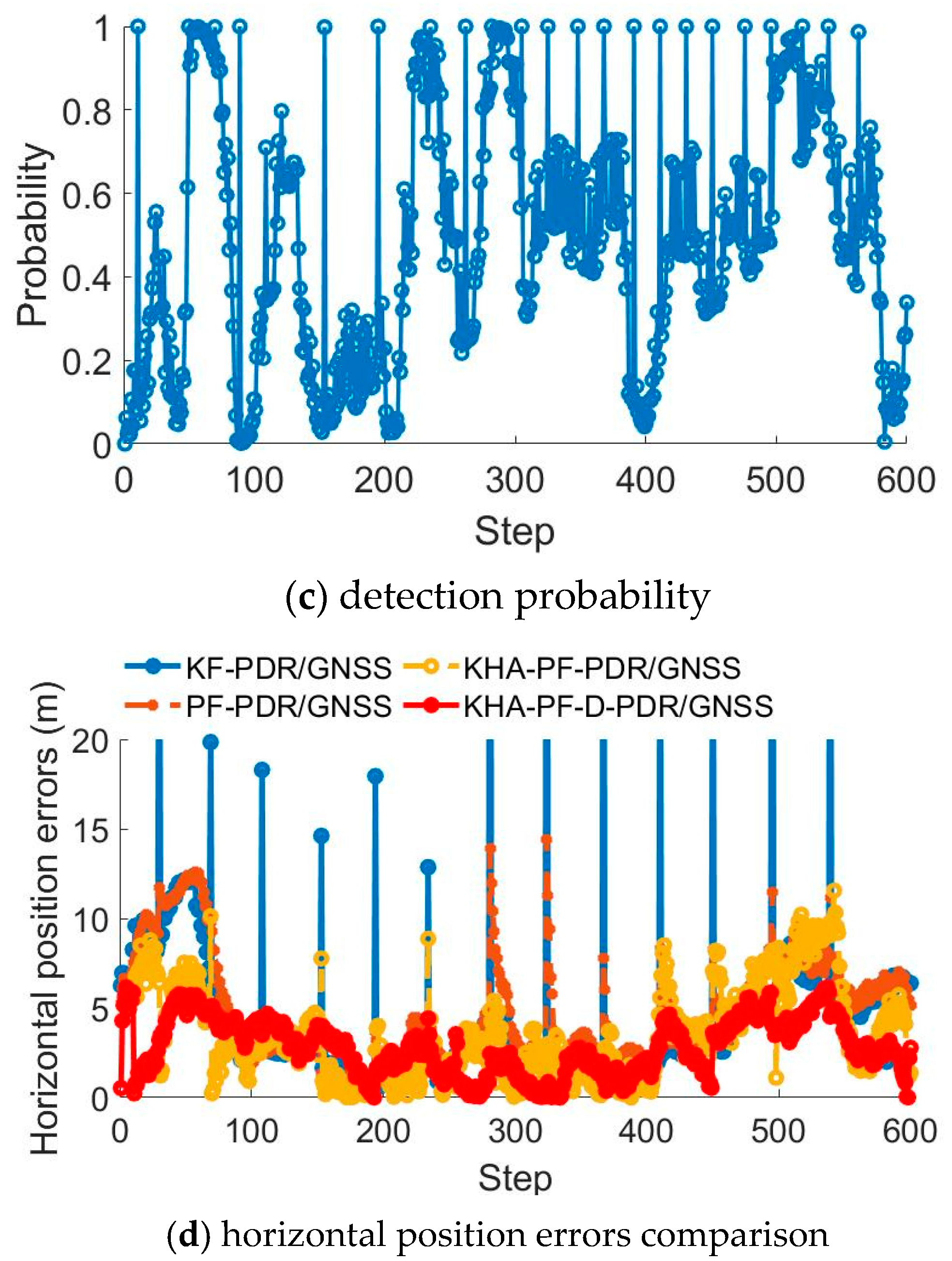
5. Results
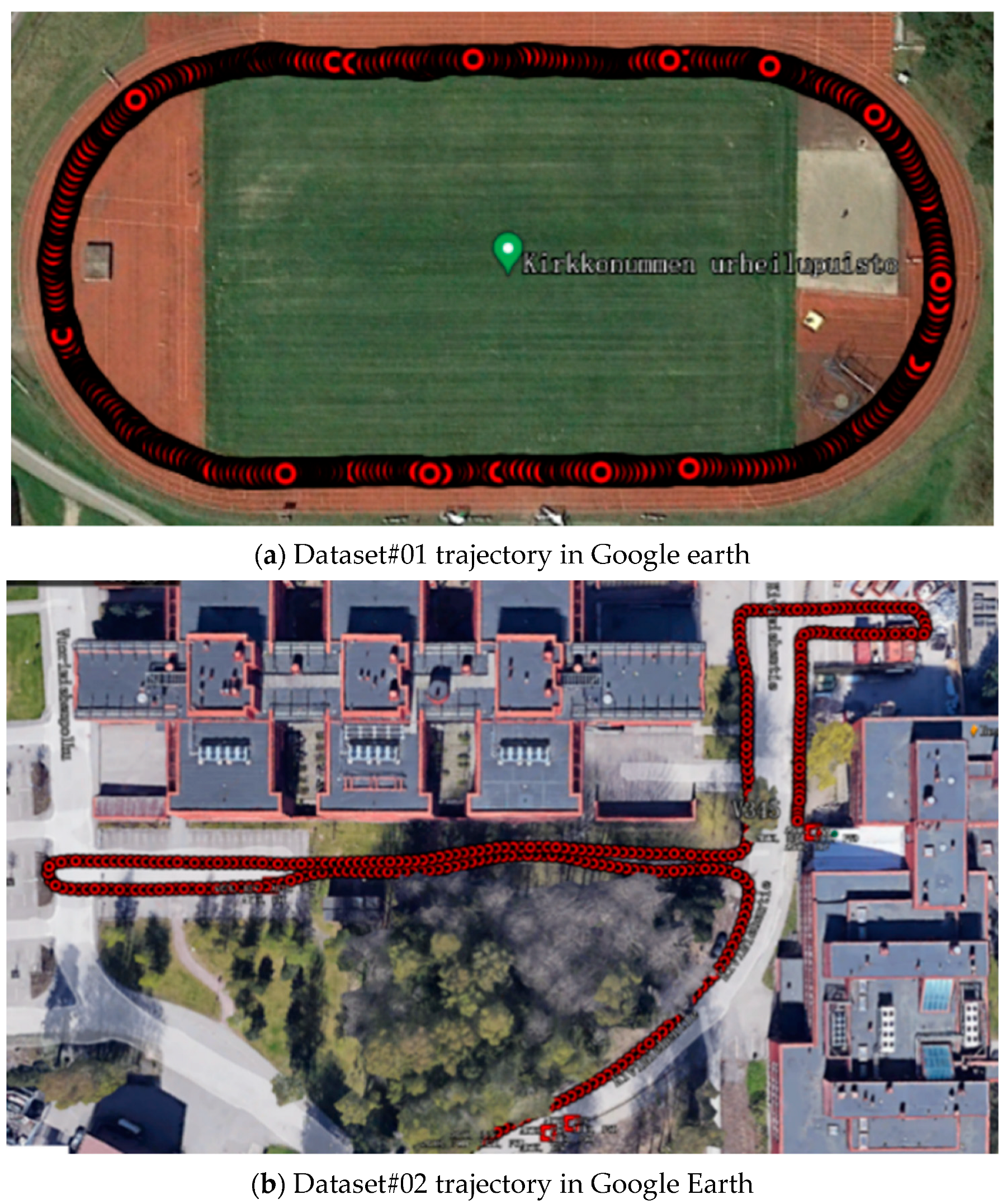
5.1. Sports Track Experiments in Open-Sky Environments
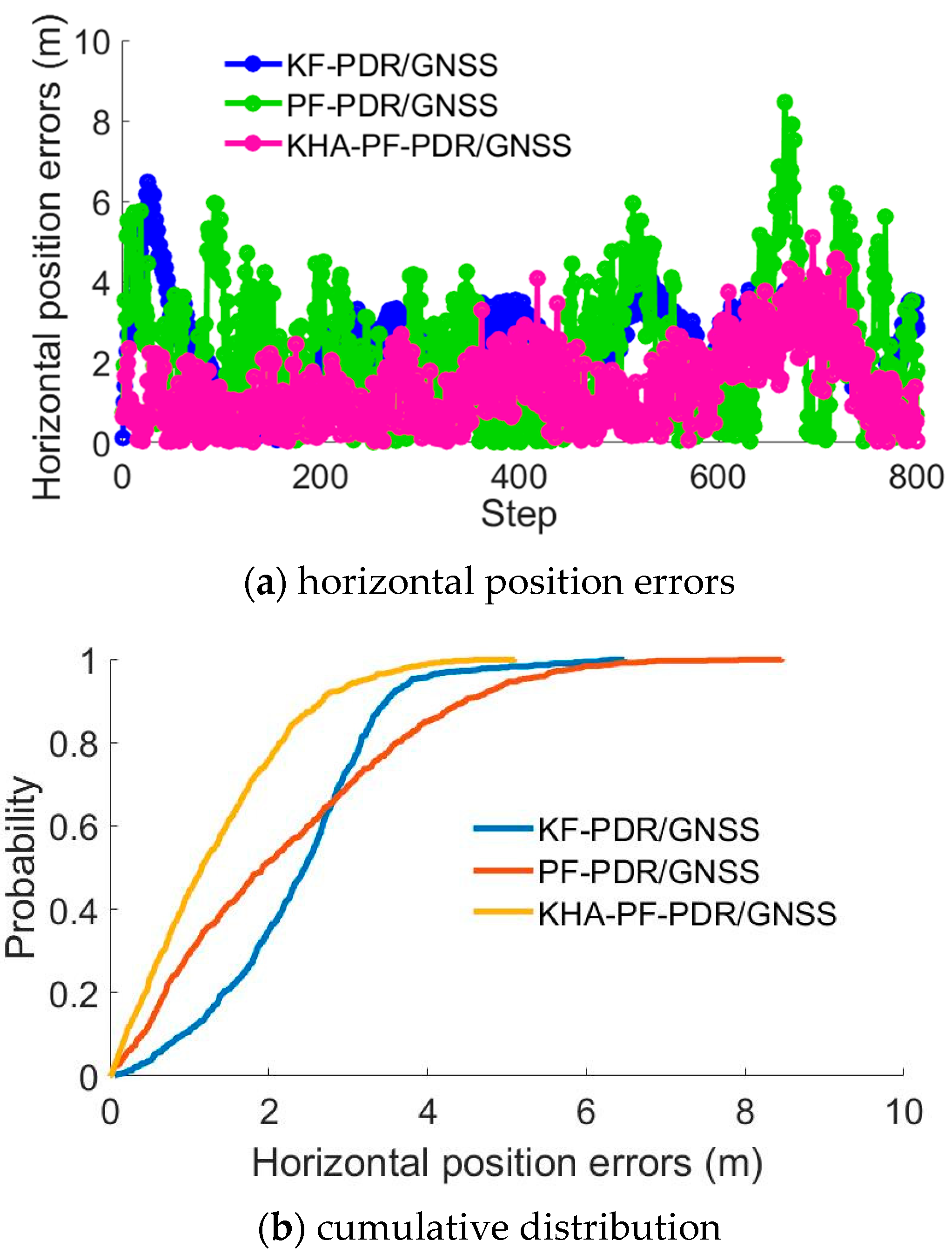
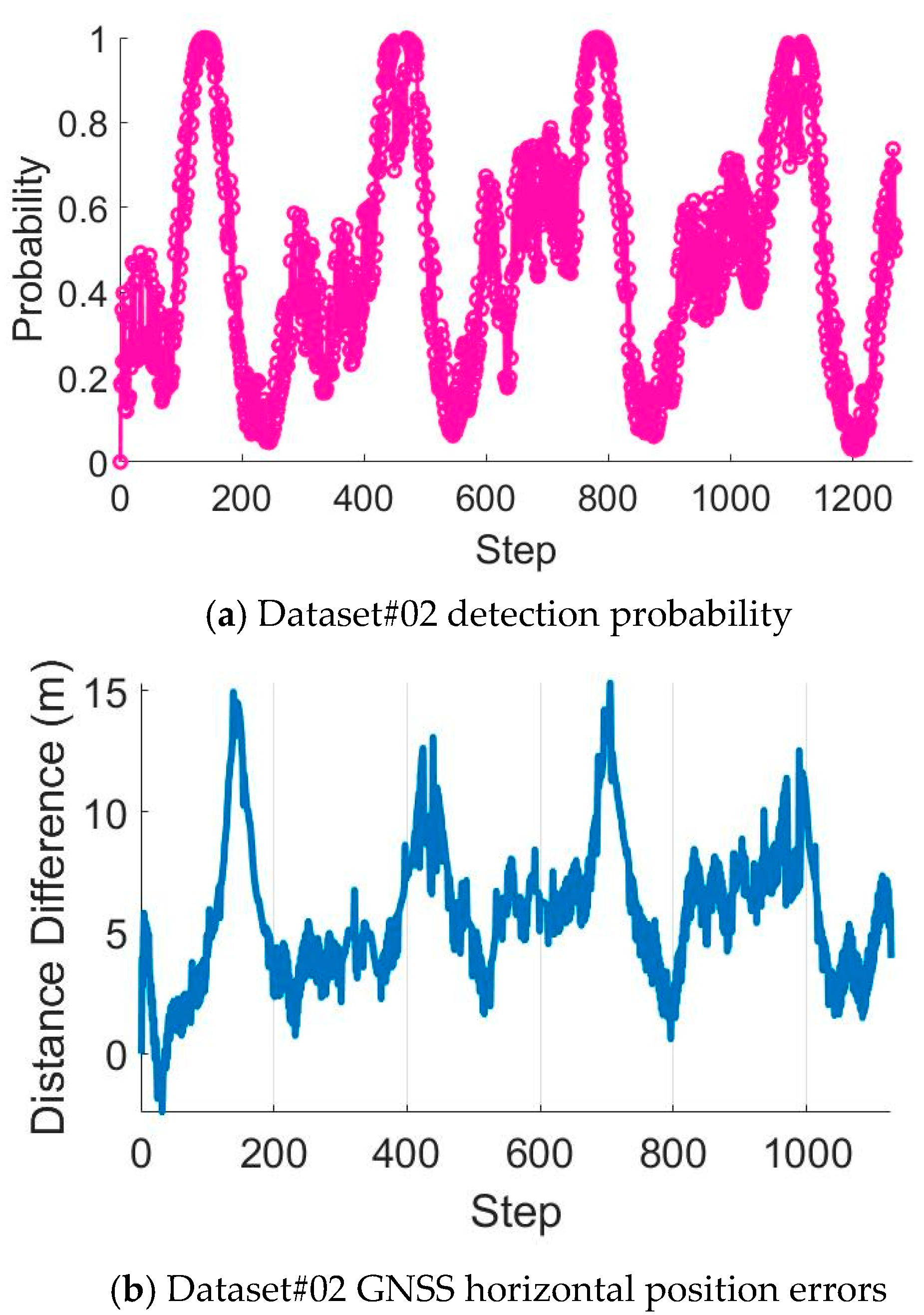
5.2. Fault Detection Experiments and Analysis
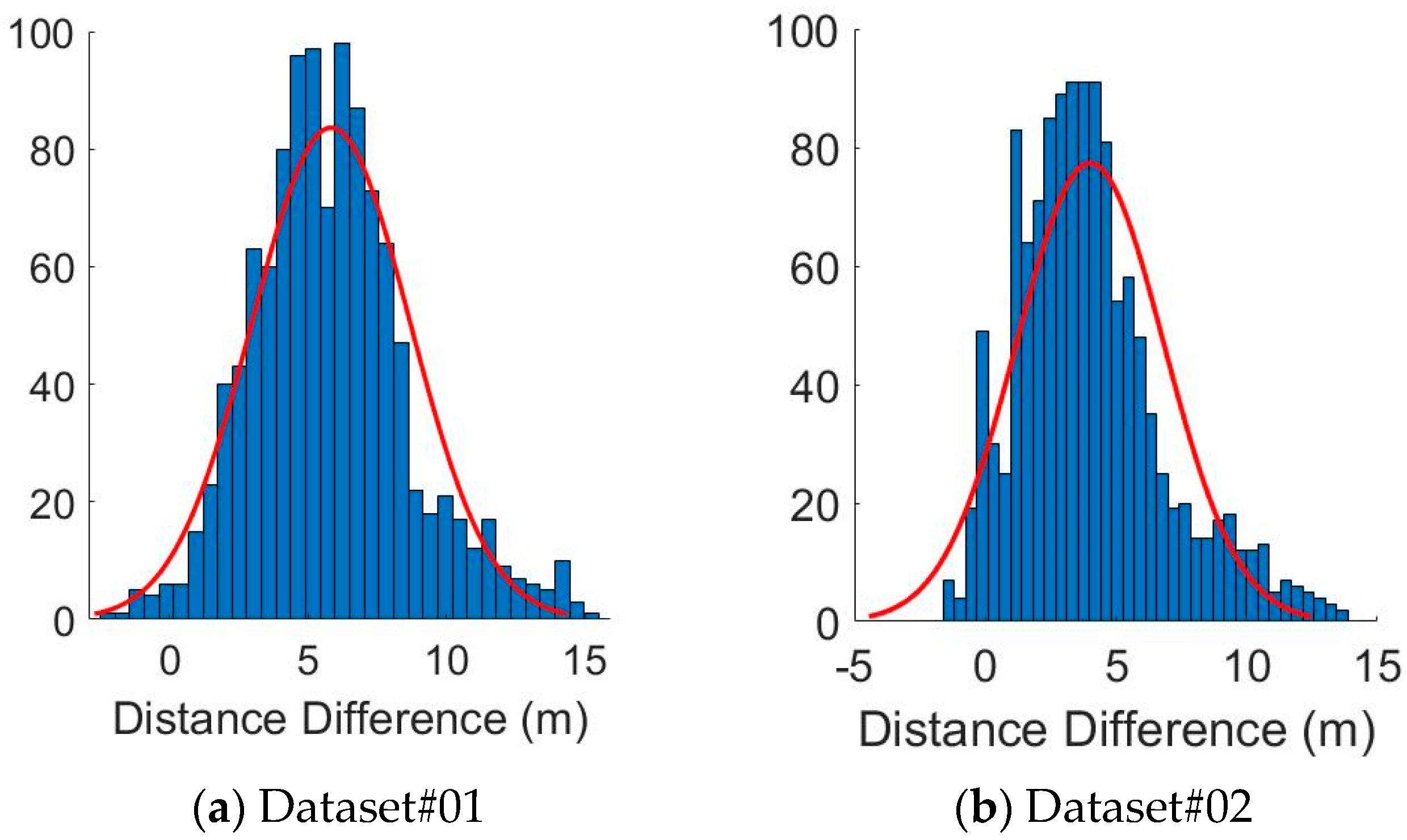
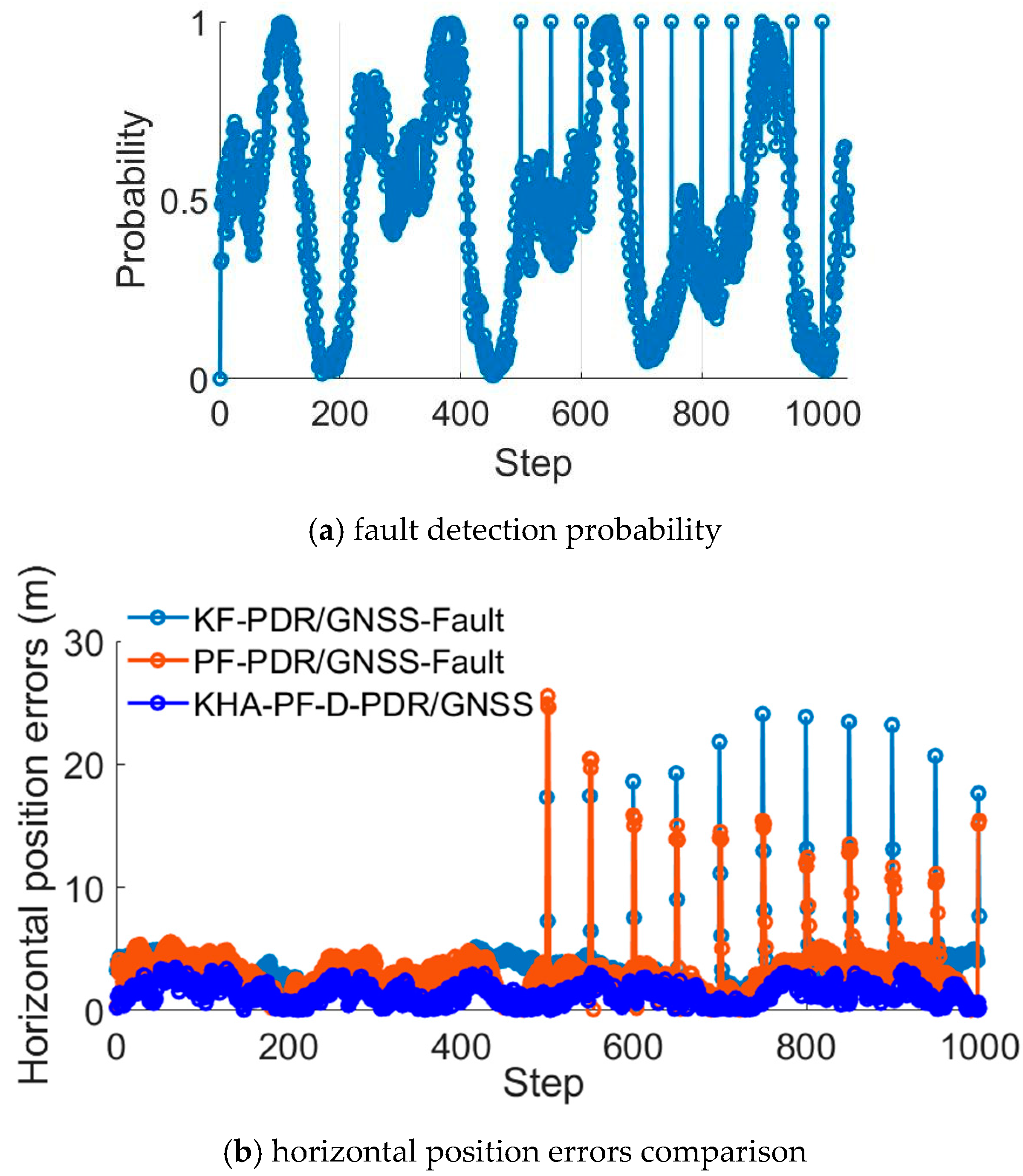
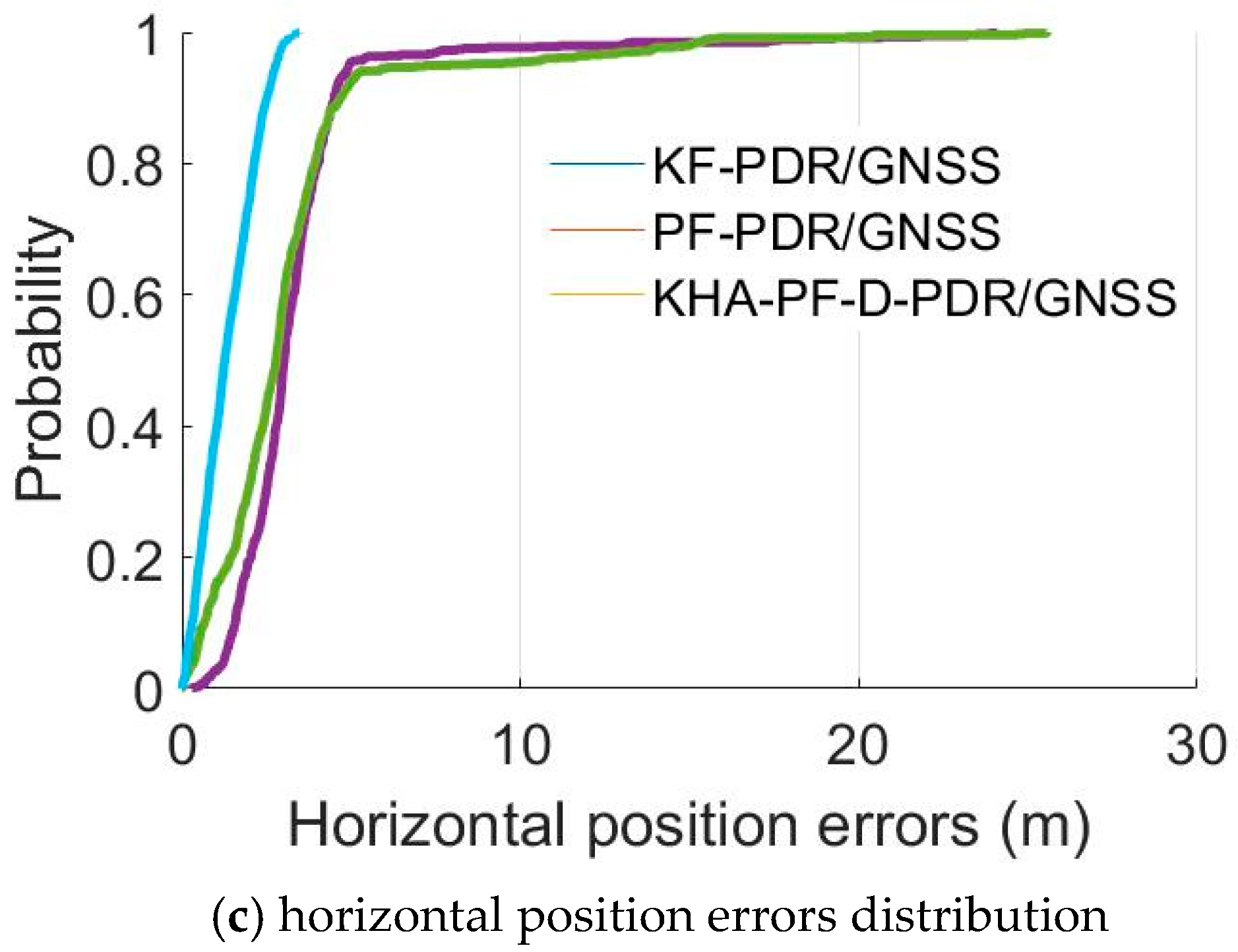
5.3. Fault Detection Experiments with Simulated Faults
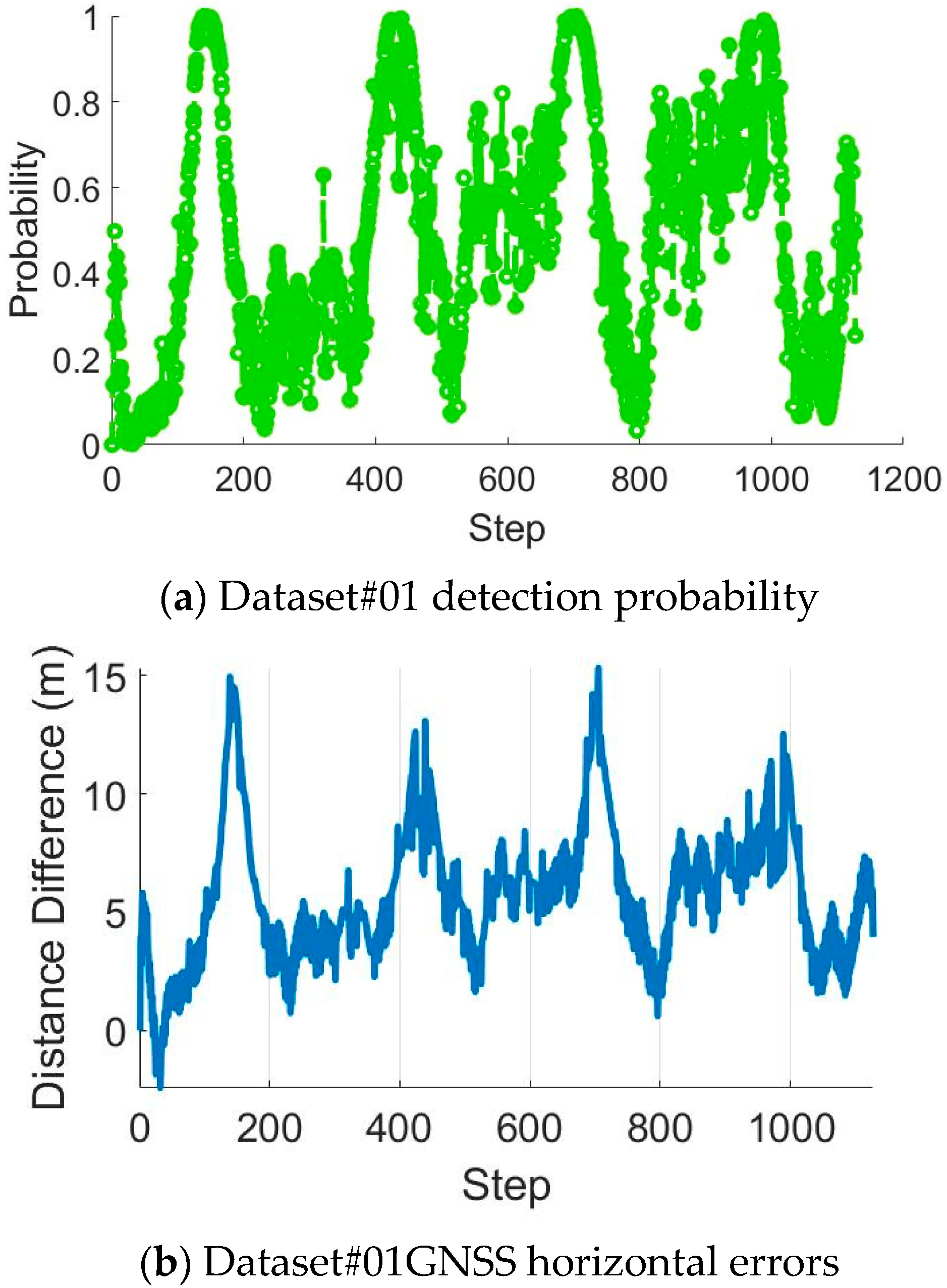
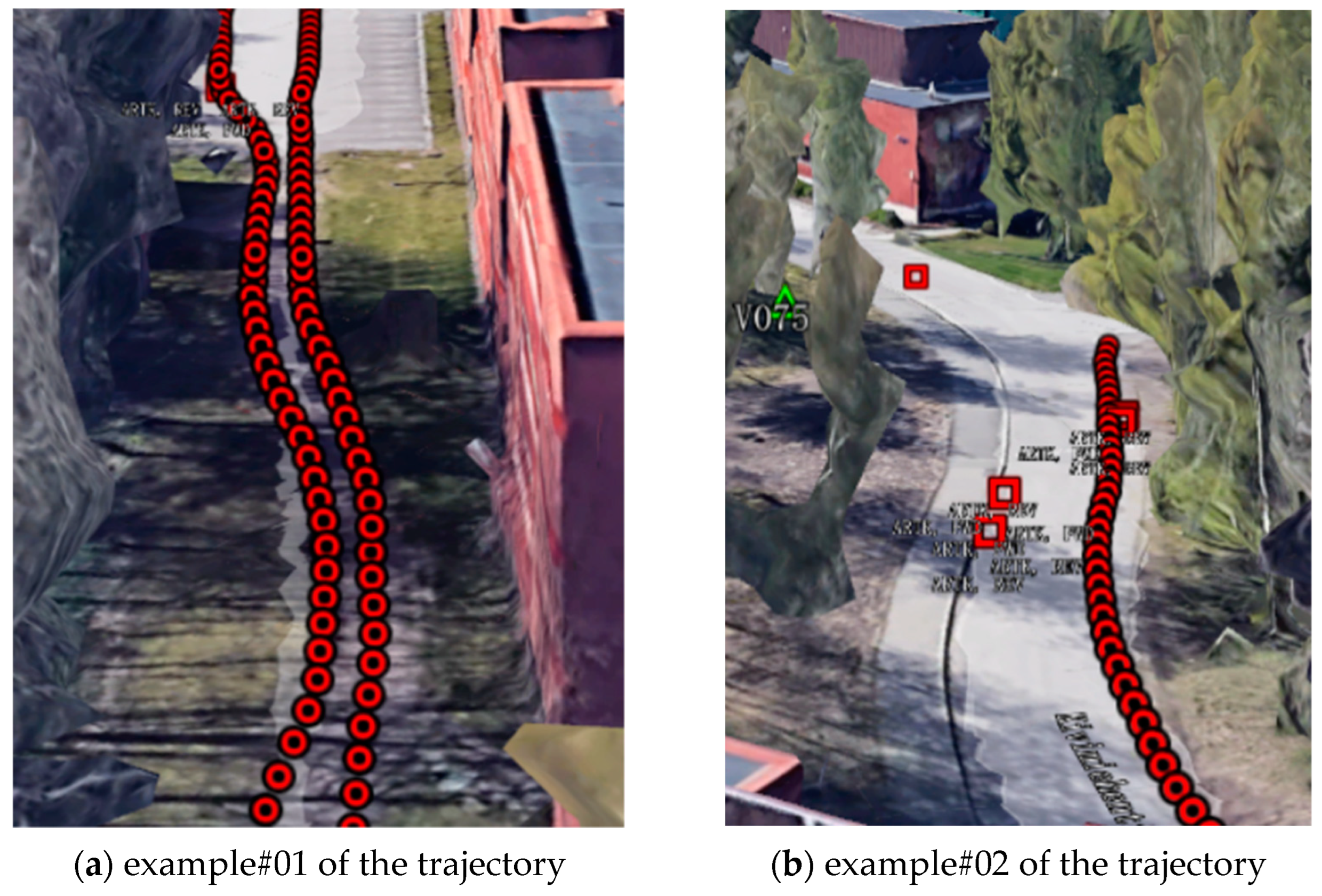
5.4. Fault Detection Experiments in Urban Areas
6. Discussion and Future Work
- (1)
- In this paper, we utilize the Gaussian distribution to model the distance difference measurements; in Equations (28) and (29), we assume that the pedestrian walks straight when building the model. Although the results show that the Gaussian distribution fit the data well, it would still be interesting to build a more universal model with other probability distribution models.
- (2)
- The fault detection method requires some prepared datasets to fit the model, which might be a disadvantage when extending the method to smartphones for real-time applications. Different individuals are likely to have different step length parameters in the Gaussian distribution. GNSS measurements under different conditions have different statistical parameters. It would be valuable to explore more practical solutions to improve the smartphone GNSS robustness, Artificial Intelligence (AI) is a prospective method.
- (1)
- In this paper, PDR is integrated with GNSS; however, there are many other sensors in smartphones, i.e., Wi-Fi, Bluetooth. Integrating more sensors to PDR/GNSS could be a more reliable solution to generate navigation solutions under different conditions.
- (2)
- In the PDR/GNSS integration method described in this paper, the position from GNSS is integrated with PDR; in fact, there is potential to carry out investigations integrating GNSS pseudo-ranges and pseudo-range rates measurements with PDR.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, D.; Dong, Y.; Li, Z.; Li, Q.; Wu, J. Constrained MEMS-based GNSS/INS tightly coupled system with robust Kalman filter for accurate land vehicular navigation. IEEE Trans. Instrum. Meas. 2019, 69, 5138–5148. [Google Scholar] [CrossRef]
- Gong, Z.; Liu, P.; Wen, F.; Ying, R.; Ji, X.; Miao, R.; Xue, W. Graph-based adaptive fusion of GNSS and VIO under intermittent GNSS-degraded environment. IEEE Trans. Instrum. Meas. 2020, 70, 1–16. [Google Scholar] [CrossRef]
- Groves, P.D.; Jiang, Z. Height aiding, C/N0 weighting and consistency checking for GNSS NLOS and multipath mitigation in urban areas. J. Navig. 2013, 66, 653–669. [Google Scholar] [CrossRef]
- Groves, P.D.; Adjrad, M. Likelihood-based GNSS positioning using LOS/NLOS predictions from 3D mapping and pseudoranges. GPS Solut. 2017, 21, 1805–1816. [Google Scholar] [CrossRef]
- Lyu, P.; Bai, S.; Lai, J.; Wang, B.; Sun, X.; Huang, K. Optimal Time Difference-Based TDCP-GPS/IMU Navigation Using Graph Optimization. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Li, X.; Wei, D.; Lai, Q.; Xu, Y.; Yuan, H. Smartphone-based integrated PDR/GPS/Bluetooth pedestrian location. Adv. Space Res. 2017, 59, 877–887. [Google Scholar] [CrossRef]
- Hostettler, R.; Särkkä, S. IMU and magnetometer modeling for smartphone-based PDR. In Proceedings of the 2016 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Alcala de Henares, Spain, 4–7 October 2016; pp. 1–8. [Google Scholar]
- Yao, Y.; Pan, L.; Fen, W.; Xu, X.; Liang, X.; Xu, X. A robust step detection and stride length estimation for pedestrian dead reckoning using a smartphone. IEEE Sens. J. 2020, 20, 9685–9697. [Google Scholar] [CrossRef]
- Naqvib, N.Z.; Kumar, A.; Chauhan, A.; Sahni, K. Step counting using smartphone-based accelerometer. Int. J. Comput. Sci. Eng. 2012, 4, 675. [Google Scholar]
- Gu, F.; Khoshelham, K.; Shang, J.; Yu, F.; Wei, Z. Robust and accurate smartphone-based step counting for indoor localization. IEEE Sens. J. 2017, 17, 3453–3460. [Google Scholar] [CrossRef]
- Al Abiad, N.; Kone, Y.; Renaudin, V.; Robert, T. Smartstep: A Robust STEP Detection Method Based on SMARTphone Inertial Signals Driven by Gait Learning. IEEE Sens. J. 2022, 22, 12288–12297. [Google Scholar] [CrossRef]
- Rehman, A.; Shahid, H.; Afzal, M.A.; Bhatti, H.M.A. Accurate and direct GNSS/PDR integration using extended Kalman filter for pedestrian smartphone navigation. Gyroscopy Navig. 2020, 11, 124–137. [Google Scholar] [CrossRef]
- Angrisano, A.; Vultaggio, M.; Gaglione, S.; Crocetto, N. Pedestrian localization with PDR supplemented by GNSS. In Proceedings of the 2019 European Navigation Conference (ENC), Warsaw, Poland, 9–12 April 2019; pp. 1–6. [Google Scholar]
- Hsu, L.T.; Gu, Y.; Huang, Y.; Kamijo, S. Urban pedestrian navigation using smartphone-based dead reckoning and 3-D map-aided GNSS. IEEE Sens. J. 2015, 16, 1281–1293. [Google Scholar] [CrossRef]
- Jiang, C.; Chen, Y.; Chen, C.; Jia, J.; Sun, H.; Wang, T.; Hyyppä, J. Smartphone PDR/GNSS Integration via Factor Graph Optimization for Pedestrian Navigation. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Qian, Y.; Chen, X. An improved particle filter based indoor tracking system via joint Wi-Fi/PDR localization. Meas. Sci. Technol. 2020, 32, 014004. [Google Scholar] [CrossRef]
- Liu, W.; Li, J.; Deng, Z.; Fu, X.; Cheng, Q. A calibrated-RSSI/PDR/Map integrated system based on a novel particle filter for indoor navigation. In Proceedings of the IEEE International Conference on Indoor Positioning and Indoor Navigation (IPIN), Pisa, Italy, 30 September–3 October 2019; pp. 1–8. [Google Scholar]
- Hsu, L.T.; Tokura, H.; Kubo, N.; Gu, Y.; Kamijo, S. Multiple faulty GNSS measurement exclusion based on consistency check in urban canyons. IEEE Sens. J. 2017, 17, 1909–1917. [Google Scholar] [CrossRef]
- Yang, L.; Knight, N.L.; Li, Y.; Rizos, C. Optimal fault detection and exclusion applied in GNSS positioning. J. Navig. 2013, 66, 683–700. [Google Scholar] [CrossRef]
- Sun, R.; Wang, J.; Cheng, Q.; Mao, Y.; Ochieng, W.Y. A new IMU-aided multiple GNSS fault detection and exclusion algorithm for integrated navigation in urban environments. GPS Solut. 2021, 25, 147. [Google Scholar] [CrossRef]
- Yang, L.; Li, Y.; Wu, Y.; Rizos, C. An enhanced MEMS-INS/GNSS integrated system with fault detection and exclusion capability for land vehicle navigation in urban areas. GPS Solut. 2014, 18, 593–603. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, X.; Pang, C.; Wang, Y.; Zhang, L.; Feng, B. Improved fault detection method based on robust estimation and sliding window test for INS/GNSS integration. J. Navig. 2020, 73, 776–796. [Google Scholar] [CrossRef]
- Yan, D.; Shi, C.; Li, T. An improved PDR system with accurate heading and step length estimation using handheld smartphone. J. Navig. 2022, 75, 141–159. [Google Scholar] [CrossRef]
- Jiang, C.; Chen, Y.; Chen, C.; Jia, J.; Sun, H.; Wang, T.; Hyyppa, J. Implementation and performance analysis of the PDR/GNSS integration on a smartphone. GPS Solut. 2022, 26, 81. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, B.; Huang, P.; Xue, W.; Li, Q.; Zhu, J.; Qiu, L. Kalman filter-based data fusion of WI-FI RTT and PDR for indoor localization. IEEE Sens. J. 2021, 21, 8479–8490. [Google Scholar] [CrossRef]
- Shi, L.F.; Yu, M.X.; Yin, W. PDR/Geomagnetic Fusion Localization Method Based on AOFA-Improved Particle Filter. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. Krill herd: A new bio-inspired optimization algorithm. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4831–4845. [Google Scholar] [CrossRef]






| Mean (m) | Median (m) | |
|---|---|---|
| KF-PDR/GNSS | 2.37 | 2.45 |
| PF-PDR/GNSS | 2.22 | 1.92 |
| KHA-PDR/GNSS | 1.34 | 1.16 |
| Mean (m) | Median (m) | |
|---|---|---|
| KF-PDR/GNSS | 2.04 | 2.11 |
| PF-PDR/GNSS | 2.03 | 1.74 |
| KHA-PDR/GNSS | 1.39 | 1.17 |
| Mean (m) | Median (m) | |
|---|---|---|
| KF-PDR/GNSS | 3.36 | 3.02 |
| PF-PDR/GNSS | 3.17 | 2.78 |
| KHA-PF-D-PDR/GNSS | 1.51 | 1.40 |
| Mean (m) | Median (m) | |
|---|---|---|
| KF-PDR/GNSS | 4.76 | 2.90 |
| PF-PDR/GNSS | 4.73 | 3.67 |
| KHA-PDR/GNSS | 3.54 | 3.09 |
| KHA-PDR-D-/GNSS | 2.81 | 2.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, C.; Chen, Y.; Liu, Z.; Xia, Q.; Chen, C.; Hyyppa, J. A Probabilistic Method-Based Smartphone GNSS Fault Detection and Exclusion System Utilizing PDR Step Length. Remote Sens. 2023, 15, 4993. https://doi.org/10.3390/rs15204993
Jiang C, Chen Y, Liu Z, Xia Q, Chen C, Hyyppa J. A Probabilistic Method-Based Smartphone GNSS Fault Detection and Exclusion System Utilizing PDR Step Length. Remote Sensing. 2023; 15(20):4993. https://doi.org/10.3390/rs15204993
Chicago/Turabian StyleJiang, Changhui, Yuwei Chen, Zuoya Liu, Qingyuan Xia, Chen Chen, and Juha Hyyppa. 2023. "A Probabilistic Method-Based Smartphone GNSS Fault Detection and Exclusion System Utilizing PDR Step Length" Remote Sensing 15, no. 20: 4993. https://doi.org/10.3390/rs15204993
APA StyleJiang, C., Chen, Y., Liu, Z., Xia, Q., Chen, C., & Hyyppa, J. (2023). A Probabilistic Method-Based Smartphone GNSS Fault Detection and Exclusion System Utilizing PDR Step Length. Remote Sensing, 15(20), 4993. https://doi.org/10.3390/rs15204993










