Next Article in Journal
2OC: A General Automated Orientation and Orthorectification Method for Corona KH-4B Panoramic Imagery
Previous Article in Journal
Mapping Fractional Vegetation Cover Using Unoccupied Aerial Vehicle Imagery to Guide Conservation of a Rare Riparian Shrub Ecosystem in Southern California
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 15
Issue 21
10.3390/rs15215115
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Two Mw ≥ 6.5 Earthquakes in Central Pamir Constrained by Satellite SAR Observations

by
Shuai Wang
1,
Chuang Song
2 and
Zhuohui Xiao
3,*
1
School of Geomatics Science and Technology, Nanjing Tech University, Nanjing 211816, China
2
College of Geological Engineering and Geomatics, Chang’an University, Xi’an 710054, China
3
Faculty of Land and Resources Engineering, Kunming University of Science and Technology, Kunming 650031, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2023, 15(21), 5115; https://doi.org/10.3390/rs15215115
Submission received: 11 September 2023 / Revised: 23 October 2023 / Accepted: 24 October 2023 / Published: 26 October 2023
(This article belongs to the Topic Advances in Earth Observation and Geosciences)
Browse Figures
Versions Notes

Abstract

:
The Pamir, situated in central Asia, is a result of the ongoing northward advance of the Indian continent, leading to compression of the Asian landmass. While geodetic and seismic data typically indicate that the most significant deformation in Pamir is along its northern boundary, an Mw 7.2 earthquake on 7 December 2015 and an Mw 6.8 earthquake on 23 February 2023 have occurred in the remote interior of Pamir. These two Mw ≥ 6.5 earthquakes, with good observations of satellite synthetic aperture radar data, provide a rare opportunity to gain insights into rupture mechanics and deformation patterns in this challenging-to-reach region. Here, we utilize spaceborne synthetic aperture radar data to determine the seismogenic faults and finite slip models for these two earthquakes. Our results reveal that the 2015 earthquake ruptured a ~88 km long, left-lateral strike-slip fault that dips to northwest. The rupture of the 2015 earthquake extended to the ground surface over a length of ~50 km with a maximum slip of ~3.5 m. In contrast, the 2023 earthquake did not rupture the ground surface, with a maximum slip of ~2.2 m estimated at a depth of ~9 km. Notably, the seismogenic fault of the 2015 earthquake does not align with the primary strand of the Sarez–Karakul fault system (SKFS), and the 2023 earthquake occurred on a previously unmapped fault. The well-determined seismogenic faults for the 2015 and 2023 earthquakes, along with the SKFS and other distributed faults in the region, suggest the existence of a wide shear zone extending from south to north within the central Pamir.

1. Introduction

The Pamir, situated immediately to the north of the western Himalayan syntaxis, is one of the most prominent regions undergoing lithospheric deformation worldwide. Both Pamir and Tibet share a common terrane structure and evolutionary history, having formed as a result of the India–Asia collision over the past ~55 Ma [1,2,3,4,5]. Although Pamir and Tibet exhibit a similar average crustal thickness of ~70 km [6], the Pamir is believed to have experienced significantly greater shortening, because a similar amount of total convergence has been accommodated over a much smaller distance in Pamir during the Cenozoic convergence of the Indian and Asian plates [7]. The shortening level in Pamir is two to three times higher than that observed in Tibet [7], which has led to lateral extrusion and deep subduction of the lithosphere [8].
As the Pamir Plateau moved northward, it overrode the previously existing connection between the Tajik basin and the Tarim basin. Presently, the last remnant of this diminishing segment of crust is represented by the Alai Valley, which is wedged between the north Pamir and the south Tien Shan (Figure 1). Currently, the main Pamir thrust (MPT) absorbs the majority of the convergence between the Pamir and the Tien Shan mountain range. Global Navigation Satellite System (GNSS) measurements estimate this convergence at ~13–15 mm/yr [9,10,11,12], accounting for more than one-third of the total convergence observed between the Indian and Asian tectonic plates. Consequently, the MPT ranks among the regions with the highest strain rates within the Pamir.
In addition to the substantial north–south shortening, GNSS measurements also reveal a dextral slip of ~5 mm/yr along the eastward-trending MPT [9]. The substantial deformation occurring along the MPT makes the region highly susceptible to large earthquakes. Since 1976, four Mw ≥ 6.0 earthquakes with epicenter depths shallower than 40 km have been documented along the MPT (Figure 1).
In the interior of the Pamir, thrusting activities have ceased, and the present-day crustal motion primarily consists of substantial northward motion and east–west extension [10,15]. Previous studies showed that the east–west extension is driven by the westward gravitational collapse of the thickened Pamir crust into the Tajik basin [16,17,18]. Strike-slip active faults are widely developed in western Pamir and are believed to accommodate the shear stress between the northward moving Pamir and the Tajik basin [17]. Within the Pamir, however, the only prominent strike-slip fault system with clear morphological expression and seismic activities is the transtensional sinistral Sarez–Karakul fault system (SKFS) [17,19,20]. The SKFS effectively separates the mostly undeformed eastern Pamir from the seismically active western Pamir, and it facilitates sinistral shear and roughly east–west extension between these two regions [17]. To the north, the SKFS extends beyond the Lake Karakul and connects to the MPT; to the south, it spans across the Lake Sarez and probably links up with active sinistral faults trending approximately north–northeast in the south Pamir (Figure 1).
In addition to the predominant crustal shortening and extensive shallow large earthquakes, another noteworthy characteristic of the Pamir is the vigorous occurrence of intermediate-depth earthquakes. These intermediate-depth earthquakes are typically enveloped by the subcrustal low velocity zone at depths ranging from 70 to 180 km [8,21,22]. Subcrustal low velocity zones housing intermediate-depth earthquakes are commonly found in many oceanic subduction zones, such as Alaska and Cascadia [23]. However, in the Pamir, the subducting oceanic crust is believed to vanish at these depths due to ongoing subduction and potential detachment since the India–Asia collision [21,22]. Therefore, previous studies proposed that the low velocity material in the Pamir may originate from continents [21,22]. Combining tomographic data and modeling results, Sippl et al. [21] suggested that a substantial amount of crustal material is being drawn beneath the Pamir by the cold mantle lithosphere, reaching depths of at least 80-100 km. They also showed that, beyond this depth, only the lower crust and mantle lithosphere continue their subduction. The occurrence of these intermediate-depth earthquakes is proposed to be related to metamorphic reactions [8,21]. It is interesting to observe how such a deep-seated process affects the short-term shallow crustal deformation seen in crustal earthquakes and geodetic surface strain, as well as the long-term tectonics reflected in Cenozoic geological structures.
On 7 December 2015, at 7:50:05 (UTC time), an Mw 7.2 earthquake, with a focal depth of ~12 km, jolted the central Pamir at 72.780°E, 38.211°E. Remarkably, this earthquake marked the most significant seismic recorded by instruments in the region in nearly a century. On 23 February 2023, another earthquake of Mw 6.8 struck the central Pamir, with the epicenter located in the southeast of the 2015 earthquake. Historically, on 18 February 1911, an earthquake of Mw ~7.3 occurred in the same region as the 2015 event [24,25]. The close proximity, along with the similarities in terms of mechanism and magnitude of these two earthquakes [25], raises the question of whether the 2015 event ruptured the same fault responsible for the 1911 earthquake. At present, the 1911 Mw 7.3, the 2015 Mw 7.2, and the 2023 Mw 6.8 earthquakes are the only three Mw ≥ 6.0 events that have been recorded in the central Pamir region.
The central Pamir experiences a significant deficiency in crustal deformation monitoring due to its challenging natural environment and remote location. Fortunately, the spaceborne synthetic aperture radar has high-quality observations for both the 2015 Mw 7.2 and the 2023 Mw 6.8 earthquakes, presenting a valuable opportunity to gain insights into the tectonism of this remote area. We note that some published studies have utilized geodetic data from spaceborne satellites to map the coseismic deformation and to invert for the seismogenic fault and distributed slip model of the 2015 Mw 7.2 event. However, these studies yielded considerably different results. For instance, Elliott et al. [26] estimated a maximum slip of up to ~5 m, which contrasts with the ~3 m observed by Metzger et al. [27] and the ~3.5 m observed by Sangha et al. [28]. Jin et al. [29] estimated the maximum slip at ~4 m. Another notable difference among various models of the 2015 Mw 7.2 earthquake lies in the location of the peak slip. Regarding the 2023 Mw 6.8 event, only one study [30] reported the fault slip mechanism using synthetic aperture radar data. In this study, we revisit these two earthquakes from the following aspects: (1) we employ a more precise procedure to process interferometric synthetic aperture radar (InSAR) data; (2) we refine the downsampling procedure to effectively minimize the effects of far-field noisy data on geodetic inversion; (3) we systematically evaluate each potential fault scenario presented by the focal slip mechanism solutions to identify the most suitable fault model; (4) we discuss the potential seismic risk along the SKFS zone; (5) we explore the relationship between crustal tectonic activities and deep subduction processes occurring within the Pamir.

2. Coseismic Surface Deformation

In contrast to the northern Pamir, where earthquakes are frequent, conducting field observations in the central Pamir is exceptionally challenging due to its remote and rugged terrain. Consequently, there are fewer than five GNSS stations within a 100 km radius of the two earthquake epicenters. Furthermore, most of these sites are campaign stations, and the infrequent observations do not allow for effective monitoring of the coseismic deformation caused by the 2015 and 2023 earthquakes. The Sentinel-1 synthetic aperture radar (SAR) satellites offer a unique advantage by revisiting the study area every 12 or 24 days, helping to mitigate the issues related to temporal coherence, particularly in areas prone to snow and ice cover, as is the case in the Pamir. Accordingly, we collect Sentinel-1 SAR images from three tracks to assess the kinematic responses of the Earth’s surface to these two earthquakes, which consist of one ascending track (100) and two descending tracks (5 and 107) as detailed in Table 1.

2.1. Data Processing

We apply the conventional two-pass differential interferometry technique to process the collected images [31]. Each pair of single-look complex (SLC) images acquired before and after the earthquake, from the same track, are processed into an interferogram using the Gamma software (v 2019) [32]. The topographic effects are removed by using the precise orbit data provided by the European Space Agency and the 30 m resolution Shuttle Radar Topography Mission digital elevation model. The number of multi-looks in the range and azimuth directions is specified to 10:2. To reduce phase noise and prevent signal distortion simultaneously, we filter the interferograms using an adaptive filtering method [33] with a relatively small pixel window of 32 × 32. Subsequently, we use the minimum cost network method [34] to unwrap the interferograms and then geocode them into the WGS-84 coordinate system. In contrast to previous studies of these two earthquakes, our study meticulously addresses potential atmospheric phase delays in the interferograms. Initially, we use the Generic Atmospheric Correction Online Service for InSAR (GACOS) to correct the tropospheric phases [35,36]. Following this, by masking out the coseismic deformation, we employ an empirical phase-elevation linear model [37] and a quadratic polynomial function to estimate the residual stratified atmospheric delays and long-wavelength artifacts that may result from potential orbital artifacts and residual tropospheric delays, respectively. To ensure high-quality coseismic deformation measurements, we mask pixels with a coherence below 0.5. We utilize SAR acquisitions captured immediately before and after the onset of each earthquake to create the coseismic interferograms for both earthquakes. Nevertheless, in the case of the 2023 earthquake, we find noticeable artifacts that could be related to phase unwrapping errors in the interferogram created from acquisitions between 15 February 2023 and 27 February 2023, along the ascending track 100. As a result, we choose to use the measurements from another interferogram spanning from 3 February 2023 to 11 March 2023 to represent the observed coseismic deformation in this track.
Considering the possibility of surface rupture of the 2015 Mw 7.2 earthquake as reported by previous studies [26,27,28,29], InSAR observations could experience issues with near-field decorrelation. Consequently, we employ SAR pixel offset tracking to capture the coseismic surface displacements in the near-field using data from descending track 5 and ascending track 100, based on pixel-by-pixel cross-correlation of SAR intensity [38,39]. In line with our previous study [40], here, we calculate only the range offset displacements, considering the theoretical accuracy of Sentinel-1 azimuth offsets (~0.70 m) is lower than that of the range offset (~0.23 m). We specify the square search window at 300 × 60 pixels during the calculations. Additionally, we set the window size for calculating the cross-correlation function between pixels, along with the acceptance threshold of cross-correlation coherence, at 32 × 32 pixels and 0.1, respectively. To reduce noise in the estimated offsets, we apply a median filter with a window size of 32 × 32 pixels. We also calculate the range offsets resulting from the 2023 Mw 6.8 earthquake following the same procedure described above, but no apparent deformation is observed.

2.2. Coseismic Surface Observations

As illustrated in Figure 2, the 2015 Mw 7.2 earthquake resulted in a relatively intricate pattern of coseismic surface deformation along the mapped fault trace. The maximum coseismic range offset and InSAR displacement are ~1.0 m and ~0.6 m, respectively, in the line-of-sight (LOS) direction. The coseismic InSAR and range offset observations, obtained from ascending and descending tracks, exhibit distinct fringe patterns on either side of the fault trace; the western side of the fault displays movement toward the satellite from the ascending orbit and away from the satellite from the descending orbit. This suggests that the earthquake is predominantly characterized by left-lateral strike-slip motion. Notably, the range offset maps clearly reveal discontinuities in ground displacements (Figure 2(a1,b1)), suggesting that slip during the earthquake had reached the Earth’s surface. Additionally, a more significant deformation extent is observed on the western side of the fault trace compared to the eastern side (Figure 2), suggesting the potential northwestward dip of the seismogenic fault associated with the 2015 earthquake.
Regarding the 2023 Mw 6.8 earthquake, the coseismic deformation acquired from the descending track illustrates a distinctive four-lobed deformation pattern (Figure 3), indicating that this earthquake is characterized by strike-slip motion on close to vertical fault. Notably, there are no apparent displacement discontinuities in the coseismic deformation maps, implying that the earthquake did not rupture the surface and can be categorized as a blind-source event. The maximum coseismic displacement observed for the 2023 earthquake is ~0.15 m (Figure 3).

3. Inversion Methods and Results

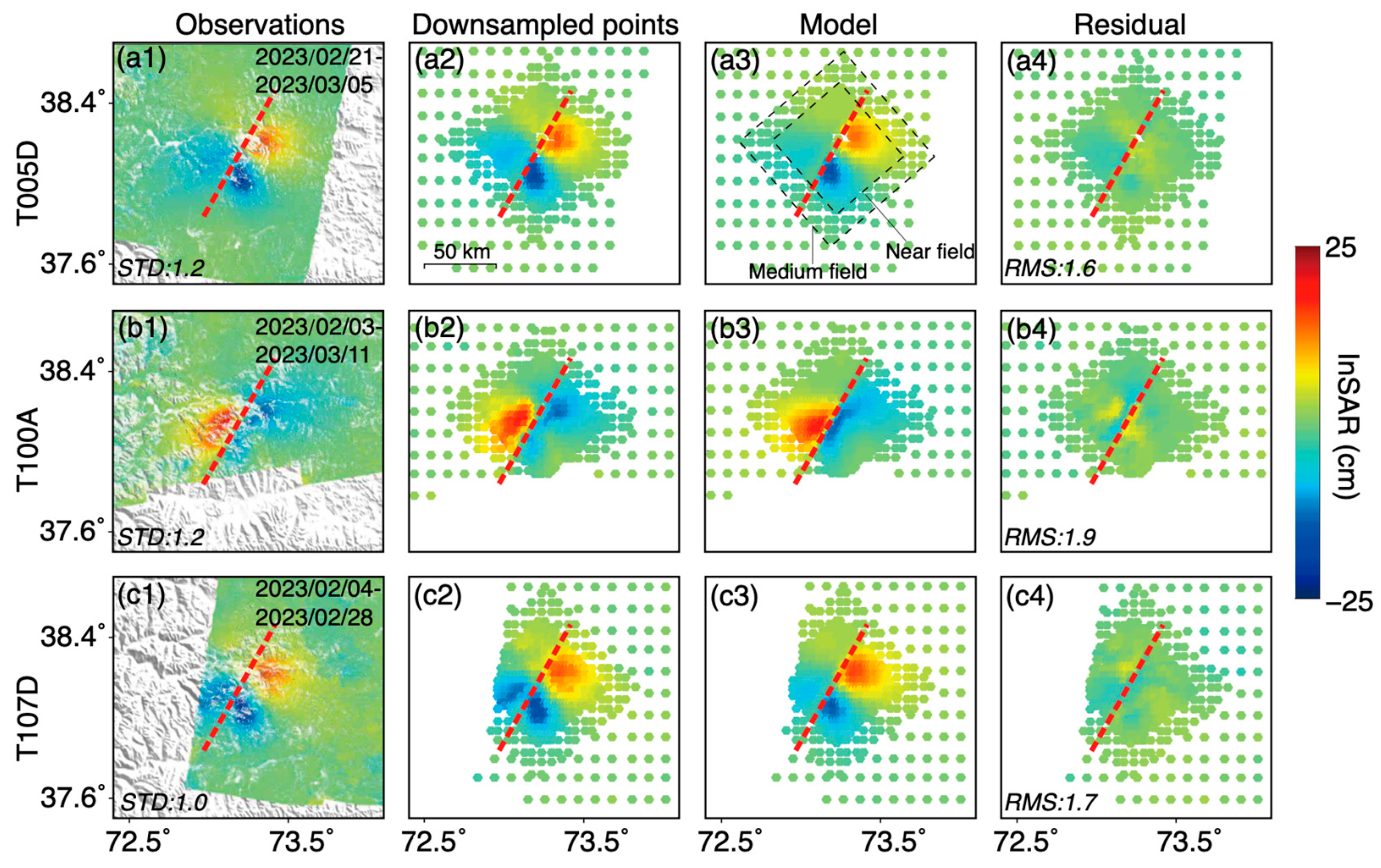
3.1. Coseismic Deformation Downsampling

Each selected interferogram provides an extensive dataset of over 105 observations that exhibit a high degree of spatial correlation. Including all of these observations in the modeling process can be somewhat impractical. To reduce redundancy and facilitate the modeling, we need to downsample the original high-resolution coseismic ground deformation without degrading the contained information. To achieve this, similar to our previous study [40], we employ a uniform downsampling method for the near-, medium-, and far-field observations, respectively. Different from the quadtree [41,42] and model resolution-based downsampling schemes [43,44], our method here not only effectively addresses the issue of oversampling data in regions with significant phase noise but also performs without requiring an initial slip model. Figure 2 and Figure 3 illustrate our downsampled observations for the two earthquakes, demonstrating that we have preserved detailed surface rupture information in the near-field regions.

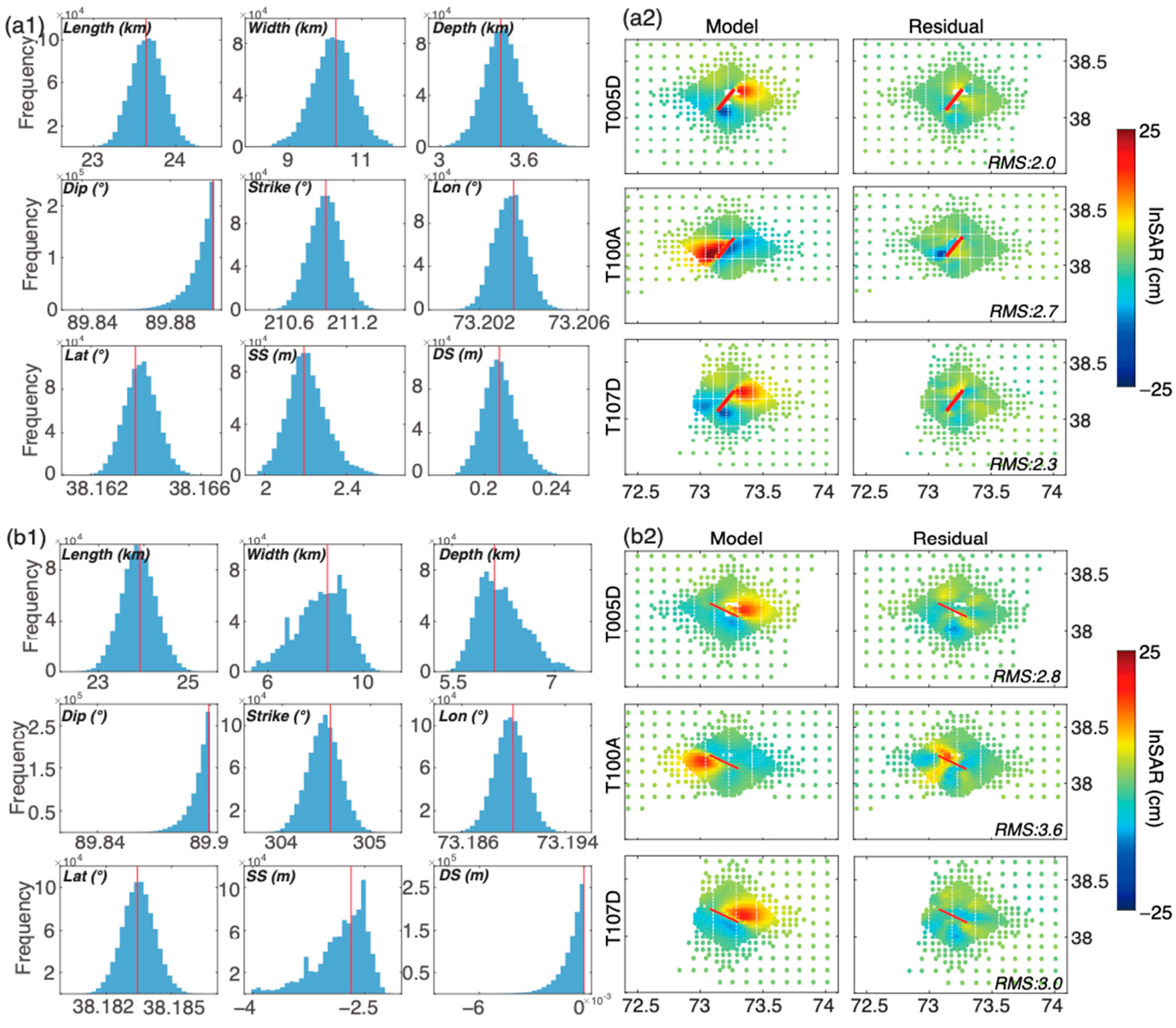
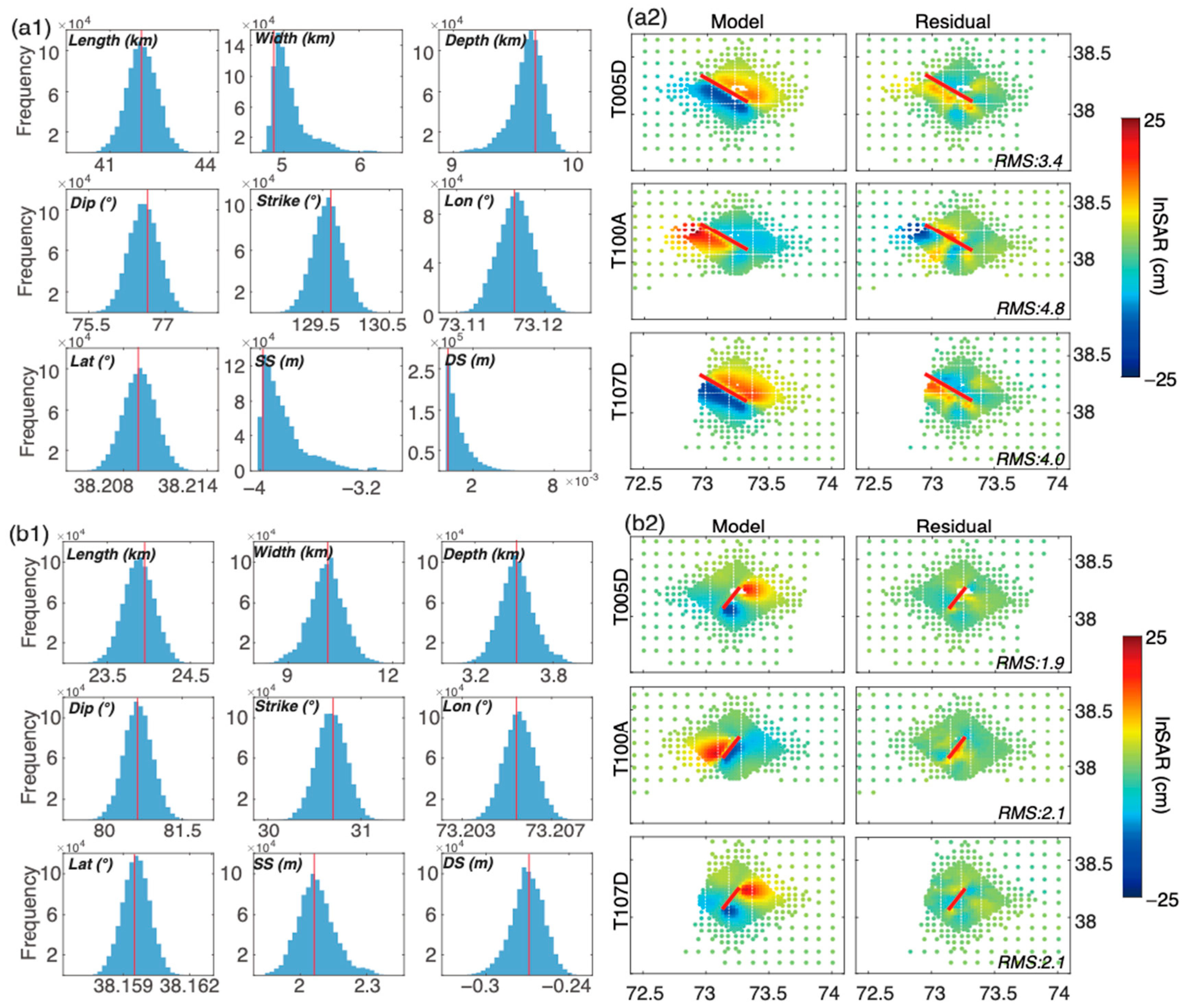
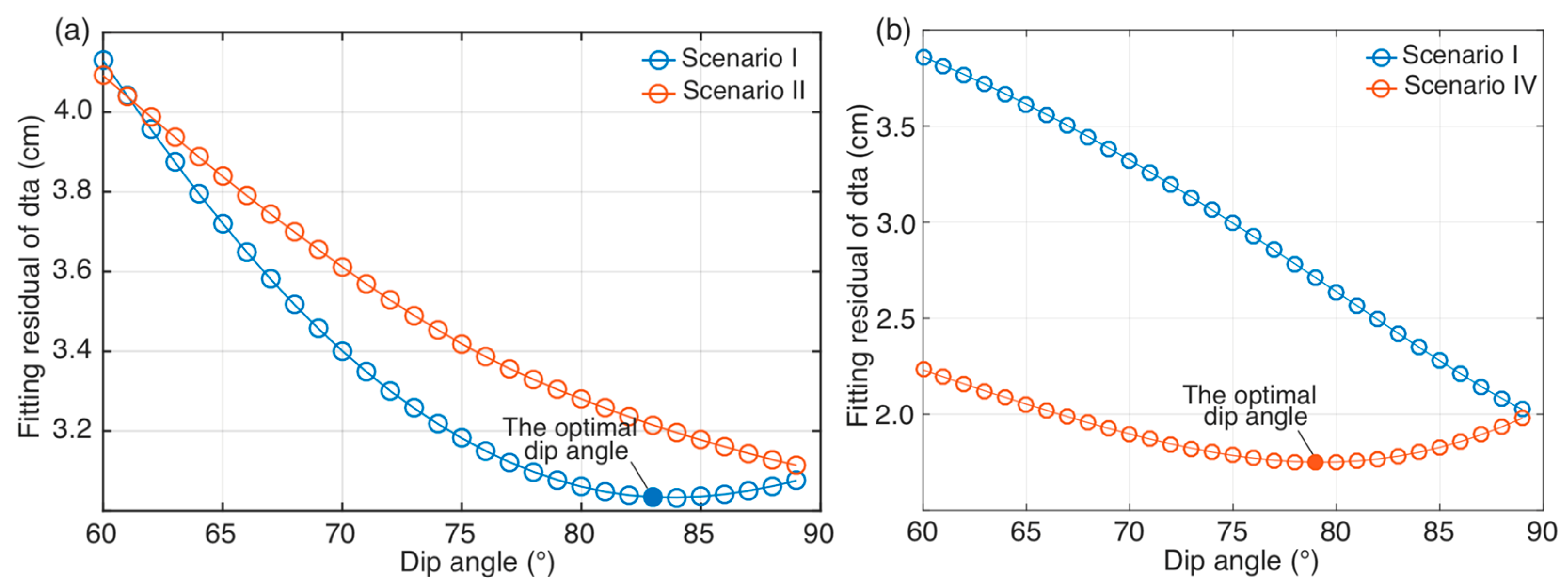
3.2. Location and Geometry of Seismogenic Faults

Regarding the 2015 event, high-resolution range offset displacement maps are particularly valuable for constraining its rupture details, particularly in near-field areas where InSAR observations experience decorrelation due to potential surface ruptures of the earthquake and potential snow coverage. Figure 2(a1,b1) illustrates that the 2015 Mw 7.2 earthquake indeed caused significant range offset displacements, indicating a surface rupture of the earthquake. The magnitude of displacement on either side of the fault can reach around 1 m. In this study, we use range offset maps to locate the surface trace of the seismogenic fault responsible for the 2015 earthquake. Once the fault location is determined, we have two possible scenarios for the seismogenic fault that ruptured in the 2015 earthquake: one dipping to the northwest and the other to the southeast, as suggested by focal mechanisms from GCMT, USGS, and GFZ (Table 2). We will determine the optimal fault dip direction and dip angle in the distributed slip modeling process.
Regarding the 2023 Mw 6.8 event, as previously mentioned, no surface rupture was observed for this earthquake, indicating that the fault responsible for this seismic event is buried at depth. To determine both the location and geometry of the seismogenic faults associated with the 2023 earthquake, we conduct non-linear geodetic inversions assuming uniform slip on the fault plane. To accomplish this, we employ the geodetic Bayesian inversion method developed by [45], which enables us to estimate the parameters of the source model by analyzing the posterior probability density. The Green’s function, relating uniform slip on test faults to InSAR downsampled observations, is calculated with an elastic half-space dislocation model [46]. During the inversion process, we determine weight ratios based on the estimated standard deviations. The previously reported focal mechanism solutions constrained by global seismic waveforms provide four candidate faults associated with the 2023 earthquake, characterized by strike angles of ~200°, ~300°, ~120°, and ~25°, respectively (Table 2). Consequently, we conduct four distinct scenarios of inversions with ranges for fault parameters including location, strike, dip, fault length, and fault width.
The non-linear inversion results show that the seismogenic faults deduced from scenarios II (~300°) and III (~120°) cannot adequately account for the observed four-quadrant deformation pattern in the descending track (Figure 4(b1,b2) and Figure 5(a1,a2)). Under scenario I, corresponding to the ~200° case (Figure 4(a1,a2)), the optimal seismogenic fault inferred from the inversion dips to the northwest with a strike angle of 210°. However, it is noteworthy that the dip angle tends to converge near the upper boundary of 90°. Under scenario IV (Figure 5(b1,b2)), associated with the ~25° case, the inversions exhibit strong convergence, and the inferred fault plane aligns well with the respective nodal plane of the focal mechanism and can effectively explain the observations. It is important to note that previous studies have indicated that the optimal fault dip angle derived from uniform slip modeling may not be suitable for a distributed slip model [47]. Consequently, it may not be possible to confidently identify the seismogenic fault based on scenarios I and IV. Therefore, we will include these two scenarios in subsequent linear inversions for further validation and verification.

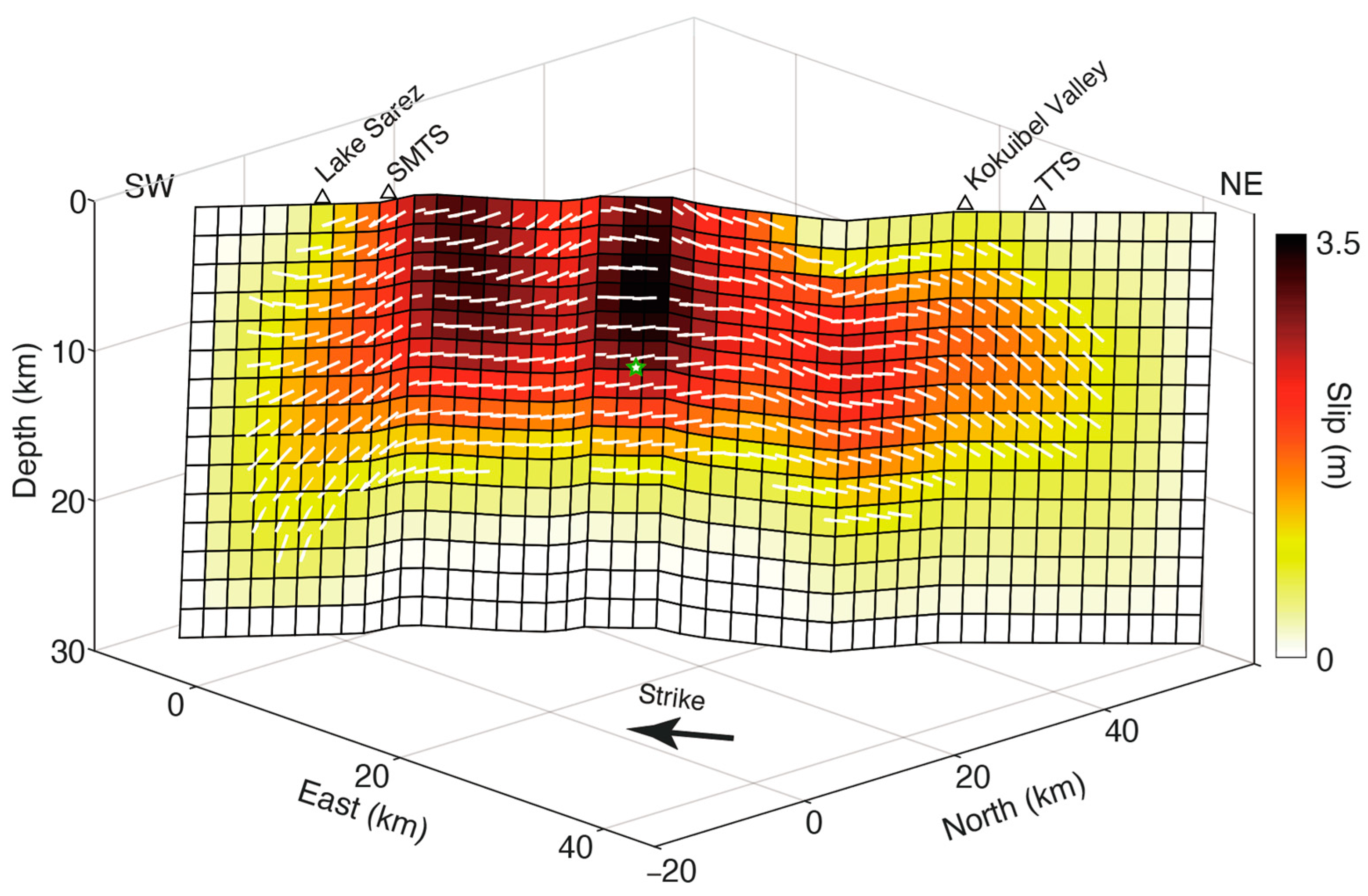
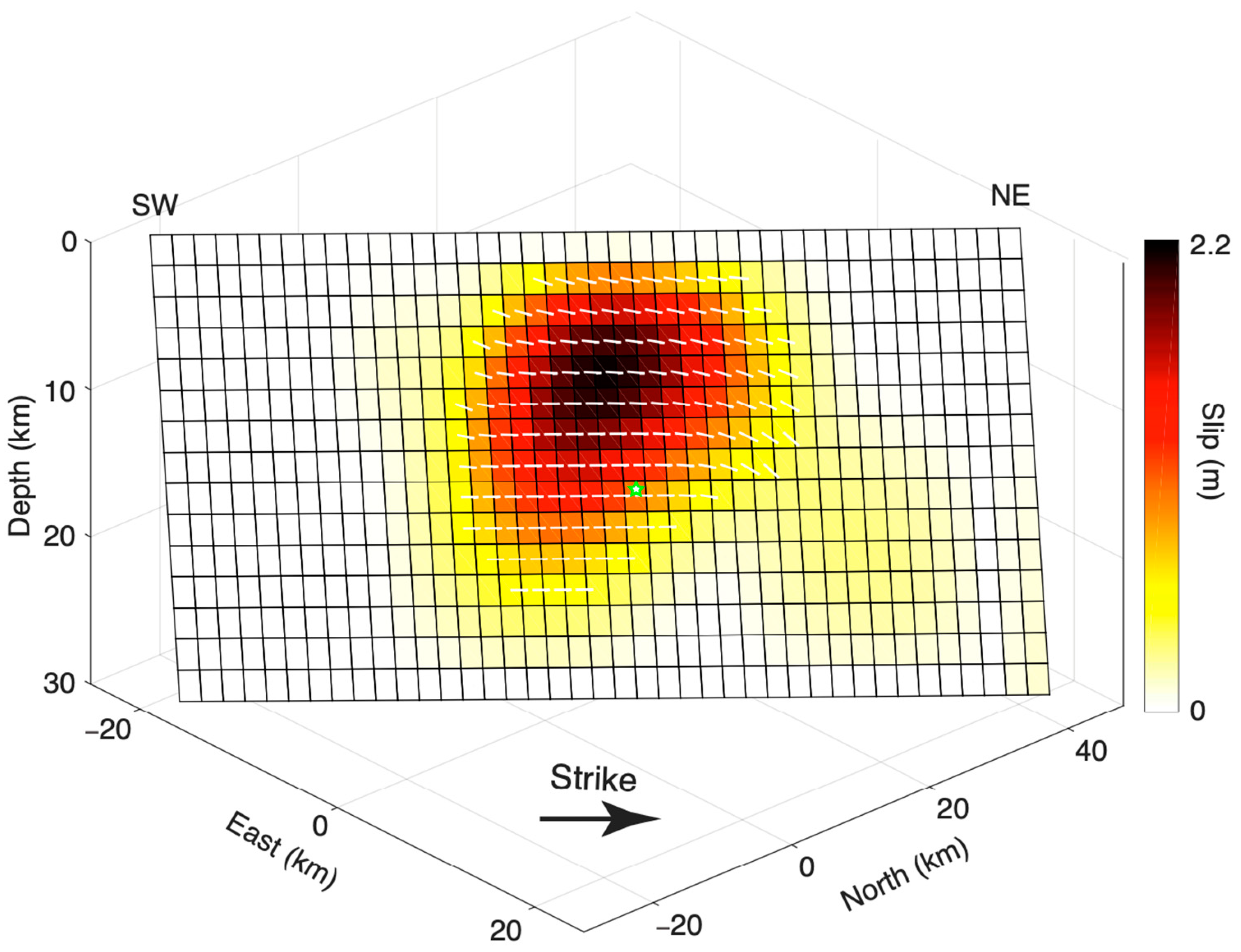
3.3. Distributed Slip Models

To obtain finite fault slip models for these two earthquakes, we further conduct linear inversions using the CosInv software (v1.1) with the bounded variable least squares algorithm [48,49,50,51]. Considering the spatial extent of coseismic deformation, the candidate seismogenic faults identified for the 2015 earthquake based on the range offset maps are extended to ~88 km in length and ~30 km in width. Similarly, for the 2023 earthquake, the candidate seismogenic faults determined from the non-linear inversions are extended to ~80 km in length and ~30 km in width. We discretize the surface plane of each candidate fault model into 2 × 2 km rectangular dislocation patches to capture the rupture details. When assessing the sensitivity of dip directions for the 2015 earthquake, we exclude the incorporation of range offset data maps due to their relatively large uncertainties, particularly in remote areas; this strategy closely mirrors the methodology employed by [26]. We weigh the influence of InSAR data on inversions based on the variance of each dataset, estimated from the non-deforming area (Table 1). We calculate the Green’s functions between the slip on each sub-fault patch and the downsampled points using the elastic half-space dislocation model [46]. To avoid non-physical oscillation in the slip distribution, we adopt a modified Laplacian smoothing operator [49] to constrain the fault motion, which is particularly suitable for earthquakes with potential surface ruptures. The optimal smoothing factor is determined by examining the trade-off curve, which defines the balance between data misfit and slip roughness. Once we determine the optimal dip angle for the 2015 earthquake, we incorporate both the InSAR and range offset deformation maps to estimate a detailed slip distribution for the earthquake.
Unlike earlier studies [26,27,28,29] that developed fault models with varying dip angles for the 2015 earthquake, in this study, we simply assume that sub-fault patches in each candidate fault model share the same dip angle, but the strike angle of the fault model is varied where the fault trace aligns with the surface ruptures, identified from the range offset maps (Figure 2(a1,b1)). For each scenario of the fault model of the 2015 earthquake, we vary the dip angle from 60° to 90°. The optimal dip angle is determined based on when the root-mean-square (RMS) of fitting residuals between the data and model prediction reaches the minimum. Our analysis of the optimal dip orientation for the seismogenic fault reveals that the fitting residual of the data reaches its minimum value, ~3.0 cm, when the dip angle is 83°, for the candidate fault model dipping to northwest (scenario I; Figure 6a). However, for scenario II, where the fault dips to the southeast direction, we are unable to estimate an optimal dip angle as the RMS monotonically decreases with an increasing dip angle and the value is still higher than in scenario I (Figure 6a). Thus, we conclude that the seismogenic fault responsible for the 2015 earthquake is dipping to northwest, with a dip angle of 83°. The result is consistent with the observations of extensive deformation occurring to west of the fault.
The inverted coseismic slip model (Figure 7) shows three primary characteristics: (1) The earthquake ruptured the Earth’s surface. (2) The predominant fault slip is concentrated at depths shallower than 20 km, and a maximum slip of ~3.5 m is observed at depths ranging from the surface to ~10 km. (3) Along-strike variations are evident in the fault rupture. Our optimal coseismic slip model effectively explains the prominent ground motions observed from the SAR data (Figure 2), with the RMS fitting residuals closely matching the standard deviations of the observations. While the fitting residuals of the range offset measurements are smaller than the standard deviations of the data, the simulation results have not exhibited apparent overfitting and the standard deviations of the data are significantly influenced by far-field noisy pixels. The optimal coseismic slip model results in a geodetic seismic moment of 8.68 × 1019 N·m, corresponding to an Mw 7.23 event, assuming a shear modulus of 30 GPa.
Regarding the 2023 earthquake, we conduct slip distribution inversions for two potential candidate seismogenic faults, as we distinguish from the non-linear inversions, with strikes of ~200° (scenario I) and ~25° (scenario IV). Under scenario I, with a strike of ~200°, the RMS fitting residuals decreases as the dip angle increases, but we cannot obtain the optimal dip angle, even under extreme conditions with a dip angle of ~90° (Figure 6b). In contrast, under scenario IV, with a strike of ~25°, the re-estimated optimal dip angle for the distributed slip model is ~79° (Figure 6b), which closely aligns with the corresponding values from reported focal mechanisms (Table 2). Considering that scenario IV exhibits a good fit to the InSAR observations, it is more convincing to conclude that the seismogenic fault for the 2023 event is dipping to the northeast. Figure 8 illustrates the optimal distributed slip model obtained for scenario IV. The 2023 earthquake is characterized by left-lateral strike-slip faulting, with a maximum slip of 2.2 m observed at a depth of ~9 km. The optimal slip distribution produces a geodetic seismic moment of 2.41 × 1019 N·m, corresponding to an Mw 6.89 event, assuming a shear modulus of 30 GPa.

4. Discussion

4.1. Comparison to Different Slip Models

In order to describe the potential geometric variations of the 2015 Mw 7.2 earthquake, both [27,28] have built a three-segment fault model to study the distributed slip model of the earthquake. In the fault model proposed by [27], the three segments, from southwest to northeast, have dips of 87.7° to the northwest, 81.8° to the northwest, and 89.3° to the southeast, respectively. Conversely, the dips for the relevant segments are 89.0° to the southeast, 80° to the northwest, and 83° to the northwest for the model of [28]. Elliott et al. [26] employed a nine-segment fault model to define the seismogenic fault associated with the 2015 earthquake. All of the fault segments in their model are dipping to the northwest, with the dip angles spanning from 67.7° to 87.8°. Compared to the two three-segment fault models above, the nine-segment fault model can be better in illustrating the curved surface traces, i.e., fault bends, of the 2015 earthquake. Contrastingly, the location of our fault model is defined directly from the displacement discontinuities in the range offset maps, making it the most accurate representation of actual surface traces with curved features resulting from the earthquake. Concerning the 2015 earthquake, prior studies have revealed that geodetic data cannot effectively differentiate between a northwest-dipping fault model and a southeast-dipping fault model [26,27,28,29]. Furthermore, the 2015 earthquake is characterized by strike-slip faulting and a relatively steep dip angle, indicating that the difference between the northwest-dipping and the southeast-dipping fault models is relatively small, as indicated by studies of other strike-slip earthquakes [47]. Consequently, similar to [26], we make a simple assumption that the fault model of the 2015 earthquake maintains a consistent dip orientation.
Another notable difference among various models of the 2015 Mw 7.2 earthquake lies in the peak slip and its location. In our study, we estimate a peak slip of ~3.5 m, which closely matches the estimate of ~3.5 m in [28] and is similar to the estimate of ~3.1 m reported by [27]. However, our estimation is notably lower than the maximum slip values estimated by [26,29], which range from 4 to 5 m. It is worth noting that, except for [26], all slip models, including ours, identify the maximum slip amplitude at the Earth’s surface, in line with the potential occurrence of supershear rupture of the earthquake, as indicated by the time progression of high-frequency radiation at speeds of ~4.3-5 km/s [28]. Elliott et al. [26] observed a minor deep-seated slip to the south of Lake Sarez, which is spatially isolated from the primary slip and not evident in the other four models, including ours (Figure 7). We think that such deep slip patches may not be reliable and could arise from potential residual tropospheric phase effects in the far-field displacements within the interferograms. Elliott et al. [26] noted another deep region of relatively high slip, ranging from 2–3 m at depths greater than 15 km beneath Kokuibel Valley. However, they acknowledged that this deep slip might not be resolved accurately by geodetic data and could result from over-smoothing of the slip on the fault plane. The geodetic seismic moment derived in our study is 8.68 × 1019 N·m, which is most consistent with the GCMT solution, with a value of 7.8 × 1019 N·m; however, it is greater than the result of 6.2 × 1019 N·m reported by [27] and smaller than the results of 13.7 × 1019 N·m in [28] and 9.098 × 1019 N·m in [29]. Nevertheless, we should acknowledge that the calculated geodetic seismic moment might be slightly overestimated due to the potential inclusion of post-seismic deformation in our coseismic deformation data.
Regarding the 2015 Mw 7.2 event, while various aspects of a slip model can be influenced by different types of data and the specific details of the chosen inversion method, there are certain characteristics that are consistent among the existing models, including ours. These common features include (Figure 7): (1) The primary motion of the 2015 earthquake is dominated by left-lateral strike-slip faulting, with the most significant slip concentrated in the region between TTS and SMTS. (2) The sections exhibiting the highest slip amplitudes are situated between Lake Sarez and the epicenter determined by GCMT. (3) The majority of the slip is concentrated at depths shallower than 20 km. (4) There is a gradual decrease in the slip towards the northern section of the fault, following the curved configuration of the fault.
For the 2023 Mw 6.8 event, we have determined the strike and dip angels to be 30.7° and 79°, respectively (Figure 5(b1,b2), Figure 6b and Figure 8), which align with the corresponding findings of [30], who reported values of ~28° and ~73°, respectively. Both our slip distribution model and that of [30] exhibit a circular spatial pattern and reflect a left-lateral strike-slip faulting mechanism, with most of the slip occurring at a depth shallower than 20 km. However, we note that the maximum slip of 2.2 m which we estimated in this study is slightly larger than the value of ~1.53 m reported by [30]. This difference may be attributed to the fact that the slip model in [30] appears to be somewhat over-smoothed. In contrast to [30], our study includes an additional descending interferogram in the inversion, as well as optimally selected acquisition dates and corrections for atmospheric phase effects. Furthermore, we implement a coherence threshold, masking out pixels with values below 0.5. In theory, these steps have contributed to enhancing the accuracy of our results.

4.2. Implications for Seismic Hazards along the SKFS Zone

The SKFS, with a north–northeast orientation, acts as a distinct boundary separating the relatively undeformed eastern Pamir from the seismically active western Pamir. The overall SKFS consists of multiple parallel fault segments and is intersected by several perpendicular faults at various locations across the central and northern Pamir (Figure 9). This fault system, being one of the most active structures in the central Pamir, facilitates left-lateral shear and approximately east–west extension between these two regions.
Our observations suggest a spatial correlation between the coseismic slip of the 2015 Mw 7.2 earthquake and geometric variations along the fault, such as fault bends (Figure 7 and Figure 9). Specifically, the coseismic slip of the 2015 event is constrained by two major structures: the SMTS in the south and the TTS in the north. Previous studies have suggested that structural complexities within fault networks, including gaps, bends, stepovers, and fault intersections, can play a dual role in influencing the mode and timing of multi-segment failure. These complexities can act as rupture barriers, determining whether multiple segments rupture together as a single large earthquake or separately as multiple events. They can also control the timing and sequence of subsequent earthquakes in a prolonged seismic sequence [52]. Moreover, the bends and intersections within fault systems can impact the spatial distribution of seismic coupling, the location of high-frequency radiation, and the variety of slip behavior [53]. Fault segments characterized by structural complexities may exhibit high initial stress, potentially leading to the generation of supershear rupture during earthquakes. For instance, in the recent 2023 Mw 7.8 Kahramanmaras earthquake in southeast Turkey, Wang et al. [54] proposed that the high initial stress at fault intersections could result in supershear rupture and backward propagation of rupture [55]. Figure 7 and Figure 9 clearly reflect that the seismogenic fault of the 2015 Mw 7.2 earthquake features multiple fault bends, and its primary slip is confined between the TTS and SMTS. These observations suggest that the fault rupture of the earthquake is influenced by fault geometry. If sufficient stress accumulates here, these geometric barriers could potentially rupture, leading to significant earthquakes with ruptures extending to the north of TTS and to the south of SMTS.
Across the globe, there are numerous instances of strike-slip earthquakes that involve the activation of two or even multiple faults simultaneously. This phenomenon has been observed in both historical seismic events, such as the 1992 Mw 7.3 Landers earthquake [56] and the 1999 Mw 7.1 Hector Mine earthquake [57], as well as more recent earthquakes, like the 2016 Mw 7.8 Kaikoura earthquake [58], the 2019 Ridgecrest earthquake sequence [59,60], the 2021 Mw 7.4 Madoi earthquake [40], and the 2023 Kahramanmaras Turkey earthquake doublet [54,55]. These events have highlighted the possibility of simultaneous fault ruptures. Taufiq et al. [61] has provided insights into how a combination of regional tectonics and stress changes induced by historical earthquakes can influence the occurrence of earthquake sequence over both space and time. As Figure 9 illustrates, active faults are distributed widely along the SKFS; when multiple faults rupture concurrently, there is the potential for these events to cascade into highly destructive, large earthquakes.
The SKFS can be traced across a network of distributed and fragmented faults, stretching from Lake Karakul in the north to Lake Sarez in the south, and extending further into southern regions [17]. However, it is notable that the seismogenic fault we have identified for the 2015 Mw 7.2 earthquake does not align with the geologically mapped strand of the SKFS. This suggests that the main strand of the SKFS still presents a significant seismic risk if it has accumulated enough elastic energy over time. There is no recorded Mw 6.0 ≥ earthquake to the north of the TTS (Figure 1); however, the 2015 earthquake had generated a positive stress of ~1 bar in the region, suggesting a high seismic risk in the future [62,63] (Figure 10). Additionally, the 2015 and 2023 earthquakes have induced a positive stress change in the southern end regions of the seismogenic fault of the 2015 earthquake, where numerous north–northeast-trending faults with lengths of ~20 km or more are prevalent. This, combined with their potential for left-lateral strike-slip faulting under the current tectonic stress field, suggests that the region may also feature a high seismic risk in the future.
The 2023 Mw 6.8 earthquake occurred on a previously unidentified fault. However, Figure 10d shows that the 2015 Mw 7.2 earthquake imposed a positive coulomb stress of ~0.07 bar on the seismogenic fault related to the 2023 earthquake (Figure 10). This suggests that the 2015 event may have played a role in triggering the 2023 earthquake. The seismogenic faults associated with the 2015 and the 2023 earthquakes, along with the faults within the SKFS, collectively highlight a wide zone of left-lateral shear deformation in the central Pamir. Thus, the seismic risk in this area is a matter of concern, necessitating an accurate assessment of the magnitude, spatial distribution, and allocation of shear strain.

4.3. Potential Role of SKFS in Regional Tectonics

The Pamir region is well known for its continental deep subduction, a phenomenon that has been extensively studied to comprehend the underlying processes. At depths beneath the crust, the indentation of India has given rise to a zone of intermediate-depth seismicity [13,64,65] (Figure 1). This seismicity is attributed to the ongoing process of continental subduction and delamination beneath the Hindu Kush and Pamir, which is supported by the detection of high-velocity zones in tomographic studies [1,13,22,65]. In addition to the deep subduction processes, the Pamir and its surrounding areas have also experienced significant crustal seismic activities, such as the 2016 Mw 6.5 Nura earthquake [66] and the 2016 Mw 6.6 Aketao earthquake [49], highlighting the high seismic levels within the crust. Previous studies have linked the crustal deformation pattern in Pamir to its westward gravitational collapse, as evidenced by changes in the orientation of surface velocity observed in GNSS data [9,10,15] (Figure 1). However, our understanding of the interactions between the deep subduction process and shallow crustal tectonism, as well as the role played by the SKFS in these interactions, remains limited.
Kufner et al. [67] conducted an analysis using seismic data from stations deployed in the Pamir–Hindu Kush area to determine the focal mechanisms of the regional earthquakes and to understand the interactions between the deep subduction process and shallow crustal tectonism. Their analysis revealed that the subcrustal lithospheric boundaries exert a significant influence on the crustal deformation of the Pamir, establishing a transfer conduit along the SKFS. In the southwestern Pamir, there is a belt of shallow crustal earthquakes trending northeastward, which closely aligns with an intermediate-depth seismicity zone showing a similar orientation (Figure 9). This alignment likely traces the eastern boundary of the cratonic Indian Plate at mantle depth [67]. The nodal planes and slip vectors of these shallow crustal earthquakes also conform to this northeast trend. The prevalence of strike-slip faulting suggests that crustal deformation is related to a network of interconnected faults (Figure 9).

5. Conclusions

As one of the most active tectonic units in the world, the Pamir experiences frequent significant earthquakes. However, the challenging natural conditions makes the central Pamir region difficult to access, limiting our understanding of its tectonism. The occurrences of the 2015 Mw 7.2 and 2023 Mw 6.8 earthquakes provide a unique opportunity to gain insights into the regional tectonic processes. In this study, we have utilized high-quality satellite radar observations of coseismic surface deformation to uncover subsurface fault slip variations for these two earthquakes. Our analysis reveals that the 2015 earthquake ruptured the Earth’s surface with a substantial slip of ~3.5 m. In contrast, the 2023 earthquake is a blind-source event, with a maximum slip of ~2.2 m observed at a depth of ~9 km. We find that the seismogenic fault responsible for the 2015 earthquake did not align with the main strand of the SKFS and that the 2023 earthquake occurred on a previously unmapped fault. The well-defined seismogenic faults for both earthquakes, along with the SKFS and other distributed faults, collectively suggest the presence of a broad shear zone extending from south to north in the central Pamir. If this region accumulates sufficient stress over time, it could pose an exceptionally high seismic risk.

Author Contributions

Conceptualization, S.W. and Z.X.; methodology, S.W. and C.S.; software, S.W. and C.S.; validation, S.W., C.S. and Z.X.; formal analysis, S.W., C.S. and Z.X.; investigation, S.W. and Z.X.; resources, S.W. and C.S.; data curation, S.W. and C.S.; writing—original draft preparation, S.W.; writing—review and editing, S.W., C.S. and Z.X.; visualization, S.W., C.S. and Z.X.; supervision, Z.X.; project administration, S.W.; funding acquisition, S.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China under Grant 42204001 and by the Natural Science Foundation of Jiangsu Province under Grant BK20200712.

Data Availability Statement

The Sentinel-1 data are copyright of the European Space Agency (ESA) and are freely available through the Copernicus Open Access Hub (https://scihub.copernicus.eu; accessed on 1 September 2023). The GACOS product can be freely accessed from http://www.gacos.net (accessed on 20 September 2023). The CosInv software we used to conduct the distributed slip model in this study can be freely accessed from http://doi.org/10.5281/zenodo.5098387 (accessed on 1 September 2023).

Acknowledgments

We would like to thank Rishabh Dutta and the other three anonymous reviewers for their valuable comments. Figures are prepared using Generic Mapping Tools [68].

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Burtman, V.S.; Molnar, P. Geological and geophysical evidence for deep sub-duction of continental crust beneath the Pamir. Spec. Pap. Geol. Soc. Am. 1993, 281, 1–76. [Google Scholar]
  2. Cowgill, E. Cenozoic right-slip faulting along the eastern margin of the Pamir salient, northwestern China. Geol. Soc. Am. Bull. 2010, 122, 145–161. [Google Scholar] [CrossRef]
  3. Fu, B.; Ninomiya, Y.; Guo, J. Slip partitioning in the northeast Pamir-Tian Shan convergence zone. Tectonophysics 2010, 483, 344–364. [Google Scholar] [CrossRef]
  4. Schwab, M.; Ratschbacher, L.; Siebel, W.; McWilliams, M.; Minacv, V.; Lutkov, V.; Chen, F.; Stanek, K.; Nelson, B.; Frisch, W.; et al. Assembly of the Pamirs: Age and origin of magmatic belts from the southern Tien Shan to the southern Pamirs and their relation to Tibet. Tectonics 2004, 23, TC4002. [Google Scholar] [CrossRef]
  5. Sun, J.; Xiao, W.; Windley, B.F.; Ji, W.; Fu, B.; Wang, J.; Jin, C. Provenance change of sediment input in the northeastern foreland of Pamir related to collision of the Indian Plate with the Kohistan-Ladakh arc at around 47 Ma. Tectonics 2016, 35, 315–338. [Google Scholar] [CrossRef]
  6. Mechie, J.; Yuan, X.; Schurr, B.; Schneider, F.; Sippl, C.; Ratschbacher, L.; Minaev, V.; Gadoev, M.; Oimahmadov, I.; Abdybachaev, U.; et al. Crustal and uppermost mantle velocity structure along a profile across the Pamir and southern Tien Shan as derived from project TIPAGE wide-angle seismic data. Geophys. J. Int. 2012, 188, 385–407. [Google Scholar] [CrossRef]
  7. Schmidt, J.; Hacker, B.R.; Ratschbacher, L.; Stubner, K.; Stearns, M.; Kylander-Clark, A.; Cottle, J.M.; Alexander, A.; Webb, G.; Gehrels, G.; et al. Cenozoic deep crust in the Pamir. Earth Planet. Sci. Lett. 2011, 312, 411–421. [Google Scholar] [CrossRef]
  8. Li, W.; Chen, Y.; Yuan, X.; Schurr, B.; Mechie, J.; Oimahmadov, I.; Fu, B. Continental lithospheric subduction and intermediate-depth seismicity: Constraints from S-wave velocity structures in the Pamir and Hindu Kush. Earth Planet. Sci. Lett. 2018, 482, 478–489. [Google Scholar] [CrossRef]
  9. Zubovich, A.V.; Wang, X.Q.; Scherba, Y.G.; Schelochkov, G.G.; Reilinger, R.; Reigber, C.; Mosienko, O.I.; Molnar, P.; Michajljow, W.; Makarov, V.I.; et al. GPS velocity field for the Tien Shan and surrounding regions. Tectonics 2010, 29, TC6014. [Google Scholar] [CrossRef]
  10. Ischuk, A.; Bendick, R.; Rybin, A.; Molnar, P.; Khan, F.S.; Kuzikov, S.; Zubovich, A.V. Kinematics of the Pamir and Hindu Kush regions from GPS geodesy. J. Geophys. Res. Solid Earth 2013, 118, 2408–2416. [Google Scholar] [CrossRef]
  11. Reigber, C.; Michel, G.W.; Galas, R.; Angermann, D.; Klotz, J.; Chen, J.Y.; Ishanov, M.C. New space geodetic constraints on the distribution of deformation in Central Asia. Earth Planet. Sci. Lett. 2001, 191, 157–165. [Google Scholar] [CrossRef]
  12. Mohadjer, S.; Bendick, R.; Ischuk, A.; Kuzikov, S.; Kostuk, A.; Saydullaev, U.; Lodi, S.; Kakar, D.M.; Wasy, A.; Khan, M.A.; et al. Partitioning of India-Eurasia convergence in the Pamir-Hindu Kush from GPS measurements. Geophys. Res. Lett. 2010, 37, L04305. [Google Scholar] [CrossRef]
  13. Sippl, C.; Schurr, B.; Yuan, X.; Mechie, J.; Schneider, F.M.; Gadoev, M.; Radjabov, N. Geometry of the Pamir-Hindu Kush intermediate-depth earthquake zone from local seismic data. J. Geophys. Res. Solid Earth 2013, 118, 1438–1457. [Google Scholar] [CrossRef]
  14. Mohadjer, S.; Ehlers, T.A.; Bendick, R.; Stübner, K.; Strube, T. A Quaternary fault database for central Asia. Nat. Hazard Earth Syst. 2016, 16, 529–542. [Google Scholar] [CrossRef]
  15. Zhou, Y.; He, J.; Oimahmadov, I.; Gadoev, M.; Pan, Z.; Wang, W.; Rajabov, N. Present-day crustal motion around the Pamir Plateau from GPS measurements. Gondwana Res. 2016, 35, 144–154. [Google Scholar] [CrossRef]
  16. Nikolaev, V. Afghan-Tajik depression: Architecture of sedimentary cover and evolution. Russ. J. Earth Sci. 2002, 4, 399–421. [Google Scholar] [CrossRef]
  17. Schurr, B.; Ratschbacher, L.; Sippl, C.; Gloaguen, R.; Yuan, X.; Mechie, J. Seismotectonics of the Pamir. Tectonics 2014, 33, 1501–1518. [Google Scholar] [CrossRef]
  18. Stübner, K.; Ratschbacher, L.; Rutte, D.; Stanek, K.; Minaev, V.; Wiesinger, R.; Project TIPAGE Members. The giant Shakhdara migmatitic gneiss dome, Pamir, India-Asia collision zone. 1: Geometry and kinematics. Tectonics 2013, 32, 948–979. [Google Scholar] [CrossRef]
  19. Rutte, D.; Ratschbacher, L.; Schneider, S.; Stübner, K.; Stearns, M.A.; Gulzar, M.A.; Hacker, B.R. Building the Pamir-Tibet Plateau-Crustal stacking, extensional collapse, and lateral extrusion in the Central Pamir: 1. Geometry and kinematics. Tectonics 2017, 36, 342–384. [Google Scholar] [CrossRef]
  20. Strecker, M.R.; Frisch, W.; Hamburger, M.W.; Ratschbacher, L.; Semiletkin, S.; Zamoruyev, A.; Sturchio, N. Quaternary deformation in the Eastern Pamirs, Tadzhikistan and Kyrgyzstan. Tectonics 1995, 14, 1061–1079. [Google Scholar] [CrossRef]
  21. Sippl, C.; Schurr, B.; Tympel, J.; Angiboust, S.; Mechie, J.; Yuan, X.; Schneider, F.M.; Sobolev, S.V.; Ratschbacher, L.; Haberland, C.; et al. Deep burial of Asian continental crust beneath the Pamir imaged with local earthquake tomography. Earth Planet. Sci. Lett. 2013, 384, 165–177. [Google Scholar] [CrossRef]
  22. Schneider, F.M.; Yuan, X.; Schurr, B.; Mechie, J.; Sippl, C.; Haberland, C.; Negmatullaev, S. Seismic imaging of subducting continental lower crust beneath the Pamir. Earth Planet. Sci. Lett. 2013, 375, 101–112. [Google Scholar] [CrossRef]
  23. Bostock, M.G. The Moho in subduction zones. Tectonophysics 2013, 609, 547–557. [Google Scholar] [CrossRef]
  24. Ambraseys, N.; Bilham, R. The Sarez-Pamir earthquake and landslide of 18 February 1911. Seismol. Res. Lett. 2012, 83, 294–314. [Google Scholar] [CrossRef]
  25. Kulikova, G.; Schurr, B.; Krüger, F.; Brzoska, E.; Heimann, S. Source parameters of the Sarez-Pamir earthquake of 1911 February 18. Geophys. J. Int. 2016, 205, 1086–1098. [Google Scholar] [CrossRef]
  26. Elliott, A.; Elliott, J.; Hollingsworth, J.; Kulikova, G.; Parsons, B.; Walker, R. Satellite imaging of the 2015 M7.2 earthquake in the Central Pamir, Tajikistan, elucidates a sequence of shallow strike-slip ruptures of the Sarez-Karakul fault. Geophys. J. Int. 2020, 221, 1696–1718. [Google Scholar] [CrossRef]
  27. Metzger, S.; Schurr, B.; Ratschbacher, L.; Sudhaus, H.; Kufner, S.-K.; Schöne, T.; Bendick, R. The 2015 Mw7.2 Sarez strike-slip earthquake in the Pamir interior: Response to the underthrusting of India’s western promontory. Tectonics 2017, 36, 2407–2421. [Google Scholar] [CrossRef]
  28. Sangha, S.; Peltzer, G.; Zhang, A.; Meng, L.; Liang, C.; Lundgren, P.; Fielding, E. Fault geometry of 2015, Mw7. 2 Murghab, Tajikistan earthquake controls rupture propagation: Insights from InSAR and seismological data. Earth Planet. Sci. Lett. 2017, 462, 132–141. [Google Scholar] [CrossRef]
  29. Jin, Z.; Fialko, Y.; Zubovich, A.; Schöne, T. Lithospheric deformation due to the 2015 M7. 2 Sarez (Pamir) earthquake constrained by 5 years of space geodetic observations. J. Geophys. Res. Solid Earth 2022, 127, e2021JB022461. [Google Scholar] [CrossRef]
  30. Shi, Y.; Wang, Y.; Bian, Y. Coseismic Source Model of the February 2023 Mw 6.8 Tajikistan Earthquake from Sentinel-1A InSAR Observations and Its Associated Earthquake Hazard. Remote Sens. 2023, 15, 3010. [Google Scholar] [CrossRef]
  31. Massonnet, D.; Rossi, M.; Carmona, C.; Adragna, F.; Peltzer, G.; Feigl, K.; Rabaute, T. The displacement field of the Landers earthquake mapped by radar interferometry. Nature 1993, 364, 138–142. [Google Scholar] [CrossRef]
  32. Werner, C.; Wegmuller, U.; Strozzi, T.; Wiesmann, A. GAMMA SAR and interferometric processing software. In Proceedings of the ERS ENVISAT Symposium, Gothenburg, Sweden, 16–20 October 2001. [Google Scholar]
  33. Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
  34. Chen, C.W.; Zebker, H.A. Network approaches to two-dimensional phase unwrapping: Intractability and two new algorithms. J. Opt. Soc. Am. 2000, 17, 401–414. [Google Scholar] [CrossRef]
  35. Yu, C.; Li, Z.; Penna, N.T. Interferometric synthetic aperture radar atmospheric correction using a GPS-based iterative tropospheric decomposition model. Remote Sens. Environ. 2008, 204, 109–121. [Google Scholar] [CrossRef]
  36. Yu, C.; Li, Z.; Penna, N.T.; Crippa, P. Generic atmospheric correction model for interferometric synthetic aperture radar observations. J. Geophys. Res. Solid Earth 2018, 123, 9202–9222. [Google Scholar] [CrossRef]
  37. Cavalié, O.; Doin, M.P.; Lasserre, C.; Briole, P. Ground motion measurement in the Lake Mead area, Nevada, by differential syn- thetic aperture radar interferometry time series analysis: Probing the lithosphere rheological structure. J. Geophys. Res. 2007, 112, B03403. [Google Scholar] [CrossRef]
  38. Michel, R.; Avouac, J.P.; Taboury, J. Measuring ground displacements from SAR amplitude images: Application to the Landers earthquake. Geophys. Res. Lett. 1999, 26, 875–878. [Google Scholar] [CrossRef]
  39. De Zan, F. Accuracy of incoherent speckle tracking for circular Gaussian signals. IEEE Geosci Remote Sens. Lett. 2014, 11, 264–267. [Google Scholar] [CrossRef]
  40. Wang, S.; Song, C.; Li, S.S.; Li, X. Resolving co- and early post-seismic slip variations of the 2021 MW 7.4 Madoi earthquake in east Bayan Har block with a block-wide distributed deformation mode from satellite synthetic aperture radar data. Earth Planet. Phys. 2022, 6, 108–122. [Google Scholar] [CrossRef]
  41. Jónsson, S.; Segall, P.; Pedersen, R.; Björnsson, G. Post-earthquake ground movements correlated to pore-pressure transients. Nature 2003, 424, 179–183. [Google Scholar] [CrossRef]
  42. Simons, M.; Fialko, Y.; Rivera, L. Coseismic deformation from the 1999 M w 7.1 Hector Mine, California, earthquake as inferred from InSAR and GPS observations. Bull. Seismol. Soc. Am. 2002, 92, 1390–1402. [Google Scholar] [CrossRef]
  43. Wang, K.; Fialko, Y. Slip model of the 2015 Mw 7.8 Gorkha (Nepal) earthquake from inversions of ALOS-2 and GPS data. Geophys. Res. Lett. 2015, 42, 7452–7458. [Google Scholar] [CrossRef]
  44. Wang, K.; Bürgmann, R. Co-and early postseismic deformation due to the 2019 Ridgecrest earthquake sequence constrained by Sentinel-1 and COSMO-SkyMed SAR data. Seismol. Res. Lett. 2020, 91, 1998–2009. [Google Scholar] [CrossRef]
  45. Bagnardi, M.; Hooper, A. Inversion of surface deformation data for rapid estimates of source parameters and uncertainties: A Bayesian approach. Geochem. Geophys. Geosyst. 2018, 19, 2194–2211. [Google Scholar] [CrossRef]
  46. Okada, Y. Internal deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1992, 82, 1018–1040. [Google Scholar] [CrossRef]
  47. Wang, S.; Jiang, G.; Lei, X.; Barbour, A.J.; Tan, X.; Xu, C.; Xu, X. Three Mw ≥ 4.7 earthquakes within the Changning (China) shale gas field ruptured shallow faults intersecting with hydraulic fracturing wells. J. Geophys. Res. Solid Earth 2022, 127, e2021JB022946. [Google Scholar] [CrossRef]
  48. Stark, P.B.; Parker, R.L. Bounded-variable least-squares: An algorithm and applications. Comput. Stat. 1995, 10, 129. [Google Scholar]
  49. Wang, S.; Xu, C.J.; Wen, Y.M.; Yin, Z.; Jiang, G.Y.; Fang, L.H. Slip model for the 25 November 2016 Mw 6.6 Aketao earthquake, western China, revealed by Sentinel-1 and ALOS-2 observations. Remote Sens. 2017, 9, 325. [Google Scholar] [CrossRef]
  50. Wang, S.; Jiang, G.Y.; Weingarten, M.; Niu, Y.F. InSAR evidence indicates a link between fluid injection for salt mining and the 2019 Changning (China) earthquake sequence. Geophys. Res. Lett. 2020, 47, e2020GL087603. [Google Scholar] [CrossRef]
  51. Wang, S.; Xu, W.B.; Xu, C.J.; Yin, Z.; Bürgmann, R.; Liu, L.; Jiang, G.Y. Changes in groundwater level possibly encourage shallow earthquakes in central Australia: The 2016 Petermann Ranges earthquake. Geophys. Res. Lett. 2019, 46, 3189–3198. [Google Scholar] [CrossRef]
  52. Walters, R.J.; Gregory, L.C.; Wedmore, L.N.; Craig, T.J.; McCaffrey, K.; Wilkinson, M.; Vittori, E. Dual control of fault intersections on stop-start rupture in the 2016 Central Italy seismic sequence. Earth Planet. Sci. Lett. 2018, 500, 1–14. [Google Scholar] [CrossRef]
  53. Luo, Y.; Ampuero, J.P. Stability of faults with heterogeneous friction properties and effective normal stress. Tectonophysics 2018, 733, 257–272. [Google Scholar] [CrossRef]
  54. Wang, Z.; Zhang, W.; Taymaz, T.; He, Z.; Xu, T.; Zhang, Z. Dynamic rupture process of the 2023 Mw 7.8 Kahramanmaraş earthquake (SE Türkiye): Variable rupture speed and implications for seismic hazard. Geophys. Res. Lett. 2023, 50, e2023GL104787. [Google Scholar] [CrossRef]
  55. Jia, Z.; Jin, Z.; Marchandon, M.; Ulrich, T.; Gabriel, A.A.; Fan, W.; Fialko, Y. The complex dynamics of the 2023 Kahramanmaraş, Turkey, M w 7.8-7.7 earthquake doublet. Science 2023, 381, 985–990. [Google Scholar] [CrossRef]
  56. Sieh, K.; Jones, L.; Hauksson, E.; Hudnut, K.; Eberhart-Phillips, D.; Heaton, T. Near-field investigations of the Landers earthquake sequence, April to July 1992. Science 1993, 260, 171–176. [Google Scholar] [CrossRef]
  57. Jónsson, S.; Zebker, H.; Segall, P.; Amelung, F. Fault slip distribution of the 1999 Mw 7.1 Hector Mine, California, earthquake, estimated from satellite radar and GPS measurements. Bull. Seismol. Soc. Am. 2002, 92, 1377–1389. [Google Scholar] [CrossRef]
  58. Xu, W.; Feng, G.; Meng, L.; Zhang, A.; Ampuero, J.P.; Bürgmann, R.; Fang, L. Transpressional rupture cascade of the 2016 Mw 7.8 Kaikoura earthquake, New Zealand. J. Geophys. Res. Solid Earth 2018, 123, 2396–2409. [Google Scholar] [CrossRef]
  59. Feng, W.; Samsonov, S.; Qiu, Q.; Wang, Y.; Zhang, P.; Li, T.; Zheng, W. Orthogonal fault rupture and rapid postseismic deformation following 2019 Ridgecrest, California, earthquake sequence revealed from geodetic observations. Geophys. Res. Lett. 2020, 47, e2019GL086888. [Google Scholar] [CrossRef]
  60. Jin, Z.; Fialko, Y. Finite slip models of the 2019 Ridgecrest earthquake sequence constrained by space geodetic data and aftershock locations. Bull. Seismol. Soc. Am. 2020, 110, 1660–1679. [Google Scholar] [CrossRef]
  61. Taufiqurrahman, T.; Gabriel, A.A.; Li, D.; Ulrich, T.; Li, B.; Carena, S.; Gallovič, F. Dynamics, interactions and delays of the 2019 Ridgecrest rupture sequence. Nature 2023, 618, 308–315. [Google Scholar] [CrossRef]
  62. Toda, S.; Stein, R.S.; Richards-Dinger, K.; Bozkurt, S.B. Forecasting the evolution of seismicity in southern California: Animations built on earthquake stress transfer. J. Geophys. Res. 2005, 110, B05S16. [Google Scholar] [CrossRef]
  63. Lin, J.; Stein, R.R. Stress triggering in thrust and subduction earthquakes, and stress interaction between the southern San Andreas and nearby thrust and strike-slip faults. J. Geophys. Res. 2004, 109, B02303. [Google Scholar] [CrossRef]
  64. Fan, G.; Ni, J.F.; Wallace, T.C. Active tectonics of the Pamirs and Karakorum. J. Geophys. Res. Solid Earth 1994, 99, 7131–7160. [Google Scholar] [CrossRef]
  65. Kufner, S.-K.; Schurr, B.; Sippl, C.; Yuan, X.H.; Ratschbacher, L.; Akbar, A.S.M.; Ischuk, A.; Murodkulov, S.; Schneider, F.; Mechie, J.; et al. Deep India meets deep Asia: Lithospheric indentation, delamination and break-off under Pamir and Hindu Kush (Central Asia). Earth Planet. Sci. Lett. 2016, 435, 171–184. [Google Scholar] [CrossRef]
  66. He, P.; Hetland, E.A.; Niemi, N.A.; Wang, Q.; Wen, Y.; Ding, K. The 2016 Mw 6.5 Nura earthquake in the Trans Alai range, northern Pamir: Possible rupture on a back-thrust fault constrained by Sentinel-1A radar interferometry. Tectonophysics 2018, 749, 62–71. [Google Scholar] [CrossRef]
  67. Kufner, S.-K.; Schurr, B.; Ratschbacher, L.; Murodkulov, S.; Abdulhameed, S.; Ischuk, A.; Metzger, S.; Kakar, N. Seismotectonics of the Tajik basin and surrounding mountain ranges. Tectonics 2018, 37, 2404–2424. [Google Scholar] [CrossRef]
  68. Wessel, P.; Smith, W.H.F.; Scharroo, R.; Luis, J.; Wobbe, F. Generic mapping tools: Improved version released. Eos Trans. AGU 2013, 94, 409–410. [Google Scholar] [CrossRef]
Remotesensing 15 05115 g001
Figure 1. Tectonic settings of the study area. The blue beach balls represent the global Centroid Moment Tensor (GCMT) focal mechanisms of Mw ≥ 6.0 earthquakes that occurred in Pamir from January 1976 to February 2023, while the two red beach balls represent the 7 December 2015 Mw 7.2 earthquake and the 23 February 2023 Mw 6.8 earthquake, respectively. The dots indicate the seismic events, color-coded based on their depths [13]. The black lines are regional active faults [14]. Blue arrows represent the GNSS-measured horizontal deformation with respect to the Eurasian plate [9,10,15]. The thick red lines show the surface traces of the seismogenic faults we determined for the two earthquakes. The red box in the top right inset indicates the location of the main panel. Colored rectangles outline the spatial coverage of the Sentinel-1 data used in this study. The red stars mark the epicenters of the 2015 Mw 7.2 earthquake and the 2023 Mw 6.8 earthquake. SKFS: Sarez–Karakul fault system, MPT: main Pamir thrust, TTS: Tanymas thrust system, SMTS: Sarez–Murghab thrust system.
Figure 1. Tectonic settings of the study area. The blue beach balls represent the global Centroid Moment Tensor (GCMT) focal mechanisms of Mw ≥ 6.0 earthquakes that occurred in Pamir from January 1976 to February 2023, while the two red beach balls represent the 7 December 2015 Mw 7.2 earthquake and the 23 February 2023 Mw 6.8 earthquake, respectively. The dots indicate the seismic events, color-coded based on their depths [13]. The black lines are regional active faults [14]. Blue arrows represent the GNSS-measured horizontal deformation with respect to the Eurasian plate [9,10,15]. The thick red lines show the surface traces of the seismogenic faults we determined for the two earthquakes. The red box in the top right inset indicates the location of the main panel. Colored rectangles outline the spatial coverage of the Sentinel-1 data used in this study. The red stars mark the epicenters of the 2015 Mw 7.2 earthquake and the 2023 Mw 6.8 earthquake. SKFS: Sarez–Karakul fault system, MPT: main Pamir thrust, TTS: Tanymas thrust system, SMTS: Sarez–Murghab thrust system.
Remotesensing 15 05115 g001
Remotesensing 15 05115 g002
Figure 2. Coseismic deformation of the 7 December 2015 Mw 7.2 earthquake. The first column (a1–e1) shows the observed interferograms, while the second column (a2–e2) shows the observations at the downsampled points. The third (a3–e3) and last (a4–e4) columns are the predicted observations and fitting residuals derived from the optimal distributed slip model, respectively. The dashed red line indicates the surface traces identified from range offset maps (a1,b1).
Figure 2. Coseismic deformation of the 7 December 2015 Mw 7.2 earthquake. The first column (a1–e1) shows the observed interferograms, while the second column (a2–e2) shows the observations at the downsampled points. The third (a3–e3) and last (a4–e4) columns are the predicted observations and fitting residuals derived from the optimal distributed slip model, respectively. The dashed red line indicates the surface traces identified from range offset maps (a1,b1).
Remotesensing 15 05115 g002
Remotesensing 15 05115 g003
Figure 3. Coseismic deformation of the 23 February 2023 Mw 6.8 earthquake. The first column (a1–c1) shows the observed interferograms, while the second column (a2–c2) shows the observations at the downsampled points. The third (a3–c3) and last (a4–c4) columns are the predicted observations and fitting residuals derived from the optimal distributed slip model, respectively. The dashed red line shows the surface projection of the optimal InSAR-derived source fault of the earthquake.
Figure 3. Coseismic deformation of the 23 February 2023 Mw 6.8 earthquake. The first column (a1–c1) shows the observed interferograms, while the second column (a2–c2) shows the observations at the downsampled points. The third (a3–c3) and last (a4–c4) columns are the predicted observations and fitting residuals derived from the optimal distributed slip model, respectively. The dashed red line shows the surface projection of the optimal InSAR-derived source fault of the earthquake.
Remotesensing 15 05115 g003
Remotesensing 15 05115 g004
Figure 4. Non-linear inversions for the candidate seismogenic faults of the 2023 Mw 6.8 earthquake. (a1) Posterior density distributions of the source parameters derived from inversions under scenario I (~200°). Red lines present the optimal values. (a2) InSAR predictions (1st column) and fitting residuals (2nd column) derived from the optimal non-linear inversion results shown in panel (a1). (b1,b2) The same as (a1,a2) but for inversion results under scenario II (~300°).
Figure 4. Non-linear inversions for the candidate seismogenic faults of the 2023 Mw 6.8 earthquake. (a1) Posterior density distributions of the source parameters derived from inversions under scenario I (~200°). Red lines present the optimal values. (a2) InSAR predictions (1st column) and fitting residuals (2nd column) derived from the optimal non-linear inversion results shown in panel (a1). (b1,b2) The same as (a1,a2) but for inversion results under scenario II (~300°).
Remotesensing 15 05115 g004
Remotesensing 15 05115 g005
Figure 5. Non-linear inversions for the candidate seismogenic faults of the 2023 Mw 6.8 earthquake. (a1,a2) The same as Figure 4(a1,a2) but for inversion results under scenario III (~120°). (b1,b2) The same as (a1,a2), but for inversion results under scenario IV (~25°).
Figure 5. Non-linear inversions for the candidate seismogenic faults of the 2023 Mw 6.8 earthquake. (a1,a2) The same as Figure 4(a1,a2) but for inversion results under scenario III (~120°). (b1,b2) The same as (a1,a2), but for inversion results under scenario IV (~25°).
Remotesensing 15 05115 g005
Remotesensing 15 05115 g006
Figure 6. (a) Trade-off curves between the model residuals and the roughness of the slip models for the two candidate fault models of the 2015 Mw 7.2 earthquake. (a) The same as (b) but for the two candidate fault models of the 2023 Mw 6.8 earthquake.
Figure 6. (a) Trade-off curves between the model residuals and the roughness of the slip models for the two candidate fault models of the 2015 Mw 7.2 earthquake. (a) The same as (b) but for the two candidate fault models of the 2023 Mw 6.8 earthquake.
Remotesensing 15 05115 g006
Remotesensing 15 05115 g007
Figure 7. The optimal distributed slip model for the 2015 Mw 7.2 earthquake, with white arrows indicating the slip direction of the hanging wall patches. Locations of Lake Sarez, Kokuibel Valley, and two major faults (SMTS and TTS) that are perpendicular to the seismogenic fault are also labeled. The green star marks the hypocenter determined in GCMT solution.
Figure 7. The optimal distributed slip model for the 2015 Mw 7.2 earthquake, with white arrows indicating the slip direction of the hanging wall patches. Locations of Lake Sarez, Kokuibel Valley, and two major faults (SMTS and TTS) that are perpendicular to the seismogenic fault are also labeled. The green star marks the hypocenter determined in GCMT solution.
Remotesensing 15 05115 g007
Remotesensing 15 05115 g008
Figure 8. The optimal distributed slip model for the 2023 Mw 6.8 earthquake, with white arrows indicating the slip direction of the hanging wall patches. The green star marks the hypocenter determined in GCMT solution.
Figure 8. The optimal distributed slip model for the 2023 Mw 6.8 earthquake, with white arrows indicating the slip direction of the hanging wall patches. The green star marks the hypocenter determined in GCMT solution.
Remotesensing 15 05115 g008
Remotesensing 15 05115 g009
Figure 9. Close-up view of the distributed faults along the SKFS. The dots are the seismic events, color-coded by their depths [13]. The color-coded lines represent the along-strike variations in inferred slip models of the 2015 Mw 7.2 and the 2023 Mw 6.8 earthquakes.
Figure 9. Close-up view of the distributed faults along the SKFS. The dots are the seismic events, color-coded by their depths [13]. The color-coded lines represent the along-strike variations in inferred slip models of the 2015 Mw 7.2 and the 2023 Mw 6.8 earthquakes.
Remotesensing 15 05115 g009
Remotesensing 15 05115 g010
Figure 10. (a,b) Coulomb failure stress changes at a depth of 10 km induced by the 2015 Mw 7.2 and 2023 Mw 6.8 earthquakes, respectively. The receiver fault is specified with a strike of 30°, a dip angle of 80°, and a rake angle of 0° (indicating left-lateral strike-slip faulting). (c) Summation of (a,b). (d) Static coulomb tress changes on the fault plane of the 2023 earthquake induced by the 2015 earthquake. The red star roughly marks the epicenter of the 2023 earthquake. Note that the effective friction coefficient was assumed to be 0.4, a typical value commonly used for strike-slip faults.
Figure 10. (a,b) Coulomb failure stress changes at a depth of 10 km induced by the 2015 Mw 7.2 and 2023 Mw 6.8 earthquakes, respectively. The receiver fault is specified with a strike of 30°, a dip angle of 80°, and a rake angle of 0° (indicating left-lateral strike-slip faulting). (c) Summation of (a,b). (d) Static coulomb tress changes on the fault plane of the 2023 earthquake induced by the 2015 earthquake. The red star roughly marks the epicenter of the 2023 earthquake. Note that the effective friction coefficient was assumed to be 0.4, a typical value commonly used for strike-slip faults.
Remotesensing 15 05115 g010
Table 1. Sentinel-1 data used in this study to measure the coseismic ground deformation caused by the 2015 Mw 7.2 and 2023 Mw 6.8 earthquakes.
Table 1. Sentinel-1 data used in this study to measure the coseismic ground deformation caused by the 2015 Mw 7.2 and 2023 Mw 6.8 earthquakes.
EventDef. TypeTrackReferenceRepeatσ (cm) †
7 December 2015
Mw 7.2		Range offset5 (Descending)201511182015121266.9
100 (Ascending)201512062015123077.4
InSAR5 (Descending)20151118201512122.3
100 (Ascending)20151206201512302.9
107 (Descending)20151207201512311.8
23 February 2023
Mw 6.8		InSAR5 (Descending)20230221202303051.2
100 (Ascending)20230203202303111.2
107 (Descending)20230204202302281.0
† σ is the standard deviation estimated from pixels by masking out the median- and near-field regions shown in Figure 2 and Figure 3.
Table 2. Solutions of focal mechanisms for the two earthquakes in this study.
Table 2. Solutions of focal mechanisms for the two earthquakes in this study.
EventLon
(°)		Lat
(°)		Depth
(km)		MwNode Plane INode Plane IISource
Strike (°)Dip (°)Rake (°)Strike (°)Dip (°)Rake (°)
7 December 2015
Mw 7.2		72.78038.21119.57.221483812382172USGS
72.9138.39127.221280−730483−170GCMT
72.9438.13117.212485−1613371−4GFZ
23 February 2023
Mw 6.8		73.23038.05613.56.920357−2130572−146USGS
73.2238.1516.96.821088112089178GCMT
73.2938.06106.812273−1582567−18GFZ
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Wang, S.; Song, C.; Xiao, Z. Two Mw ≥ 6.5 Earthquakes in Central Pamir Constrained by Satellite SAR Observations. Remote Sens. 2023, 15, 5115. https://doi.org/10.3390/rs15215115

AMA Style

Wang S, Song C, Xiao Z. Two Mw ≥ 6.5 Earthquakes in Central Pamir Constrained by Satellite SAR Observations. Remote Sensing. 2023; 15(21):5115. https://doi.org/10.3390/rs15215115

Chicago/Turabian Style

Wang, Shuai, Chuang Song, and Zhuohui Xiao. 2023. "Two Mw ≥ 6.5 Earthquakes in Central Pamir Constrained by Satellite SAR Observations" Remote Sensing 15, no. 21: 5115. https://doi.org/10.3390/rs15215115

APA Style

Wang, S., Song, C., & Xiao, Z. (2023). Two Mw ≥ 6.5 Earthquakes in Central Pamir Constrained by Satellite SAR Observations. Remote Sensing, 15(21), 5115. https://doi.org/10.3390/rs15215115

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop