1. Introduction
Point clouds provide precise 3D geometric information. They are used in digital twin cities [
1,
2], railways [
3], cultural heritage [
4], power line extraction and reconstruction [
5], and autonomous driving [
6]. However, they lack semantic information, hindering machine comprehension and usage. High-precision semantic segmentation is necessary for many applications.
Supervised machine learning methods like SVM [
7] and Random Forest [
8] are often used in early point cloud segmentation research and rely on hand-crafted features to extract low-dimensional data. However, with the increase in GPU computing power, deep learning methods have become more common in recent years for processing point cloud data and tackling complex semantic segmentation tasks [
9].
Convolution is an important branch in the field of 3D deep learning, known for its advantages of weight sharing and local perception [
10]. The deep learning method KPCONV [
11] extends convolution to 3D point cloud processing, achieving competitive results. It uses convolution kernel points with fixed spatial generation, calculates the weight matrix through the kernel function, and performs calculations with points in the spherical neighborhood. KPCONV bypasses the problem of direct, high-complexity regular grid convolution by obtaining points in the spherical neighborhood through Poisson disks or random points to reduce operational complexity.
However, recognizing objects in 3D scenes can be challenging due to their complexity. For instance, buildings often have multiple sides and facades, while streets look flat. Additionally, trees have a tall vertical structure and a large crown. The rigid convolutional kernel point strategy of KPCONV inhibits its potential to recognize buildings, trees, and other objects from point clouds. For example, when dealing with large-scale airborne laser scanning (ALS) data, planar structures with multiple sides and facades are often present in the point cloud data of buildings, roads, and other similar categories, while structures with one side larger than the others, such as a spherical cone, are typically found in vegetation data. The convolution kernel used by KPCONV employs a system composed of attraction and repulsion and indiscriminately considers the characteristics of local neighborhood points. Pursuing more detailed semantic segmentation effects may slightly constrain the network effect due to this characteristic.
Based on the larger variance of ALS point cloud coordinates in the XY plane than along the
Z-axis, LGENet [
12] created a hybrid 2D and 3D convolutional module using the original KPCONV convolution. Similar to the principle of LGENet, with a better disparity in its 3D structure, the cylindrical convolutional kernel generation solves the inconsistency between the XY and Z planes often found in buildings and roads. Furthermore, the dataset often contains vegetation, and those features can be further explored. The spherical cone convolution kernel generation is designed to improve the recognition accuracy of trees and shrubs.
Optimizing the effectiveness of a network involves judiciously leveraging the diverse capabilities of convolutional kernels, a facet that often remains untapped when employing only a single kernel per downsampling layer. Drawing inspiration from the domain of image analysis, where many convolution kernels prove invaluable for robust feature extraction, we recognize the potential of a richer kernel ensemble. Building upon the conceptual foundation of KPCONV, we introduce a novel and streamlined architecture called Integrated Point Convolution (IPCONV), fusing multiple computational elements to enhance network performance.
We introduce the Multi-Shape Neighborhood System (MSNS) during the downsampling phase. This sophisticated construct synergizes the insights derived from two distinct convolution kernel types: cylindrical and spherical cone kernels. The resultant hybrid kernel framework is illustrated in
Figure 1, juxtaposing the novel IPCONV with the traditional KPCONV, wherein IPCONV replaces the conventional single-layer spherical convolution kernels with an array of different convolution kernels. The significant contributions of this work are as follows:
- (1)
Innovative Kernel Generation Methodology: Our study pioneers the development of two distinct methodologies for generating cylindrical convolution kernel points and spherical cone kernel points. Our proposed network optimally captures idiosyncrasies in ground object characteristics by meticulously tuning these parameters, enhancing feature learning.
- (2)
Enhanced Local Category Differentiation: Addressing the need for precise discrimination between local categories, we introduce the MSNS. This system effectively concatenates knowledge acquired through diverse convolutional kernel point generation methods, elevating the proficiency of feature learning. This approach enhances the discernment capabilities of the network and augments its grasp on complex local features.
- (3)
Benchmark Validation: The efficacy of our proposed model is demonstrated through comprehensive evaluations on multiple 3D benchmark datasets. Comparisons with established baseline methods consistently highlight the progress achieved. Specifically, on the ISPRS Vaihingen 3D dataset [
13], our model achieves an impressive Avg.F1 score of 70.7%, with a corresponding overall accuracy (OA) index of 84.5%. Performance on the LASDU dataset [
14] further underscores the prowess of our model, with an Avg.F1 score of 75.67% and an OA of 86.66%. On the DFC 2019 dataset [
15], our model attains a remarkable Avg.F1 score of 87.9%, and OA score of 97.1%.
In essence, our work, IPCONV, builds upon the KP-FCNN architecture of KPCONV and harnesses the combined potential of various convolutional kernels and kernel generation methodologies. The network significantly enhances feature learning, local categorization, and benchmark performance. This study thereby contributes substantively to the domain of 3D benchmark dataset analysis and serves as a testament to the efficacy of our proposed IPCONV model.
3. Method
In this section, we outline our approach, beginning with two novel convolution kernel point generation strategies and introducing the fundamental principles of convolution in
Section 3.1. These strategies encompass cylindrical convolution kernel point generation and spherical cone kernel point generation, aligned with the KPCONV-based convolution rules. Subsequently,
Section 3.2 describes the MSNS, while
Section 3.3 illustrates the comprehensive network architecture.
3.1. Convolution Kernel Point Generation
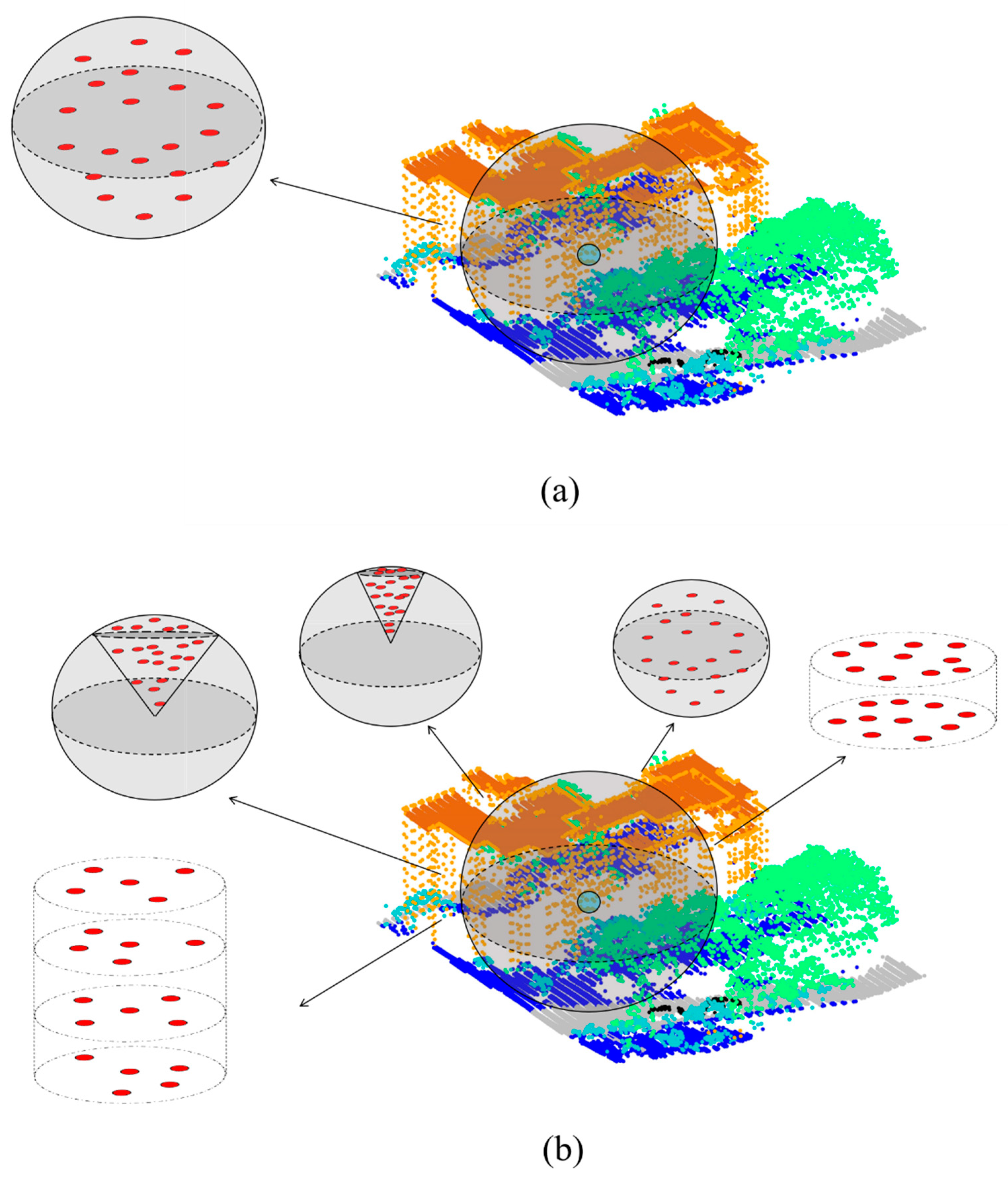
We propose a novel approach for distributing convolution kernel points to enhance the efficacy of capturing point cloud features. Departing from the rigid convolution generation operator of the traditional KPCONV, which optimizes kernel point spacing within a designated sphere by applying an attractive potential at the center of the sphere to prevent divergence (as shown in
Figure 2a), we propose two supplementary strategies: cylindrical convolution kernel point generation and spherical cone convolution kernel point generation. These methods serve as a valuable augmentation to the original KPCONV, designed to broaden its capabilities.
3.1.1. Cylindrical Convolution Kernel Point Generation
The cylindrical convolution kernel point generation strategy proves highly effective in enhancing the discernment of planar and flat structures featuring multiple height layers, such as buildings, as depicted in
Figure 2b. This strategy unfolds in two distinct phases.
Initially, a plane is established parallel to the base of the cylinder. The intersection between this plane and the cylinder creates a circle. By subsequently moving the plane along the cylindrical axis, adhering to a predetermined step, a series of
circles akin to the initial one is generated. The position of each plane, denoted as
, is calculated using Equation (1).
where
and
represent opposite values, with their absolute magnitudes equating to half the cylindrical height.
In the subsequent phase, a specified number of kernel points is extracted for each derived circle through Equation (2). These kernel points adopt a 2D version of the initial KPCONV, a technique employed to enhance the comprehension of planar entities [
12]. The kernel points show a clear tendency to avoid each other, ensuring a level of separation while also possessing an attraction that draws them within a certain radius. The formulation for generating the 2D KPCONV is outlined in Equations (3) and (4).
where the radius of the cylinder is denoted as
, the number of kernel points
per layer is
,
signifies the overall count of kernel points, the kernel points for each layer are represented by
, and
represents the combined constraint that encompasses both repulsion and attraction effects.
Finally, akin to KPCONV, the kernel points at each layer undergo random rotations around the Z-axis and are subject to random coordinate offsets.
3.1.2. Spherical Cone Convolution Kernel Point Generation
While cylindrical convolution kernel point generation excels in distributing points across height multilayers with plane symmetry, it may fall short in recognizing objects that do not fit this assumption, like trees. Trees often exhibit significant size discrepancies between their canopy and trunk regions, resulting in sparse trunk point representation. To address this, we propose the spherical cone convolution kernel point generation.
Spherical convolutional kernel point generation closely resembles the spherical cone approach. Additionally, the parameters can be adjusted to yield a dual spherical cone or accommodate a versatile complement within the spherical neighborhood, as described earlier. This configuration offers substantial flexibility to suit various scenarios.
Firstly, an initial set of candidate points is randomly generated within a sphere.
Secondly, as depicted in
Figure 3, a line segment is traced from a point on the surface of the sphere to the center of the sphere, forming an angle of
with the
Z-axis. A spherical cone is formed by rotating this line segment around the
Z-axis. This spherical cone can be represented as
, as indicated below:
where
signifies the threshold angle between a point and the
-axis,
stands for the kernel points located within the spherical cone, and
denotes the positions of kernel points.
Furthermore, Equation (5) incorporates a range of parameters that have been strategically devised to enhance the versatility of the convolution process. These parameters offer multiple configurations, such as concatenating them to derive dual-volume kernel points in the “both-side” mode and modifying the direction of the inequality to generate reverse points in the “complementary” mode. This adaptability allows the convolution process to cater to diverse scenarios and requirements.
Lastly, the resulting convolution kernel points are randomly selected to fulfill the specified count as the definitive kernel points. Analogous to KPCONV, these kernel points undergo random 3D rotations and are subject to random coordinate offsets to complete the process.
The point cloud generation process associated with spherical cone convolution yields denser results than cylindrical forms, closely mirroring the morphology of the tree. This convolutional kernel point generation relies on the concept of a sphere neighborhood. As illustrated in
Figure 3, its base mode is instrumental in capturing tree features. This nuanced convolutional kernel point generation is anticipated to unlock additional layers of point cloud feature information.
3.1.3. Convolution Rules Based on KPCONV
After kernel point generation, the convolution process is the same as for KPCONV. The convolution procedure
for a given point
can be delineated as follows:
here,
signifies the previously acquired convolution kernel points, with their positions denoted as
. The points within the spherical neighborhood are represented as
from
, and their point features
are represented as
.
The convolution commences by selecting an arbitrary neighboring point , then iterating through each kernel point to calculate the positional weight . This involves subtracting the normalized position of the specific point from the neighboring point . Subsequently, the weights for each kernel point are obtained by multiplying the positional weights with the feature weight mapping matrix , where the input dimension of the feature mapping matrix is and the output dimension is , and the weight for neighborhood point is obtained by summing the weights of each kernel point. The outcome of multiplying the weight obtained from with the corresponding feature serves as the convolution feature of the neighboring point . The convolutional features of all neighboring points for a particular point are aggregated to derive the final convolutional feature, which becomes the output feature for that specific point.
IPCONV builds upon the KP-FCNN framework and employs cylindrical convolution kernel point generation and spherical cone convolution kernel point generation for generating kernel points. These kernel points, utilizing geometric relationships between kernel points and the neighboring point through Equation (6) of the convolution rules, impact the efficacy of the feature learning process for each particular point p.
3.2. Multi-Shape Neighborhood System
After the preceding convolution process, we employ a singular convolution operator for downsampling to learn neighborhood points. Building upon these convolution kernels, we focus on refining convolutional intricacies by creating a highly adaptable MSNS. Our aim with the MSNS is to augment the features of the convolution kernels, mitigating the potential imbalance inherent in employing a solitary convolution kernel for a given category. To achieve this, we incorporate diverse convolutional kernel point generation methods for each layer, including cylindrical convolution and spherical cone point generation. The accumulated knowledge from these distinct convolution patterns results in
and
representing the acquired features. Subsequently, the MSNS process involves dimensionality reduction and feature concatenation. Illustrated in
Figure 4, our proposed MSNS integrates multiple convolutional kernels of varying types, fostering enriched feature learning.
Before feeding the network with data, the MSNS initially applies a batch normalization and ReLU layer to the original features .
Next, features are learned through the generated cylindrical and spherical convolutional kernels, designated as
and
. These features are concatenated to yield
, expressed as:
is normalized, resulting in a dimensionality reduction denoted as . Concurrently, the processed total network features are integrated with the input network features. This integration entails combining the input network features with the processed total network features to establish short-circuit connections, thereby finalizing the module.
3.3. Network Architecture
The fundamental network structure utilized in this study is KP-FCNN, wherein the conventional KPCONV module is substituted with the MSNS.
Figure 5 provides a visual depiction, highlighting that IPCONV predominantly enriches the feature learning process during downsampling. The network framework is an amalgamation of distinct elements, encompassing upsampling paired with feature concatenation, 1D convolution, skip link, the MSNS module, and the Strided Multi-Shape Neighborhood System module (Strided MSNS).
The encoder consists of 5 convolutional layers. IPCONV uses the MSNS module and the Strided MSNS module for all convolutional blocks for each layer. The MSNS module keeps both the input and output feature dimensions and points the same. The Strided MSNS can be likened to image stride convolution grounded in KPCONV, where the output feature dimension is twice as large as the input dimension , and the output number of points is fewer than the input point count .
In the decoder, nearest neighbor upsampling is used to obtain the final point-by-point features. There are four skip links that pass intermediate features from the encoder to the decoder. These features are concatenated using the upsampled features and point-by-point features, then passed through a 1D convolution block.
6. Ablation Study
In this section, we discuss the impact of different convolutional kernel point generation methods and the MSNS on the ISPRS benchmark dataset.
6.1. Effect of Difference Convolution Kernel Point Generation
This section evaluates the impact of difference convolution kernel point generation methods when implemented individually within the same type.
Table 6 presents the results, demonstrating the efficacy of single cylindrical convolution generation and single spherical cone convolution kernel point generation over the baseline network.
For single cylindrical convolution generation, an Avg.F1 of 69.5% and an OA of 83.8% are achieved. Similarly, for single spherical cone convolution kernel point generation, the Avg.F1 is 69.4%, and the OA is 83.9%, both showing improvements.
Compared to the benchmark KPCONV, single cylindrical convolution generation focuses on enhancing the accuracy of the facade, impervious surfaces, and low vegetation categories, with F1 scores improved by 1.8%, 3.6%, and 3.5%, respectively. However, accuracy for the fence/hedge category decreases by 9.0%, possibly due to the insensitivity of the network to short, linear geometries like fences/hedges. Slight decreases in the accuracy of the tree, power, and car categories are attributed to the multilayer generation of kernel points in cylindrical convolutional generation struggling to learn narrow or low features in height space layers during feature recognition.
For single spherical cone convolution kernel generation, the F1 scores for low vegetation, fence/hedge, shrub, and tree improve by 2.7% compared to the benchmark network KPCONV. Notably, the strategy improves vegetation features while maintaining overall category accuracy. However, recognition accuracy for power decreases by 21.1%, likely due to the scarcity of power line categories leading to more misclassifications.
This study highlights the strengths of spherical cone convolution kernel generation for tree features and cylindrical convolution kernel generation for features extending along the XY plane, showcasing promising results.
6.2. Effect of the MSNS
An examination of the impact of the MSNS is presented in
Table 7, where the baseline for the ablation study is KPCONV. Various combinations of the original rigid convolution kernels are designed to showcase the effectiveness of the parallel algorithm in contrast to the vanilla version consisting of six rigid KPCONV convolution kernels.
Experimental results reveal that the accuracy has been moderately improved, reaching 83.9%. However, the extent of the improvement is limited, suggesting that the undifferentiated spherical convolutional kernel point generation approach encounters constraints in processing our point cloud data. Notably, its recognition accuracy for the “power” category is higher, achieving a 67.5% in F1 score. Nonetheless, the OA performance in other feature categories remains average. Nevertheless, the OA still demonstrates an enhancement of approximately 2.2% compared to a single cylindrical convolutional generation.
Meanwhile, an investigation was conducted by incorporating multiple instances of cylindrical convolution kernel point generations to analyze their impact on the results. As the cylindrical convolution kernel point generation is designed to specifically address building features, and given that the majority of categories in the ISPRS benchmark dataset pertain to buildings, commendable outcomes were achieved. With an Avg.F1 reaching 69.8% and an OA reaching 84.3%, it demonstrates promising performance, particularly on the roof, facade, and shrub categories. Nonetheless, it fell slightly short of the performance achieved by a single spherical cone convolution.
The parallel spherical cone convolution kernel point generation attained an OA result of 84.3%. However, we noted a slight decline in Avg.F1, indicating that it slightly underperforms compared to parallel cylindrical convolution kernel point generation in terms of overall accuracy. However, it achieved an impressive 82.9% classification accuracy on tree features, while the results for low vegetation and shrub categories were less effective than anticipated.
Ultimately, by considering various combinations of cylindrical convolution kernel point generations and spherical cone convolution kernel point generations, specifically focusing on building and tree categories, the optimal combination was selected from these permutations to achieve the current noteworthy semantic segmentation outcomes.
7. Conclusions
We have introduced IPCONV, a straightforward yet highly effective deep learning network tailored for semantic segmentation tasks on point cloud data, particularly in urban settings. Our proposed IPCONV demonstrates a superior performance compared to the KPCONV baseline, showcasing its enhanced capabilities in processing urban datasets. One of the key innovations is the integration of the MSNS, which empowers each convolution layer to incorporate a variety of convolution kernels through customizable configurations. This flexibility allows us to tailor the kernel combination according to specific feature recognition needs, such as using cylindrical convolution kernel point generation for architectural categories and spherical cone convolution kernel point generation for tree categories. The simplicity and straightforwardness of the MSNS parameters facilitate easy integration and experimentation.
The advantages of IPCONV are comprehensively validated through ablation experiments conducted on the ISPRS benchmark dataset. IPCONV showcases an improved OA and an average F1 score of 70.7% over the KPCONV baseline. Furthermore, compared to the LGENet strategy, which is also an enhancement based on KPCONV, IPCONV achieves a similar performance while offering a simpler approach, with an OA index of around 84.5%. Additionally, the efficacy of IPCONV is further demonstrated through evaluations of the LASDU and DFC 2019 datasets.
In the future, we hope to design a more practical network framework for point cloud semantic segmentation tasks. At the same time, we also need to consider the effectiveness of the model for large-scale point cloud datasets to improve network performance. We attempt a feature screening strategy to accomplish feature selection and reduce the dependence on unnecessary features.