Integration of Residual Terrain Modelling and the Equivalent Source Layer Method in Gravity Field Synthesis for Airborne Gravity Gradiometer Test Site Determination
Abstract
1. Introduction
- The site should exhibit pronounced high-frequency and shallow gravity field features.
- It should be with moderate terrain.
- The site should be minimally impacted by human activities.
- There should be no restrictions on flight altitudes.
2. Methodology
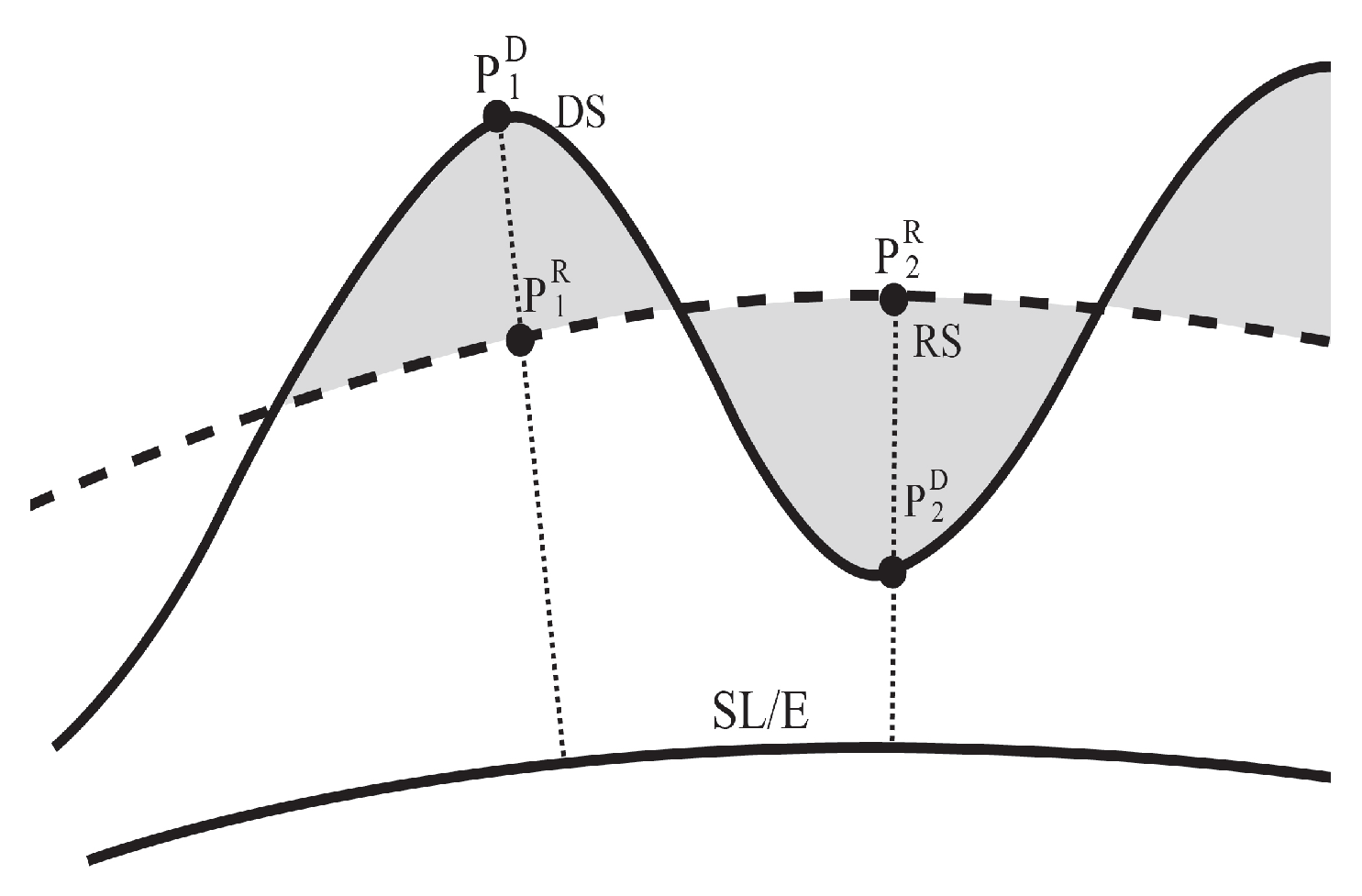
2.1. The Principle of RTM Technique
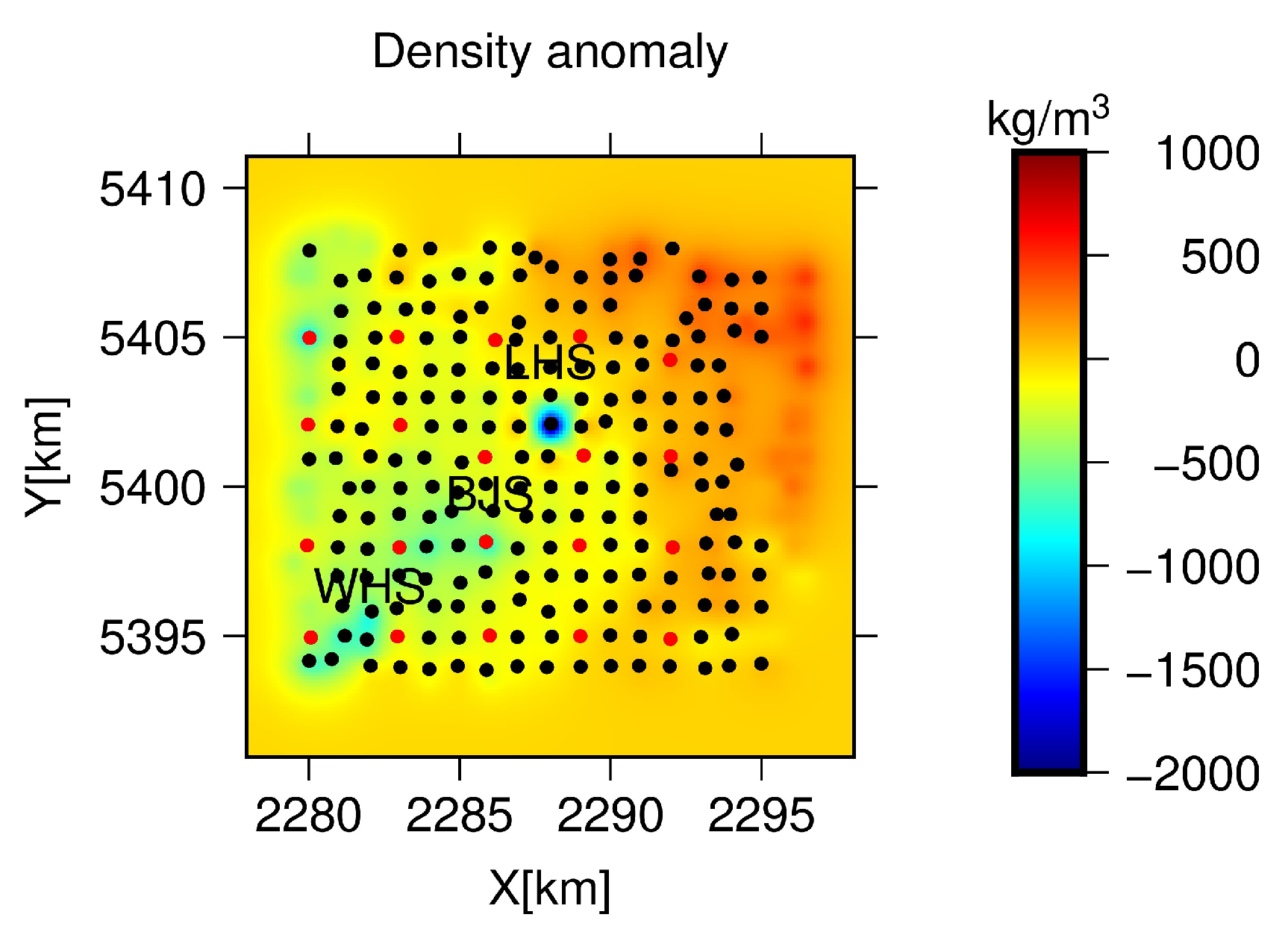
2.2. Description of Equivalent Source Layer (ESL) Setting
3. Numerical Study
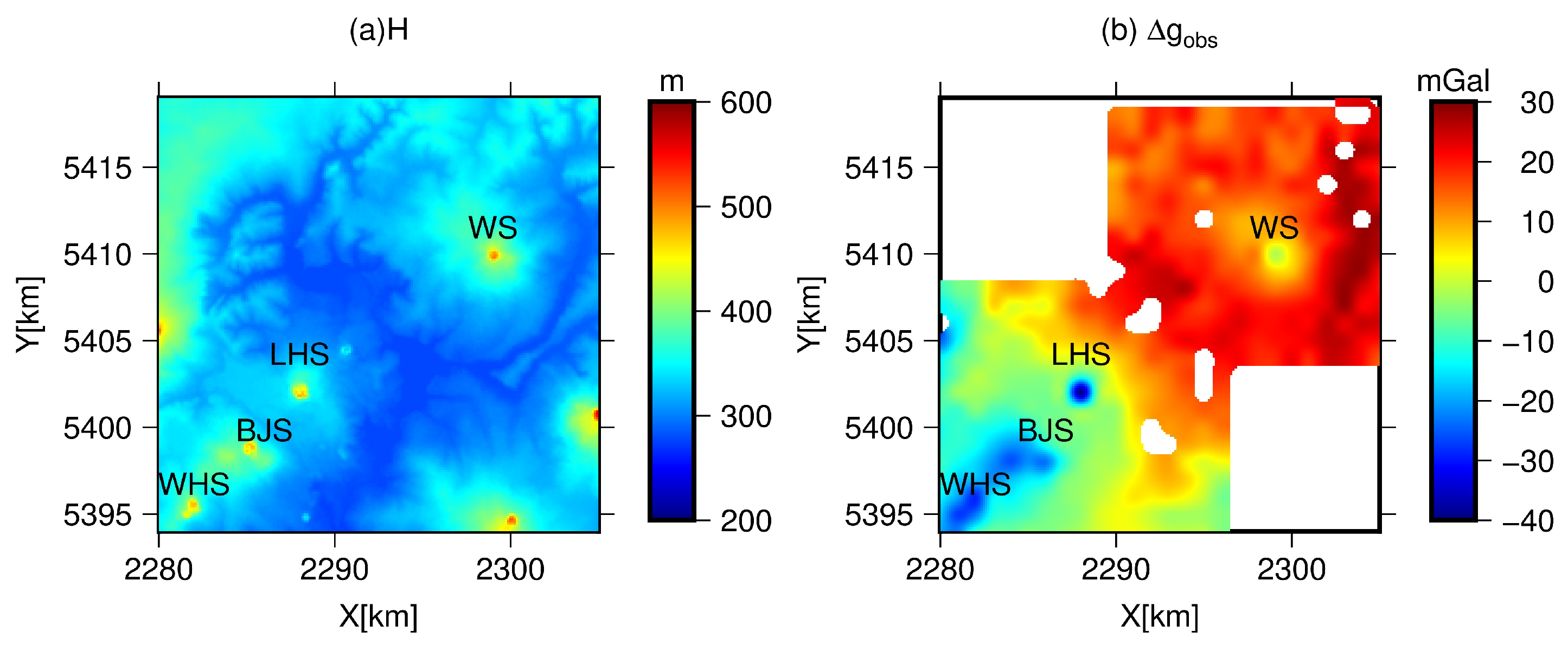
3.1. The Wudalianchi Volcano Field
3.2. The Calculation Method of Gravity Filed Features over WVF
3.3. The Gravity Field Signals over the Southwestern Area
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jekeli, C. A review of gravity gradiometer survey system data analyses. Geophysics 1993, 58, 508–514. [Google Scholar] [CrossRef]
- Dransfield, M.; Milkereit, B. Airborne gravity gradiometry in the search for mineral deposits. Proc. Explor. 2007, 7, 341–354. [Google Scholar]
- Wetherley, S.; Moore, D. Using FALCON® airborne gravity gradiometry for oil and gas exploration: Recent case studies. In Proceedings of the 12th SEGJ International Symposium, Tokyo, Japan, 18–20 November 2015; Society of Exploration Geophysicists. 2015; pp. 60–63. [Google Scholar] [CrossRef]
- DiFrancesco, D.; Grierson, A.; Kaputa, D.; Meyer, T. Gravity gradiometer systems–advances and challenges. Geophys. Prospect. 2009, 57, 615–623. [Google Scholar] [CrossRef]
- Evstifeev, M. The state of the art in the development of onboard gravity gradiometers. Gyroscopy Navig. 2017, 8, 68–79. [Google Scholar] [CrossRef]
- Janvier, C.; Menoret, V.; Desruelle, B.; Merlet, S.; dos Santos, F.P.; Landragin, A. Recent advances in quantum gravity sensors. In Proceedings of the SEG/AAPG/SEPM First International Meeting for Applied Geoscience & Energy, Denver, CO, USA, 26 September–1 October 2021; OnePetro: Richardson, TX, USA, 2021. [Google Scholar] [CrossRef]
- Eötvös, L. Untersuchungen über gravitation und erdmagnetismus. Ann. Phys. 1896, 295, 354–400. [Google Scholar] [CrossRef]
- Jekeli, C. The Gravity Gradiometer Survey System (GGSS); EOS: Norwell, MA, USA, 1988; Volume 69, p. 105. ISSN 0096-3941. [Google Scholar]
- DiFrancesco, D. Gravity gradiometry developments at Lockheed Martin. In Proceedings of the EGS-AGU-EUG Joint Assembly, Nice, France, 6–11 April 2003; p. 1069. [Google Scholar]
- Dransfield, M.H.; Lee, J.B. The FALCON airborne gravity gradiometer survey systems. In Proceedings of the ASEG-PESA Airborne Gravity 2004 Workshop, Sydney, Australia, 15 August 2004; pp. 15–19. [Google Scholar]
- Murphy, C.A. The Air-FTG airborne gravity gradiometer system. In Airborne Gravity; Commonwealth of Australia: Canberra City, Australia, 2004; pp. 7–14. [Google Scholar]
- Rummel, R.; Yi, W.; Stummer, C. GOCE gravitational gradiometry. J. Geod. 2011, 85, 777–790. [Google Scholar] [CrossRef]
- Moody, M. A superconducting gravity gradiometer for measurements from a moving vehicle. Rev. Sci. Instrum. 2011, 82, 094501. [Google Scholar] [CrossRef]
- Cuperus, R.; Flokstra, F.; Wiegerink, R.; Flokstra, J. MEMS based gravimeters and gravity gradiometers. In Proceedings of the Poster, presented at the MEMS Conference/University of Twente, Enschede, The Netherlands, 26–29 September 2010. [Google Scholar]
- Biedermann, G.; Wu, X.; Deslauriers, L.; Roy, S.; Mahadeswaraswamy, C.; Kasevich, M. Testing gravity with cold-atom interferometers. Phys. Rev. A 2015, 91, 033629. [Google Scholar] [CrossRef]
- Snadden, M.; McGuirk, J.; Bouyer, P.; Haritos, K.; Kasevich, M. Measurement of the Earth’s gravity gradient with an atom interferometer-based gravity gradiometer. Phys. Rev. Lett. 1998, 81, 971. [Google Scholar] [CrossRef]
- Fixler, J.B. Atom Interferometer-Based Gravity Gradiometer Measurements. Ph.D. Thesis, Yale University, New Haven, CT, USA, 2003. [Google Scholar]
- Dowling, J.P.; Milburn, G.J. Quantum technology: The second quantum revolution. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2003, 361, 1655–1674. [Google Scholar] [CrossRef]
- Hu, L.; Poli, N.; Salvi, L.; Tino, G.M. Atom interferometry with the Sr optical clock transition. Phys. Rev. Lett. 2017, 119, 263601. [Google Scholar] [CrossRef] [PubMed]
- Hu, L.; Wang, E.; Salvi, L.; Tinsley, J.N.; Tino, G.M.; Poli, N. Sr atom interferometry with the optical clock transition as a gravimeter and a gravity gradiometer. Class. Quantum Gravity 2019, 37, 014001. [Google Scholar] [CrossRef]
- Bresson, A.; Bidel, Y.; Bouyer, P.; Leone, B.; Murphy, E.; Silvestrin, P. Quantum mechanics for space applications. Appl. Phys. B 2006, 84, 545–550. [Google Scholar] [CrossRef][Green Version]
- Duan, X.C.; Zhou, M.K.; Mao, D.K.; Yao, H.B.; Deng, X.B.; Luo, J.; Hu, Z.K. Operating an atom-interferometry-based gravity gradiometer by the dual-fringe-locking method. Phys. Rev. A 2014, 90, 023617. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, C.; Huang, X.; Wu, W.; Hu, F.; Liu, H.; Tu, L. Scale Factor Calibration for a Rotating Accelerometer Gravity Gradiometer. Sensors 2018, 18, 4386. [Google Scholar] [CrossRef] [PubMed]
- Meng, Z.; Yang, Y.; Li, Z. Development of airborne gravity gradiometer based on a quartz flexible accelerometer. Acta Geol. Sin. Engl. Ed. 2019, 93, 352–364. [Google Scholar] [CrossRef]
- Zhang, H.; Mao, D.K.; Luo, Q.; Hu, Z.K.; Chen, L.L.; Zhou, M.K. The self-attraction effect in an atom gravity gradiometer. Metrologia 2020, 57, 045011. [Google Scholar] [CrossRef]
- Barzaghi, R.; Borghi, A.; Keller, K.; Forsberg, R.; Giori, I.; Loretti, I.; Olesen, A.V.; Stenseng, L. Airborne gravity tests in the Italian area to improve the geoid model of Italy. Geophys. Prospect. 2009, 57, 625–632. [Google Scholar] [CrossRef]
- Christensen, A.N.; Dransfield, M.H. Noise and repeatability of airborne gravity gradiometry. In Proceedings of the 76th EAGE Conference and Exhibition 2014, European Association of Geoscientists & Engineers, Amsterdam, The Netherlands, 16–19 June 2014; Volume 2014, pp. 1–5. [Google Scholar] [CrossRef]
- Christensen, A. Results from Falcon Airborne Gravity Gradiometer surveys over the Kauring AGG test site. Aseg Ext. Abstr. 2013, 2013, 1–4. [Google Scholar] [CrossRef]
- Bruton, A.; Hammada, Y.; Ferguson, S.; Schwarz, K.; Wei, M.; Halpenny, J. A comparison of inertial platform, damped 2-axis platform and strapdown airborne gravimetry. In Proceedings of the International Symposium on Kinematic Systems in Geodesy, Geomatics and Navigation, Banff, AB, Canada, 5–8 June 2001; pp. 542–550. [Google Scholar]
- Healey, D. Application of gravity data to geologic problems at Nevada Test Site. Nev. Test Site Geol. Soc. Am. Mem. 1968, 110, 147–156. [Google Scholar]
- Dal Pozzo, H.A.; Shukowsky, W.; Molina, E.C. Tietê Airborne Gravity Test Area. In Proceedings of the 10th International Congress of the Brazilian Geophysical Society, European Association of Geoscientists & Engineers, Rio de Janeiro, Brazil, 19–23 November 2007; pp. cp–172. [Google Scholar] [CrossRef]
- Peirce, J.; Sander, S.; Charters, R.; Lavoie, V. Turner Valley, Canada—A case history in contemporary airborne gravity. In SEG Technical Program Expanded Abstracts 2002; Society of Exploration Geophysicists: Houston, TX, USA, 2002; pp. 783–787. [Google Scholar] [CrossRef]
- Elieff, S.; Sander, S. AIRGrav airborne gravity survey in Timmins, Ontario. In Proceedings of the ASEG-PESA Airborne Gravity 2004 Workshop, Sydney, Australia, 15 August 2004; Volume 1519, p. 111119. [Google Scholar]
- Moritz, H. Least-squares collocation. Rev. Geophys. 1978, 16, 421–430. [Google Scholar] [CrossRef]
- Forsberg, R.; Tscherning, C.C. The use of height data in gravity field approximation by collocation. J. Geophys. Res. Solid Earth 1981, 86, 7843–7854. [Google Scholar] [CrossRef]
- Willberg, M.; Zingerle, P.; Liu, Q.; Schmidt, M.; Pail, R. The 1 cm geoid experiment with Least Squares Collocation. In Geophysical Research Abstracts; EBSCO Industries, Inc.: Birmingham, AL, USA, 2019; Volume 21. [Google Scholar]
- Klees, R.; Tenzer, R.; Prutkin, I.; Wittwer, T. A data-driven approach to local gravity field modelling using spherical radial basis functions. J. Geod. 2008, 82, 457–471. [Google Scholar] [CrossRef]
- Liu, Q.; Schmidt, M.; Sánchez, L.; Willberg, M. Regional gravity field refinement for (quasi-) geoid determination based on spherical radial basis functions in Colorado. J. Geod. 2020, 94, 99. [Google Scholar] [CrossRef]
- Mahbuby, H.; Amerian, Y.; Nikoofard, A.; Eshagh, M. Application of the nonlinear optimisation in regional gravity field modelling using spherical radial base functions. Stud. Geophys. Geod. 2021, 65, 261–290. [Google Scholar] [CrossRef]
- Sjöberg, L.E. Least Squares Modification of Stokes’ and Vening Meinesz’formulas by Accounting for Errors of Truncation, Potential Coefficients and Gravity Data; University of Uppsala, Institute of Geophysics, Department of Geodesy: Uppsala, Sweden, 1984. [Google Scholar]
- Bouman, J.; Koop, R. Calibration of GOCE SGG data combining terrestrial gravity data and global gravity field models. In Proceedings of the Gravity and Geoid 2002; 3rd Meeting of the IGGC Ziti Editions, Thessaloniki, Greece, 26–30 August 2002; pp. 275–280. [Google Scholar]
- Bouman, J.; Koop, R.; Tscherning, C.; Visser, P. Calibration of GOCE SGG data using high–low SST, terrestrial gravity data and global gravity field models. J. Geod. 2004, 78, 124–137. [Google Scholar] [CrossRef]
- Arabelos, D.; Tscherning, C.; Veicherts, M. External calibration of GOCE SGG data with terrestrial gravity data: A simulation study. In Proceedings of the Dynamic Planet: Monitoring and Understanding a Dynamic Planet with Geodetic and Oceanographic Tools IAG Symposium Cairns, Cairns, Australia, 22–26 August 2005; Springer: Berlin/Heidelberg, Germany, 2007; pp. 337–344. [Google Scholar]
- Bucha, B.; Janák, J.; Papčo, J.; Bezděk, A. High-resolution regional gravity field modelling in a mountainous area from terrestrial gravity data. Geophys. J. Int. 2016, 207, 949–966. [Google Scholar] [CrossRef]
- Kern, M.; Haagmans, R. Determination of gravity gradients from terrestrial gravity data for calibration and validation of gradiometric GOCE data. In Proceedings of the Gravity, Geoid and Space Missions; Jekeli, C., Bastos, L., Fernandes, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 95–100. [Google Scholar]
- Rexer, M.; Hirt, C.; Pail, R.; Claessens, S. Evaluation of the third-and fourth-generation GOCE Earth gravity field models with Australian terrestrial gravity data in spherical harmonics. J. Geod. 2014, 88, 319–333. [Google Scholar] [CrossRef]
- Denker, H. Computation of gravity gradients over Europe for calibration/validation of GOCE data. In Proceedings of the 3rd Meeting of the International Gravity and Geoid Commission: Gravity and Geoid, Thessaloniki, Greece, 26–30 August 2002. [Google Scholar]
- Forsberg, R. A Study of Terrain Reductions, Density Anomalies and Geophysical Inversion Methods in Gravity Field Modelling; Technical report; Ohio State Univ Columbus Dept of Geodetic Science and Surveying: Columbus, OH, USA, 1984. [Google Scholar]
- Zhu, L.; Jekeli, C. Gravity gradient modeling using gravity and DEM. J. Geod. 2009, 83, 557–567. [Google Scholar] [CrossRef]
- Hirt, C.; Claessens, S.; Fecher, T.; Kuhn, M.; Pail, R.; Rexer, M. New ultrahigh-resolution picture of Earth’s gravity field. Geophys. Res. Lett. 2013, 40, 4279–4283. [Google Scholar] [CrossRef]
- Hirt, C.; Yang, M.; Kuhn, M.; Bucha, B.; Kurzmann, A.; Pail, R. SRTM2gravity: An ultrahigh resolution global model of gravimetric terrain corrections. Geophys. Res. Lett. 2019, 46, 4618–4627. [Google Scholar] [CrossRef]
- Yang, M.; Hirt, C.; Tenzer, R.; Pail, R. Experiences with the use of mass-density maps in residual gravity forward modelling. Stud. Geophys. Geod. 2018, 62, 596–623. [Google Scholar] [CrossRef]
- Yang, M.; Hirt, C.; Pail, R. TGF: A New MATLAB-based Software for Terrain-related Gravity Field Calculations. Remote Sens. 2020, 12, 1063. [Google Scholar] [CrossRef]
- Li, Z.; Ni, S.; Zhang, B.; Bao, F.; Zhang, S.; Deng, Y.; Yuen, D.A. Shallow magma chamber under the Wudalianchi Volcanic Field unveiled by seismic imaging with dense array. Geophys. Res. Lett. 2016, 43, 4954–4961. [Google Scholar] [CrossRef]
- Oldenburg, D.W.; Li, Y. Inversion for applied geophysics: A tutorial. Near-Surf. Geophys. 2005, 89–150. [Google Scholar] [CrossRef]
- Hirt, C.; Bucha, B.; Yang, M.; Kuhn, M. A numerical study of residual terrain modelling (RTM) techniques and the harmonic correction using ultra-high-degree spectral gravity modelling. J. Geod. 2019, 93, 1469–1486. [Google Scholar] [CrossRef]
- Yang, M.; Hirt, C.; Wu, B.; Deng, X.L.; Tsoulis, D.; Feng, W.; Wang, C.Q.; Zhong, M. Residual Terrain Modelling: The Harmonic Correction for Geoid Heights. Surv. Geophys. 2022, 43, 1201–1231. [Google Scholar] [CrossRef]
- Klees, R.; Seitz, K.; Slobbe, D. The RTM harmonic correction revisited. J. Geod. 2022, 96, 39. [Google Scholar] [CrossRef]
- Klees, R.; Seitz, K.; Slobbe, C. Exact closed-form expressions for the complete RTM correction. J. Geod. 2023, 97, 33. [Google Scholar] [CrossRef]
- Nagy, D.; Papp, G.; Benedek, J. The gravitational potential and its derivatives for the prism. J. Geod. 2000, 74, 552–560. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. 3-D inversion of gravity data. Geophysics 1998, 63, 109–119. [Google Scholar] [CrossRef]
- Lawson, C.L.; Hanson, R. Linear least squares with linear inequality constraints. In Solving Least Squares Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1974; pp. 158–173. [Google Scholar]
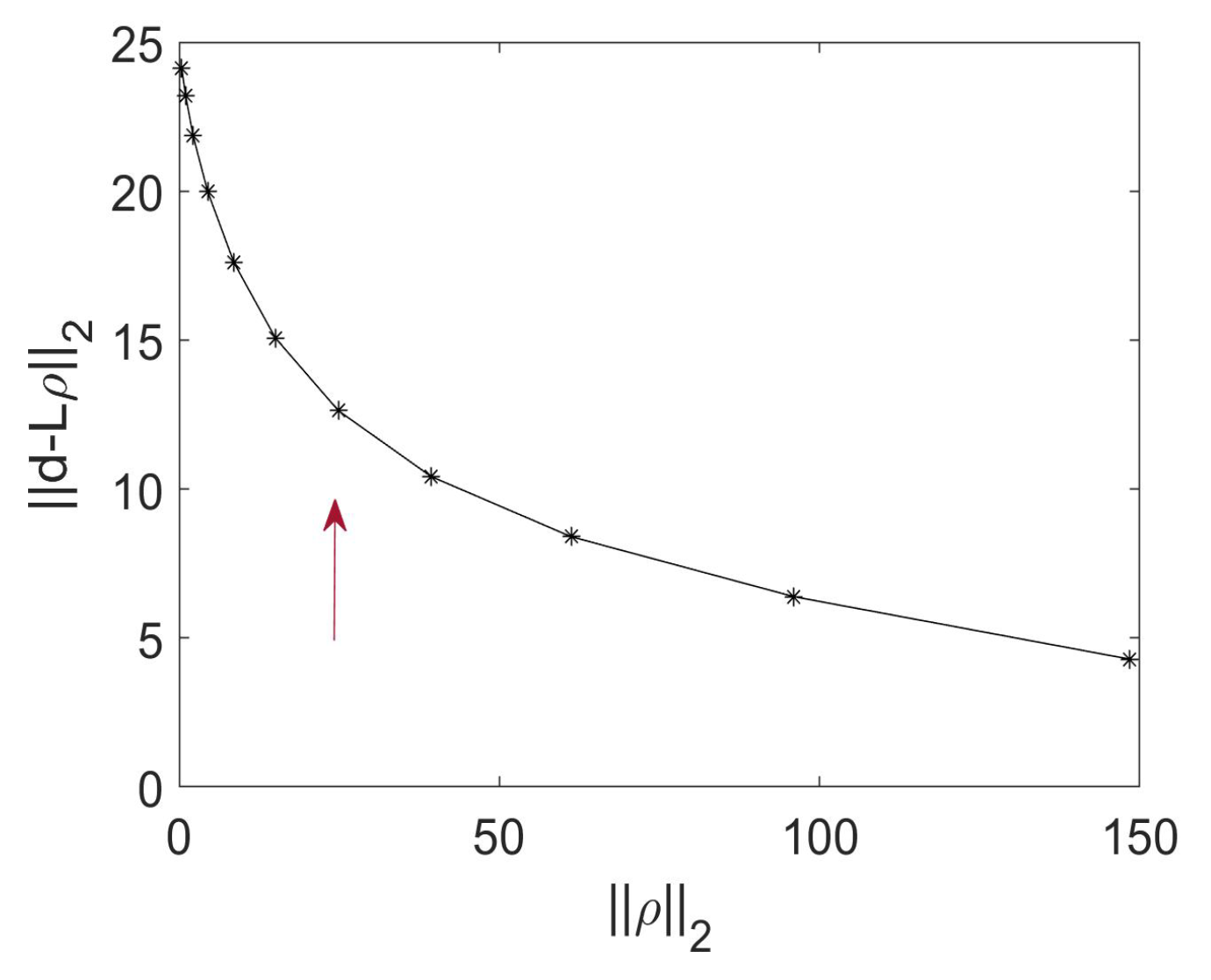
- Hansen, P.C. The L-curve and its use in the numerical treatment of inverse problems. In Computational Inverse Problems in Electrocardiology; Johnston, P., Ed.; WIT Press: Southampton, UK, 2001; pp. 119–142. [Google Scholar]
- Zhang, S.; Jia, X.; Zhang, Y.; Li, S.; Li, Z.; Tian, P.; Ming, Y.; Zhang, C. Volcanic Magma Chamber Survey and Geothermal Geological Condition Analysis for Hot Dry Rock at Weishan Volcano in Wudalianchi Region, Heilongjiang Province. Acta Geol. Sin. 2017, 91, 1506–1521. [Google Scholar]
- Bucha, B.; Janák, J. Definition of Functionals of the Geopotential Used in GrafLab Software; Scientific Technical Report; Slovak University of Technology in Bratislava: Bratislava, Slovak, 2021. [Google Scholar]
- Yamazaki, D.; Ikeshima, D.; Tawatari, R.; Yamaguchi, T.; O’Loughlin, F.; Neal, J.C.; Sampson, C.C.; Kanae, S.; Bates, P.D. A high-accuracy map of global terrain elevations. Geophys. Res. Lett. 2017, 44, 5844–5853. [Google Scholar] [CrossRef]
- Li, W.; Yang, M.; Zhong, M.; Feng, W. Methodology to calculate full tensor of airborne gravity gradient based on 3Dgravity inversion. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2022, 50, 90–95. [Google Scholar] [CrossRef]
- DiFrancesco, D.; Meyer, T.; Christensen, A.; FitzGerald, D. Gravity gradiometry–today and tomorrow. In Proceedings of the 11th SAGA Biennial Technical Meeting and Exhibition, European Association of Geoscientists & Engineers, Swaziland, South Africa, 16–18 September 2009; pp. cp–241. [Google Scholar] [CrossRef]
- Ďuríčková, Z.; Janák, J. RTM-based omission error corrections for global geopotential models: Case study in Central Europe. Stud. Geophys. Geod. 2016, 60, 622–643. [Google Scholar] [CrossRef]
- Bucha, B.; Hirt, C.; Yang, M.; Kuhn, M.; Rexer, M. Residual terrain modelling (RTM) in terms of the cap-modified spectral technique: RTM from a new perspective. J. Geod. 2019, 93, 2089–2108. [Google Scholar] [CrossRef]
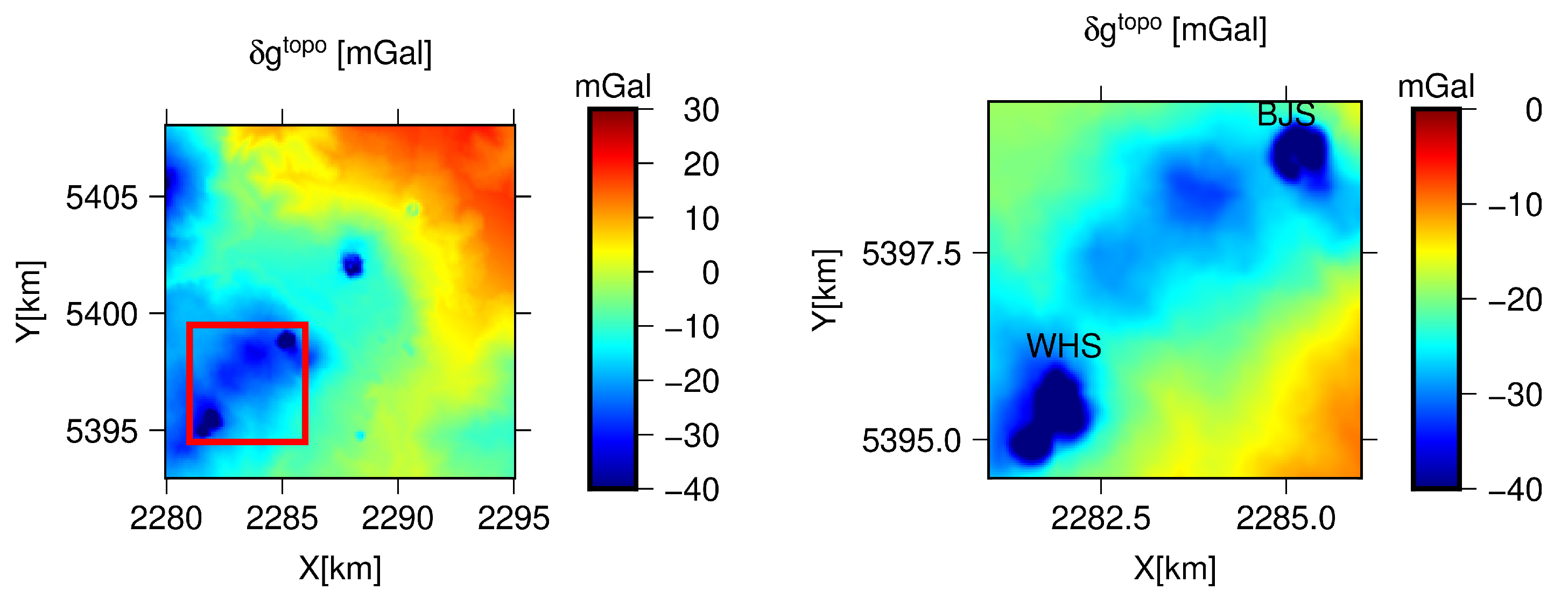
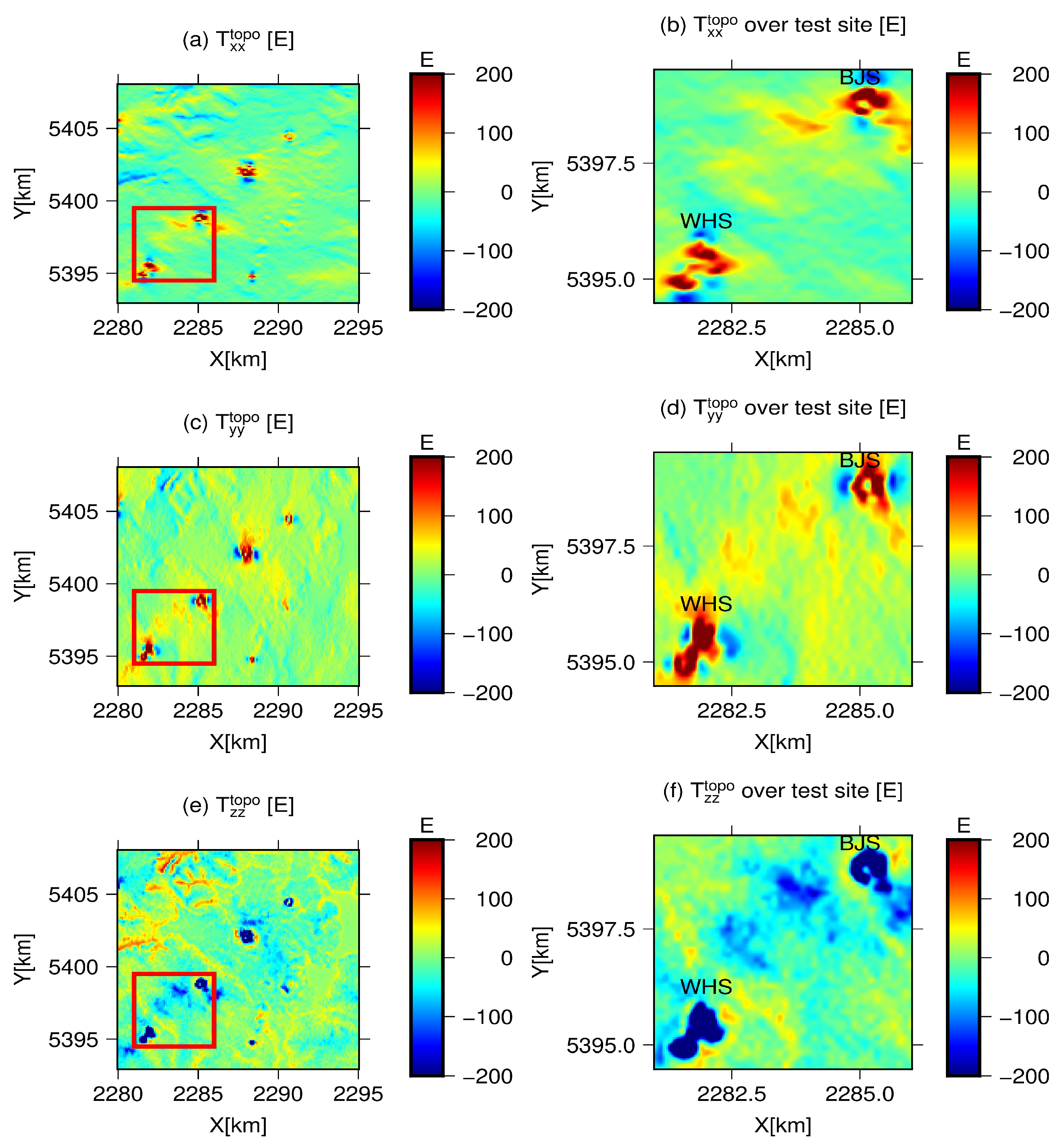
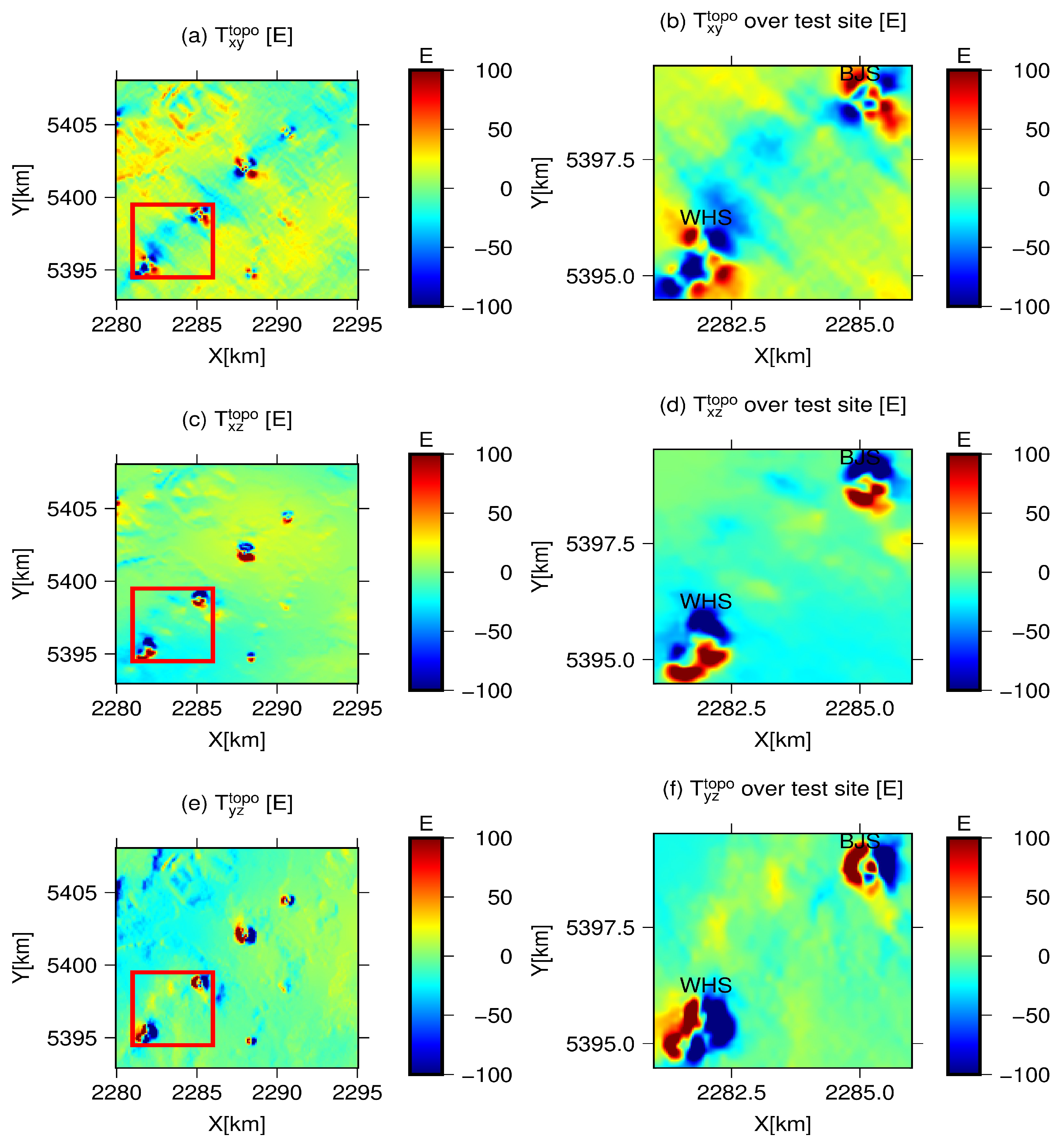

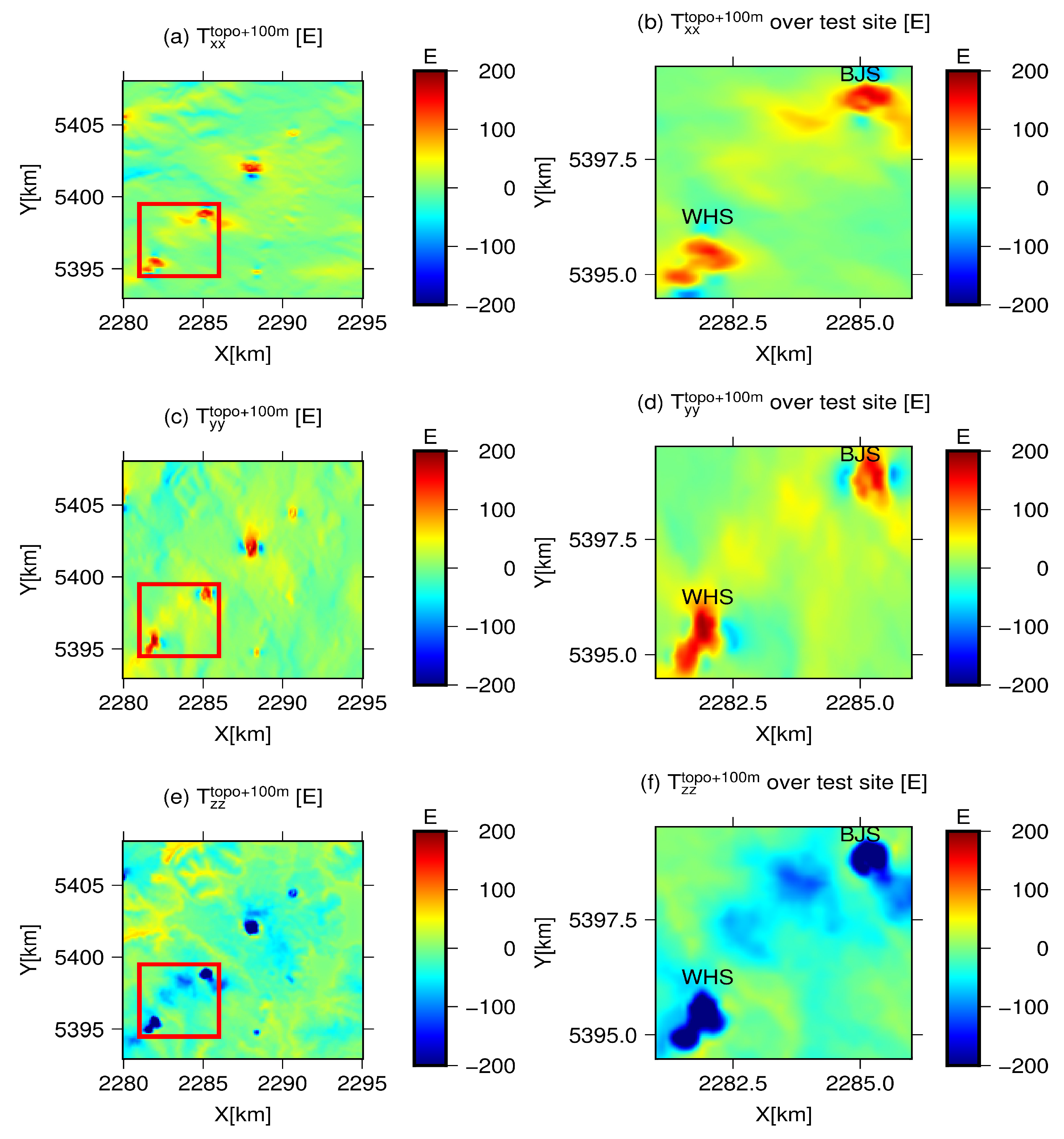
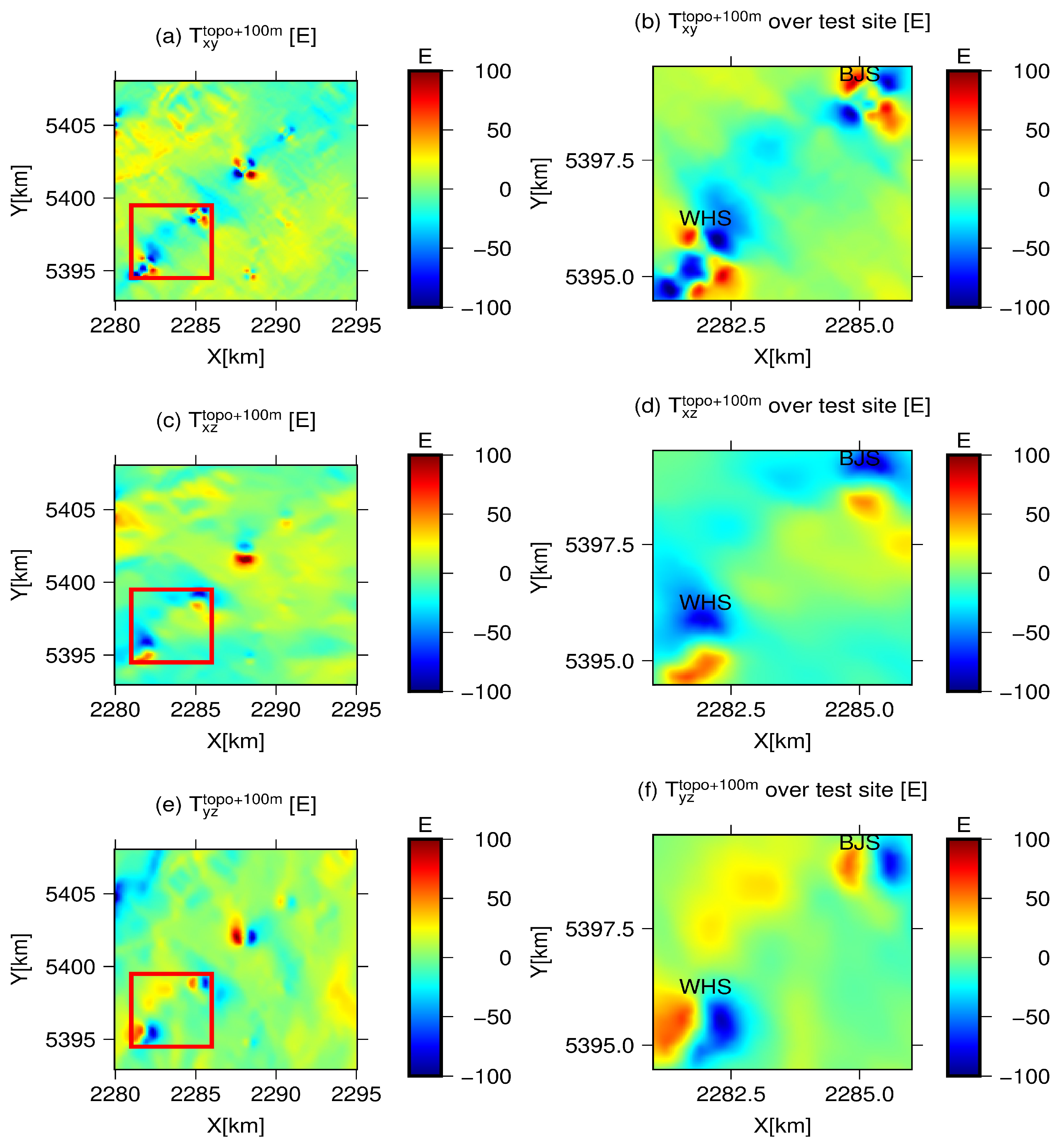
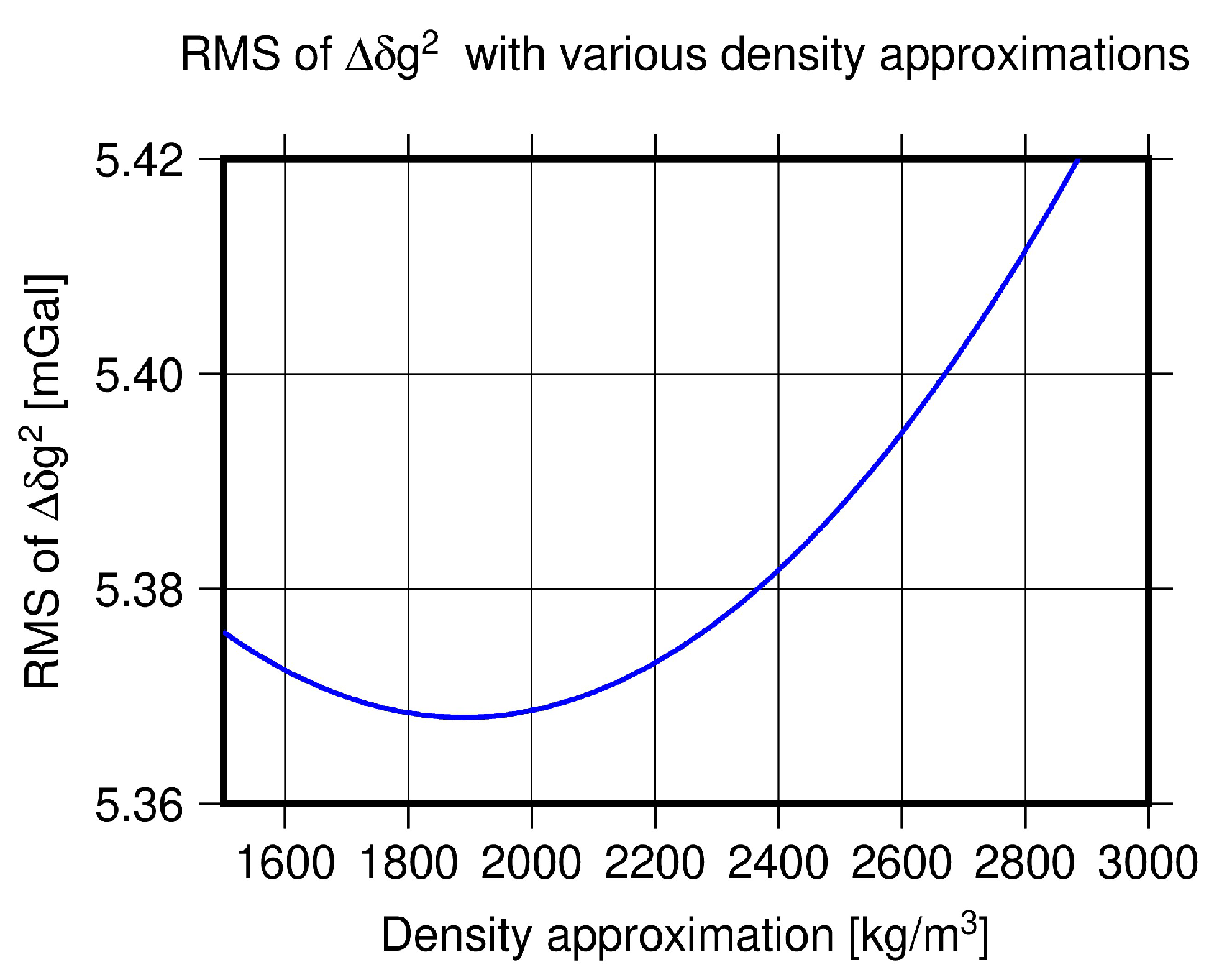
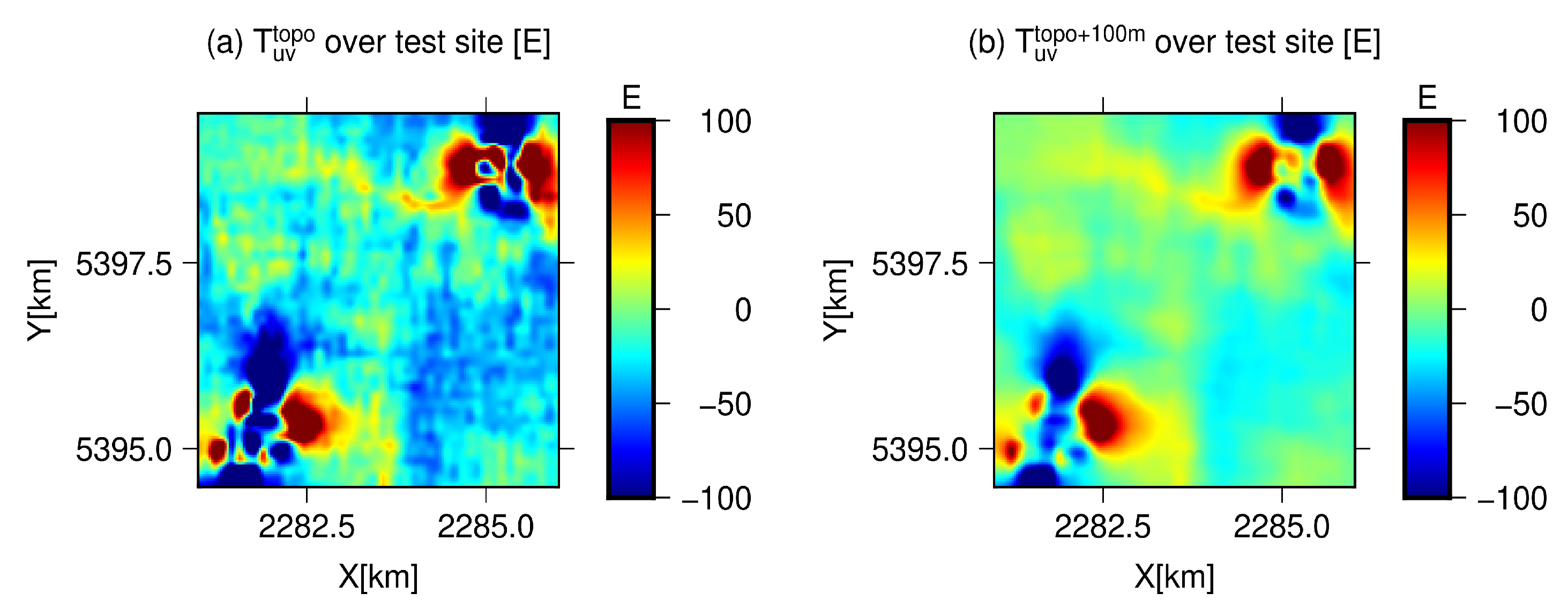
| Variants | Min | Max | Mean | STD | RMS | |
|---|---|---|---|---|---|---|
| (mGal) | −24.61 | 15.36 | −4.44 | 11.33 | 11.90 | |
| (mGal) | −7.47 | 14.07 | 1.80 | 5.14 | 5.93 | 50.17% |
| (mGal) | −5.44 | 11.76 | 1.99 | 5.10 | 5.40 | 54.62% |
| (mGal) | −4.42 | 1.63 | −0.29 | 1.13 | 1.64 | 86.22% |
| Variants | Min | Max | Mean | STD | RMS |
|---|---|---|---|---|---|
| (mGal) | −68.53 | 20.41 | −0.62 | 13.29 | 13.30 |
| (E) | −209.82 | 525.94 | −10.89 | 26.02 | 28.21 |
| (E) | −202.70 | 506.91 | 11.59 | 28.91 | 31.15 |
| (E) | −895.57 | 218.54 | −0.70 | 44.71 | 44.71 |
| (E) | −173.90 | 143.72 | 2.97 | 16.03 | 16.30 |
| (E) | −224.14 | 348.19 | −2.04 | 16.78 | 16.91 |
| (E) | −397.25 | 347.02 | −7.62 | 19.79 | 21.20 |
| Variants | Min | Max | Mean | STD | RMS |
|---|---|---|---|---|---|
| (mGal) | −63.32 | 20.08 | −0.35 | 13.26 | 13.27 |
| (E) | −133.75 | 187.27 | 0.73 | 17.70 | 17.72 |
| (E) | −122.30 | 202.74 | 6.85 | 18.88 | 20.09 |
| (E) | −364.66 | 89.53 | −7.58 | 29.45 | 30.42 |
| (E) | −137.08 | 115.04 | 0.21 | 13.14 | 13.14 |
| (E) | −215.18 | 314.53 | −0.52 | 20.91 | 20.91 |
| (E) | −292.92 | 254.83 | 2.07 | 21.51 | 21.61 |
| Variants | Min of | Max of | Mean of | RMS of | RMS of | RMS of | RMS of |
|---|---|---|---|---|---|---|---|
| g | g | g | g | ||||
| (mGal) | −56.52 | −9.82 | −22.67 | 23.71 | 17.98 | 5.04 | 10.91 |
| (E) | −150.23 | 389.12 | 1.93 | 40.97 | 6.75 | 40.49 | 10.52 |
| (E) | −166.49 | 467.23 | 23.56 | 50.92 | 4.41 | 47.46 | 12.07 |
| (E) | −839.521 | 95.35 | −25.49 | 75.36 | 11.01 | 71.29 | 22.49 |
| (E) | −136.38 | 120.10 | 1.61 | 26.91 | 1.47 | 26.524 | 1.90 |
| (E) | −224.14 | 222.27 | −10.42 | 32.50 | 6.14 | 30.97 | 7.21 |
| (E) | −338.91 | 276.69 | −8.75 | 39.08 | 7.18 | 38.88 | 7.24 |
| (E) | −390.99 | 293.28 | −21.62 | 53.50 | 2.99 | 51.99 | 2.53 |
| Variants | Min of | Max of | Mean of | RMS of | RMS of | RMS of | RMS of |
|---|---|---|---|---|---|---|---|
| g | g | g | g | ||||
| (mGal) | −52.04 | −9.00 | −22.41 | 23.36 | 17.89 | 4.54 | 10.69 |
| (E) | −101.66 | 161.60 | 12.68 | 30.07 | 6.64 | 28.26 | 10.18 |
| (E) | −100.84 | 186.48 | 18.33 | 34.08 | 4.26 | 30.18 | 11.76 |
| (E) | −330.88 | 41.35 | −31.01 | 55.14 | 10.76 | 48.49 | 21.86 |
| (E) | −112.38 | 91.45 | −0.88 | 21.25 | 1.40 | 20.65 | 1.76 |
| (E) | −215.18 | 187.33 | −11.76 | 34.90 | 6.00 | 35.39 | 6.88 |
| (E) | −236.20 | 190.93 | 2.72 | 34.37 | 7.13 | 35.77 | 7.05 |
| (E) | −199.91 | 183.29 | −5.65 | 33.04 | 2.98 | 32.69 | 2.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Li, W.-K.; Feng, W.; Pail, R.; Wu, Y.-G.; Zhong, M. Integration of Residual Terrain Modelling and the Equivalent Source Layer Method in Gravity Field Synthesis for Airborne Gravity Gradiometer Test Site Determination. Remote Sens. 2023, 15, 5190. https://doi.org/10.3390/rs15215190
Yang M, Li W-K, Feng W, Pail R, Wu Y-G, Zhong M. Integration of Residual Terrain Modelling and the Equivalent Source Layer Method in Gravity Field Synthesis for Airborne Gravity Gradiometer Test Site Determination. Remote Sensing. 2023; 15(21):5190. https://doi.org/10.3390/rs15215190
Chicago/Turabian StyleYang, Meng, Wei-Kai Li, Wei Feng, Roland Pail, Yan-Gang Wu, and Min Zhong. 2023. "Integration of Residual Terrain Modelling and the Equivalent Source Layer Method in Gravity Field Synthesis for Airborne Gravity Gradiometer Test Site Determination" Remote Sensing 15, no. 21: 5190. https://doi.org/10.3390/rs15215190
APA StyleYang, M., Li, W.-K., Feng, W., Pail, R., Wu, Y.-G., & Zhong, M. (2023). Integration of Residual Terrain Modelling and the Equivalent Source Layer Method in Gravity Field Synthesis for Airborne Gravity Gradiometer Test Site Determination. Remote Sensing, 15(21), 5190. https://doi.org/10.3390/rs15215190








