The Wave Period Parameterization of Ocean Waves and Its Application to Ocean Wave Simulations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Introduction
2.2. SWAN Model Introduction
2.2.1. Ocean Wave Energy Spectrum Equation
2.2.2. Original Function Term Introduction
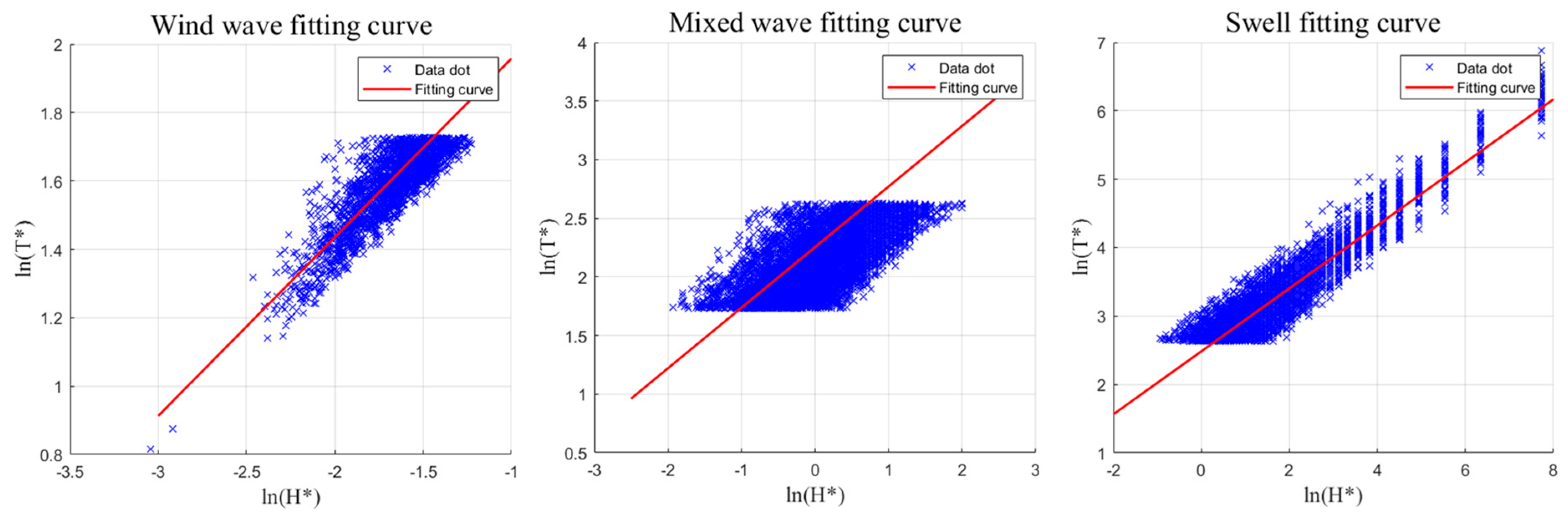
2.3. Statistical Analysis Test
3. Results
3.1. Validation between Wind Data and SWAN Wave Field Results
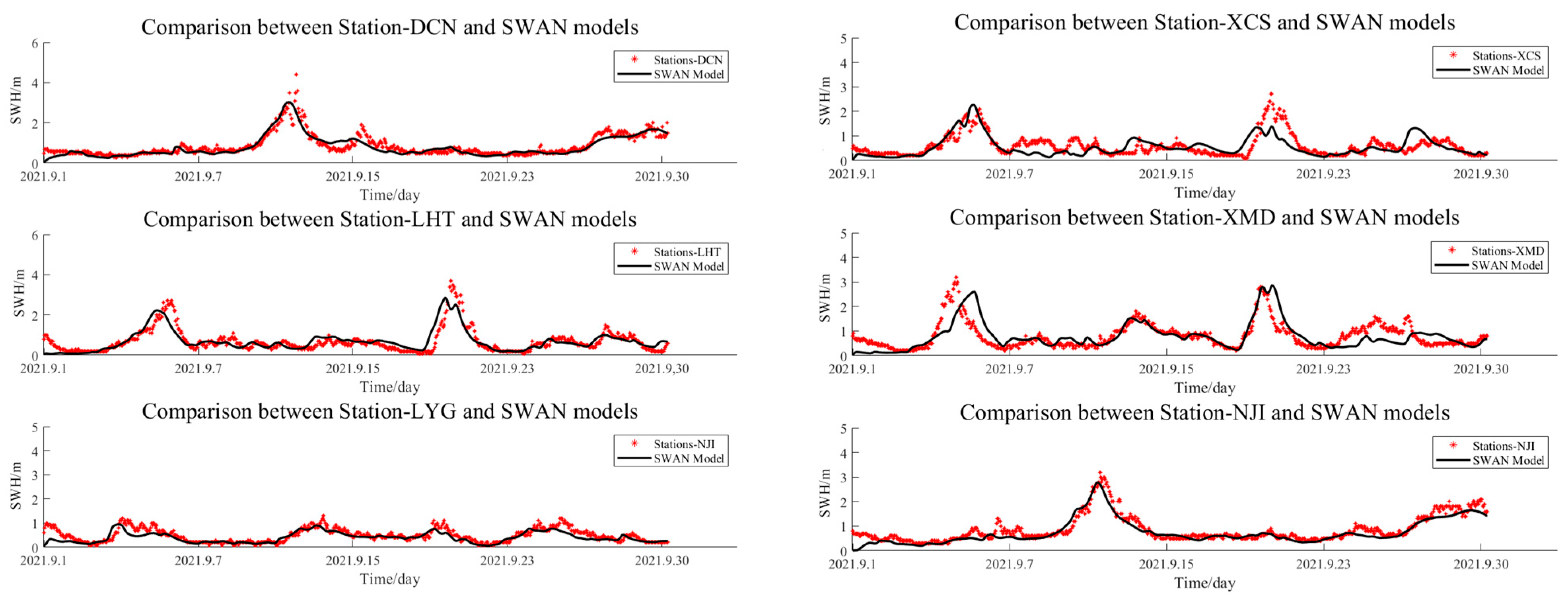
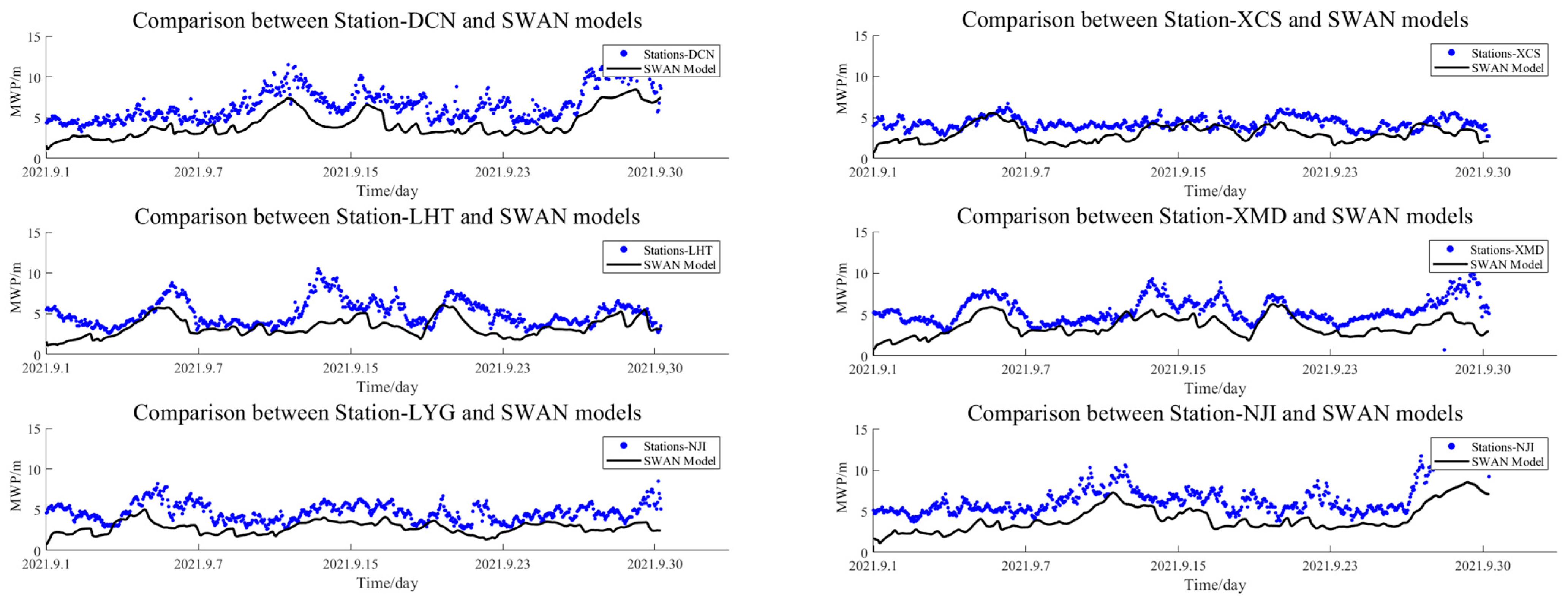
3.2. Validation with NMDC Station Observation Data
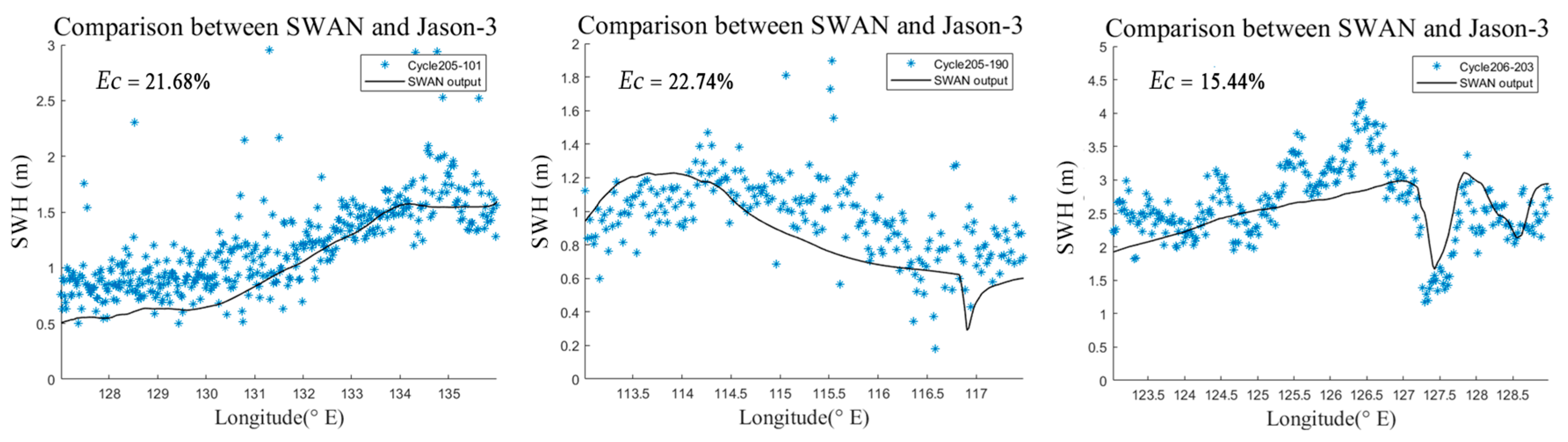
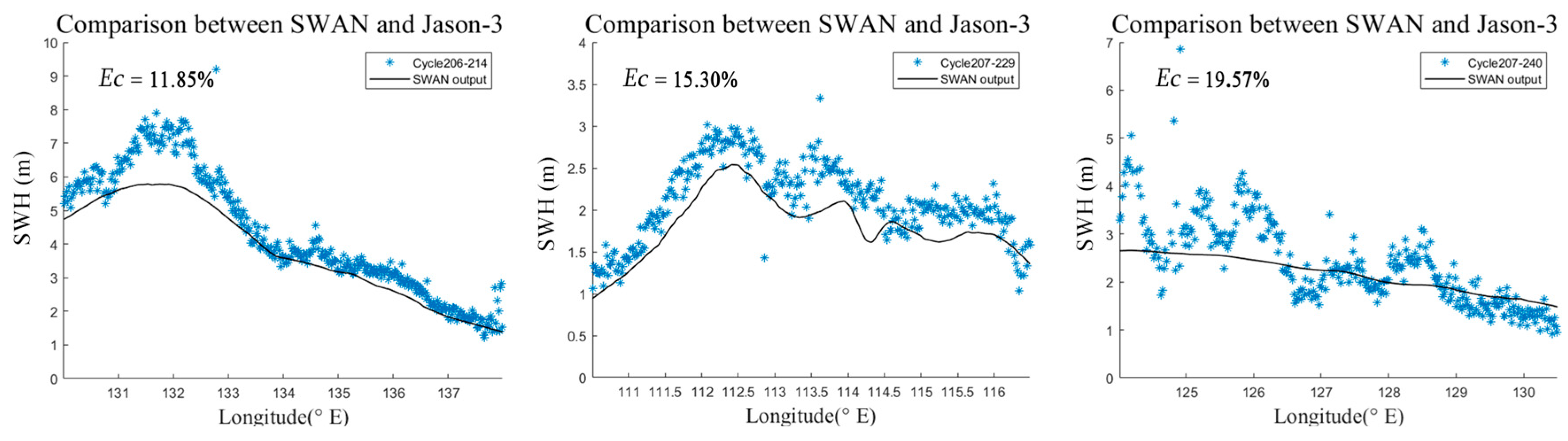
3.3. Validation with NCEI Satellite Data
4. Discussion
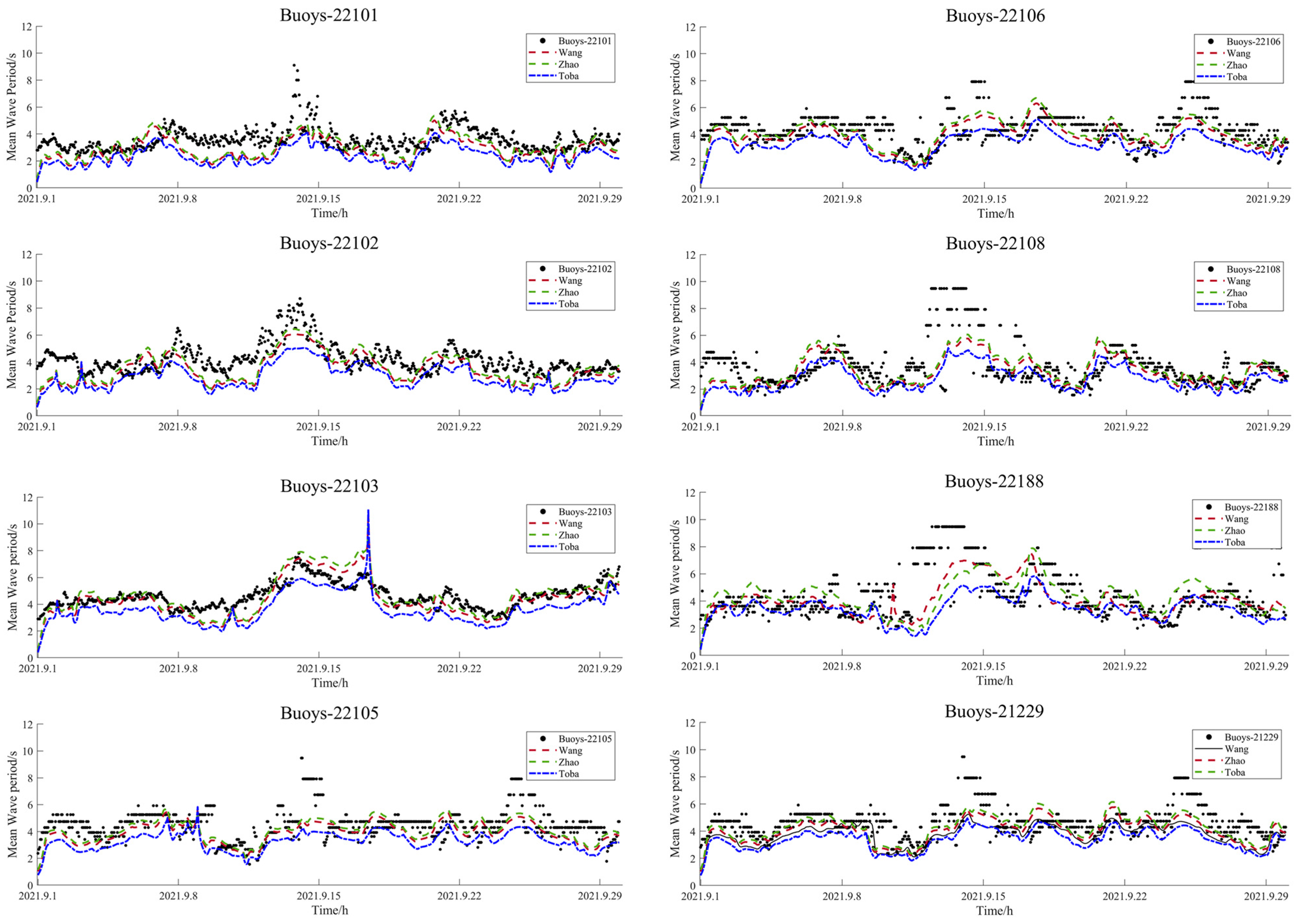
4.1. Previous Parametric Scheme Results
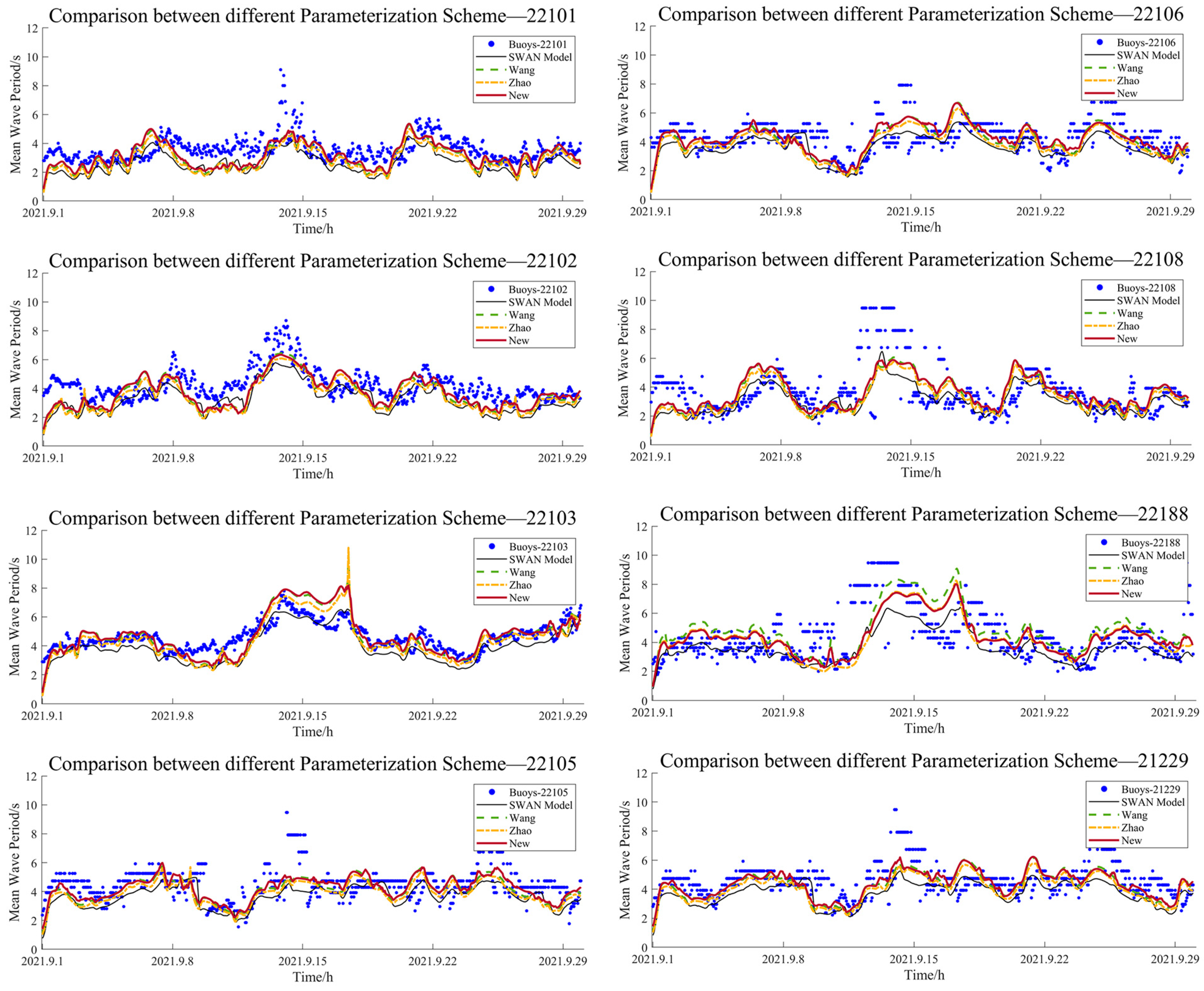
4.2. Parameter Application and Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tan, K.; Xie, L.; Bai, P.; Zheng, Q.; Li, J.; Xu, Y.; Li, M. Modulation Effects of Mesoscale Eddies on Sea Surface Wave Fields in the South China Sea Derived from a Wave Spectrometer Onboard the China-France Ocean Satellite. J. Geophys. Res. Ocean. 2023, 128, e2021JC018088. [Google Scholar] [CrossRef]
- Rasool, S.; Muttaqi, K.M.; Sutanto, D.; Iqbal, S. Modeling Ocean waves and investigation of oceanic wave spectra for wave to-wire system. J. Eng. Res. 2022, 10, 1–17. [Google Scholar] [CrossRef]
- Chang, Z.M.; Han, F.X.; Sun, Z.Q.; Gao, Z.H.; Wang, L.L. Three-dimensional dynamic sea surface modeling based on ocean wave spectrum. J. Oceanogr. 2021, 40, 11. [Google Scholar] [CrossRef]
- Shao, W.Z.; Yu, W.P.; Jiang, X.W.; Shi, J.; Wei, Y.L.; Ji, Q.Y. Analysis of Wave Distributions Using the WAVEWATCH-III Model in the Arctic Ocean. J. Ocean Univ. China 2022, 21, 15–27. [Google Scholar] [CrossRef]
- Polnikov, V.G.; Pogarskii, F.A. Features of the atmospheric boundary layer block for three versions of the WAM wind wave model. Izv. Atmos. Ocean. Phys. 2016, 52, 659–666. [Google Scholar] [CrossRef]
- Bjrkqvist, J.V.; Vh-Piikki, O.; Alari, V.; Kuznetsova, A.; Tuomi, L. WAM, SWAN and WAVEWATCH III in the Finnish archipelago—The effect of spectral performance on bulk wave parameters. J. Oper. Oceanogr. 2020, 13, 55–70. [Google Scholar] [CrossRef]
- Liu, C.X.; Zhao, Z.K.; Bi, X.Y.; Yuan, J.N.; Wen, G.H.; Huang, H.J. Development and application of ocean circulation and wave model. J. Adv. Meteorol. Sci. Technol. 2017, 7, 12–22. [Google Scholar]
- Umesh, P.A.; Swain, J.; Balchand, A.N. Inter-comparison of WAM and WAVEWATCH-III in the North Indian Ocean using ERA-40 and Quik-SCAT/NCEP blended winds. J. Ocean Eng. 2018, 164, 298–321. [Google Scholar] [CrossRef]
- Miyamoto, Y.; Fudeyasu, H.; Wada, A. Intensity and Structural Changes of Numerically Simulated Typhoon Faxai (1915) before Landfall. J. Meteorol. Soc. Jpn. 2022, 100, 181–196. [Google Scholar] [CrossRef]
- Zhang, M.; Zhou, C.; Zhang, J.; Zhang, X.; Tang, Z. Numerical Simulation and Analysis of Storm Surges Under Different Extreme Weather Event and Typhoon Experiments in the South Yellow Sea. J. Ocean Univ. China 2022, 21, 1–14. [Google Scholar] [CrossRef]
- Yu, J.M.; Ji, Q.Y.; Zheng, H.; Yang, L.Y.; Wang, R.Q.; Chen, C.J. Evaluation of wave energy resources in Zhoushan sea area based on SWAN model. J. Ocean. Forecast 2020, 37, 38–49. [Google Scholar]
- Fan, L.L. Long-Term Evaluation of Wave Energy Resources in the South China Sea Based on WAVEWATCH-III Model; Tianjin University: Tianjin, China, 2019. [Google Scholar]
- Jiang, L.F.; Zhang, Z.X.; Qi, Y.Q.; Chen, R. Comparative Analysis of Wave Simulation Results of WAVEWATCH-III and SWAN Models in the Northern South China Sea. J. Trop. Oceanogr. 2011, 30, 27–37. [Google Scholar]
- Atan, R.; Nash, S.; Goggins, J. Development of a nested local scale wave model for a 1/4 scale wave energy test site using SWAN. J. Oper. Oceanogr. 2017, 10, 59–78. [Google Scholar] [CrossRef]
- Umesh, P.A.; Behera Manasa, R. On the improvements in nearshore wave height predictions using nested SWAN-SWASH modelling in the eastern coastal waters of India. J. Ocean Eng. 2021, 236, 109550. [Google Scholar] [CrossRef]
- Trossman, D.S.; Arbic, B.K.; Garner, S.T.; Goff, J.A.; Jayne, S.R.; Metzger, E.J.; Wallcraft, A.J. Impact of parameterized lee wave drag on the energy budget of an eddying global ocean model. J. Ocean Model. 2013, 72, 119–142. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.G.; Ling, T.J.; Zuo, J.Q. Introduction of vertical hybrid parameterization scheme in ocean model. J. Ocean Predict. 2014, 5, 93–104. [Google Scholar]
- Li, X.; Wu, H.D.; Wang, H. Study on the influence of sea surface state parameterization on numerical simulation of marine atmospheric boundary layer. J. Mar. Sci. Bull. 2011, 30, 8. [Google Scholar]
- Wang, H.L. Study on Wave-Induced Mixing and Parameterization of Ocean upper Boundary Layer; Nanjing University of Information Science and Technology: Nanjing, China, 2020. [Google Scholar]
- Taylor Peter, K.; Yelland Margaret, J. The Dependence of Sea Surface Roughness on the Height and Steepness of the Waves. J. Phys. Oceanogr. 2001, 31, 572. [Google Scholar] [CrossRef]
- Wang, C.; Fei, J.; Ding, J.; Hu, R.; Huang, X.; Cheng, X. Development of a new significant wave height and dominant wave period parameterization scheme. J. Ocean Eng. 2017, 135, 170–182. [Google Scholar] [CrossRef]
- Andreas Edgar, L.; Wang, S. Predicting significant wave height off the northeast coast of the United States. J. Ocean Eng. 2007, 34, 1328–1335. [Google Scholar] [CrossRef]
- Sun, D.F.; Song, J.Q.; Li, X.Y.; Ren, K.J.; Leng, H.Z. A Novel Sea Surface Roughness Parameterization Based on Wave State and Sea Foam. J. Mar. Sci. Eng. 2021, 9, 246. [Google Scholar] [CrossRef]
- Li, W.B.; Li, X.; Li, Q.J.; Chen, M.; Wang, L.P. Application of a new parameterization scheme of drag coefficient in numerical simulation of sea waves during hurricanes Katrina and Rita. J. Ocean Forecast 2022, 39, 8–16. [Google Scholar]
- Bourassa Mark, A.; Vincent Dayton, G.; Wood William, L. A Sea State Parameterization with Nonarbitrary Wave Age Applicable to Low and Moderate Wind Speeds. J. Phys. Oceanogr. 2001, 31, 2840. [Google Scholar] [CrossRef]
- Wu, J. Wind-Stress Coefficients Over Sea Surface from Breeze to Hurricane. J. Geophys. Res. Part C Ocean. 1982, 87, 9704–9706. [Google Scholar] [CrossRef]
- Powell, M.D.; Vickery, P.J.; Reinhold, T.A. Reinhold. Reduced drag coefficient for high wind speeds in tropical cyclones. J. Nat. 2003, V422, 279–283. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Weisberg, R.H.; Zheng, L.; Zijlema, M. Gulf of Mexico hurricane wave simulations using SWAN: Bulk formula-based drag coefficient sensitivity for Hurricane Ike. J. Geophys. Res. Ocean. 2013, 118, 3916–3938. [Google Scholar] [CrossRef]
- Li, J.K.; Zhou, L.M.; Li, S.Q. Inversion of wave period in the North Pacific Ocean from TOPEX altimeter data. J. Mar. Sci. Bull. 2012, 3, 268–277. [Google Scholar]
- Gommenginger, C.P.; Srokosz, M.A.; Challenor, P.G. Development and validation of altimeter wind speed algorithms using an extended collocated buoy/Topex dataset. J. Geosci. Remote Sens. 2002, 40, 251–260. [Google Scholar] [CrossRef]
- Mackay, E.B.L.; Retzler, C.H.; Challenor, P.G.; Gommenginger, C.P. A parametric model for ocean wave period from Ku band altimeter data. J. Geophys. Res. Ocean. 2008, 113, C03029. [Google Scholar] [CrossRef]
- Lv, J.L.; Shi, J.; Zhang, W.J.; Xia, J.M.; Wang, Q.H. Numerical simulations on waves in the Northwest Pacific Ocean based on SWAN models. J. Phys. Conf. Ser. 2023, 2486, 12034. [Google Scholar] [CrossRef]
- Wang, M.J.; Shi, J.; Li, R.J.; Dai, L.; Xiao, Q.L. Parameterization scheme of mean wave period and application in SWAN model. J. Trans. Oceanol. Limnol. 2017, 1, 23–28. [Google Scholar]
- Jia, N.; Zhao, D.L. Influence of swell on wind wave energy in ocean. J. Ocean Univ. China (Nat. Sci. Ed.) 2019, 49, 1–6. [Google Scholar]
- Zhao, D.L. Preliminary study on wave characteristics under natural sea conditions. J. Qingdao Ocean Univ. 2002, 6, 853–858. [Google Scholar]
- Wang, H.L.; Wang, C.Z. What caused the increase of tropical cyclones in the western North Pacific during the period of 2011–2020? J. Clim. Dyn. 2023, 60, 165–177. [Google Scholar] [CrossRef]
- Ying, M.; Zhang, W.; Yu, H.; Lu, X.Q.; Feng, J.X.; Fan, Y.X.; Zhu, Y.T.; Chen, D.Q. An Overview of the China Meteorological Administration Tropical Cyclone Database. J. Atmos. Ocean. Technol. 2014, 31, 287–301. [Google Scholar] [CrossRef]
- Lu, X.Q.; Yu, H.; Ying, M.; Zhao, B.K.; Zhang, S.; Lin, L.M.; Bai, L.N.; Wan, R.J. Western North Pacific Tropical Cyclone Database Created by the China Meteorological Administration. J. Prog. Atmos. Sci. (Engl. Version) 2021, 38, 690–699. [Google Scholar] [CrossRef]
- Yoshizawa, T. Fast Fourier Transform and its Applications. J. Soc. Instrum. Control Eng. 1969, 8, 851–860. [Google Scholar]
- SWAN Group. SWAN User Manual-SWAN Cycle III Version 40.91, Chap. 4; Delft University of Technology: Delft, The Netherlands, 2012. [Google Scholar]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, A.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of wind-wave growth and decay during the Joint North Sea Wave Project (JONSWAP). Dtsch. Hydrogr. Z 1973, A8, 1–95. [Google Scholar]
- Toba, Y. Local balance in the air-sea boundary processes. J. Oceanogr. 1972, 28, 109–120. [Google Scholar] [CrossRef]
- Glazman, R.E.; Greysukh, A. Satellite altimeter measurements of surface wind. J. Geophys. Res. 1993, 98, 2475–2483. [Google Scholar] [CrossRef]
- Wang, X.F. Wave Period Retrieval Based on Satellite Altimeter Data. Master’s Degree, Ocean University of China, Qingdao, China, 2006. [Google Scholar]
- Toba, T.; Adachi, S. Hydrolysis of Lactose by Microbial β-Galactosidases. Formation of Oligosaccharides with Special Reference to 2-0-β-D-galactopyranosyl-D-glucose. J. Dairy Sci. 1978, 61, 33–38. [Google Scholar] [CrossRef]
- Weisberg Robert, H.; Zheng, L.Y. Hurricane storm surge simulations comparing three-dimensional with two-dimensional formulations based on an Ivan-like storm over the Tampa Bay, Florida region. J. Geophys. Res. Ocean. 2008, 113, C12001. [Google Scholar] [CrossRef]
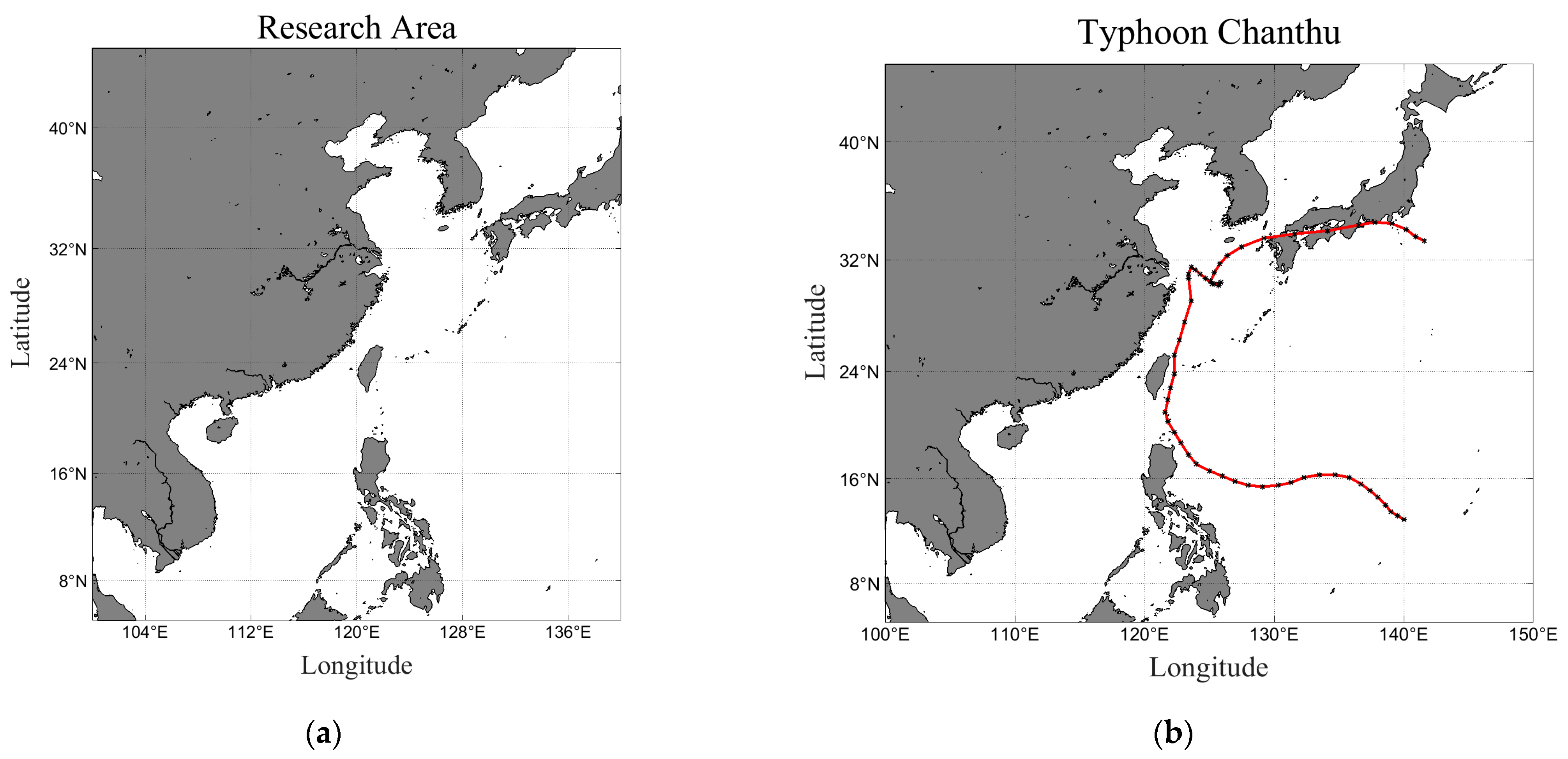
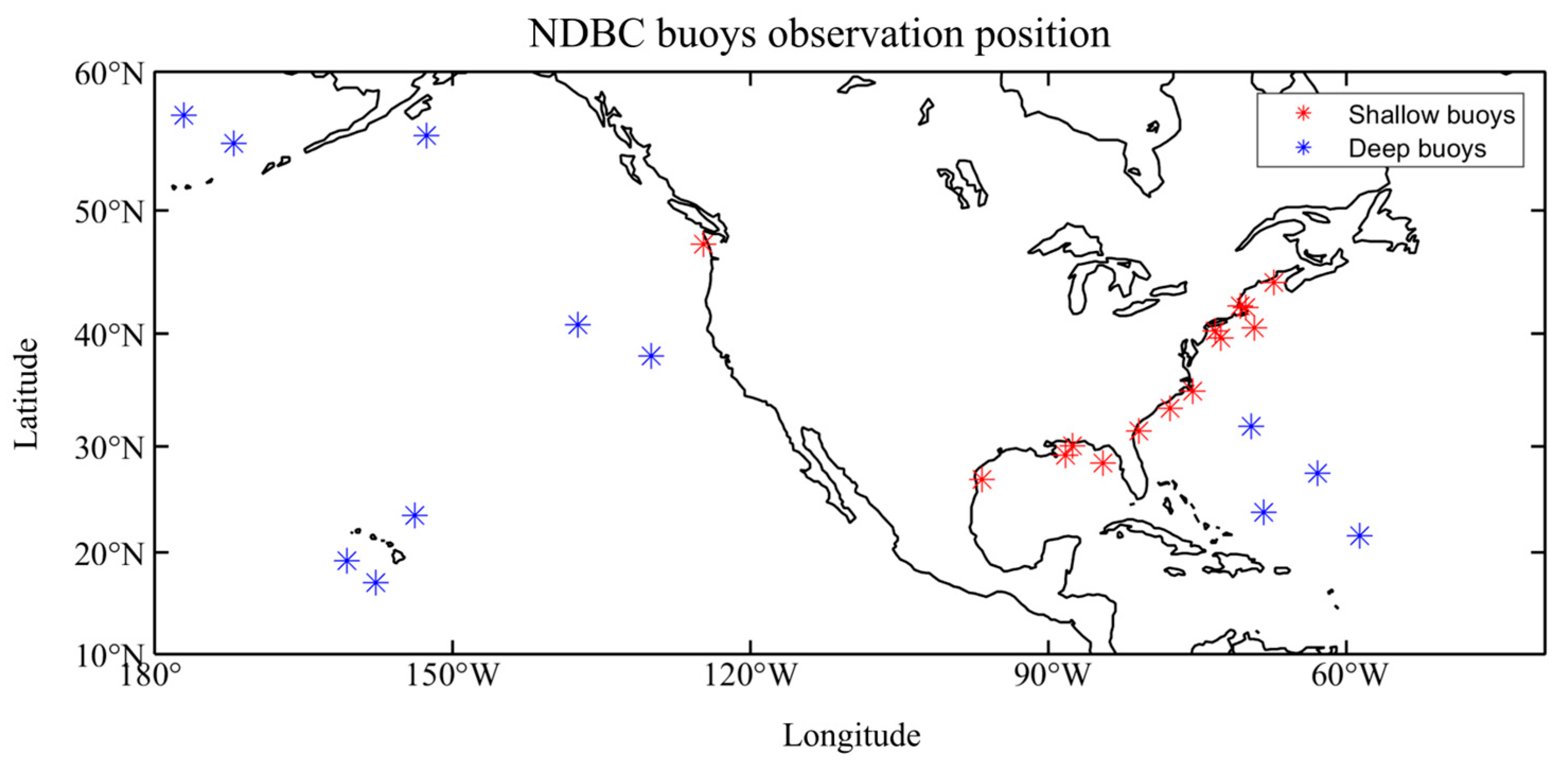
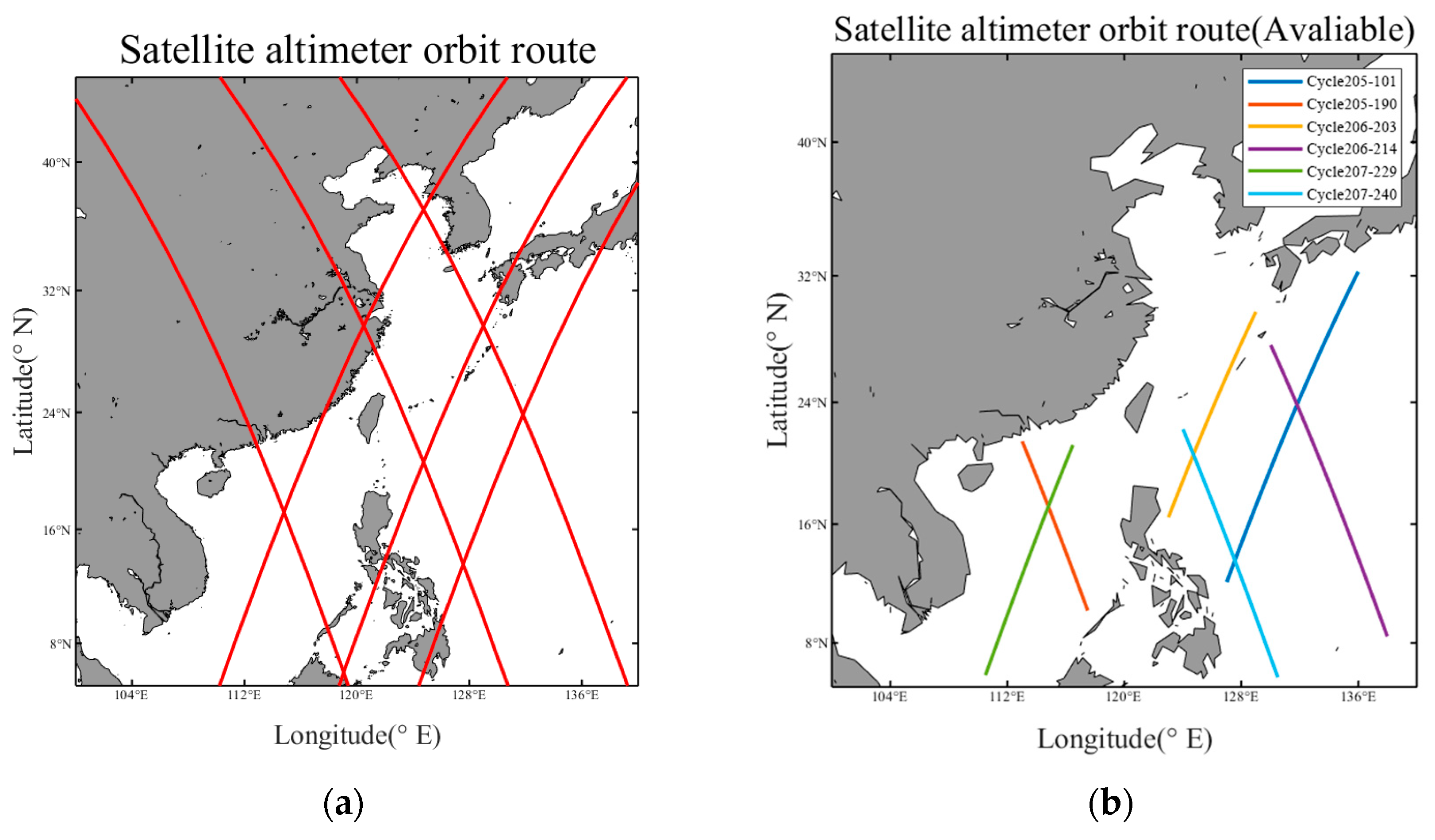
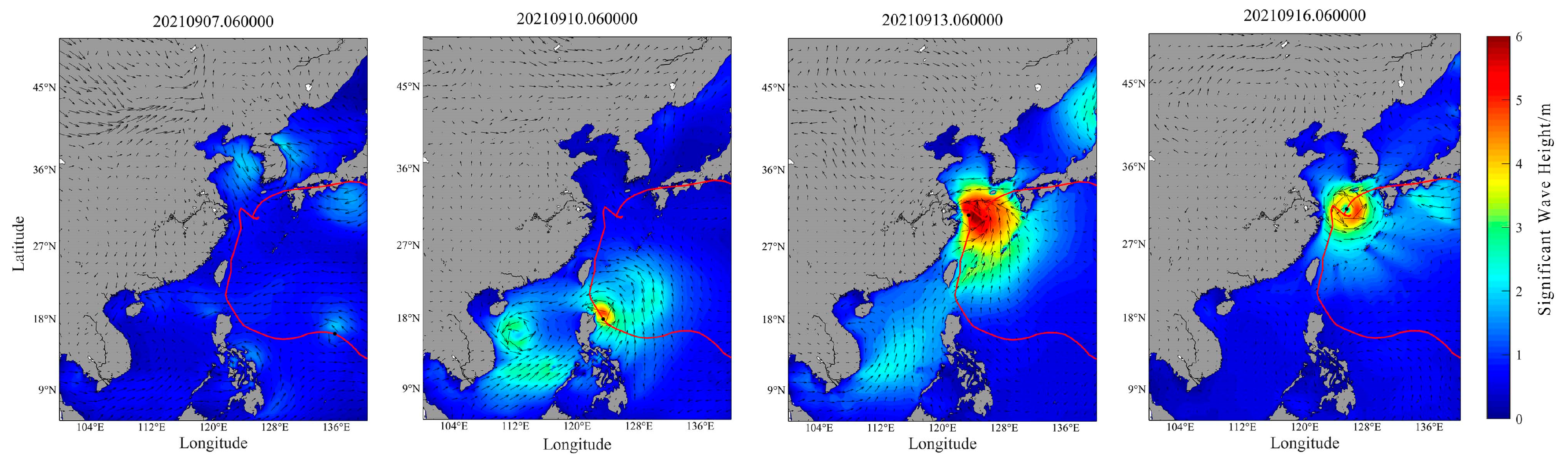

| Time | Level | Latitude | Longitude | Centre Pressure (hPa) | Max Wind Speed (m/s) |
|---|---|---|---|---|---|
| 09.06 6:00 | 8 | 14.0 | 138.6 | 1002 | 15 |
| 09.07 6:00 | 10 | 16.1 | 135.8 | 970 | 35 |
| 09.08 6:00 | 15 | 15.7 | 131.3 | 915 | 62 |
| 09.09 6:00 | 18 | 15.8 | 127.0 | 920 | 58 |
| 09.10 6:00 | 16 | 17.8 | 123.4 | 910 | 68 |
| 09.11 6:00 | 18 | 21.0 | 121.6 | 930 | 58 |
| 09.12 6:00 | 16 | 25.2 | 122.3 | 935 | 50 |
| 09.13 6:00 | 15 | 30.7 | 123.4 | 955 | 42 |
| 09.14 6:00 | 12 | 31.0 | 124.3 | 970 | 28 |
| 09.15 6:00 | 10 | 30.4 | 125.9 | 982 | 28 |
| 09.16 6:00 | 11 | 31.1 | 125.4 | 990 | 28 |
| 09.17 6:00 | 10 | 33.5 | 129.2 | 995 | 23 |
| 09.18 6:00 | 8 | 34.6 | 137.8 | 1002 | 15 |
| 09.19 6:00 | 8 | 33.3 | 141.6 | 1008 | 13 |
| Name | Longitude | Latitude | Area | Name | Longitude | Latitude | Area |
|---|---|---|---|---|---|---|---|
| 41008 | 80.87°W | 31.40°N | Shallow | 46041 | 124.74°W | 47.35°N | Shallow |
| 41013 | 77.76°W | 33.44°N | Shallow | 41044 | 58.63°W | 21.58°N | Deep |
| 41025 | 75.45°W | 35.01°N | Shallow | 41046 | 68.34°W | 23.82°N | Deep |
| 42012 | 87.55°W | 30.06°N | Shallow | 41048 | 69.57°W | 31.83°N | Deep |
| 42020 | 96.69°W | 26.97°N | Shallow | 41049 | 62.94°W | 27.49°N | Deep |
| 42036 | 84.51°W | 28.50°N | Shallow | 46006 | 137.38°W | 40.76°N | Deep |
| 42040 | 88.24°W | 29.21°N | Shallow | 46035 | 177.03°W | 57.02°N | Deep |
| 44008 | 69.25°W | 40.50°N | Shallow | 46059 | 129.97°W | 38.05°N | Deep |
| 44013 | 70.65°W | 42.35°N | Shallow | 46073 | 172.01°W | 55.01°N | Deep |
| 44018 | 70.15°W | 42.20°N | Shallow | 46078 | 152.64°W | 55.58°N | Deep |
| 44025 | 73.16°W | 40.25°N | Shallow | 51000 | 153.79°W | 23.53°N | Deep |
| 44027 | 67.30°W | 44.28°N | Shallow | 51002 | 157.75°W | 17.04°N | Deep |
| 44066 | 72.64°W | 39.62°N | Shallow | 51003 | 160.64°W | 19.20°N | Deep |
| Name | Longitude | Latitude | Element | Time |
|---|---|---|---|---|
| 22101 | 126.01°E | 37.24°N | wind speed, and | 2021.09 |
| 22102 | 125.77°E | 34.79°N | wind speed, and | 2021.09 |
| 22103 | 127.50°E | 34.00°N | wind speed, and | 2021.09 |
| 22105 | 129.95°E | 37.48°N | wind speed, and | 2021.09 |
| 22106 | 129.78°E | 36.25°N | wind speed, and | 2021.09 |
| 22108 | 125.75°E | 36.25°N | wind speed, and | 2021.09 |
| 22188 | 128.23°E | 34.39°N | wind speed, and | 2021.09 |
| 21229 | 131.11°E | 37.46°N | wind speed, and | 2021.09 |
| Station | ||||||||
|---|---|---|---|---|---|---|---|---|
| DCN | 0.170 | 2.416 | 0.203 | 0.369 | 0.241 | 2.631 | 0.905 | 0.652 |
| LHT | 0.229 | 1.734 | 0.445 | 0.324 | 0.339 | 2.156 | 0.820 | 0.521 |
| LYG | 0.136 | 1.879 | 0.290 | 0.384 | 0.192 | 2.145 | 0.773 | 0.380 |
| XCS | 0.254 | 1.332 | 0.495 | 0.311 | 0.356 | 1.554 | 0.655 | 0.434 |
| XMD | 0.302 | 1.947 | 0.410 | 0.354 | 0.439 | 2.249 | 0.693 | 0.627 |
| NJI | 0.163 | 2.551 | 0.198 | 0.388 | 0.225 | 2.787 | 0.930 | 0.650 |
| Parameter | α | β | SE (α) | SE (β) |
|---|---|---|---|---|
| Swell | 12.982 | 0.5170 | 0.0035 | 0.0064 |
| Mixed wave | 13.611 | 0.5227 | 0.0073 | 0.0081 |
| Wind wave | 14.585 | 0.5747 | 0.0070 | 0.0104 |
| Buoys | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SWAN | Zhao | Wang | WS-23 | SWAN | Zhao | Wang | WS-23 | SWAN | Zhao | Wang | WS-23 | SWAN | Zhao | Wang | WS-23 | |
| 22101 | 1.04 | 0.84 | 0.92 | 0.78 | 0.29 | 0.23 | 0.25 | 0.22 | 1.21 | 1.03 | 1.11 | 0.97 | 0.47 | 0.48 | 0.49 | 0.56 |
| 22102 | 1.04 | 0.98 | 1.04 | 0.92 | 0.24 | 0.23 | 0.25 | 0.22 | 1.25 | 1.15 | 1.22 | 1.09 | 0.59 | 0.61 | 0.61 | 0.67 |
| 22103 | 0.75 | 0.69 | 0.67 | 0.65 | 0.17 | 0.15 | 0.15 | 0.14 | 0.87 | 0.88 | 0.84 | 0.83 | 0.84 | 0.83 | 0.83 | 0.86 |
| 22105 | 0.98 | 0.87 | 0.94 | 0.83 | 0.20 | 0.19 | 0.20 | 0.18 | 1.31 | 1.13 | 1.21 | 1.09 | 0.48 | 0.49 | 0.49 | 0.51 |
| 22106 | 0.95 | 0.83 | 0.88 | 0.79 | 0.20 | 0.19 | 0.20 | 0.18 | 1.21 | 1.07 | 1.12 | 1.03 | 0.54 | 0.53 | 0.54 | 0.57 |
| 22108 | 1.23 | 1.34 | 1.27 | 1.20 | 0.23 | 0.31 | 0.27 | 0.26 | 1.74 | 1.73 | 1.73 | 1.62 | 0.52 | 0.50 | 0.47 | 0.58 |
| 22188 | 1.09 | 1.07 | 1.08 | 1.05 | 0.26 | 0.28 | 0.27 | 0.28 | 1.56 | 1.50 | 1.52 | 1.47 | 0.52 | 0.52 | 0.53 | 0.58 |
| 21229 | 1.03 | 0.85 | 0.92 | 0.82 | 0.21 | 0.18 | 0.19 | 0.17 | 1.32 | 1.09 | 1.17 | 1.06 | 0.52 | 0.53 | 0.54 | 0.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, J.; Zhang, W.; Shi, J.; Wu, J.; Wang, H.; Cao, X.; Wang, Q.; Zhao, Z. The Wave Period Parameterization of Ocean Waves and Its Application to Ocean Wave Simulations. Remote Sens. 2023, 15, 5279. https://doi.org/10.3390/rs15225279
Lv J, Zhang W, Shi J, Wu J, Wang H, Cao X, Wang Q, Zhao Z. The Wave Period Parameterization of Ocean Waves and Its Application to Ocean Wave Simulations. Remote Sensing. 2023; 15(22):5279. https://doi.org/10.3390/rs15225279
Chicago/Turabian StyleLv, Jialei, Wenjing Zhang, Jian Shi, Jie Wu, Hanshi Wang, Xuhui Cao, Qianhui Wang, and Zeqi Zhao. 2023. "The Wave Period Parameterization of Ocean Waves and Its Application to Ocean Wave Simulations" Remote Sensing 15, no. 22: 5279. https://doi.org/10.3390/rs15225279
APA StyleLv, J., Zhang, W., Shi, J., Wu, J., Wang, H., Cao, X., Wang, Q., & Zhao, Z. (2023). The Wave Period Parameterization of Ocean Waves and Its Application to Ocean Wave Simulations. Remote Sensing, 15(22), 5279. https://doi.org/10.3390/rs15225279





