TD3-Based Optimization Framework for RSMA-Enhanced UAV-Aided Downlink Communications in Remote Areas
Abstract
:1. Introduction
- We introduce an RSMA-enhanced FlyBS system, where the FlyBS equipped with a multi-antenna array serves mobile ground users in hard-to-reach areas. At the same time, the communication channel is improved by RSMA technology. To maximize the downlink sum rate, we formulate an optimization problem that considers the 3D FlyBS trajectory and RSMA parameters, i.e., the precoding matrix and common rate vector, while considering the mobility of ground users.
- We transform the problem into a Markov decision process (MDP) by carefully defining the state space, action space, and reward function. To solve the MDP model, we develop the TD3-RFBS optimization framework, which stands for Twin-Delayed Deep Deterministic policy gradient for Rate-splitting multiple access-enhanced Flying Base Station. The TD3 algorithm is used to overcome the overestimation bias issue present in the well-known DDPG algorithm. In the framework, the FlyBS engages, monitors, and acquires knowledge of channel patterns without any pre-existing channel state information (CSI) to optimize its actions.
- We conduct extensive simulations to evaluate the performance of the TD3-RFBS framework. The results confirm that the framework outperforms baseline solutions, including DDPG and local search-based counterparts regarding the learning convergence and total achievable rate.
2. Related Work
3. System Model and Problem Formulation
3.1. System Model
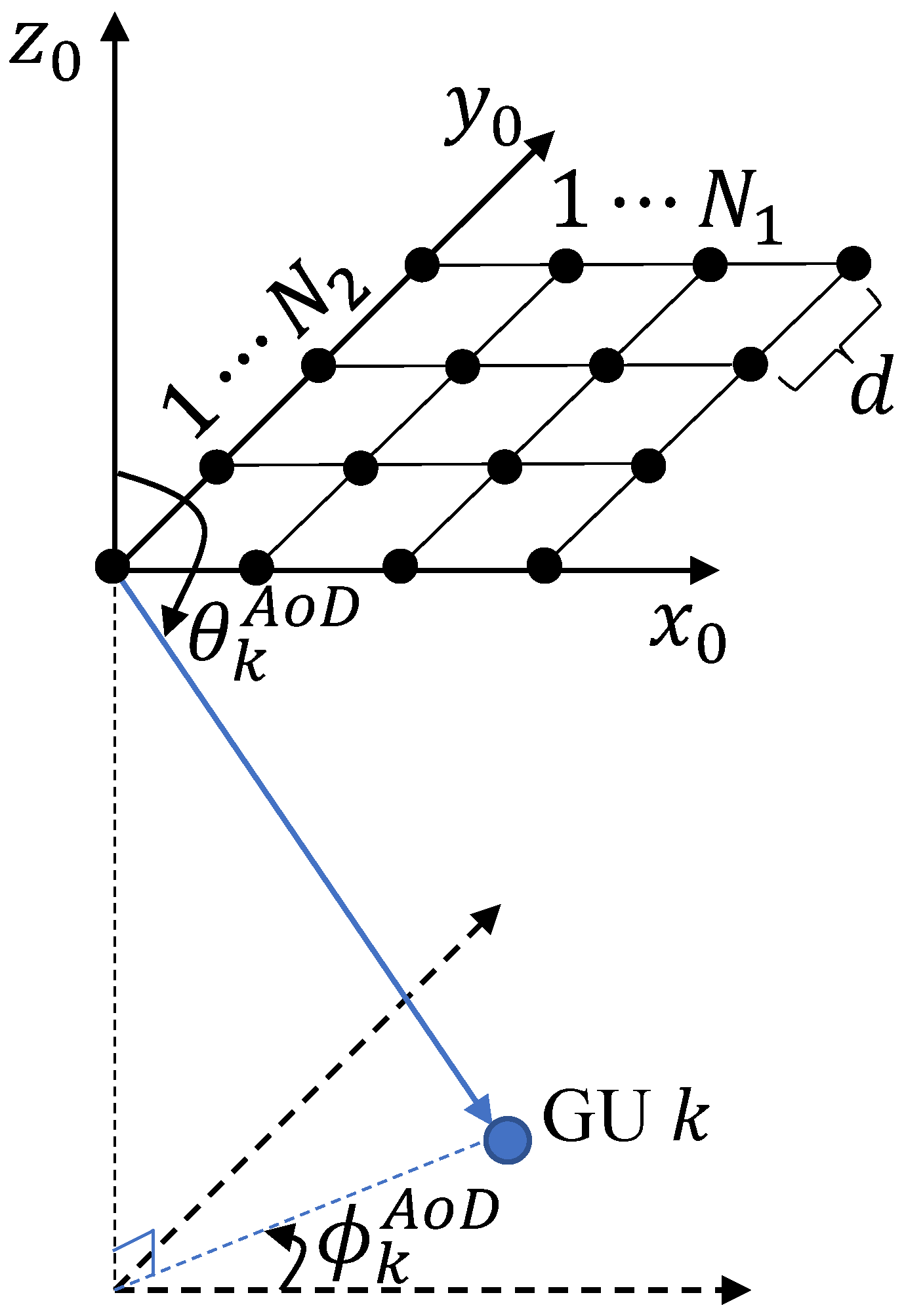
3.1.1. Mobility Model
3.1.2. Channel Model
3.1.3. Signal Model
3.2. Problem Formulation
4. TD3-RFBS Optimization Framework for RSMA-Enhanced FlyBS System
4.1. Markov Decision Process Transformation
- State: At every time interval, the state comprises the present location information of both the FlyBS and K GUs. By utilizing these observed locations, it is possible to estimate the CSI between the FlyBS and the respective GUs [34]. The state is represented as
- Action: At each state , the agent makes decisions on the joint action , which encompasses the optimization variables of the precoding matrix , the common rate vector , and the parameters of the FlyBS (i.e., the azimuth angle , elevation angle , and velocity ). It is formally given aswhere is the complex-valued linear precoder for the signal and . It is worth noting that the action defined in the above equation contains both discrete, continuous, and complex-valued variables which are not directly accessible to the DRL-based learning algorithms. To address this issue, we redefine the precoding matrix as , where is reformed as and [35]. Hence, the original value of can be computed bywhere . In addition, by applying the softmax function to the element of , we define as the normalized vector of , where the is calculated asFurthermore, we define as normalized variables of , , and , respectively, to eliminate the effect of diversity of the variables. Thus, we haveAs a result, all the action variables are normalized in the range of . The action can be rewritten by
- Reward: The agent is given an immediate reward upon performing action . This study aims to maximize the system sum-rate. Therefore, the reward is determined by the combined achievable rate of all GUs, which is represented asThe agent aims to maximize the discounted cumulative reward, expressed as
4.2. TD3-RFBS Optimization Framework
- Clipped double Q-learning: TD3 uses two critic networks instead of one, as in DDPG. By using the minimum Q-value from the target networks, TD3 improves the accuracy of value estimates and reduces the overestimation bias.
- Target policy smoothing: TD3 adds noise to the target action when updating the policy. This makes the policy more robust to Q-value estimation errors.
- Delayed policy updates: TD3 updates the policy and target networks less frequently than the critic networks. This prevents the policy from exploiting the overestimated Q-values.
| Algorithm 1 Training process for the TD3-RFBS optimization framework. |
|
4.3. Computational Complexity
5. Performance Evaluation and Discussion
5.1. Simulation Setup
- TD3-RFBS: Our proposed optimization framework is based on the TD3 algorithm with a normalized action space. It optimizes the precoding matrix, common rate vector, and 3D trajectory for the RSMA-enabled FlyBS to maximize the system sum-rate.
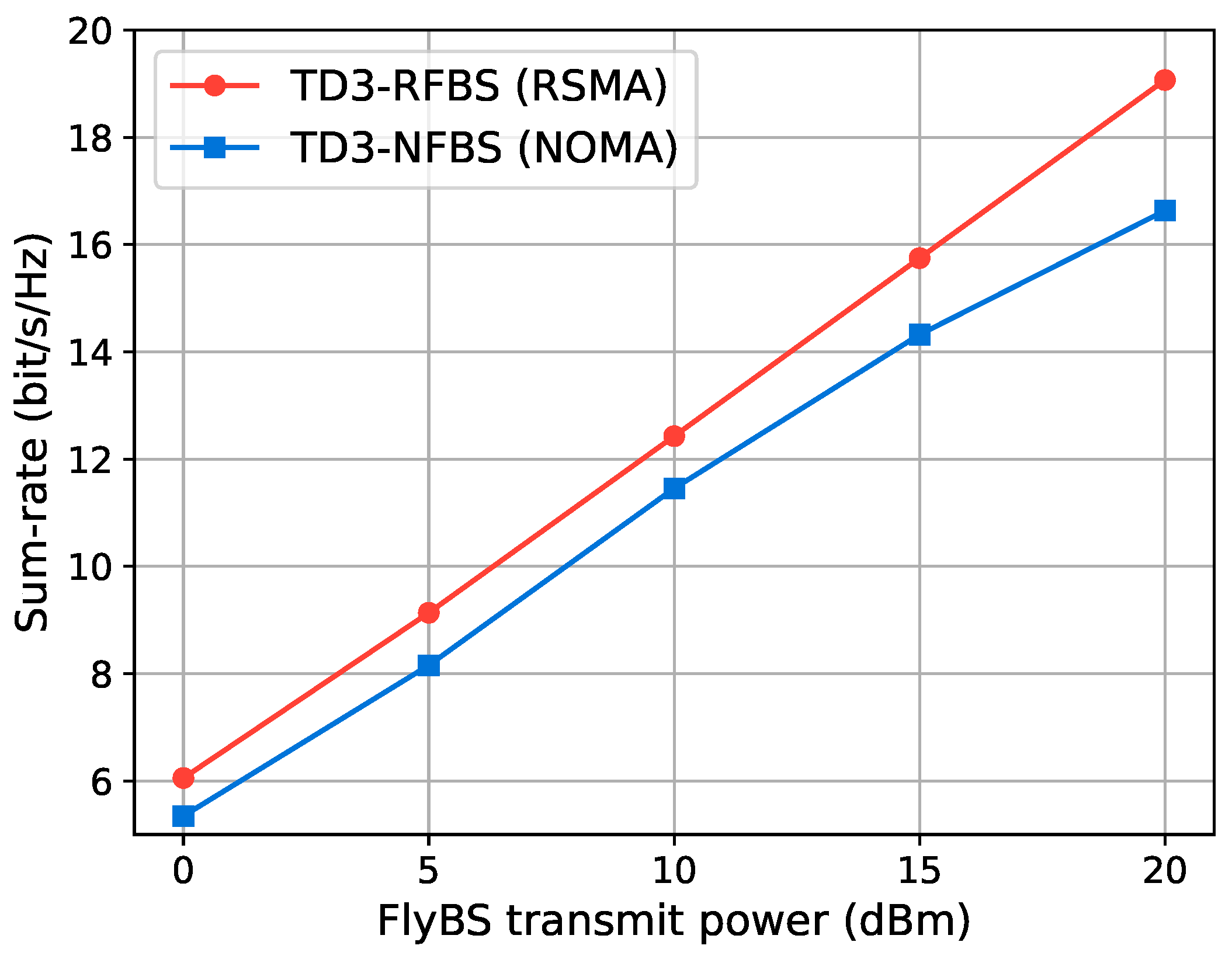
- TD3 algorithm for NOMA-based FlyBS (TD3-NFBS): TD3-NFBS uses the NOMA scheme for the communication channel between the FlyBS and GUs, as opposed to the RSMA scheme in TD3-RFBS. In NOMA, the user with the stronger signal must decode all other users’ messages before accessing its own [7]. The TD3 algorithm optimizes the precoding matrix and 3D trajectory to maximize the system sum-rate.
5.2. Convergence Analysis
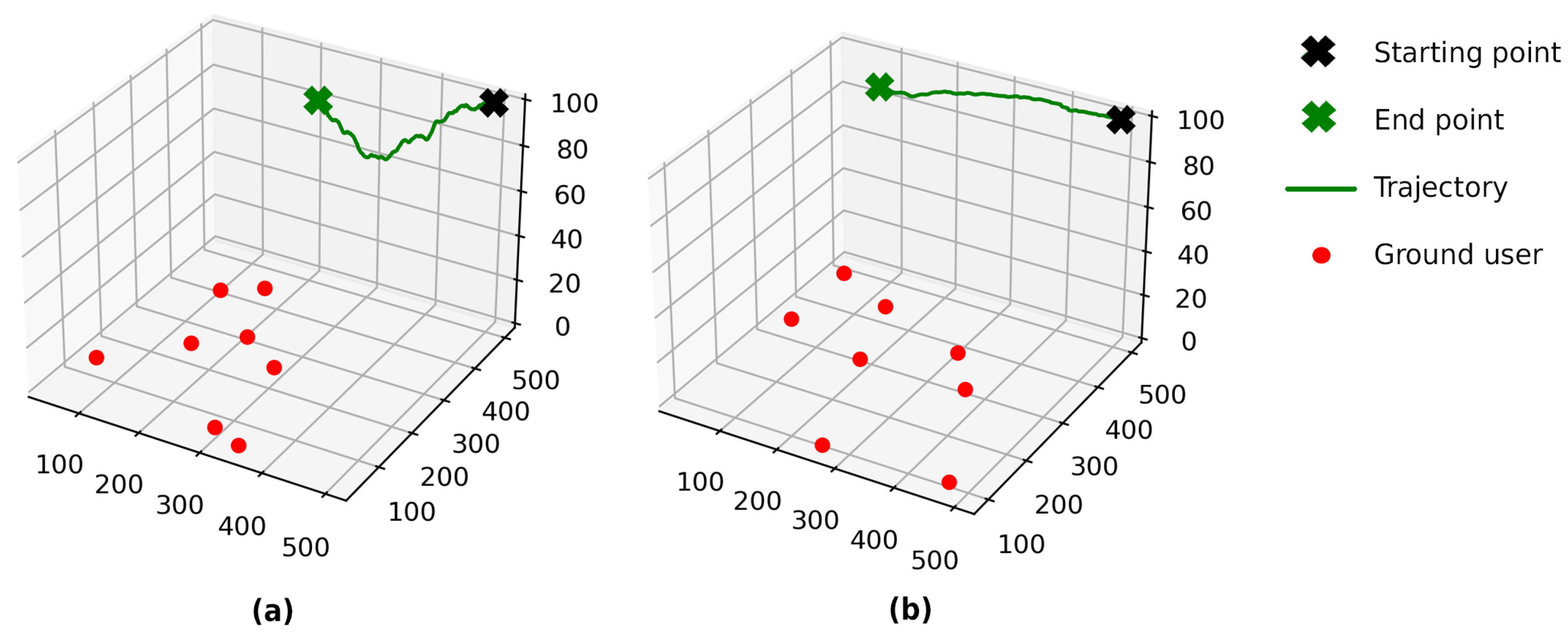
5.3. Performance Analysis
5.3.1. Comparison of Multiple Access Schemes
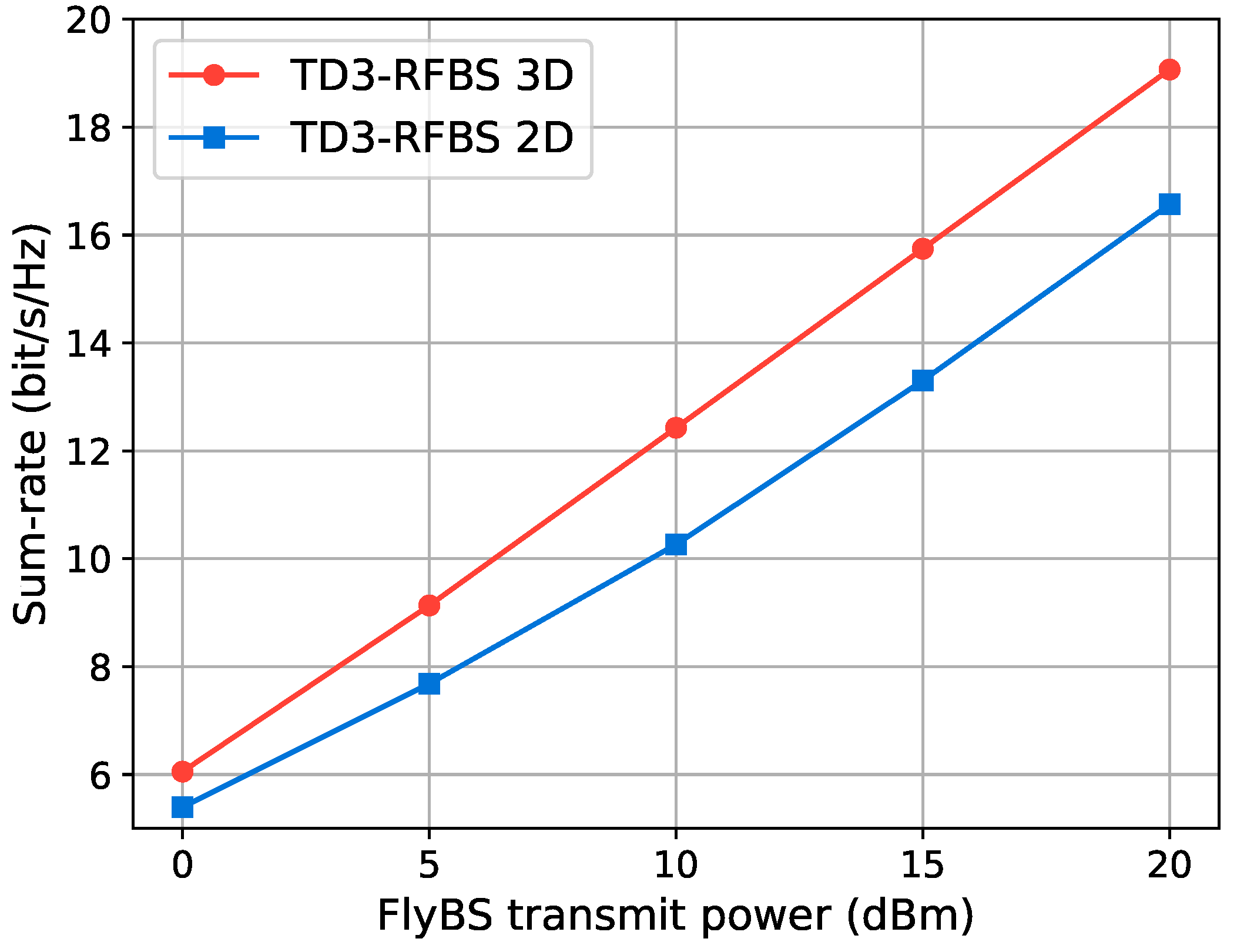
5.3.2. Comparison of 3D and 2D FlyBS Trajectories
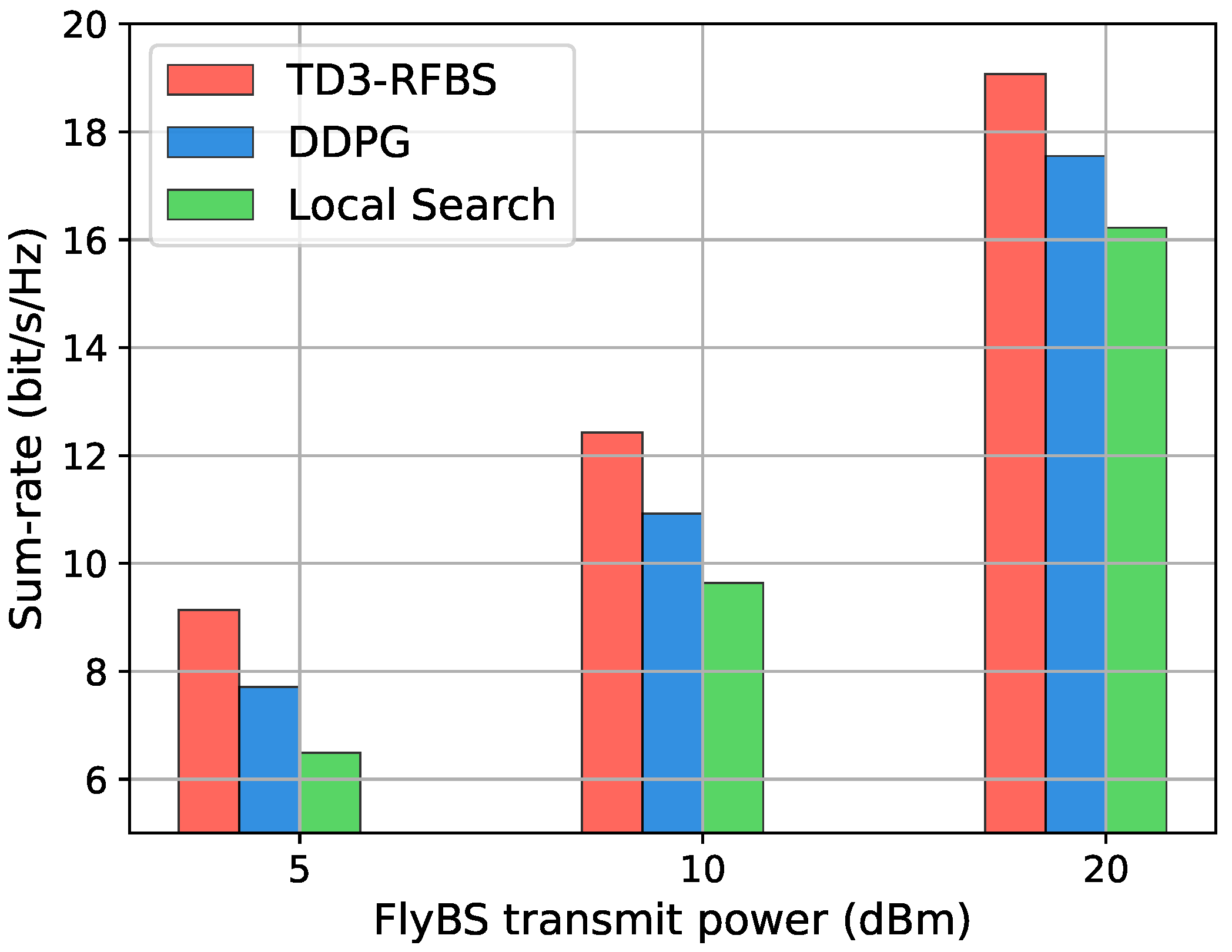
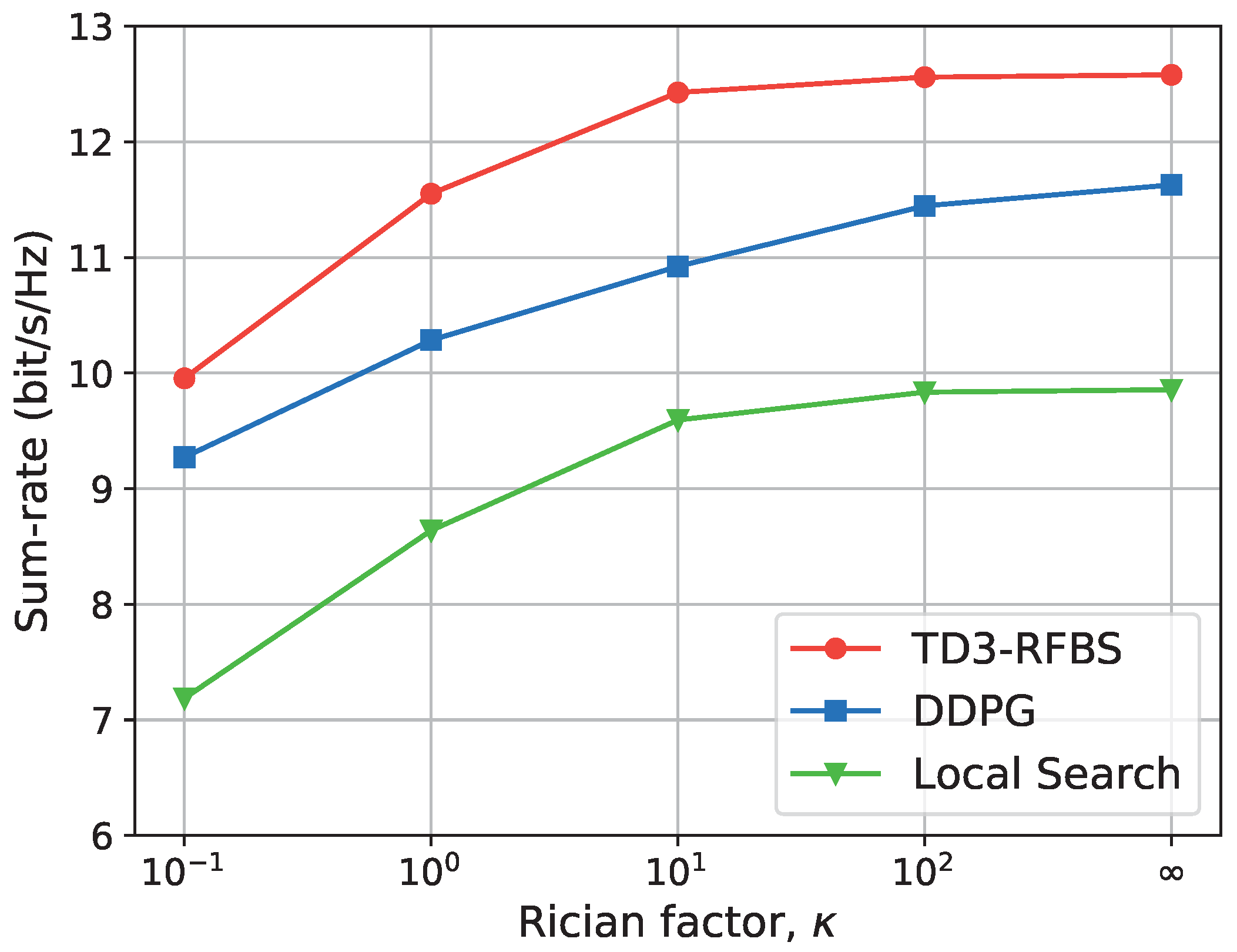
5.3.3. Comparison of Algorithms
5.4. Practical System Implication
- Disaster management: FlyBSs can provide communication coverage in areas where terrestrial BSs have been damaged or destroyed by natural disasters, such as hurricanes and earthquakes. The TD3-RFBS optimization framework can improve the performance of these systems, leading to more reliable and efficient communications in disaster areas, which can be critical for search and rescue efforts.
- Remote sensing: FlyBSs can collect data on remote areas, such as forests, mountains, and oceans, for various applications, including environmental monitoring and remote control of critical infrastructure. The TD3-RFBS optimization framework can increase the spectral efficiency of these systems, leading to more timely and accurate data collection.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 2D | Two-dimensional |
| 3D | Three-dimensional |
| BS | Base station |
| CSI | Channel state information |
| DDPG | Deep deterministic policy gradient |
| DNN | Deep neural network |
| DRL | Deep reinforcement learning |
| FlyBS | Flying base station |
| GU | Ground user |
| IoT | Internet of Things |
| LoS | Line-of-sight |
| MDP | Markov decision process |
| NLoS | Non-line-of-sight |
| NOMA | Non-orthogonal multiple access |
| QoS | Quality of service |
| RSMA | Rate-splitting multiple access |
| SIC | Successive interference cancellation |
| TD3 | Twin-delayed deep deterministic policy gradient |
| UAV | Unmanned aerial vehicle |
| URA | Uniform rectangular array |
References
- Dao, N.N.; Pham, Q.V.; Tu, N.H.; Thanh, T.T.; Bao, V.N.Q.; Lakew, D.S.; Cho, S. Survey on Aerial Radio Access Networks: Toward a Comprehensive 6G Access Infrastructure. IEEE Commun. Surv. Tutor. 2021, 23, 1193–1225. [Google Scholar] [CrossRef]
- Zhao, M.; Chen, C.; Liu, L.; Lan, D.; Wan, S. Orbital collaborative learning in 6G space-air-ground integrated networks. Neurocomputing 2022, 497, 94–109. [Google Scholar] [CrossRef]
- Dong, F.; Song, J.; Zhang, Y.; Wang, Y.; Huang, T. DRL-Based Load-Balancing Routing Scheme for 6G Space–Air–Ground Integrated Networks. Remote Sens. 2023, 15, 2801. [Google Scholar] [CrossRef]
- Lakew, D.S.; Tran, A.T.; Dao, N.N.; Cho, S. Intelligent Offloading and Resource Allocation in Heterogeneous Aerial Access IoT Networks. IEEE Internet Things J. 2023, 10, 5704–5718. [Google Scholar] [CrossRef]
- Geraci, G.; Garcia-Rodriguez, A.; Azari, M.M.; Lozano, A.; Mezzavilla, M.; Chatzinotas, S.; Chen, Y.; Rangan, S.; Renzo, M.D. What Will the Future of UAV Cellular Communications Be? A Flight From 5G to 6G. IEEE Commun. Surv. Tutor. 2022, 24, 1304–1335. [Google Scholar] [CrossRef]
- Shi, J.; Cong, P.; Zhao, L.; Wang, X.; Wan, S.; Guizani, M. A Two-Stage Strategy for UAV-enabled Wireless Power Transfer in Unknown Environments. IEEE Trans. Mob. Comput. 2023, in press. [Google Scholar] [CrossRef]
- Dai, L.; Wang, B.; Yuan, Y.; Han, S.; Chih-lin, I.; Wang, Z. Non-orthogonal multiple access for 5G: Solutions, challenges, opportunities, and future research trends. IEEE Commun. Mag. 2015, 53, 74–81. [Google Scholar] [CrossRef]
- Mao, Y.; Dizdar, O.; Clerckx, B.; Schober, R.; Popovski, P.; Poor, H.V. Rate-Splitting Multiple Access: Fundamentals, Survey, and Future Research Trends. IEEE Commun. Surv. Tutor. 2022, 24, 2073–2126. [Google Scholar] [CrossRef]
- Clerckx, B.; Mao, Y.; Jorswieck, E.A.; Yuan, J.; Love, D.J.; Erkip, E.; Niyato, D. A Primer on Rate-Splitting Multiple Access: Tutorial, Myths, and Frequently Asked Questions. IEEE J. Sel. Areas Commun. 2023, 41, 1265–1308. [Google Scholar] [CrossRef]
- Mao, Y.; Clerckx, B.; Li, V.O. Rate-splitting multiple access for downlink communication systems: Bridging, generalizing, and outperforming SDMA and NOMA. EURASIP J. Wirel. Commun. Netw. 2018, 2018, 133. [Google Scholar] [CrossRef]
- Mao, Y.; Clerckx, B.; Li, V.O.K. Rate-Splitting for Multi-Antenna Non-Orthogonal Unicast and Multicast Transmission: Spectral and Energy Efficiency Analysis. IEEE Trans. Commun. 2019, 67, 8754–8770. [Google Scholar] [CrossRef]
- Sen, S.; Santhapuri, N.; Choudhury, R.R.; Nelakuditi, S. Successive Interference Cancellation: Carving Out MAC Layer Opportunities. IEEE Trans. Mob. Comput. 2013, 12, 346–357. [Google Scholar] [CrossRef]
- Hieu, N.Q.; Hoang, D.T.; Niyato, D.; Kim, D.I. Optimal Power Allocation for Rate Splitting Communications with Deep Reinforcement Learning. IEEE Wirel. Commun. Lett. 2021, 10, 2820–2823. [Google Scholar] [CrossRef]
- Xu, Y.; Mao, Y.; Dizdar, O.; Clerckx, B. Rate-Splitting Multiple Access with Finite Blocklength for Short-Packet and Low-Latency Downlink Communications. IEEE Trans. Veh. Technol. 2022, 71, 12333–12337. [Google Scholar] [CrossRef]
- Van, N.T.T.; Luong, N.C.; Feng, S.; Nguyen, V.D.; Kim, D.I. Evolutionary Games for Dynamic Network Resource Selection in RSMA-Enabled 6G Networks. IEEE J. Sel. Areas Commun. 2023, 41, 1320–1335. [Google Scholar] [CrossRef]
- Yu, D.; Kim, J.; Park, S.H. An Efficient Rate-Splitting Multiple Access Scheme for the Downlink of C-RAN Systems. IEEE Wirel. Commun. Lett. 2019, 8, 1555–1558. [Google Scholar] [CrossRef]
- Xu, Y.; Mao, Y.; Dizdar, O.; Clerckx, B. Max-Min Fairness of Rate-Splitting Multiple Access with Finite Blocklength Communications. IEEE Trans. Veh. Technol. 2023, 72, 6816–6821. [Google Scholar] [CrossRef]
- Zhou, G.; Mao, Y.; Clerckx, B. Rate-Splitting Multiple Access for Multi-Antenna Downlink Communication Systems: Spectral and Energy Efficiency Tradeoff. IEEE Trans. Wirel. Commun. 2022, 21, 4816–4828. [Google Scholar] [CrossRef]
- Truong, T.P.; Dao, N.N.; Cho, S. HAMEC-RSMA: Enhanced Aerial Computing Systems with Rate Splitting Multiple Access. IEEE Access 2022, 10, 52398–52409. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Park, L. HAP-Assisted RSMA-Enabled Vehicular Edge Computing: A DRL-Based Optimization Framework. Mathematics 2023, 11, 2376. [Google Scholar] [CrossRef]
- Jaafar, W.; Naser, S.; Muhaidat, S.; Sofotasios, P.C.; Yanikomeroglu, H. On the Downlink Performance of RSMA-Based UAV Communications. IEEE Trans. Veh. Technol. 2020, 69, 16258–16263. [Google Scholar] [CrossRef]
- Singh, S.K.; Agrawal, K.; Singh, K.; Li, C.P. Ergodic Capacity and Placement Optimization for RSMA-Enabled UAV-Assisted Communication. IEEE Syst. J. 2023, 17, 2586–2589. [Google Scholar] [CrossRef]
- Singh, S.K.; Agrawal, K.; Singh, K.; Chen, Y.M.; Li, C.P. Performance Analysis and Optimization of RSMA Enabled UAV-Aided IBL and FBL Communication with Imperfect SIC and CSI. IEEE Trans. Wirel. Commun. 2023, 22, 3714–3732. [Google Scholar] [CrossRef]
- Xiao, M.; Cui, H.; Huang, D.; Zhao, Z.; Cao, X.; Wu, D.O. Traffic-Aware Energy-Efficient Resource Allocation for RSMA Based UAV Communications. IEEE Trans. Netw. Sci. Eng. 2023, in press. [Google Scholar] [CrossRef]
- Ji, J.; Cai, L.; Zhu, K.; Niyato, D. Decoupled Association with Rate Splitting Multiple Access in UAV-assisted Cellular Networks Using Multi-agent Deep Reinforcement Learning. IEEE Trans. Mob. Comput. 2023, in press. [Google Scholar] [CrossRef]
- Hua, D.T.; Do, Q.T.; Dao, N.N.; Cho, S. On sum-rate maximization in downlink UAV-aided RSMA systems. ICT Express 2023, in press. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Sánchez, J.A.H.; Casilimas, K.; Rendon, O.M.C. Deep Reinforcement Learning for Resource Management on Network Slicing: A Survey. Sensors 2022, 22, 3031. [Google Scholar] [CrossRef]
- Wang, Z.; Pan, W.; Li, H.; Wang, X.; Zuo, Q. Review of Deep Reinforcement Learning Approaches for Conflict Resolution in Air Traffic Control. Aerospace 2022, 9, 294. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Park, L. A Survey on Deep Reinforcement Learning-driven Task Offloading in Aerial Access Networks. In Proceedings of the 2022 13th International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Republic of Korea, 19–21 October 2022; pp. 822–827. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Park, H.; Park, L. Recent Studies on Deep Reinforcement Learning in RIS-UAV Communication Networks. In Proceedings of the 2023 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Bali, Indonesia, 20–23 February 2023; pp. 378–381. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Park, H.; Seol, K.; So, S.; Park, L. Applications of Deep Learning and Deep Reinforcement Learning in 6G Networks. In Proceedings of the 2023 Fourteenth International Conference on Ubiquitous and Future Networks (ICUFN), Paris, France, 4–7 July 2023; pp. 427–432. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. In Proceedings of the 4th International Conference on Learning Representations (ICLR 2016), San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Truong, T.P.; Tuong, V.D.; Dao, N.N.; Cho, S. FlyReflect: Joint Flying IRS Trajectory and Phase Shift Design Using Deep Reinforcement Learning. IEEE Internet Things J. 2023, 10, 4605–4620. [Google Scholar] [CrossRef]
- Hua, D.T.; Do, Q.T.; Dao, N.N.; Nguyen, T.V.; Lakew, D.S.; Cho, S. Learning-based Reconfigurable Intelligent Surface-aided Rate-Splitting Multiple Access Networks. IEEE Internet Things J. 2023, 10, 17603–17619. [Google Scholar] [CrossRef]
- Fujimoto, S.; Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1587–1596. [Google Scholar]
- Nguyen, T.H.; Truong, T.P.; Dao, N.N.; Na, W.; Park, H.; Park, L. Deep Reinforcement Learning-based Partial Task Offloading in High Altitude Platform-aided Vehicular Networks. In Proceedings of the 2022 13th International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Republic of Korea, 19–21 October 2022; pp. 1341–1346. [Google Scholar] [CrossRef]
- Yong, S.K.; Thompson, J. Three-dimensional spatial fading correlation models for compact MIMO receivers. IEEE Trans. Wirel. Commun. 2005, 4, 2856–2869. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 15 July 2023).



| References | Optimization Objective | Optimization Method | FlyBS | FlyBS Trajectory | Time-Varying Environment |
|---|---|---|---|---|---|
| [10] | Sum-rate maximization | Alternating optimization | ✗ | Not applicable | ✗ |
| [11] | Energy efficiency | Successive convex approximation | ✗ | Not applicable | ✗ |
| [13] | Sum-rate maximization | DRL (i.e., PPO) | ✗ | Not applicable | ✓ |
| [14] | Sum-rate maximization | Successive convex approximation | ✗ | Not applicable | ✗ |
| [15] | Sum-rate maximization | Evolutionary game | ✗ | Not applicable | ✓ |
| [16] | Max–min rate fairness | Iterative algorithm | ✗ | Not applicable | ✗ |
| [17] | Max–min rate fairness | Successive convex approximation | ✗ | Not applicable | ✗ |
| [18] | Energy efficiency | Successive convex approximation | ✗ | Not applicable | ✗ |
| [21] | Sum-rate maximization | Alternating optimization | ✓ | Optimal position | ✗ |
| [22] | Sum-rate maximization | Alternating optimization | ✓ | Optimal position | ✗ |
| [23] | Sum-rate maximization | Alternating optimization | ✓ | Optimal position | ✗ |
| [24] | Energy efficiency | Sub-problem decomposition | ✓ | Optimal position | ✗ |
| [25] | Sum-rate maximization | DRL (i.e., PPO) | ✓ | Fixed position | ✓ |
| [26] | Sum-rate maximization | DRL (i.e., DDPG) | ✓ | 2D trajectory | ✓ |
| Our work | Sum-rate maximization | DRL (i.e., TD3) | ✓ | 3D trajectory | ✓ |
| Parameter | Value |
|---|---|
| System | |
| Number of GUs, K | 8 |
| Channel bandwidth, B | 1 MHz |
| Noise power, | −174 dBm/Hz |
| GUs’ maximum velocity | 5 m/s |
| FlyBS’s maximum velocity | 20 m/s |
| FlyBS’s maximum transmit power, | 10 dBm |
| Number of antennas, N | 16 |
| Rician factor, | 10 |
| Large-scale path loss, | dB |
| Time slot duration, | 0.1 s |
| Algorithm | |
| Optimizer | Adam |
| Discount factor, | 0.95 |
| Size of replay buffer | |
| Size of mini-batch, S | 64 |
| Actor learning rate, | |
| Critic learning rate, | |
| Frequency of policy updates, f | 2 |
| Policy noise variance, | 0.2 |
| Noise clip, c | 0.2 |
| Soft update rate, | |
| Number of training episodes | 2000 |
| Number of testing episodes | 100 |
| Number of time slots in each episode | 300 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.-H.; Nguyen, L.V.; Dang, L.M.; Hoang, V.T.; Park, L. TD3-Based Optimization Framework for RSMA-Enhanced UAV-Aided Downlink Communications in Remote Areas. Remote Sens. 2023, 15, 5284. https://doi.org/10.3390/rs15225284
Nguyen T-H, Nguyen LV, Dang LM, Hoang VT, Park L. TD3-Based Optimization Framework for RSMA-Enhanced UAV-Aided Downlink Communications in Remote Areas. Remote Sensing. 2023; 15(22):5284. https://doi.org/10.3390/rs15225284
Chicago/Turabian StyleNguyen, Tri-Hai, Luong Vuong Nguyen, L. Minh Dang, Vinh Truong Hoang, and Laihyuk Park. 2023. "TD3-Based Optimization Framework for RSMA-Enhanced UAV-Aided Downlink Communications in Remote Areas" Remote Sensing 15, no. 22: 5284. https://doi.org/10.3390/rs15225284
APA StyleNguyen, T.-H., Nguyen, L. V., Dang, L. M., Hoang, V. T., & Park, L. (2023). TD3-Based Optimization Framework for RSMA-Enhanced UAV-Aided Downlink Communications in Remote Areas. Remote Sensing, 15(22), 5284. https://doi.org/10.3390/rs15225284








