Few-Shot High-Resolution Range Profile Ship Target Recognition Based on Task-Specific Meta-Learning with Mixed Training and Meta Embedding

Abstract

High-resolution range profile (HRRP), characterized by its high availability and rich target structural information, has been extensively studied. However, HRRP-based target recognition methods using closed datasets exhibit limitations when it comes to identifying new classes of targets. The scarcity of samples for new classes leads to overfitting during the deep learning process, and the similarity in the scattering structures of different ships, combined with the significant structural differences among samples of the same ship, contribute to a high level of confusion among targets. To address these challenges, this paper proposed Task-Specific Mate-learning (TSML) for few-shot HRRP. Firstly, a Task-Adaptive Mixed Transfer (TAMT) strategy is proposed, which combines basic learning with meta-learning, to reduce the likelihood of overfitting and enhance adaptability for recognizing new classes of ships. Secondly, a Prototype Network is introduced to enable the recognition of new classes of targets with limited samples. Additionally, a Space-Adjusted Meta Embedding (SAME) is proposed based on the Prototype Network. This embedding function, designed for HRRP data, modifies the distances between samples in meta-tasks by increasing the distances between samples from different ships and decreasing the distances between samples from the same ship. The proposed method is evaluated based on an actual measured HRRP dataset and the experimental results prove that the proposed method can more accurately recognize the unknown ship classes with a small number of labels by learning the known classes of ships. In addition, the method has a degree of robustness to the number of training samples and a certain generalization ability, which can produce improved results when applied to other backbones.

1. Introduction

Maritime control and situational awareness have garnered increasing significance, especially in the context of classifying and identifying maritime targets. In this regard, considerable attention has been devoted by researchers to radar automatic target recognition (RATR), which has led to the development of various classification approaches. Based on the type of radar data, target classification methods can be broadly categorized as radar cross section (RCS)-based methods [1,2], synthetic aperture radar (SAR)-image-based methods [3,4,5,6,7,8] and high-resolution range profiles (HRRP)-based methods [9,10,11]. HRRP, which is the projection of the spatial scattering structure of the target in the direction of the radar line of sight (LOS) [12], provides essential information such as target size, scattering structure, and position. In comparison to SAR images, HRRP offers the benefits of simple acquisition, easy storage, and straightforward processing. Consequently, HRRP-based target recognition methods have gained popularity in the field of RATR.

Traditional target recognition techniques have the advantage of requiring less data. For instance, Ning et al. [13] proposed a non-equidistant margin plane (NM) in high-dimensional feature space to enhance object recognition accuracy for HRRP data. Wang et al. [14] incorporated a defined separability measure based on the distribution of training samples into the construction of a decision tree, and proposed an improved support vector machine (SVM) decision tree. Furthermore, Chai et al. [15] developed a weighted k-nearest neighbors (KNN) classifier to mitigate the effects of outliers before cooperative target identification. However, the majority of feature extraction methods are unsupervised and lossy, as well as highly dependent on the knowledge and experience with HRRP data of researchers. This means that these methods do not focus well on the maximum separability features, and it can be challenging to obtain the expected results. Compared with the above methods, deep learning can produce better results when applied to HRRP-based RATR [16,17,18,19]. It is essential to note, however, that these methods are primarily trained and tested on specific datasets, and the classifiers used during testing have been exposed to a substantial number of samples from known categories. This category-complete, azimuthally comprehensive scenario is referred to as the closed dataset setting for HRRP target recognition. Networks trained under this paradigm are limited to recognizing specific target types.

In reality, a more intricate situation arises in which radar target recognition systems are required to identify novel classes of targets. However, typically, samples are scarce for these novel classes, giving rise to a class of open-set recognition problems which we refer to as the few-shot problem. When the number of labeled HRRP samples is limited, existing research has predominantly employed two approaches to address overfitting during deep learning. The first approach involves expanding existing data to generate additional samples [20,21,22], while the second strategy combines semi-supervised learning with transfer learning to facilitate knowledge-sharing [23,24]. Nevertheless, when data are seriously lacking, the effectiveness of these techniques is limited. Sufficient training data may not be generated through data expansion to cover diverse data distributions, and transfer learning may only transfer general prior knowledge among related domains, which may prove insufficient for efficient model learning when significant amounts of data are missing. Therefore, these methods are insufficient to address the problem of insufficient data and overfitting in deep learning.

Few-shot learning (FSL) [25] is a type of meta-learning that addresses the challenge of target classification when only a limited number of labeled instances are available. FSL involves two sets of visual concepts: seen classes that have sufficient labeled instances and unseen classes that have few labeled instances. The objective of FSL is to develop a visual classifier that can identify unseen classes using seen classes, making it task-agnostic. This means that the trained model can be applied to the recognition task of novel classes. However, FSL is still in the developmental stage in the field of optical images, and there are fewer studies on HRRP-based few-shot target recognition [24,26]. Moreover, existing FSL methods are not entirely applicable to HRRP due to two primary reasons. Firstly, the scattering structures of different ship classes are still very similar, which leads to small differences between HRRP samples of different ship classes. Secondly, high-resolution radar, being a large integrated system, is inevitably affected by various environmental factors when acquiring the HRRPs of a target. When the attitude of the target changes relative to the LOS, the position of each scatter on the target changes relative to the position of the radar. This change causes relatively substantial differences between HRRP samples of the same target. Applying current FSL methods for optical images to the field of HRRP is challenging due to the difficulty in accurately classifying ship samples that belong to the same class but have relatively large differences. Therefore, it is essential to emphasize the distinctions between classes and reduce the variation within each class when working with HRRP data.

To address the challenge of recognizing new classes of HRRP targets with limited samples and high target confusability, a method for HRRP target recognition is introduced in this paper. Firstly, base-learning and meta-learning methods are employed to mitigate the issue of overfitting in few-shot HRRP recognition. Few-shot recognition of HRRP is addressed during the meta-learning phase. And in the base-training phase, the feature extractor, through modeling all HRRP samples, acquires robust feature extraction capabilities, thereby providing a solid foundation for initializing the weights in the meta-learning phase. During the weight transfer process, the training parameters are reduced by freezing shallow-level blocks and retaining feature weights acquired during the base learning phase to extract envelope features and local physical characteristics from HRRP samples. Several fine-tuning strategies are applied to the deep-level block weights to adapt them to new classification tasks. This transfer strategy alleviates issues related to feature loss and poor adaptability to new tasks during the transfer process, reducing data redundancy and, consequently, minimizing overfitting risk in meta-training. Furthermore, the proposed method enhances discriminative embeddings through an additional embedding function based on prototype networks during meta-training. Specifically, Graph Convolutional Networks (GCNs) are utilized in the meta-training phase to embed support set samples. GCNs capture sample relationships and similarities, aligning samples of the same class in the embedding space, which results in prototypes, defined as the mean embedding vectors for each class. Multi-head Attention is applied to prototype embeddings, assigning feature weights to accentuate subtle feature distinctions among categories, thereby improving prototype distinguishability in the embedding space. Samples in the query set, once embedded by GCN, are classified based on their proximity to the nearest class prototypes. This part, based on the prototype network, not only addresses the problem of recognizing novel classes, but also, by embedding samples and prototypes differently, reduces classification confusion, thereby enhancing recognition accuracy.

Our overall contribution is thus four-fold:

(1)

To address the limitations of recognizing specific target types in the HRRP target identification task on a closed dataset, the prototype network is introduced in this paper. This enables the identification of novel class targets with limited samples.

(2)

To mitigate the overfitting issues that can arise when dealing with a high number of network parameters during meta-training, the Task-Adaptive Mixed Transfer is proposed, which reduces the training parameters, avoiding the redundancy in parameter fine-tuning and computational resource wastage, without introducing information loss during the transfer process.

(3)

To address the challenge of high target confusion during the identification process, a Space-Adjusted Meta Embedding for HRRP based on the prototype network is proposed, which generates discriminative embedding vectors and prototypes, thus improving the accuracy of target classification in HRRP.

(4)

The proposed method in this paper is evaluated based on the actual measured HRRP data. Experiments, both in terms of quantitative results and visualizations, demonstrate that the proposed method can more accurately identify unknown ship classes with a small number of labels by learning the known classes of ships. Furthermore, by varying the number of training samples, we find that the method exhibits a degree of robustness to the number of training samples.

2. Background

2.1. HRRP

HRRP [12] is a technique used for projecting the spatial scattering structure of a target in the direction of LOS, as shown in Figure 1. The scattering point model employed by this technique partitions the target along the LOS into several distance units. Assuming the absence of noise and interference, let the i distance unit contain $N_i$ scattering points of the target, $i=1,2,3,\dots ,n$, and n is the total number of distance units. The sum of all target scattering point echoes is superimposed in the i distance unit, and the expression can be represented as follows:

$$x\left(i\right)=\sum _{j=1}^{N_i}{a}_{ij}{e}^{j2\pi f{\tau }_{ij}}$$

(1)

where $a_{ij}$ represents the intensity coefficient of the j scattering point; ${\tau }_{ij}$ is the echo delay caused by the j scattering point. $x\left(i\right)$ contains the amplitude information and phase information of the target, in which the amplitude information is generally used in radar target identification. Thus, each ship sample can be expressed as:

$$x=\left[\left|x\left(1\right)\right|,\left|x\left(2\right)\right|,\cdots ,\left|x\left(n\right)\right|\right]$$

(2)

2.2. Few-Shot Learning

FSL is an application of meta-learning within the domain of supervised learning. Meta-learning, also known as “learning to learn” [25], involves converting the training set into a large number of few-shot tasks during the training phase, with the goal of learning the generalization ability of the model in the presence of class changes. In the testing phase, the model can perform classification tasks using existing learned knowledge, without the need for further changes. Most of the few-shot classification studies are based on optical images and can be broadly classified into the following categories:

(1)

Meta-learning based on data expansion (Refs. [27,28,29]). This approach involves generating additional positive or negative data based on the labeled data provided, which can then be incorporated as auxiliary information to the meta-learner. The aim of this technique is to provide deeper insights and enhance the information fed to the deep neural network.

(2)

Metric-based learning methods, also called comparison learning [30,31,32,33]. This approach centers on the construction of a suitable embedding space that facilitates the generation of corresponding data feature representations. Subsequently, these representations are classified by comparing their similarity with labeled instances and test data features.

(3)

Optimization-based meta-learning approaches, also referred to as learning optimization [34,35], seek to develop a well-initialized optimizer that can rapidly adapt to unseen classes over multiple training iterations.

(4)

External memory-based meta-learning methods [36] replicate the processes of storage, retrieval and knowledge application in the human brain by introducing a memory module. The method stores acquired experiential information in the memory module and retrieves stored knowledge as required to perform classification tasks.

This paper is centered on the construction of an appropriate embedding space.

3. Proposed Method

Acquiring a large number of labeled samples of non-cooperative targets for HRRPs is a challenging task. Additionally, the scattering structures of different classes of ships are similar, and environmental factors significantly affect the HRRP samples of the same class, resulting in a considerable challenge for few-shot HRRP target recognition. Therefore, in this paper, a twofold objective is pursued by the proposed few-shot HRRP target recognition method: firstly, to fully extract the available information from the HRRPs of cooperative ship targets and employ appropriate transfer strategies for non-cooperative target recognition; and secondly, to enhance recognition accuracy by highlighting commonalities among samples of the same class and differences among samples of different classes to mitigate strong confusability during HRRP classification. To achieve this, transfer learning and meta-learning are employed to construct a suitable embedding space $\Phi \left(·\right)$ using cooperative target data with a large number of labeled samples.

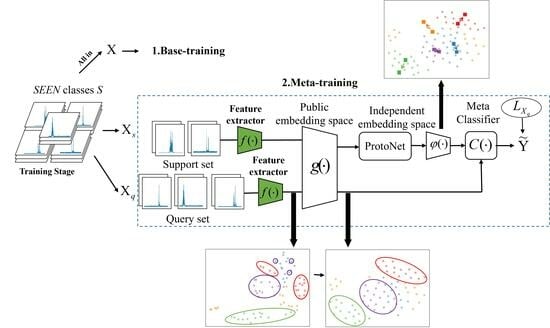
As depicted in Figure 2, the method in this paper can be delineated into three primary stages: the base-training, meta-training, and meta-testing phases. The first stage, termed base-training, defines the task as HRRP target recognition on a closed dataset. In this stage, the feature extractor $f_{\theta }(·)$ and classifier $C_{base}(·)$ are trained using the complete dataset of cooperative HRRP targets. Subsequently, the weights of the feature extractor with superior classification performance are selected as the initial weights for the feature extractor in the meta-training phase. The second stage is designed to tackle the open-set recognition problem, specifically the challenge of dealing with few-shot HRRP target recognition. In this phase, a substantial number of tasks are sampled from the cooperative HRRP dataset to train and adapt the parameters $\theta$, the embedding space function $g(·)$, and $\phi (·)$. Each task includes a support set $X_k$ for network training and a query set $X_q$ for evaluating network performance. Firstly, the feature extractor $f_{\theta }(·)$ and the embedding space function $g(·)$ transform the samples from the support set $X_k$ into feature representations conducive to classification, facilitating the closer proximity of samples from the same class in the metric space. Secondly, the prototype network creates class prototypes by calculating the mean embedding vectors for each class. Finally, $\phi (·)$ accentuates the inter-class differences, enabling better differentiation of class prototypes in the embedding space. An in-depth explanation of the transfer strategy for the parameter $\theta$ during the training phase and the embedding space functions will be provided in Section 3.2. The third stage is the meta-testing phase. Based on the well-trained feature extractor $f_{\theta }(·)$, and the embedding space functions $g(·)$ and $\phi (·)$, a small number of samples is employed to establish prototype representations in the metric space for new classes. The class of a given sample can then be ascertained by calculating the distance between the embedding vector of the sample and the prototype representation. It is noteworthy that our research is based on Resent12, a widely used convolutional neural network.

In the standard formulation of FSL, a task is represented as an N-way K-shot classification problem with N classes sampled from a set of visual concepts and K labeled examples per class. The goal of FSL is to find a function that classifies unlabeled examples into one of the N classes. However, in FSL, K is often small (e.g., K = 1 or K = 5), making it challenging to construct complex functions. To this end, the learning algorithm is also supplied with additional data consisting of ample labeled instances (SEEN classes). The original few-shot task is referred to as the target task, which discerns N UNSEEN classes that do not overlap with SEEN classes. To avoid confusion, the dataset from the SEEN classes used for training are denoted as $D_{train}$, comprising a total of $N_t$ ship classes. In practical applications, cooperative targets with ample labeled samples are considered as SEEN classes, while non-cooperative targets with limited labeled samples are regarded as UNSEEN classes.

3.1. Base-Training

The aim of this study is to extract as much information as possible from the cooperative HRRP data available for non-cooperative target identification. To achieve this, a feature extractor is trained utilizing all available cooperative target HRRP data. This phase is base-learning, and is intended to model the HRRP data distribution for each class of ships to accomplish the single task of classification referred to as the source task. Base-training facilitates the complete learning of cooperative ship target features based on the entire HRRP training data, leading to a well-initialized network for the meta-training phase. Consequently, meta-learning can converge quickly with fewer tasks. It should be noted that this phase solely relies on the SEEN class dataset $D_{train}$ and does not consider adaptation from other datasets.

In the initial learning phase, a classifier is trained for the $N_t$ class, consisting of a linear classifier $C_{base}$$\left(·\right)$, as shown in Figure 3, and a convolutional feature extractor $f_{\theta }(·)$, both of which are initialized randomly and updated via gradient descent:

$$\begin{array}{c}\left[f_{\theta }(·),\right.C_{base}\left(·\right)=:\left[f_{\theta }(·),\right.C_{base}\left(·\right)-\gamma ▽L_{D_{train}}\left(\left[f_{\theta }(·),\right.\right.C_{base}\left(·\right)\hfill \end{array}$$

(3)

where $L_{D_{train}}$$\left(·\right)$ is the cross-entropy loss function and $\gamma$ is the learning rate.

The trained feature extractor and classifier effectively extract HRRP features to improve the ship classification task performance, based on the complete dataset $D_{train}$. The feature extractor acquires enhanced feature extraction capability by learning the separability features of large-scale data, and its weights are utilized as the initialization weights of the network in the meta-training phase. However, the classifier $C_{base}$ is not used during the meta-learning phase due to modifications made to the classification task.

3.2. Task-Specific Meta-Training

The problem of a limited number of labeled instances and high confusion in HRRP ship classification can be addressed through meta-learning. In the initial stage, the learning of each class of cooperative ship is completed by the feature extractor, and improved feature extraction weights are obtained. However, the features extracted by the current feature extractor may be insufficient or redundant for the new task. Therefore, the meta-training phase involves not only learning how to classify N-way K-shot tasks across a large number of similar tasks, but also accurately and efficiently transferring the trained feature weights to the new task and adapting them to the new task.

There are a series of episodes in the meta-training set. Each episode in this study is randomly sampled from dataset $D_{train}$, and comprises two subsets: a support set and a query set. The support set is similar to a traditional training set in machine learning, and includes N classes, each with K training samples. The query set, on the other hand, resembles a test set and comprises Q samples of the same classes as the support set, but without any overlapping samples. Additionally, the meta-learning process is divided into two phases: the meta-training and the meta-testing. For a task $T_i$ within the meta-training phase, its dataset can be represented as $D_{trai{n}_i}$ = {($X_k$, $Y_k$), ($X_q$, $X_q$)}, where ($X_k$, $Y_k$) constitutes the support set, and ($X_q$, $X_q$) forms the query set. The number of classes contained in $X_k$ and $X_q$ is denoted as N. Let $X_{n,k}$ represent the subset of classes in $X_k$ for n = 1, 2, 3…N, with corresponding labels $Y_{n,k}$.

(1) Task-Adaptive Mixed Transfer.

The training objectives diverge between the base-training phase and the meta-training phase. Consequently, freezing all the weights $\theta$ of the feature extractor would render the network unable to adapt to new tasks. Nonetheless, whether dealing with SEEN or UNSEEN classes, the structural differences among ships are marginal, and the discriminative feature types necessary for ship HRRP data classification remain consistent. Completely relearning all the initial weights $\theta$ could potentially introduce redundancy and squander computational resources. To address these challenges, a Task-Adaptive Mixed Transfer (TAMT) method is proposed, which fine-tunes the parameters in different ways based on the distinct roles of various network blocks in feature extraction. Specifically, the shallow blocks are frozen to preserve the memory of the pre-trained model in extracting ship data envelope features and local physical structure features, while adjusting the deep blocks to adapt to the new few-shot tasks.

The fine-tuning process involves two methods: Neuron-level Scaling and Shifting (SS), and Parameter-level Fine-Tuning (FT). SS involves freezing neurons and then performing scaling and shifting based on their original weights and biases, as shown in Figure 4b. Given the trained $f_{\theta }(·)$, for its l-th layer containing M neurons, there are M pairs of parameters, respectively, as weight and bias, denoted as {($W_{l,m}$,$b_{l,m}$ )}. Note that the neuron location l, m will be omitted for readability. Based on the methods in this paper, we learn M pairs of scalars. Assuming $X_k$ is input, we apply $S_{\{1,2\}}$ to (W, b) as

$$SS(X_k;W,b;S_{\{1,2\}})=(W\odot S_1)X_k+(b+S_2)$$

(4)

where ⊙ denotes the element-wise multiplication. Taking Figure 4b as an example of a single 1 × 6 filter, after SS operations, this filter is scaled by $S_1^{\prime }$ then the feature maps after convolutions are shifted by $S_2^{\prime }$ in addition to the original bias b.

$$SS(X_k;W,b;S_{\{1,2\}})=(W\odot S_1^{\prime })X_k+(b+S_2^{\prime })$$

(5)

Figure 4b illustrates FT, which involves making small adjustments to all the neural network weight parameters of the model to make it better suited to specific tasks or data. It is evident that FT updates the entire values of W and b, encompassing a large number of parameters, making it susceptible to overfitting when the sample size is limited. Furthermore, performing FT on the entire network may result in the complete forgetting of pre-training memory, known as “catastrophic forgetting”. By contrast, as seen in the examples in the Figure 4, SS reduces the number of training parameters, significantly reducing the computational and memory overhead. However, when SS is applied to all neurons, the adaptation of the network to few-shot tasks may be somewhat lacking.

Assume that the feature extractor $f_{\theta }(·)$, initialized with weights, acquires new network weights denoted as ${\theta }_i$}${}_{i=1}^{N_b}$ after the base-training, and considering that the number of network blocks $N_b$ is 4 due to our use of ResNet12 for feature extraction. During the meta-training phase, in addition to learning the parameters for the introduced meta embedding, there is a need to fine-tune the existing feature extractor network weights ${\theta }_i$}${}_{i=1}^{N_b}$ to adapt to the changing recognition task. Based on FT and SS, the transfer strategy designed in this paper is depicted in Figure 5, which includes the mapping of network parameters before and after meta-training.

The frozen blocks are referred to as shallow static blocks, while the ones that need adjustment to adapt to the new task are referred to as deep dynamic blocks. Initially, the neurons in shallow blocks, including block 1 and block 2, are frozen to preserve their capability to extract HRRP sample envelope features and initial separability features. Thus, the network parameters ${\theta }_i$}${}_{i=1}^{N_b=2}$ remain unchanged before and after training. Subsequently, to adapt to new few-shot tasks and extract relevant features based on task characteristics, block 3 and block 4 are fine-tuned using different fine-tuning methods. Block 3, serving as the deep dynamic block that bridges the two training modes, adopts FT, meaning that the neuron weights of the entire block can be learned. Its main task is to flexibly transform feature vectors from the shallow static module, thoroughly sift, and further extract relevant information to obtain useful features for the new task, initiating the initial adaptation learning for the new task. Block 4 undergoes scaling and shifting based on the initialized weights. Given that its channel count is eight times that of block 1, FT would significantly increase the number of parameters to be learned. In this paper, SS is employed to fine-tune Block 4, a method that substantially reduces the computational and memory overhead while allowing for further adaptation to new classification tasks built on the foundation of Block 3.

This transfer strategy accomplishes several key objectives. Firstly, it preserves the feature extraction capabilities of the feature extractor during the base-training phase for effective HRRP sample extraction, thereby preventing the occurrence of “catastrophic forgetting” that may arise when fine-tuning the entire network. Secondly, it ensures network flexibility and adaptability to new tasks. Finally, by freezing certain neurons and applying SS to others, the number of training parameters in the meta-training phase is reduced, thereby preventing overfitting when dealing with a limited number of labeled ship HRRP samples.

(2) Space-Adjusted Meta Embedding based on GCN and Multi-head Attention.

Achieving the goal of reducing the diversity within the same ships while increasing the differences between different classes is a challenging task when using only a uniform feature extraction network. To address the problem of high confusion about ship HRRP targets in the classification process, this paper introduces a task adaptation step that employs an embedding function focusing on instances and relationships between classes. The embedding function, based on the GCN with a good clustering effect and Multi-head Attention that can emphasize critical classification features, involves all instances entering a new embedding space. This space comprises a sample-based public embedding space and an independent embedding space based on prototypes, as illustrated in Figure 6, designed to perform opposite and complementary functions. The “public” embedding space aims to resolve the problem of significant sample differences within the same type of ships in HRRP, while the “independent” embedding space addresses the issue of slight variations between different ship classes.

Fully connected layers, such as classifier $C_{base}$$\left(·\right)$ during base-training, are less flexible, since they cannot adapt to changes in the number of classifications. To enhance model flexibility and avoid learning complex recognition models from a limited number of labeled examples of HRRP ships, this study proposes using a prototype network to dynamically construct prototypes and perform the nearest prototype classification. In TAMT, initial adaptation to the new task from a feature extraction perspective is performed by adjusting the weights of the deep blocks. In contrast, the proposed embedding function facilitates further adaptation to the new task from the perspective of class classification and optimal prototype acquisition. The support set samples $X_k$ are processed through the feature extractor $f_{\theta }(·)$ to obtain $F_k$, which represents the features of the input samples. Correspondingly, within $F_k$, the subset for categories where $n=1,2,3\dots N$ is denoted as $F_{n,k}$, with their respective class labels $Y_{n,k}$.

The GCN, initially utilized for irregular data structures, particularly graph structures, focuses on the relationships between nodes and exhibits a good clustering effect on the embedded data points. To address the relatively large differences between HRRP samples of the same ship target, GCN serves as a public embedding space $g(·)$ based on samples to decrease the distance between samples of the same ships.

Each HRRP instance is considered a data point. For each data point, the GCN can consider both the adjacent data points and the feature information contained in itself. The input to the GCN is denoted as $F_k$, where feature representation vector of each sample is considered as a separate data point. The similarity between each instance is represented by an adjacency matrix A. Specifically, if two ship instances belong to the same class, the corresponding element in A is set to 1, otherwise to 0. $F_k$ and A are fed as inputs to the GCN. The adjacency matrix A is symmetrized and normalized to obtain the matrix:

$$S=D^{-\frac{1}{2}}\left(A+I\right)D^{-\frac{1}{2}}$$

(6)

where I is the identity matrix and D is the diagonal matrix whose elements are equal to the sum of the elements in the corresponding rows of $A+I$. The relationship between instances could be propagated based on S:

$$H^{t+1}=ReLU\left(S{H}^{t}W\right),t=1,2,\dots ,T-1$$

(7)

where W is a projection matrix for feature transformation. $H^t$ is the input feature matrix of each layer, and $H^0$ is the output of the feature extractor $F_k$. In GCN, the embedding in the set is transformed based on Equation (7) multiple times, which eventually produces the embedding result. The output result of GCN is denoted by $G_k$:

$$G_k=g\left(F_k\right)$$

(8)

After the instances are embedded into the public embedding space using GCN, the data points belonging to the same ship are more tightly aggregated, exhibiting less variability. This reduces the probability of misclassifying instances that belong to the same ship but with large differences to different classes.

Prototype $c_n(n=1,2,\cdots ,N)$ is obtained by calculating the average of all vectors belonging to a class of ships in $G_k$:

$$c_n=\frac{1}{\left|X_{n,s}\right|}\sum _{x_i\in X_{n,s}}^{}{f}_{\theta }\left(x_i\right),n=1,2,3,\cdots ,N$$

(9)

Therefore, the prototypes for the task $T_i$ are recorded as $C_i$=$c_n$}${}_{n=1}^N$.

As ships are the only classification objects considered in this paper, their target structures exhibit a significant degree of similarity. Furthermore, the HRRP reflects the projection of the target scatterer in the direction of the LOS, causing the HRRP data returned by ships with similar structures to be highly similar as well. As a result, treating the prototype as a data point means that the distance between prototypes of different ships would be relatively small. To overcome this issue, an independent embedding space $\phi (·)$ is required for the prototype to accentuate the distinguishable differences between different ship classes.

The Multi-head Attention has the ability to focus on context, extracting important information from an extensive amount of data and highlighting it, while disregarding the rest of the information which is mostly irrelevant. By employing this mechanism in the embedding of the prototype, the Multi-head Attention highlights the vital information from the prototype set. For the classification task, this means enhancing the discernible information between prototypes of different ship classes by assigning weights to them and reducing their commonality. This process increases the distance between different class prototypes and reduces the probability of classifying different classes of ships into the same class. To accomplish this, we first apply the self-attention mechanism to the matrix $C_i$=$c_n$}${}_{n=1}^N$:

$$Q=C_i·W^Q$$

(10)

$$K=C_i·W^K$$

(11)

$$V=C_i·W^V$$

(12)

$$O=Attention\left(Q,K,V\right)=softmax\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$

(13)

where $\sqrt{d_k}$ represents the vector length.

Then, the output matrix of each self-attention operation is concatenated along the feature dimension to form a new matrix, which is subsequently fed into a fully connected layer to generate the final output:

$$C_i^{\prime }=MultiHead(C_i,C_i,C_i)=Concat(O_1,O_2,\cdots ,O_{multi})W^O$$

(14)

where W is a projection matrix for feature transformation, and $C_i^{\prime }$=$c_n^{\prime }$}${}_{n=1}^N$ is the result of prototype processed by the Multi-head Attention.

For all the embedding points $x\in X_q$, the Euclidean distance d to a certain class prototype $c_n^{\prime }$ can be represented as:

$$d({\Phi }_q\left(x\right),c_n^{\prime })=\sqrt{{({\Phi }_q\left(x\right)-c_n^{\prime })}^2}$$

(15)

where ${\Phi }_q\left(·\right)=g\left(f\left(·\right)\right)$.

Normalizing the distances from embedded samples to all prototypes using the Softmax can transform the distances into probabilities for the corresponding classes:

$$p\left(y=n|x\right)=\frac{exp\left(-d\left({\Phi }_q\left(x\right),c_n^{}{}^{\prime }\right)\right)}{{\sum }_{n=1}^{N}exp\left(-d\left({\Phi }_q\left(x\right),c_n^{}{}^{\prime }\right)\right)}$$

(16)

So, the loss function for this network on a single training sample is the negative natural logarithm of the true class probability:

$$L=-logp(y=n|x\in X_{n,q})$$

(17)

The presented process describes one task in the meta-training procedure. And the overarching objective is to learn the meta-function $\Phi \left(·\right)$, which comprises the functions $f\left(·\right)$, $g\left(·\right)$ and $\phi \left(·\right)$.

4. Results

In this section, the proposed method was evaluated based on the actual measured HRRP data. To initiate the analysis, the measured data were introduced and pre-processed in preparation for the experiment. Subsequently, the proposed method was compared with the state-of-the-art few-shot learning methods, and the performance of both was analyzed. Moreover, the effects of embedding function and transfer strategy change on the experimental results were investigated. All experiments were conducted using PyTorch on an NVIDIA GeForce RTX 2080 Ti graphics card.

4.1. Data and Preprocessing

Figure 7 displays the distribution of data samples and the normalized representation of certain three types of ships, as utilized in this paper. All statistics were measured by a shore-based radar with a bandwidth of 600 MHz, containing 137,702 measured HRRP samples with 95 different ship targets. Each HRRP is a 4096-dimensional vector, encapsulating one-dimensional structural information of various ships. As observed in Figure 7b–d, the position of the ship relative to the radar at various instances contributes to the incorporation of diverse information about the ship across a range of azimuth and pitch angles within the sample.

The goal of the few-shot meta-learning is to train a meta-learner with the ability to train a learner to converge quickly and accurately for new tasks. Specifically, 60 classes were randomly selected as the training set $D_{train}$ among the classes with ample labeled samples, to investigate the impact of the number of training samples on recognition accuracy. The remaining classes were divided into 15 and 20 for validation set $D_{val}$ and testing set $D_{test}$, respectively. It is worth noting that the classes of the dataset do not intersect with each other. As shown in Figure 8, according to the meta-learning formulation settings, $D_{train}$ and $D_{test}$ contain different episodes, which are divided into a support set and a query set. We defined the support set and query set of the meta-training set as $D_{train-s}$ and $D_{train-q}$; similarly, we defined the support set and query set of the meta-testing dataset as $D_{test-s}$ and $D_{test-q}$. Different classes of HRRP samples are treated as meta-training set and meta-testing set as above described. The classification tasks of different azimuth angle HRRP samples are divided into different tasks in the field of meta-learning formulation, as indicated by the markers in Figure 8.

As a complex and integrated system, the intensity of the HRRP data obtained through high-resolution radar can be influenced by several factors, including radar transmit power, target distance, radar antenna gain, and radar receiver gain. The collected data will have an inconsistent intensity problem. This problem is also called intensity sensitivity. Before using HRRP for target recognition, the original HRRP echo is processed by normalization to improve the intensity sensitivity problem.

If the raw HRRP sample can be expressed as $x=[x_1,x_2,\cdots ,x_m]$, where m is the total number of range cells contained in the HRRP, the intensity normalized HRRP sample $x_{norm}$ can be expressed as

$$x_{norm}=\frac{x-x_{min}}{x_{max}-x_{min}}$$

(18)

where the intensity is scaled to [0, 1]. Since the convolution, as well as pooling operations, are robust to sample shifts, there is no need for additional processing of translation sensitivity, making the recognition process more complete and reducing human manipulation.

4.2. Evaluation Metrics

This paper evaluates the classification accuracy of five-way one-shot and five-way five-shot, using Q instances from the same categories as test data. The final classification results are obtained by calculating the average accuracy of classification for 10,000 tasks based on the test set, and the calculation is as follows:

$$acc=E_T\left[E_c\left[\frac{{\sum }_{x\in X_{c,q}}^{}p(y==c)}{CARD\left(X_{c,q}\right)}\right]\right]$$

(19)

where $X_{c,q}$ is the set of samples in the query set with the class label c, $CARD(·)$ represents the number of elements in a set, $p(·)$ represents the probability, y is the predicted class for sample x, c is the true class, and T represents a test task. The formula first calculates the average category recognition rate within a task and then computes the expected value of the average category recognition rate across all tasks.

4.3. Results and Analysis

4.3.1. Compared with State-of-the-Art Methods

The comparison results of the proposed method with several state-of-the-art few-shot methods are presented in

Table 1. Recognition accuracy of different methods.

Method	Accuracy%
	One-Shot Five-Way	Five-Shot Five-Way
Matchnet [33]	64.54	75.41
Protonet [30]	65.51	76.04
MTL [37]	70.52	80.10
FEAT [38]	73.89	84.39
Ours	75.23	86.46

The bolded parts are the methods with the best recognition results.

and Figure 9. The results indicate that although these methods exhibit good performance in the field of optical images, their performance is average in the field of HRRP-based RATA. The possible reason for this discrepancy is that these methods have good performance in recognizing 2D optical images, but are not suitable for 1D HRRP data. Notably, both MTL and FEAT classify ships based on ResNet12. However, the recognition accuracy of MTL is 5.28% and 6.36% lower than the method proposed in this paper, primarily because the linear classifier used in MTL requires learning with a small number of samples, which can limit its effectiveness due to insufficient learning or fewer parameters. In contrast, the proposed method achieves 1.34% and 2.07% higher accuracy than FEAT, because the clustering effect of the GCN reduces the differences between samples within the same class, thereby decreasing the probability of misclassification. Furthermore, the Multi-head Attention embeds prototypes, increasing the distance between prototypes of different classes, thereby enhancing their representativeness, which is another contributing factor to the reduction of misclassifications. The visualization results are shown in Figure 10.

4.3.2. Comparison with Different Transfer Strategies

When a network comprises multiple blocks, it is common to utilize shallow blocks to extract envelope features and local physical structure features of the HRRP, while the deep blocks are leveraged to adapt to a specific task. The base-trained feature extractor is already equipped with good initialization weights and can effectively extract features. However, it is not well-suited to the new task. Therefore, this study proposes a transfer strategy, where the shallow blocks are frozen and the deep blocks are fine-tuned to adapt to the new task. The effectiveness of this transfer strategy is demonstrated through two experimental scenarios. The first scenario involves no common embedding space GCN, while the second scenario employs a common embedding space GCN. The results of these experiments are presented in

Table 2. Recognition accuracy of different transfer strategies.

	Accuracy %
Transfer Strategy	Embedding without GCN		Embedding with GCN
	One-Shot Five-Way	Five-Shot Five-Way	One-Shot Five-Way	Five-Shot Five-Way
Fully FT	73.89	84.39	75.52	85.67
Fully SS	73.72	82.74	75.13	84.65
23Frozen	73.20	83.99	74.99	85.30
34Frozen	70.69	82.36	73.93	84.43
Ours	74.17	84.69	75.23	86.46

The bolded parts are the methods with the best recognition results.

, and the contrast chart is presented in Figure 11.

In the absence of GCN embedding, the current study finds that the proposed method is comparable to the results obtained through full parameter fine-tuning. This suggests that the proposed transfer strategy effectively extracts features and adapts to the task, despite freezing some network blocks. Moreover, the proposed method is more computationally efficient and does not compromise accuracy. In contrast, the results indicate that freezing the deep blocks and training only the shallow blocks yield the worst performance, with recognition accuracies of 70.69% and 82.36%, respectively. These accuracies are 3.48% and 2.33% lower than those obtained through the proposed method. This inferior performance can be attributed to the attempt to extract new features, by training only the shallow blocks but keeping the initialized weights unchanged in the deep blocks. This approach not only diminishes the feature extraction capability established during base-training, but also fails to adapt to the new task. Furthermore, the full SS yields recognition accuracies of 73.72% and 83.74%, respectively, which are lower than the proposed method with differences of 0.45% and 1.95%. The results suggest that adapting to new tasks solely through SS is still insufficient.

In the presence of GCN embedding, the gap between all methods decreases when identifying tasks of one-shot, five-way, but differs from the approach proposed in this paper by only +0.29%, −0.1%, −0.24%, and −1.3%. This is because the GCN is responsible for adapting to the new task, masking inadequate task adaptation. However, freezing the deep blocks and training only the shallow blocks still performs the worst in this case, with 1.3% lower than the proposed method in this paper. When the number of labeled samples per class is increased to 5, the proposed methods show better performance, with accuracies of 0.79%, 1.81%, 1.16%, and 2.02% higher than the other methods, respectively. This increased gap between methods is due to the fact that, as the number of labeled samples increases, the remaining methods are unable to take full advantage of the labeled samples to learn the adjustable parameters, although they ensure that the base-training memory is fully utilized. It is worth noting that the proposed method is also 0.79% higher than the full fine-tuning of the parameters. This indicates that full fine-tuning of the parameters may suffer from “forgetting the base-training information” as the number of labeled samples increases.

The number of parameters. Based on the presented table, it is evident that the Full FT, 23Frozen, and 34Frozen transfer methods yield unsatisfactory recognition results when compared to the transfer strategy proposed in this study. This outcome can be attributed to incomplete adaptation to the new task or insufficient feature extraction. Furthermore, only the full FT yields similar recognition results to the transfer strategy in this paper. However, it requires 1.23 M training parameters for complete fine-tuning, which is more than twice the number of training parameters required for the proposed method in this study, which is 495.57 K. Thus, the transfer strategy proposed in this paper achieved improved recognition accuracy by fully extracting target features and adapting to the new task with a smaller number of parameters.

4.3.3. Comparison with Different Embedding Functions

The present experiment investigates the effect of different embedding functions on recognition accuracy in terms of independent embedding space only, public embedding space only, and a combination of different embedding functions. As shown in

Table 3. Recognition accuracy of different embedding functions.

Embedding Function		Accuracy%
		One-Shot Five-Way	Five-Shot Five-Way
	NONE-NONE	70.83	84.61
	Attention	74.17	84.69
Independent	BiLstm	72.31	83.10
	Attention+BiLstm	72.99	84.40
	GCN	72.27	84.64
Public	Deepset	72.00	84.41
	GCN-BiLstm	72.30	85.16
	Deepset-Attention	73.42	83.95
Dual-task	GCN-Deepset	71.98	85.02
	GCN-Attention	75.23	86.46

The bolded parts are the methods with the best recognition results.

and Figure 12, all three types of embedding methods improve recognition accuracy compared to no embedding at all.

The first part of the experiment focuses on the independent embedding space only. For the recognition of a one-shot, five-way task, the embedding space with Multi-head Attention demonstrates significantly higher recognition accuracy compared to other embedding functions. Specifically, the recognition accuracy of the attention mechanism is 1.4% higher than that of GCN, 1.86% higher than BiLSTM, and 1.5% higher than Deepset. This result can be attributed to the embedding space’s purpose of embedding prototypes of different classes, with the main task being to highlight differences between different classes. While GCN primarily concerns the relationship between data points, it is effective in clustering similar samples. BiLSTM is concerned with sequence correlation, while Deepset lacks the feature of highlighting the weak differences between class prototypes of different classes of ships. The experimental results demonstrate that the recognition accuracy improvement is not significant, even with the addition of other embedding functions on top of the Multi-head Attention. For the five-shot, five-way task recognition, the recognition accuracy of the embedding functions excluding attention decreases rather than increases when compared to no embedding. This is due to the fact that the added embedding functions not only fail to highlight differences between class prototypes but also increase network complexity, making network training more difficult.

The second part of the experiment focuses on the public embedding space only. Compared to Deepset, GCN improves recognition accuracy by 0.27% and 0.23% with fewer parameters. In the third part, different combinations of embedding functions are examined, demonstrating that the combination in this study does not rely on increasing network complexity to improve recognition accuracy. As shown in Table 3, the recognition accuracy of the embedding space combination with GCN as the public embedding function is higher than that of the embedding space combination with Deepset as the public embedding function for the five-shot, five-way task by 1.21%, 1.07%, and 2.51%. This result is due to the excellent clustering function of GCN, which weakens the variability between similar samples, making the samples more clustered, and reducing the chance of class prototypes. The GCN-Attention embeddings have higher recognition accuracy than the combined effect of other functions because GCN and attention play different and irreplaceable roles for HRRP characteristics, respectively. GCN weakens the differences between HRRP samples of the same class by clustering, while attention highlights the weak difference of the prototypes between different classes by calculating the weights.

The Number of parameters.

Table 4. Number of parameters.

Embedding Function	GCN-BiLstm	Deepset-Attention	GCN-Deepset	GCN-Attention
params (M)	3.67 M	6.30 M	7.35 M	3.15 M

The bolded parts are the methods with the best recognition results.

shows the parameter count for various embedding functions. The results indicate that the GCN-Attention embedding function has the lowest number of parameters in comparison to other dual-task embedding functions while also achieving superior accuracy. This suggests that the GCN-Attention embedding function has higher parameter efficiency.

4.3.4. Ablation Studies

This section examines the method proposed in this paper and its ablation variants. As presented in

Table 5. Recognition accuracy of ablation variants.

					Accuracy%
	Fully FT	TATS	GCN	Attention	One-Shot Five-Way	Five-Shot Five-Way
1	√			√	73.89	84.39
2	√		√	√	75.52	85.67
3		√			70.83	84.61
4		√	√		72.27	84.64
5		√		√	74.17	84.69
6		√	√	√	75.23	86.46

The bolded parts are the methods with the best recognition results.

, with full parameters of the feature extractor trained, the recognition accuracy attained during the meta-training phase is 75.52% and 85.67%. Subsequently, after applying the transfer strategy proposed in this study, the accuracy is 75.2% and 86.46%. Notably, there is no reduction in accuracy and a gain of 0.79% when the number of labeled samples is only 5. These results indicate that our transfer strategy ensures no loss of information when adapting to new tasks and prevents “information forgetting” to the full fine-tuning method. Moreover, as presented in Figure 13, compared with the fully FT, the convergence speed of the method in this paper is faster.

Compared to no embedding function, attention as independent embedding space only and GCN as public embedding space only, respectively, enhance recognition accuracy, with Attention improving by 3.34% and 0.08%, and GCN improving by 1.44% and 0.03%. These findings highlight the crucial roles of Attention and GCN in improving accuracy in the classification process.

Moreover, the dual-task embedding function that utilizes Attention and GCN for instance embedding and prototype embedding, respectively, boosts accuracy by 4.4% and 1.85% compared to without embedding. These results demonstrate that Attention and GCN play different roles in the classification process and are critical to the success of the proposed method.

4.3.5. Effect of Network Parameters

The effect of the network parameters on the recognition accuracy was discussed in this subsection. Specifically, the variety of the recognition accuracy of the proposed method in different learning rates was studied on one-shot five-way and five-shot five-way tasks, as well as the effect of the number of heads of the Multi-head Attention of the five-shot, five-way task.

a. Learning rate. The influence of learning rate on recognition accuracy was discussed and the results were shown in Figure 14. As seen from Figure 14, a too large or too small learning rate will make the recognition accuracy unsatisfactory. A large learning rate will make the instability of the recognition accuracy and a small learning rate will lead to slow learning.

Table 6. Recognition accuracy of different learning rates.

Learning Rate	Accuracy%
	One-Shot Five-Way	Five-Shot Five-Way
${10}^{-3}$	53.90	56.17
${10}^{-4}$	75.02	85.51
${10}^{-5}$	74.89	86.46
${10}^{-6}$	75.23	85.86
${10}^{-7}$	71.04	80.22

The bolded parts are the methods with the best recognition results.

shows the accuracy curves of different learning rates. It can be seen from Table 6 that the performance for classification of one-shot, five-way of the proposed method is best when the learning rate is set to ${10}^{-6}$. And the learning rate is set to ${10}^{-5}$ for the five-shot, five-way tasks.

b. Number of heads of the Multi-head Attention.

Table 7. Recognition accuracy of different numbers of heads.

Number of Head	Accuracy % Five-Shot Five-Way
1	86.46
2	85.99
3	86.61
4	86.10

The bolded parts are the methods with the best recognition results.

presents the impact of the number of heads in Multi-head Attention on the recognition accuracy of five-shot five-way tasks. The results indicate that there is no improvement in accuracy as the number of heads increases. On the contrary, increasing the number of heads leads to a rise in the number of training parameters and can result in overfitting when the number of samples is limited. As a consequence, the number of heads is set to 1 in this paper.

4.3.6. Effect of Number of Training Samples

In this experiment, the effect of the number of samples in the training set on the recognition accuracy is investigated. To this end, the training curves for different numbers of HRRP samples are obtained. Specifically, we perform meta-training based on initialized weights obtained from base-training with different sample sizes by keeping the number of samples in the test set constant but varying the number of HRRP samples in the training set.

Figure 15 shows the training curve with the different numbers of training samples. As expected, the accuracy increases with the increase in the number of samples in the training set.

Table 8. Recognition accuracy of different numbers of training samples.

Number of Samples	Accuracy % Five-Shot Five-Way
100	83.36
200	85.72
400	85.78
500	86.35
600	86.46

The bolded parts are the methods with the best recognition results.

presents the accuracy of the test set for different training sample sizes. We observe that the recognition accuracy decreases by only 0.74% when the number of samples is reduced from 600 to 200. This result indicates that our method is robust to changes in the sample size. Notably, the proposed method outperforms MatchNet, Protonet, and MTL even when the number of samples is only 100. Moreover, when the number of training samples is 200, our method achieves higher recognition accuracy than FEAT.

In conclusion, our experiments demonstrate the effectiveness and robustness of our proposed method in recognizing HRRP patterns. These findings are valuable for future research in this area.

4.3.7. Generalization Verification

This experiment employed the method of this paper in Conv4, Resnet12 (the network of this paper), and Resnet18, respectively, as shown in

Table 9. Recognition accuracy of different backbones in five-shot conditions.

	Accuracy %
	Conv4	Resnet12	Resnet18
Ours	77.98	86.46	83.60
FEAT	75.12	84.39	80.96
Change the Embedding Function
GCN-Bilstm	77.67	85.16	82.61
Deepset-attention	78.14	83.95	83.04
Change Transfer Strategy
Fully FT	-	85.67	83.53
Fully SS	-	84.65	81.77
23Frozen	-	85.30	81.87
34Frozen	-	84.43	81.48

The bolded parts are the methods with the best recognition results.

. Due to the simple structure of Conv4, no base-training and transfer operations were performed, and only the embedding function was assessed using this network.

It can be seen from the table that increasing the depth of the network does not necessarily enhance the recognition accuracy, due to the limited number of samples. Moreover, the dual-task embedding function in this paper performs well in both Resnet12 and Resnet18, surpassing the state-of-the-art few-shot method FEAT by 1.96% and 2.64%, respectively. Additionally, compared with Deepset-attention, which has the highest number of parameters, the accuracy achieved by the method in this paper is 2.4% and 0.56% higher for Resnet12 and Resnet18, respectively. In Conv4, Deepset-attention yields a slightly better accuracy of 0.16% than the method proposed in this paper, but with twice as many parameters. Notably, in Resnet18, the transfer methods used during the meta-training stage, namely fully SS, 23frozen, and 34frozen, show significantly lower accuracy than the method proposed in this paper, by 1.83%, 1.73%, and 2.12%, respectively. This could be attributed to inadequate transferring, memory loss, and insufficient adaptation to the task. In conclusion, the method presented in this paper outperforms other methods across different network skeletons.

5. Conclusions

In this study, a novel few-shot HRRP target recognition approach, denoted as Task-Specific Mate-learning, is introduced to address the challenge posed by limited labeled samples and high target variability. Initially, the base learning and meta-learning are employed to mitigate the prevalent overfitting issues within the few-shot HRRP recognition domain. Subsequently, the Task-Adaptive Mixed Transfer technique is proposed, which achieves a classification accuracy no less than that of complete fine-tuning, even when training with only half the number of parameters as compared to full fine-tuning. This highlights the effectiveness of this strategy in preserving valuable information while minimizing information loss during the transfer process, as supported by the recognition accuracy curve. Furthermore, upon visualizing the classification results, it is evident that Space-Adjusted Meta Embedding reduces intra-class sample variations, enhances the separability among distinct ship classes, and alleviates the challenges associated with high target variability during the target recognition process. This adjustment enables instance embeddings to better align with class prototypes in the HRRP target classification task.The actual measured HRRP data are also employed in the proposed method. In comparison to state-of-the-art few-shot learning methods, superior performance in the identification of unknown ship classes with limited labels is achieved by our approach, attributed to its ability to learn from known ship classes. Furthermore, our method demonstrates a degree of generalization and robustness concerning variations in the number of training samples. Specifically, the recognition accuracy of our approach experiences only a marginal decrease of 0.74%, even when the training sample size is reduced from 600 to 200. However, in reality, a more complex scenario exists where radar target recognition systems must identify new class targets with zero samples, a challenge known as zero-shot recognition. Our paper has not addressed this scenario, and as such, we will explore zero-shot learning to enable the zero-shot recognition of new class HRRP targets our future work.