A Multiple Agile Satellite Staring Observation Mission Planning Method for Dense Regions
Abstract
:1. Introduction
- Traditional clustering methods used in the scanning observation mode cannot be directly applied to the emerging staring observation mode. This is because the rectangular field of view constraint in the staring mode is more stringent and demanding compared to the strip field of view constraint in the scanning mode. Additionally, in staring imaging, the imaging is not constrained by the motion direction during the imaging of the Earth’s surface, allowing for more flexible maneuverability.
- In the current research, the assumption is made that the satellite’s attitude transition time is independent of the satellite’s actual position and is considered constant. However, in reality, the attitude transition time depends on various factors such as the attitude torque of the satellite, the angular velocity of the axes, and the angular acceleration. When performing transitions for Earth observation tasks, it is not appropriate to simply set a fixed value for the attitude transition time. These factors need to be taken into account to accurately model the attitude transition time during the task transitions.
- In the current mission planning and modeling process, the simultaneous consideration of satellite’s attitude transition time, energy consumption during attitude maneuvers, and balanced utilization of on-board resources between adjacent tasks is lacking. This incomplete modeling approach may not be conducive to practical applications. To achieve more accurate mission planning, it is necessary to comprehensively consider these factors and ensure efficient utilization of resources and energy during task execution. This will help improve the efficiency and performance of task execution.
2. Materials and Methods
2.1. Target Clustering in Staring Observation Mode
2.1.1. Clustering Model Construction
2.1.2. Solution Modelling via the DBSCAN Algorithm
2.2. Mission Planning Based on the Heuristic ACO Algorithm
2.2.1. Mission Planning Process Assumptions and Simplifications
- Presume that the targets, clustered by field of view, remain stationary.
- Adherence to the satellite’s resource constraints is requisite, specifically, energy limitations and storage capacity restrictions.
- Each observation target needs to be observed by the satellite only once, and the staring observation time is the same for each observation target.
- The satellite can only observe one mission at the same time.
- Neglecting the potentiality of satellite malfunction.
2.2.2. Mission Planning Model Construction
- Problem description
- Constriants
- Visible time window constraints. The time window constraint for each target observation moment, the satellite observable time, must be within the visible time window.
- Start observation time constraints. The start time of adjacent observation tasks cannot overlap.
- Slew angle constraints. When the mission is converted, the slew angle cannot exceed the maximum slew angle of the satellite.
- Solar altitude angle constraints. For optical cameras, only a certain range of solar altitude angles can be observed.
- Energy constraints. The sum of the energy consumed by the th satellite observation mission and the energy consumed by the mission switch cannot exceed the total energy of the satellite.
- Storage capacity constraints. The sum of storage space consumed by the th satellite observation mission cannot exceed the total storage capacity of the satellite.
- Attitude transfer time constraints. In reality, this time period is influenced by the satellite’s position, the target’s location, and the moment of attitude control, and as such, it cannot be determined using fixed constants. It is assumed that the satellite maneuvers using the shortest possible path, that is, the satellite acceleration–uniform speed–deceleration process completes the attitude transfer. The attitude transfer time according to the above maneuver process can be calculated in two cases, as shown in Figure 3:By installing the optical load on the platform, the rotary axis can be oriented in various directions, and the platform can be adjusted along the rotary axis. To ensure reliability, a drive mechanism is employed that restricts the maximum angular velocity of the rotary axis during platform adjustment. To quickly stabilize the optical axis, the adjustment operation is typically carried out at an angular velocity of zero. The strategy, depicted in Figure 3, involves accelerating and decelerating at the maximum angular acceleration without surpassing the maximum speed . The two typical adjustment requirements described by Equation (9) are as follows:where represents the transition angle from the th mission to the th mission. It follows that the attitude transfer time constraint should satisfy the following condition:
- Optimization objective function
2.2.3. Based on Heuristic ACO Algorithm
- Ant transfer strategy
- Pheromone concentration :represents the pheromone concentration between task and task . Once every ant in the current generation has finalized constructing their solution, it becomes necessary to update the pheromone within the solution space.
- Interval mission transfer time :signifies the inverse of the time interval during which the satellite initiates the execution of task following the completion of task , that is:Equation (14) delineates the influence of the time interval between task executions on the transfer probability, where a larger time interval suggests that the satellite spends more time in unproductive waiting, thereby potentially reducing the number of tasks it can perform within a fixed time range.
- Prioritization of transfer tasks :signifies the priority of undertaking the ensuing task. In the progression to the subsequent task, the higher the task’s priority, the greater its value becomes, thereby optimizing the final total observed benefit.
- Length of time a task can start observation :signifies the duration of available initiation time for executing the subsequent task, namely:Equation (15) signifies the time span within which the ants can transition to task . The sigmoid function can map any real value to a value between 0 and 1. From the properties of the function, it can be observed that when is small, the value of tends to 1, indicating a higher probability of selecting tasks that are closer to the latest observable start time. Conversely, as increases, the probability decreases. This constitutes the critical heuristic element proposed by the algorithm in this study.
- Pheromone update strategy
- Heuristic ACO algorithm process
- Obtain algorithm input information, such as time windows, task point information, and satellite properties.
- Initialize algorithm data by clearing the planning information.
- Calculate the observation time windows and maneuvering time for all feasible tasks based on the given constraints. Calculate the transition probability based on these calculations. Use the roulette wheel selection method to determine the next task (task i) to be observed.
- Add the selected task (task i) to the planning sequence.
- Repeat steps 3 and 4 until all feasible tasks are planned for the current ant.
- Repeat steps 3, 4, and 5 until all ants in the current generation have completed their traversal.
- Check if the maximum iteration limit has been reached. If not, update the pheromone information and global best planning solution. Continue with the algorithm iteration. Otherwise, end the algorithm iteration and output the planning result.
3. Results
3.1. Experimental Setup
3.2. Analysis of ACO Algorithm Parameter Settings
3.3. Algorithm Stability Test
3.4. Simulation Experiment Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, X.; Reinelt, G.; Dai, G.; Spitz, A. A mixed integer linear programming model for multi-satellite scheduling. Eur. J. Oper. Res. 2019, 275, 694–707. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O.; Adam, E.; Ismail, R. Intra-and-Inter Species Biomass Prediction in a Plantation Forest: Testing the Utility of High Spatial Resolution Spaceborne Multispectral RapidEye Sensor and Advanced Machine Learning Algorithms. Sensors 2014, 14, 15348–15370. [Google Scholar] [CrossRef]
- Shakhmatov, E.; Belokonov, I.; Timbai, I.; Ustiugov, E.; Nikitin, A.; Shafran, S. SSAU Project of the nanosatellite SamSat-QB50 for monitoring the Earth’s thermosphere parameters. In Proceedings of the Scientific and Technological Experiments on Automatic Space Vehicles and Small Satellites, Amsterdam, The Netherlands, 31 May 2015; Volume 104, pp. 139–146. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, M.; Liu, W.; Li, X.; Yu, S.; Lu, C.; Wickert, J. Initial assessment of the COMPASS/BeiDou-3: New-generation navigation signals. J. Geod. 2017, 91, 1225–1240. [Google Scholar] [CrossRef]
- Zacharias, N.; Dorland, B. The concept of a stare-mode astrometric space mission. Publ. Astron. Soc. Pac. 2006, 118, 1419–1427. [Google Scholar] [CrossRef]
- Lemaitre, M.; Verfaillie, G.; Jouhaud, F.; Lachiver, J.M.; Bataille, N. Selecting and scheduling observations of agile satellites. Aerosp. Sci. Technol. 2002, 6, 367–381. [Google Scholar] [CrossRef]
- Habet, D.; Vasquez, M.; Vimont, Y. Bounding the optimum for the problem of scheduling the photographs of an Agile Earth Observing Satellite. Comput. Optim. Appl. 2010, 47, 307–333. [Google Scholar] [CrossRef]
- Xu, R.; Chen, H.; Liang, X.; Wang, H. Priority-based constructive algorithms for scheduling agile earth observation satellites with total priority maximization. Expert Syst. Appl. 2016, 51, 195–206. [Google Scholar] [CrossRef]
- Mok, S.H.; Jo, S.; Bang, H.; Leeghim, H. Heuristic-Based Mission Planning for an Agile Earth Observation Satellite. Int. J. Aeronaut. Space Sci. 2019, 20, 781–791. [Google Scholar] [CrossRef]
- Qiu, W.; Xu, C.; Ren, Z.; Teo, K.L. Scheduling and Planning Framework for Time Delay Integration Imaging by Agile Satellite. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 189–205. [Google Scholar] [CrossRef]
- Du, B.; Li, S.; She, Y.; Li, W.; Liao, H.; Wang, H. Area targets observation mission planning of agile satellite considering the drift angle constraint. J. Astron. Telesc. Instrum. Syst. 2018, 4, 047002. [Google Scholar] [CrossRef]
- Yu, Y.; Hou, Q.; Zhang, J.; Zhang, W. Mission scheduling optimization of multi-optical satellites for multi-aerial targets staring surveillance. J. Frankl. Inst.-Eng. Appl. Math. 2020, 357, 8657–8677. [Google Scholar] [CrossRef]
- Cui, K.; Xiang, J.; Zhang, Y. Mission planning optimization of video satellite for ground multi-object staring imaging. Adv. Space Res. 2018, 61, 1476–1489. [Google Scholar] [CrossRef]
- Ji, H.; Huang, D. A mission planning method for multi-satellite wide area observation. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419890715. [Google Scholar] [CrossRef]
- Vasquez, M.; Hao, J.K. A “logic-constrained” knapsack formulation and a tabu algorithm for the daily photograph scheduling of an earth observation satellite. Comput. Optim. Appl. 2001, 20, 137–157. [Google Scholar] [CrossRef]
- Xhafa, F.; Herrero, X.; Barolli, A.; Takizawa, M. Using STK Toolkit for Evaluating a GA base Algorithm for Ground Station Scheduling. In Proceedings of the 2013 Seventh International Conference on Complex, Intelligent, and Software Intensive Systems (CISIS), New York, NY, USA, 3–5 July 2013; pp. 265–273. [Google Scholar] [CrossRef]
- Tangpattanakul, P.; Jozefowiez, N.; Lopez, P. A multi-objective local search heuristic for scheduling Earth observations taken by an agile satellite. Eur. J. Oper. Res. 2015, 245, 542–554. [Google Scholar] [CrossRef]
- Song, Y.; Ou, J.; Wu, J.; Wu, Y.; Xing, L.; Chen, Y. A cluster-based genetic optimization method for satellite range scheduling system. Swarm Evol. Comput. 2023, 79, 101316. [Google Scholar] [CrossRef]
- Liu, X.; Laporte, G.; Chen, Y.; He, R. An adaptive large neighborhood search metaheuristic for agile satellite scheduling with time-dependent transition time. Comput. Oper. Res. 2017, 86, 41–53. [Google Scholar] [CrossRef]
- Long, X.; Wu, S.; Wu, X.; Huang, Y.; Mu, Z. A GA-SA Hybrid Planning Algorithm Combined with Improved Clustering for LEO Observation Satellite Missions. Algorithms 2019, 12, 231. [Google Scholar] [CrossRef]
- Lu, Z.; Shen, X.; Li, D.; Chen, Y. Integrated Imaging Mission Planning Modeling Method for Multi-Type Targets for Super-Agile Earth Observation Satellite. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2022, 15, 4156–4169. [Google Scholar] [CrossRef]
- Bianchessi, N.; Cordeau, J.F.; Desrosiers, J.; Laporte, G.; Raymond, V. A heuristic for the multi-satellite, multi-orbit and multi-user management of Earth observation satellites. Eur. J. Oper. Res. 2007, 177, 750–762. [Google Scholar] [CrossRef]
- Kebin, G.; Guohua, W.U.; Jianghan, Z. Multi-Satellite Observation Scheduling Based on a Hybrid Ant Colony Optimization. Adv. Mater. Res. 2013, 765–767, 532–536. [Google Scholar] [CrossRef]
- Song, Y.; Ou, J.; Suganthan, P.N.; Pedrycz, W.; Yang, Q.; Xing, L. Learning Adaptive Genetic Algorithm for Earth Electromagnetic Satellite Scheduling. IEEE Trans. Aerosp. Electron. Syst. 2023, 1–17. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, M.; Shen, X.; Zhang, G.; Lu, Z.; Xu, J. A Multi-Objective Modeling Method of Multi-Satellite Imaging Task Planning for Large Regional Mapping. Remote Sens. 2020, 12, 344. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Q.; Li, C.; Wang, F. Mission planning for Earth observation satellite with competitive learning strategy. Aerosp. Sci. Technol. 2021, 118, 107047. [Google Scholar] [CrossRef]
- Deng, X.; Dong, Y.; Xie, S. Multi-Granularity Mission Negotiation for a Decentralized Remote Sensing Satellite Cluster. Remote Sens. 2020, 12, 3595. [Google Scholar] [CrossRef]
- Song, Y.; Wei, L.; Yang, Q.; Wu, J.; Xing, L.; Chen, Y. RL-GA: A Reinforcement Learning-based Genetic Algorithm for Electromagnetic Detection Satellite Scheduling Problem. Swarm Evol. Comput. 2023, 77, 101236. [Google Scholar] [CrossRef]
- Ou, J.; Xing, L.; Yao, F.; Li, M.; Lv, J.; He, Y.; Song, Y.; Wu, J.; Zhang, G. Deep reinforcement learning method for satellite range scheduling problem. Swarm Evol. Comput. 2023, 77, 101233. [Google Scholar] [CrossRef]
- He, C.; Dong, Y.; Li, H.; Liew, Y. Reasoning-Based Scheduling Method for Agile Earth Observation Satellite with Multi-Subsystem Coupling. Remote Sens. 2023, 15, 1577. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, L.; Bouguila, N.; Wang, C.; Chen, Y.; Du, J. BLOCK-DBSCAN: Fast clustering for large scale data. Pattern Recognit. 2021, 109, 107624. [Google Scholar] [CrossRef]
- Merkle, D.; Middendorf, M.; Schmeck, H. Ant colony optimization for resource-constrained project scheduling. IEEE Trans. Evol. Comput. 2002, 6, 333–346. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Cuckoo Search via Levey Flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NABIC 2009), New York, NY, USA, 9–11 December 2009; pp. 210–214. [Google Scholar] [CrossRef]




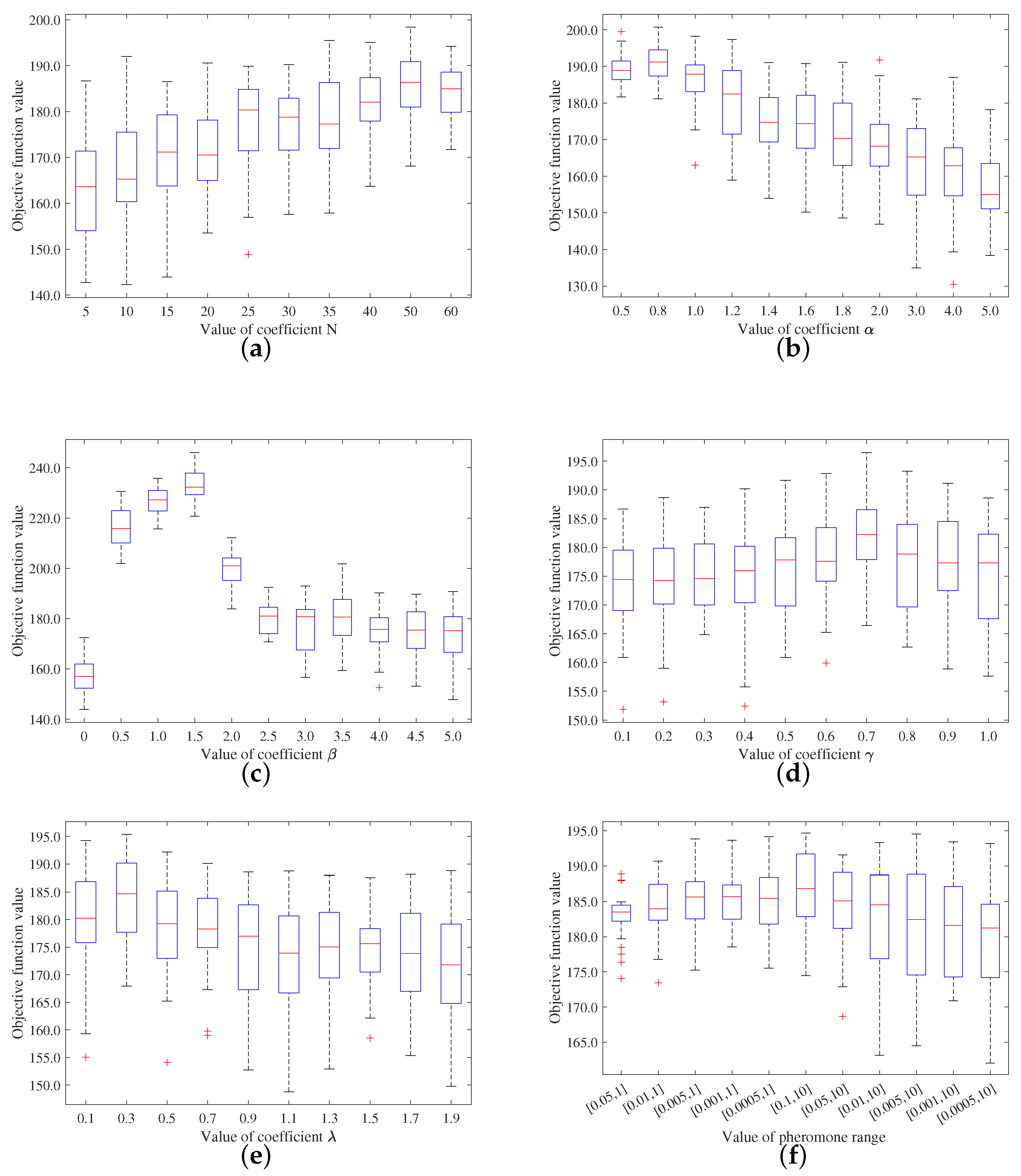
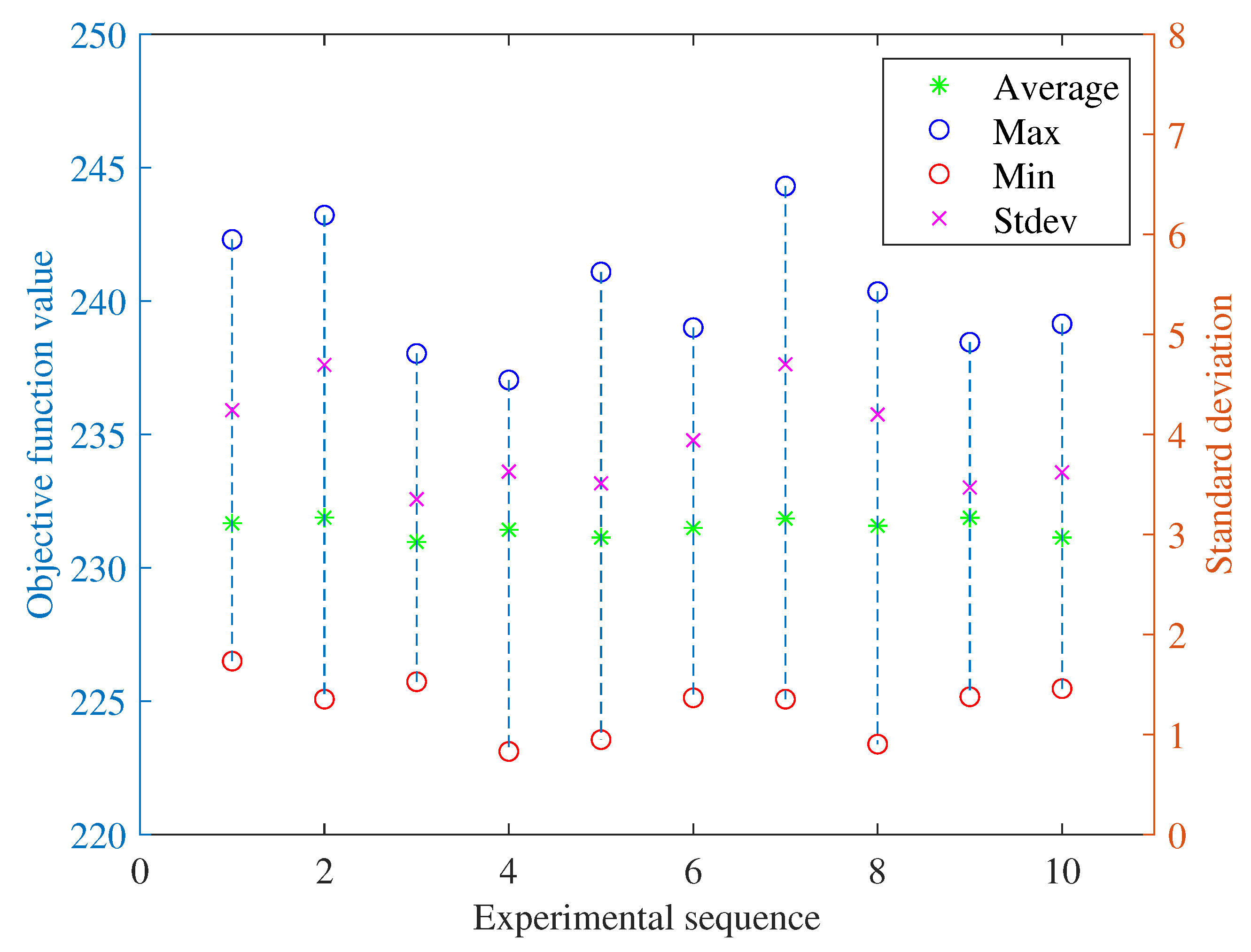

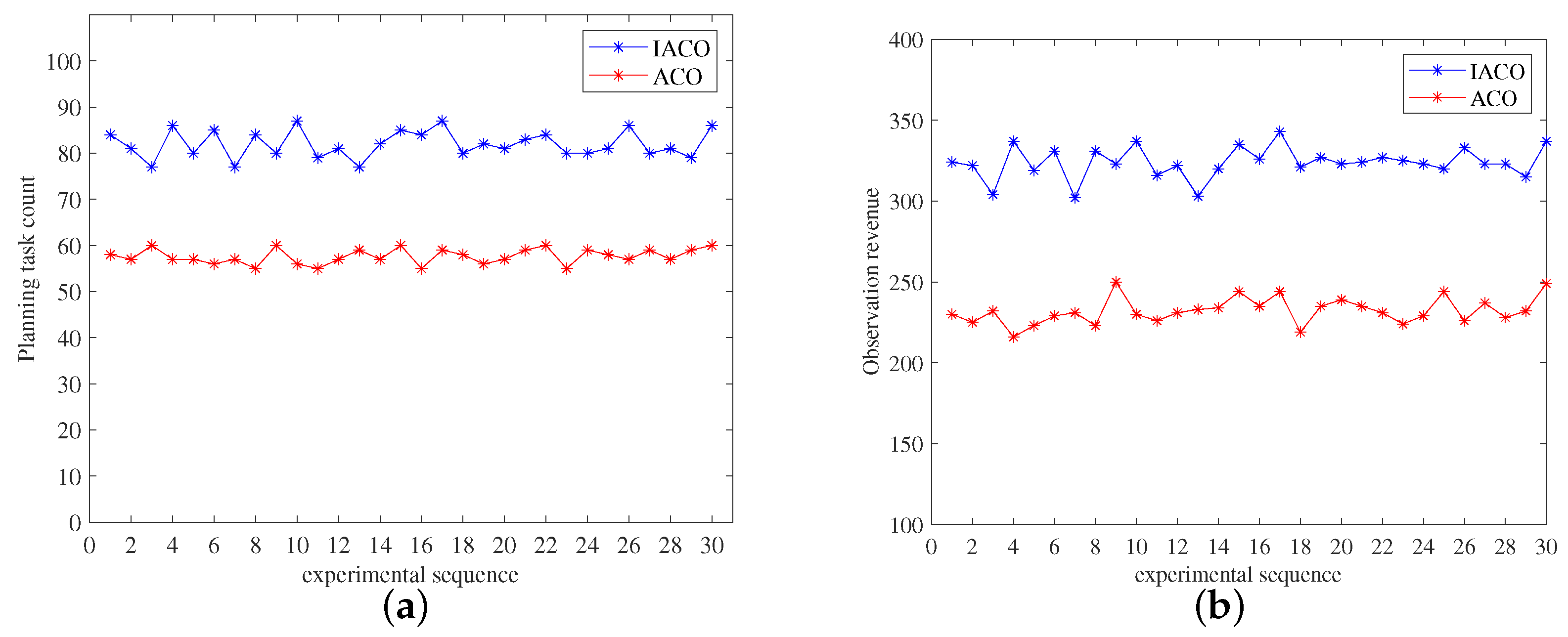
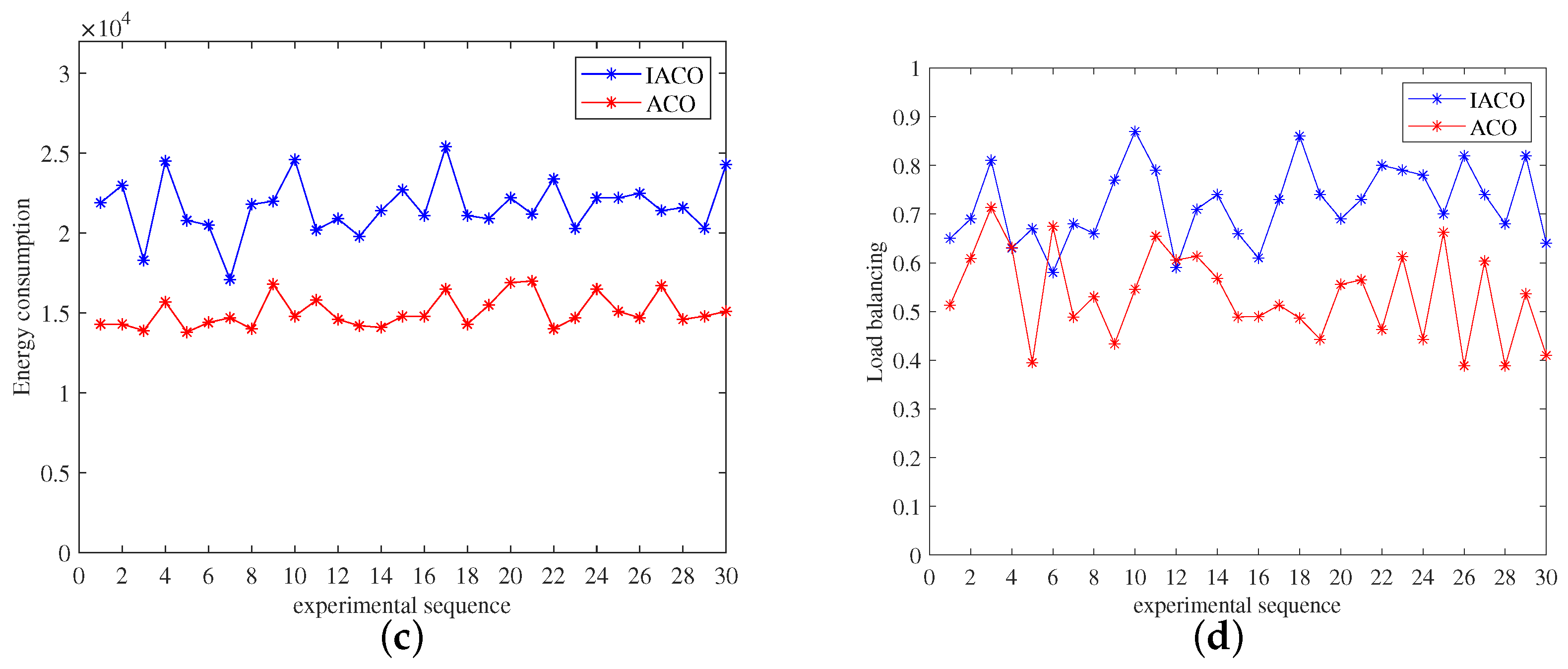
| Notation | Definition |
|---|---|
| , where represents the set of satellites, n represents the number of satellites. | |
| C | , where C represents the set of observation missions after clustering, m represents the number of missions. |
| L | , where L represents the load set of satellites, n represents the number of satellites. |
| , where represents the slew angle set of the satellites, represents the slew angle when the th satellite observes the th mission, represents the maximum slew angle of the satellite. | |
| represents the maximum angular velocity of the satellites. | |
| represents the maximum angular acceleration of the satellites. | |
| , where represents the set of visible time windows, k represents the number of the windows , represents the th visible time window, represents the visible start time, represents the visible end time, represents the visible duration. | |
| , where represents the set of observable time windows, l represents the number of the windows, , represents the th observable time window, represents the observable begin time, represents the observable finalization time, represents the observable duration. | |
| represents the attitude transfer time of the th mission to the th mission. | |
| represents the actual begin observation time of the th mission. | |
| , where represents the energy set of the satellites, n represents the number of satellites. | |
| represents the energy consumed by the th satellite for the th mission. | |
| represents the energy consumption per unit time of the th satellite during the mission observation. | |
| represents the energy consumption per unit time of the attitude maneuver of the th satellite during mission transition. | |
| , where the set of storage capacity of the satellite, n represents the number of satellites. | |
| represents the storage space consumed by the th satellite observing the th mission. | |
| , where represents the set of mission priorities, m represents the number of missions. | |
| represents the maximum single-axis attitude control moment of the satellite. | |
| represents minimum solar altitude angle of the satellite. | |
| z | z represents a bool variable, the execution mission is 1, otherwise it is 0. |
| represents a bool variable, taking the value 1 if the th satellite observes the th mission, and 0 otherwise. | |
| represents a bool variable, taking the value 1 if the th mission is the successor observation mission to the th mission, and 0 otherwise. |
| Satellite Parameters | Satellite 1 | Satellite 2 | Satellite 3 |
|---|---|---|---|
| Inclination | |||
| Right Ascension of Ascending Node | 0 | 0 | 0 |
| Eccentricity | 0 | 0 | 0 |
| Argument of Perigee | 0 | 0 | 0 |
| Initial True Anomaly | |||
| Orbit radius | 7200 km | 7200 km | 7200 km |
| Maximum attitude angular acceleration | |||
| Maximum attitude angular velocity | |||
| Single-axis maximum attitude control moment | 10 | 10 | 10 |
| Maximum roll and pitch angle | |||
| Visible light camera field of view angle |
| Algorithm Parameters | Range of Values |
|---|---|
| N | |
| pheromone range |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.; Wang, H.; Yi, D.; Wang, S.; Zhang, B.; Cui, J. A Multiple Agile Satellite Staring Observation Mission Planning Method for Dense Regions. Remote Sens. 2023, 15, 5317. https://doi.org/10.3390/rs15225317
Huang W, Wang H, Yi D, Wang S, Zhang B, Cui J. A Multiple Agile Satellite Staring Observation Mission Planning Method for Dense Regions. Remote Sensing. 2023; 15(22):5317. https://doi.org/10.3390/rs15225317
Chicago/Turabian StyleHuang, Weiquan, He Wang, Dongbo Yi, Song Wang, Binchi Zhang, and Jingwen Cui. 2023. "A Multiple Agile Satellite Staring Observation Mission Planning Method for Dense Regions" Remote Sensing 15, no. 22: 5317. https://doi.org/10.3390/rs15225317
APA StyleHuang, W., Wang, H., Yi, D., Wang, S., Zhang, B., & Cui, J. (2023). A Multiple Agile Satellite Staring Observation Mission Planning Method for Dense Regions. Remote Sensing, 15(22), 5317. https://doi.org/10.3390/rs15225317







