Surface Motion and Topographic Effects on Ice Thickness Inversion for High Mountain Asia Glaciers: A Comparison Study from Three Numerical Models
Abstract
:1. Introduction
2. Study Area and Datasets
2.1. Study Area
2.2. Datasets
3. Methods
3.1. GlabTop2 Ice Thickness Model Description
3.2. VOLTA Ice-Thickness Inversion Model
3.3. Ice Velocity-Based Model Description
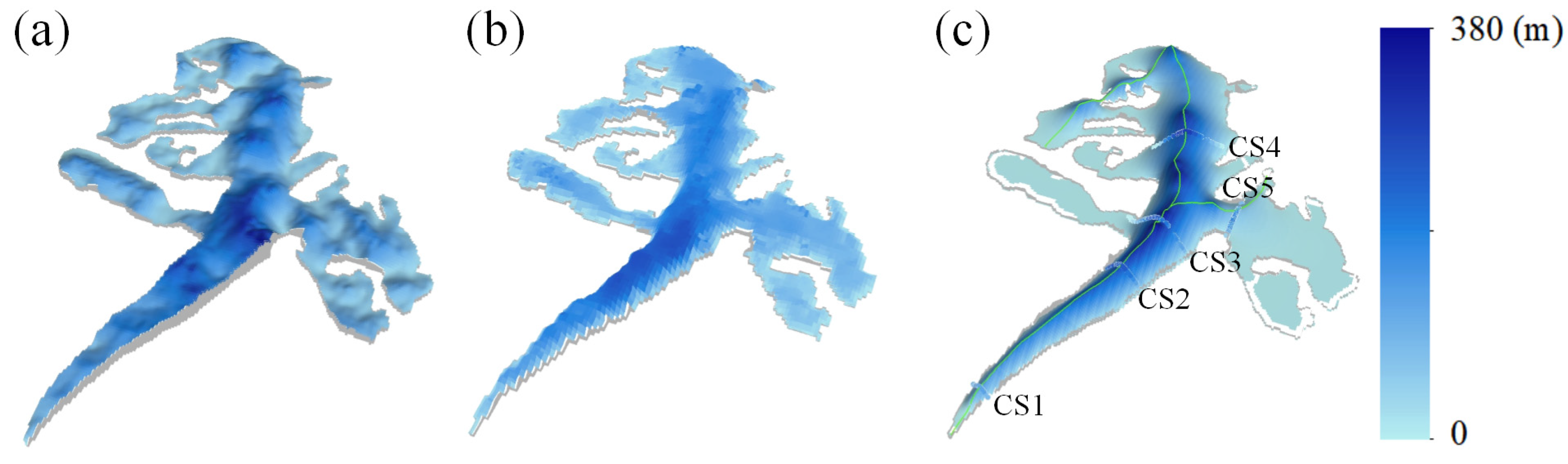
3.4. Accuracy Assessment
4. Results and Analysis
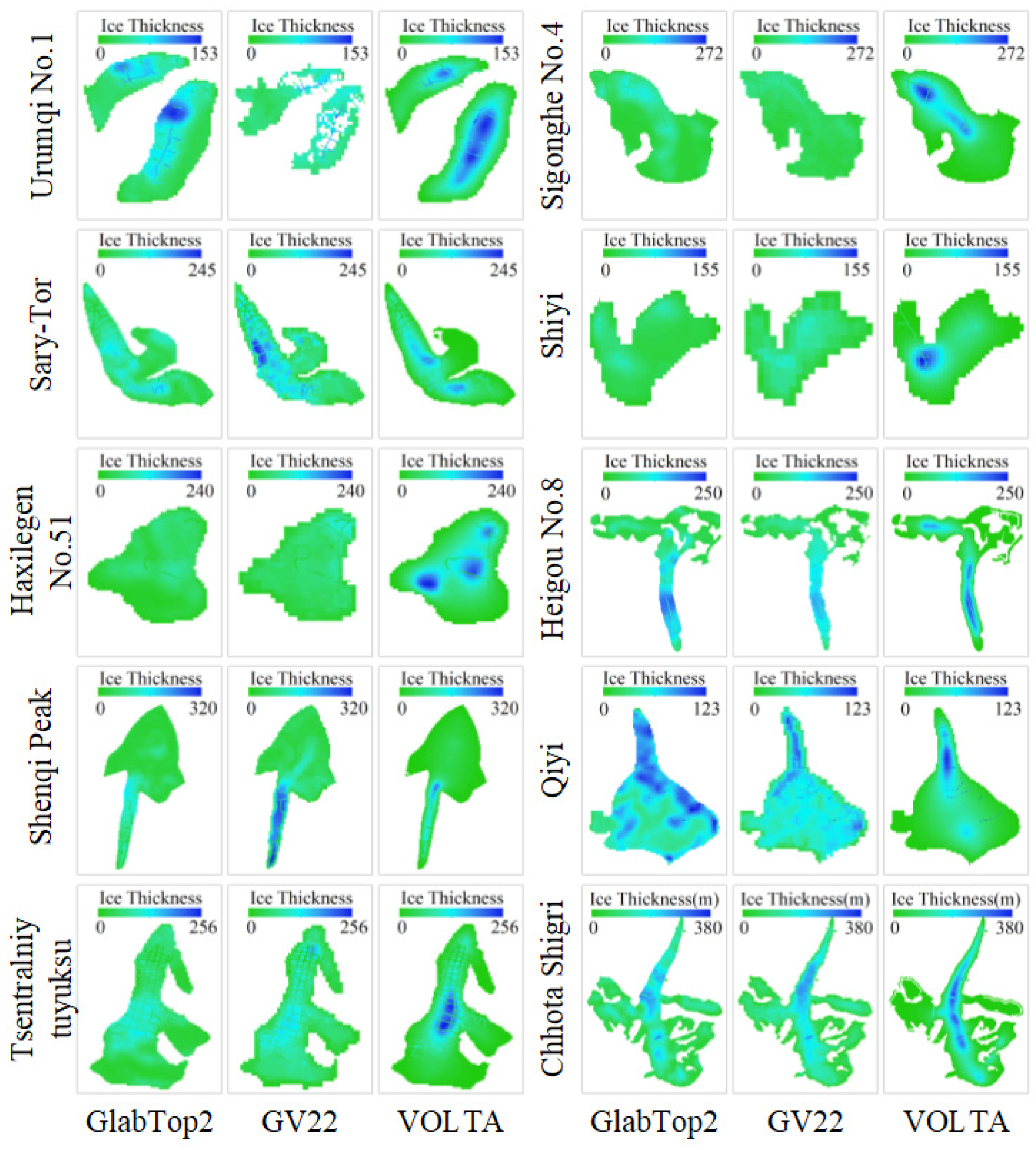
4.1. Spatial Distribution of Simulated Ice Thickness
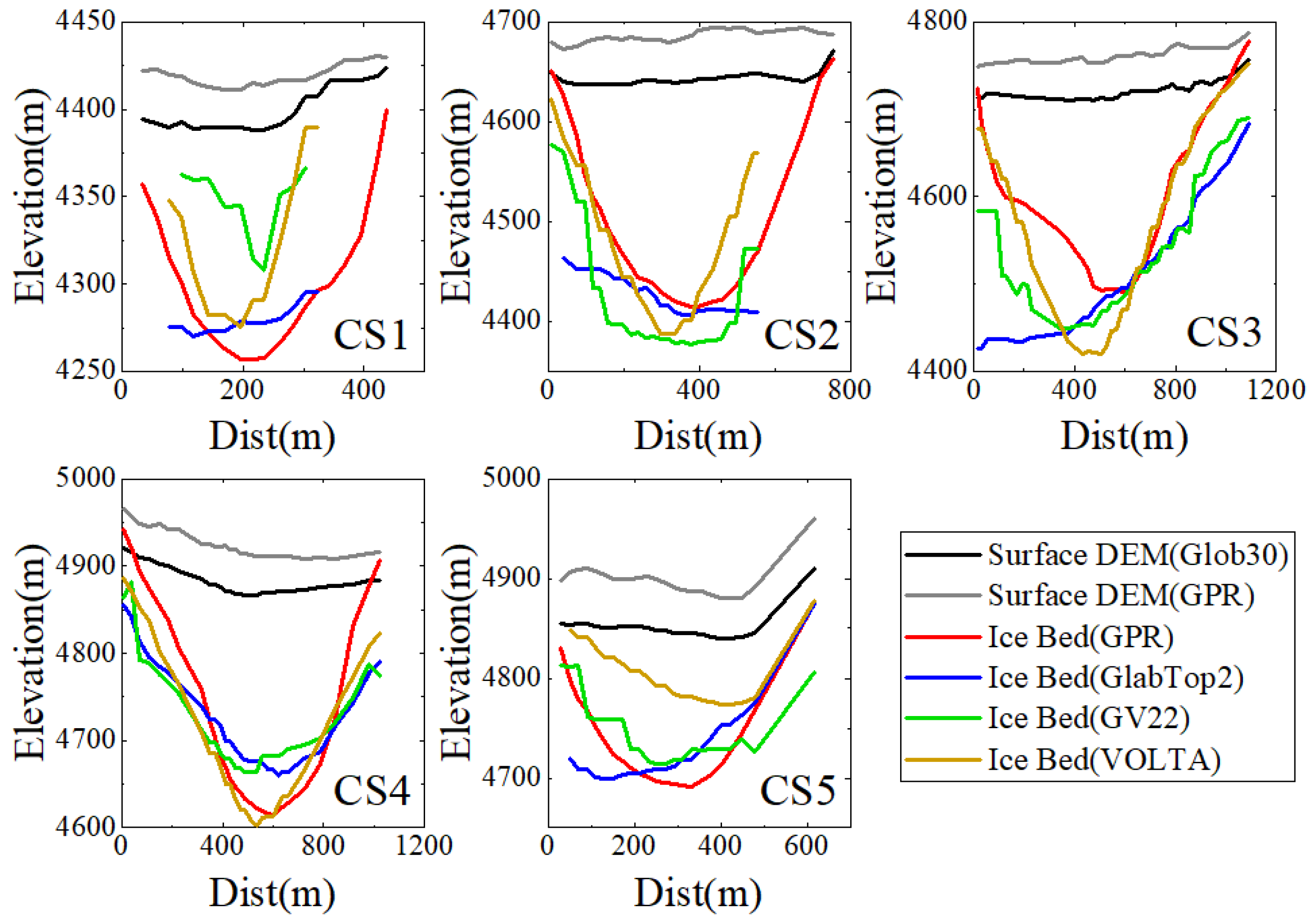
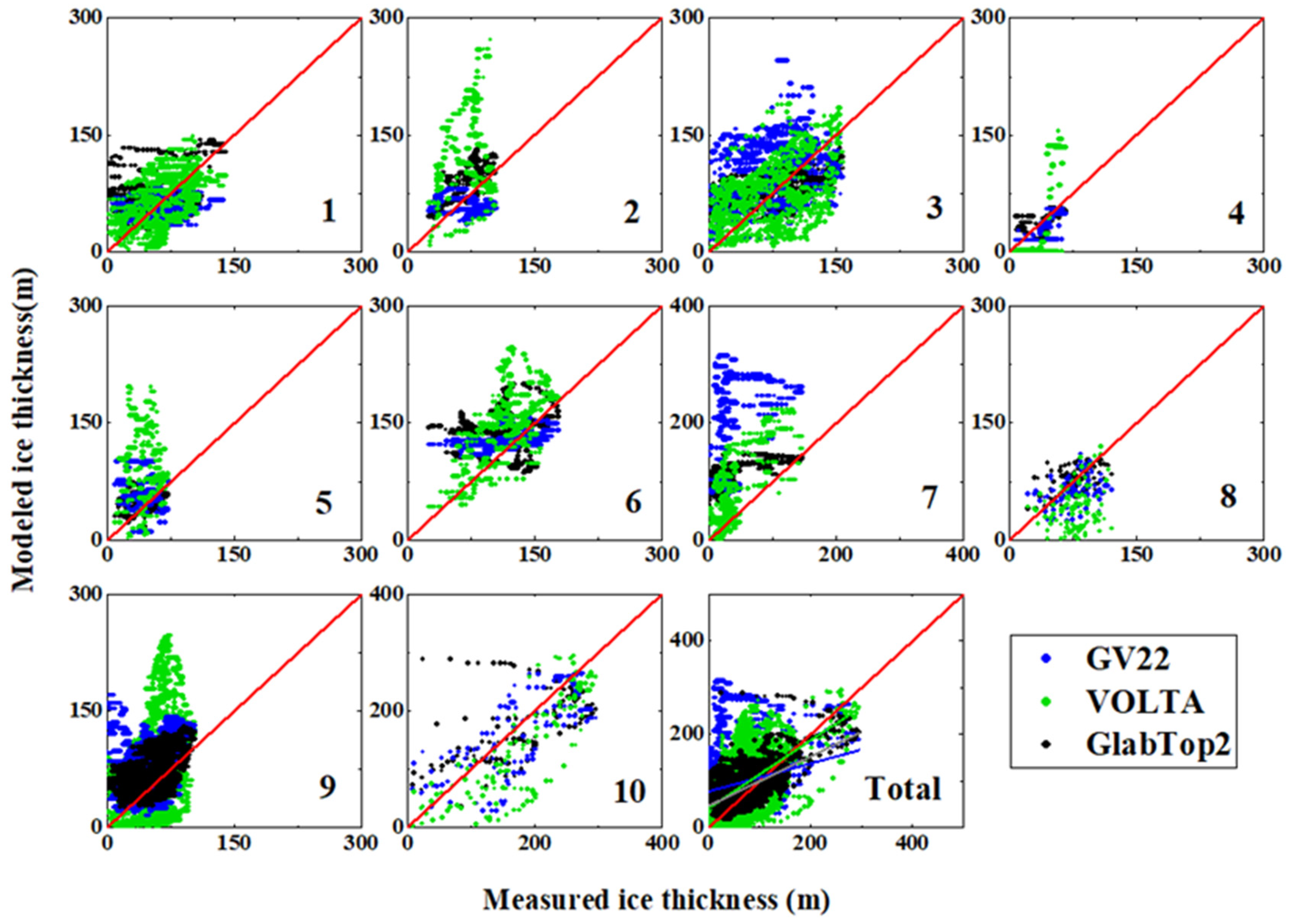
4.2. Accuracy of Simulated Ice Thickness
5. Discussion
5.1. Comparison with Previous Research
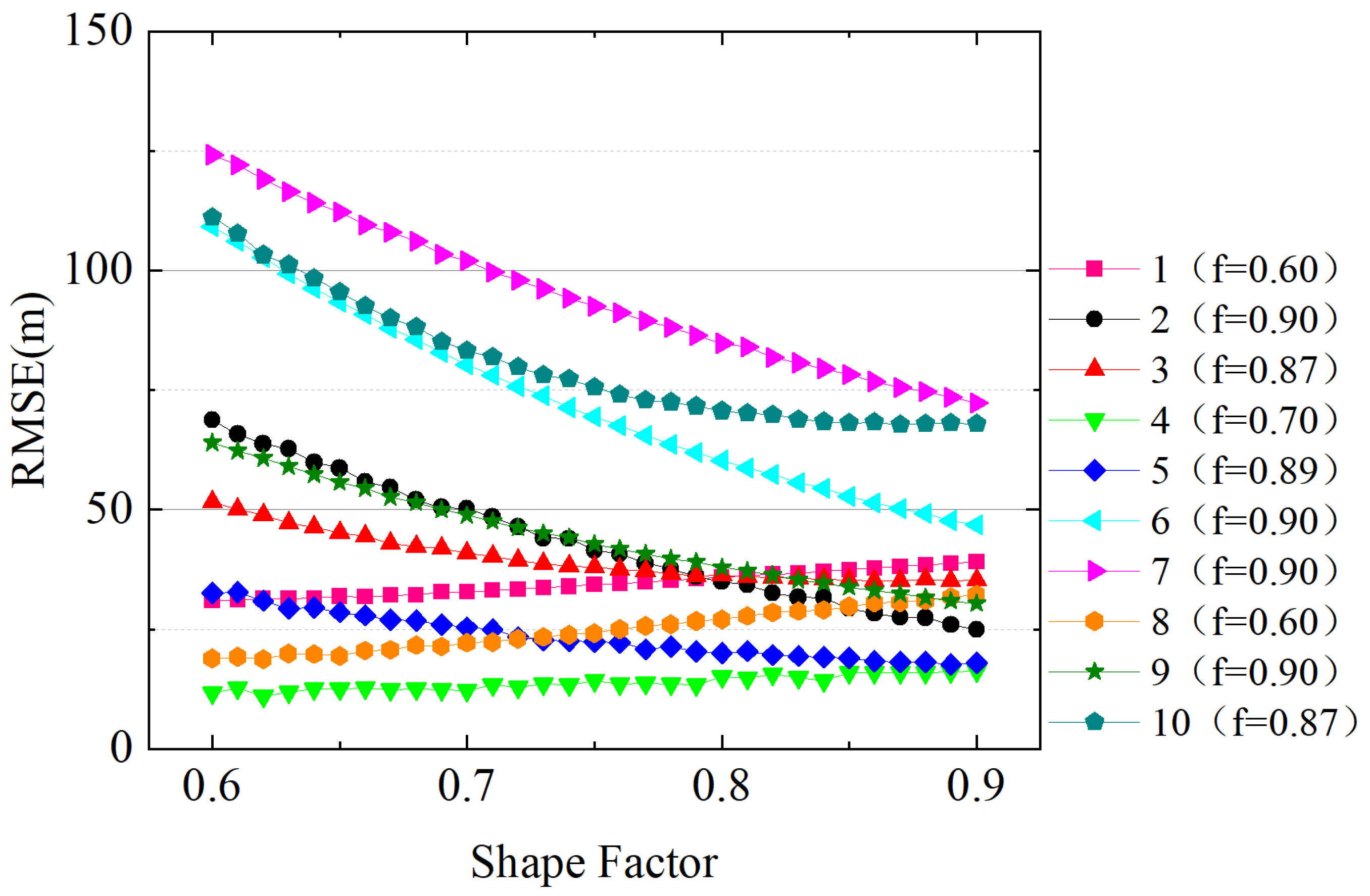
5.2. Sensitivity Analysis of Modeling
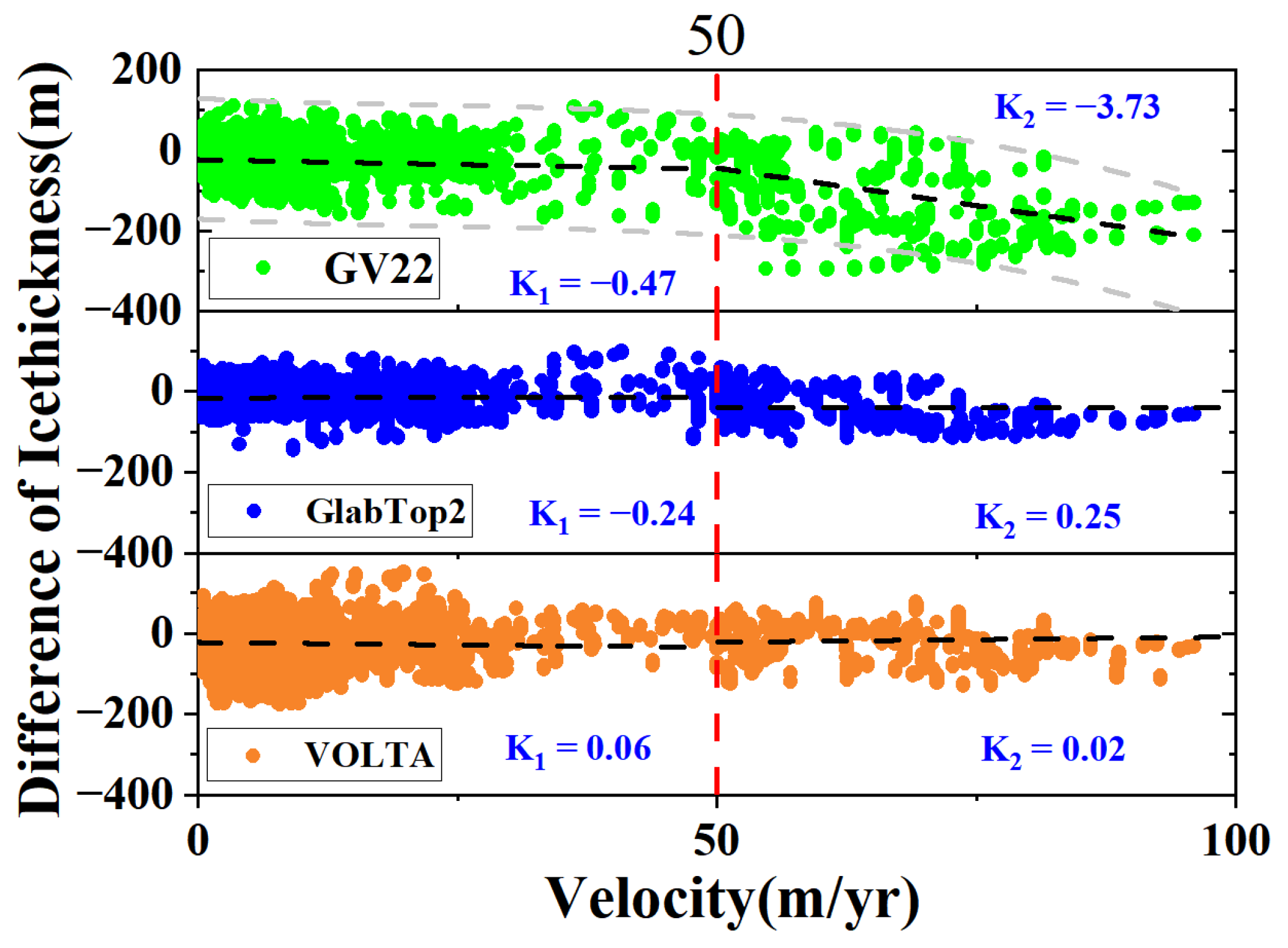
5.3. Influence of Glacier Velocity on Ice Thickness Estimate
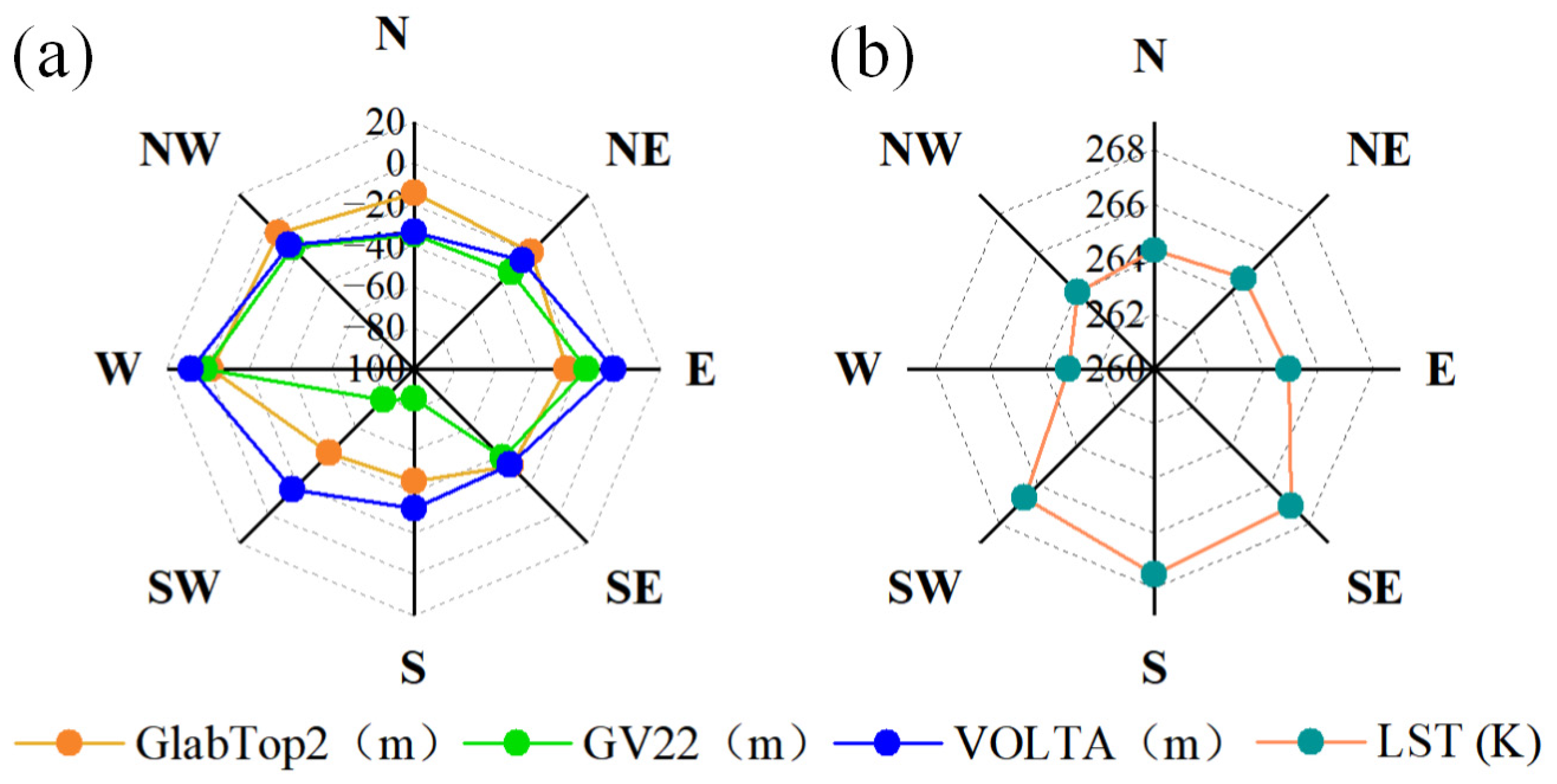
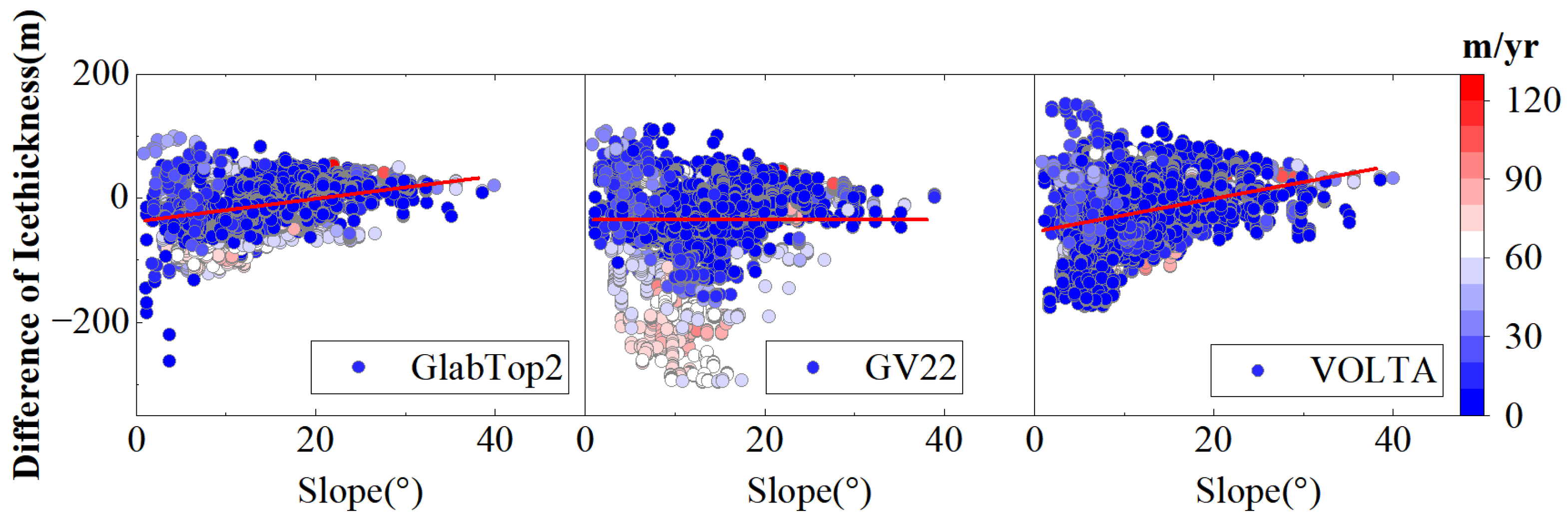
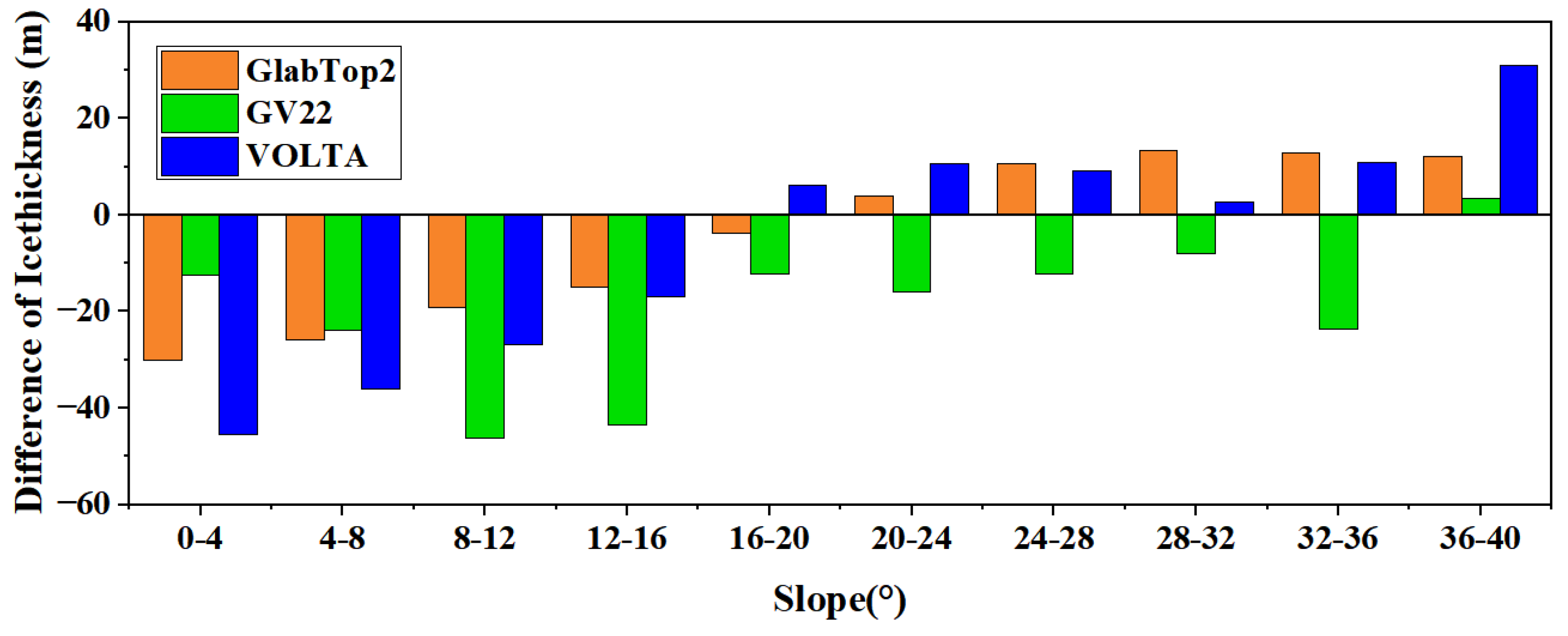
5.4. Influence of Terrain Factors on Ice Thickness Estimate
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zou, X.; Gao, H.; Zhang, Y.; Ma, N.; Wu, J.; Bin Farhan, S. Quantifying ice storage in upper Indus river basin using ground-penetrating radar measurements and glacier bed topography model version 2. Hydrol. Process. 2021, 35, 14. [Google Scholar] [CrossRef]
- Liang, P.-B.; Tian, L.-D. Estimation of glacier ice storage in western China constrained by field ground-penetrating Radar surveys. Adv. Clim. Change Res. 2022, 13, 359–374. [Google Scholar] [CrossRef]
- Yao, T.D.; Thompson, L.; Yang, W.; Yu, W.S.; Gao, Y.; Guo, X.J.; Yang, X.X.; Duan, K.Q.; Zhao, H.B.; Xu, B.Q.; et al. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Change 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Bhambri, R.; Schmidt, S.; Chand, P.; Nusser, M.; Haritashya, U.; Sain, K.; Tiwari, S.K.; Yadav, J.S. Heterogeneity in glacier thinning and slowdown of ice movement in the Garhwal Himalaya, India. Sci. Total Environ. 2023, 875, 162625. [Google Scholar] [CrossRef]
- Mannan Afzal, M.; Wang, X.; Sun, L.; Jiang, T.; Kong, Q.; Luo, Y. Hydrological and dynamical response of glaciers to climate change based on their dimensions in the Hunza Basin, Karakoram. J. Hydrol. 2023, 617, 128948. [Google Scholar] [CrossRef]
- Zhang, Z.; Tao, P.; Liu, S.; Zhang, S.; Huang, D.; Hu, K.; Lu, Y. What controls the surging of Karayaylak glacier in eastern Pamir? New insights from remote sensing data. J. Hydrol. 2022, 607, 127577. [Google Scholar] [CrossRef]
- Shugar, D.H.; Jacquemart, M.; Shean, D.; Bhushan, S.; Upadhyay, K.; Sattar, A.; Schwanghart, W.; McBride, S.; de Vries, M.V.; Mergili, M.; et al. A massive rock and ice avalanche caused the 2021 disaster at Chamoli, Indian Himalaya. Science 2021, 373, 300–306. [Google Scholar] [CrossRef]
- Guo, R.; Jiang, L.; Xu, Z.; Li, C.; Huang, R.; Zhou, Z.; Li, T.; Liu, Y.; Wang, H.; Fan, X. Seismic and hydrological triggers for a complex cascading geohazard of the Tianmo Gully in the southeastern Tibetan Plateau. Eng. Geol. 2023, 324, 107269. [Google Scholar] [CrossRef]
- Kraaijenbrink, P.D.A.; Bierkens, M.F.P.; Lutz, A.F.; Immerzeel, W.W. Impact of a global temperature rise of 1.5 degrees Celsius on Asia’s glaciers. Nature 2017, 549, 257–260. [Google Scholar] [CrossRef]
- Li, F.; Maussion, F.; Wu, G.; Chen, W.; Yu, Z.; Li, Y.; Liu, G. Influence of glacier inventories on ice thickness estimates and future glacier change projections in the Tian Shan range, Central Asia. J. Glaciol. 2022, 69, 266–280. [Google Scholar] [CrossRef]
- Sommer, C.; Fürst, J.J.; Huss, M.; Braun, M.H. Constraining regional glacier reconstructions using past ice thickness of deglaciating areas—A case study in the European Alps. Cryosphere 2023, 17, 2285–2303. [Google Scholar] [CrossRef]
- Welty, E.; Zemp, M.; Navarro, F.; Huss, M.; Fürst, J.J.; Gärtner-Roer, I.; Landmann, J.; Machguth, H.; Naegeli, K.; Andreassen, L.M.; et al. Worldwide version-controlled database of glacier thickness observations. Earth Syst. Sci. Data 2020, 12, 3039–3055. [Google Scholar] [CrossRef]
- Farinotti, D.; Brinkerhoff, D.J.; Clarke, G.K.C.; Fürst, J.J.; Frey, H.; Gantayat, P.; Gillet-Chaulet, F.; Girard, C.; Huss, M.; Leclercq, P.W.; et al. How accurate are estimates of glacier ice thickness? Results from ITMIX, the Ice Thickness Models Intercomparison eXperiment. Cryosphere 2017, 11, 949–970. [Google Scholar] [CrossRef]
- Zorzut, V.; Ruiz, L.; Rivera, A.; Pitte, P.; Villalba, R.; Medrzycka, D. Slope estimation influences on ice thickness inversion models: A case study for Monte Tronador glaciers, North Patagonian Andes. J. Glaciol. 2020, 66, 996–1005. [Google Scholar] [CrossRef]
- Farinotti, D.; Huss, M.; Fürst, J.J.; Landmann, J.; Machguth, H.; Maussion, F.; Pandit, A. A consensus estimate for the ice thickness distribution of all glaciers on Earth. Nat. Geosci. 2019, 12, 168–173. [Google Scholar] [CrossRef]
- Frey, H.; Machguth, H.; Huss, M.; Huggel, C.; Bajracharya, S.; Bolch, T.; Kulkarni, A.; Linsbauer, A.; Salzmann, N.; Stoffel, M. Estimating the volume of glaciers in the Himalayan–Karakoram region using different methods. Cryosphere 2014, 8, 2313–2333. [Google Scholar] [CrossRef]
- Millan, R.; Mouginot, J.; Rabatel, A.; Morlighem, M. Ice velocity and thickness of the world’s glaciers. Nat. Geosci. 2022, 15, 124–129. [Google Scholar] [CrossRef]
- James, W.H.M.; Carrivick, J.L. Automated modelling of spatially-distributed glacier ice thickness and volume. Comput. Geosci. 2016, 92, 90–103. [Google Scholar] [CrossRef]
- Bahr, D.B.; Pfeffer, W.T.; Kaser, G. A review of volume-area scaling of glaciers. Rev. Geophys. 2015, 53, 95–140. [Google Scholar] [CrossRef]
- Fürst, J.J.; Gillet-Chaulet, F.; Benham, T.J.; Dowdeswell, J.A.; Grabiec, M.; Navarro, F.; Pettersson, R.; Moholdt, G.; Nuth, C.; Sass, B.; et al. Application of a two-step approach for mapping ice thickness to various glacier types on Svalbard. Cryosphere 2017, 11, 2003–2032. [Google Scholar] [CrossRef]
- Gantayat, P.; Kulkarni, A.V.; Srinivasan, J. Estimation of ice thickness using surface velocities and slope: Case study at Gangotri Glacier, India. J. Glaciol. 2014, 60, 277–282. [Google Scholar] [CrossRef]
- Wu, K.; Liu, S.; Zhu, Y.; Liu, Q.; Jiang, Z. Dynamics of glacier surface velocity and ice thickness for maritime glaciers in the southeastern Tibetan Plateau. J. Hydrol. 2020, 590, 125527. [Google Scholar] [CrossRef]
- Farinotti, D.; Huss, M.; Bauder, A.; Funk, M.; Truffer, M. A method to estimate the ice volume and ice-thickness distribution of alpine glaciers. J. Glaciol. 2009, 55, 422–430. [Google Scholar] [CrossRef]
- Maussion, F.; Butenko, A.; Champollion, N.; Dusch, M.; Eis, J.; Fourteau, K.; Gregor, P.; Jarosch, A.H.; Landmann, J.; Oesterle, F.; et al. The Open Global Glacier Model (OGGM) v1.1. Geosci. Model Dev. 2019, 12, 909–931. [Google Scholar] [CrossRef]
- Radić, V.; Hock, R. Regional and global volumes of glaciers derived from statistical upscaling of glacier inventory data. J. Geophys. Res. 2010, 115, F01010. [Google Scholar] [CrossRef]
- Huss, M.; Farinotti, D. Distributed ice thickness and volume of all glaciers around the globe. J. Geophys. Res. Earth Surf. 2012, 117, F04010. [Google Scholar] [CrossRef]
- Pieczonka, T.; Bolch, T.; KrÖHnert, M.; Peters, J.; Liu, S. Glacier branch lines and glacier ice thickness estimation for debris-covered glaciers in the Central Tien Shan. J. Glaciol. 2018, 64, 835–849. [Google Scholar] [CrossRef]
- Ramsankaran, R.; Pandit, A.; Azam, M.F. Spatially distributed ice-thickness modelling for Chhota Shigri Glacier in western Himalayas, India. Int. J. Remote Sens. 2018, 39, 3320–3343. [Google Scholar] [CrossRef]
- Li, H.L.; Ng, F.; Li, Z.Q.; Qin, D.H.; Cheng, G.D. An extended “perfect-plasticity” method for estimating ice thickness along the flow line of mountain glaciers. J. Geophys. Res. Earth Surf. 2012, 117, 1020–1030. [Google Scholar] [CrossRef]
- Chen, W.F.; Yao, T.D.; Zhang, G.Q.; Li, F.; Zheng, G.X.; Zhou, Y.S.; Xu, F.L. Towards ice-thickness inversion: An evaluation of global digital elevation models (DEMs) in the glacierized Tibetan Plateau. Cryosphere 2022, 16, 197–218. [Google Scholar] [CrossRef]
- Su, F.; Pritchard, H.D.; Yao, T.; Huang, J.; Ou, T.; Meng, F.; Sun, H.; Li, Y.; Xu, B.; Zhu, M. Contrasting fate of western Third Pole’s water resources under 21st century climate change. Earth’s Future 2022, 10, e2022EF002776. [Google Scholar] [CrossRef]
- Pfeffer, W.T.; Arendt, A.A.; Bliss, A.; Bolch, T.; Cogley, J.G.; Gardner, A.S.; Hagen, J.-O.; Hock, R.; Kaser, G.; Kienholz, C.; et al. The Randolph Glacier Inventory: A globally complete inventory of glaciers. J. Glaciol. 2014, 60, 537–552. [Google Scholar] [CrossRef]
- Zhan, J.; Shi, H.; Wang, Y.; Yao, Y. Complex principal component analysis of mass balance changes on the Qinghai–Tibetan Plateau. Cryosphere 2017, 11, 1487–1499. [Google Scholar] [CrossRef]
- Farinotti, D.; Brinkerhoff, D.J.; Furst, J.J.; Gantayat, P.; Gillet-Chaulet, F.; Huss, M.; Leclercq, P.W.; Maurer, H.; Morlighem, M.; Pandit, A.; et al. Results from the Ice Thickness Models Intercomparison eXperiment Phase 2 (ITMIX2). Front. Earth Sci 2021, 8, 21. [Google Scholar] [CrossRef]
- Azam, M.F.; Wagnon, P.; Ramanathan, A.; Vincent, C.; Sharma, P.; Arnaud, Y.; Linda, A.; Pottakkal, J.G.; Chevallier, P.; Singh, V.B. From balance to imbalance: A shift in the dynamic behaviour of Chhota Shigri glacier, western Himalaya, India. J. Glaciol. 2012, 58, 315–324. [Google Scholar] [CrossRef]
- Reuter, H.I.; Nelson, A.; Jarvis, A. An evaluation of void-filling interpolation methods for SRTM data. Int. J. Geogr. Inf. Sci. 2007, 21, 983–1008. [Google Scholar] [CrossRef]
- González-Moradas, M.d.R.; Viveen, W. Evaluation of ASTER GDEM2, SRTMv3.0, ALOS AW3D30 and TanDEM-X DEMs for the Peruvian Andes against highly accurate GNSS ground control points and geomorphological-hydrological metrics. Remote Sens. Environ. 2020, 237, 111509. [Google Scholar] [CrossRef]
- Hawker, L.; Uhe, P.; Paulo, L.; Sosa, J.; Savage, J.; Sampson, C.; Neal, J. A 30 m global map of elevation with forests and buildings removed. Environ. Res. Lett. 2022, 17, 024016. [Google Scholar] [CrossRef]
- Becek, K.; Koppe, W.; Kutoğlu, Ş. Evaluation of Vertical Accuracy of the WorldDEM™ Using the Runway Method. Remote Sens. 2016, 8, 934. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, J.; Göttsche, F.M.; Zhan, W.; Liu, S.; Cao, R. A Method Based on Temporal Component Decomposition for Estimating 1-km All-Weather Land Surface Temperature by Merging Satellite Thermal Infrared and Passive Microwave Observations. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4670–4691. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, J.; Liang, S.; Wang, D. A practical reanalysis data and thermal infrared remote sensing data merging (RTM) method for reconstruction of a 1-km all-weather land surface temperature. Remote Sens. Environ. 2021, 260, 112437. [Google Scholar] [CrossRef]
- Millan, R.; Mouginot, J.; Rabatel, A.; Jeong, S.; Cusicanqui, D.; Derkacheva, A.; Chekki, M. Mapping Surface Flow Velocity of Glaciers at Regional Scale Using a Multiple Sensors Approach. Remote Sens. 2019, 11, 2498. [Google Scholar] [CrossRef]
- Linsbauer, A.; Paul, F.; Hoelzle, M.; Frey, H.; Haeberli, W. The Swiss Alps Without Glaciers—A GIS-based Modelling Approach for Reconstruction of Glacier Beds. In Geomorphometry 2009 International Conference; Department of Geography, University of Zurich: Zurich, Switzerland, 2009. [Google Scholar]
- Haeberli, W.; Hoelzle, M. Application of inventory data for estimating characteristics of and regional climate-change effects on mountain glaciers: A pilot study with the European Alps. Ann. Glaciol. 1995, 21, 206–212. [Google Scholar] [CrossRef]
- Gharehchahi, S.; James, W.H.M.; Bhardwaj, A.; Jensen, J.L.R.; Sam, L.; Ballinger, T.J.; Butler, D.R. Glacier Ice Thickness Estimation and Future Lake Formation in Swiss Southwestern Alps—The Upper Rhône Catchment: A VOLTA Application. Remote Sens. 2020, 12, 3443. [Google Scholar] [CrossRef]
- Driedger, C.L.; Kennard, P.M. Glacier Volume Estimation on Cascade Volcanoes: An Analysis and Comparison with Other Methods. Ann. Glaciol. 1986, 8, 59–64. [Google Scholar] [CrossRef]
- Lei, Y.; Gardner, A.; Agram, P. Autonomous Repeat Image Feature Tracking (autoRIFT) and Its Application for Tracking Ice Displacement. Remote Sens. 2021, 13, 749. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, J.; Cheng, X. Glacier Velocity Changes in the Himalayas in Relation to Ice Mass Balance. Remote Sens. 2021, 13, 3825. [Google Scholar] [CrossRef]
- Glen, J.W. The creep of polycrystalline ice. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 1955, 228, 519–538. [Google Scholar]
- Höhle, J.; Höhle, M. Accuracy assessment of digital elevation models by means of robust statistical methods. ISPRS J. Photogramm. Remote Sens. 2009, 64, 398–406. [Google Scholar] [CrossRef]
- Muhuri, A.; Gascoin, S.; Menzel, L.; Kostadinov, T.S.; Harpold, A.A.; Sanmiguel-Vallelado, A.; Lopez-Moreno, J.I. Performance Assessment of Optical Satellite-Based Operational Snow Cover Monitoring Algorithms in Forested Landscapes. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7159–7178. [Google Scholar] [CrossRef]
- Chymyrov, A. Comparison of different DEMs for hydrological studies in the mountainous areas. Egypt. J. Remote Sens. Space Sci. 2021, 24, 587–594. [Google Scholar] [CrossRef]
- Wang, P.Y.; Li, Z.Q.; Wang, W.B.; Li, H.L.; Wang, F.T. Glacier Volume Calculation from Ice-Thickness Data for Mountain Glaciers-A Case Study of Glacier No. 4 of Sigong River over Mt. Bogda, Eastern Tianshan, Central Asia. J. Earth Sci. 2014, 25, 371–378. [Google Scholar] [CrossRef]
- Patel, A.; Goswami, A.; Dharpure, J.K.; Sharma, P.; Patel, L.K.; Thamban, M. Monitoring glacier characteristics and their mass balance using a multidimensional approach over the glaciers of the Chandra basin, western Himalaya. Hydrol. Sci. J. 2022, 67, 419–435. [Google Scholar] [CrossRef]
- Chen, F.; Wang, J.; Li, B.; Yang, A.; Zhang, M. Spatial variability in melting on Himalayan debris-covered glaciers from 2000 to 2013. Remote Sens. Environ. 2023, 291, 113560. [Google Scholar] [CrossRef]
- Compagno, L.; Huss, M.; Miles, E.S.; McCarthy, M.J.; Zekollari, H.; Dehecq, A.; Pellicciotti, F.; Farinotti, D. Modelling supraglacial debris-cover evolution from the single-glacier to the regional scale: An application to High Mountain Asia. Cryosphere 2022, 16, 1697–1718. [Google Scholar] [CrossRef]
- Iverson, N.R.; Helanow, C.; Zoet, L.K. Debris-bed friction during glacier sliding with ice–bed separation. Ann. Glaciol. 2020, 60, 30–36. [Google Scholar] [CrossRef]
- Shukla, A.; Garg, P.K. Evolution of a debris-covered glacier in the western Himalaya during the last four decades (1971–2016): A multiparametric assessment using remote sensing and field observations. Geomorphology 2019, 341, 1–14. [Google Scholar] [CrossRef]
- Neckel, N.; Loibl, D.; Rankl, M. Recent slowdown and thinning of debris-covered glaciers in south-eastern Tibet. Earth Planet. Sci. Lett. 2017, 464, 95–102. [Google Scholar] [CrossRef]
- Rounce, D.R.; Hock, R.; McNabb, R.W.; Millan, R.; Sommer, C.; Braun, M.H.; Malz, P.; Maussion, F.; Mouginot, J.; Seehaus, T.C.; et al. Distributed Global Debris Thickness Estimates Reveal Debris Significantly Impacts Glacier Mass Balance. Geophys. Res. Lett. 2021, 48, 12. [Google Scholar] [CrossRef]
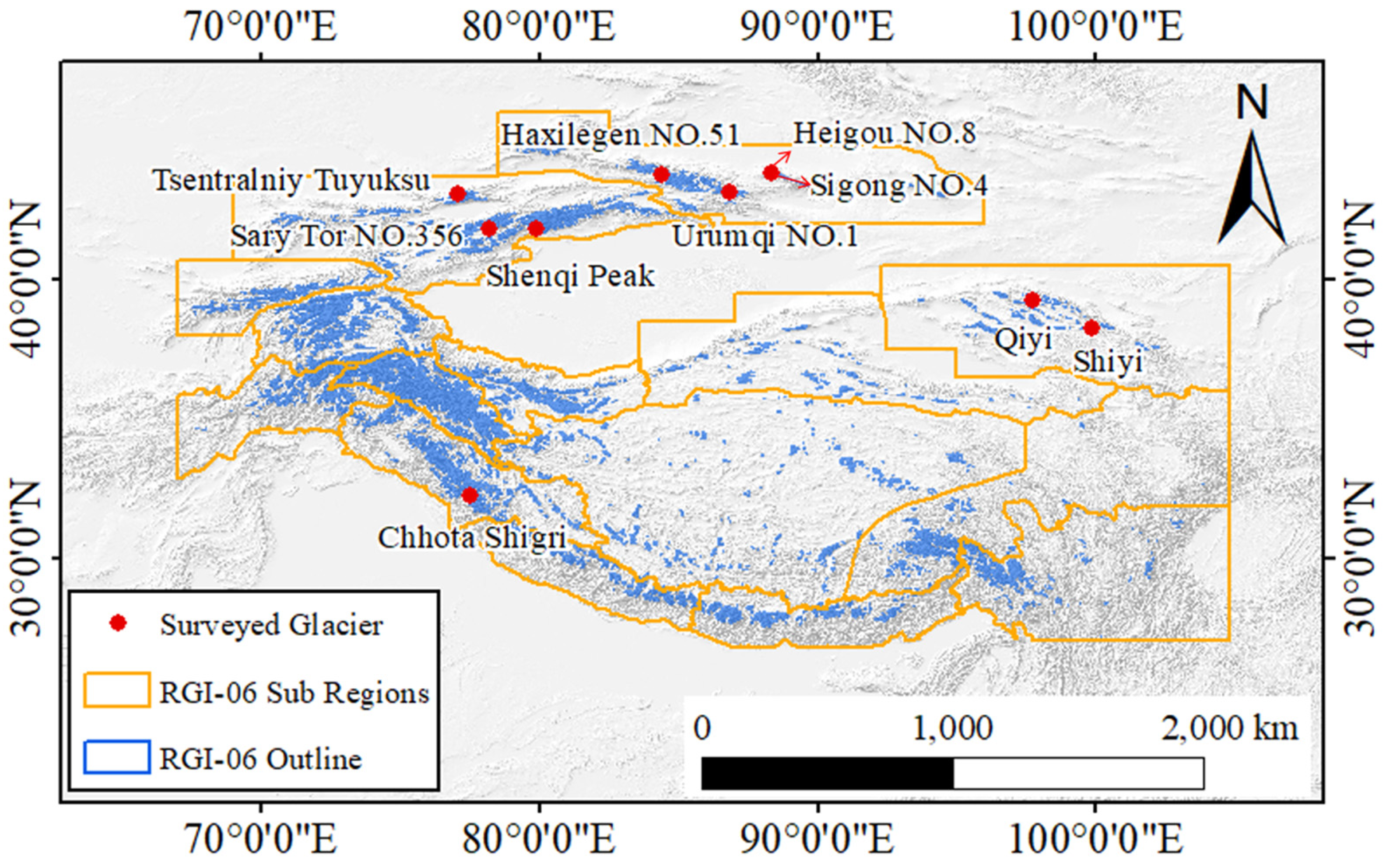



| ID | Glacier | DEM | Source | Time | Area_(km2) |
|---|---|---|---|---|---|
| 1 | Urumqi No.1 | COPDEM30 | GlaThiDa | 2014 | 1.581 |
| 2 | Sigonghe No.4 | COPDEM30 | GlaThiDa | 2009 | 2.643 |
| 3 | Sary-Tor | COPDEM30 | GlaThiDa | 2013 | 2.925 |
| 4 | Shiyi | COPDEM30 | GlaThiDa | 2010 | 0.495 |
| 5 | Haxilegen No.51 | COPDEM30 | GlaThiDa | 2010 | 1.099 |
| 6 | Heigou No.8 | COPDEM30 | GlaThiDa | 2009 | 6.078 |
| 7 | Shenqi Peak | COPDEM30 | GlaThiDa | 2008 | 6.595 |
| 8 | Qiyi | SRTM-C | GlaThiDa | 1980 | 2.531 |
| 9 | Tsentralniy Tuyuksu | COPDEM30 | GlaThiDa | 2013 | 2.838 |
| 10 | Chhota Shigri | COPDEM30 | [34,35] | 2009 | 16.764 |
| Glacier | Area (km2) | Average Ice Thickness at Measurement Sites (m) | Volume (km3) | Maximum Ice Thickness (m) | RE (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GPR | GT2 | GV22 | VOLTA | GT2 | GV22 | VOLTA | GT2 | GV22 | VOLTA | GT2 | GV22 | VOLTA | ||
| Urumqi No.1 | 1.58 | 69.95 | 64.45 | 57.47 | 66.82 | 0.077 | 0.073 | 0.074 | 153.37 | 98.41 | 149.05 | −7.86 | −17.84 | −4.47 |
| Sigonghe No.4 | 2.64 | 68.87 | 88.61 | 59.22 | 121.26 | 0.122 | 0.103 | 0.143 | 130.41 | 81.38 | 272.23 | 28.66 | −14.01 | 76.07 |
| Sary-Tor | 2.93 | 75.47 | 77.87 | 106.30 | 75.65 | 0.177 | 0.234 | 0.131 | 132.97 | 245.49 | 189.82 | 3.18 | 40.85 | 0.24 |
| Shiyi | 0.50 | 39.27 | 39.96 | 34.42 | 42.50 | 0.012 | 0.015 | 0.013 | 56.02 | 62.79 | 155.01 | 1.76 | −12.35 | 8.23 |
| Haxilegen No.51 | 1.10 | 43.89 | 46.61 | 63.10 | 96.62 | 0.037 | 0.045 | 0.072 | 77.20 | 100.80 | 240.10 | 6.20 | 43.77 | 120.14 |
| Heigou No.8 | 6.07 | 114.83 | 142.21 | 129.78 | 150.40 | 0.431 | 0.358 | 0.269 | 214.60 | 166.68 | 246.27 | 23.84 | 13.02 | 30.98 |
| Shenqi Peak | 6.59 | 38.65 | 106.54 | 200.79 | 72.81 | 0.338 | 0.536 | 0.206 | 172.17 | 314.60 | 246.81 | 175.65 | 419.51 | 88.38 |
| Qiyi | 2.53 | 76.82 | 76.70 | 61.21 | 41.61 | 0.158 | 0.133 | 0.063 | 123.13 | 109.96 | 118.94 | −0.16 | −20.32 | −45.83 |
| Tsentralniy Tuyuksu | 2.84 | 50.92 | 72.80 | 86.79 | 80.43 | 0.151 | 0.178 | 0.137 | 137.43 | 170.11 | 256.55 | 42.97 | 70.44 | 57.95 |
| Chhota Shigri | 13.48 | 172.88 | 176.01 | 161.29 | 135.32 | 1.299 | 1.300 | 0.872 | 295.41 | 268.76 | 379.46 | 1.81 | −6.70 | −21.73 |
| Cross Section | RMSE | ||
|---|---|---|---|
| GlabTop2 | GV22 | VOLTA | |
| CS1 | 30.33 | 98.21 | 72.68 |
| CS2 | 43.34 | 29.35 | 69.27 |
| CS3 | 91.02 | 42.14 | 40.43 |
| CS4 | 69.95 | 69.92 | 34.02 |
| CS5 | 53.94 | 64.81 | 124.68 |
| Total | 67.82 | 57.77 | 68.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, X.; Jiang, L.; Guo, R.; Xu, Z.; Li, X.; Lu, X. Surface Motion and Topographic Effects on Ice Thickness Inversion for High Mountain Asia Glaciers: A Comparison Study from Three Numerical Models. Remote Sens. 2023, 15, 5378. https://doi.org/10.3390/rs15225378
Pang X, Jiang L, Guo R, Xu Z, Li X, Lu X. Surface Motion and Topographic Effects on Ice Thickness Inversion for High Mountain Asia Glaciers: A Comparison Study from Three Numerical Models. Remote Sensing. 2023; 15(22):5378. https://doi.org/10.3390/rs15225378
Chicago/Turabian StylePang, Xiaoguang, Liming Jiang, Rui Guo, Zhida Xu, Xiaoen Li, and Xi Lu. 2023. "Surface Motion and Topographic Effects on Ice Thickness Inversion for High Mountain Asia Glaciers: A Comparison Study from Three Numerical Models" Remote Sensing 15, no. 22: 5378. https://doi.org/10.3390/rs15225378
APA StylePang, X., Jiang, L., Guo, R., Xu, Z., Li, X., & Lu, X. (2023). Surface Motion and Topographic Effects on Ice Thickness Inversion for High Mountain Asia Glaciers: A Comparison Study from Three Numerical Models. Remote Sensing, 15(22), 5378. https://doi.org/10.3390/rs15225378






