Infrared Small-Target Detection Based on Background-Suppression Proximal Gradient and GPU Acceleration
Abstract
:1. Introduction
- A novel continuation strategy based on the Proximal Gradient (PG) algorithm is introduced to suppress strong edges. This continuation strategy preserves heterogeneous backgrounds as low-rank components, hence reducing false alarms.
- The APSVD is proposed for solving the LRSD problem, which is more efficient than the original SVD. Subsequently, parallel strategies are presented to accelerate the construction and reconstruction of patch images. These designs can reduce the computation time at the algorithmic and hardware levels, facilitating rapid and accurate solution.
- Implementation of the proposed method on GPU is executed and experimentally validate its effectiveness with respect to the detection accuracy and computation time. The obtained results demonstrate that the proposed method out-performs nine state-of-the-art methods.
2. Related Work
2.1. HVS-Based Methods
2.2. Deep Learning-Based Methods
2.3. Patch-Based Methods
2.4. Acceleration Strategies for Patch-Based Methods
3. Method
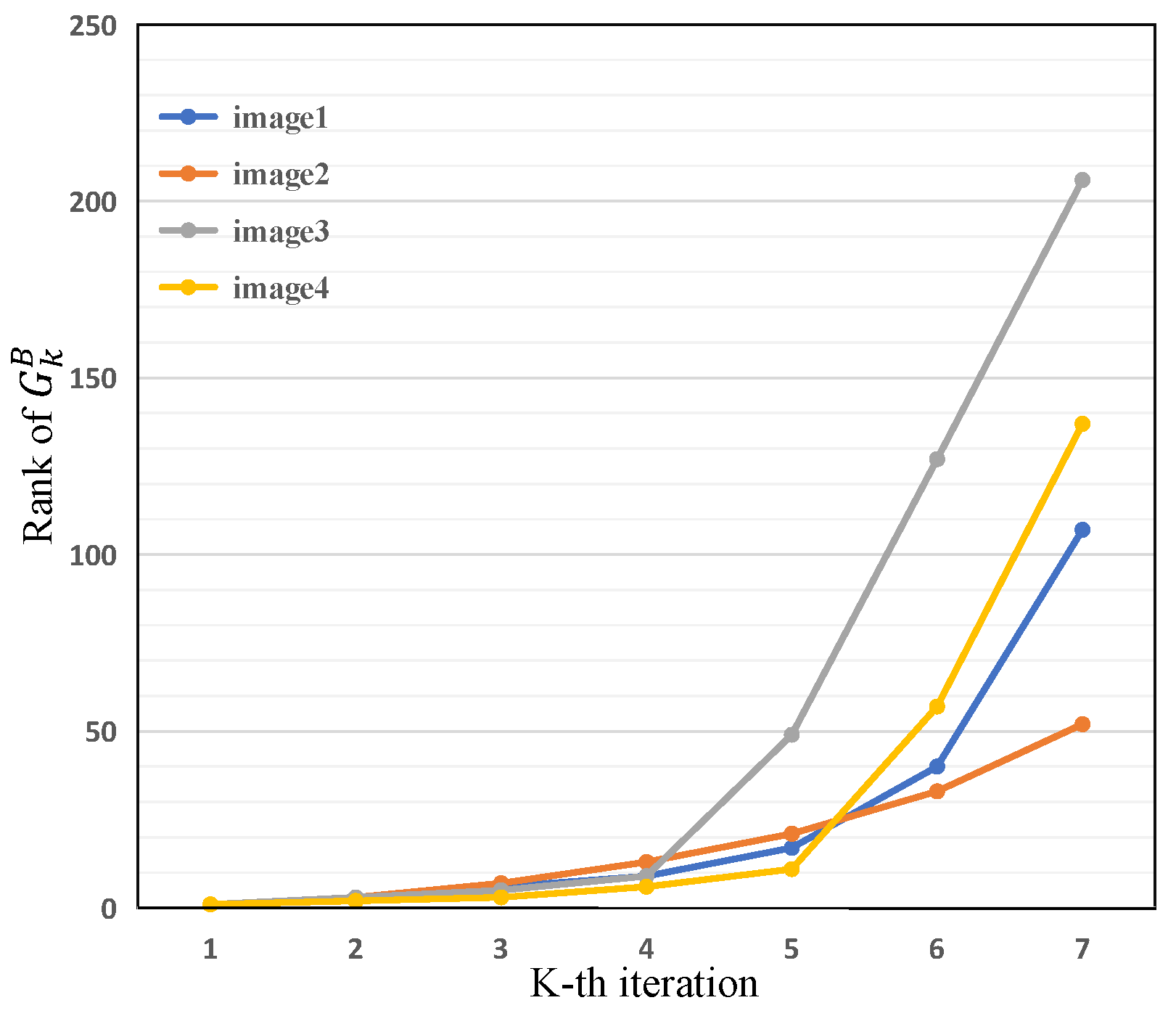
3.1. BSPG Model
| Algorithm 1: BSPG solution via APSVD |
 |
3.2. APSVD
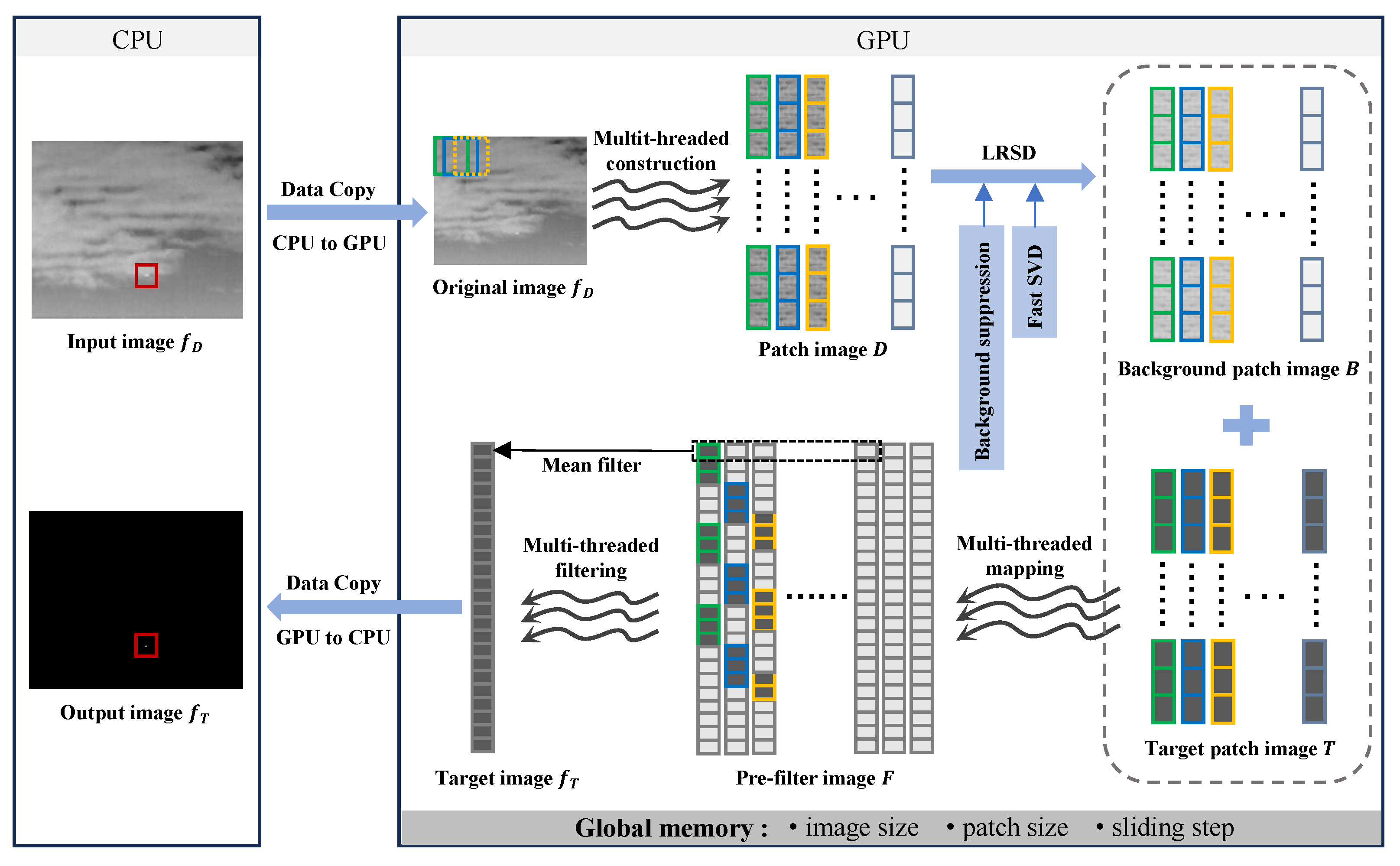
3.3. GPU Parallel Implementation
3.3.1. Construction
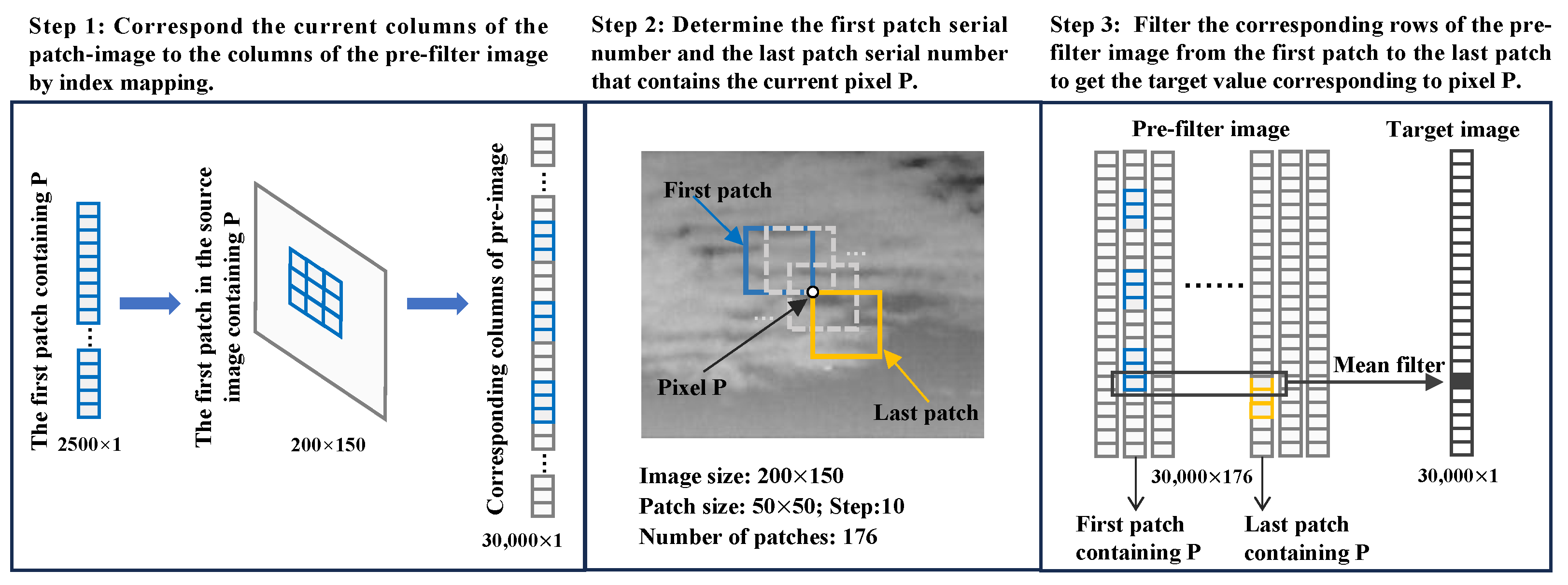
3.3.2. Reconstruction
| Algorithm 2: The mapping of patch image and pre-filter image |
| Input: Patch image D, original image size w and h, patch size and , step s, patch number of per row Output: pre-filter image F
|
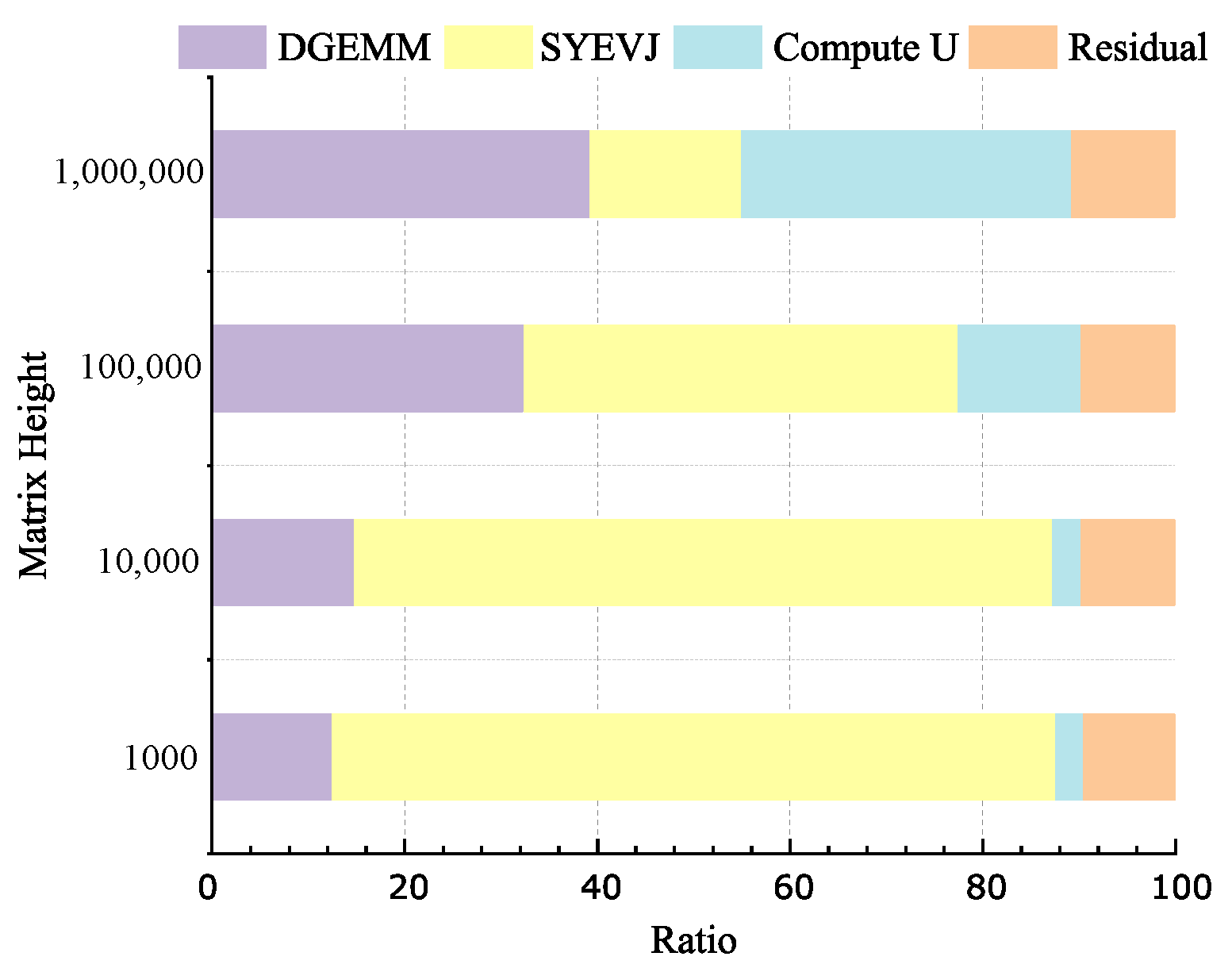
3.3.3. APSVD Using CUDA
4. Experiments and Analysis
4.1. Experimental Setup
4.2. Visual Comparison with Baselines
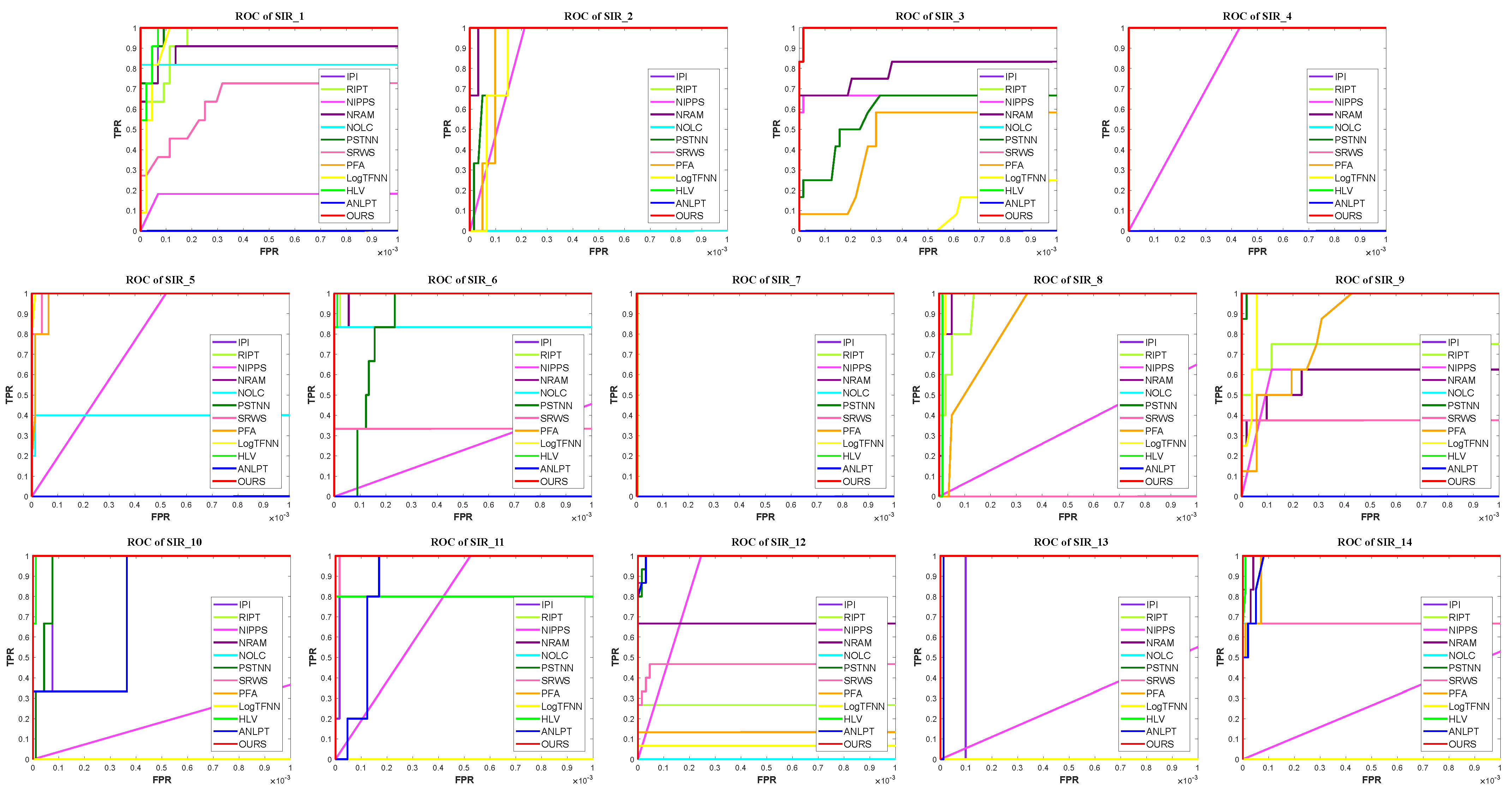
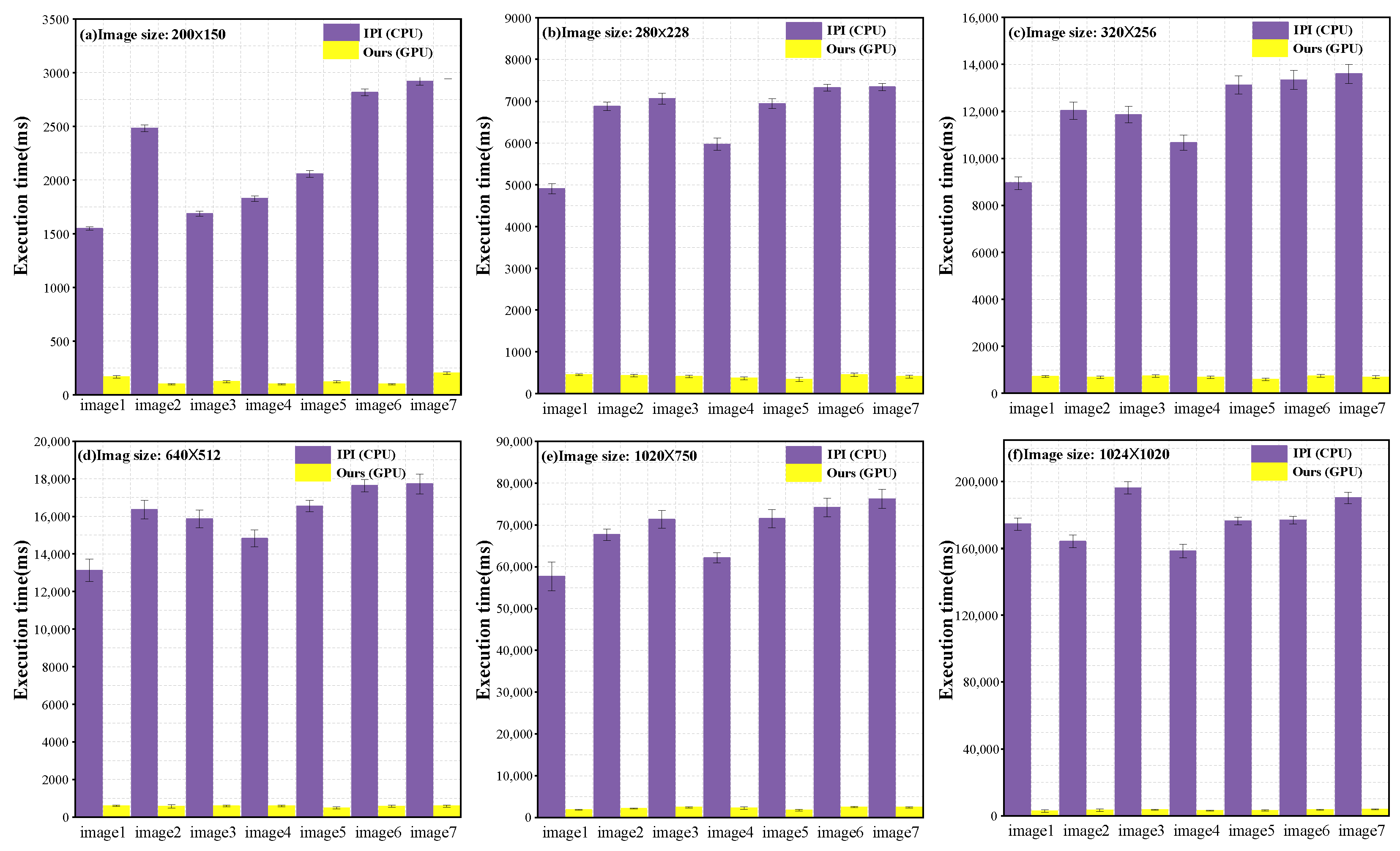
4.3. Quantitative Evaluation and Analysis
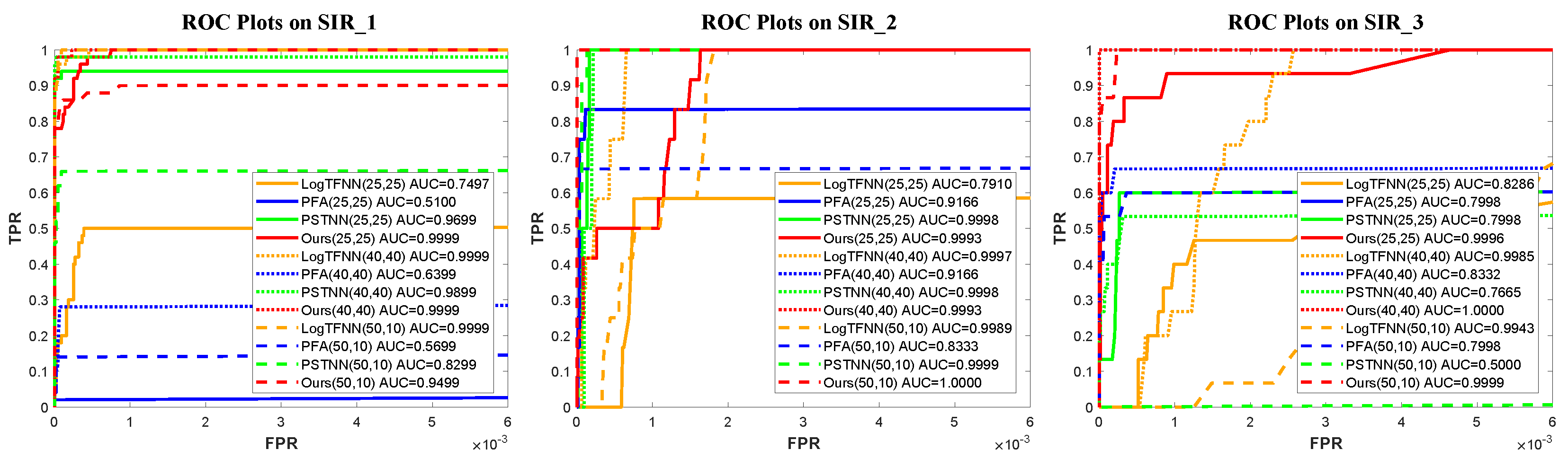
4.4. Ablation Study
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, C.P.; Li, H.; Wei, Y.; Xia, T.; Tang, Y.Y. A local contrast method for small infrared target detection. IEEE Trans. Geosci. Remote Sens. 2013, 52, 574–581. [Google Scholar] [CrossRef]
- Zhang, C.; He, Y.; Tang, Q.; Chen, Z.; Mu, T. Infrared Small Target Detection via Interpatch Correlation Enhancement and Joint Local Visual Saliency Prior. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5001314. [Google Scholar] [CrossRef]
- Bai, X.; Zhou, F. Analysis of new top-hat transformation and the application for infrared dim small target detection. Pattern Recognit. 2010, 43, 2145–2156. [Google Scholar] [CrossRef]
- Zhao, Y.; Pan, H.; Du, C.; Peng, Y.; Zheng, Y. Bilateral two-dimensional least mean square filter for infrared small target detection. Infrared Phys. Technol. 2014, 65, 17–23. [Google Scholar] [CrossRef]
- Deshpande, S.D.; Er, M.H.; Venkateswarlu, R.; Chan, P. Max-mean and max-median filters for detection of small targets. In Proceedings of the Signal and Data Processing of Small Targets, Denver, CO, USA, 20–22 July 1999; Volume 3809, pp. 74–83. [Google Scholar]
- Liu, X.; Li, L.; Liu, L.; Su, X.; Chen, F. Moving dim and small target detection in multiframe infrared sequence with low SCR based on temporal profile similarity. IEEE Geosci. Remote Sens. Lett. 2022, 19, 7507005. [Google Scholar] [CrossRef]
- Qin, Y.; Li, B. Effective infrared small target detection utilizing a novel local contrast method. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1890–1894. [Google Scholar] [CrossRef]
- Han, J.; Liang, K.; Zhou, B.; Zhu, X.; Zhao, J.; Zhao, L. Infrared small target detection utilizing the multiscale relative local contrast measure. IEEE Geosci. Remote Sens. Lett. 2018, 15, 612–616. [Google Scholar] [CrossRef]
- Wei, Y.; You, X.; Li, H. Multiscale patch-based contrast measure for small infrared target detection. Pattern Recognit. 2016, 58, 216–226. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, G.; Ma, Y.; Kang, J.U.; Kwan, C. Small infrared target detection based on fast adaptive masking and scaling with iterative segmentation. IEEE Geosci. Remote Sens. Lett. 2021, 19, 7000605. [Google Scholar] [CrossRef]
- Cui, H.; Li, L.; Liu, X.; Su, X.; Chen, F. Infrared small target detection based on weighted three-layer window local contrast. IEEE Geosci. Remote Sens. Lett. 2021, 19, 7505705. [Google Scholar] [CrossRef]
- Du, J.; Lu, H.; Hu, M.; Zhang, L.; Shen, X. CNN-based infrared dim small target detection algorithm using target-oriented shallow-deep features and effective small anchor. IET Image Process. 2021, 15, 1–15. [Google Scholar] [CrossRef]
- Du, J.; Lu, H.; Zhang, L.; Hu, M.; Chen, S.; Deng, Y.; Shen, X.; Zhang, Y. A spatial-temporal feature-based detection framework for infrared dim small target. IEEE Trans. Geosci. Remote Sens. 2021, 60, 3000412. [Google Scholar] [CrossRef]
- Zhang, M.; Dong, L.; Ma, D.; Xu, W. Infrared target detection in marine images with heavy waves via local patch similarity. Infrared Phys. Technol. 2022, 125, 104283. [Google Scholar] [CrossRef]
- Li, B.; Xiao, C.; Wang, L.; Wang, Y.; Lin, Z.; Li, M.; An, W.; Guo, Y. Dense nested attention network for infrared small target detection. IEEE Trans. Image Process. 2022, 32, 1745–1758. [Google Scholar] [CrossRef]
- Zhong, S.; Zhou, H.; Cui, X.; Cao, X.; Zhang, F. Infrared small target detection based on local-image construction and maximum correntropy. Measurement 2023, 211, 112662. [Google Scholar] [CrossRef]
- Gao, C.; Meng, D.; Yang, Y.; Wang, Y.; Zhou, X.; Hauptmann, A.G. Infrared patch-image model for small target detection in a single image. IEEE Trans. Image Process. 2013, 22, 4996–5009. [Google Scholar] [CrossRef] [PubMed]
- Dai, Y.; Wu, Y.; Song, Y. Infrared small target and background separation via column-wise weighted robust principal component analysis. Infrared Phys. Technol. 2016, 77, 421–430. [Google Scholar] [CrossRef]
- Wang, X.; Peng, Z.; Kong, D.; Zhang, P.; He, Y. Infrared dim target detection based on total variation regularization and principal component pursuit. Image Vis. Comput. 2017, 63, 1–9. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y.; Song, Y.; Guo, J. Non-negative infrared patch-image model: Robust target-background separation via partial sum minimization of singular values. Infrared Phys. Technol. 2017, 81, 182–194. [Google Scholar] [CrossRef]
- Guo, J.; Wu, Y.; Dai, Y. Small target detection based on reweighted infrared patch-image model. IET Image Process. 2018, 12, 70–79. [Google Scholar] [CrossRef]
- Zhang, L.; Peng, L.; Zhang, T.; Cao, S.; Peng, Z. Infrared small target detection via non-convex rank approximation minimization joint l 2, 1 norm. Remote Sens. 2018, 10, 1821. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, H.; Liu, Y.; Peng, L.; Yang, C.; Peng, Z. Infrared small target detection based on non-convex optimization with Lp-norm constraint. Remote Sens. 2019, 11, 559. [Google Scholar] [CrossRef]
- Chen, X.; Xu, W.; Tao, S.; Gao, T.; Feng, Q.; Piao, Y. Total Variation Weighted Low-Rank Constraint for Infrared Dim Small Target Detection. Remote Sens. 2022, 14, 4615. [Google Scholar] [CrossRef]
- Yan, F.; Xu, G.; Wu, Q.; Wang, J.; Li, Z. Infrared small target detection using kernel low-rank approximation and regularization terms for constraints. Infrared Phys. Technol. 2022, 125, 104222. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Hao, X.; Tang, W.; Zhang, S.; Lei, T. Single-Frame Infrared Small Target Detection by High Local Variance, Low-Rank and Sparse Decomposition. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5614317. [Google Scholar] [CrossRef]
- Deng, H.; Sun, X.; Liu, M.; Ye, C.; Zhou, X. Entropy-based window selection for detecting dim and small infrared targets. Pattern Recognit. 2017, 61, 66–77. [Google Scholar] [CrossRef]
- Bai, X.; Bi, Y. Derivative entropy-based contrast measure for infrared small-target detection. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2452–2466. [Google Scholar] [CrossRef]
- Xu, Y.; Wan, M.; Zhang, X.; Wu, J.; Chen, Y.; Chen, Q.; Gu, G. Infrared Small Target Detection Based on Local Contrast-Weighted Multidirectional Derivative. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5000816. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, L.; Yuan, D.; Chen, H. Infrared small target detection based on local intensity and gradient properties. Infrared Phys. Technol. 2018, 89, 88–96. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Li, W.; Liu, Y. Infrared Small Target Detection Based on Gradient-Intensity Joint Saliency Measure. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 7687–7699. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y.; Zhou, F.; Barnard, K. Attentional local contrast networks for infrared small target detection. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9813–9824. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, L.; Wang, L. Miss detection vs. false alarm: Adversarial learning for small object segmentation in infrared images. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 8509–8518. [Google Scholar]
- Zhang, T.; Peng, Z.; Wu, H.; He, Y.; Li, C.; Yang, C. Infrared small target detection via self-regularized weighted sparse model. Neurocomputing 2021, 420, 124–148. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, J.Q.; Huang, X.; Liu, D.L. Separable convolution template (SCT) background prediction accelerated by CUDA for infrared small target detection. Infrared Phys. Technol. 2013, 60, 300–305. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y. Reweighted infrared patch-tensor model with both nonlocal and local priors for single-frame small target detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3752–3767. [Google Scholar] [CrossRef]
- Xu, L.; Wei, Y.; Zhang, H.; Shang, S. Robust and fast infrared small target detection based on pareto frontier optimization. Infrared Phys. Technol. 2022, 123, 104192. [Google Scholar] [CrossRef]
- Zhang, L.; Peng, Z. Infrared small target detection based on partial sum of the tensor nuclear norm. Remote Sens. 2019, 11, 382. [Google Scholar] [CrossRef]
- Kong, X.; Yang, C.; Cao, S.; Li, C.; Peng, Z. Infrared small target detection via nonconvex tensor fibered rank approximation. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5000321. [Google Scholar] [CrossRef]
- Wang, G.; Tao, B.; Kong, X.; Peng, Z. Infrared Small Target Detection Using Nonoverlapping Patch Spatial—Temporal Tensor Factorization With Capped Nuclear Norm Regularization. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5001417. [Google Scholar] [CrossRef]
- Li, J.; Zhang, P.; Zhang, L.; Zhang, Z. Sparse Regularization-Based Spatial-Temporal Twist Tensor Model for Infrared Small Target Detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5000417. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, C.; Gao, Z.; Xie, C. ANLPT: Self-Adaptive and Non-Local Patch-Tensor Model for Infrared Small Target Detection. Remote Sens. 2023, 15, 1021. [Google Scholar] [CrossRef]
- Toh, K.C.; Yun, S. An accelerated proximal gradient algorithm for nuclear norm regularized linear least squares problems. Pac. J. Optim. 2010, 6, 15. [Google Scholar]
- Lin, Z.; Ganesh, A.; Wright, J.; Wu, L.; Chen, M.; Ma, Y. Fast Convex Optimization Algorithms for Exact Recovery of a Corrupted Low-Rank Matrix. Coordinated Science Laboratory Report no. UILU-ENG-09-2214, DC-246. 2009. Available online: https://people.eecs.berkeley.edu/~yima/matrix-rank/Files/rpca_algorithms.pdf (accessed on 30 September 2023).
- Ordóñez, Á.; Argüello, F.; Heras, D.B.; Demir, B. GPU-accelerated registration of hyperspectral images using KAZE features. J. Supercomput. 2020, 76, 9478–9492. [Google Scholar] [CrossRef]
- Seznec, M.; Gac, N.; Orieux, F.; Naik, A.S. Real-time optical flow processing on embedded GPU: An hardware-aware algorithm to implementation strategy. J. Real Time Image Process. 2022, 19, 317–329. [Google Scholar] [CrossRef]


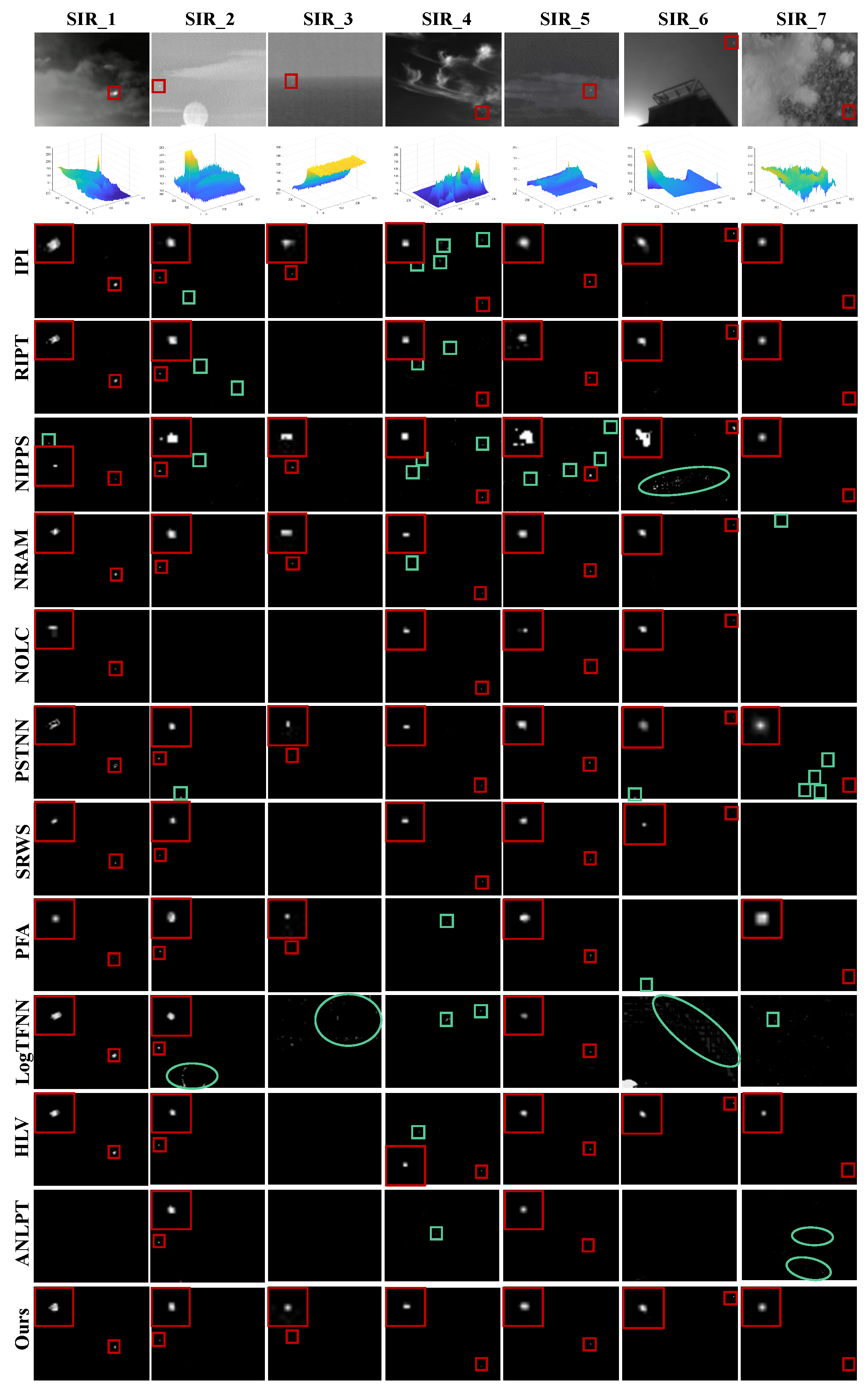



| Data | Image Size | Target Size | SCR | Background Type | Target Type | Detection Challenges | |||
|---|---|---|---|---|---|---|---|---|---|
| Strong Edge | Low Contrast | Heavy Noise | Cloud Clutter | ||||||
| SIR_1 | 256 × 172 | 11 | 6.52 | cloud + sky | Irregular shape | ✓ | |||
| SIR_2 | 256 × 239 | 3 | 8.63 | building + sky | Weak | ✓ | ✓ | ✓ | |
| SIR_3 | 300 × 209 | 12 | 1.04 | sea + sky | Low intensity | ✓ | ✓ | ||
| SIR_4 | 280 × 228 | 2 | 3.09 | cloud + sky | Weak, hidden | ✓ | ✓ | ||
| SIR_5 | 320 × 240 | 7 | 11.11 | cloud + sky | Hidden | ✓ | |||
| SIR_6 | 359 × 249 | 6 | 6.14 | building + sky | Irregular shape | ✓ | |||
| SIR_7 | 640 × 512 | 4 | 10.52 | cloud + sky | Weak, hidden | ✓ | ✓ | ||
| SIR_8 | 320 × 256 | 5 | 5.36 | sea + sky | Weak | ✓ | |||
| SIR_9 | 283 × 182 | 8 | 1.59 | cloud + sea | Hidden | ✓ | ✓ | ||
| SIR_10 | 379 × 246 | 3 | 10.57 | building + sky | Low intensity | ✓ | ✓ | ||
| SIR_11 | 315 × 206 | 5 | 9.61 | cloud + sky | Low intensity | ✓ | ✓ | ||
| SIR_12 | 305 × 214 | 17 | 8.43 | tree + sky | Irregular shape | ✓ | |||
| SIR_13 | 320 × 255 | 4 | 4.12 | cloud + sky | Low intensity | ✓ | ✓ | ✓ | |
| SIR_14 | 377 × 261 | 6 | 2.38 | cloud + sky | Low intensity | ✓ | ✓ | ||
| Method | Patch Size | Step | Parameter |
|---|---|---|---|
| IPI [17] | 10 | ||
| RIPT [36] | 10 | ||
| NIPPS [20] | 10 | ||
| NRAM [22] | 10 | ||
| NOLC [23] | 10 | ||
| PSTNN [38] | 40 | ||
| SRWS [34] | 10 | ||
| PFA [37] | 25 | ||
| LogTFNN [39] | 40 | , , | |
| HLV [26] | 10 | ||
| ANLPT [42] | 10 | , | |
| Ours | 10 |
| Methods | IPI [17] | RIPT [17] | NIPPS [20] | NRAM [22] | NOLC [23] | PSTNN [38] | SRWS [34] | PFA [37] | LogTFNN [39] | HLV [26] | ANLPT [42] | Ours | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SIR_1 | SCRG | 2.08 | 2.55 | 0.05 | 2.76 | 2.58 | 1.81 | 2.78 | 0.03 | 1.56 | 2.85 | NaN | 20.67 |
| BSF | 1.51 | 2.26 | 3.45 | 2.82 | 1.98 | 1.31 | 5.54 | 4.50 | 1.14 | 2.14 | Inf | 32.40 | |
| SIR_2 | SCRG | 3.29 | 2.38 | 1.17 | 2.89 | NaN | 3.13 | 5.20 | 0.91 | 1.82 | 4.24 | 3.40 | 23.50 |
| BSF | 1.05 | 0.59 | 0.26 | 0.75 | Inf | 0.80 | 2.48 | 0.40 | 0.48 | 1.08 | 0.83 | 7.20 | |
| SIR_3 | SCRG | 137.56 | NaN | 102.47 | 235.38 | NaN | 90.23 | NaN | 32.40 | 11.80 | NaN | NaN | 151.21 |
| BSF | 11.39 | Inf | 5.99 | 17.02 | Inf | 18.42 | Inf | 12.10 | 1.28 | Inf | Inf | 19.48 | |
| SIR_4 | SCRG | 16.36 | 15.36 | 9.46 | Inf | 39.94 | Inf | 60.86 | NaN | NaN | 16.74 | NaN | Inf |
| BSF | 3.55 | 3.47 | 2.04 | Inf | 8.80 | Inf | 13.90 | Inf | Inf | 3.61 | Inf | Inf | |
| SIR_5 | SCRG | 2.18 | 5.60 | 0.68 | 4.79 | 4.96 | 1.53 | 6.57 | 2.39 | 1.41 | 1.82 | 0.01 | 7.81 |
| BSF | 0.77 | 2.07 | 0.16 | 1.63 | 1.72 | 0.49 | 2.49 | 0.80 | 0.71 | 0.61 | 0.68 | 3.59 | |
| SIR_6 | SCRG | 28.99 | 17.08 | 7.77 | Inf | 26.84 | NaN | Inf | NaN | NaN | 2.56 | NaN | Inf |
| BSF | 32.21 | 6.18 | 1.96 | Inf | 8.08 | Inf | Inf | Inf | Inf | 0.90 | Inf | Inf | |
| SIR_7 | SCRG | 275.57 | Inf | Inf | NaN | NaN | 5.36 | NaN | 2.13 | 3.42 | 351.29 | NaN | Inf |
| BSF | 169.41 | Inf | Inf | Inf | Inf | 3.30 | Inf | 1.69 | 2.47 | 215.97 | Inf | Inf | |
| SIR_8 | SCRG | 7.53 | 32.22 | 7.89 | 17.04 | 41.07 | 6.16 | NaN | 2.40 | 3.48 | 8.75 | 4.76 | 90.97 |
| BSF | 3.98 | 25.67 | 3.28 | 9.77 | 43.57 | 4.50 | Inf | 192.28 | 1.82 | 4.88 | 2.39 | 69.74 | |
| SIR_9 | SCRG | 24.34 | 25.51 | 11.86 | Inf | NaN | 14.85 | Inf | 5.41 | 18.08 | 23.11 | NaN | Inf |
| BSF | 12.92 | 24.33 | 9.04 | Inf | Inf | 7.95 | Inf | 10.00 | 9.44 | 12.42 | Inf | Inf | |
| SIR_10 | SCRG | 1.94 | Inf | 0.38 | Inf | 3.37 | Inf | 4.31 | NaN | NaN | 2.39 | 2.02 | Inf |
| BSF | 1.04 | Inf | 0.16 | Inf | 1.85 | Inf | 2.47 | Inf | Inf | 1.30 | 1.36 | Inf | |
| SIR_11 | SCRG | 2.57 | NaN | 0.87 | NaN | NaN | NaN | 10.58 | NaN | 0.06 | Inf | 1.73 | Inf |
| BSF | 0.28 | Inf | 0.07 | Inf | Inf | Inf | 1.46 | Inf | 0.05 | Inf | 0.18 | Inf | |
| SIR_12 | SCRG | 1.47 | Inf | 1.42 | Inf | NaN | 1.91 | 1.11 | Inf | 0.52 | 1.75 | 1.14 | Inf |
| BSF | 0.73 | Inf | 0.62 | Inf | Inf | 1.02 | 1.75 | Inf | 0.25 | 0.91 | 0.55 | Inf | |
| SIR_13 | SCRG | 1.58 | Inf | 0.30 | Inf | Inf | 5.67 | Inf | NaN | NaN | 31.94 | Inf | Inf |
| BSF | 0.53 | Inf | 0.08 | Inf | Inf | 3.40 | Inf | Inf | Inf | 6.23 | Inf | Inf | |
| SIR_14 | SCRG | 4.28 | 7.69 | 1.87 | 8.26 | Inf | 3.25 | Inf | 1.58 | 0.52 | 7.25 | 5.73 | Inf |
| BSF | 1.55 | 2.79 | 0.48 | 3.09 | Inf | 1.14 | Inf | 0.63 | 0.19 | 2.88 | 2.06 | Inf | |
| Image id | SIR_1 | SIR_2 | SIR_3 | SIR_4 | SIR_5 | SIR_6 | SIR_7 | SIR_8 | SIR_9 | SIR_10 | SIR_11 | SIR_12 | SIR_13 | SIR_14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IPI [17] | 3.28 | 5.23 | 7.63 | 6.45 | 12.52 | 12.93 | 12.67 | 11.28 | 4.12 | 15.32 | 7.88 | 7.29 | 14.87 | 18.72 |
| RIPT [36] | 1.17 | 2.76 | 2.02 | 2.82 | 4.70 | 2.88 | 8.01 | 4.35 | 0.96 | 1.85 | 1.02 | 1.40 | 2.12 | 2.14 |
| NIPPS [20] | 1.88 | 3.34 | 3.60 | 3.56 | 5.51 | 6.82 | 7.11 | 6.71 | 2.84 | 9.18 | 3.95 | 3.99 | 7.51 | 9.96 |
| NRAM [22] | 2.17 | 2.14 | 1.55 | 2.61 | 2.99 | 3.88 | 2.38 | 4.79 | 1.44 | 4.20 | 2.09 | 2.27 | 3.94 | 4.20 |
| NOLC [23] | 0.72 | 0.86 | 1.11 | 1.15 | 1.24 | 1.67 | 3.62 | 1.64 | 0.94 | 3.17 | 1.55 | 1.28 | 1.33 | 2.11 |
| SRWS [34] | 2.01 | 2.01 | 1.10 | 3.12 | 2.12 | 2.60 | 3.65 | 1.63 | 0.78 | 1.57 | 1.01 | 1.29 | 1.46 | 1.77 |
| HLV [26] | 1.13 | 1.76 | 2.32 | 1.55 | 2.86 | 4.51 | 4.26 | 3.54 | 1.44 | 4.47 | 2.30 | 2.27 | 4.01 | 6.09 |
| ANLPT [42] | 1.53 | 1.79 | 1.91 | 1.73 | 2.05 | 2.18 | 8.07 | 2.57 | 1.53 | 2.29 | 1.99 | 2.15 | 2.52 | 2.80 |
| Ours (CPU) | 0.49 | 0.76 | 0.94 | 0.93 | 1.55 | 1.94 | 2.10 | 1.29 | 0.53 | 1.77 | 0.86 | 0.87 | 1.64 | 1.89 |
| Ours (GPU) | 0.34 | 0.42 | 0.54 | 0.52 | 0.87 | 0.98 | 0.54 | 0.90 | 0.36 | 0.84 | 0.47 | 0.42 | 0.82 | 0.85 |
| Method | SIR_1 | SIR_2 | SIR_3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| (Patch, Step) | (25,25) | (40,40) | (50,10) | (25,25) | (40,40) | (50,10) | (25,25) | (40,40) | (50,10) |
| PFA [37] | 9.96 | 0.33 | 1.39 | 12.68 | 0.26 | 1.69 | 0.33 | 0.26 | 2.19 |
| PSTNN [38] | 0.04 | 0.05 | 1.15 | 0.06 | 0.07 | 3.90 | 0.16 | 0.06 | 1.44 |
| LogTFNN [39] | 0.89 | 1.33 | 15.06 | 1.22 | 1.81 | 11.63 | 1.27 | 1.38 | 26.92 |
| Ours(CPU) | 0.12 | 0.13 | 0.49 | 0.19 | 0.17 | 0.76 | 0.16 | 0.14 | 0.94 |
| Ours(GPU) | 0.02 | 0.02 | 0.34 | 0.04 | 0.02 | 0.42 | 0.02 | 0.01 | 0.54 |
| Matrix Height | MATLAB | CUDA | ||||||
|---|---|---|---|---|---|---|---|---|
| SVD | SVDS | Lanczos | RSVD | APSVD | SGESVD | SGESVDJ | APSVD | |
| 1000 | 1.03 | 6.68 | 4.59 | 7.67 | 0.53 | 9.07 | 5.75 | 1.06 |
| 10,000 | 6.27 | 19.93 | 22.08 | 10.05 | 1.83 | 16.71 | 7.36 | 1.24 |
| 100,000 | 280.12 | 406.70 | 298.77 | 50.82 | 11.82 | / | 24.06 | 9.58 |
| Image Size | Base | +PASVD | +New Continuation | +GPU Parallelism |
|---|---|---|---|---|
| 1.42 | 0.86 | 0.29 | 0.09 | |
| 6.23 | 4.91 | 1.12 | 0.41 | |
| 12.77 | 9.24 | 1.99 | 0.74 | |
| 13.60 | 7.33 | 2.31 | 0.59 | |
| 57.79 | 34.6 | 7.32 | 2.38 | |
| 207.13 | 116.58 | 22.20 | 3.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, X.; Liu, X.; Liu, Y.; Cui, Y.; Lei, T. Infrared Small-Target Detection Based on Background-Suppression Proximal Gradient and GPU Acceleration. Remote Sens. 2023, 15, 5424. https://doi.org/10.3390/rs15225424
Hao X, Liu X, Liu Y, Cui Y, Lei T. Infrared Small-Target Detection Based on Background-Suppression Proximal Gradient and GPU Acceleration. Remote Sensing. 2023; 15(22):5424. https://doi.org/10.3390/rs15225424
Chicago/Turabian StyleHao, Xuying, Xianyuan Liu, Yujia Liu, Yi Cui, and Tao Lei. 2023. "Infrared Small-Target Detection Based on Background-Suppression Proximal Gradient and GPU Acceleration" Remote Sensing 15, no. 22: 5424. https://doi.org/10.3390/rs15225424
APA StyleHao, X., Liu, X., Liu, Y., Cui, Y., & Lei, T. (2023). Infrared Small-Target Detection Based on Background-Suppression Proximal Gradient and GPU Acceleration. Remote Sensing, 15(22), 5424. https://doi.org/10.3390/rs15225424






