Deceptive Jamming Algorithm against Synthetic Aperture Radar in Large Squint Angle Mode Based on Non-Linear Chirp Scaling and Low Azimuth Sampling Reconstruction
Abstract
:1. Introduction
1.1. Background
1.2. Problem Statement and Contributions
2. Deceptive Jamming Algorithm Based on Non-Linear Chirp Scaling and Low Azimuth Sampling Reconstruction
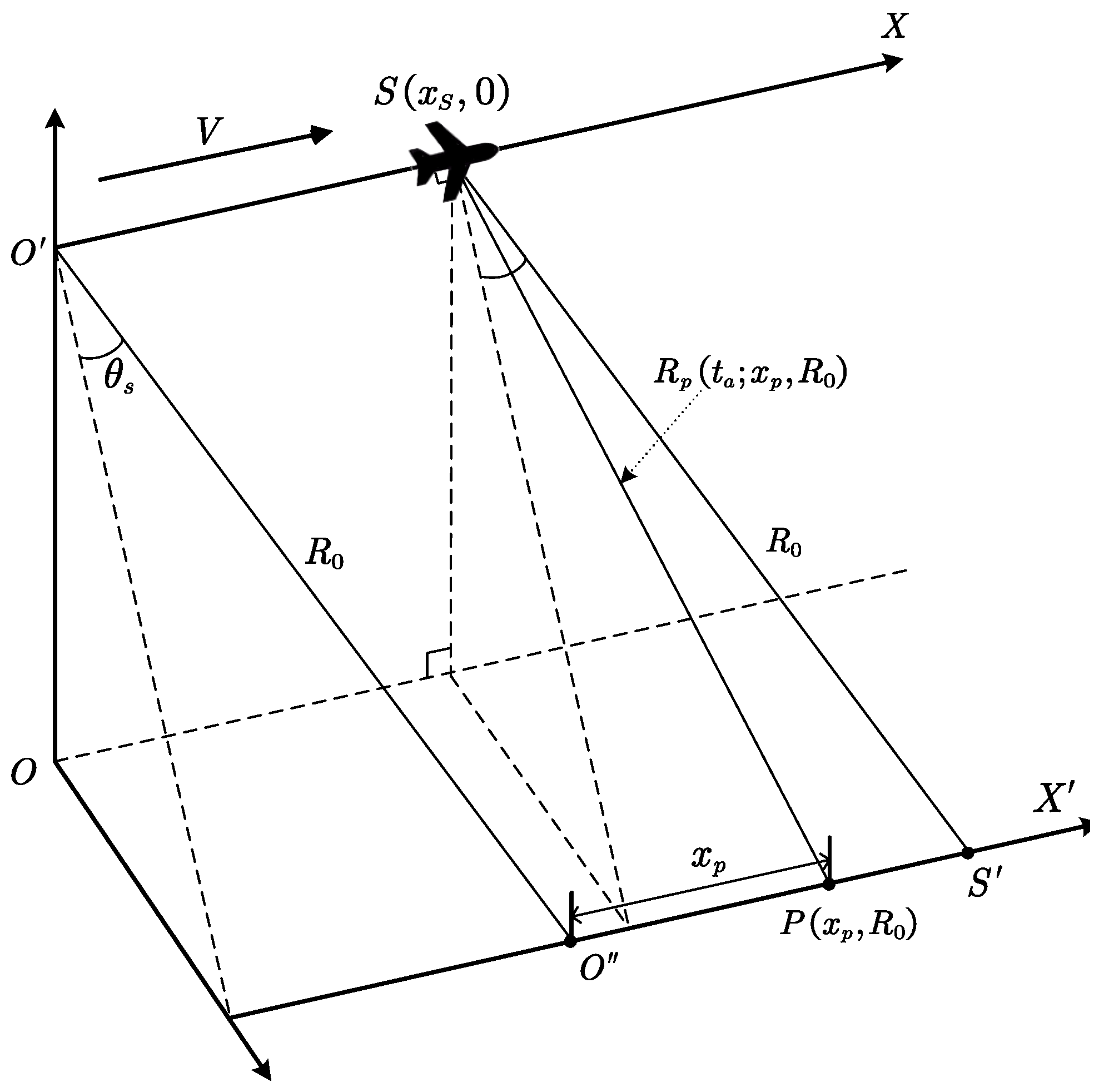
2.1. Squint Angle SAR Signal Model
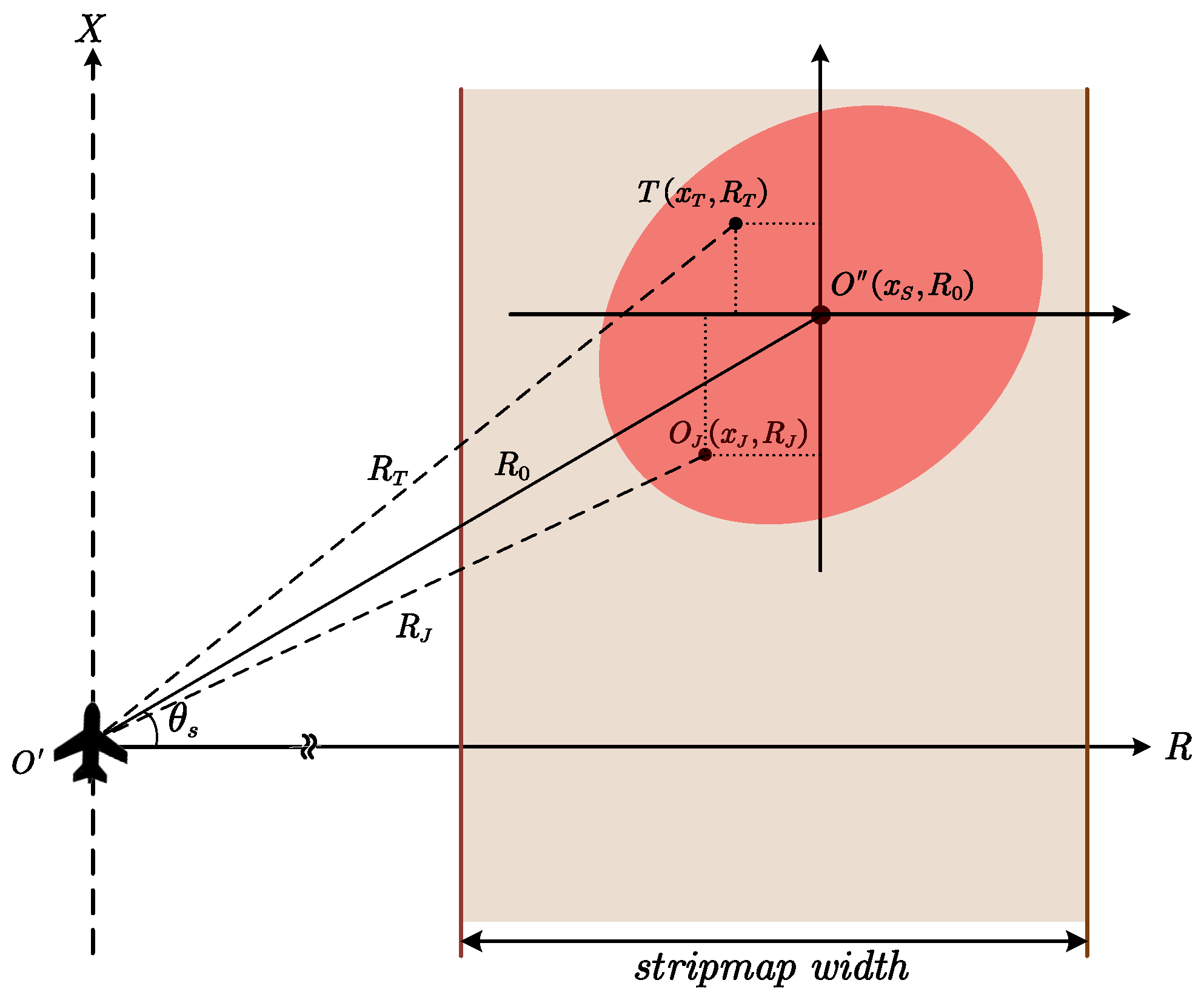
2.2. SAR Deceptive Jamming Model
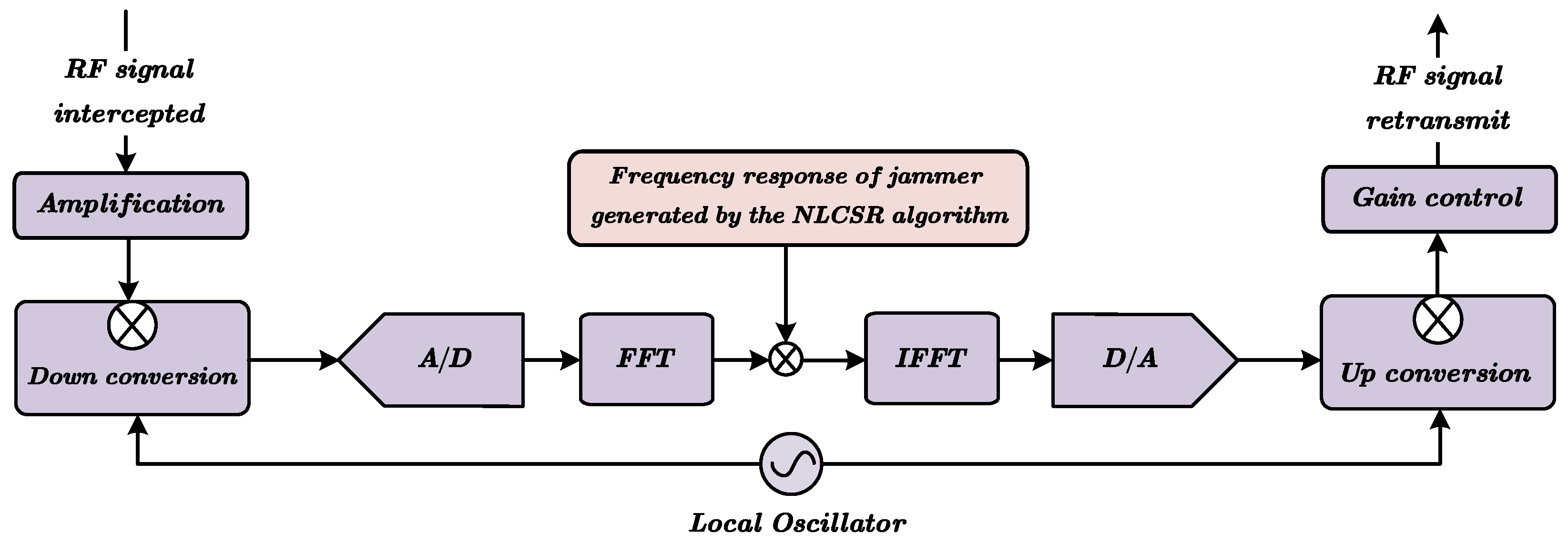
2.3. NLCSR-Based Deceptive Jamming
2.3.1. Consistent Construction of the Cross-Coupling Term
2.3.2. Construction of Azimuth Modulation Term Based on Non-Linear Chirp Scaling
- First, multiply the factor in the range frequency domain and azimuth time domain to achieve the range translation of the deceptive jamming template;
- Second, adjust the azimuth sampling interval of the deceptive template, divide the original sampling interval by to achieve the azimuth scaling of the deceptive jamming template, and the Equation (36) can be obtained.
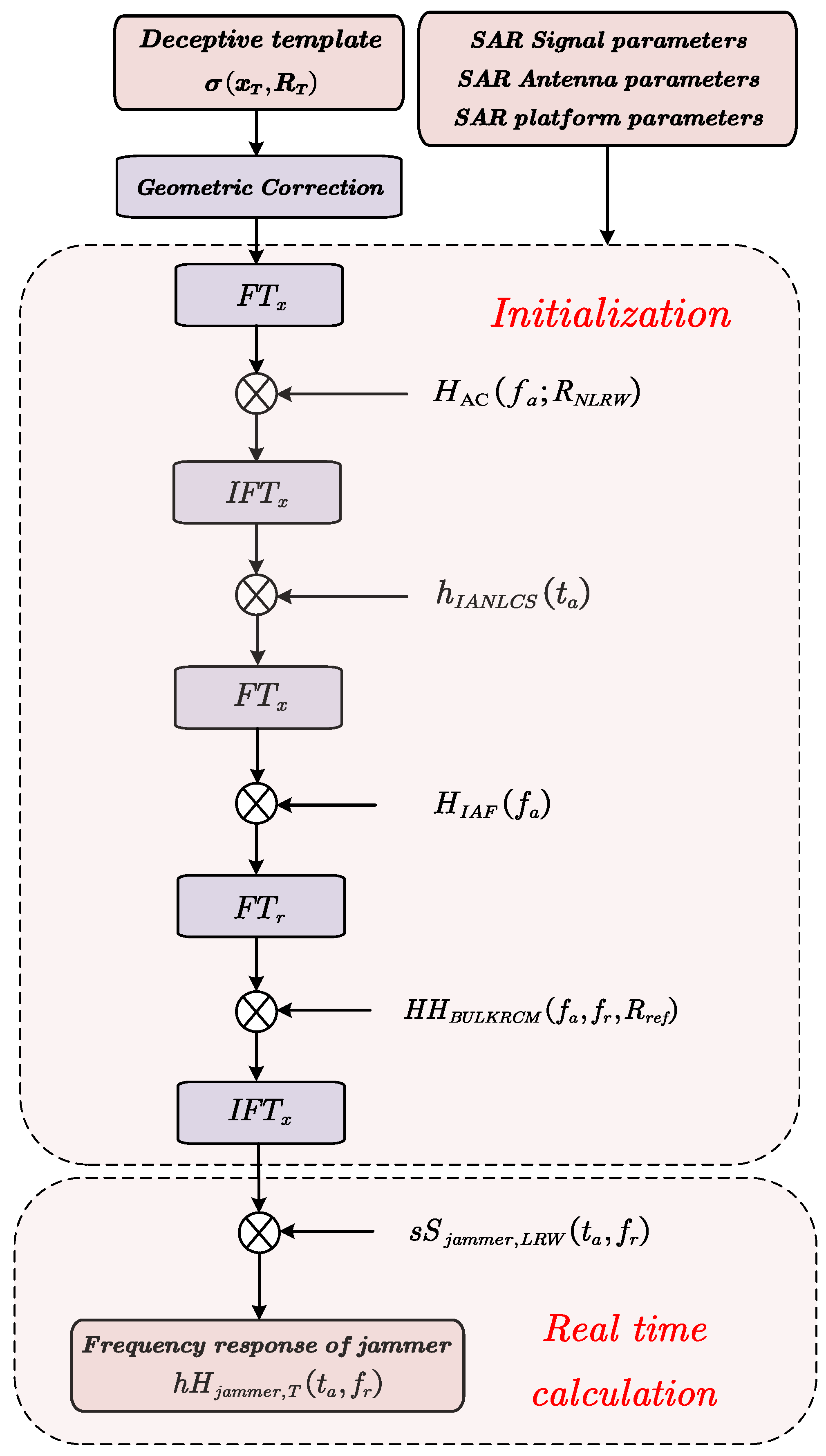
2.3.3. Construction Process of Jamming Signal Based on NLCSR Algorithm
- SAR signal parameters, such as center frequency , signal bandwidth , signal pulse width , and pulse repetition frequency ;
- SAR antenna parameters, such as synthetic aperture length , squint angle and pitch angle ;
- SAR platform parameters, such as flight speed V, and SAR flight height H.
3. Analysis and Simulation of NLCSR Algorithm
3.1. Simulation and Result
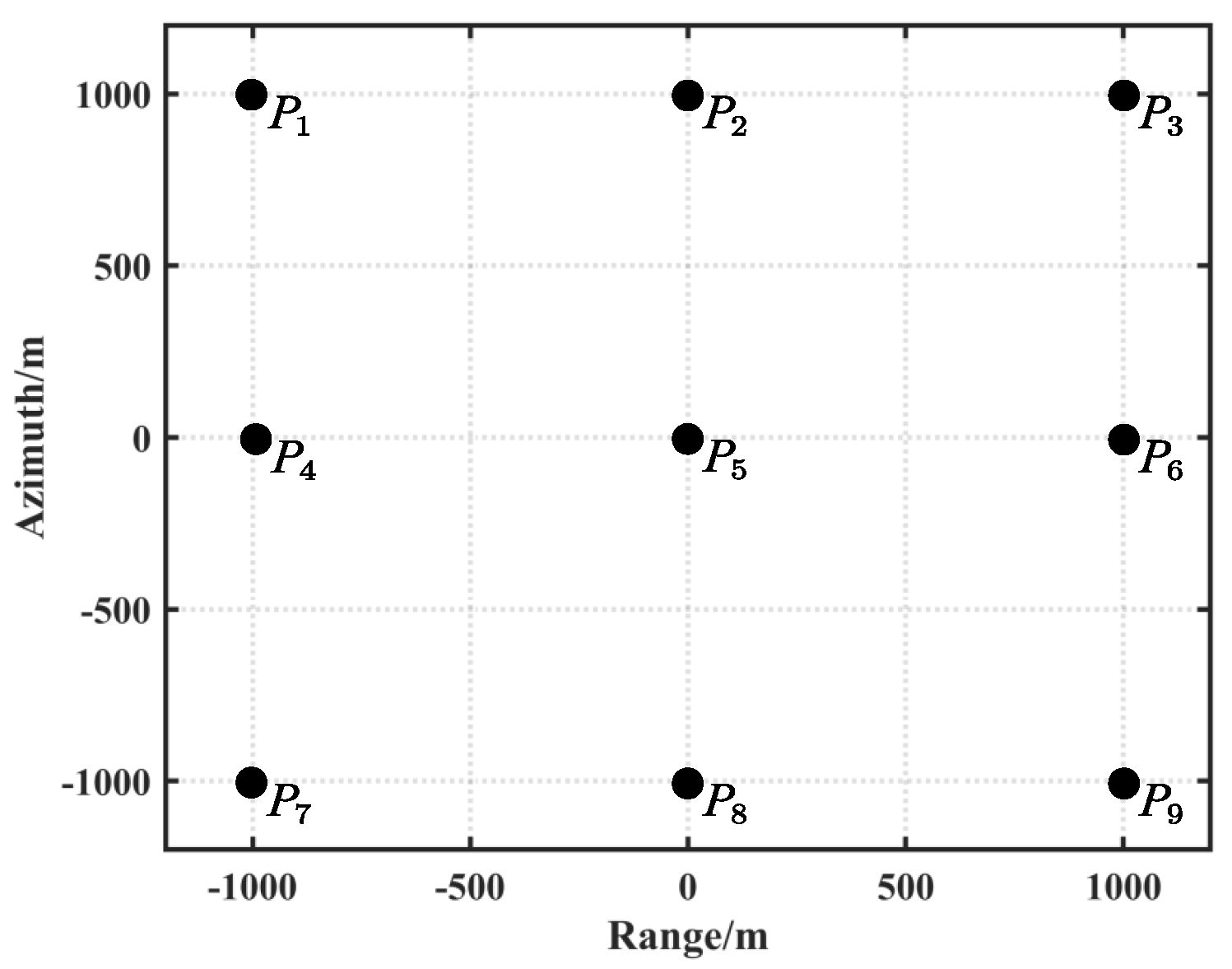
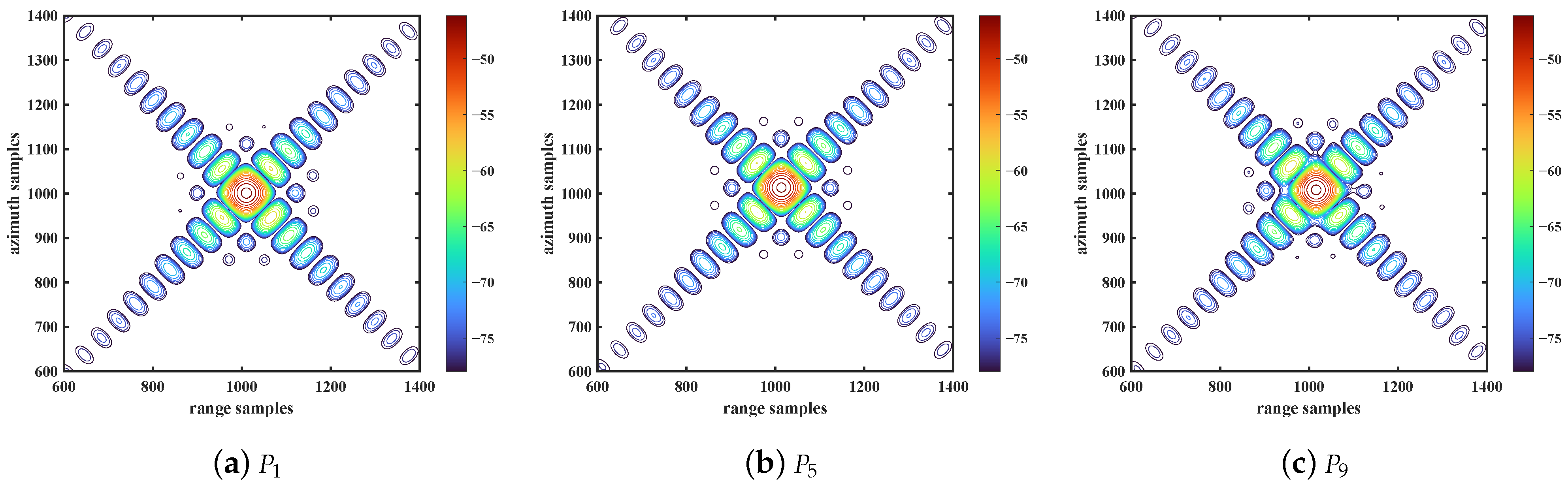
3.1.1. False Point Target Simulation
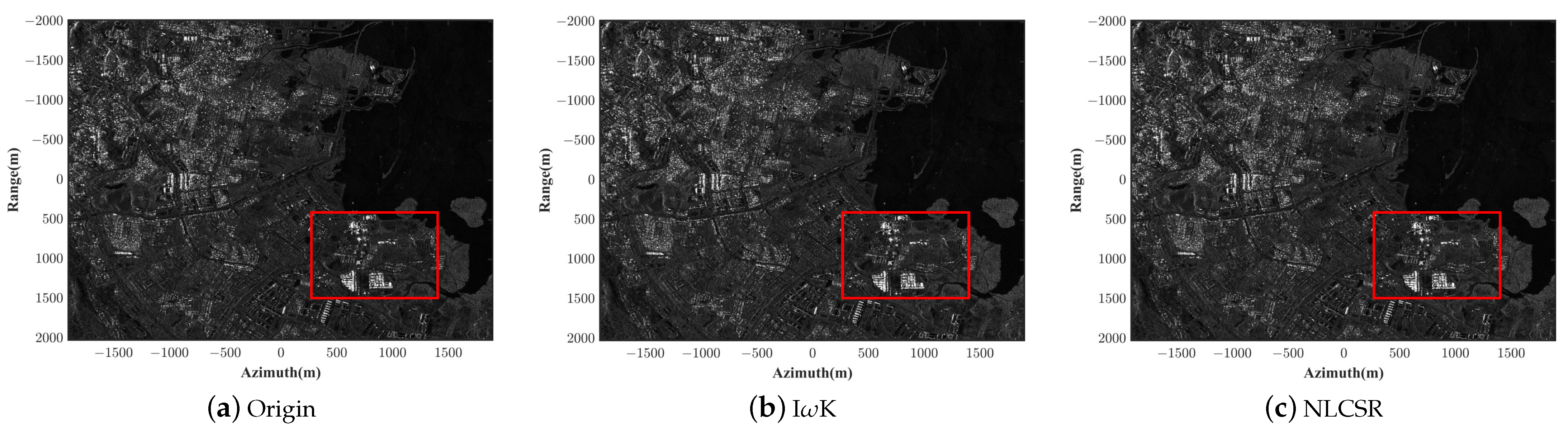
3.1.2. Actual Scene Deceptive Simulation
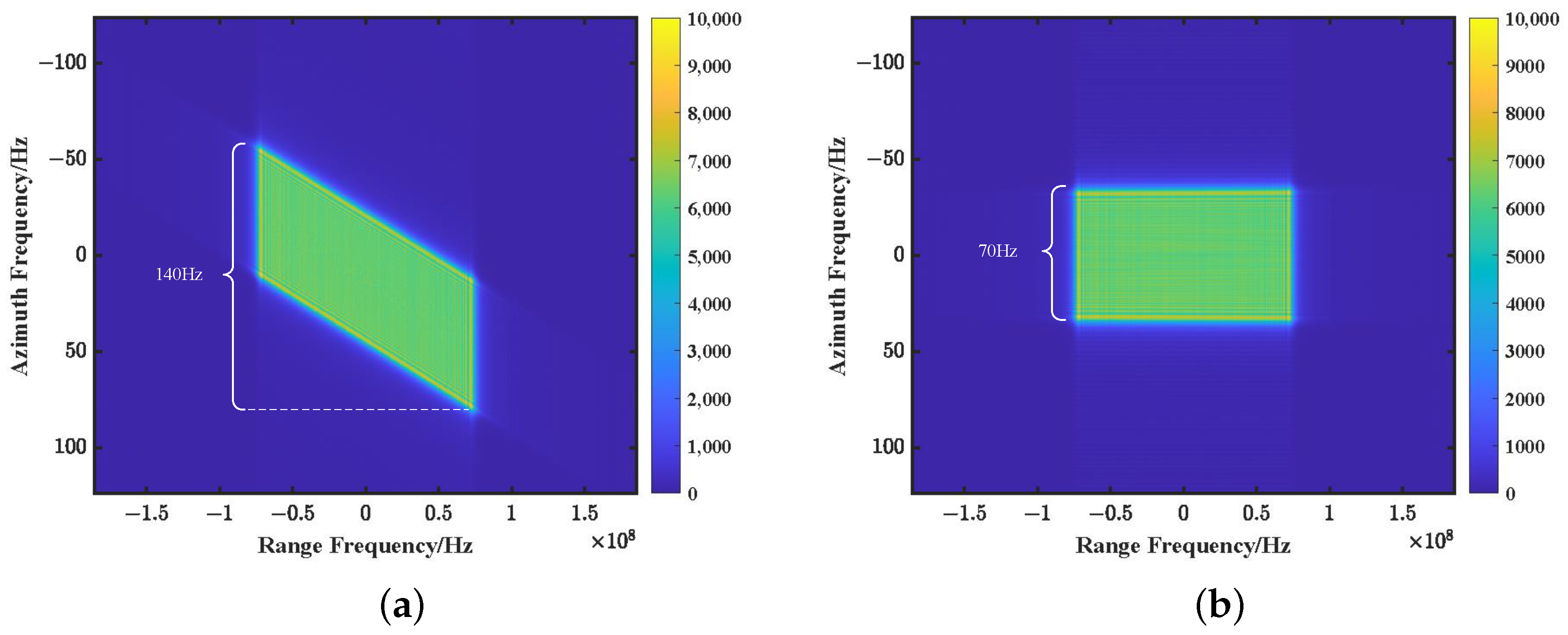
3.2. Validity Analysis
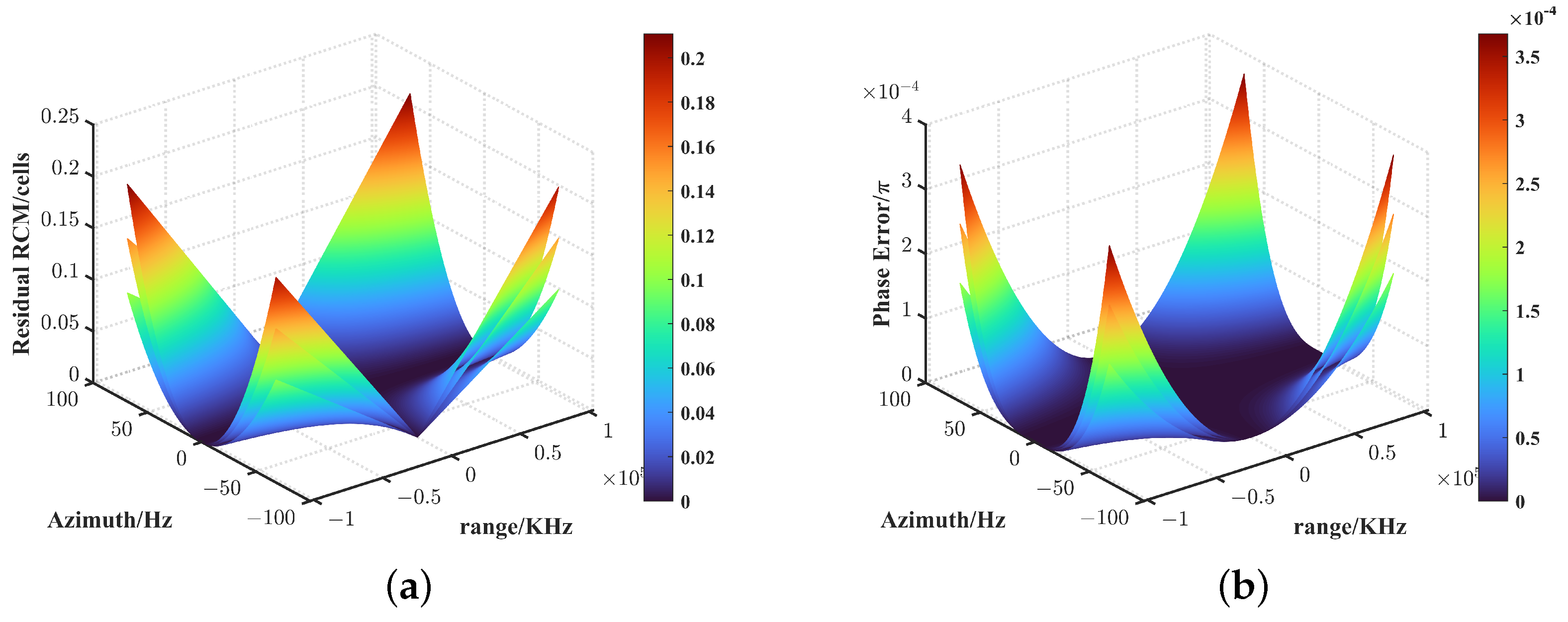
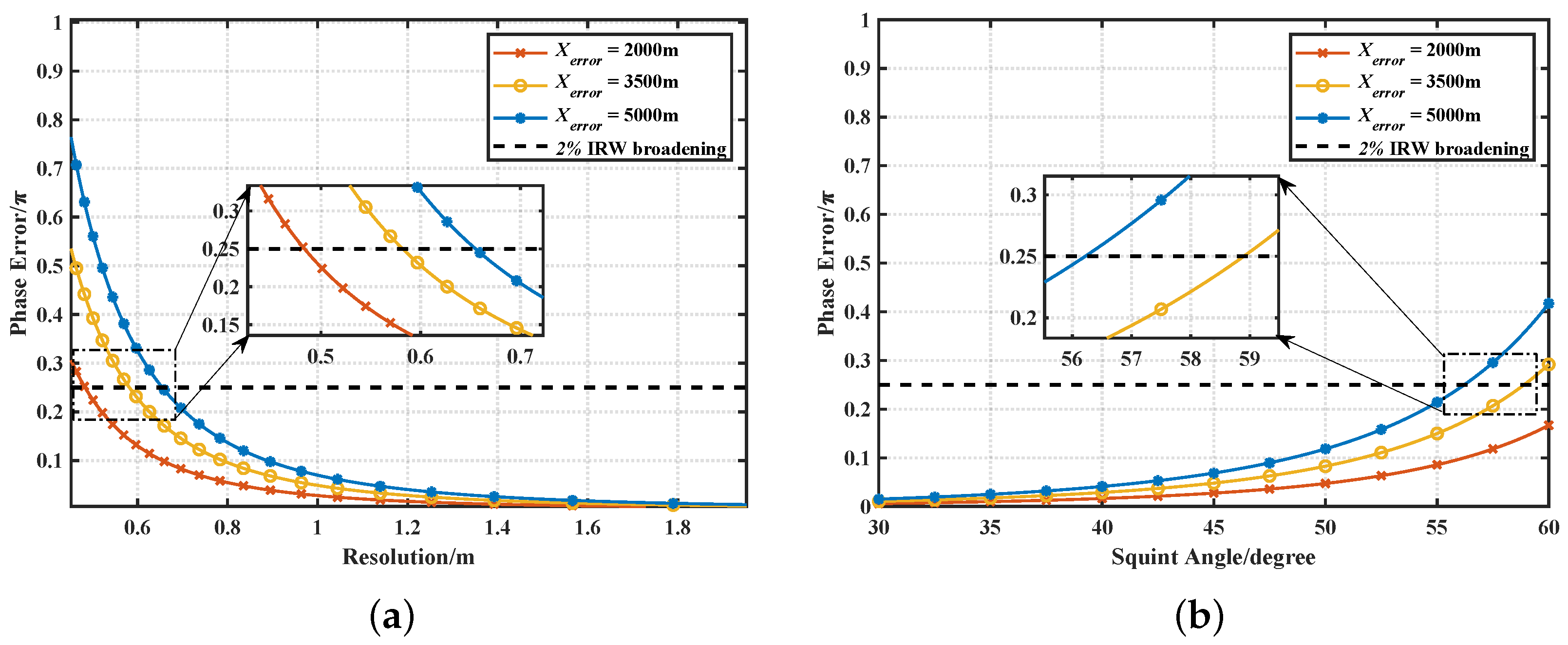
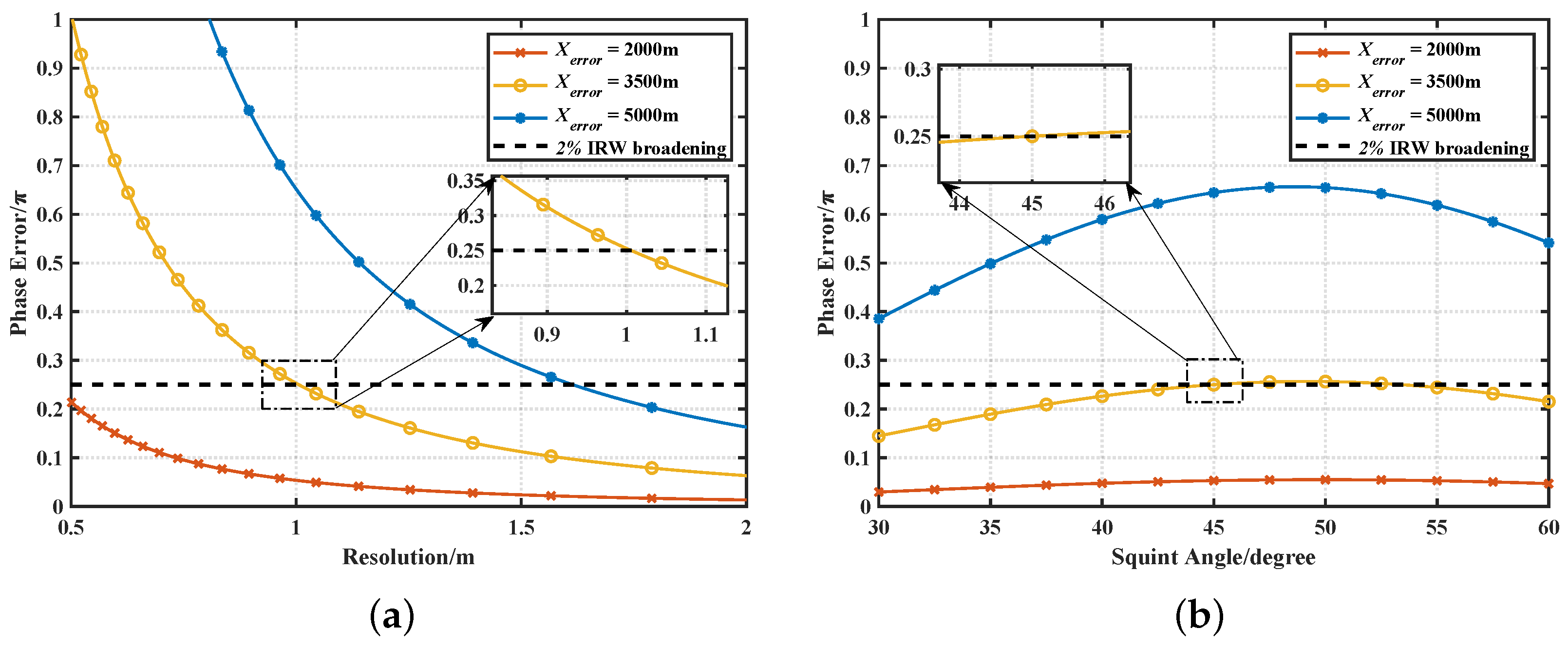
3.2.1. Validation of the Cross-Coupling Signal Model
3.2.2. Validation of the Azimuth Signal Model
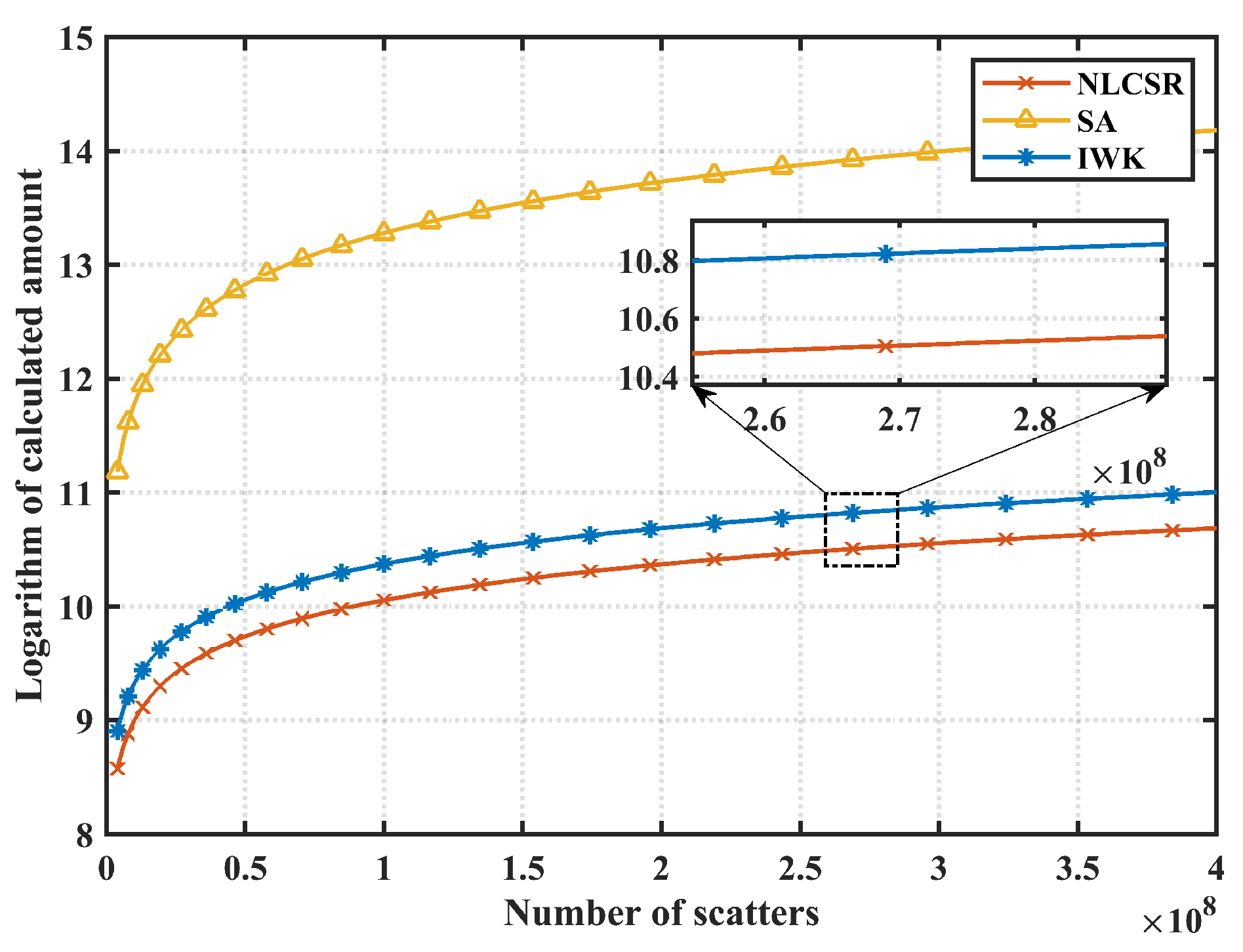
3.3. Computational Complexity Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SAR | Synthetic aperture radar |
| NLCSR | Non-linear chirp scaling and low azimuth sampling reconstruction algorithm |
| SA | Superposition calculation algorithm |
| IK | Inverse Omega-K algorithm |
| JFR | Jamming frequency response |
| PRI | Pulse repetition interval |
| DRFM | Digital radio frequency memory |
| LRW | Linear range walking |
| QPE | Quadratic phase error |
| ANCS | Azimuth non-linear chirp scaling algorithm |
| CSA | Chirp scaling imaging algorithm |
| IRW | Impulse response width |
| PSLR | Peak sidelobe ratio |
| ISLR | Integral sidelobe ratio |
| SSIM | Structural similarity |
Appendix A. Derivation of Equations (30)∼(33)
References
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data; Artech House Publishers: Boston, MA, USA, 2005; pp. 473–476. [Google Scholar]
- Condley, C. Some System Considerations for Electronic Countermeasures to Synthetic Aperture Radar. In Proceedings of the IEE Colloquium on Electronic Warfare Systems, London, UK, 14 January 1991; pp. 8/1–8/7. [Google Scholar]
- Goi, W.W.; Goj, W.W. Synthetic-Aperture Radar and Electronic Warfare; Artech House Publishers: Boston, MA, USA, 1993. [Google Scholar]
- Song, C.; Wang, Y.; Jin, G.; Wang, Y.; Dong, Q.; Wang, B.; Zhou, L.; Lu, P.; Wu, Y. A Novel Jamming Method against SAR Using Nonlinear Frequency Modulation Waveform with Very High Sidelobes. Remote Sens. 2022, 14, 5370. [Google Scholar] [CrossRef]
- Liu, G.; Li, L.; Ming, F.; Sun, X.; Hong, J. A Controllable Suppression Jamming Method against SAR Based on Active Radar Transponder. Remote Sens. 2022, 14, 3949. [Google Scholar] [CrossRef]
- Wang, S.; Li, Y.U.; Jin, N.I.; Zhang, G. A Study on the Active Deception Jamming to SAR. Acta Electron. Sin. 2003, 31, 1900–1902. [Google Scholar]
- Yan, Z.; Guoqing, Z.; Yu, Z. Research on SAR Jamming Technique Based on Man-made Map. In Proceedings of the 2006 CIE International Conference on Radar, Shanghai, China, 16–19 October 2006; pp. 1–4. [Google Scholar] [CrossRef]
- Zhou, F.; Zhao, B.; Tao, M.; Bai, X.; Chen, B.; Sun, G. A Large Scene Deceptive Jamming Method for Space-Borne SAR. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4486–4495. [Google Scholar] [CrossRef]
- Sun, Q.; Shu, T.; Zhou, S.; Tang, B.; Yu, W. A Novel Jamming Signal Generation Method for Deceptive SAR Jammer. In Proceedings of the 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 1174–1178. [Google Scholar] [CrossRef]
- Yang, K.; Ye, W.; Ma, F.; Li, G.; Tong, Q. A Large-Scene Deceptive Jamming Method for Space-Borne SAR Based on Time-Delay and Frequency-Shift with Template Segmentation. Remote Sens. 2019, 12, 53. [Google Scholar] [CrossRef]
- Liu, Y.; Wei, W.; Pan, X.; Dai, D.; Feng, D. A Frequency-Domain Three-Stage Algorithm for Active Deception Jamming against Synthetic Aperture Radar. IET Radar Sonar Navig. 2014, 8, 639–646. [Google Scholar] [CrossRef]
- Lin, X.; Liu, P.; Xue, G. Fast Generation of SAR Deceptive Jamming Signal Based on Inverse Range Doppler Algorithm. In Proceedings of the IET International Radar Conference 2013, Xi’an, China, 14–16 April 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, W.; Pan, X.; Fu, Q.; Wang, G. Inverse Omega-K Algorithm for the Electromagnetic Deception of Synthetic Aperture Radar. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3037–3049. [Google Scholar] [CrossRef]
- Sun, Q.; Shu, T.; Yu, K.B.; Yu, W. Efficient Deceptive Jamming Method of Static and Moving Targets Against SAR. IEEE Sens. J. 2018, 18, 3610–3618. [Google Scholar] [CrossRef]
- He, X.; Zhu, J.; Wang, J.; Du, D.; Tang, B. False Target Deceptive Jamming for Countering Missile-Borne SAR. In Proceedings of the 2014 IEEE 17th International Conference on Computational Science and Engineering, Chengdu, China, 19–21 December 2014; pp. 1974–1978. [Google Scholar] [CrossRef]
- Zhao, B.; Zhou, F.; Bao, Z. Deception Jamming for Squint SAR Based on Multiple Receivers. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3988–3998. [Google Scholar] [CrossRef]
- Zhao, B.; Huang, L.; Zhou, F.; Zhang, J. Performance Improvement of Deception Jamming Against SAR Based on Minimum Condition Number. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1039–1055. [Google Scholar] [CrossRef]
- Zhao, B.; Huang, L.; Li, J.; Liu, M.; Wang, J. Deceptive SAR Jamming Based on 1-Bit Sampling and Time-Varying Thresholds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 939–950. [Google Scholar] [CrossRef]
- Yang, K.; Ma, F.; Ran, D.; Ye, W.; Li, G. Fast Generation of Deceptive Jamming Signal Against Spaceborne SAR Based on Spatial Frequency Domain Interpolation. IEEE Trans. Geosci. Remote Sens. 2022. [Google Scholar] [CrossRef]
- Li, N.; Cheng, D.; Lu, P.; Shu, G.; Guo, Z. Smart Jamming Against SAR Based on Non-Linear Frequency-Modulated Signal. IEEE Trans. Aerosp. Electron. Syst. 2022, 1–19. [Google Scholar] [CrossRef]
- Dong, J.; Zhang, Q.; Lu, W.; Cheng, W.; Liu, X. Hybrid Domain Efficient Modulation-Based Deceptive Jamming Algorithm for Nonlinear-Trajectory Synthetic Aperture Radar. Remote Sens. 2023, 15, 2446. [Google Scholar] [CrossRef]
- Liu, Y.X.; Zhang, Q.; Xiong, S.C.; Ni, J.C.; Wang, D.; Wang, H.B. An ISAR Shape Deception Jamming Method Based on Template Multiplication and Time Delay. Remote Sens. 2023, 15, 2762. [Google Scholar] [CrossRef]
- Shenghua, Z.; Dazhuan, X.; Xueming, J.; Hua, H. A Study on Active Jamming to Synthetic Aperture Radar. In Proceedings of the ICCEA 2004 3rd International Conference on Computational Electromagnetics and Its Applications, 2004, Beijing, China, 1–4 November 2004; pp. 403–406. [Google Scholar] [CrossRef]
- Dai, D.H.; Wu, X.F.; Wang, X.S.; Xiao, S.P. SAR Active-Decoys Jamming Based on DRFM. In Proceedings of the 2007 IET International Conference on Radar Systems, Edinburgh, UK, 15–18 October 2007; pp. 1–4. [Google Scholar]
- Zaugg, E.C.; Long, D.G. Generalized Frequency-Domain SAR Processing. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3761–3773. [Google Scholar] [CrossRef]
- Li, Z.; Bethel, J. Image Coregistration in Sar Interferometry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, XXXVII, 433–438. [Google Scholar]
- Sun, G.; Jiang, X.; Xing, M.; Qiao, Z.J.; Wu, Y.; Bao, Z. Focus Improvement of Highly Squinted Data Based on Azimuth Nonlinear Scaling. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2308–2322. [Google Scholar] [CrossRef]
- Liu, R.; Wang, Y. Extended Nonlinear Chirp Scaling Algorithm for Highly Squinted Missile-Borne Synthetic Aperture Radar with Diving Acceleration. J. Appl. Remote Sens. 2016, 10, 025005. [Google Scholar] [CrossRef]
- Yi, T.; He, Z.; He, F.; Dong, Z.; Wu, M. Generalized Nonlinear Chirp Scaling Algorithm for High-Resolution Highly Squint SAR Imaging. Sensors 2017, 17, 2568. [Google Scholar] [CrossRef]
- Sample Imagery Detail. Available online: https://www.intelligence-airbusds.com/en/9317-sample-imagery-detail?product=37970&keyword=&type=364 (accessed on 24 June 2023).
- SAR Data–Pathfinder Radar ISR & SAR Systems. Available online: https://www.sandia.gov/radar/pathfinder-radar-isr-and-synthetic-aperture-radar-sar-systems/complex-data/ (accessed on 5 July 2023).




| Parameters | Values |
|---|---|
| Transmitted Radar Signal | LFM |
| Center Frequency | 10 GHz |
| Pulse Bandwidth | 150 MHz |
| Pulse Repetition Interval | ms |
| Pulse Duration | 10 s |
| Velocity | 100 m/s |
| Aperture Length | m |
| Squint Angle | |
| Center Slant Range | 20 km |
| Scatters | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Range | IRW(m) | SA | 0.8860 | 0.8860 | 0.8859 | 0.8860 | 0.8860 | 0.8859 | 0.8860 | 0.8860 | 0.8859 |
| IK | 0.8861 | 0.8859 | 0.8859 | 0.8861 | 0.8861 | 0.8859 | 0.8861 | 0.8861 | 0.8861 | ||
| NLCSR | 0.8860 | 0.8862 | 0.8858 | 0.8860 | 0.8860 | 0.8862 | 0.8862 | 0.8862 | 0.8868 | ||
| IRWB(%) | IK | 0.00% | 0.02% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.02% | |
| IRWB(%) | NLCSR | 0.00% | 0.02% | 0.00% | 0.00% | 0.00% | 0.04% | 0.02% | 0.02% | 0.11% | |
| PSLR(dB) | SA | −13.2638 | −13.2621 | −13.2602 | −13.2615 | −13.2597 | −13.2608 | −13.2608 | −13.2593 | −13.2591 | |
| IK | −13.2670 | −13.2639 | −13.2587 | −13.2652 | −13.2620 | −13.2590 | −13.2645 | −13.2600 | −13.2568 | ||
| NLCSR | −13.2588 | −13.2578 | −13.2526 | −13.2646 | −13.2647 | −13.2592 | −13.2670 | −13.2663 | −13.3032 | ||
| PSLRB(dB) | IK | 0.0032 | 0.0018 | 0.0015 | 0.0036 | 0.0022 | 0.0018 | 0.0037 | 0.0007 | 0.0022 | |
| PSLRB(dB) | NLCSR | 0.0049 | 0.0043 | 0.0077 | 0.0031 | 0.0050 | 0.0015 | 0.0062 | 0.0070 | 0.0441 | |
| ISLR(dB) | SA | −10.3014 | −10.3016 | −10.3011 | −10.3008 | −10.3010 | −10.3012 | −10.3007 | −10.3007 | −10.3007 | |
| IK | −10.3052 | −10.3043 | −10.3055 | −10.3046 | −10.3047 | −10.3055 | −10.3045 | −10.3042 | −10.3056 | ||
| NLCSR | −10.5878 | −10.5859 | −10.5856 | −10.5855 | −10.5867 | −10.5880 | −10.5870 | −10.5867 | −10.6330 | ||
| ISLRB(dB) | IK | 0.0037 | 0.0027 | 0.0044 | 0.0038 | 0.0037 | 0.0043 | 0.0038 | 0.0035 | 0.0048 | |
| ISLRB(dB) | NLCSR | 0.2864 | 0.2843 | 0.2844 | 0.2847 | 0.2858 | 0.2868 | 0.2863 | 0.2860 | 0.3323 | |
| Azimuth | IRW(m) | SA | 0.8860 | 0.8860 | 0.8860 | 0.8860 | 0.8860 | 0.8860 | 0.8860 | 0.8860 | 0.8860 |
| IK | 0.8861 | 0.8859 | 0.8859 | 0.8861 | 0.8859 | 0.8859 | 0.8861 | 0.8859 | 0.8859 | ||
| NLCSR | 0.8864 | 0.8860 | 0.8860 | 0.8858 | 0.8860 | 0.8862 | 0.8858 | 0.8860 | 0.8874 | ||
| IRWB(%) | IK | 0.00% | 0.02% | 0.02% | 0.00% | 0.02% | 0.02% | 0.00% | 0.02% | 0.02% | |
| IRWB(%) | NLCSR | 0.04% | 0.00% | 0.00% | 0.02% | 0.00% | 0.02% | 0.02% | 0.00% | 0.15% | |
| PSLR(dB) | SA | −13.2595 | −13.2609 | −13.2634 | −13.2594 | −13.2613 | −13.2636 | −13.2595 | −13.2624 | −13.2642 | |
| IK | −13.2569 | −13.2621 | −13.2684 | −13.2569 | −13.2620 | −13.2688 | −13.2570 | −13.2624 | −13.2691 | ||
| NLCSR | −12.2789 | −12.7784 | −13.2695 | −12.7769 | −13.2618 | −13.7728 | −13.2633 | −13.7704 | −14.2932 | ||
| PSLRB(dB) | IK | 0.0026 | 0.0012 | 0.0051 | 0.0025 | 0.0007 | 0.0052 | 0.0025 | 0.0000 | 0.0049 | |
| PSLRB(dB) | NLCSR | 0.9806 | 0.4825 | 0.0062 | 0.4825 | 0.0005 | 0.5092 | 0.0037 | 0.5080 | 1.0290 | |
| ISLR(dB) | SA | −10.3169 | −10.3168 | −10.3172 | −10.3174 | −10.3169 | −10.3175 | −10.3174 | −10.3174 | −10.3176 | |
| IK | −10.3184 | −10.3171 | −10.3189 | −10.3185 | −10.3171 | −10.3191 | −10.3185 | −10.3173 | −10.3192 | ||
| NLCSR | −10.5088 | −10.5658 | −10.5816 | −10.5669 | −10.5800 | −10.5690 | −10.5809 | −10.5677 | −10.5583 | ||
| ISLRB(dB) | IK | 0.0015 | 0.0003 | 0.0016 | 0.0012 | 0.0002 | 0.0016 | 0.0011 | 0.0001 | 0.0016 | |
| ISLRB(dB) | NLCSR | 0.1918 | 0.2491 | 0.2643 | 0.2496 | 0.2631 | 0.2515 | 0.2635 | 0.2502 | 0.2407 | |
| Algorithm | Basic Operations |
|---|---|
| SA | |
| IK | |
| NLCSR | |
| Template Size | Signal Sampling | Runnig Time(s) | ||
|---|---|---|---|---|
| SA | IωK | NLCSR | ||
| 6824 | 10.425 | 1.626 | ||
| 187,248 | 10.837 | 1.593 | ||
| 31,848 | 45.553 | 5.926 | ||
| 386,928 | 46.145 | 5.947 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, J.; Zhang, Q.; Huang, W.; Wang, H.; Lu, W.; Liu, X. Deceptive Jamming Algorithm against Synthetic Aperture Radar in Large Squint Angle Mode Based on Non-Linear Chirp Scaling and Low Azimuth Sampling Reconstruction. Remote Sens. 2023, 15, 5446. https://doi.org/10.3390/rs15235446
Dong J, Zhang Q, Huang W, Wang H, Lu W, Liu X. Deceptive Jamming Algorithm against Synthetic Aperture Radar in Large Squint Angle Mode Based on Non-Linear Chirp Scaling and Low Azimuth Sampling Reconstruction. Remote Sensing. 2023; 15(23):5446. https://doi.org/10.3390/rs15235446
Chicago/Turabian StyleDong, Jiaming, Qunying Zhang, Wenqiang Huang, Haiying Wang, Wei Lu, and Xiaojun Liu. 2023. "Deceptive Jamming Algorithm against Synthetic Aperture Radar in Large Squint Angle Mode Based on Non-Linear Chirp Scaling and Low Azimuth Sampling Reconstruction" Remote Sensing 15, no. 23: 5446. https://doi.org/10.3390/rs15235446
APA StyleDong, J., Zhang, Q., Huang, W., Wang, H., Lu, W., & Liu, X. (2023). Deceptive Jamming Algorithm against Synthetic Aperture Radar in Large Squint Angle Mode Based on Non-Linear Chirp Scaling and Low Azimuth Sampling Reconstruction. Remote Sensing, 15(23), 5446. https://doi.org/10.3390/rs15235446







