A Grid-Based Gradient Descent Extended Target Clustering Method and Ship Target Inverse Synthetic Aperture Radar Imaging for UHF Radar
Abstract
:1. Introduction
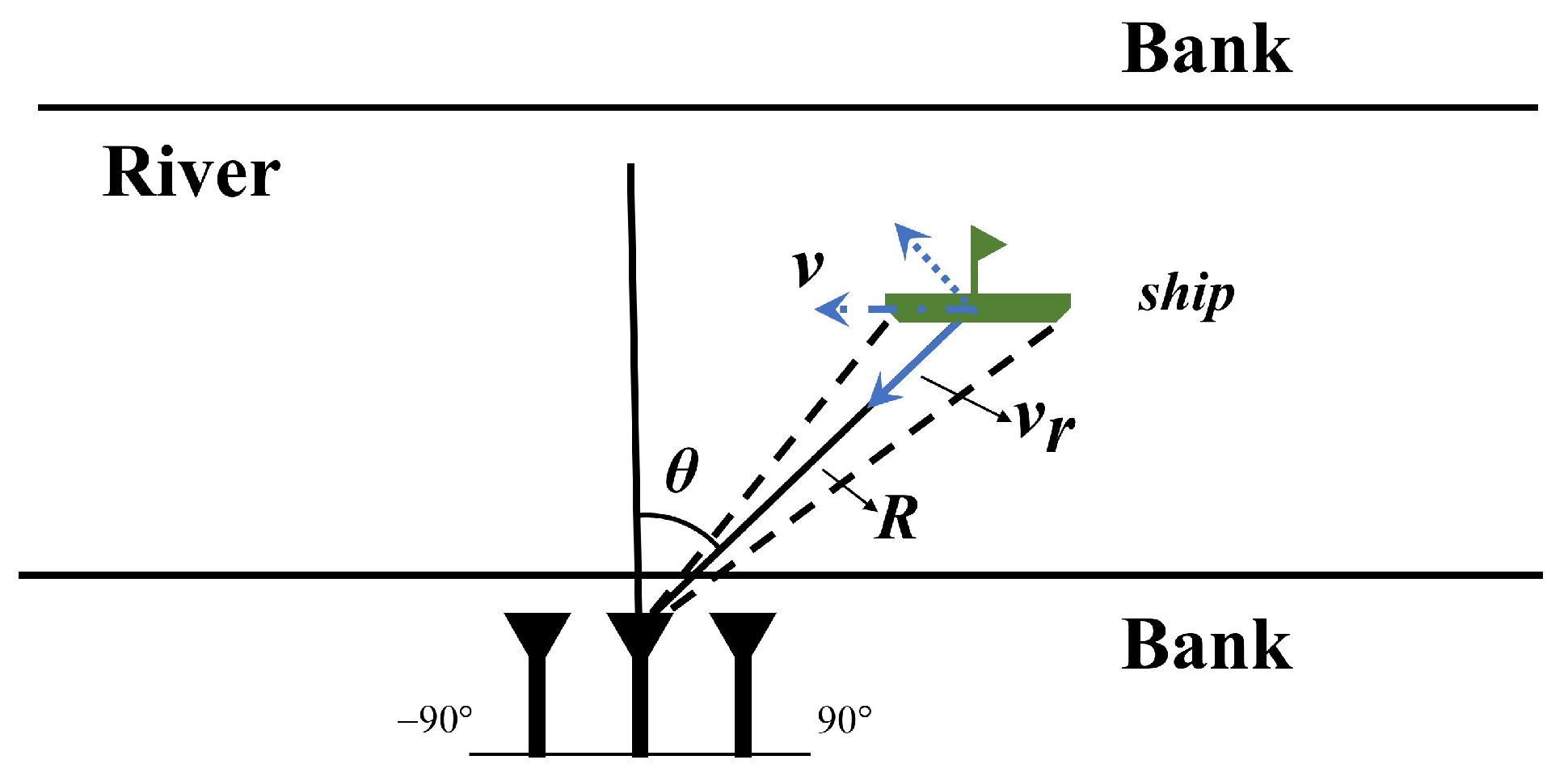
2. Characteristics of Extended Ship Target and ISAR Signal Model
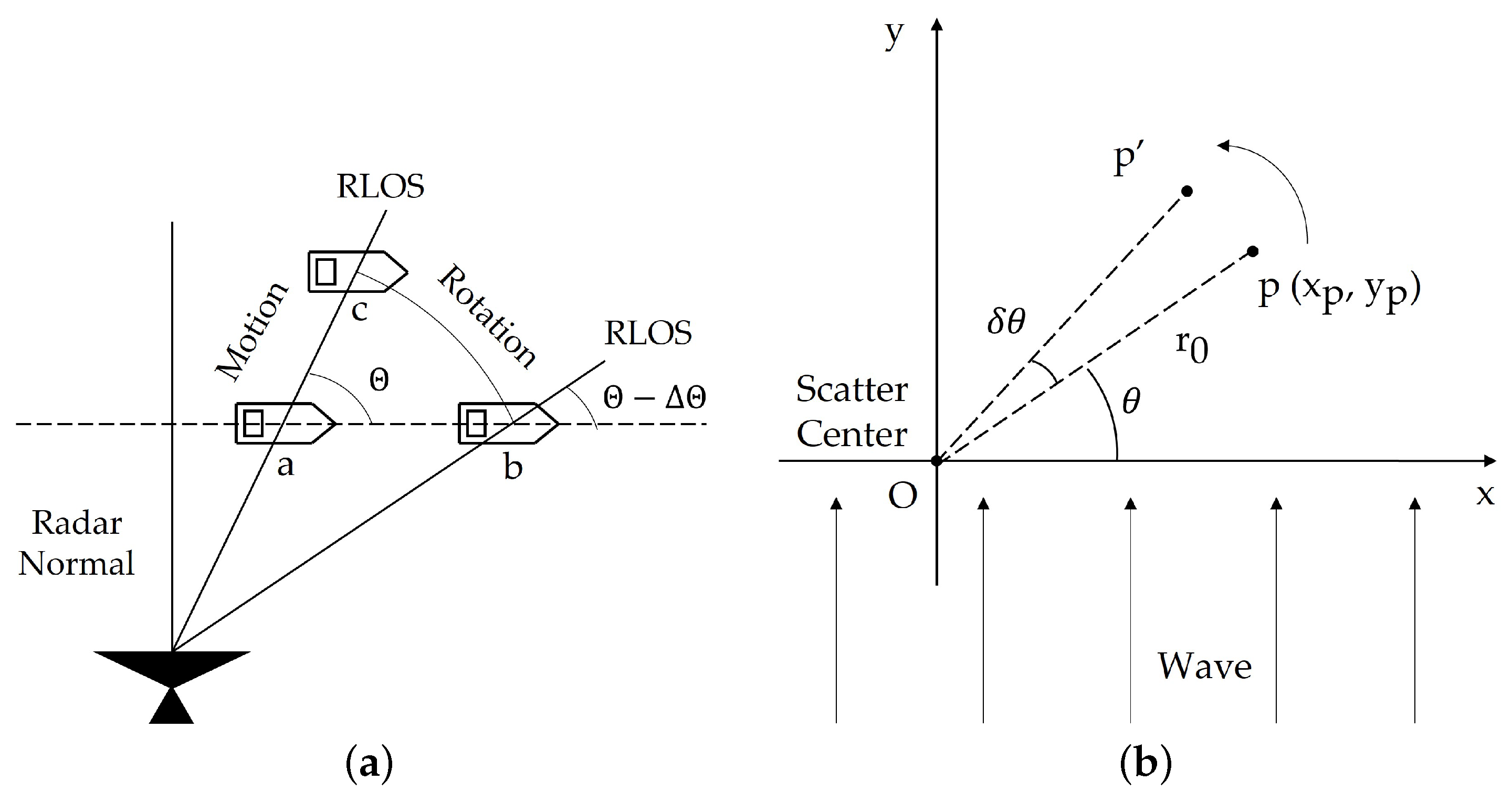
2.1. Characteristics of Extended Ship Target
2.2. Characteristics of ISAR Signal Model
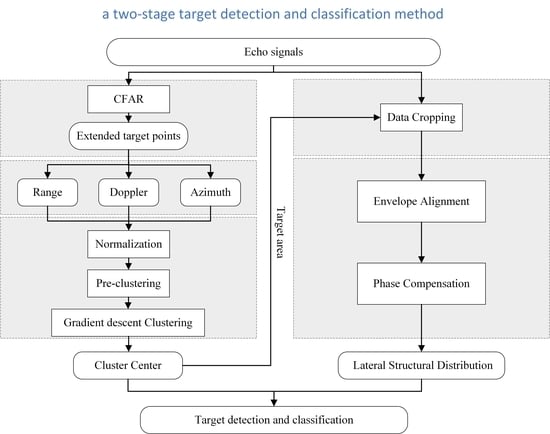
3. Proposed Methods
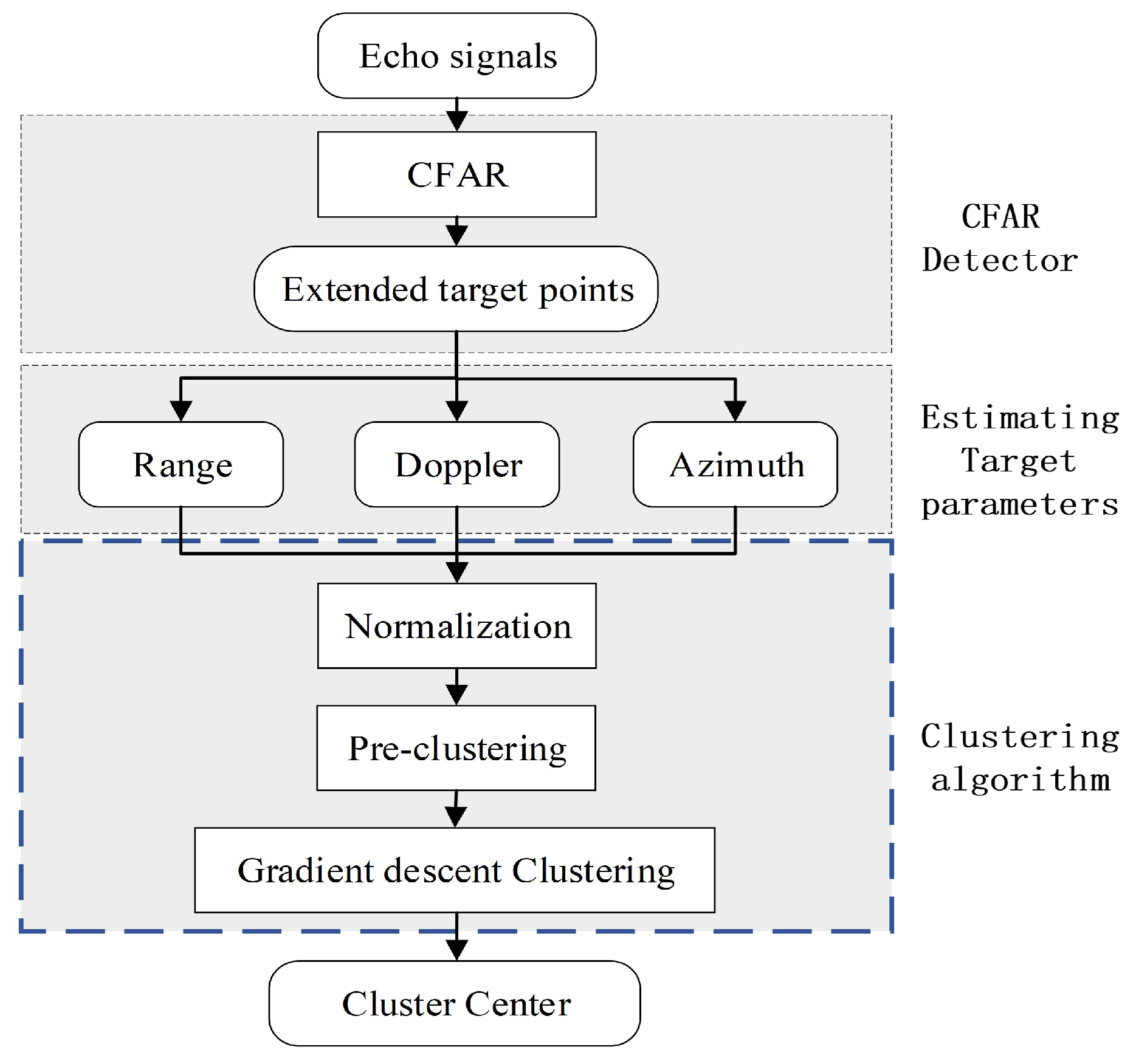
3.1. Clustering Algorithm
3.1.1. Normalization
3.1.2. Pre-Clustering
- Divide the grid into several big chunks. The chunk sizes here are chosen as 8 cells for range and Doppler and 20 cells for azimuth.
- Calculate the attribute parameters of each chunk, including the mean and variance of the range, Doppler, and azimuth.
- Remove discrete false points based on azimuth concentration and the number of points in each chunk. The extended target points are numerous, and their azimuth distribution is concentrated, while the false points perform the opposite characteristics. These properties can be used as a basis to eliminate false points. The associated chunks are then grouped into the same cluster.
3.1.3. Gradient Descent Clustering
| Algorithm 1: GBGD-Cluster |
 |
| Algorithm 2: Associate |
| Data: , , and are the thresholds for m, n, and in Equation (16), respectively. Set , , . C is an existing cluster created by GBGD-Clustering. Input: cell under processing b. the end cell of an existing cluster c 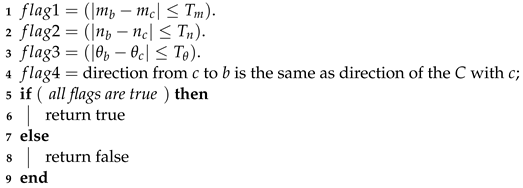 |
3.2. ISAR Imaging Method
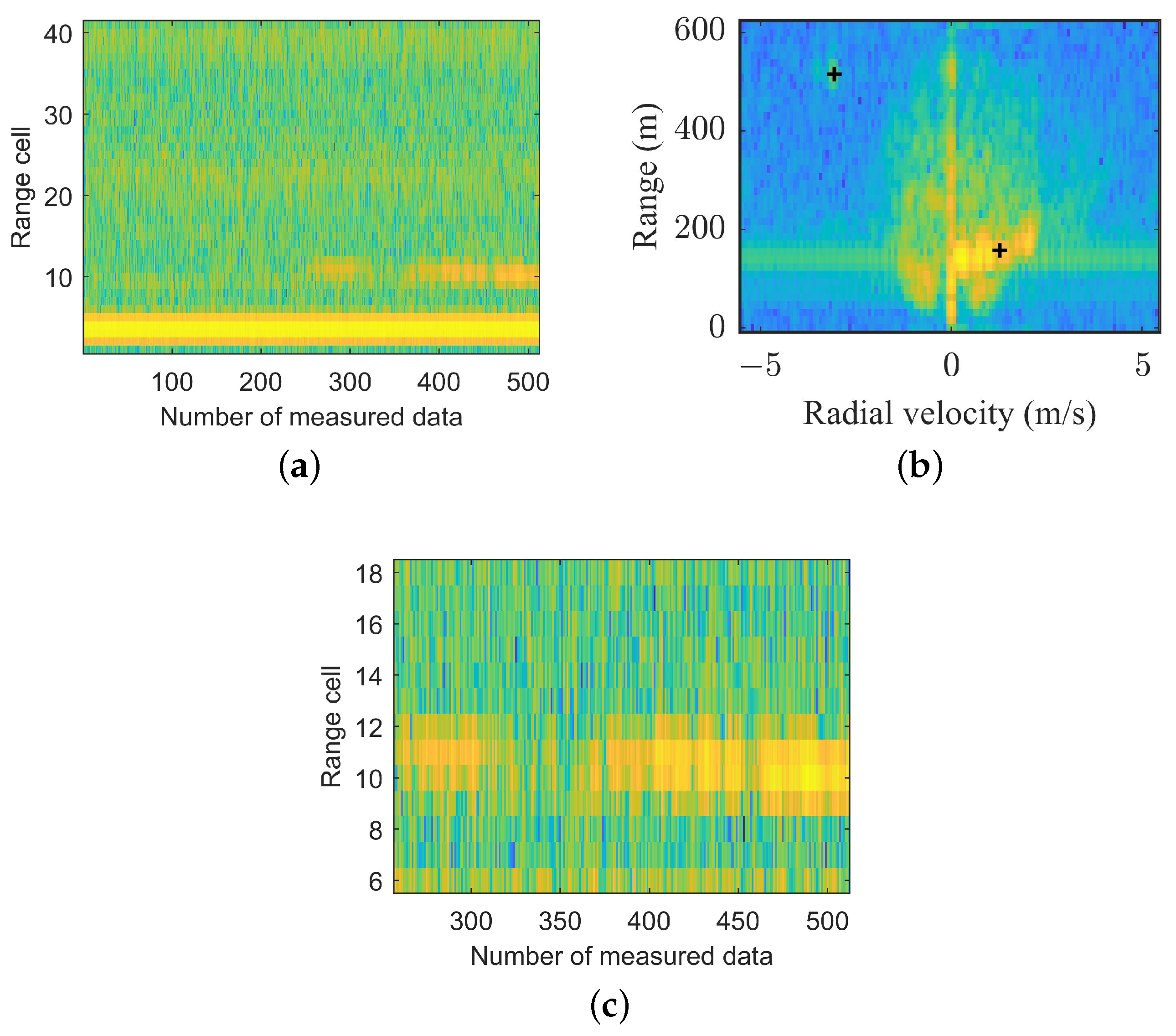
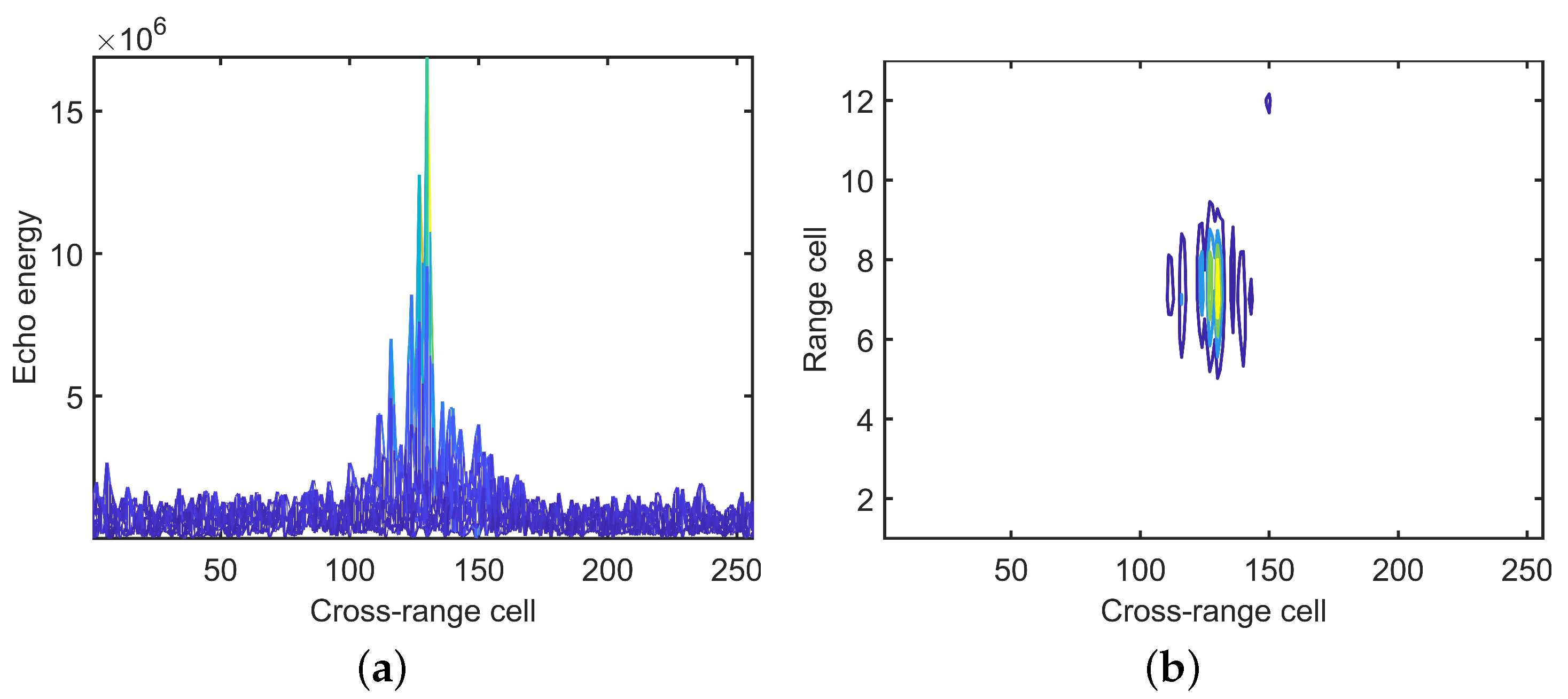
3.2.1. Envelope Alignment
3.2.2. Phase Compensation
4. Results
4.1. Simulation Results
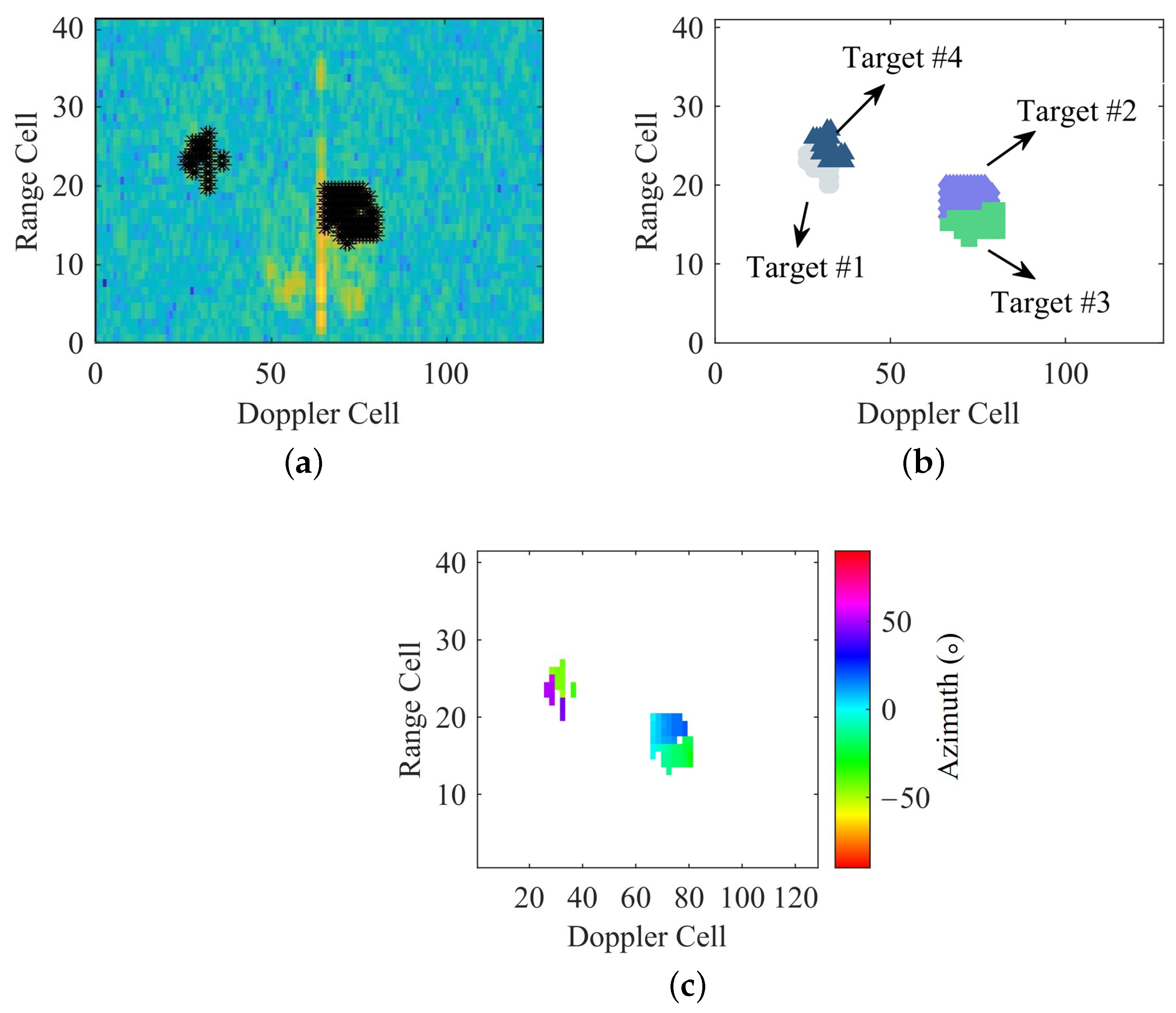
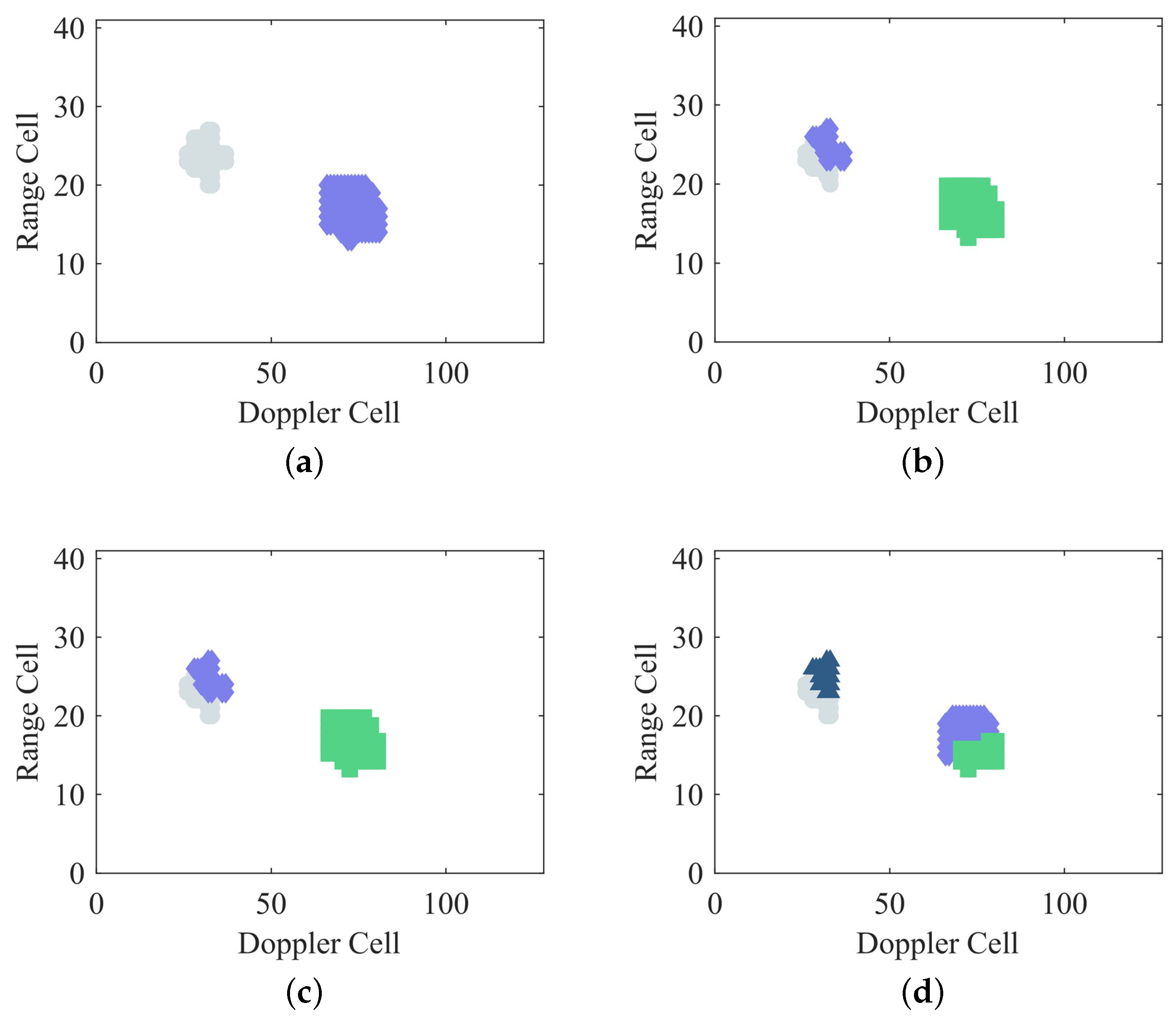
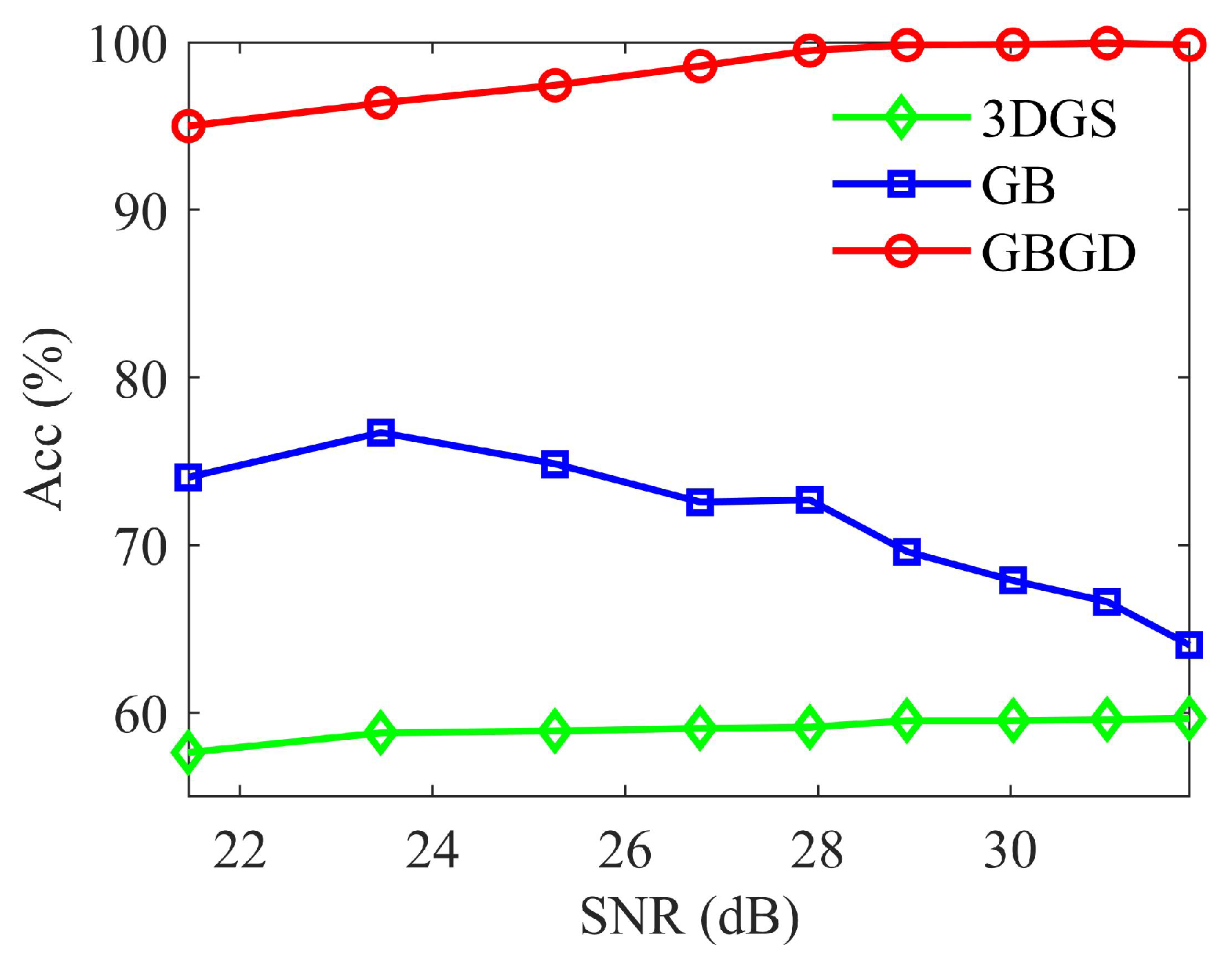
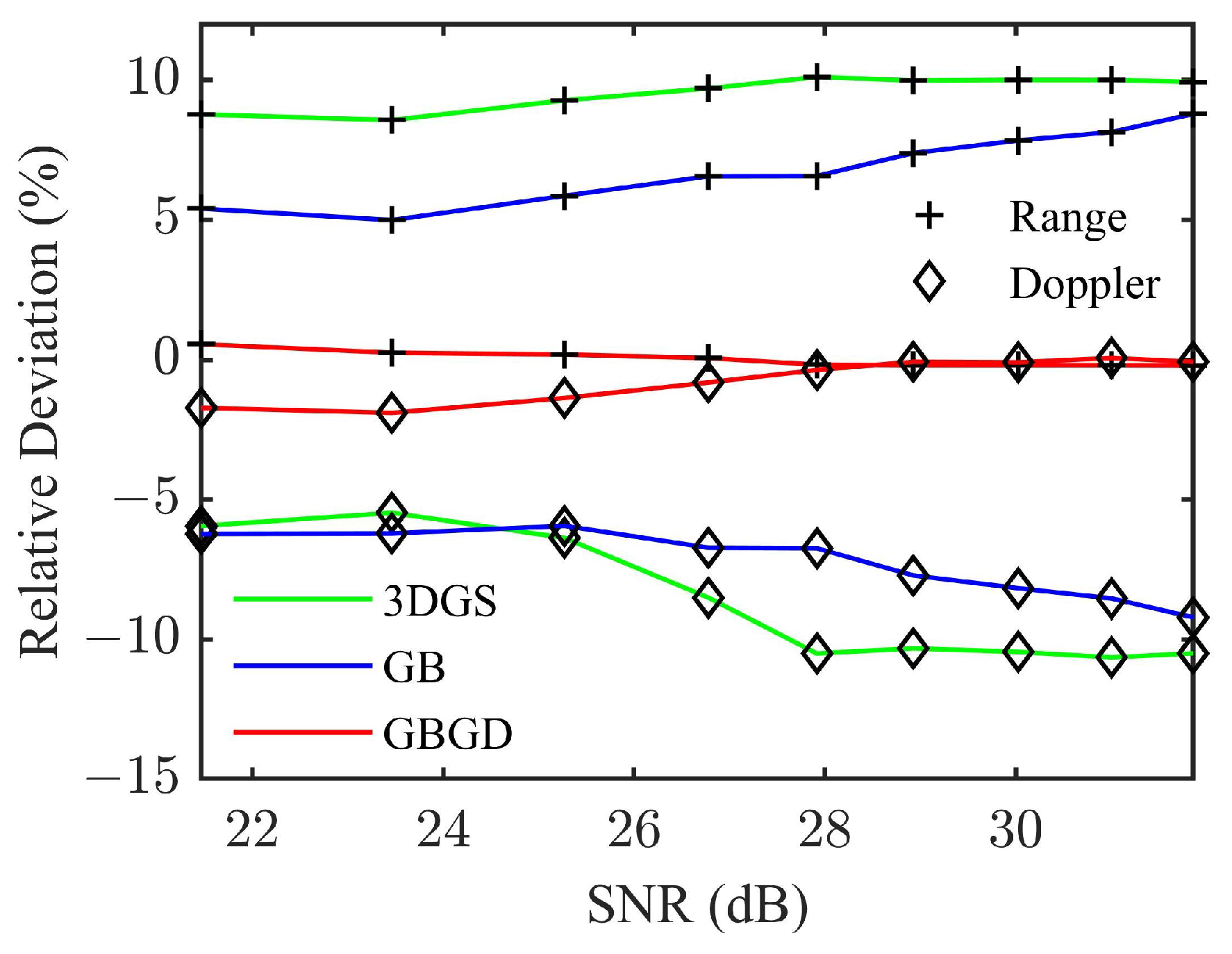
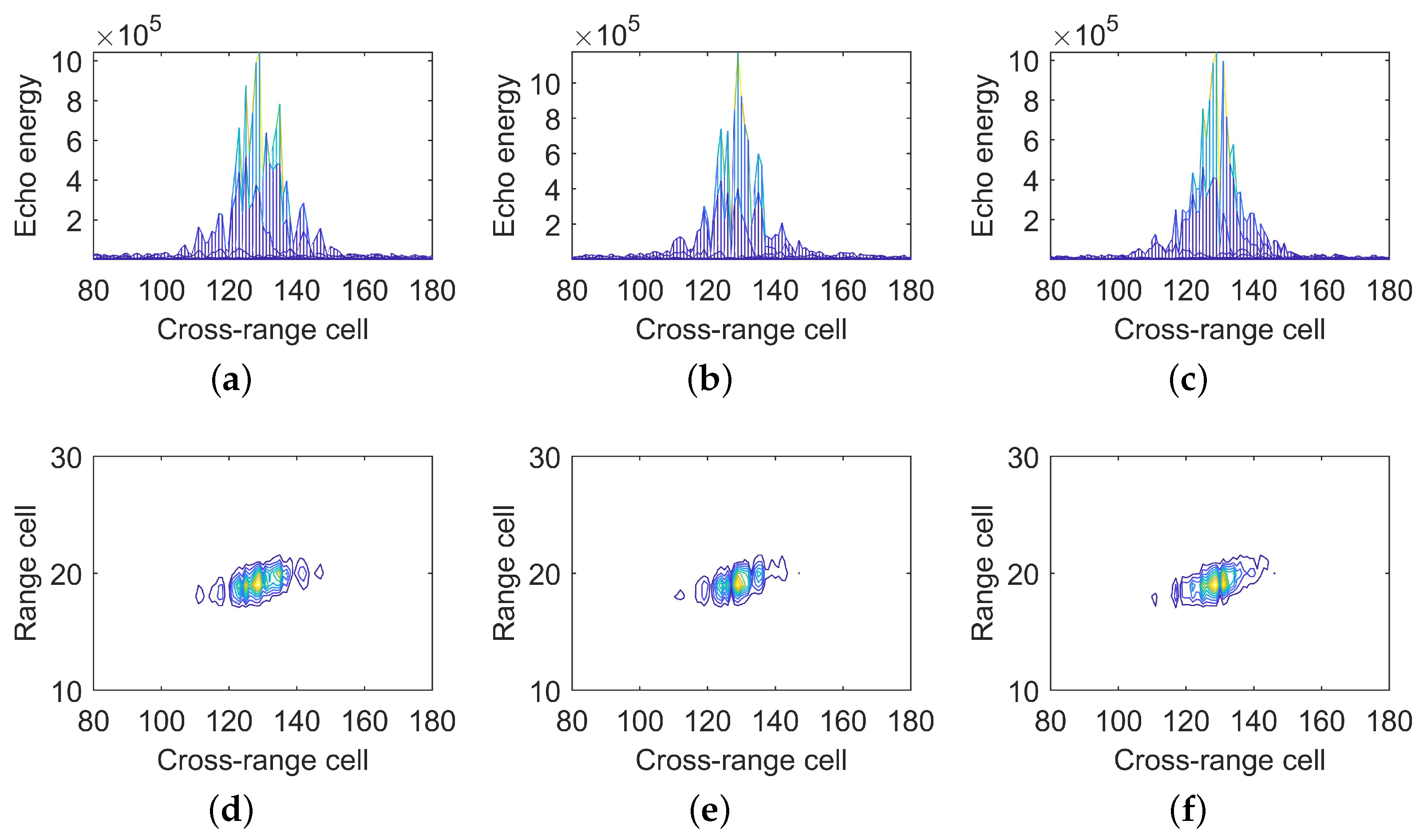
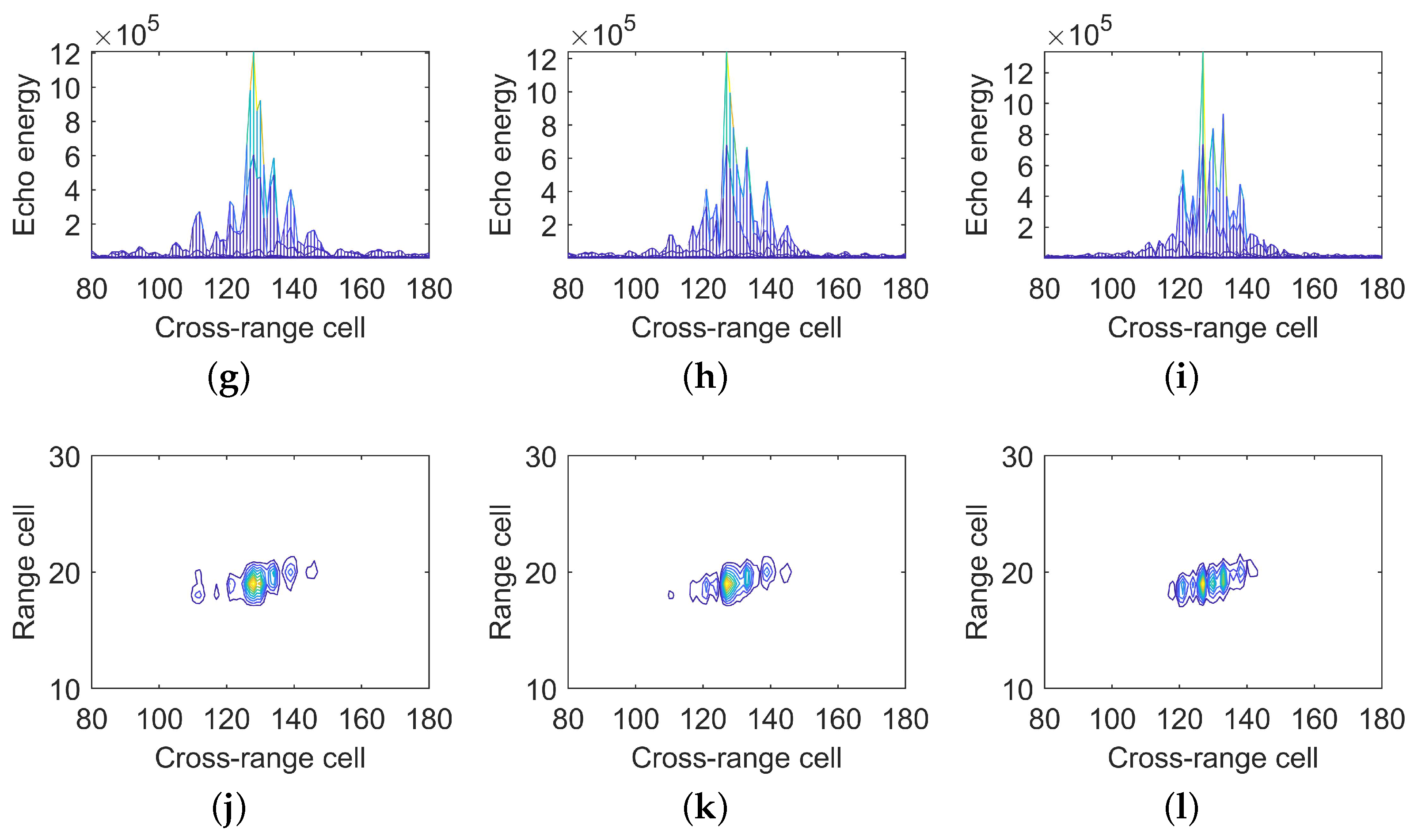
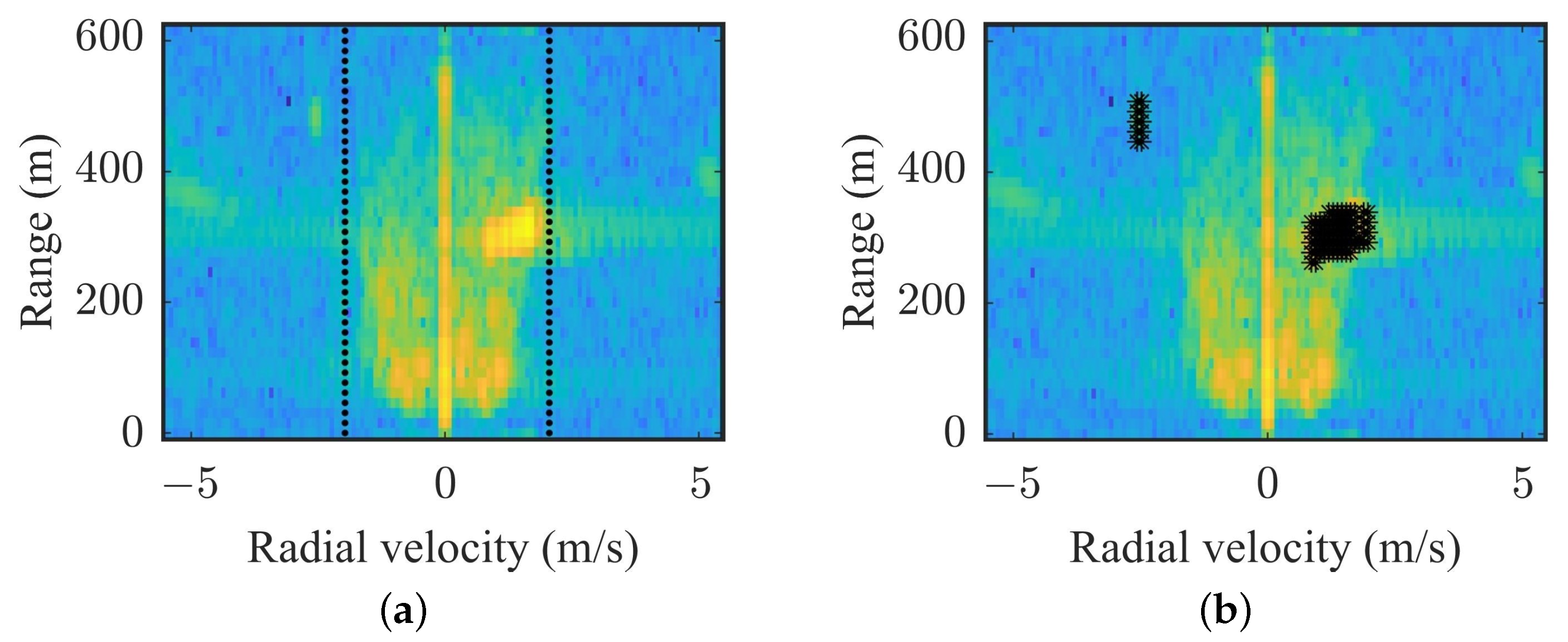
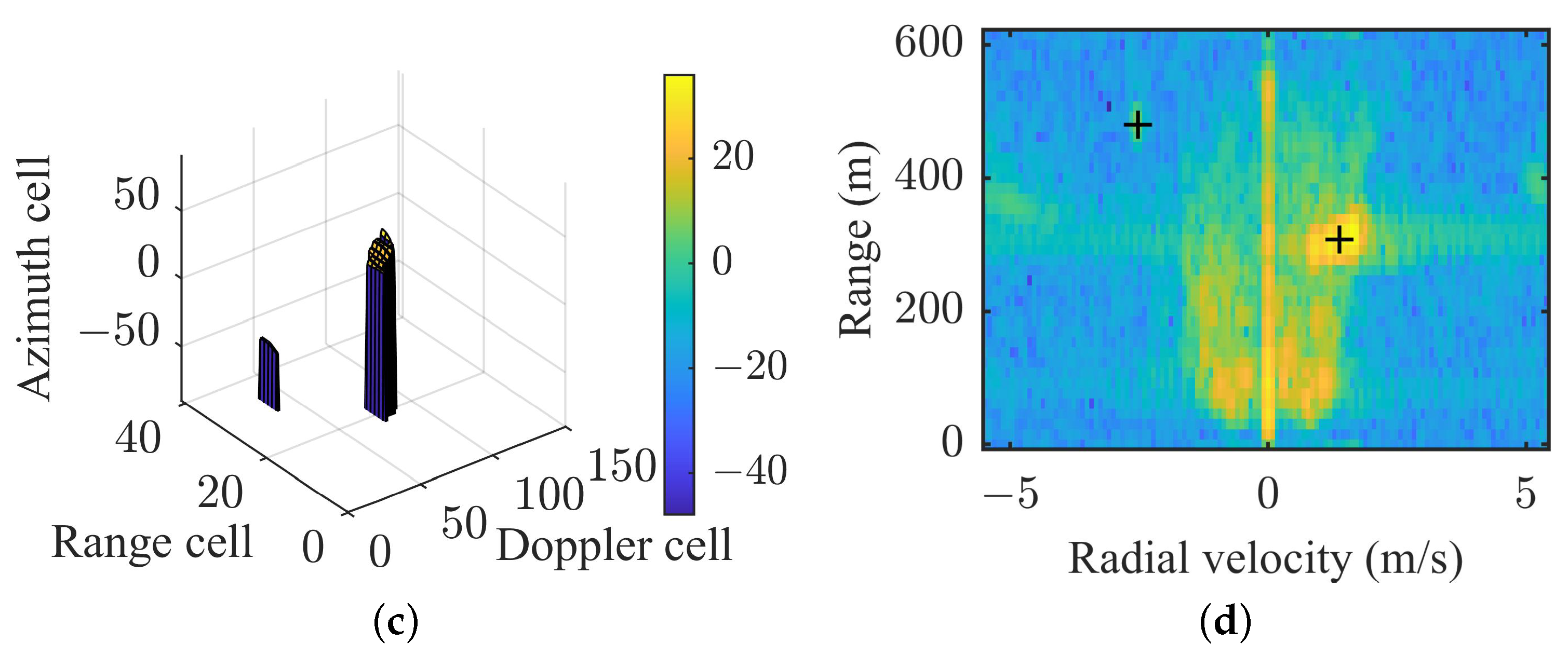
4.1.1. The GBGD-Clustering Algorithm
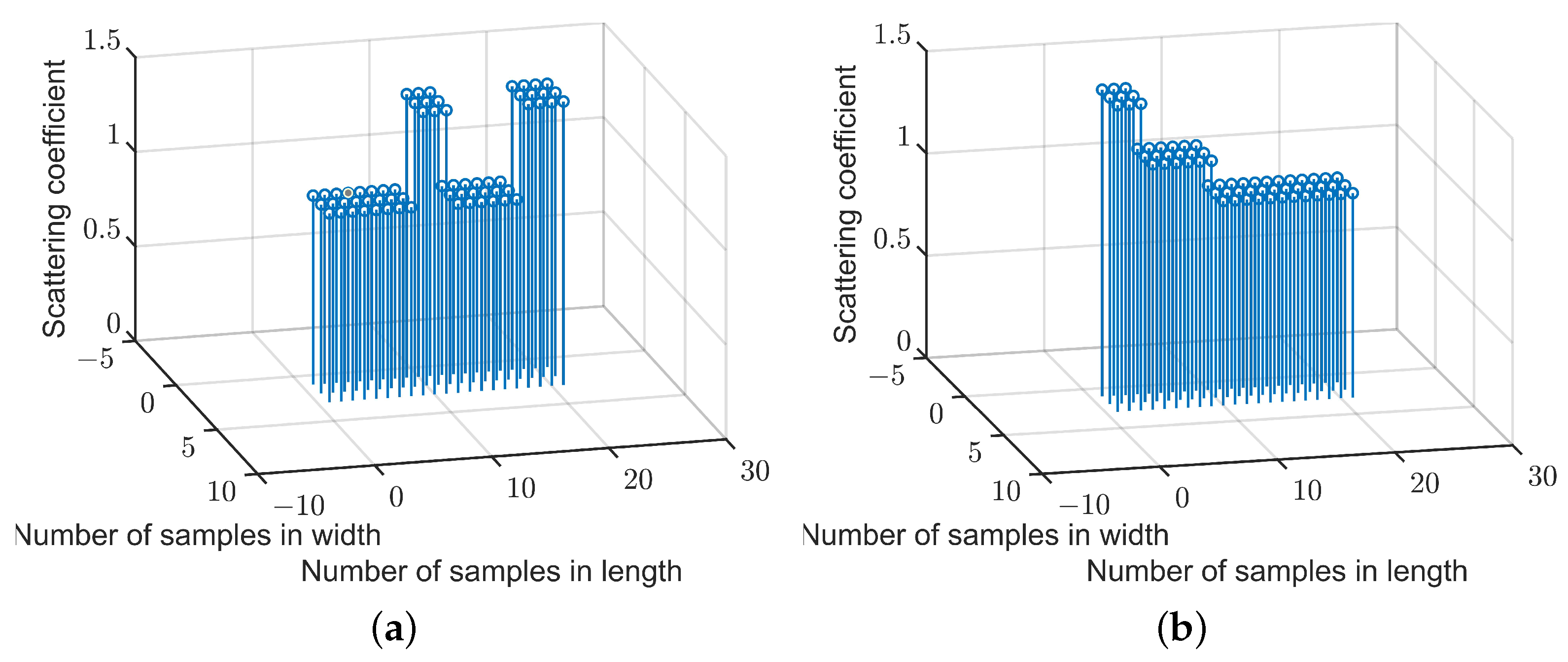
4.1.2. ISAR Imaging
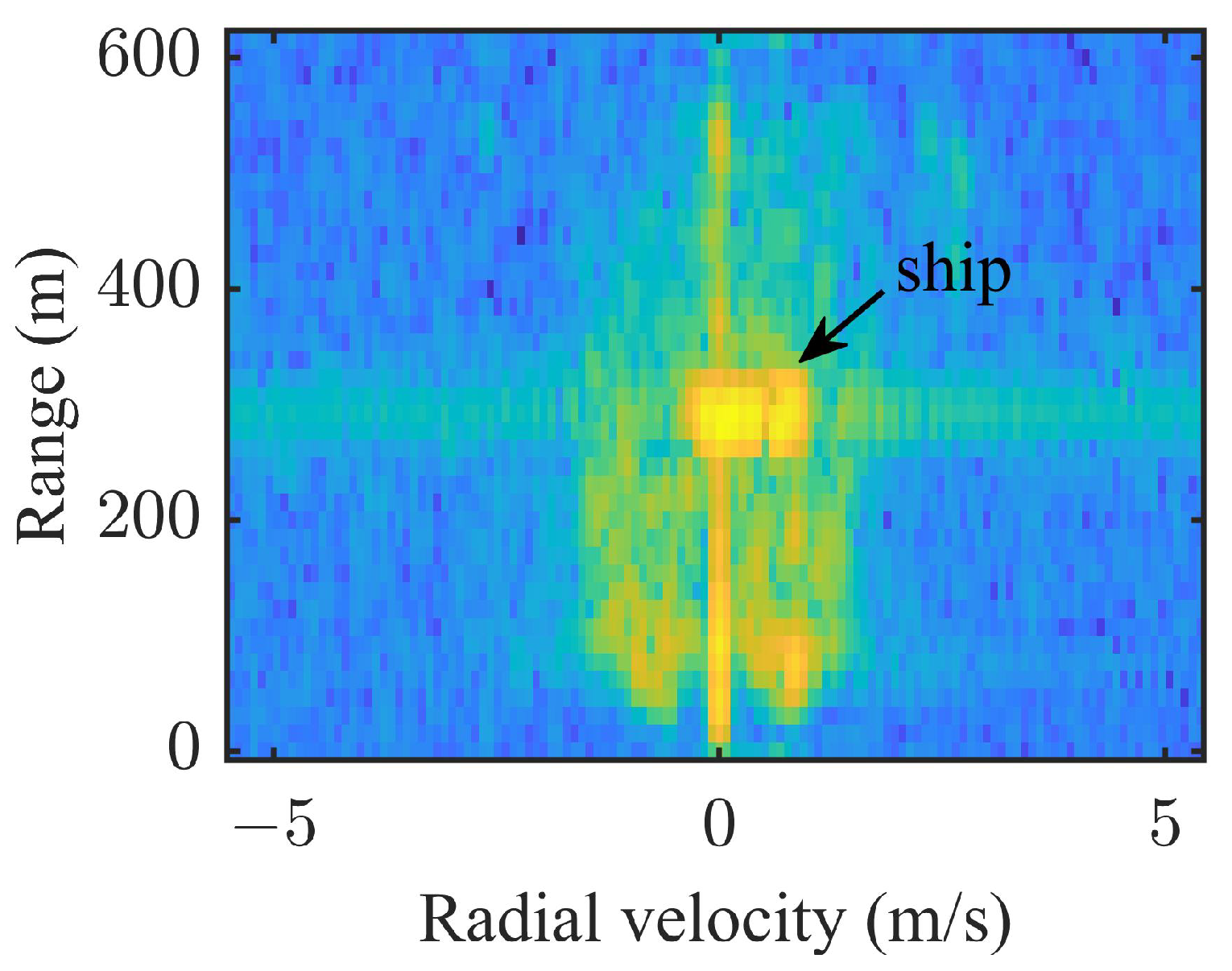
4.2. Real Data Results
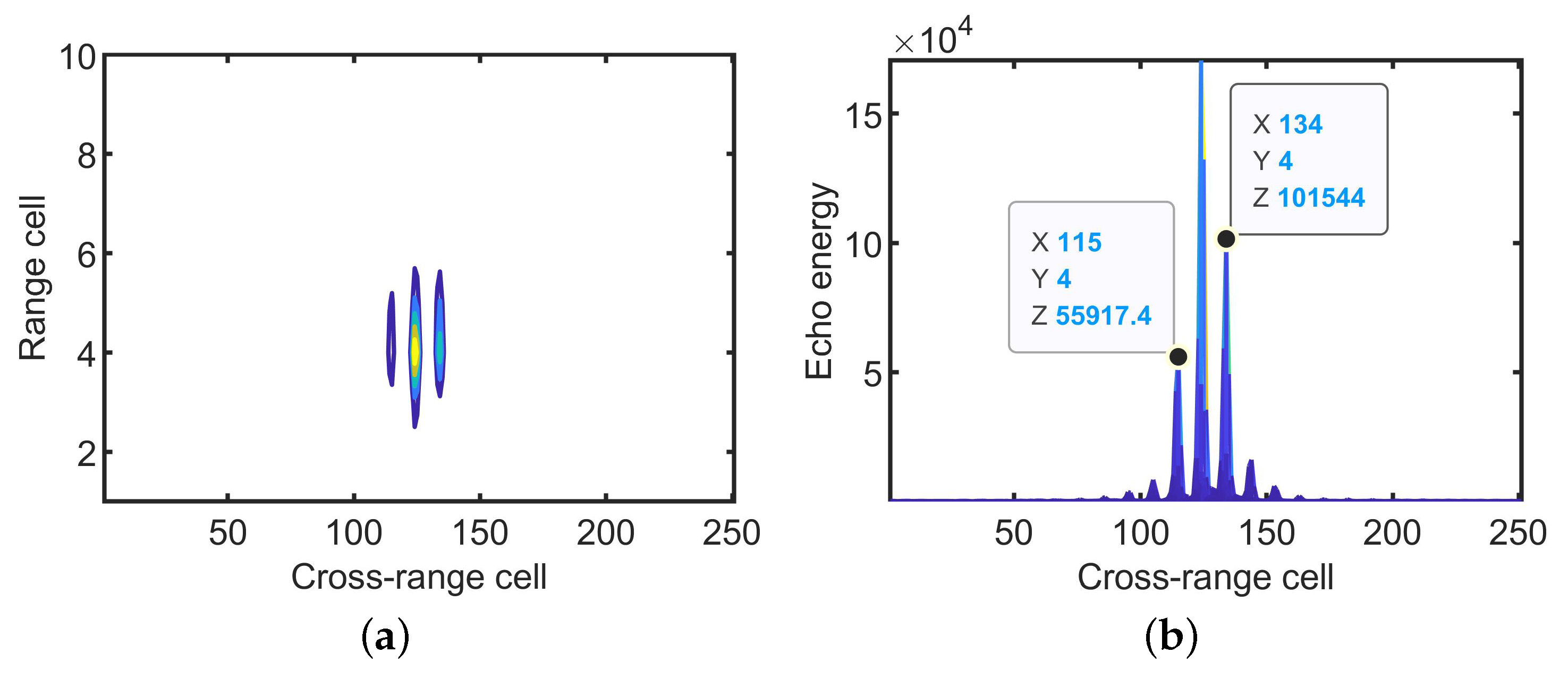
4.2.1. The Clustering Results
4.2.2. The ISAR Imaging Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Obad, D.; Bosnjak-Cihlar, Z. Benefits of automatic identification system within framework of river information services. In Elmar-2004, Proceedings of the 46th International Symposium on Electronics in Marine, Zadar, Croatia, 18 June 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 143–147. [Google Scholar]
- Jin, X.; Su, F.; Li, H.; Xu, Z.; Deng, J. Automatic ISAR Ship Detection Using Triangle-Points Affine Transform Reconstruction Algorithm. Remote Sens. 2023, 15, 2507. [Google Scholar] [CrossRef]
- Kuang, C.; Wang, C.; Wen, B.; Hou, Y.; Lai, Y. An improved CA-CFAR method for ship target detection in strong clutter using UHF radar. IEEE Signal Process. Lett. 2020, 27, 1445–1449. [Google Scholar] [CrossRef]
- Wang, C.; Tian, Y.; Yang, J.; Zhou, H.; Wen, B.; Hou, Y. A practical calibration method of linear UHF Yagi arrays for ship target detection application. IEEE Access 2020, 8, 46472–46479. [Google Scholar] [CrossRef]
- Yang, Y.; Wen, B.; Wang, C.; Hou, Y. Real-time and automatic river discharge measurement with UHF radar. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1851–1855. [Google Scholar] [CrossRef]
- El Mekkaoui, S.; Benabbou, L.; Berrado, A. Predicting ships estimated time of arrival based on AIS data. In Proceedings of the 13th International Conference on Intelligent Systems: Theories and Applications, Rabat, Morocco, 23–24 September 2020; pp. 1–6. [Google Scholar]
- Xiao, F.; Ligteringen, H.; Van Gulijk, C.; Ale, B. Comparison study on AIS data of ship traffic behavior. Ocean Eng. 2015, 95, 84–93. [Google Scholar] [CrossRef]
- Wawrzyniak, N.; Hyla, T.; Popik, A. Vessel detection and tracking method based on video surveillance. Sensors 2019, 19, 5230. [Google Scholar] [CrossRef]
- Shao, Z.; Wang, L.; Wang, Z.; Du, W.; Wu, W. Saliency-aware convolution neural network for ship detection in surveillance video. IEEE Trans. Circuits Syst. Video Technol. 2019, 30, 781–794. [Google Scholar] [CrossRef]
- Cao, X.; Gao, S.; Chen, L.; Wang, Y. Ship recognition method combined with image segmentation and deep learning feature extraction in video surveillance. Multimed. Tools Appl. 2020, 79, 9177–9192. [Google Scholar] [CrossRef]
- Arifin, A.S.; Firdaus, T.S. Ship location detection using wireless sensor networks with cooperative nodes. In Proceedings of the 2017 Ninth International Conference on Ubiquitous and Future Networks (ICUFN), Milan, Italy, 4–7 July 2017; pp. 433–437. [Google Scholar]
- Zhang, C.; Liu, P.; Wang, H.; Jin, Y. Saliency-Based Centernet for Ship Detection in SAR Images. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 1552–1555. [Google Scholar]
- Deng, Y.; Guan, D.; Chen, Y.; Yuan, W.; Ji, J.; Wei, M. Sar-Shipnet: Sar-Ship Detection Neural Network via Bidirectional Coordinate Attention and Multi-Resolution Feature Fusion. In Proceedings of the ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022; pp. 3973–3977. [Google Scholar]
- Kang, M.; Leng, X.; Lin, Z.; Ji, K. A modified faster R-CNN based on CFAR algorithm for SAR ship detection. In Proceedings of the 2017 International Workshop on Remote Sensing with Intelligent Processing (RSIP), Shanghai, China, 18–21 May 2017; pp. 1–4. [Google Scholar]
- Ma, Z.; Wen, B.; Zhou, H.; Wang, C.; Yan, W. UHF surface currents radar hardware system design. IEEE Microw. Wirel. Compon. Lett. 2005, 15, 904–906. [Google Scholar]
- Granstrom, K.; Baum, M.; Reuter, S. Extended object tracking: Introduction, overview and applications. arXiv 2016, arXiv:1604.00970. [Google Scholar]
- Li, M.D.; Cui, X.C.; Chen, S.W. Adaptive superpixel-level CFAR detector for SAR inshore dense ship detection. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Zhou, H.; Wen, B.; Wu, S.; Liu, X. Linear time-frequency MUSIC algorithm. In Proceedings of the IEEE 6th Circuits and Systems Symposium on Emerging Technologies: Frontiers of Mobile and Wireless Communication (IEEE Cat. No. 04EX710), Shanghai, China, 31 May–2 June 2004; Volume 2, pp. 689–692. [Google Scholar]
- Huang, B.; He, B.; Wu, L.; Lin, Y. A deep learning approach to detecting ships from high-resolution aerial remote sensing images. J. Coast. Res. 2020, 111, 16–20. [Google Scholar] [CrossRef]
- Sun, Z.; Meng, C.; Cheng, J.; Zhang, Z.; Chang, S. A multi-scale feature pyramid network for detection and instance segmentation of marine ships in SAR images. Remote Sens. 2022, 14, 6312. [Google Scholar] [CrossRef]
- Zhang, L.; You, W.; Wu, Q.J.; Qi, S.; Ji, Y. Deep learning-based automatic clutter/interference detection for HFSWR. Remote Sens. 2018, 10, 1517. [Google Scholar] [CrossRef]
- Chi, L.-j.; Feng, X.-x.; Miao, L. A new measurement partition for extended target tracking based on CFSFDP algorithm. In Proceedings of the 2017 3rd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 13–16 December 2017; pp. 1731–1735. [Google Scholar]
- Li, H.; Bu, F.; Li, L.; Zhou, J. Extended Target Measurement Set Partition Algorithm Based on KFCM Clustering. In Proceedings of the 2020 IEEE 5th International Conference on Signal and Image Processing (ICSIP), Nanjing, China, 23–25 October 2020; pp. 1065–1070. [Google Scholar]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; Volume 96, pp. 226–231. [Google Scholar]
- Kuang, C.; Wang, C.; Wen, B.; Huang, W. An applied method for clustering extended targets with UHF radar. IEEE Access 2020, 8, 98670–98678. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, H.; Yang, L.; Bai, Y. Estimating the Location of HFSWR Extended Targets Based on Clustering Algorithm. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021; pp. 7674–7679. [Google Scholar]
- Wagner, T.; Feger, R.; Stelzer, A. A fast grid-based clustering algorithm for range/Doppler/DoA measurements. In Proceedings of the 2016 European Radar Conference (EuRAD), London, UK, 5–7 October 2016; pp. 105–108. [Google Scholar]
- Huang, L.; Li, W.; Chen, C.; Zhang, F.; Lang, H. Multiple features learning for ship classification in optical imagery. Multimed. Tools Appl. 2018, 77, 13363–13389. [Google Scholar] [CrossRef]
- Ren, Y.; Yang, J.; Zhang, Q.; Guo, Z. Multi-feature fusion with convolutional neural network for ship classification in optical images. Appl. Sci. 2019, 9, 4209. [Google Scholar] [CrossRef]
- Du, X.; Wang, J.; Li, Y.; Tang, B. Marine Ship Identification Algorithm Based on Object Detection and Fine-Grained Recognition. In Advanced Intelligent Technologies for Industry, Proceedings of the 2nd International Conference on Advanced Intelligent Technologies (ICAIT 2021), Xi’an, China, 19 May 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 207–215. [Google Scholar]
- Karine, A.; Toumi, A.; Khenchaf, A.; El Hassouni, M. Radar target recognition using salient keypoint descriptors and multitask sparse representation. Remote Sens. 2018, 10, 843. [Google Scholar] [CrossRef]
- Ni, P.; Liu, Y.; Pei, H.; Du, H.; Li, H.; Xu, G. CLISAR-Net: A Deformation-Robust ISAR Image Classification Network Using Contrastive Learning. Remote Sens. 2022, 15, 33. [Google Scholar] [CrossRef]
- Musman, S.; Kerr, D.; Bachmann, C. Automatic recognition of ISAR ship images. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1392–1404. [Google Scholar] [CrossRef]
- Wang, J.; Kasilingam, D. Global range alignment for ISAR. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 351–357. [Google Scholar] [CrossRef]
- Ye, W.; Yeo, T.S.; Bao, Z. Weighted least-squares estimation of phase errors for SAR/ISAR autofocus. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2487–2494. [Google Scholar] [CrossRef]
- Chen, C.C.; Andrews, H.C. Target-motion-induced radar imaging. IEEE Trans. Aerosp. Electron. Syst. 1980, AES-16, 2–14. [Google Scholar] [CrossRef]

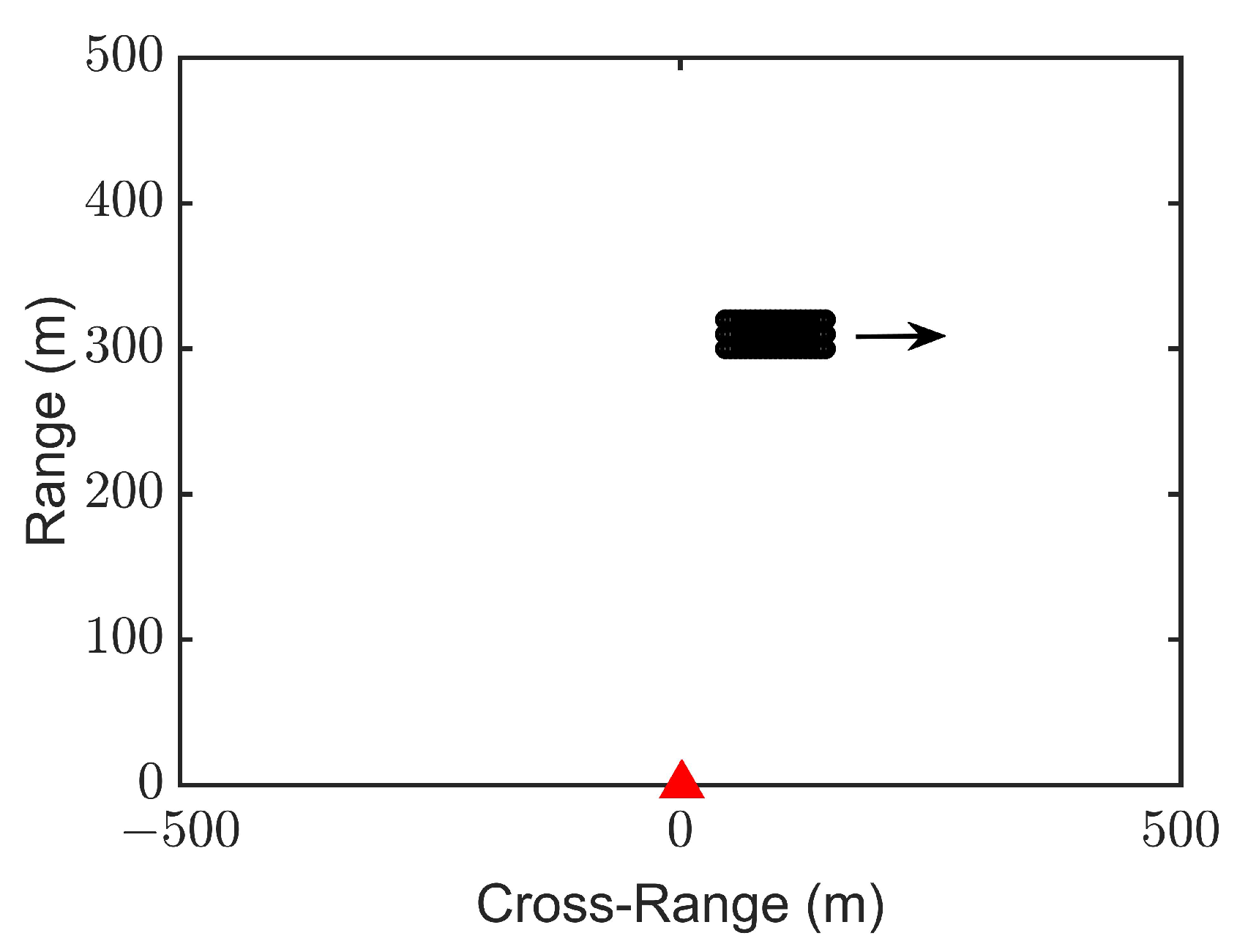
| Parameters | Value |
|---|---|
| Frequency, | 340 MHz |
| Pulse width, | 0.04 s |
| Bandwidth, B | 10 MHz |
| Pulse repetition time, | 0.041 s |
| Number of integrated pulses, M | 128 |
| Target | Value | Target #1 | Target #2 | Target #3 | Target #4 |
|---|---|---|---|---|---|
| Target parameters | 323.1221 | 272.5765 | 223.3154 | 378.2689 | |
| −2.346 | 0.5372 | 0.672 | −1.599 | ||
| 48.9818 | 12.5918 | −15.3926 | −43.0374 |
| Clustering Algorithm | 3DGS | GB | GBGD | |
|---|---|---|---|---|
| Target | Acc | 0.5965 | 0.6727 | 0.9979 |
| Target | (m) | −0.9924 | 0.2769 | 0.2769 |
| (m/s) | 0.0006 | −0.0012 | −0.0012 | |
| −0.0971 | 0.0445 | 0.0445 | ||
| Target | (m) | 26.8438 | 20.8284 | −0.6354 |
| (m/s) | −0.1096 | −0.0845 | −0.0044 | |
| 12.2482 | 11.1209 | −0.1292 | ||
| Target | (m) | −25.0277 | −19.9638 | −0.1863 |
| (m/s) | 0.0916 | 0.0789 | 0.0042 | |
| −13.4646 | −10.695 | −0.112 | ||
| Target | (m) | −0.0166 | −0.0166 | −0.0166 |
| (m/s) | 0.0012 | 0.0012 | 0.0012 | |
| 0.0156 | 0.0156 | 0.0156 |
| Point No. | Cross-Range (m) | Range (m) | Scattering Coefficient |
|---|---|---|---|
| 1 | 0 | 350 | 2 |
| 2 | 50 | 350 | 1.5 |
| 3 | −50 | 350 | 1 |
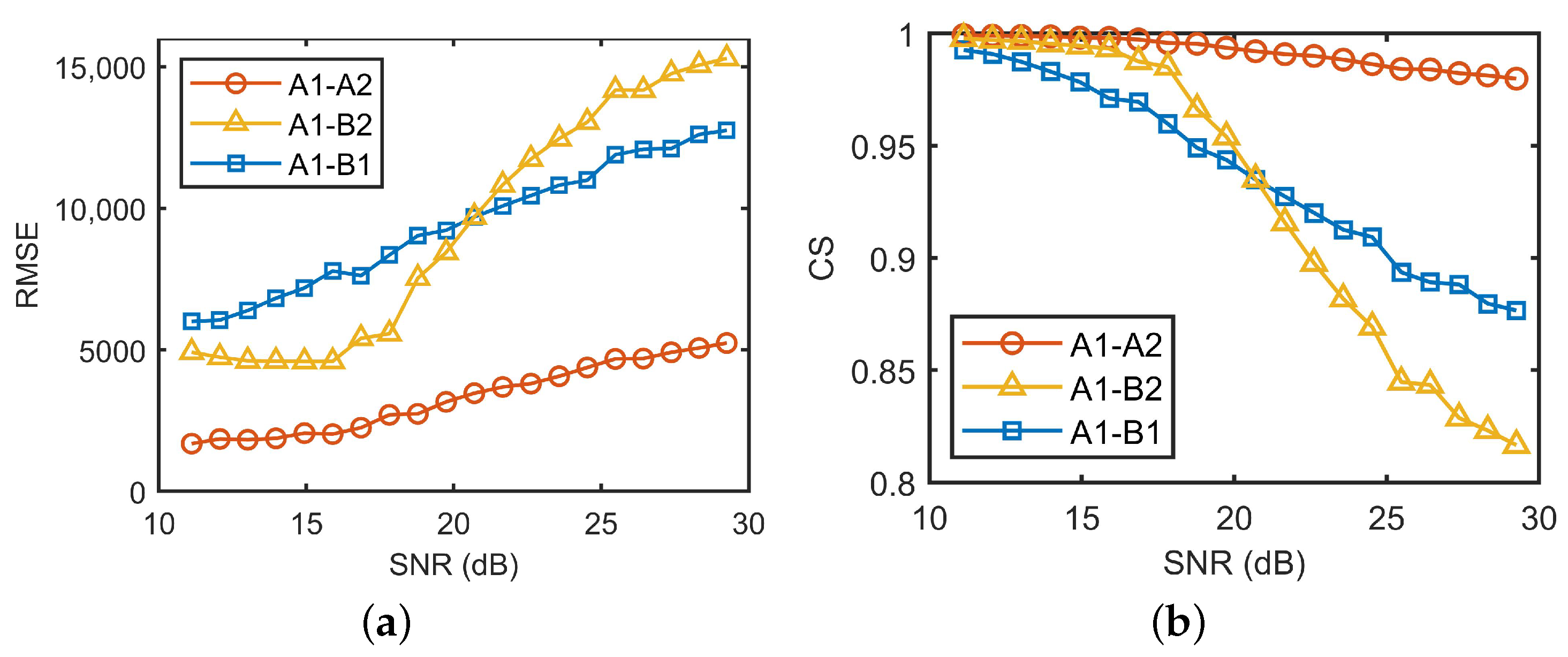
| Target Type | A-A | B-B | A-B | |||
|---|---|---|---|---|---|---|
| RMSE | CS | RMSE | CS | RMSE | CS | |
| 1-2 | 7524.6 | 0.9613 | 9477.0 | 0.9299 | 19,883 | 0.7107 |
| 2-3 | 9321.6 | 0.9394 | 8781.6 | 0.9402 | 13,239 | 0.8700 |
| 1-1 | 0 | 1 | 0 | 1 | 17,443 | 0.7835 |
| 2-2 | 0 | 1 | 0 | 1 | 16,813 | 0.7908 |
| 3-3 | 0 | 1 | 0 | 1 | 13,771 | 0.8623 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Zhou, H.; Bai, L.; Tian, Y. A Grid-Based Gradient Descent Extended Target Clustering Method and Ship Target Inverse Synthetic Aperture Radar Imaging for UHF Radar. Remote Sens. 2023, 15, 5466. https://doi.org/10.3390/rs15235466
Zhang L, Zhou H, Bai L, Tian Y. A Grid-Based Gradient Descent Extended Target Clustering Method and Ship Target Inverse Synthetic Aperture Radar Imaging for UHF Radar. Remote Sensing. 2023; 15(23):5466. https://doi.org/10.3390/rs15235466
Chicago/Turabian StyleZhang, Lizun, Hao Zhou, Liyun Bai, and Yingwei Tian. 2023. "A Grid-Based Gradient Descent Extended Target Clustering Method and Ship Target Inverse Synthetic Aperture Radar Imaging for UHF Radar" Remote Sensing 15, no. 23: 5466. https://doi.org/10.3390/rs15235466
APA StyleZhang, L., Zhou, H., Bai, L., & Tian, Y. (2023). A Grid-Based Gradient Descent Extended Target Clustering Method and Ship Target Inverse Synthetic Aperture Radar Imaging for UHF Radar. Remote Sensing, 15(23), 5466. https://doi.org/10.3390/rs15235466