Optimizing the Retrieval of Wheat Crop Traits from UAV-Borne Hyperspectral Image with Radiative Transfer Modelling Using Gaussian Process Regression
Abstract
:1. Introduction
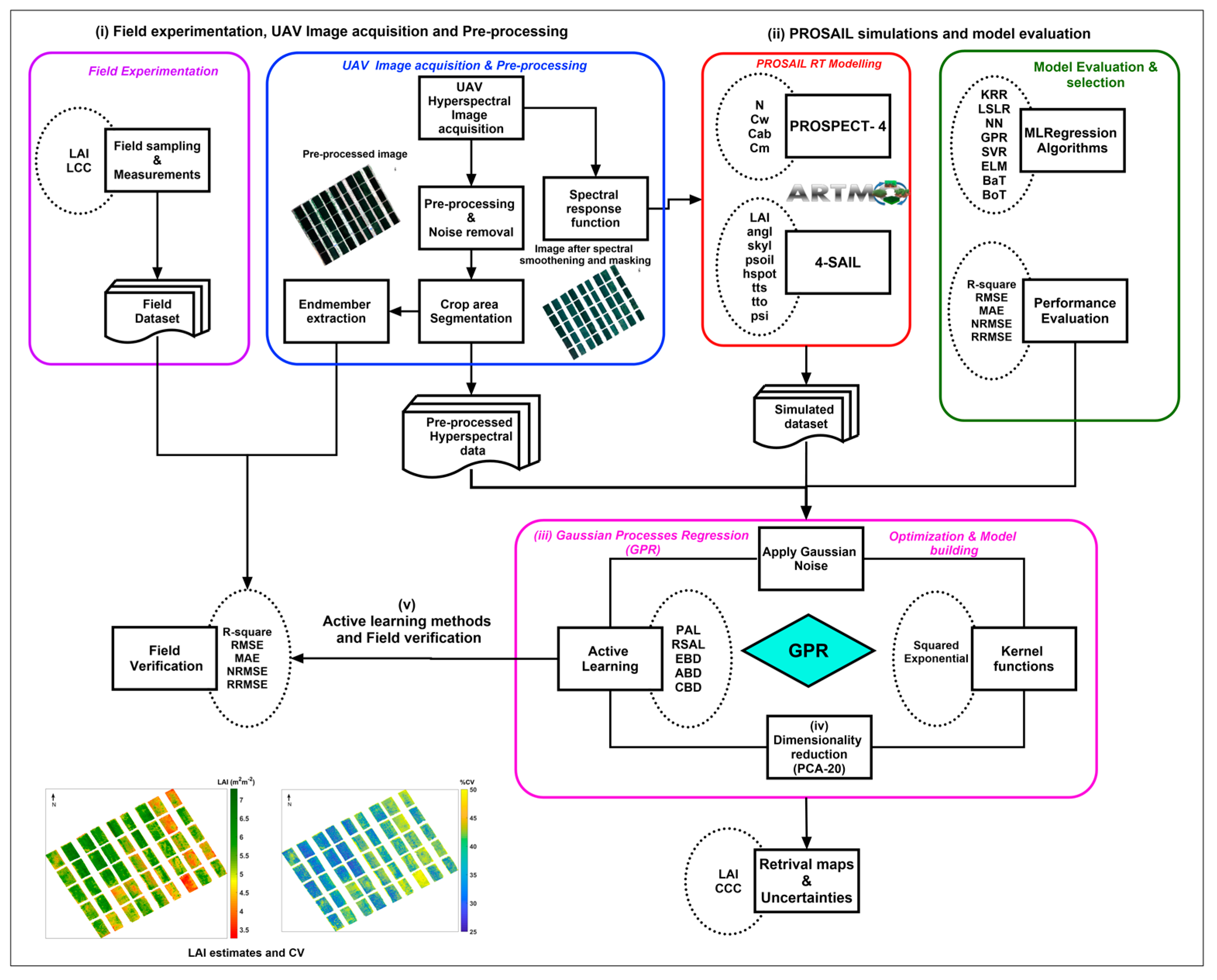
2. Materials and Methods
2.1. Field Experimentation and UAV Image Acquisition
2.2. PROSAIL Simulations and Model Evaluation
2.3. Gaussian Process Regression (GPR)
2.4. Dimensionality Reduction Using Principal Component Analysis (PCA)
2.5. Active Learning Methods and Field Verification
3. Results
3.1. Model Evaluation and Selection of GPR
3.2. Performance of AL Techniques
3.3. Validation of Crop-Trait Models
3.4. Retrieval of LAI and CCC
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Weiss, M.; Jacob, F.; Duveiller, G. Remote Sensing for Agricultural Applications: A Meta-Review. Remote Sens. Environ. 2020, 236, 111402. [Google Scholar] [CrossRef]
- Gonsamo, A.; Pellikka, P. Methodology Comparison for Slope Correction in Canopy Leaf Area Index Estimation Using Hemispherical Photography. For. Ecol. Manage. 2008, 256, 749–759. [Google Scholar] [CrossRef]
- Gower, S.T.; Kucharik, C.J.; Norman, J.M. Direct and Indirect Estimation of Leaf Area Index, FAPAR, and Net Primary Production of Terrestrial Ecosystems. Remote Sens. Environ. 1999, 70, 29–51. [Google Scholar] [CrossRef]
- Liang, L.; Geng, D.; Yan, J.; Qiu, S.; Di, L.; Wang, S.; Xu, L.; Wang, L.; Kang, J.; Li, L. Estimating Crop Lai Using Spectral Feature Extraction and the Hybrid Inversion Method. Remote Sens. 2020, 12, 3534. [Google Scholar] [CrossRef]
- Yan, G.; Hu, R.; Luo, J.; Weiss, M.; Jiang, H.; Mu, X.; Xie, D.; Zhang, W. Review of Indirect Optical Measurements of Leaf Area Index: Recent Advances, Challenges, and Perspectives. Agric. For. Meteorol. 2019, 265, 390–411. [Google Scholar] [CrossRef]
- Behera, S.K.; Srivastava, P.; Pathre, U.V.; Tuli, R. An indirect method of estimating leaf area index in Jatropha curcas L. using LAI-2000 Plant Canopy Analyzer. Agric. For. Meteorol. 2010, 150, 307–311. [Google Scholar] [CrossRef]
- Orlando, F.; Movedi, E.; Paleari, L.; Gilardelli, C.; Foi, M.; Dell’Oro, M.; Confalonieri, R. Estimating Leaf Area Index in Tree Species Using the Pocket LAI Smart App. Appl. Veg. Sci. 2015, 18, 716–723. [Google Scholar] [CrossRef]
- Francone, C.; Pagani, V.; Foi, M.; Cappelli, G.; Confalonieri, R. Comparison of Leaf Area Index Estimates by Ceptometer and PocketLAI Smart App in Canopies with Different Structures. Field Crops Res. 2014, 155, 38–41. [Google Scholar] [CrossRef]
- Zhu, X.; Yang, Q.; Chen, X.; Ding, Z. An Approach for Joint Estimation of Grassland Leaf Area Index and Leaf Chlorophyll Content from UAV Hyperspectral Data. Remote Sens. 2023, 15, 2525. [Google Scholar] [CrossRef]
- Nie, C.; Shi, L.; Li, Z.; Xu, X.; Yin, D.; Li, S.; Jin, X. A Comparison of Methods to Estimate Leaf Area Index Using Either Crop-Specific or Generic Proximal Hyperspectral Datasets. Eur. J. Agron. 2023, 142, 126664. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Gitelson, A.; Delegido, J.; Moreno, J.; Camps-Valls, G. Spectral Band Selection for Vegetation Properties Retrieval Using Gaussian Processes Regression. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 554–567. [Google Scholar] [CrossRef]
- Tripathi, R.; Sahoo, R.N.; Gupta, V.K.; Sehgal, V.K.; Sahoo, P.M. Retrieval of Leaf Area Index Using IRS-P6, LISS-III Data and Validation of MODIS LAI Product (MOD15 V5) over Trans Gangetic Plains of India. Indian J. Agric. Sci. 2013, 83, 380–385. [Google Scholar]
- Tripathi, R.; Sahoo, R.N.; Gupta, V.K.; Sehgal, V.K.; Sahoo, P.M. Developing Vegetation Health Index from Biophysical Variables Derived Using MODIS Satellite Data in the Trans-Gangetic Plains of India. Emirates J. Food Agric. 2013, 25, 376–384. [Google Scholar] [CrossRef]
- Thomas, H.; Howarth, C.J. Five Ways to Stay Green. J. Exp. Bot. 2000, 51, 329–337. [Google Scholar] [CrossRef]
- Hotta, Y.; Tanaka, T.; Takaoka, H.; Takeuchi, Y.; Konnai, M. New Physiological Effects of 5-Aminolevulinic Acid in Plants: The Increase of Photosynthesis, Chlorophyll Content, and Plant Growth. Biosci. Biotechnol. Biochem. 1997, 61, 2025–2028. [Google Scholar] [CrossRef] [PubMed]
- Shibghatallah, M.A.H.; Khotimah, S.N.; Suhandono, S.; Viridi, S.; Kesuma, T. Measuring Leaf Chlorophyll Concentration from Its Color: A Way in Monitoring Environment Change to Plantations. In Proceedings of the AIP Conference, Kabupaten Sumedang, Indonesia, 7–9 May 2013; Volume 1554. [Google Scholar]
- Daughtry, C.S.T.; Walthall, C.L.; Kim, M.S.; De Colstoun, E.B.; McMurtrey, J.E. Estimating Corn Leaf Chlorophyll Concentration from Leaf and Canopy Reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Parry, C.; Blonquist, J.M.; Bugbee, B. In Situ Measurement of Leaf Chlorophyll Concentration: Analysis of the Optical/Absolute Relationship. Plant Cell Environ. 2014, 37, 2508–2520. [Google Scholar] [CrossRef] [PubMed]
- Patane, P.; Vibhute, A. Chlorophyll and Nitrogen Estimation Techniques: A Review. Int. J. Eng. Res. Rev. 2014, 2, 33–41. [Google Scholar]
- Simic, A.; Chen, J.M.; Noland, T.L. Retrieval of Forest Chlorophyll Content Using Canopy Structure Parameters Derived from Multi-Angle Data: The Measurement Concept of Combining Nadir Hyperspectral and off-Nadir Multispectral Data. Int. J. Remote Sens. 2011, 32, 5621–5644. [Google Scholar] [CrossRef]
- Zhang, X.; He, Y.; Wang, C.; Xu, F.; Li, X.; Tan, C.; Chen, D.; Wang, G.; Shi, L. Estimation of Corn Canopy Chlorophyll Content Using Derivative Spectra in the O2–A Absorption Band. Front. Plant Sci. 2019, 10, 1047. [Google Scholar] [CrossRef]
- Haboudane, D.; Tremblay, N.; Miller, J.R.; Vigneault, P. Remote Estimation of Crop Chlorophyll Content Using Spectral Indices Derived from Hyperspectral Data. In IEEE Transactions on Geoscience and Remote Sensing; IEEE: Piscateville, NJ, USA, 2008; Volume 46. [Google Scholar]
- Fitzgerald, G.; Rodriguez, D.; O’Leary, G. Measuring and Predicting Canopy Nitrogen Nutrition in Wheat Using a Spectral Index-The Canopy Chlorophyll Content Index (CCCI). Field Crops Res. 2010, 116, 318–324. [Google Scholar] [CrossRef]
- Hunt, E.R.; Doraiswamy, P.C.; McMurtrey, J.E.; Daughtry, C.S.T.; Perry, E.M.; Akhmedov, B. A Visible Band Index for Remote Sensing Leaf Chlorophyll Content at the Canopy Scale. Int. J. Appl. Earth Obs. Geoinf. 2012, 21, 103–112. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Miller, J.R.; Morales, A.; Berjón, A.; Agüera, J. Hyperspectral Indices and Model Simulation for Chlorophyll Estimation in Open-Canopy Tree Crops. Remote Sens. Environ. 2004, 90, 463–476. [Google Scholar] [CrossRef]
- Verrelst, J.; Malenovský, Z.; Van der Tol, C.; Camps-Valls, G.; Gastellu-Etchegorry, J.P.; Lewis, P.; North, P.; Moreno, J. Quantifying Vegetation Biophysical Variables from Imaging Spectroscopy Data: A Review on Retrieval Methods. Surv. Geophys. 2019, 40, 589–629. [Google Scholar] [CrossRef] [PubMed]
- Grahn, H.F.; Geladi, P. Techniques and Applications of Hyperspectral Image Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Ravikanth, L.; Jayas, D.S.; White, N.D.G.; Fields, P.G.; Sun, D.W. Extraction of Spectral Information from Hyperspectral Data and Application of Hyperspectral Imaging for Food and Agricultural Products. Food Bioprocess Technol. 2017, 10, 1–33. [Google Scholar] [CrossRef]
- Ma, J.; Zheng, B.; He, Y. Applications of a Hyperspectral Imaging System Used to Estimate Wheat Grain Protein: A Review. Front. Plant Sci. 2022, 13, 837200. [Google Scholar] [CrossRef]
- Liu, H.; Bruning, B.; Garnett, T.; Berger, B. Hyperspectral Imaging and 3D Technologies for Plant Phenotyping: From Satellite to Close-Range Sensing. Comput. Electron. Agric. 2020, 175, 105621. [Google Scholar] [CrossRef]
- Negash, L.; Kim, H.Y.; Choi, H.L. Emerging UAV Applications in Agriculture. In Proceedings of the 2019 7th International Conference on Robot Intelligence Technology and Applications (RiTA 2019), Daejeon, Republic of Korea, 1–3 November 2019. [Google Scholar]
- Perz, R.; Wronowski, K. UAV Application for Precision Agriculture. Aircr. Eng. Aerosp. Technol. 2019, 91, 257–263. [Google Scholar] [CrossRef]
- Radoglou-Grammatikis, P.; Sarigiannidis, P.; Lagkas, T.; Moscholios, I. A Compilation of UAV Applications for Precision Agriculture. Comput. Netw. 2020, 172, 107148. [Google Scholar] [CrossRef]
- Tang, L.; Shao, G. Drone Remote Sensing for Forestry Research and Practices. J. For. Res. 2015, 26, 791–797. [Google Scholar] [CrossRef]
- de Castro, A.I.; Shi, Y.; Maja, J.M.; Peña, J.M. Uavs for Vegetation Monitoring: Overview and Recent Scientific Contributions. Remote Sens. 2021, 13, 2139. [Google Scholar] [CrossRef]
- Tripathi, R.; Sahoo, R.N.; Sehgal, V.K.; Tomar, R.K.; Chakraborty, D.; Nagarajan, S. Inversion of PROSAIL Model for Retrieval of Plant Biophysical Parameters. J. Indian Soc. Remote Sens. 2012, 40, 19–28. [Google Scholar] [CrossRef]
- Sehgal, V.K.; Chakraborty, D.; Sahoo, R.N. Inversion of Radiative Transfer Model for Retrieval of Wheat Biophysical Parameters from Broadband Reflectance Measurements. Inf. Process. Agric. 2016, 3, 107–118. [Google Scholar] [CrossRef]
- Srivastava, P.K.; Gupta, M.; Singh, U.; Prasad, R.; Pandey, P.C.; Raghubanshi, A.S.; Petropoulos, G.P. Sensitivity Analysis of Artificial Neural Network for Chlorophyll Prediction Using Hyperspectral Data. Environ. Dev. Sustain. 2021, 23, 5504–5519. [Google Scholar] [CrossRef]
- Lin, H.; Liang, L.; Zhang, L.; Du, P. Wheat Leaf Area Index Inversion with Hyperspectral Remote Sensing Based on Support Vector Regression Algorithm. Nongye Gongcheng Xuebao/Trans. Chin. Soc. Agric. Eng. 2013, 29, 139–146. [Google Scholar] [CrossRef]
- Mridha, N.; Sahoo, R.N.; Sehgal, V.K.; Krishna, G.; Pargal, S.; Pradhan, S.; Gupta, V.K.; Kumar, D.N. Comparative Evaluation of Inversion Approaches of the Radiative Transfer Model for Estimation of Crop Biophysical Parameters. Int. Agrophys. 2015, 29, 201–212. [Google Scholar] [CrossRef]
- Verrelst, J.; Alonso, L.; Camps-Valls, G.; Delegido, J.; Moreno, J. Retrieval of Vegetation Biophysical Parameters Using Gaussian Process Techniques. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1832–1843. [Google Scholar] [CrossRef]
- Xie, R.; Darvishzadeh, R.; Skidmore, A.K.; Heurich, M.; Holzwarth, S.; Gara, T.W.; Reusen, I. Mapping Leaf Area Index in a Mixed Temperate Forest Using Fenix Airborne Hyperspectral Data and Gaussian Processes Regression. Int. J. Appl. Earth Obs. Geoinf. 2021, 95, 102242. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Leonenko, G.; Alonso, L.; Moreno, J. Optimizing LUT-Based RTM Inversion for Semiautomatic Mapping of Crop Biophysical Parameters from Sentinel-2 and -3 Data: Role of Cost Functions. IEEE Trans. Geosci. Remote Sens. 2014, 52, 257–269. [Google Scholar] [CrossRef]
- le Maire, G.; François, C.; Soudani, K.; Berveiller, D.; Pontailler, J.Y.; Bréda, N.; Genet, H.; Davi, H.; Dufrêne, E. Calibration and Validation of Hyperspectral Indices for the Estimation of Broadleaved Forest Leaf Chlorophyll Content, Leaf Mass per Area, Leaf Area Index and Leaf Canopy Biomass. Remote Sens. Environ. 2008, 112, 3846–3864. [Google Scholar] [CrossRef]
- Duan, S.B.; Li, Z.L.; Wu, H.; Tang, B.H.; Ma, L.; Zhao, E.; Li, C. Inversion of the PROSAIL Model to Estimate Leaf Area Index of Maize, Potato, and Sunflower Fields from Unmanned Aerial Vehicle Hyperspectral Data. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 12–20. [Google Scholar] [CrossRef]
- Xu, L.; Shi, S.; Gong, W.; Shi, Z.; Qu, F.; Tang, X.; Chen, B.; Sun, J. Improving Leaf Chlorophyll Content Estimation through Constrained PROSAIL Model from Airborne Hyperspectral and LiDAR Data. Int. J. Appl. Earth Obs. Geoinf. 2022, 115, 103128. [Google Scholar] [CrossRef]
- Verrelst, J.; Muñoz, J.; Alonso, L.; Delegido, J.; Rivera, J.P.; Camps-Valls, G.; Moreno, J. Machine Learning Regression Algorithms for Biophysical Parameter Retrieval: Opportunities for Sentinel-2 and -3. Remote Sens. Environ. 2012, 118, 127–139. [Google Scholar] [CrossRef]
- Caicedo, J.P.R.; Verrelst, J.; Munoz-Mari, J.; Moreno, J.; Camps-Valls, G. Toward a Semiautomatic Machine Learning Retrieval of Biophysical Parameters. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1249–1259. [Google Scholar] [CrossRef]
- Sinha, S.K.; Padalia, H.; Dasgupta, A.; Verrelst, J.; Rivera, J.P. Estimation of Leaf Area Index Using PROSAIL Based LUT Inversion, MLRA-GPR and Empirical Models: Case Study of Tropical Deciduous Forest Plantation, North India. Int. J. Appl. Earth Obs. Geoinf. 2020, 86, 102027. [Google Scholar] [CrossRef] [PubMed]
- Adeluyi, O.; Harris, A.; Verrelst, J.; Foster, T.; Clay, G.D. Estimating the Phenological Dynamics of Irrigated Rice Leaf Area Index Using the Combination of PROSAIL and Gaussian Process Regression. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102454. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Moreno, J.; Camps-Valls, G. Gaussian Processes Uncertainty Estimates in Experimental Sentinel-2 LAI and Leaf Chlorophyll Content Retrieval. ISPRS J. Photogramm. Remote Sens. 2013, 86, 157–167. [Google Scholar] [CrossRef]
- Lázaro-Gredilla, M.; Titsias, M.K.; Verrelst, J.; Camps-Valls, G. Retrieval of Biophysical Parameters with Heteroscedastic Gaussian Processes. IEEE Geosci. Remote Sens. Lett. 2014, 11, 838–842. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera-Caicedo, J.P.; Reyes-Muñoz, P.; Morata, M.; Amin, E.; Tagliabue, G.; Panigada, C.; Hank, T.; Berger, K. Mapping Landscape Canopy Nitrogen Content from Space Using PRISMA Data. ISPRS J. Photogramm. Remote Sens. 2021, 178, 382–395. [Google Scholar] [CrossRef]
- Rivera-Caicedo, J.P.; Verrelst, J.; Muñoz-Marí, J.; Camps-Valls, G.; Moreno, J. Hyperspectral Dimensionality Reduction for Biophysical Variable Statistical Retrieval. ISPRS J. Photogramm. Remote Sens. 2017, 132, 88–101. [Google Scholar] [CrossRef]
- Berger, K.; Hank, T.; Halabuk, A.; Rivera-Caicedo, J.P.; Wocher, M.; Mojses, M.; Gerhátová, K.; Tagliabue, G.; Dolz, M.M.; Venteo, A.B.P.; et al. Assessing Non-Photosynthetic Cropland Biomass from Spaceborne Hyperspectral Imagery. Remote Sens. 2021, 13, 4711. [Google Scholar] [CrossRef] [PubMed]
- Pascual-Venteo, A.B.; Portalés, E.; Berger, K.; Tagliabue, G.; Garcia, J.L.; Pérez-Suay, A.; Rivera-Caicedo, J.P.; Verrelst, J. Prototyping Crop Traits Retrieval Models for CHIME: Dimensionality Reduction Strategies Applied to PRISMA Data. Remote Sens. 2022, 14, 2448. [Google Scholar] [CrossRef] [PubMed]
- Wocher, M.; Berger, K.; Verrelst, J.; Hank, T. Retrieval of Carbon Content and Biomass from Hyperspectral Imagery over Cultivated Areas. ISPRS J. Photogramm. Remote Sens. 2022, 193, 104–114. [Google Scholar] [CrossRef] [PubMed]
- Abdelbaki, A.; Schlerf, M.; Retzlaff, R.; Machwitz, M.; Verrelst, J.; Udelhoven, T. Comparison of Crop Trait Retrieval Strategies Using UAV-Based VNIR Hyperspectral Imaging. Remote Sens. 2021, 13, 1748. [Google Scholar] [CrossRef]
- Kayad, A.; Rodrigues, F.A.; Naranjo, S.; Sozzi, M.; Pirotti, F.; Marinello, F.; Schulthess, U.; Defourny, P.; Gerard, B.; Weiss, M. Radiative Transfer Model Inversion Using High-Resolution Hyperspectral Airborne Imagery—Retrieving Maize LAI to Access Biomass and Grain Yield. Field Crops Res. 2022, 282, 108449. [Google Scholar] [CrossRef] [PubMed]
- Chakhvashvili, E.; Siegmann, B.; Muller, O.; Verrelst, J.; Bendig, J.; Kraska, T.; Rascher, U. Retrieval of Crop Variables from Proximal Multispectral UAV Image Data Using PROSAIL in Maize Canopy. Remote Sens. 2022, 14, 1247. [Google Scholar] [CrossRef]
- Yu, F.H.; Xu, T.Y.; Du, W.; Ma, H.; Zhang, G.S.; Chen, C.L. Radiative Transfer Models (RTMs) for Field Phenotyping Inversion of Rice Based on UAV Hyperspectral Remote Sensing. Int. J. Agric. Biol. Eng. 2017, 10, 150–157. [Google Scholar] [CrossRef]
- Arnon, D.I. Copper Enzymes in Isolated Chloroplasts. Polyphenoloxidase in Beta vulgaris. Plant Physiol. 1949, 24, 1–15. [Google Scholar] [CrossRef]
- Lama, G.F.C.; Errico, A.; Pasquino, V.; Mirzaei, S.; Preti, F.; Chirico, G.B. Velocity Uncertainty Quantification Based on Riparian Vegetation Indices in Open Channels Colonized by Phragmites Australis. J. Ecohydraulics 2022, 7, 71–76. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Ciganda, V.; Rundquist, D.C.; Arkebauer, T.J. Remote Estimation of Canopy Chlorophyll Content in Crops. Geophys. Res. Lett. 2005, 32, L08403. [Google Scholar] [CrossRef]
- Ge, X.; Wang, J.; Ding, J.; Cao, X.; Zhang, Z.; Liu, J.; Li, X. Combining UAV-Based Hyperspectral Imagery and Machine Learning Algorithms for Soil Moisture Content Monitoring. PeerJ 2019, 7, e6926. [Google Scholar] [CrossRef] [PubMed]
- Sahoo, R.N.; Gakhar, S.; Rejith, R.G.; Ranjan, R.; Meena, M.C.; Dey, A.; Mukherjee, J.; Dhakar, R.; Arya, S.; Daas, A.; et al. Unmanned Aerial Vehicle (UAV)–Based Imaging Spectroscopy for Predicting Wheat Leaf Nitrogen. Photogramm. Eng. Remote Sens. 2023, 89, 107–116. [Google Scholar] [CrossRef]
- Chancia, R.; Bates, T.; Heuvel, J.V.; van Aardt, J. Assessing Grapevine Nutrient Status from Unmanned Aerial System (UAS) Hyperspectral Imagery. Remote Sens. 2021, 13, 4489. [Google Scholar] [CrossRef]
- Wei, L.; Yu, M.; Liang, Y.; Yuan, Z.; Huang, C.; Li, R.; Yu, Y. Precise Crop Classification Using Spectral-Spatial-Location Fusion Based on Conditional Random Fields for UAV-Borne Hyperspectral Remote Sensing Imagery. Remote Sens. 2019, 11, 2011. [Google Scholar] [CrossRef]
- Aggarwal, A.; Garg, R.D. Systematic Approach towards Extracting Endmember Spectra from Hyperspectral Image Using PPI and SMACC and Its Evaluation Using Spectral Library. Appl. Geomatics 2015, 7, 37–48. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT + SAIL Models: A Review of Use for Vegetation Characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Mridha, N. Assessing Crop Biophysical Parameters from Hyper-Spectral and Multispectral Remote Sensing and Multispectral Remote Sensing Data through Radiative Transfer Modeling; Indian Agricultural Research Institute: New Delhi, India, 2014. [Google Scholar]
- Chakraborty, D.; Sehgal, V.K.; Sahoo, R.N.; Pradhan, S.; Gupta, V.K. Study of the Anisotropic Reflectance Behaviour of Wheat Canopy to Evaluate the Performance of Radiative Transfer Model PROSAIL5B. J. Indian Soc. Remote Sens. 2015, 43, 297–310. [Google Scholar] [CrossRef]
- Barman, D.; Sehgal, V.K.; Sahoo, R.N.; Nagarajan, S. Relationship of Bidirectional Reflectance of Wheat with Biophysical Parameters and Its Radiative Transfer Modeling Using Prosail. J. Indian Soc. Remote Sens. 2010, 38, 35–44. [Google Scholar] [CrossRef]
- Tripathi, R.; Sahoo, R.N.; Sehgal, V.K.; Gupta, V.K.; Bhattacharya, B.B.K.; Gupta, K.; Bhattacharya, B.B.K. Remote Sensing Derived Composite Vegetation Health Index Through Inversion of Prosail for Monitoring of Wheat Growth in Trans Gangetic Plains of India. ISPRS Arch. XXXVIII-8/W3 Work. Proc. Impact Clim. Chang. Agric. 2009, 38, W3. [Google Scholar]
- Ranghetti, M.; Boschetti, M.; Ranghetti, L.; Tagliabue, G.; Panigada, C.; Gianinetto, M.; Verrelst, J.; Candiani, G. Assessment of Maize Nitrogen Uptake from PRISMA Hyperspectral Data through Hybrid Modelling. Eur. J. Remote Sens. 2022, 1–17. [Google Scholar] [CrossRef]
- Verrelst, J.; Romijn, E.; Kooistra, L. Mapping Vegetation Density in a Heterogeneous River Floodplain Ecosystem Using Pointable CHRIS/PROBA Data. Remote Sens. 2012, 4, 2866. [Google Scholar] [CrossRef]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Estévez, J.; Berger, K.; Vicent, J.; Rivera-Caicedo, J.P.; Wocher, M.; Verrelst, J. Top-of-Atmosphere Retrieval of Multiple Crop Traits Using Variational Heteroscedastic Gaussian Processes within a Hybrid Workflow. Remote Sens. 2021, 13, 1589. [Google Scholar] [CrossRef]
- Ayala Izurieta, J.E.; Jara Santillán, C.A.; Márquez, C.O.; García, V.J.; Rivera-Caicedo, J.P.; Van Wittenberghe, S.; Delegido, J.; Verrelst, J. Improving the Remote Estimation of Soil Organic Carbon in Complex Ecosystems with Sentinel-2 and GIS Using Gaussian Processes Regression. Plant Soil 2022, 479, 159–183. [Google Scholar] [CrossRef] [PubMed]
- Reyes-Muñoz, P.; Pipia, L.; Salinero-Delgado, M.; De Grave, C.; Estévez, J.; Belda, S.; Verrelst, J. Mapping essential vegetation variables over europe using gaussian process regression and sentinel-3 data in Google Earth Engine. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Brussels, Belgium, 11–16 July 2021. [Google Scholar]
- Zhang, Y.; Yang, J.; Du, L. Analyzing the Effects of Hyperspectral Zhuhai-1 Band Combinations on Lai Estimation Based on the Prosail Model. Sensors 2021, 21, 1869. [Google Scholar] [CrossRef] [PubMed]
- Pipia, L.; Amin, E.; Belda, S.; Salinero-Delgado, M.; Verrelst, J. Green Lai Mapping and Cloud Gap-Filling Using Gaussian Process Regression in Google Earth Engine. Remote Sens. 2021, 13, 403. [Google Scholar] [CrossRef] [PubMed]
- Berger, K.; Rivera Caicedo, J.P.; Martino, L.; Wocher, M.; Hank, T.; Verrelst, J. A Survey of Active Learning for Quantifying Vegetation Traits from Terrestrial Earth Observation Data. Remote Sens. 2021, 13, 287. [Google Scholar] [CrossRef]
- Verrelst, J.; Berger, K.; Rivera-Caicedo, J.P. Intelligent Sampling for Vegetation Nitrogen Mapping Based on Hybrid Machine Learning Algorithms. IEEE Geosci. Remote Sens. Lett. 2021, 18, 2038–2042. [Google Scholar] [CrossRef]
- Verrelst, J.; Dethier, S.; Rivera, J.P.; Munoz-Mari, J.; Camps-Valls, G.; Moreno, J. Active Learning Methods for Efficient Hybrid Biophysical Variable Retrieval. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1012–1016. [Google Scholar] [CrossRef]
- ElRafey, A.; Wojtusiak, J. A Hybrid Active Learning and Progressive Sampling Algorithm. Int. J. Mach. Learn. Comput. 2018, 8, 423–427. [Google Scholar] [CrossRef]
- Douak, F.; Benoudjit, N.; Melgani, F. A Two-Stage Regression Approach for Spectroscopic Quantitative Analysis. Chemom. Intell. Lab. Syst. 2011, 109, 34–41. [Google Scholar] [CrossRef]
- Douak, F.; Melgani, F.; Benoudjit, N. Kernel Ridge Regression with Active Learning for Wind Speed Prediction. Appl. Energy 2013, 103, 328–340. [Google Scholar] [CrossRef]
- Binh, N.A.; Hauser, L.T.; Viet Hoa, P.; Thi Phuong Thao, G.; An, N.N.; Nhut, H.S.; Phuong, T.A.; Verrelst, J. Quantifying Mangrove Leaf Area Index from Sentinel-2 Imagery Using Hybrid Models and Active Learning. Int. J. Remote Sens. 2022, 43, 5636–5657. [Google Scholar] [CrossRef] [PubMed]
- Estévez, J.; Salinero-Delgado, M.; Berger, K.; Pipia, L.; Rivera-Caicedo, J.P.; Wocher, M.; Reyes-Muñoz, P.; Tagliabue, G.; Boschetti, M.; Verrelst, J. Gaussian Processes Retrieval of Crop Traits in Google Earth Engine Based on Sentinel-2 Top-of-Atmosphere Data. Remote Sens. Environ. 2022, 273, 112958. [Google Scholar] [CrossRef] [PubMed]
- Salinero-Delgado, M.; Estévez, J.; Pipia, L.; Belda, S.; Berger, K.; Gómez, V.P.; Verrelst, J. Monitoring Cropland Phenology on Google Earth Engine Using Gaussian Process Regression. Remote Sens. 2022, 14, 146. [Google Scholar] [CrossRef] [PubMed]
- Estévez, J.; Vicent, J.; Rivera-Caicedo, J.P.; Morcillo-Pallarés, P.; Vuolo, F.; Sabater, N.; Camps-Valls, G.; Moreno, J.; Verrelst, J. Gaussian Processes Retrieval of LAI from Sentinel-2 Top-of-Atmosphere Radiance Data. ISPRS J. Photogramm. Remote Sens. 2020, 167, 289–304. [Google Scholar] [CrossRef]
- Verrelst, J.; Alonso, L.; Rivera Caicedo, J.P.; Moreno, J.; Camps-Valls, G. Gaussian Process Retrieval of Chlorophyll Content from Imaging Spectroscopy Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 867–874. [Google Scholar] [CrossRef]
- Tuia, D.; Volpi, M.; Copa, L.; Kanevski, M.; Muñoz-Marí, J. A Survey of Active Learning Algorithms for Supervised Remote Sensing Image Classification. IEEE J. Sel. Top. Signal Process. 2011, 5, 606–617. [Google Scholar] [CrossRef]
- Shen, X.J.; Wu, H.X.; Zhu, Q. Training Support Vector Machine through Redundant Data Reduction. In Proceedings of the 4th International Conference on Internet Multimedia Computing and Service, Wuhan, China, 9–11 September 2012. ACM International Conference Proceeding Series. [Google Scholar]
- Candiani, G.; Tagliabue, G.; Panigada, C.; Verrelst, J.; Picchi, V.; Caicedo, J.P.R.; Boschetti, M. Evaluation of Hybrid Models to Estimate Chlorophyll and Nitrogen Content of Maize Crops in the Framework of the Future CHIME Mission. Remote Sens. 2022, 14, 1792. [Google Scholar] [CrossRef]
- Croft, H.; Arabian, J.; Chen, J.M.; Shang, J.; Liu, J. Mapping Within-Field Leaf Chlorophyll Content in Agricultural Crops for Nitrogen Management Using Landsat-8 Imagery. Precis. Agric. 2020, 21, 856–880. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Veroustraete, F.; Muñoz-Marí, J.; Clevers, J.G.P.W.; Camps-Valls, G.; Moreno, J. Experimental Sentinel-2 LAI Estimation Using Parametric, Non-Parametric and Physical Retrieval Methods—A Comparison. ISPRS J. Photogramm. Remote Sens. 2015, 108, 260–272. [Google Scholar] [CrossRef]




| S. No. | Parameter | Abbreviation | Unit | Values |
|---|---|---|---|---|
| Leaf Model: PROSPECT-4 | ||||
| 1. | Leaf structure coefficient | N | Dimensionless | 1 |
| 2. | Equivalent water thickness | Cw | cm | 0.01–0.045 (0.001 interval) |
| 3. | Leaf chlorophyll content | Cab | µcm−2 | 0–80 (0.2 interval) |
| 4. | Dry matter content | Cm | g cm−2 | 0.0046 |
| Canopy Model: 4-SAIL | ||||
| 5. | Leaf area index | LAI | m2 m−2 | 0.1–7.5 (0.01 interval) |
| 6. | Average leaf angle | angl | Degree | 70, 57, 45 |
| 7. | Fraction of diffuse incoming solar radiation | skyl | Dimensionless | 0.1 |
| 8. | Soil brightness coefficient | psoil | Dimensionless | 0.1 |
| 9. | Hot-spot size parameter | hspot | mm−1 | 0.78, 0.40, 0.32 |
| 10. | Solar zenith angle | tts | Degree | 51, 45, 33 |
| 11. | Sensor/view zenith angle | tto | Degree | 0 |
| 12. | Relative azimuth | psi | Degree | 0 |
| S. No. | Algorithm | Principle | Formula and Description |
|---|---|---|---|
| 1. | Kernel ridge regression (KRR) [77] |
| where is the new test point, is the solution, , and . Adding bias |
| 2. | Least squares linear regression (LSLR) |
| where is the mean of all the values in input x and ȳ is the mean of all the values in desired output y. m is the slope of the line, and c is the y-intercept. |
| 3. | Neural network (NN) |
| where —output; —input; —activation function; —weight; —bias; —error; and —ground truth, for instance. |
| 4. | Support vector regression (SVR) |
| where is the sample dataset, for which SVM finds weights such that the data points in the dataset are separated using the most optimum hyperplane. Further, is differentiated with respect to . |
| 5. | Extreme learning machine (ELM) |
| where —hidden nodes; —output function at hidden node; —hidden node parameters; —weight vector; —activation function; and —hidden-layer output matrix. |
| 6. | Bagging trees (BaTs) |
| where is the record for which a prediction is to be generated, is the bagged prediction, and are the predictions from the individual base learners. |
| 7. | Boosting trees (BoTs) |
| where final classifier is the sum of simple base classifiers . where is called the step size. where is the iteration; is the empirical loss function at each iteration; and is moved towards the negative gradient direction. |
| S. No. | MLRA | MAE | RMSE | RRMSE (%) | NRMSE (%) | R2 |
|---|---|---|---|---|---|---|
| LAI | ||||||
| 1. | GPR | 0.019 | 0.143 | 3.796 | 1.946 | 0.996 |
| 2. | KRR | 0.114 | 0.153 | 4.065 | 2.084 | 0.995 |
| 3. | NN | 0.129 | 0.232 | 6.150 | 3.153 | 0.988 |
| 4. | LS | 0.189 | 0.247 | 6.545 | 3.355 | 0.987 |
| 5. | ELM | 0.189 | 0.321 | 8.499 | 4.357 | 0.978 |
| 6. | BaT | 0.218 | 0.357 | 9.469 | 4.854 | 0.976 |
| 7. | BoT | 0.303 | 0.413 | 10.933 | 5.604 | 0.963 |
| 8. | SVR | 0.334 | 0.449 | 11.892 | 6.096 | 0.957 |
| CCC | ||||||
| 1. | KRR | 0.016 | 0.024 | 1.562 | 0.433 | 0.9997 |
| 2. | GPR | 0.031 | 0.043 | 2.756 | 0.746 | 0.999 |
| 3. | NN | 0.031 | 0.050 | 3.262 | 0.904 | 0.999 |
| 4. | LS | 0.038 | 0.050 | 3.292 | 0.912 | 0.999 |
| 5. | ELM | 0.042 | 0.063 | 4.115 | 1.140 | 0.998 |
| 6. | SVR | 0.075 | 0.093 | 6.099 | 1.690 | 0.995 |
| 7. | BaT | 0.068 | 0.109 | 7.105 | 1.969 | 0.995 |
| 8. | BoT | 0.139 | 0.176 | 11.521 | 3.192 | 0.982 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sahoo, R.N.; Gakhar, S.; Rejith, R.G.; Verrelst, J.; Ranjan, R.; Kondraju, T.; Meena, M.C.; Mukherjee, J.; Daas, A.; Kumar, S.; et al. Optimizing the Retrieval of Wheat Crop Traits from UAV-Borne Hyperspectral Image with Radiative Transfer Modelling Using Gaussian Process Regression. Remote Sens. 2023, 15, 5496. https://doi.org/10.3390/rs15235496
Sahoo RN, Gakhar S, Rejith RG, Verrelst J, Ranjan R, Kondraju T, Meena MC, Mukherjee J, Daas A, Kumar S, et al. Optimizing the Retrieval of Wheat Crop Traits from UAV-Borne Hyperspectral Image with Radiative Transfer Modelling Using Gaussian Process Regression. Remote Sensing. 2023; 15(23):5496. https://doi.org/10.3390/rs15235496
Chicago/Turabian StyleSahoo, Rabi N., Shalini Gakhar, Rajan G. Rejith, Jochem Verrelst, Rajeev Ranjan, Tarun Kondraju, Mahesh C. Meena, Joydeep Mukherjee, Anchal Daas, Sudhir Kumar, and et al. 2023. "Optimizing the Retrieval of Wheat Crop Traits from UAV-Borne Hyperspectral Image with Radiative Transfer Modelling Using Gaussian Process Regression" Remote Sensing 15, no. 23: 5496. https://doi.org/10.3390/rs15235496
APA StyleSahoo, R. N., Gakhar, S., Rejith, R. G., Verrelst, J., Ranjan, R., Kondraju, T., Meena, M. C., Mukherjee, J., Daas, A., Kumar, S., Kumar, M., Dhandapani, R., & Chinnusamy, V. (2023). Optimizing the Retrieval of Wheat Crop Traits from UAV-Borne Hyperspectral Image with Radiative Transfer Modelling Using Gaussian Process Regression. Remote Sensing, 15(23), 5496. https://doi.org/10.3390/rs15235496







