Optical and Thermal Image Processing for Monitoring Rainfall Triggered Shallow Landslides: Insights from Analogue Laboratory Experiments
Abstract
:1. Introduction
- To assess the reliability, potential, and capabilities of optical- and IRT-DIP techniques as an innovative method for monitoring shallow landslides triggered by rainfall, using RGB optical images extracted from digital videos and infrared thermal images;
- To study the deformation behaviour of shallow landslides, reproducing it in the laboratory using a flume test analogic apparatus;
- To expand knowledge on the behaviour of earth slopes involved in shallow landslide processes, to identify potential precursors of slope failure.
2. Materials and Methods
2.1. Description of the Experimental Set-Up
2.2. Description of Sensors
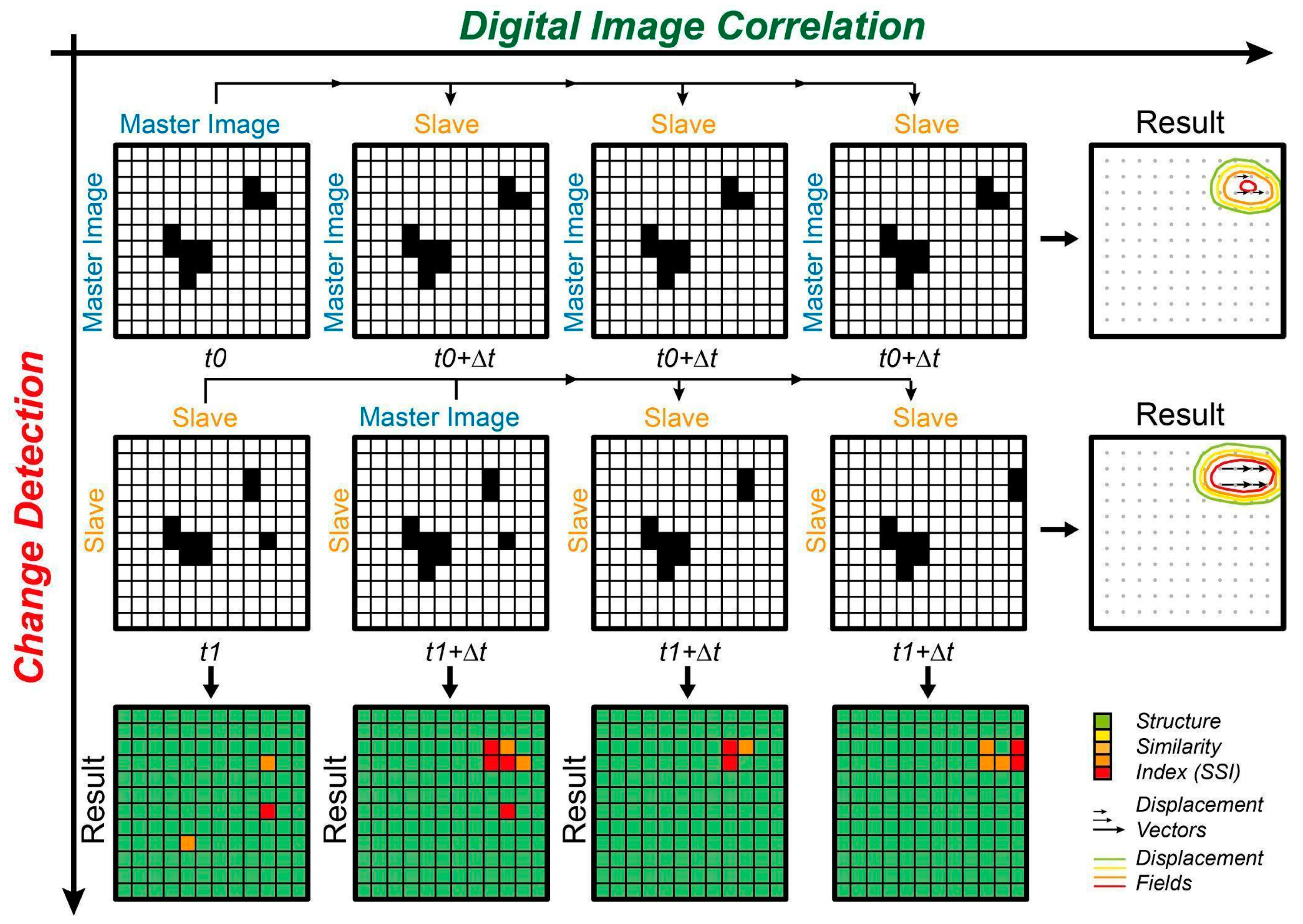
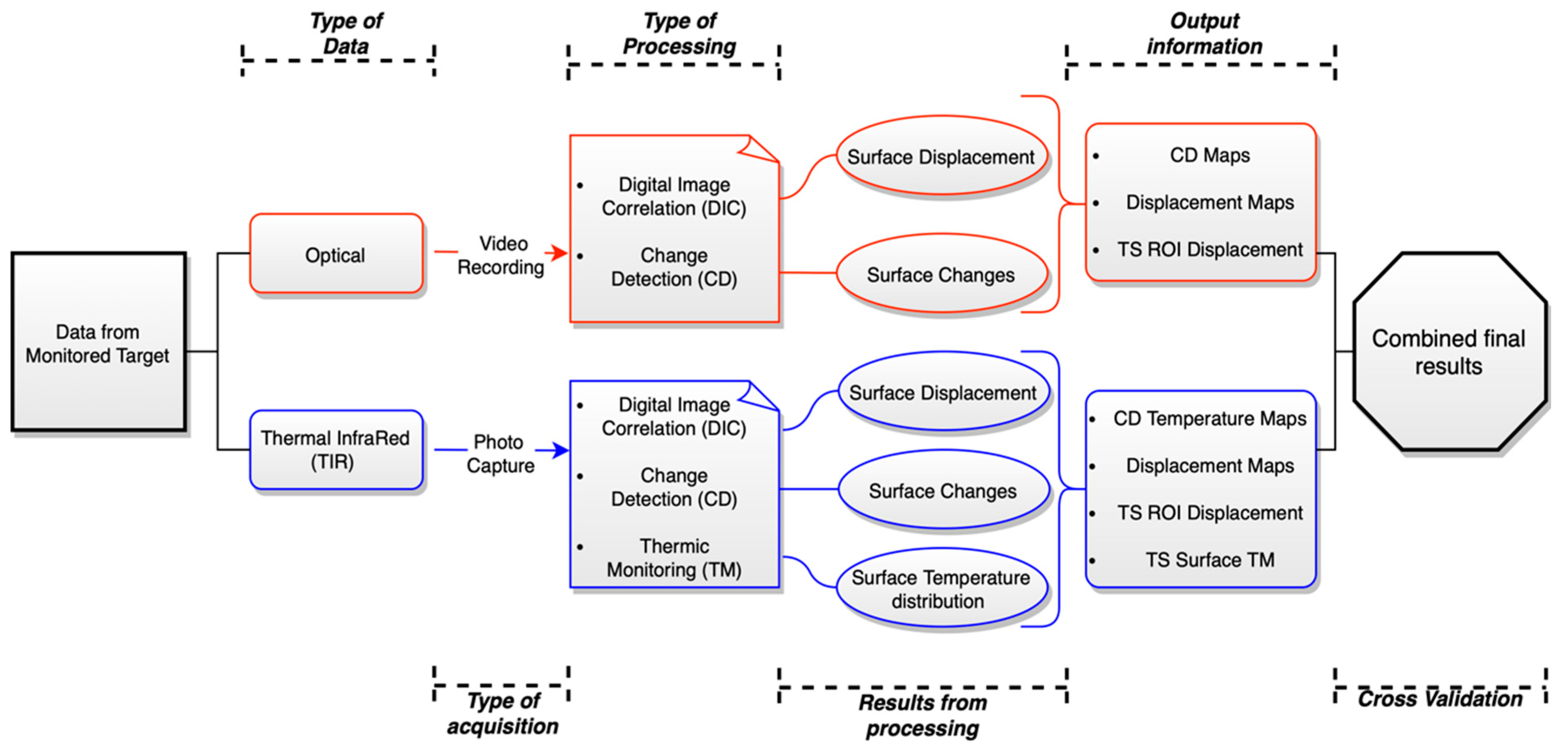
2.3. Remote Sensing Technique (RTS)
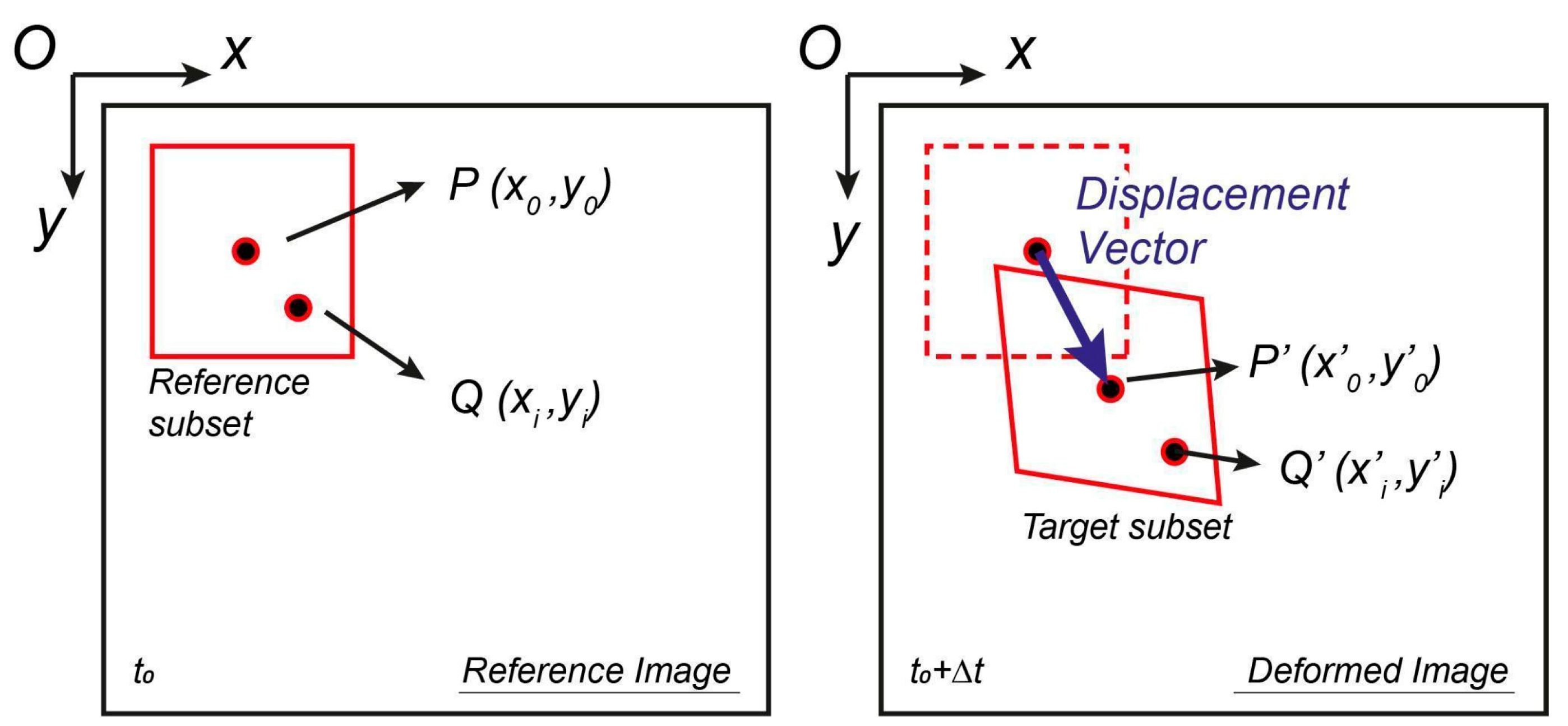
2.3.1. Principles of PhotoMonitoring
2.3.2. Data Processing
3. Results
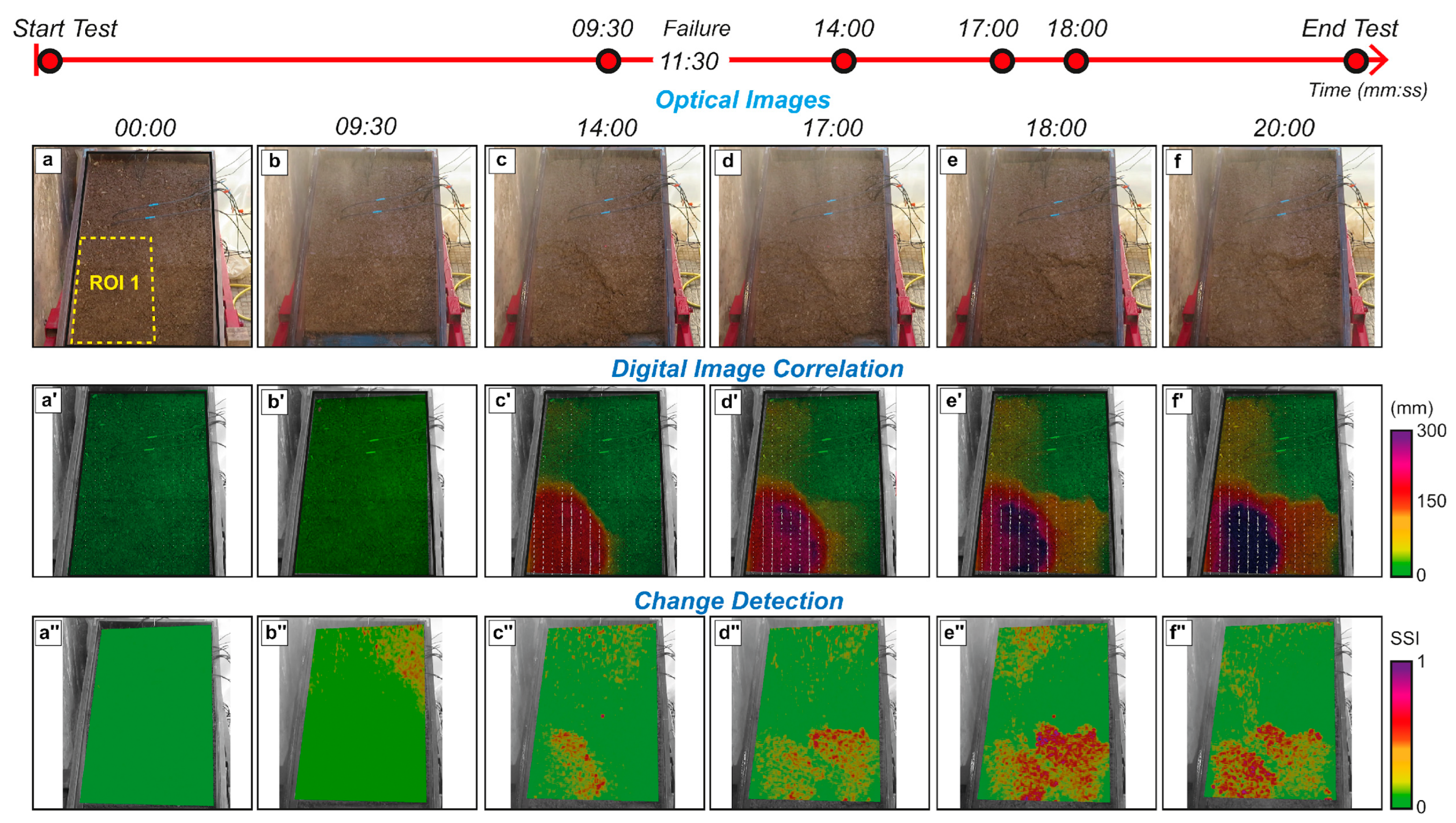
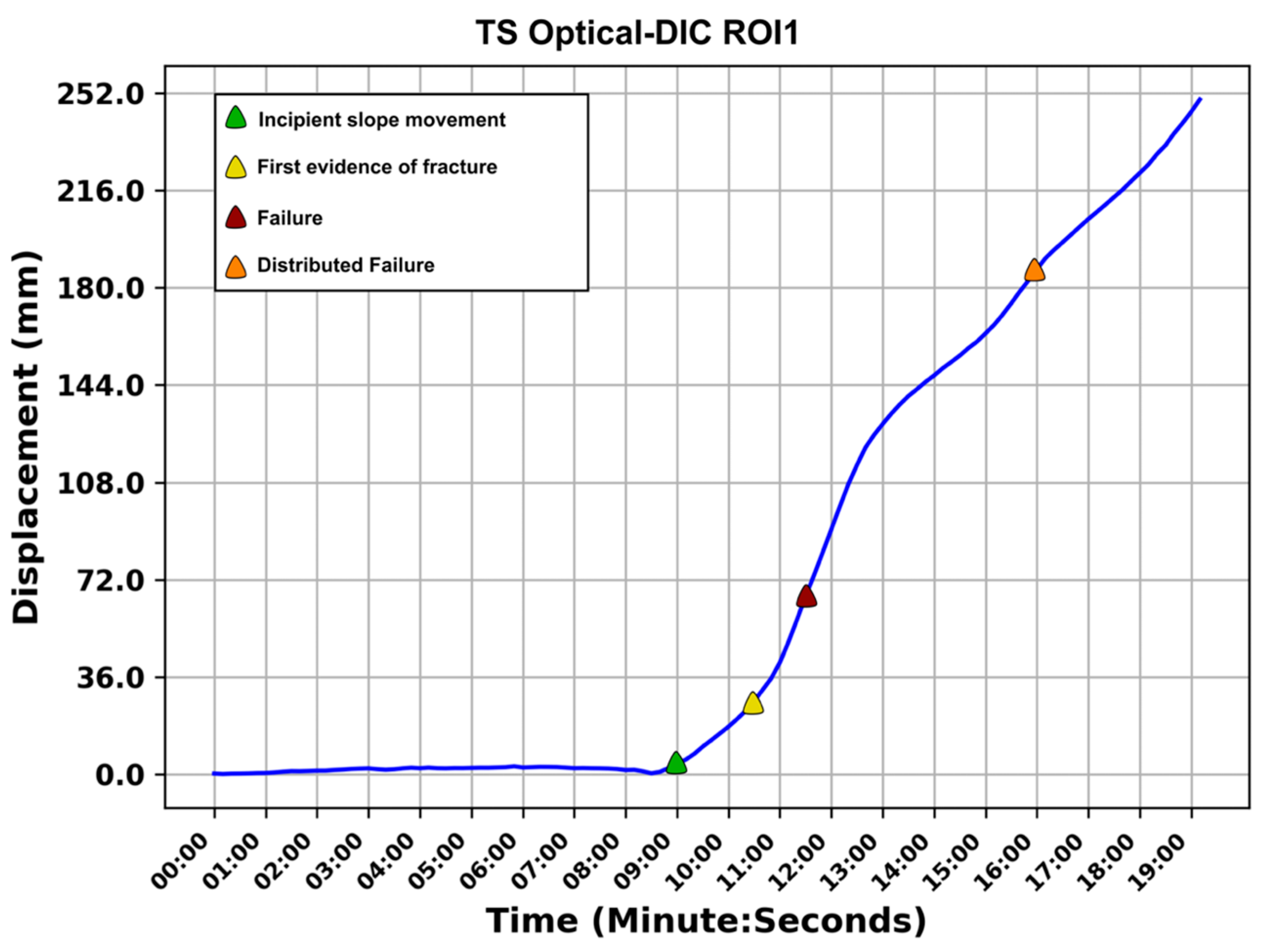
3.1. Results from Optical Camera
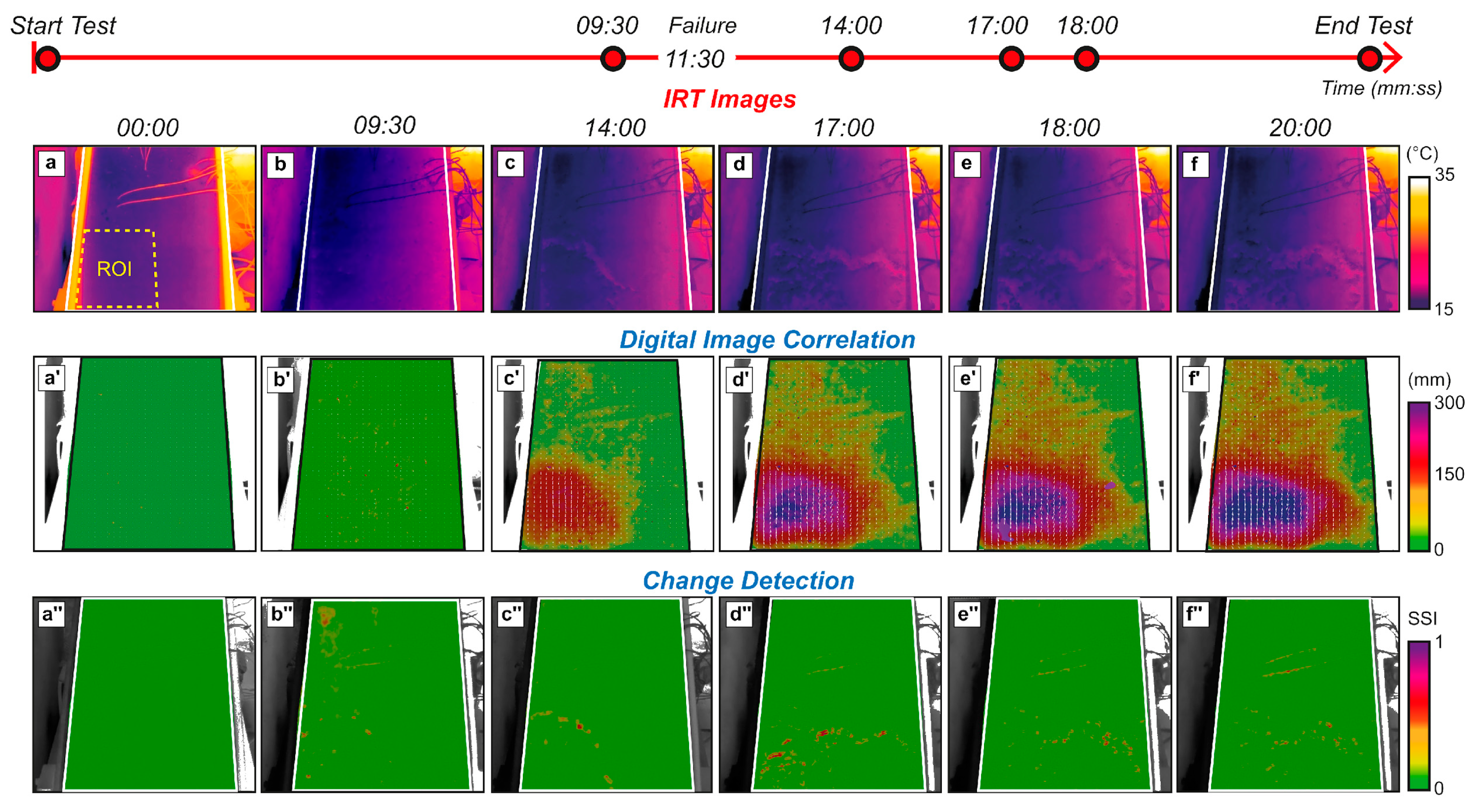
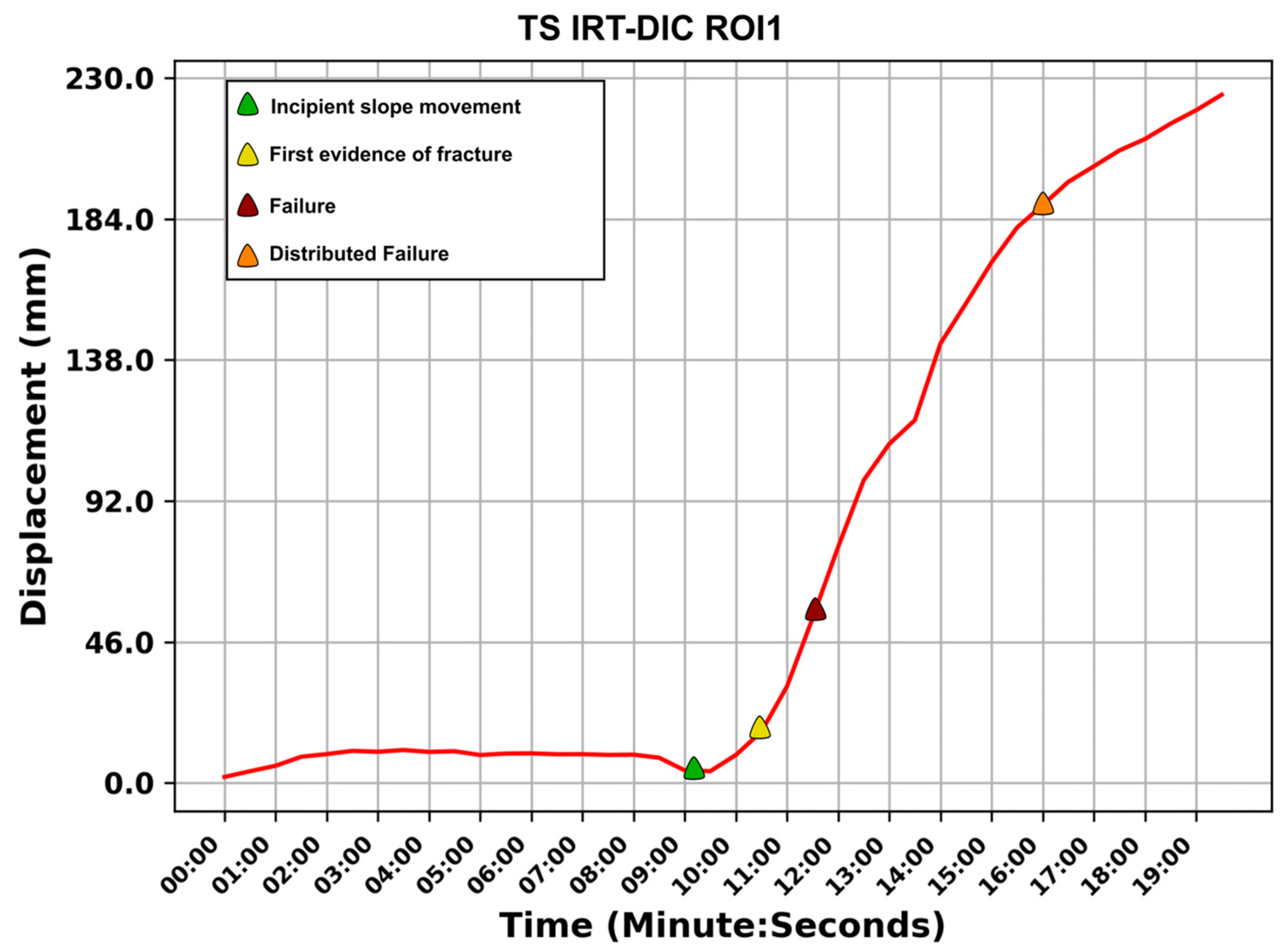
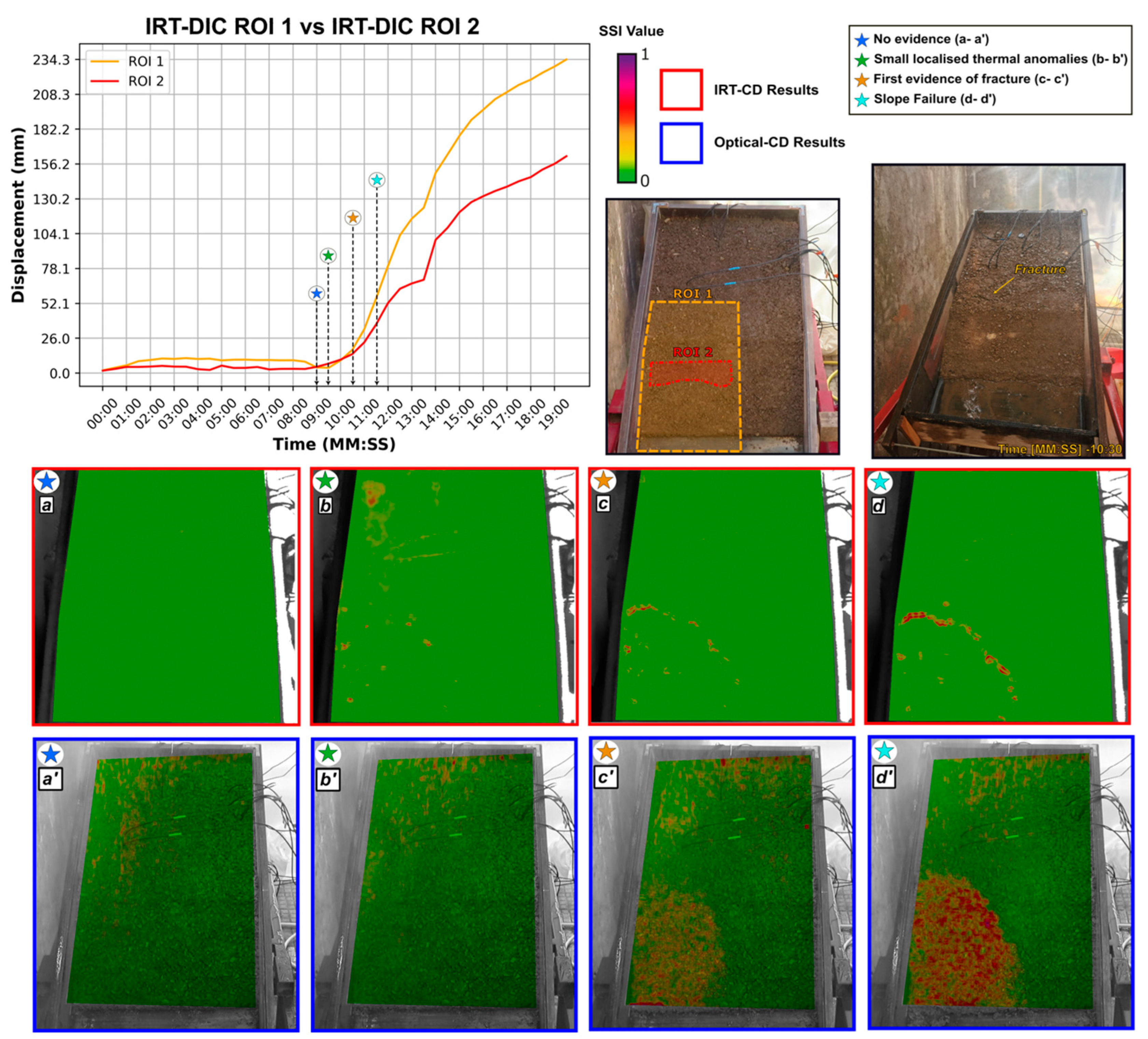
3.2. Results from IRT Sensor
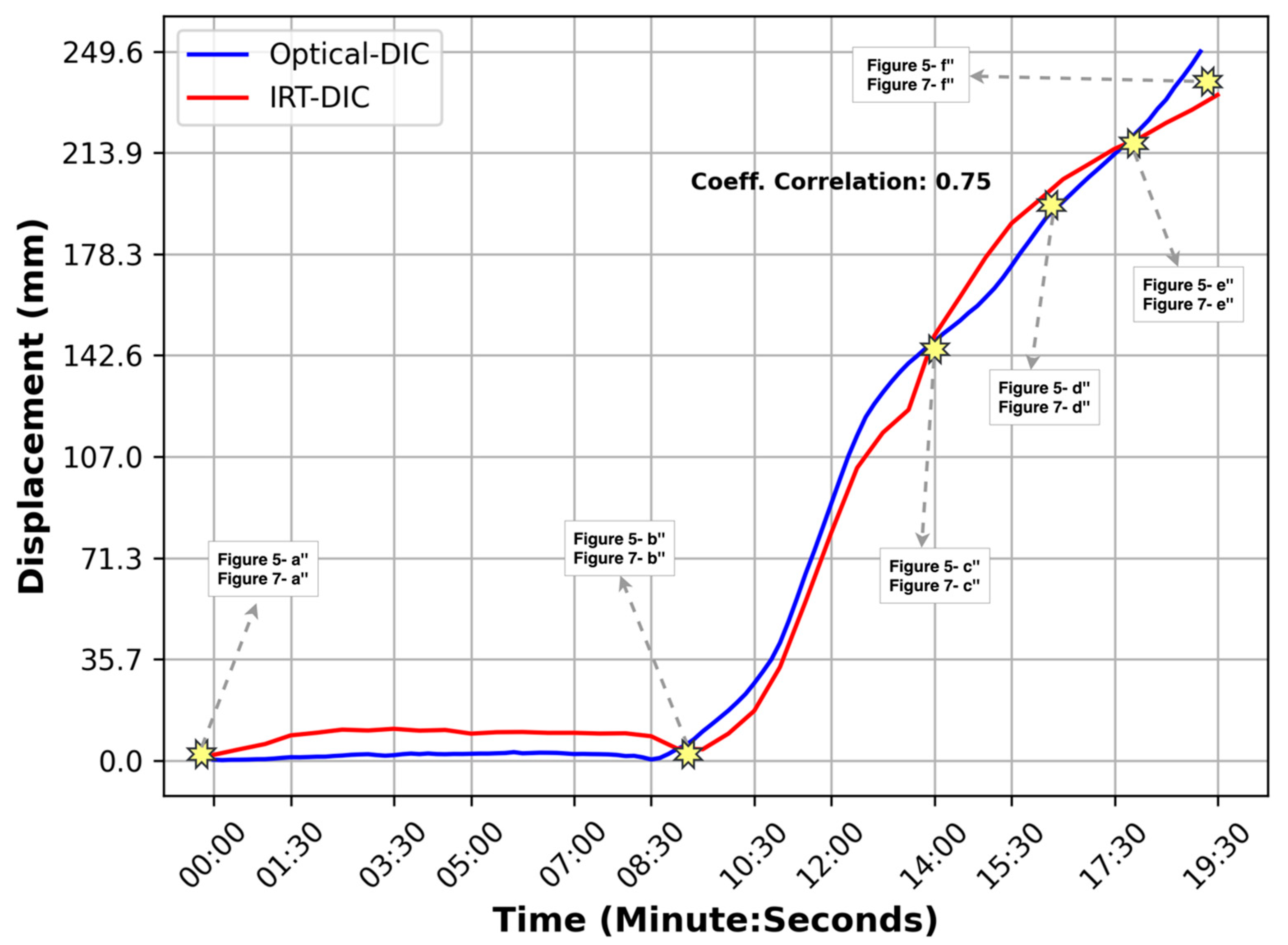
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haque, U.; Blum, P.; Da Silva, P.F.; Andersen, P.; Pilz, J.; Chalov, S.R.; Malet, J.-P.; Auflič, M.J.; Andres, N.; Poyiadji, E.; et al. Fatal Landslides in Europe. Landslides 2016, 13, 1545–1554. [Google Scholar] [CrossRef]
- Klose, M.; Maurischat, P.; Damm, B. Landslide Impacts in Germany: A Historical and Socioeconomic Perspective. Landslides 2016, 13, 183–199. [Google Scholar] [CrossRef]
- Casagli, N.; Intrieri, E.; Tofani, V.; Gigli, G.; Raspini, F. Landslide Detection, Monitoring and Prediction with Remote-Sensing Techniques. Nat. Rev. Earth Environ. 2023, 4, 51–64. [Google Scholar] [CrossRef]
- Canuti, P.; Casagli, N.; Ermini, L.; Fanti, R.; Farina, P. Landslide Activity as a Geoindicator in Italy: Significance and New Perspectives from Remote Sensing. Environ. Geol. 2004, 45, 907–919. [Google Scholar] [CrossRef]
- Gunzburger, Y.; Merrien-Soukatchoff, V.; Guglielmi, Y. Influence of Daily Surface Temperature Fluctuations on Rock Slope Stability: Case Study of the Rochers de Valabres Slope (France). Int. J. Rock Mech. Min. Sci. 2005, 42, 331–349. [Google Scholar] [CrossRef]
- Dai, F.C.; Lee, C.F.; Ngai, Y.Y. Landslide Risk Assessment and Management: An Overview. Eng. Geol. 2002, 64, 65–87. [Google Scholar] [CrossRef]
- Mantovani, F.; Soeters, R.; Van Westen, C.J. Remote Sensing Techniques for Landslide Studies and Hazard Zonation in Europe. Geomorphology 1996, 15, 213–225. [Google Scholar] [CrossRef]
- Chae, B.-G.; Park, H.-J.; Catani, F.; Simoni, A.; Berti, M. Landslide Prediction, Monitoring and Early Warning: A Concise Review of State-of-the-Art. Geosci. J. 2017, 21, 1033–1070. [Google Scholar] [CrossRef]
- Mazzanti, P.; Caporossi, P.; Muzi, R. Sliding Time Master Digital Image Correlation Analyses of CubeSat Images for Landslide Monitoring: The Rattlesnake Hills Landslide (USA). Remote Sens. 2020, 12, 592. [Google Scholar] [CrossRef]
- Guerriero, L.; Di Martire, D.; Calcaterra, D.; Francioni, M. Digital Image Correlation of Google Earth Images for Earth’s Surface Displacement Estimation. Remote Sens. 2020, 12, 3518. [Google Scholar] [CrossRef]
- Caporossi, P.; Mazzanti, P.; Bozzano, F. Digital Image Correlation (DIC) Analysis of the 3 December 2013 Montescaglioso Landslide (Basilicata, Southern Italy): Results from a Multi-Dataset Investigation. IJGI 2018, 7, 372. [Google Scholar] [CrossRef]
- Mazza, D.; Cosentino, A.; Romeo, S.; Mazzanti, P.; Guadagno, F.M.; Revellino, P. Remote Sensing Monitoring of the Pietrafitta Earth Flows in Southern Italy: An Integrated Approach Based on Multi-Sensor Data. Remote Sens. 2023, 15, 1138. [Google Scholar] [CrossRef]
- Oats, R.C.; Dai, Q.; Head, M. Digital Image Correlation Advances in Structural Evaluation Applications: A Review. Pract. Period. Struct. Des. Constr. 2022, 27, 03122007. [Google Scholar] [CrossRef]
- Mugnai, F.; Caporossi, P.; Mazzanti, P. Exploiting Image Assisted Total Station in Digital Image Correlation (DIC) Displacement Measurements: Insights from Laboratory Experiments. Eur. J. Remote Sens. 2022, 55, 115–128. [Google Scholar] [CrossRef]
- Spampinato, L.; Calvari, S.; Oppenheimer, C.; Boschi, E. Volcano Surveillance Using Infrared Cameras. Earth-Sci. Rev. 2011, 106, 63–91. [Google Scholar] [CrossRef]
- Calvari, S.; Spampinato, L.; Lodato, L.; Harris, A.J.L.; Patrick, M.R.; Dehn, J.; Burton, M.R.; Andronico, D. Chronology and Complex Volcanic Processes during the 2002–2003 Flank Eruption at Stromboli Volcano (Italy) Reconstructed from Direct Observations and Surveys with a Handheld Thermal Camera. J. Geophys. Res. 2005, 110, B02201. [Google Scholar] [CrossRef]
- Schöpa, A.; Pantaleo, M.; Walter, T.R. Scale-Dependent Location of Hydrothermal Vents: Stress Field Models and Infrared Field Observations on the Fossa Cone, Vulcano Island, Italy. J. Volcanol. Geotherm. Res. 2011, 203, 133–145. [Google Scholar] [CrossRef]
- Furukawa, Y. Infrared Thermography of the Fumarole Area in the Active Crater of the Aso Volcano, Japan, Using a Consumer Digital Camera. J. Asian Earth Sci. 2010, 38, 283–288. [Google Scholar] [CrossRef]
- Stevenson, J.A.; Varley, N. Fumarole Monitoring with a Handheld Infrared Camera: Volcán de Colima, Mexico, 2006–2007. J. Volcanol. Geotherm. Res. 2008, 177, 911–924. [Google Scholar] [CrossRef]
- Pappalardo, G.; Mineo, S.; Caliò, D.; Bognandi, A. Evaluation of Natural Stone Weathering in Heritage Building by Infrared Thermography. Heritage 2022, 5, 2594–2614. [Google Scholar] [CrossRef]
- Grinzato, E.; Bison, P.G.; Marinetti, S. Monitoring of Ancient Buildings by the Thermal Method. J. Cult. Herit. 2002, 3, 21–29. [Google Scholar] [CrossRef]
- Lucchi, E. Applications of the Infrared Thermography in the Energy Audit of Buildings: A Review. Renew. Sustain. Energy Rev. 2018, 82, 3077–3090. [Google Scholar] [CrossRef]
- Mineo, S.; Pappalardo, G. The Use of Infrared Thermography for Porosity Assessment of Intact Rock. Rock Mech. Rock Eng. 2016, 49, 3027–3039. [Google Scholar] [CrossRef]
- Mineo, S.; Pappalardo, G.; Rapisarda, F.; Cubito, A.; Di Maria, G. Integrated Geostructural, Seismic and Infrared Thermography Surveys for the Study of an Unstable Rock Slope in the Peloritani Chain (NE Sicily). Eng. Geol. 2015, 195, 225–235. [Google Scholar] [CrossRef]
- Lee, E.J.; Shin, S.Y.; Ko, B.C.; Chang, C. Early Sinkhole Detection Using a Drone-Based Thermal Camera and Image Processing. Infrared Phys. Technol. 2016, 78, 223–232. [Google Scholar] [CrossRef]
- Baroň, I.; Bečkovský, D.; Míča, L. Application of Infrared Thermography for Mapping Open Fractures in Deep-Seated Rockslides and Unstable Cliffs. Landslides 2014, 11, 15–27. [Google Scholar] [CrossRef]
- Teza, G.; Marcato, G.; Castelli, E.; Galgaro, A. IRTROCK: A MATLAB Toolbox for Contactless Recognition of Surface and Shallow Weakness of a Rock Cliff by Infrared Thermography. Comput. Geosci. 2012, 45, 109–118. [Google Scholar] [CrossRef]
- Martino, S.; Mazzanti, P. Integrating Geomechanical Surveys and Remote Sensing for Sea Cliff Slope Stability Analysis: The Mt. Pucci Case Study (Italy). Nat. Hazards Earth Syst. Sci. 2014, 14, 831–848. [Google Scholar] [CrossRef]
- Grechi, G.; Fiorucci, M.; Marmoni, G.M.; Martino, S. 3D Thermal Monitoring of Jointed Rock Masses through Infrared Thermography and Photogrammetry. Remote Sens. 2021, 13, 957. [Google Scholar] [CrossRef]
- Guerin, A.; Jaboyedoff, M.; Collins, B.D.; Stock, G.M.; Derron, M.-H.; Abellán, A.; Matasci, B. Remote Thermal Detection of Exfoliation Sheet Deformation. Landslides 2021, 18, 865–879. [Google Scholar] [CrossRef]
- Loiotine, L.; Andriani, G.F.; Derron, M.-H.; Parise, M.; Jaboyedoff, M. Evaluation of InfraRed Thermography Supported by UAV and Field Surveys for Rock Mass Characterization in Complex Settings. Geosciences 2022, 12, 116. [Google Scholar] [CrossRef]
- Vivaldi, V.; Bordoni, M.; Mineo, S.; Crozi, M.; Pappalardo, G.; Meisina, C. Airborne Combined Photogrammetry—Infrared Thermography Applied to Landslide Remote Monitoring. Landslides 2023, 20, 297–313. [Google Scholar] [CrossRef]
- Massi, A.; Ortolani, M.; Vitulano, D.; Bruni, V.; Mazzanti, P. Enhancing the Thermal Images of the Upper Scarp of the Poggio Baldi Landslide (Italy) by Physical Modeling and Image Analysis. Remote Sens. 2023, 15, 907. [Google Scholar] [CrossRef]
- Yang, H.; Liu, B.; Karekal, S. Experimental Investigation on Infrared Radiation Features of Fracturing Process in Jointed Rock under Concentrated Load. Int. J. Rock Mech. Min. Sci. 2021, 139, 104619. [Google Scholar] [CrossRef]
- Schilirò, L.; Poueme Djueyep, G.; Esposito, C.; Scarascia Mugnozza, G. The Role of Initial Soil Conditions in Shallow Landslide Triggering: Insights from Physically Based Approaches. Geofluids 2019, 2019, 2453786. [Google Scholar] [CrossRef]
- Lourenço, S.D.N.; Sassa, K.; Fukuoka, H. Failure Process and Hydrologic Response of a Two Layer Physical Model: Implications for Rainfall-Induced Landslides. Geomorphology 2006, 73, 115–130. [Google Scholar] [CrossRef]
- Scaioni, M.; Longoni, L.; Melillo, V.; Papini, M. Remote Sensing for Landslide Investigations: An Overview of Recent Achievements and Perspectives. Remote Sens. 2014, 6, 9600–9652. [Google Scholar] [CrossRef]
- Montrasio, L.; Schilirò, L.; Terrone, A. Physical and Numerical Modelling of Shallow Landslides. Landslides 2016, 13, 873–883. [Google Scholar] [CrossRef]
- Schilirò, L.; Marmoni, G.M.; Fiorucci, M.; Pecci, M.; Mugnozza, G.S. Preliminary Insights from Hydrological Field Monitoring for the Evaluation of Landslide Triggering Conditions over Large Areas. Nat Hazards 2023, 118, 1401–1426. [Google Scholar] [CrossRef]
- Ma, J.; Niu, X.; Liu, X.; Wang, Y.; Wen, T.; Zhang, J. Thermal Infrared Imagery Integrated with Terrestrial Laser Scanning and Particle Tracking Velocimetry for Characterization of Landslide Model Failure. Sensors 2019, 20, 219. [Google Scholar] [CrossRef]
- Frodella, W.; Gigli, G.; Morelli, S.; Lombardi, L.; Casagli, N. Landslide Mapping and Characterization through Infrared Thermography (IRT): Suggestions for a Methodological Approach from Some Case Studies. Remote Sens. 2017, 9, 1281. [Google Scholar] [CrossRef]
- Mugnai, F.; Cosentino, A.; Mazzanti, P.; Tucci, G. Vibration Analyses of a Gantry Structure by Mobile Phone Digital Image Correlation and Interferometric Radar. Geomatics 2021, 2, 17–35. [Google Scholar] [CrossRef]
- Pan, B.; Xie, H.; Wang, Z.; Qian, K.; Wang, Z. Study on Subset Size Selection in Digital Image Correlation for Speckle Patterns. Opt. Express 2008, 16, 7037. [Google Scholar] [CrossRef] [PubMed]
- Stumpf, A. Landslide Recognition and Monitoring with Remotely Sensed Data from Passive Optical Sensors. Ph.D. Thesis, Université de Strasbourg, Strasbourg, France, 2013. [Google Scholar]
- Leprince, S.; Berthier, E.; Ayoub, F.; Delacourt, C.; Avouac, J.-P. Monitoring Earth Surface Dynamics with Optical Imagery. Eos Trans. AGU 2008, 89, 1–2. [Google Scholar] [CrossRef]
- Mazzanti, P. Toward Transportation Asset Management: What Is the Role of Geotechnical Monitoring? J. Civ. Struct. Health Monit. 2017, 7, 645–656. [Google Scholar] [CrossRef]
- Sara, U.; Akter, M.; Uddin, M.S. Image Quality Assessment through FSIM, SSIM, MSE and PSNR—A Comparative Study. JCC 2019, 7, 8–18. [Google Scholar] [CrossRef]
- Plyer, A.; Le Besnerais, G.; Champagnat, F. Massively Parallel Lucas Kanade Optical Flow for Real-Time Video Processing Applications. J. Real-Time Image Proc. 2016, 11, 713–730. [Google Scholar] [CrossRef]
- Kim, D.; Balasubramaniam, A.S.; Gratchev, I.; Kim, S.-R.; Chang, S.-H. Application of Image Quality Assessment for Rockfall Investigation. In Proceedings of the 16th Asian Regional Conference on Soil Mechanics and Geotechnical Engineering: Geotechnique for Sustainable Development and Emerging Market Regions, ARC 2019, Taipei, Taiwan, 14–18 October 2019. [Google Scholar]
- Stumpf, A.; Malet, J.-P.; Delacourt, C. Correlation of Satellite Image Time-Series for the Detection and Monitoring of Slow-Moving Landslides. Remote Sens. Environ. 2017, 189, 40–55. [Google Scholar] [CrossRef]
- Lacroix, P.; Araujo, G.; Hollingsworth, J.; Taipe, E. Self-Entrainment Motion of a Slow-Moving Landslide Inferred From Landsat-8 Time Series. J. Geophys. Res. Earth Surf. 2019, 124, 1201–1216. [Google Scholar] [CrossRef]
- Optical Flow Estimation: An Error Analysis of Gradient-Based Methods with Local Optimization. Available online: https://www.academia.edu/19375575/Optical_Flow_Estimation_An_Error_Analysis_of_Gradient-Based_Methods_with_Local_Optimization (accessed on 1 November 1987).
- Brigot, G.; Colin-Koeniguer, E.; Plyer, A.; Janez, F. Adaptation and Evaluation of an Optical Flow Method Applied to Coregistration of Forest Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2923–2939. [Google Scholar] [CrossRef]
- Debella-Gilo, M.; Kääb, A. Sub-Pixel Precision Image Matching for Measuring Surface Displacements on Mass Movements Using Normalized Cross-Correlation. Remote Sens. Environ. 2011, 115, 130–142. [Google Scholar] [CrossRef]
- Bickel, V.; Manconi, A.; Amann, F. Quantitative Assessment of Digital Image Correlation Methods to Detect and Monitor Surface Displacements of Large Slope Instabilities. Remote Sens. 2018, 10, 865. [Google Scholar] [CrossRef]
- Singleton, A.; Li, Z.; Hoey, T.; Muller, J.-P. Evaluating Sub-Pixel Offset Techniques as an Alternative to D-InSAR for Monitoring Episodic Landslide Movements in Vegetated Terrain. Remote Sens. Environ. 2014, 147, 133–144. [Google Scholar] [CrossRef]
- Li, W.C.; Lee, L.M.; Cai, H.; Li, H.J.; Dai, F.C.; Wang, M.L. Combined Roles of Saturated Permeability and Rainfall Characteristics on Surficial Failure of Homogeneous Soil Slope. Eng. Geol. 2013, 153, 105–113. [Google Scholar] [CrossRef]
- Yubonchit, S.; Chinkulkijniwat, A.; Horpibulsuk, S.; Jothityangkoon, C.; Arulrajah, A.; Suddeepong, A. Influence Factors Involving Rainfall-Induced Shallow Slope Failure: Numerical Study. Int. J. Geomech. 2017, 17, 04016158. [Google Scholar] [CrossRef]
- Naidu, S.; Sajinkumar, K.S.; Oommen, T.; Anuja, V.J.; Samuel, R.A.; Muraleedharan, C. Early Warning System for Shallow Landslides Using Rainfall Threshold and Slope Stability Analysis. Geosci. Front. 2018, 9, 1871–1882. [Google Scholar] [CrossRef]
- Chinkulkijniwat, A.; Tirametatiparat, T.; Supotayan, C.; Yubonchit, S.; Horpibulsuk, S.; Salee, R.; Voottipruex, P. Stability Characteristics of Shallow Landslide Triggered by Rainfall. J. Mt. Sci. 2019, 16, 2171–2183. [Google Scholar] [CrossRef]
- Askarinejad, A.; Akca, D.; Springman, S.M. Precursors of Instability in a Natural Slope Due to Rainfall: A Full-Scale Experiment. Landslides 2018, 15, 1745–1759. [Google Scholar] [CrossRef]
- Askarinejad, A.; Springman, S.M. A Novel Technique to Monitor Subsurface Movements of Landslides. Can. Geotech. J. 2018, 55, 620–630. [Google Scholar] [CrossRef]


| (a) | ||
|---|---|---|
| Monitoring Tool | Specifications | |
 FLIR T840 | IR Resolution: | 464 × 348 (161,472 pixels) |
| Accuracy: | ±2 °C (±3.6 °F) or ±2% of reading | |
| Thermal Sensitivity/NETD: | <30 mK at 30 °C (42° lens) | |
| Object Temperature Range: | −20 °C to 1500 °C (−4 °F to 2732 °F) | |
| Spectral Range: | 7.5–14.0 µm | |
| Lens: | 24°; f = 17 mm | |
| (b) | ||
| Monitoring Tool | Specifications | |
 Canon PowerShot SX730 HS | Sensor Type: | 1/2.3 CMOS |
| Sensor Resolution: | 20 Mpx | |
| Focal Length: | 4.3–172.0 mm (used 35 mm) | |
| Video Resolution: | (Full HD) 1920 × 1080, 29.97 fps | |
| Experiment | Execution Date | Video Duration | Frame * | Sub-Sampling (1/300) ** |
|---|---|---|---|---|
| 1 | 1 June 2022 | 29:59 | 36,000 | 120 |
| 2 | 19 July 2022 | 23:45 | 36,000 | 120 |
| 3 | 2 September 2022 | 23:44 | 36,000 | 120 |
| Experiment | Execution Date | Number IRT Images |
|---|---|---|
| 1 | 1 June 2022 | 150 |
| 2 | 19 July 2022 | 120 |
| 3 | 2 September 2022 | 76 |
| Experiment | Execution Date | Initial Water Content (w0) | Time to Failure (hh:mm:ss) |
|---|---|---|---|
| 1 | 1 June 2022 | 9.86% | 00:29:30 |
| 2 | 19 July 2022 | 14.65% | 00:11:30 |
| 3 | 2 September 2022 | 15.51% | 00:12:90 |
| Experiment | Date | Coeff. Correlation TS |
|---|---|---|
| 1 | 1 June 2022 | 0.71 |
| 2 | 19 July 2022 | 0.75 |
| 3 | 2 September 2022 | 0.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cosentino, A.; Marmoni, G.M.; Fiorucci, M.; Mazzanti, P.; Scarascia Mugnozza, G.; Esposito, C. Optical and Thermal Image Processing for Monitoring Rainfall Triggered Shallow Landslides: Insights from Analogue Laboratory Experiments. Remote Sens. 2023, 15, 5577. https://doi.org/10.3390/rs15235577
Cosentino A, Marmoni GM, Fiorucci M, Mazzanti P, Scarascia Mugnozza G, Esposito C. Optical and Thermal Image Processing for Monitoring Rainfall Triggered Shallow Landslides: Insights from Analogue Laboratory Experiments. Remote Sensing. 2023; 15(23):5577. https://doi.org/10.3390/rs15235577
Chicago/Turabian StyleCosentino, Antonio, Gian Marco Marmoni, Matteo Fiorucci, Paolo Mazzanti, Gabriele Scarascia Mugnozza, and Carlo Esposito. 2023. "Optical and Thermal Image Processing for Monitoring Rainfall Triggered Shallow Landslides: Insights from Analogue Laboratory Experiments" Remote Sensing 15, no. 23: 5577. https://doi.org/10.3390/rs15235577
APA StyleCosentino, A., Marmoni, G. M., Fiorucci, M., Mazzanti, P., Scarascia Mugnozza, G., & Esposito, C. (2023). Optical and Thermal Image Processing for Monitoring Rainfall Triggered Shallow Landslides: Insights from Analogue Laboratory Experiments. Remote Sensing, 15(23), 5577. https://doi.org/10.3390/rs15235577









