Characteristics of Inter-System Bias between BDS-2 and BDS-3 and Its Impact on BDS Orbit and Clock Solutions
Abstract
:1. Introduction
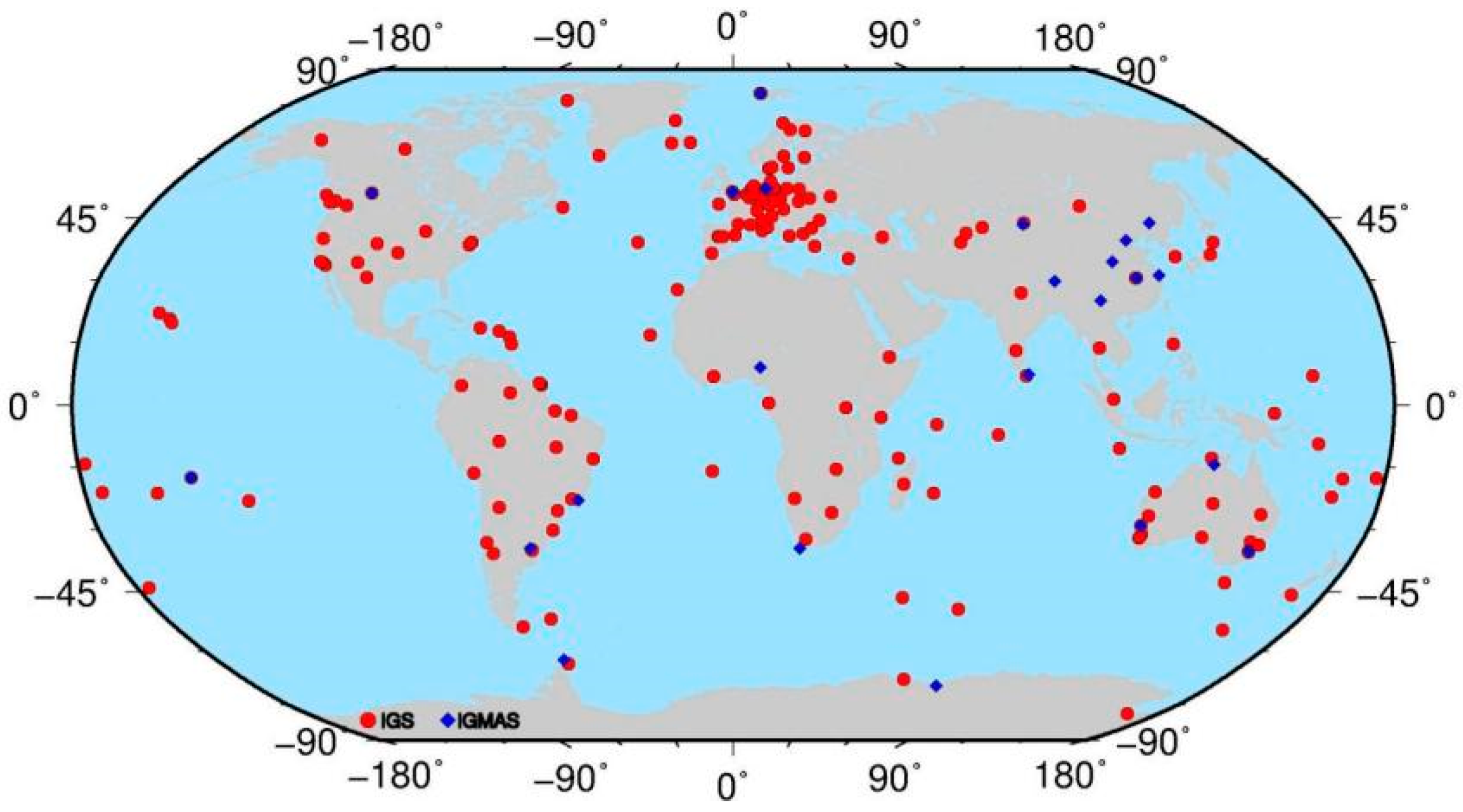
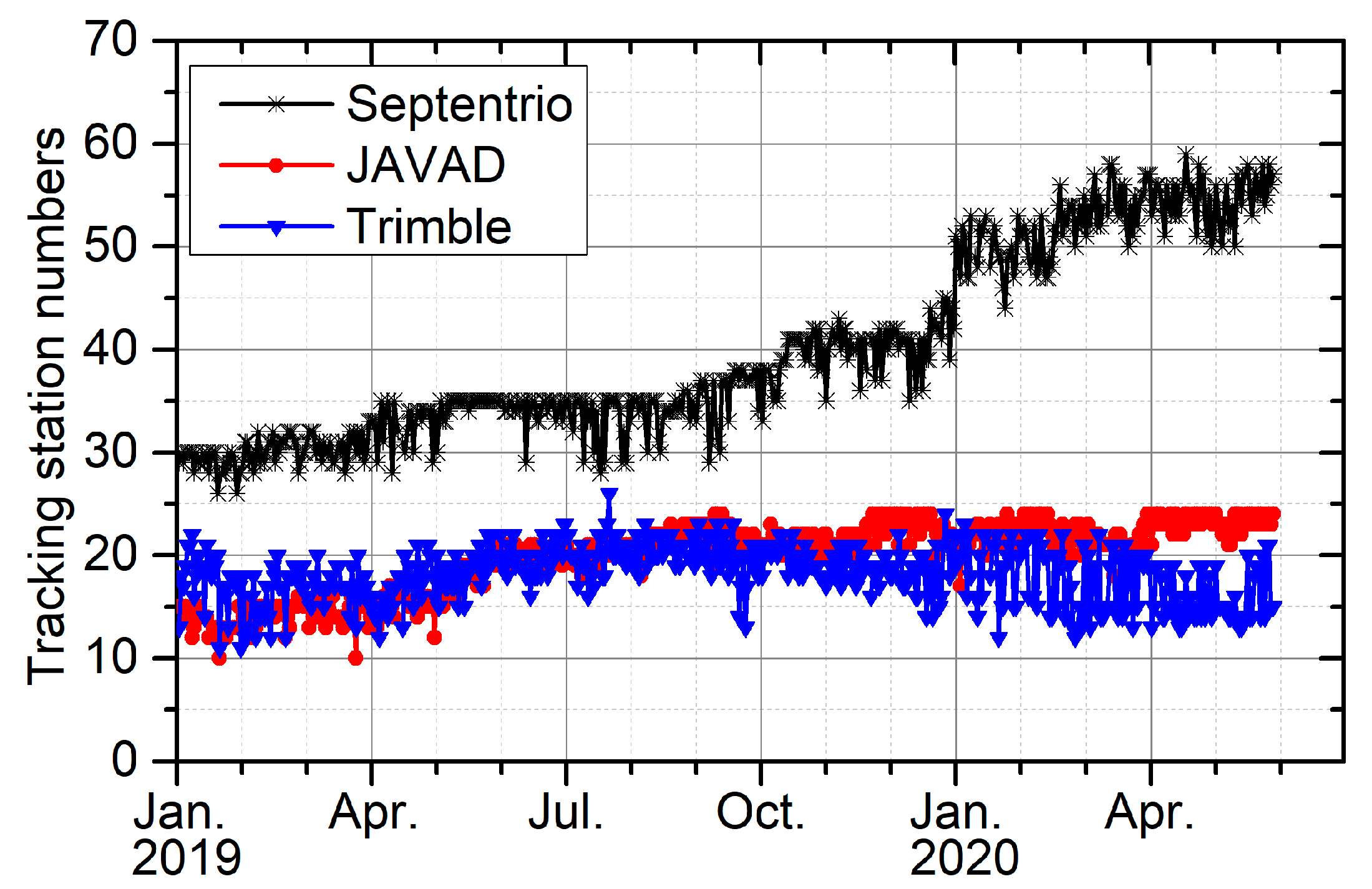
2. Data Collection
3. Method and Strategy
3.1. Method
3.2. Strategy
- BNA0 solution: The satellite-specific ISB is estimated for each BDS satellite with float ambiguity resolution.
- B1A1 solution: One ISB is estimated for both BDS-2 and BDS-3 with inter-constellation integer ambiguity resolution.
- B2A1 solution: Two ISB values are estimated for BDS-2 and BDS-3 independently with inter-constellation integer ambiguity resolution.
- B1A2 solution: One ISB is estimated for both BDS-2 and BDS-3 with intra-constellation integer ambiguity resolution.
- B2A2 solution: Two ISB values are estimated for both BDS-2 and BDS-3 with intra-constellation integer ambiguity resolution.
4. Experiments and Discussion
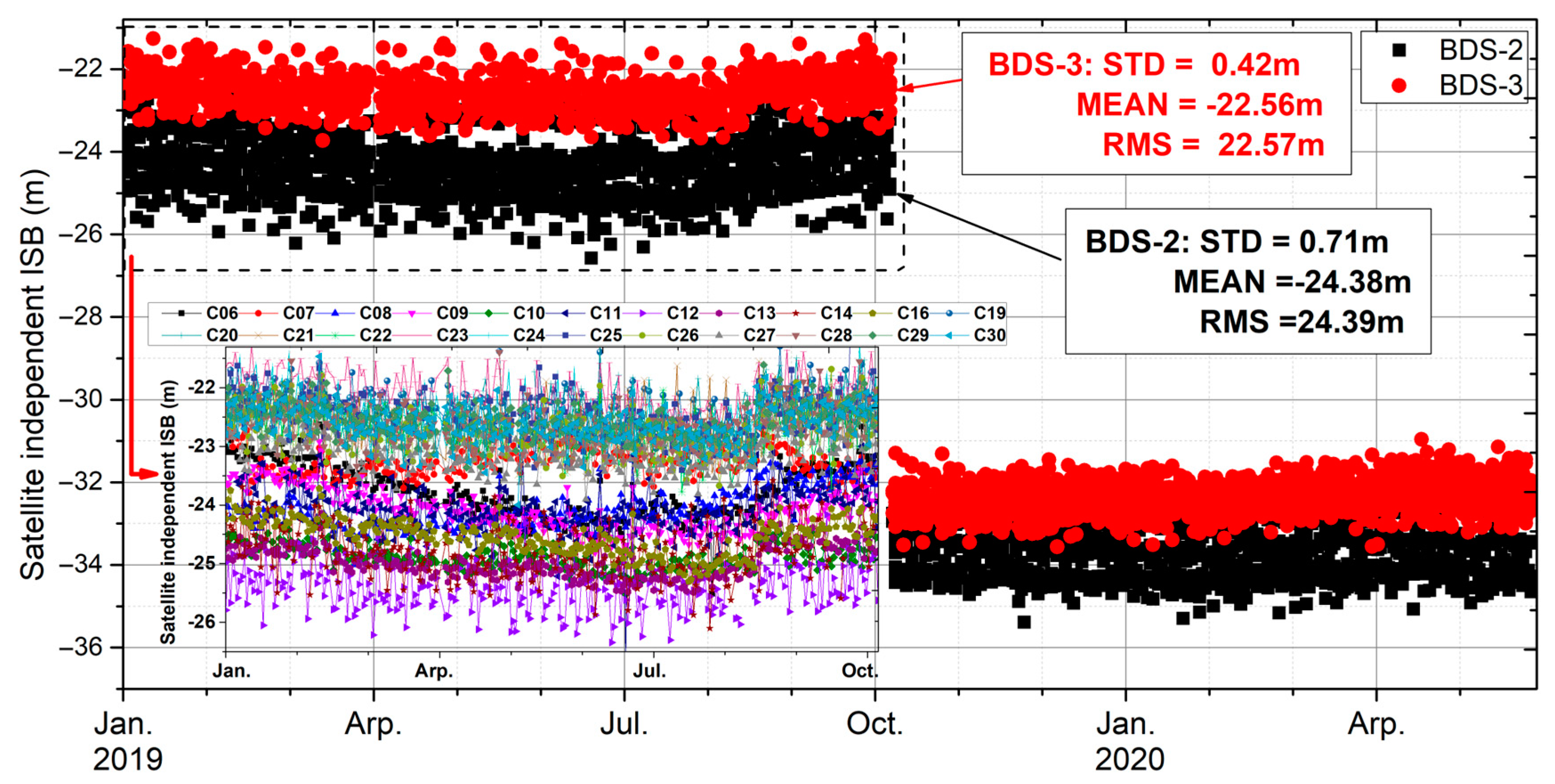
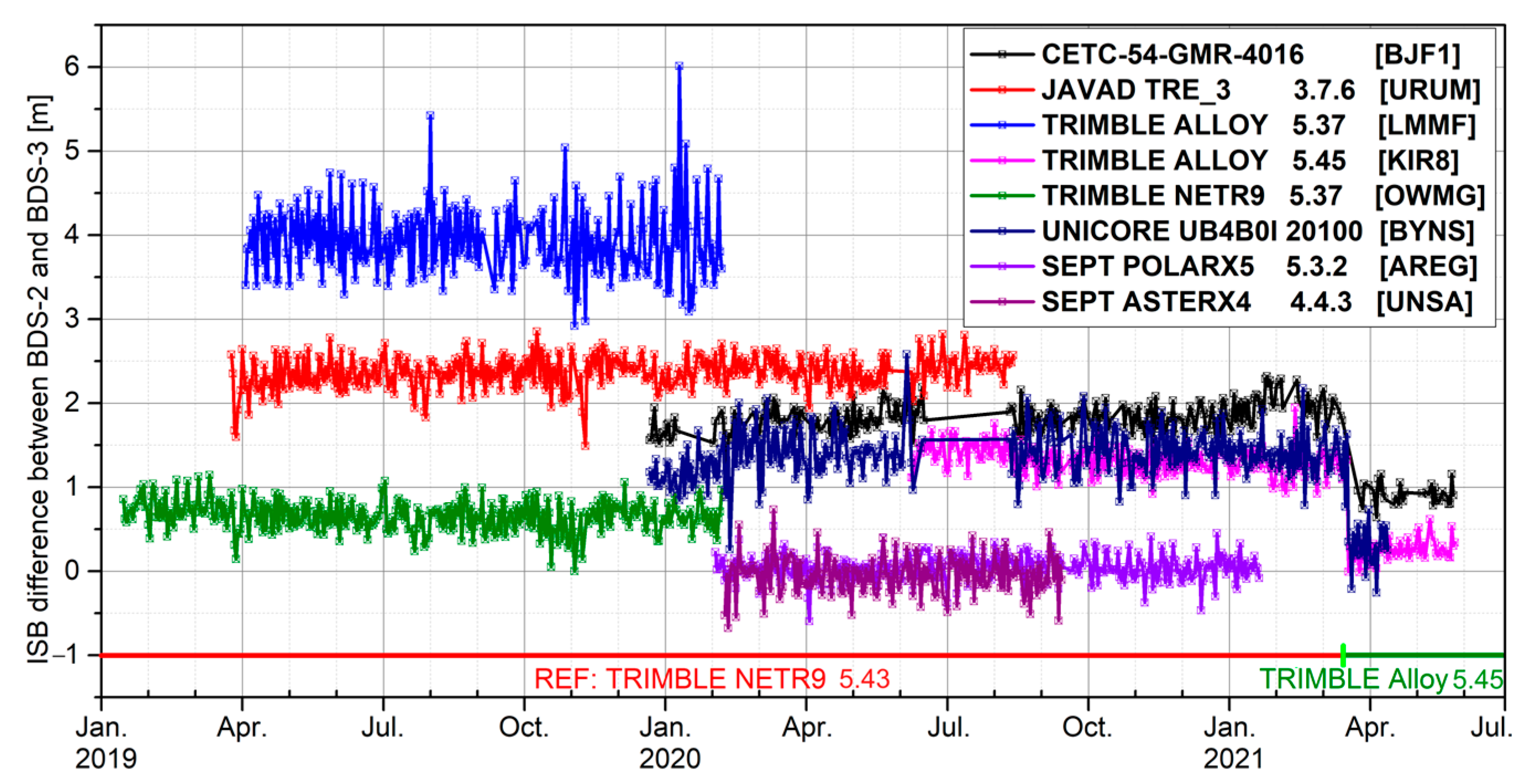
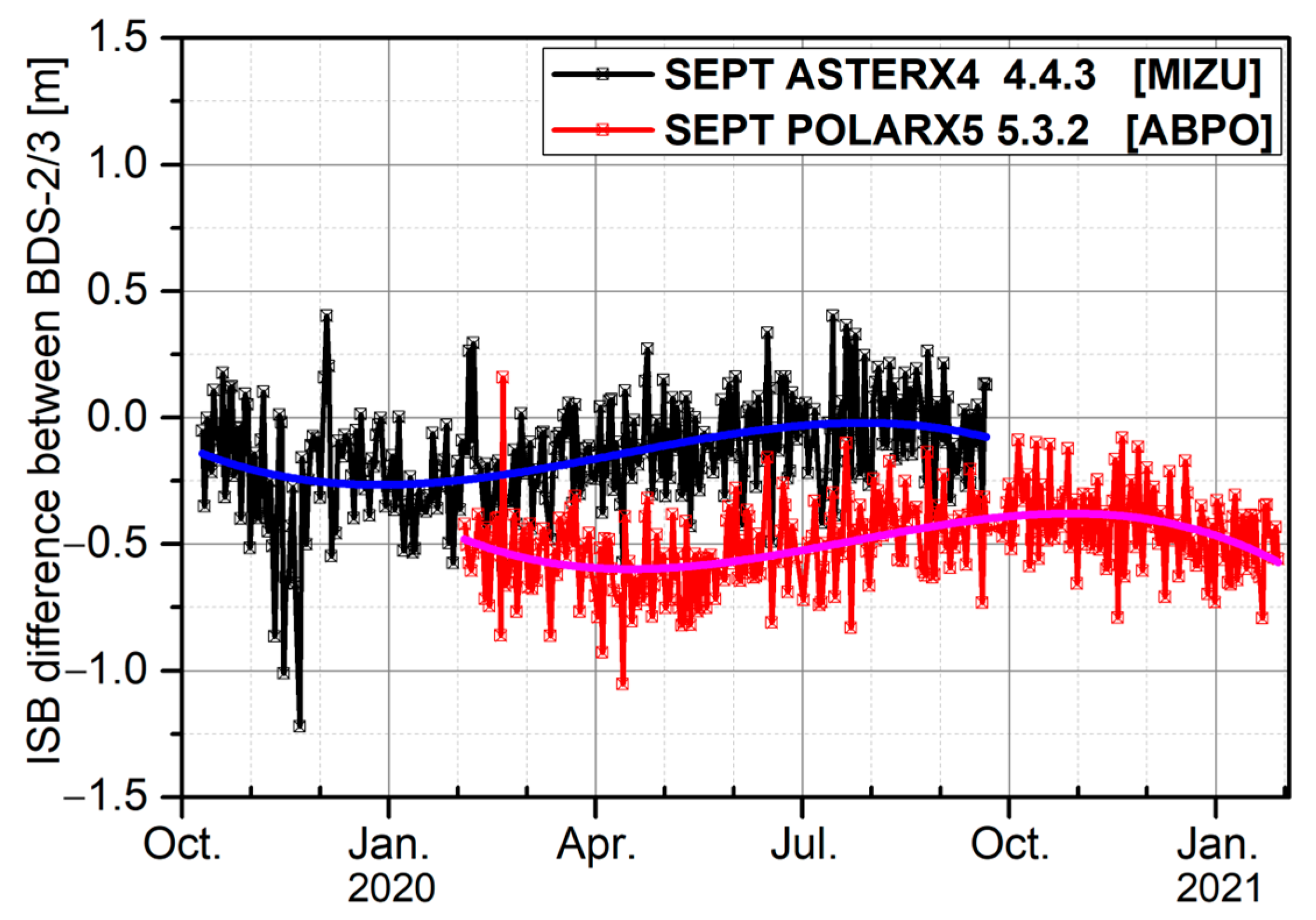
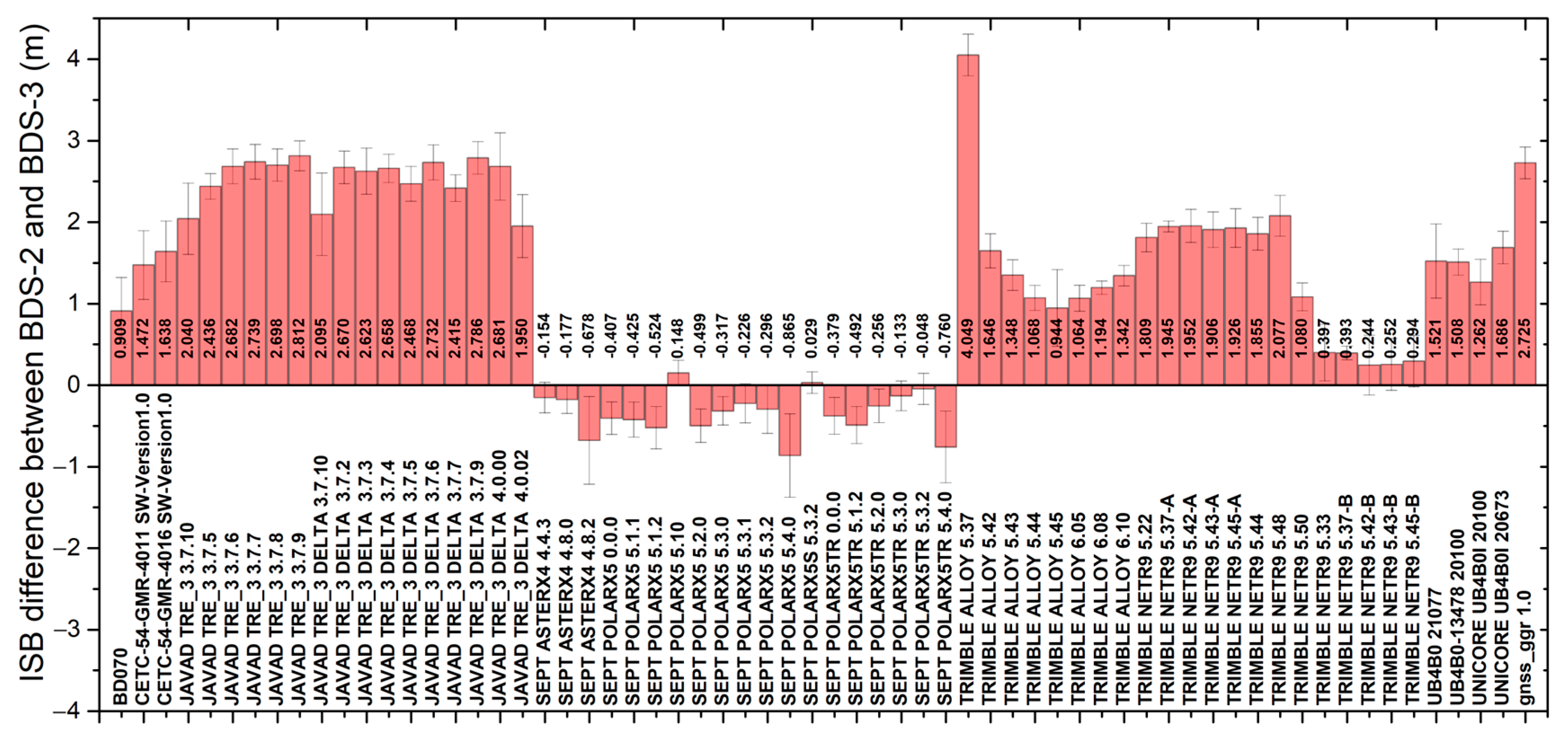
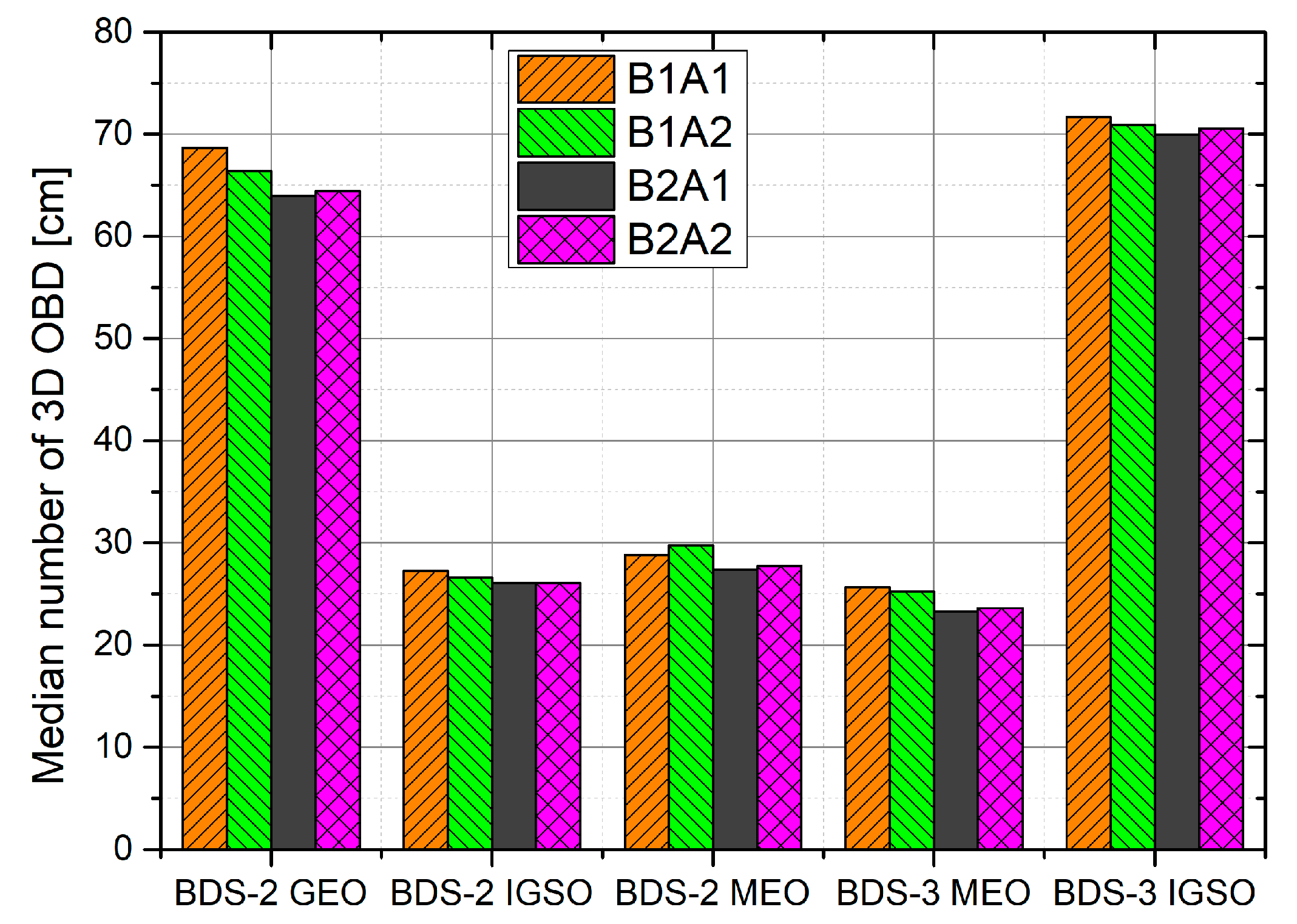
4.1. Characteristics of Inter-System-like Bias
4.2. Impacts of Inter-System-like Bias
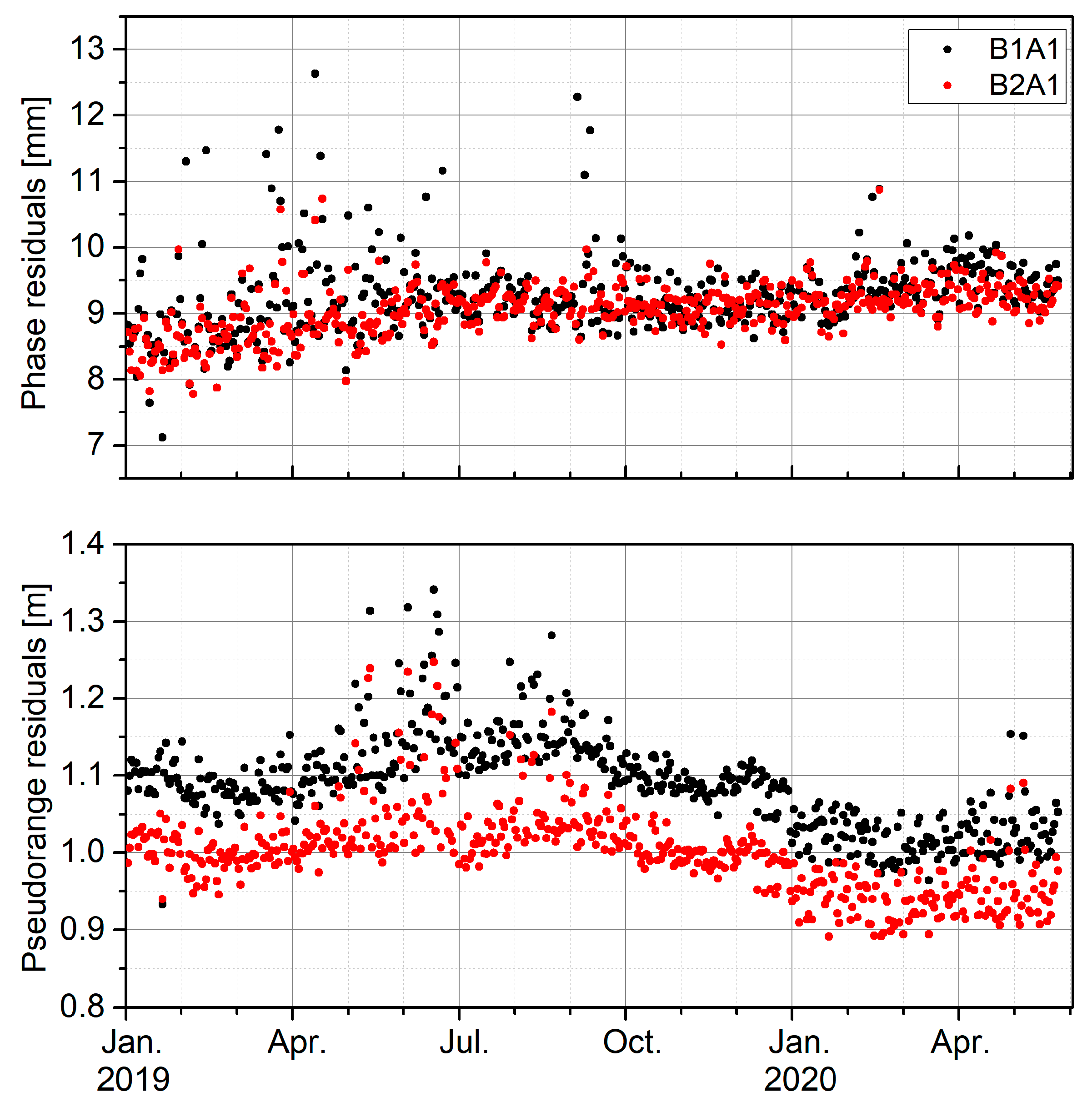
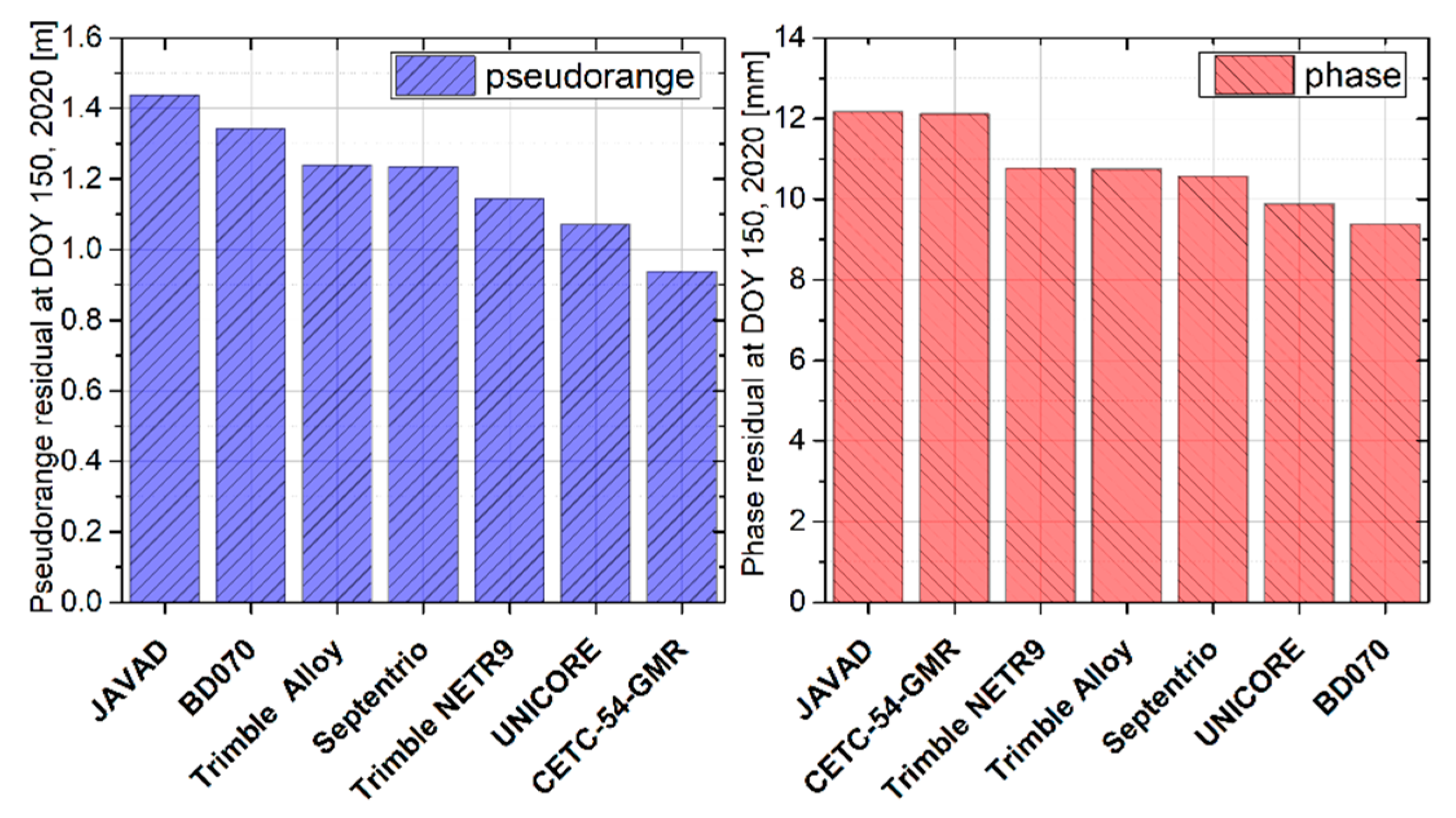
4.2.1. Code and Phase Residuals
4.2.2. Orbits
- Orbit boundary discontinuation
- SLR validation
4.2.3. Clocks
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Y.; Tang, J.; Montenbruck, O. Chinese Navigation Satellite Systems. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J., Montenbruck, O., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Yang, Y.; Ding, Q.; Gao, W.; Li, J.; Xu, Y.; Sun, B. Principle and performance of BDSBAS and PPP-B2b of BDS-3. Satell. Navig. 2022, 3, 5. [Google Scholar] [CrossRef]
- Wanninger, L.; Beer, S. BeiDou satellite-induced code pseudorange variations: Diagnosis and therapy. GPS Solut. 2015, 19, 639–648. [Google Scholar] [CrossRef]
- Zhou, R.; Hu, Z.; Zhao, Q.; Li, P.; Wang, W.; He, C.; Cai, C.; Pan, Z. Elevation-dependent pseudorange variation characteristics analysis for the new-generation BeiDou satellite navigation system. GPS Solut. 2018, 22, 60. [Google Scholar] [CrossRef]
- Gong, X.P.; Lou, Y.D.; Zheng, F.; Gu, S.F.; Shi, C.; Liu, J.N.; Jing, G.F. Evaluation and calibration of BeiDou receiver-related pseudorange biases. GPS Solut. 2018, 22, 98. [Google Scholar] [CrossRef]
- Zheng, F.; Gong, X.; Lou, Y.; Gu, S.; Jing, G.; Shi, C. Calibration of BeiDou Triple-Frequency Receiver-Related Pseudorange Biases and Their Application in BDS Precise Positioning and Ambiguity Resolution. Sensors 2019, 19, 3500. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Kubo, N.; Chen, J.; Wang, A. Calibration and analysis of BDS receiver-dependent code biases. J. Geod. 2021, 95, 43. [Google Scholar] [CrossRef]
- Li, X.X.; Xie, W.L.; Huang, J.X.; Ma, T.Z.; Zhang, X.H.; Yuan, Y.Q. Estimation and analysis of differential code biases for BDS3/BDS2 using iGMAS and MGEX observations. J. Geod. 2019, 93, 419–435. [Google Scholar] [CrossRef]
- Mi, X.; Sheng, C.; El-Mowafy, A.; Zhang, B. Characteristics of receiver-related biases between BDS-3 and BDS-2 for five frequencies including inter-system biases, differential code biases, and differential phase biases. GPS Solut. 2021, 25, 113. [Google Scholar] [CrossRef]
- Song, Z.; Chen, J.; Wang, B.; Yu, C. Analysis and Modeling of the Inter-System Bias Between BDS-2 and BDS-3. In China Satellite Navigation Conference (CSNC) 2020 Proceedings: Volume II, Singapore, 2020; Sun, J., Yang, C., Xie, J., Eds.; Springer Nature: Singapore, 2020; pp. 279–289. [Google Scholar]
- Pan, L.; Zhang, Z.; Yu, W.; Dai, W. Intersystem Bias in GPS, GLONASS, Galileo, BDS-3, and BDS-2 Integrated SPP: Characteristics and Performance Enhancement as a Priori Constraints. Remote Sens. 2021, 13, 4650. [Google Scholar] [CrossRef]
- Zhao, W.; Chen, H.; Gao, Y.; Jiang, W.; Liu, X. Evaluation of Inter-System Bias between BDS-2 and BDS-3 Satellites and Its Impact on Precise Point Positioning. Remote Sens. 2020, 12, 2185. [Google Scholar] [CrossRef]
- Mi, X.; Zhang, B.; Yuan, Y.; Luo, X. Characteristics of GPS, BDS2, BDS3 and Galileo inter-system biases and their influence on RTK positioning. Meas. Sci. Technol. 2019, 31, 015009. [Google Scholar] [CrossRef]
- Jiao, G.; Song, S.; Chen, Q.; Huang, C.; Su, K.; Wang, Z.; Cheng, N. Modeling and Analysis of BDS-2 and BDS-3 Combined Precise Time and Frequency Transfer Considering Stochastic Models of Inter-System Bias. Remote Sens. 2021, 13, 793. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, C.; Xiao, G.; Zhang, X.; Feng, X. Estimating and Analyzing Long-Term Multi-GNSS Inter-System Bias Based on Uncombined PPP. Sensors 2020, 20, 1499. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Li, Z.; Wang, N.; Tang, C.; Ma, H.; Zhang, Y.; Wang, Z.; Wu, J. Considering inter-receiver pseudorange biases for BDS-2 precise orbit determination. Measurement 2021, 177, 109251. [Google Scholar] [CrossRef]
- Steigenberger, P.; Montenbruck, O. Multi-GNSS Working Group. In International GNSS Service Technical Report 2019 (IGS Annual Report); IGS Central Bureau and University of Bern, Bern Open Publishing: Bern, Switzerland, 2019. [Google Scholar]
- Mi, X.L.; Zhang, B.C.; Odolinski, R.; Yuan, Y.B. On the temperature sensitivity of multi-GNSS intra- and inter-system biases and the impact on RTK positioning. GPS Solut. 2020, 24, 112. [Google Scholar] [CrossRef]
- Hatch, R. The synergism of GPS code and carrier measurements. In International Geodetic Symposium on Satellite Doppler Positioning; Physical Sciences Laboratory of New Mexico State University: Las Cruces, NM, USA, 1982; Volume 2, pp. 1213–1231. [Google Scholar]
- Melbourne, W.G. The case for ranging in GPS-based geodetic systems. In Proceedings of the First International Symposium on Precise Positioning with the Global Positioning System, Rockville, MD, USA, 15–19 April 1985; pp. 373–386. [Google Scholar]
- Wübbena, G. Software developments for geodetic positioning with GPS using TI-4100 code and carrier measurements. In Proceedings of the First International Symposium on Precise Positioning with the Global Positioning System, Rockvile, MD, USA, 15–19 April 1985; pp. 403–412. [Google Scholar]
- Peng, Y.; Dai, X.; Lou, Y.; Gong, X.; Zheng, F. BDS-2 and BDS-3 combined precise orbit determination with hybrid ambiguity resolution. Measurement 2022, 188, 110593. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Dick, G.; Zhang, F.P.; Rothacher, M. A new data processing strategy for huge GNSS global networks. J. Geod. 2006, 80, 199–203. [Google Scholar] [CrossRef]
- Wang, C.; Guo, J.; Zhao, Q.L.; Liu, J.N. Yaw attitude modeling for BeiDou I06 and BeiDou-3 satellites. GPS Solut. 2018, 22, 117. [Google Scholar] [CrossRef]
- Lin, X.; Bin, B.; Liu, Y.; Xiong, S.; Bai, T. Satellite geometry and attitude mode of MEO satellites of BDS-3 developed by SECM. In Proceedings of the ION GNSS 2018, Institute of Navigation, Miami, FL, USA, 24–28 September 2018; pp. 1268–1289. [Google Scholar]
- Petit, G.; Luzum, B. IERS Conventions (2010) (IERS Technical Note; 36) Frankfurt am Main: Verlag des Bundesamts für Kartographie und Geodäsie; IERS: Frankfurt, Germany, 2010. [Google Scholar]
- Wang, C.; Guo, J.; Zhao, Q.L.; Liu, J.N. Empirically derived model of solar radiation pressure for BeiDou GEO satellites. J. Geod. 2019, 93, 791–807. [Google Scholar] [CrossRef]
- Rodriguez-Solano, C.J.; Hugentobler, U.; Steigenberger, P. Impact of Albedo Radiation on GPS Satellites. Iag. Symp. 2012, 136, 113–119. [Google Scholar]
- Gong, X.; Zheng, F.; Gu, S.; Zhang, Z.; Lou, Y. The long-term characteristics of GNSS signal distortion biases and their empirical corrections. GPS Solut. 2022, 26, 52. [Google Scholar] [CrossRef]
- Griffiths, J.; Ray, J.R. On the precision and accuracy of IGS orbits. J. Geod. 2009, 83, 277–287. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, X. General design of the third generation BeiDou Navigation Satellite System. J. Nanjing Univ. Aeronaut. Astronaut. 2020, 52, 835–845. (In Chinese) [Google Scholar]
- Pearlman, M.R.; Degnan, J.J.; Bosworth, J.M. The International Laser Ranging Service. Adv. Space Res. 2002, 30, 135–143. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hugentobler, U.; Dach, R.; Steigenberger, P.; Hauschild, A. Apparent clock variations of the Block IIF-1 (SVN62) GPS satellite. GPS Solut. 2012, 16, 303–313. [Google Scholar] [CrossRef]




| Receiver | Firmware | Receiver | Firmware |
|---|---|---|---|
| BD070 | 1.0 | SEPT POLARX5TR | 0.0.0, 5.1.2, 5.2.0, |
| CETC-54-GMR-4011 | SW-version1.0 | 5.3.0, 5.3.2, 5.4.0 | |
| CETC-54-GMR-4016 | SW-version1.0 | TRIMBLE ALLOY | 5.37, 5.42, 5.43, |
| JAVAD TRE_3 | 3.7.5, 3.7.6, 3.7.7 | 5.44, 5.45, 6.05 | |
| 3.7.8, 3.7.9, 3.7.10 | 6.08, 6.10 | ||
| JAVAD TRE_3 DELTA | 3.7.2, 3.7.3, 3.7.4, | TRIMBLE NETR9 | 5.22, 5.37, 5.42, |
| 3.7.5, 3.7.6, 3.7.7, | 5.43, 5.44, 5.45, | ||
| 3.7.9, 3.7.10, | 5.48, 5.50, 5.33 | ||
| 4.0.02, 4.0.00 | LEICA GR30 | 4.31, 4.35, 4.50 | |
| SEPT ASTERX4 | 4.4.3, 4.8.0, 4.8.2 | LEICA GR50 | 4.31 4.50 |
| SEPT POLARX5 | 0.0.0, 5.1.1, 5.1.2, | gnss_ggr | 1.0 |
| 5.10, 5.2.0, 5.3.0, | UB4B0 | 21,077 | |
| 5.3.1, 5.3.2, 5.4.0 | UB4B0-13478 | 20,100 | |
| SEPT POLARX5S | 5.3.2 | UNICORE UB4B0I | 20,100, 20,673 |
| Group | PRN |
|---|---|
| 1 | C19 C20 C21 C22 C28 |
| 2 | C23 C24 C25 C26 C27 C29 C30 |
| 3 | C32 C33 C34 |
| 4 | C35 C36 C37 |
| 5 | C38 C39 C40 |
| 6 | C41 C42 |
| 7 | C43 C44 C45 C46 |
| Items | Description |
|---|---|
| Observation | Undifferentiated IF code and phase combination of B1I and B3I |
| POD arc length | 24 h |
| Sampling rate | 300 s |
| Elevation angle cutoff | 10 deg |
| Weighting | 2 cm for phase raw observations, 2 m for code raw observations for IGSOs and MEOs. Downweighing for GEOs by a factor of 4. Elevation-dependent weighting for the observations under 30° according to 1/2 sin(E) |
| Satellite antenna PCO/PCV | igs14_wwww.atx |
| Receiver antenna PCO/PCV | igs14_wwww.atx, and the GPS L1 and L2 corrections used for BDS B1I and B3I |
| Ambiguity resolution | Float resolution for BNA0 The intra-constellation double-difference ambiguities are fixed for B1A2 and B2A2 solution based on [23] The inter-constellation double-difference ambiguities are fixed for B1A1 and B2A1 solution based on [23] |
| Satellite yaw attitude | GEO satellites: orbit nominal mode BDS-2 C07, C08, C09, C10, C12, C13: yaw-steering and orbit normal mode The rest BDS-2 as well as BDS-3 MEO/IGSO CAST 1 satellites [24]; BDS-3 MEO SECM 2 satellites [25] |
| Geopotential | EGM2008 with 12 degrees and orders |
| Tidal variations in geopotential | Solid Earth tides: Applied [26] |
| Ocean tides: Not applied | |
| Solid Earth pole tide: Applied [26] | |
| Ocean pole tide: Not applied | |
| Third-body | Sun, Moon, Mercury, Venus, Mars, Jupiter, Saturn, Uranus, Neptune, Pluto |
| SRP model | 5-parameter ECOM1 with a priori SRP model for BDS-2 GEO [27] and BDS-3 MEO [27] |
| Earth albedo | Applied [28] |
| Antenna thrust | Transmit power: BDS-2 IGSO: 185W, BDS-2 MEO: 130W BDS-3 MEO CAST: 310W, BDS-3 MEO SECM: 280W |
| Relativistic effects | Schwarzschild and Lense-Thirring [26] |
| ISB | 1, 2 or satellite-dependent daily constant per stations for BDS-2 and BDS-3 |
| Solution | Solution | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| B1A1 | B1A2 | B2A1 | B2A2 | B1A1 | B1A2 | B2A1 | B2A2 | ||
| C01 | 591 | 588 | 610 | 620 | C25 | 245 | 240 | 223 | 231 |
| C02 | 716 | 695 | 573 | 579 | C26 | 259 | 261 | 247 | 248 |
| C03 | 647 | 689 | 668 | 672 | C27 | 259 | 263 | 249 | 257 |
| C04 | 687 | 630 | 715 | 713 | C28 | 274 | 270 | 270 | 288 |
| C05 | 792 | 718 | 632 | 638 | C29 | 275 | 278 | 269 | 277 |
| C06 | 267 | 260 | 263 | 253 | C30 | 232 | 240 | 219 | 225 |
| C07 | 272 | 273 | 271 | 274 | C32 | 214 | 215 | 217 | 216 |
| C08 | 264 | 252 | 248 | 249 | C33 | 248 | 245 | 230 | 236 |
| C09 | 288 | 265 | 260 | 260 | C34 | 262 | 257 | 244 | 246 |
| C10 | 273 | 271 | 266 | 263 | C35 | 257 | 251 | 243 | 248 |
| C11 | 335 | 350 | 313 | 321 | C36 | 250 | 242 | 232 | 232 |
| C12 | 262 | 279 | 253 | 253 | C37 | 259 | 237 | 235 | 243 |
| C13 | 245 | 241 | 227 | 229 | C38 | 805 | 746 | 740 | 727 |
| C14 | 315 | 316 | 294 | 302 | C39 | 606 | 593 | 585 | 602 |
| C16 | 302 | 301 | 291 | 294 | C40 | 740 | 788 | 775 | 789 |
| C19 | 178 | 179 | 170 | 174 | C41 | 302 | 295 | 252 | 255 |
| C20 | 183 | 181 | 172 | 171 | C42 | 269 | 263 | 241 | 231 |
| C21 | 194 | 198 | 184 | 188 | C43 | 398 | 382 | 319 | 320 |
| C22 | 191 | 195 | 175 | 180 | C44 | 340 | 330 | 273 | 267 |
| C23 | 223 | 220 | 199 | 200 | C45 | 310 | 305 | 262 | 265 |
| C24 | 237 | 227 | 219 | 227 | C46 | 296 | 281 | 244 | 244 |
| B1A1 | B1A2 | B2A1 | B2A2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PRN | MEAN | STD | RMS | MEAN | STD | RMS | MEAN | STD | RMS | MEAN | STD | RMS |
| C01 | 12.2 | 18.9 | 22.5 | 12.2 | 18.9 | 22.5 | −1.0 | 20.1 | 20.1 | −1.0 | 20.1 | 20.1 |
| C08 | 0.4 | 6 | 6.0 | 0.4 | 6.1 | 6.1 | 0.5 | 6.0 | 6.1 | 0.5 | 6.1 | 6.1 |
| C10 | 1.0 | 4.8 | 4.9 | 1.0 | 4.9 | 5.0 | 1.3 | 4.7 | 4.9 | 1.2 | 4.7 | 4.9 |
| C11 | 0.9 | 3.2 | 3.3 | 0.5 | 3.1 | 3.1 | 0.6 | 3.1 | 3.2 | 0.5 | 3.1 | 3.1 |
| C13 | 1.4 | 5.9 | 6.1 | 1.7 | 5.7 | 6.0 | 2.0 | 5.7 | 6.0 | 1.9 | 7.1 | 7.3 |
| C20 | 3.2 | 3.0 | 4.4 | 3.3 | 2.9 | 4.4 | 3.3 | 2.9 | 4.4 | 3.3 | 2.8 | 4.4 |
| C21 | 4.8 | 2.8 | 5.6 | 5.0 | 2.9 | 5.8 | 5.0 | 2.8 | 5.7 | 5.0 | 2.8 | 5.8 |
| C29 | 0.6 | 3.5 | 3.6 | 0.8 | 3.6 | 3.7 | 0.7 | 3.7 | 3.8 | 0.8 | 3.7 | 3.8 |
| C30 | 0.0 | 3.6 | 3.6 | 0.2 | 3.5 | 3.5 | 0.1 | 3.5 | 3.5 | 0.2 | 3.4 | 3.4 |
| Solution | Solution | Solution | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B1A1 | B1A2 | B2A1 | B2A2 | B1A1 | B1A2 | B2A1 | B2A2 | B1A1 | B1A2 | B2A1 | B2A2 | |||
| C01 | 0.128 | 0.128 | 0.128 | 0.127 | C16 | 0.066 | 0.066 | 0.061 | 0.061 | C33 | 0.039 | 0.036 | 0.033 | 0.034 |
| C02 | 0.132 | 0.132 | 0.132 | 0.132 | C19 | 0.036 | 0.036 | 0.034 | 0.036 | C34 | 0.033 | 0.031 | 0.030 | 0.031 |
| C03 | 0.127 | 0.127 | 0.128 | 0.127 | C20 | 0.040 | 0.039 | 0.038 | 0.038 | C35 | 0.049 | 0.047 | 0.041 | 0.042 |
| C04 | 0.155 | 0.154 | 0.154 | 0.154 | C21 | 0.037 | 0.037 | 0.037 | 0.038 | C36 | 0.046 | 0.044 | 0.035 | 0.036 |
| C05 | 0.088 | 0.088 | 0.085 | 0.084 | C22 | 0.043 | 0.040 | 0.040 | 0.042 | C37 | 0.047 | 0.045 | 0.040 | 0.041 |
| C06 | 0.139 | 0.138 | 0.136 | 0.136 | C23 | 0.038 | 0.036 | 0.032 | 0.033 | C38 | 0.098 | 0.096 | 0.085 | 0.086 |
| C07 | 0.191 | 0.191 | 0.191 | 0.192 | C24 | 0.039 | 0.037 | 0.035 | 0.036 | C39 | 0.086 | 0.080 | 0.074 | 0.076 |
| C08 | 0.120 | 0.119 | 0.119 | 0.119 | C25 | 0.036 | 0.034 | 0.032 | 0.033 | C40 | 0.064 | 0.061 | 0.049 | 0.047 |
| C09 | 0.114 | 0.114 | 0.113 | 0.113 | C26 | 0.035 | 0.032 | 0.031 | 0.031 | C41 | 0.067 | 0.061 | 0.034 | 0.036 |
| C10 | 0.182 | 0.181 | 0.180 | 0.180 | C27 | 0.031 | 0.028 | 0.028 | 0.029 | C42 | 0.054 | 0.051 | 0.033 | 0.035 |
| C11 | 0.100 | 0.100 | 0.099 | 0.099 | C28 | 0.027 | 0.025 | 0.026 | 0.027 | C43 | 0.060 | 0.055 | 0.041 | 0.044 |
| C12 | 0.075 | 0.075 | 0.073 | 0.073 | C29 | 0.033 | 0.030 | 0.030 | 0.031 | C44 | 0.087 | 0.082 | 0.047 | 0.047 |
| C13 | 0.160 | 0.160 | 0.161 | 0.161 | C30 | 0.030 | 0.028 | 0.028 | 0.029 | C45 | 0.139 | 0.132 | 0.081 | 0.083 |
| C14 | 0.058 | 0.058 | 0.056 | 0.056 | C32 | 0.033 | 0.030 | 0.028 | 0.029 | C46 | 0.110 | 0.106 | 0.085 | 0.087 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Cai, Z. Characteristics of Inter-System Bias between BDS-2 and BDS-3 and Its Impact on BDS Orbit and Clock Solutions. Remote Sens. 2023, 15, 5659. https://doi.org/10.3390/rs15245659
Xu X, Cai Z. Characteristics of Inter-System Bias between BDS-2 and BDS-3 and Its Impact on BDS Orbit and Clock Solutions. Remote Sensing. 2023; 15(24):5659. https://doi.org/10.3390/rs15245659
Chicago/Turabian StyleXu, Xiaolong, and Zhan Cai. 2023. "Characteristics of Inter-System Bias between BDS-2 and BDS-3 and Its Impact on BDS Orbit and Clock Solutions" Remote Sensing 15, no. 24: 5659. https://doi.org/10.3390/rs15245659
APA StyleXu, X., & Cai, Z. (2023). Characteristics of Inter-System Bias between BDS-2 and BDS-3 and Its Impact on BDS Orbit and Clock Solutions. Remote Sensing, 15(24), 5659. https://doi.org/10.3390/rs15245659







