Pasture Biomass Estimation Using Ultra-High-Resolution RGB UAVs Images and Deep Learning
Abstract
:1. Introduction
2. Materials
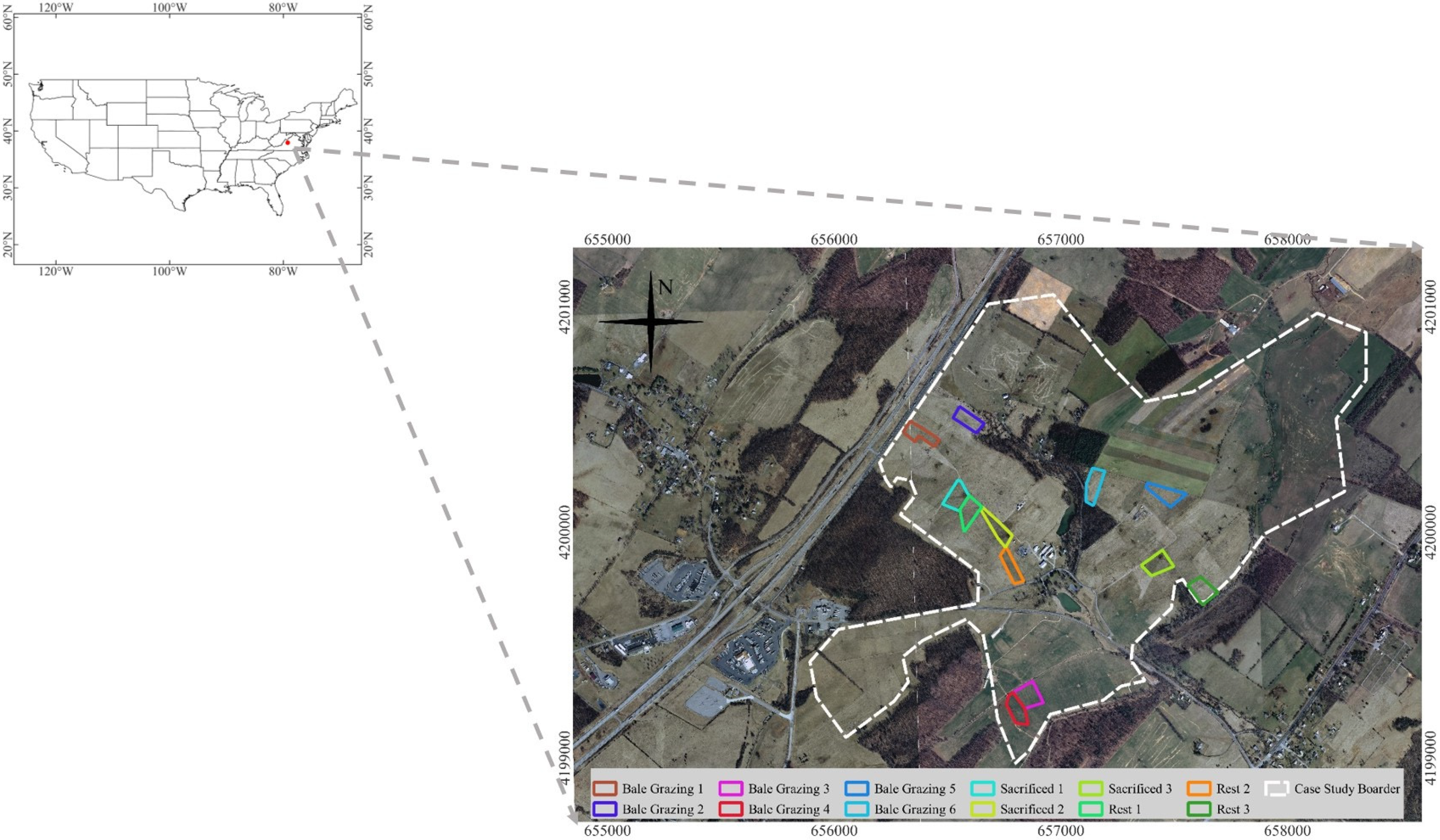
2.1. Study Area
2.2. Ground Samples
2.3. UAVs Flights
3. Methodology
3.1. Processing Station
3.1.1. Image Preprocessing
3.1.2. Image Gridding
3.1.3. Variable Extraction
3.2. Model Training
- Artificial Neural Network (ANN)
- Support Vector Regression (SVR)
- Random Forest (RF)
3.3. Evaluation Criteria
3.3.1. Common Numerical Criteria
3.3.2. Statistics on the Fitted Line between Predicted and Observed Values
4. Results and Discussion
4.1. Variable Analysis
4.1.1. Structural Variables Analysis
4.1.2. Spectral Variable Analysis
4.2. Models Performance
4.3. Comparison with Previous Studies
4.4. Biomass Maps
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Herrero, M.; Havlík, P.; Valin, H.; Notenbaert, A.; Rufino, M.C.; Thornton, P.K.; Blümmel, M.; Weiss, F.; Grace, D.; Obersteiner, M. Biomass use, production, feed efficiencies, and greenhouse gas emissions from global livestock systems. Proc. Natl. Acad. Sci. USA 2013, 110, 20888–20893. [Google Scholar] [CrossRef]
- Lobell, D.B.; Burke, M.B. Why are agricultural impacts of climate change so uncertain? The importance of temperature relative to precipitation. Environ. Res. Lett. 2008, 3, 034007. [Google Scholar] [CrossRef]
- Herrero, M.; Thornton, P.K.; Notenbaert, A.M.; Wood, S.; Msangi, S.; Freeman, H.; Bossio, D.; Dixon, J.; Peters, M.; van de Steeg, J. Smart investments in sustainable food production: Revisiting mixed crop-livestock systems. Science 2010, 327, 822–825. [Google Scholar] [CrossRef]
- Togeiro de Alckmin, G.; Kooistra, L.; Rawnsley, R.; Lucieer, A. Comparing methods to estimate perennial ryegrass biomass: Canopy height and spectral vegetation indices. Precis. Agric. 2021, 22, 205–225. [Google Scholar] [CrossRef]
- Dusseux, P.; Guyet, T.; Pattier, P.; Barbier, V.; Nicolas, H. Monitoring of grassland productivity using Sentinel-2 remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2022, 111, 102843. [Google Scholar] [CrossRef]
- Peng, J.; Zeiner, N.; Parsons, D.; Féret, J.-B.; Söderström, M.; Morel, J. Forage Biomass Estimation Using Sentinel-2 Imagery at High Latitudes. Remote Sens. 2023, 15, 2350. [Google Scholar] [CrossRef]
- Vahidi, M.; Shafian, S.; Thomas, S.; Maguire, R. Estimation of Bale Grazing and Sacrificed Pasture Biomass through the Integration of Sentinel Satellite Images and Machine Learning Techniques. Remote Sens. 2023, 15, 5014. [Google Scholar] [CrossRef]
- Matzrafi, M.; Herrmann, I.; Nansen, C.; Kliper, T.; Zait, Y.; Ignat, T.; Siso, D.; Rubin, B.; Karnieli, A.; Eizenberg, H. Hyperspectral technologies for assessing seed germination and trifloxysulfuron-methyl response in Amaranthus palmeri (Palmer amaranth). Front. Plant Sci. 2017, 8, 474. [Google Scholar] [CrossRef] [PubMed]
- Lourenço, P.; Godinho, S.; Sousa, A.; Gonçalves, A.C. Estimating tree aboveground biomass using multispectral satellite-based data in Mediterranean agroforestry system using random forest algorithm. Remote Sens. Appl. Soc. Environ. 2021, 23, 100560. [Google Scholar] [CrossRef]
- Hojas Gascon, L.; Ceccherini, G.; Garcia Haro, F.J.; Avitabile, V.; Eva, H. The potential of high resolution (5 m) RapidEye optical data to estimate above ground biomass at the national level over Tanzania. Forests 2019, 10, 107. [Google Scholar] [CrossRef]
- Sinde-González, I.; Gil-Docampo, M.; Arza-García, M.; Grefa-Sánchez, J.; Yánez-Simba, D.; Pérez-Guerrero, P.; Abril-Porras, V. Biomass estimation of pasture plots with multitemporal UAV-based photogrammetric surveys. Int. J. Appl. Earth Obs. Geoinf. 2021, 101, 102355. [Google Scholar] [CrossRef]
- Navarro, A.; Young, M.; Allan, B.; Carnell, P.; Macreadie, P.; Ierodiaconou, D. The application of Unmanned Aerial Vehicles (UAVs) to estimate above-ground biomass of mangrove ecosystems. Remote Sens. Environ. 2020, 242, 111747. [Google Scholar] [CrossRef]
- Adar, S.; Sternberg, M.; Paz-Kagan, T.; Henkin, Z.; Dovrat, G.; Zaady, E.; Argaman, E. Estimation of aboveground biomass production using an unmanned aerial vehicle (UAV) and VENμS satellite imagery in Mediterranean and semiarid rangelands. Remote Sens. Appl. Soc. Environ. 2022, 26, 100753. [Google Scholar] [CrossRef]
- Zhu, W.; Rezaei, E.E.; Nouri, H.; Sun, Z.; Li, J.; Yu, D.; Siebert, S. UAV Flight Height Impacts on Wheat Biomass Estimation via Machine and Deep Learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 7471–7485. [Google Scholar] [CrossRef]
- Xiong, D.; Shi, P.; Zhang, X.; Zou, C.B. Effects of grazing exclusion on carbon sequestration and plant diversity in grasslands of China—A meta-analysis. Ecol. Eng. 2016, 94, 647–655. [Google Scholar] [CrossRef]
- Lussem, U.; Schellberg, J.; Bareth, G. Monitoring forage mass with low-cost UAV data: Case study at the Rengen grassland experiment. PFG–J. Photogramm. Remote Sens. Geoinf. Sci. 2020, 88, 407–422. [Google Scholar] [CrossRef]
- Grüner, E.; Astor, T.; Wachendorf, M. Biomass prediction of heterogeneous temperate grasslands using an SfM approach based on UAV imaging. Agronomy 2019, 9, 54. [Google Scholar] [CrossRef]
- Smith, M.W.; Carrivick, J.L.; Quincey, D.J. Structure from motion photogrammetry in physical geography. Prog. Phys. Geogr. 2016, 40, 247–275. [Google Scholar] [CrossRef]
- Li, F.; Piasecki, C.; Millwood, R.J.; Wolfe, B.; Mazarei, M.; Stewart Jr, C.N. High-throughput switchgrass phenotyping and biomass modeling by UAV. Front. Plant Sci. 2020, 11, 574073. [Google Scholar] [CrossRef]
- Blackburn, R.C.; Barber, N.A.; Farrell, A.K.; Buscaglia, R.; Jones, H.P. Monitoring ecological characteristics of a tallgrass prairie using an unmanned aerial vehicle. Restor. Ecol. 2021, 29, e13339. [Google Scholar] [CrossRef]
- Théau, J.; Lauzier-Hudon, É.; Aube, L.; Devillers, N. Estimation of forage biomass and vegetation cover in grasslands using UAV imagery. PLoS ONE 2021, 16, e0245784. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Tang, Z.; Wang, B.; Meng, B.; Qin, Y.; Sun, Y.; Lv, Y.; Zhang, J.; Yi, S. A non-destructive method for rapid acquisition of grassland aboveground biomass for satellite ground verification using UAV RGB images. Glob. Ecol. Conserv. 2022, 33, e01999. [Google Scholar] [CrossRef]
- Zhao, X.; Su, Y.; Hu, T.; Cao, M.; Liu, X.; Yang, Q.; Guan, H.; Liu, L.; Guo, Q. Analysis of UAV lidar information loss and its influence on the estimation accuracy of structural and functional traits in a meadow steppe. Ecol. Indic. 2022, 135, 108515. [Google Scholar] [CrossRef]
- Peciña, M.V.; Bergamo, T.F.; Ward, R.; Joyce, C.; Sepp, K. A novel UAV-based approach for biomass prediction and grassland structure assessment in coastal meadows. Ecol. Indic. 2021, 122, 107227. [Google Scholar] [CrossRef]
- Geipel, J.; Bakken, A.K.; Jørgensen, M.; Korsaeth, A. Forage yield and quality estimation by means of UAV and hyperspectral imaging. Precis. Agric. 2021, 22, 1437–1463. [Google Scholar] [CrossRef]
- Geipel, J.; Korsaeth, A. Hyperspectral aerial imaging for grassland yield estimation. Adv. Anim. Biosci. 2017, 8, 770–775. [Google Scholar] [CrossRef]
- Qin, Y.; Yi, S.; Ding, Y.; Qin, Y.; Zhang, W.; Sun, Y.; Hou, X.; Yu, H.; Meng, B.; Zhang, H. Effects of plateau pikas’ foraging and burrowing activities on vegetation biomass and soil organic carbon of alpine grasslands. Plant Soil 2021, 458, 201–216. [Google Scholar] [CrossRef]
- Bazzo, C.O.G.; Kamali, B.; Hütt, C.; Bareth, G.; Gaiser, T. A review of estimation methods for aboveground biomass in grasslands using UAV. Remote Sens. 2023, 15, 639. [Google Scholar] [CrossRef]
- Kurt Menke, G.; Smith, R., Jr.; Pirelli, L.; John Van Hoesen, G. Mastering QGIS; Packt Publishing Ltd.: Birmingham, UK, 2016. [Google Scholar]
- Luo, M.; Wang, Y.; Xie, Y.; Zhou, L.; Qiao, J.; Qiu, S.; Sun, Y. Combination of feature selection and catboost for prediction: The first application to the estimation of aboveground biomass. Forests 2021, 12, 216. [Google Scholar] [CrossRef]
- Khajehyar, R.; Vahidi, M.; Tripepi, R. Determining Nitrogen Foliar Nutrition of Tissue Culture Shoots of Little-Leaf Mockorange By Using Spectral Imaging. In Proceedings of the 2021 ASHS Annual Conference, Denver, CO, USA, 5–9 August 2021. [Google Scholar]
- Vahidi, M.; Aghakhani, S.; Martín, D.; Aminzadeh, H.; Kaveh, M. Optimal Band Selection Using Evolutionary Machine Learning to Improve the Accuracy of Hyper-spectral Images Classification: A Novel Migration-Based Particle Swarm Optimization. J. Classif. 2023, 40, 552–587. [Google Scholar] [CrossRef]
- van der Merwe, D.; Baldwin, C.E.; Boyer, W. An efficient method for estimating dormant season grass biomass in tallgrass prairie from ultra-high spatial resolution aerial imaging produced with small unmanned aircraft systems. Int. J. Wildland Fire 2020, 29, 696–701. [Google Scholar] [CrossRef]
- Gebremedhin, A.; Badenhorst, P.; Wang, J.; Shi, F.; Breen, E.; Giri, K.; Spangenberg, G.C.; Smith, K. Development and validation of a phenotyping computational workflow to predict the biomass yield of a large perennial ryegrass breeding field trial. Front. Plant Sci. 2020, 11, 689. [Google Scholar] [CrossRef]
- Plaza, J.; Criado, M.; Sánchez, N.; Pérez-Sánchez, R.; Palacios, C.; Charfolé, F. UAV multispectral imaging potential to monitor and predict agronomic characteristics of different forage associations. Agronomy 2021, 11, 1697. [Google Scholar] [CrossRef]
- Adeluyi, O.; Harris, A.; Foster, T.; Clay, G.D. Exploiting centimetre resolution of drone-mounted sensors for estimating mid-late season above ground biomass in rice. Eur. J. Agron. 2022, 132, 126411. [Google Scholar] [CrossRef]
- Rueda-Ayala, V.P.; Peña, J.M.; Höglind, M.; Bengochea-Guevara, J.M.; Andújar, D. Comparing UAV-based technologies and RGB-D reconstruction methods for plant height and biomass monitoring on grass ley. Sensors 2019, 19, 535. [Google Scholar] [CrossRef] [PubMed]
- Ballesteros, R.; Ortega, J.F.; Hernandez, D.; Moreno, M.A. Onion biomass monitoring using UAV-based RGB imaging. Precis. Agric. 2018, 19, 840–857. [Google Scholar] [CrossRef]
- González-Alonso, F.; Merino-De-Miguel, S.; Roldán-Zamarrón, A.; García-Gigorro, S.; Cuevas, J. Forest biomass estimation through NDVI composites. The role of remotely sensed data to assess Spanish forests as carbon sinks. Int. J. Remote Sens. 2006, 27, 5409–5415. [Google Scholar] [CrossRef]
- Sharma, P.; Leigh, L.; Chang, J.; Maimaitijiang, M.; Caffé, M. Above-ground biomass estimation in oats using UAV remote sensing and machine learning. Sensors 2022, 22, 601. [Google Scholar] [CrossRef]
- Yue, J.; Yang, H.; Yang, G.; Fu, Y.; Wang, H.; Zhou, C. Estimating vertically growing crop above-ground biomass based on UAV remote sensing. Comput. Electron. Agric. 2023, 205, 107627. [Google Scholar] [CrossRef]
- Dreiseitl, S.; Ohno-Machado, L. Logistic regression and artificial neural network classification models: A methodology review. J. Biomed. Inform. 2002, 35, 352–359. [Google Scholar] [CrossRef]
- Ramsundar, B.; Zadeh, R.B. TensorFlow for Deep Learning: From Linear Regression to Reinforcement Learning; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2018. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Mohammadi, R.; Sahebi, M.R.; Omati, M.; Vahidi, M. Synthetic aperture radar remote sensing classification using the bag of visual words model to land cover studies. Int. J. Geol. Environ. Eng. 2018, 12, 588–591. [Google Scholar]
- Rostami, O.; Kaveh, M. Optimal feature selection for SAR image classification using biogeography-based optimization (BBO), artificial bee colony (ABC) and support vector machine (SVM): A combined approach of optimization and machine learning. Comput. Geosci. 2021, 25, 911–930. [Google Scholar] [CrossRef]
- Ghajari, Y.E.; Kaveh, M.; Martín, D. Predicting PM10 Concentrations Using Evolutionary Deep Neural Network and Satellite-Derived Aerosol Optical Depth. Mathematics 2023, 11, 4145. [Google Scholar] [CrossRef]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; pp. 278–282. [Google Scholar]
- Svetnik, V.; Liaw, A.; Tong, C.; Culberson, J.C.; Sheridan, R.P.; Feuston, B.P. Random forest: A classification and regression tool for compound classification and QSAR modeling. J. Chem. Inf. Comput. Sci. 2003, 43, 1947–1958. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Statnikov, A.; Wang, L.; Aliferis, C.F. A comprehensive comparison of random forests and support vector machines for microarray-based cancer classification. BMC Bioinform. 2008, 9, 1–10. [Google Scholar] [CrossRef]
- Plevris, V.; Solorzano, G.; Bakas, N.P.; Ben Seghier, M.E.A. Investigation of performance metrics in regression analysis and machine learning-based prediction models. In Proceedings of the 8th European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS Congress 2022), Oslo, Norway, 5–9 June 2022. [Google Scholar]
- Karunasingha, D.S.K. Root mean square error or mean absolute error? Use their ratio as well. Inf. Sci. 2022, 585, 609–629. [Google Scholar] [CrossRef]
- Pope, P.T.; Webster, J.T. The use of an F-statistic in stepwise regression procedures. Technometrics 1972, 14, 327–340. [Google Scholar] [CrossRef]
- Acquah, H.d.-G. Comparison of Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) in Selection of an Asymmetric Price Relationship. J. Dev. Agric. Econ. 2010, 2, 1–6. [Google Scholar]
- Andrade, J.; Estévez-Pérez, M. Statistical comparison of the slopes of two regression lines: A tutorial. Anal. Chim. Acta 2014, 838, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Shi, L.; Han, J.; Chen, Z.; Yu, J. A VI-based phenology adaptation approach for rice crop monitoring using UAV multispectral images. Field Crops Res. 2022, 277, 108419. [Google Scholar] [CrossRef]
- Casler, M.; Pedersen, J.F.; Undersander, D. Forage yield and economic losses associated with the brown-midrib trait in Sudangrass. Crop Sci. 2003, 43, 782–789. [Google Scholar] [CrossRef]
- Tang, Z.; Parajuli, A.; Chen, C.J.; Hu, Y.; Revolinski, S.; Medina, C.A.; Lin, S.; Zhang, Z.; Yu, L.-X. Validation of UAV-based alfalfa biomass predictability using photogrammetry with fully automatic plot segmentation. Sci. Rep. 2021, 11, 3336. [Google Scholar] [CrossRef]
- Singh, J.; Koc, A.B.; Aguerre, M.J. Aboveground Biomass Estimation of Tall Fescue using Aerial and Ground-based Systems. In Proceedings of the 2023 ASABE Annual International Meeting, Omaha, NE, USA, 9–12 July 2023; p. 1. [Google Scholar]
- Vanamburg, L.; Trlica, M.; Hoffer, R.; Weltz, M. Ground based digital imagery for grassland biomass estimation. Int. J. Remote Sens. 2006, 27, 939–950. [Google Scholar] [CrossRef]
- Liang, Y.; Kou, W.; Lai, H.; Wang, J.; Wang, Q.; Xu, W.; Wang, H.; Lu, N. Improved estimation of aboveground biomass in rubber plantations by fusing spectral and textural information from UAV-based RGB imagery. Ecol. Indic. 2022, 142, 109286. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Sagan, V.; Sidike, P.; Maimaitiyiming, M.; Hartling, S.; Peterson, K.T.; Maw, M.J.; Shakoor, N.; Mockler, T.; Fritschi, F.B. Vegetation index weighted canopy volume model (CVMVI) for soybean biomass estimation from unmanned aerial system-based RGB imagery. ISPRS J. Photogramm. Remote Sens. 2019, 151, 27–41. [Google Scholar] [CrossRef]
- Mutanga, O.; Masenyama, A.; Sibanda, M. Spectral saturation in the remote sensing of high-density vegetation traits: A systematic review of progress, challenges, and prospects. ISPRS J. Photogramm. Remote Sens. 2023, 198, 297–309. [Google Scholar] [CrossRef]
- Batistoti, J.; Marcato Junior, J.; Ítavo, L.; Matsubara, E.; Gomes, E.; Oliveira, B.; Souza, M.; Siqueira, H.; Salgado Filho, G.; Akiyama, T. Estimating pasture biomass and canopy height in Brazilian savanna using UAV photogrammetry. Remote Sens. 2019, 11, 2447. [Google Scholar] [CrossRef]
- Borra-Serrano, I.; De Swaef, T.; Muylle, H.; Nuyttens, D.; Vangeyte, J.; Mertens, K.; Saeys, W.; Somers, B.; Roldán-Ruiz, I.; Lootens, P. Canopy height measurements and non-destructive biomass estimation of Lolium perenne swards using UAV imagery. Grass Forage Sci. 2019, 74, 356–369. [Google Scholar] [CrossRef]
- Castro, W.; Marcato Junior, J.; Polidoro, C.; Osco, L.P.; Gonçalves, W.; Rodrigues, L.; Santos, M.; Jank, L.; Barrios, S.; Valle, C. Deep learning applied to phenotyping of biomass in forages with UAV-based RGB imagery. Sensors 2020, 20, 4802. [Google Scholar] [CrossRef] [PubMed]
- DiMaggio, A.M.; Perotto-Baldivieso, H.L.; Ortega-S., J.A.; Walther, C.; Labrador-Rodriguez, K.N.; Page, M.T.; Martinez, J.d.l.L.; Rideout-Hanzak, S.; Hedquist, B.C.; Wester, D.B. A pilot study to estimate forage mass from unmanned aerial vehicles in a semi-arid rangeland. Remote Sens. 2020, 12, 2431. [Google Scholar] [CrossRef]
- Lussem, U.; Bolten, A.; Menne, J.; Gnyp, M.L.; Schellberg, J.; Bareth, G. Estimating biomass in temperate grassland with high resolution canopy surface models from UAV-based RGB images and vegetation indices. J. Appl. Remote Sens. 2019, 13, 034525. [Google Scholar] [CrossRef]
- Alves Oliveira, R.; Marcato Junior, J.; Soares Costa, C.; Näsi, R.; Koivumäki, N.; Niemeläinen, O.; Kaivosoja, J.; Nyholm, L.; Pistori, H.; Honkavaara, E. Silage grass sward nitrogen concentration and dry matter yield estimation using deep regression and RGB images captured by UAV. Agronomy 2022, 12, 1352. [Google Scholar] [CrossRef]
- Shorten, P.; Trolove, M. UAV-based prediction of ryegrass dry matter yield. Int. J. Remote Sens. 2022, 43, 2393–2409. [Google Scholar] [CrossRef]
- Vogel, S.; Gebbers, R.; Oertel, M.; Kramer, E. Evaluating soil-borne causes of biomass variability in grassland by remote and proximal sensing. Sensors 2019, 19, 4593. [Google Scholar] [CrossRef]
- Wijesingha, J.; Moeckel, T.; Hensgen, F.; Wachendorf, M. Evaluation of 3D point cloud-based models for the prediction of grassland biomass. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 352–359. [Google Scholar] [CrossRef]
- Ohsowski, B.M.; Dunfield, K.E.; Klironomos, J.N.; Hart, M.M. Improving plant biomass estimation in the field using partial least squares regression and ridge regression. Botany 2016, 94, 501–508. [Google Scholar] [CrossRef]









| Flight Date | Flight Speed | Flight Altitude | Side Overlap | Front Overlap | GSD (m) |
|---|---|---|---|---|---|
| April | ~3 mph | 60 ft | %75 | %75 | 0.01 |
| May | ~3 mph | 60 ft | %75 | %75 | 0.01 |
| June | ~3 mph | 60 ft | %75 | %75 | 0.01 |
| Variable | Variable Types | Variable Name | Description |
|---|---|---|---|
| Numerical | Structural | Maximum of PH in grids | |
| Mean of PH in grids | |||
| Median PH in grids | |||
| Standard deviation of PH in grids | |||
| Variance of PH in grids | |||
| Spectral | Mean value of pixels in the red band in grid | ||
| Mean value of pixels in the green band in grid | |||
| Mean value of pixels in the blue band in the grid | |||
| Categorical | Paddock types | BG low impact | Low-impact areas in bale grazing |
| BG high impact | High-impact areas in bale grazing | ||
| Rest paddock | Livestock grazing is restricted for a period | ||
| Sacrifice paddock | heavily impacted by trampling |
| Epochs | Optimizer | Initializer | Number of Neurons | Activation Function |
|---|---|---|---|---|
| 50, 100, 200, and 500 | “SGD”, “RMSprop”, “Adam”, “Nadam” | “lecun_uniform”, “normal”, “he_normal”, “uniform” | 50, 25, 16, 10, 8, 7, 5, 3 | “Relu”, “linear”, and “Tanh” |
| Variable | Date/Treatment | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HI Bale Grazing | LI Bale Grazing | Rest | Sacrifice | |||||||||
| April | May | June | April | May | June | April | May | June | April | May | June | |
| 0.084 | 0.16 | 0.71 | 0.206 | 0.255 | 0.84 | 0.35 | 0.7 | 1.11 | 0.106 | 0.25 | 0.536 | |
| 0.034 | 0.06 | 0.38 | 0.063 | 0.104 | 0.37 | 0.21 | 0.44 | 0.69 | 0.048 | 0.12 | 0.314 | |
| 0.017 | 0.04 | 0.11 | 0.040 | 0.056 | 0.14 | 0.052 | 0.1 | 0.11 | 0.020 | 0.05 | 0.086 | |
| <0.001 | 0.001 | 0.01 | 0.002 | 0.003 | 0.02 | 0.003 | 0.008 | 0.01 | 0.000 | 0.003 | 0.007 | |
| 194 | 139 | 143 | 203 | 146 | 122 | 183 | 132 | 129 | 168 | 137 | 141 | |
| 184 | 162 | 164 | 193 | 164 | 149 | 197 | 175 | 149 | 171 | 177 | 171 | |
| 159 | 89 | 88 | 182 | 93 | 95 | 146 | 78 | 79 | 126 | 82 | 79 | |
| Model | ) | ) | |
|---|---|---|---|
| ANN | 0.93 | 62 | 44 |
| SVR | 0.91 | 64 | 48 |
| RF | 0.86 | 78 | 58 |
| Model | BIC | t-Test/Slope | t-Test/INTERCEPT | Prob (F-Statistic) | |
|---|---|---|---|---|---|
| ANN | 491.4 | 462.4 | 22.16 | 1.17 | 4.43 × 10−24 |
| SVR | 390.3 | 471.3 | 19.75 | 0.62 | 3.05 × 10−22 |
| RF | 256.1 | 487.5 | 16.03 | 0.014 | 5.50 × 10−19 |
| Author | Year | Spectral Info | Structural Info | Model | R2 | Ref |
|---|---|---|---|---|---|---|
| Batistoti et al. | 2019 | n/a | Plant height | Linear regression | 0.74 | [66] |
| Borra-Serrano et al. | 2019 | 10 spectral indices | 7 canopy metrics | PLSAR, MLR, LR and RF | 0.67, 0.81, 0.58, 0.70 | [67] |
| Castro et al. | 2020 | 4 spectral indices | n/a | CNN | 0.88 | [68] |
| DiMaggio et al. | 2020 | n/a | Plant height | LR | 0.65 | [69] |
| Grüner, et al. | 2019 | n/a | Plant height | LR | 0.72 | [17] |
| Lussem et al., | 2019 | 6 spectral indices | Plant height | MLR | 0.73 | [70] |
| Lussem, et al. | 2020 | n/a | Plant height metrics | LR | 0.86 | [16] |
| Alves Oliveira et al. | 2022 | n/a | n/a | CNN | 0.79 | [71] |
| Qin et al. | 2021 | Spectral indices | Fractional vegetation cover | LR | 0.45 | [27] |
| Rueda-Ayala et al. | 2019 | n/a | Plant height metrics | LR | 0.54 | [37] |
| Shorten and Trolove | 2022 | Mean spectral bands for vegetative and soil material | Percent vegetation cover and forage volume | LR | 0.66 | [72] |
| Sinde-González et al. | 2021 | n/a | Density factor and volume | Descriptive statistic | 0.78 | [11] |
| Van Der Merwe, Baldwin and Boyer | 2020 | n/a | Canopy height model | LR | 0.91 | [33] |
| Vogel et al. | 2019 | Reflectance of red, green, and blue; hue: saturation, value | n/a | LR | 0.81 | [73] |
| Wijesingha et al. | 2019 | n/a | 10 canopy height metrics | LR | 0.62 | [74] |
| Zhang et al. | 2022 | 6 color space indices and 3 vegetation indices | Canopy height model from point clouds | RF | 0.78 | [22] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vahidi, M.; Shafian, S.; Thomas, S.; Maguire, R. Pasture Biomass Estimation Using Ultra-High-Resolution RGB UAVs Images and Deep Learning. Remote Sens. 2023, 15, 5714. https://doi.org/10.3390/rs15245714
Vahidi M, Shafian S, Thomas S, Maguire R. Pasture Biomass Estimation Using Ultra-High-Resolution RGB UAVs Images and Deep Learning. Remote Sensing. 2023; 15(24):5714. https://doi.org/10.3390/rs15245714
Chicago/Turabian StyleVahidi, Milad, Sanaz Shafian, Summer Thomas, and Rory Maguire. 2023. "Pasture Biomass Estimation Using Ultra-High-Resolution RGB UAVs Images and Deep Learning" Remote Sensing 15, no. 24: 5714. https://doi.org/10.3390/rs15245714
APA StyleVahidi, M., Shafian, S., Thomas, S., & Maguire, R. (2023). Pasture Biomass Estimation Using Ultra-High-Resolution RGB UAVs Images and Deep Learning. Remote Sensing, 15(24), 5714. https://doi.org/10.3390/rs15245714






