Estimating the SPAD of Litchi in the Growth Period and Autumn Shoot Period Based on UAV Multi-Spectrum
Abstract
:1. Introduction
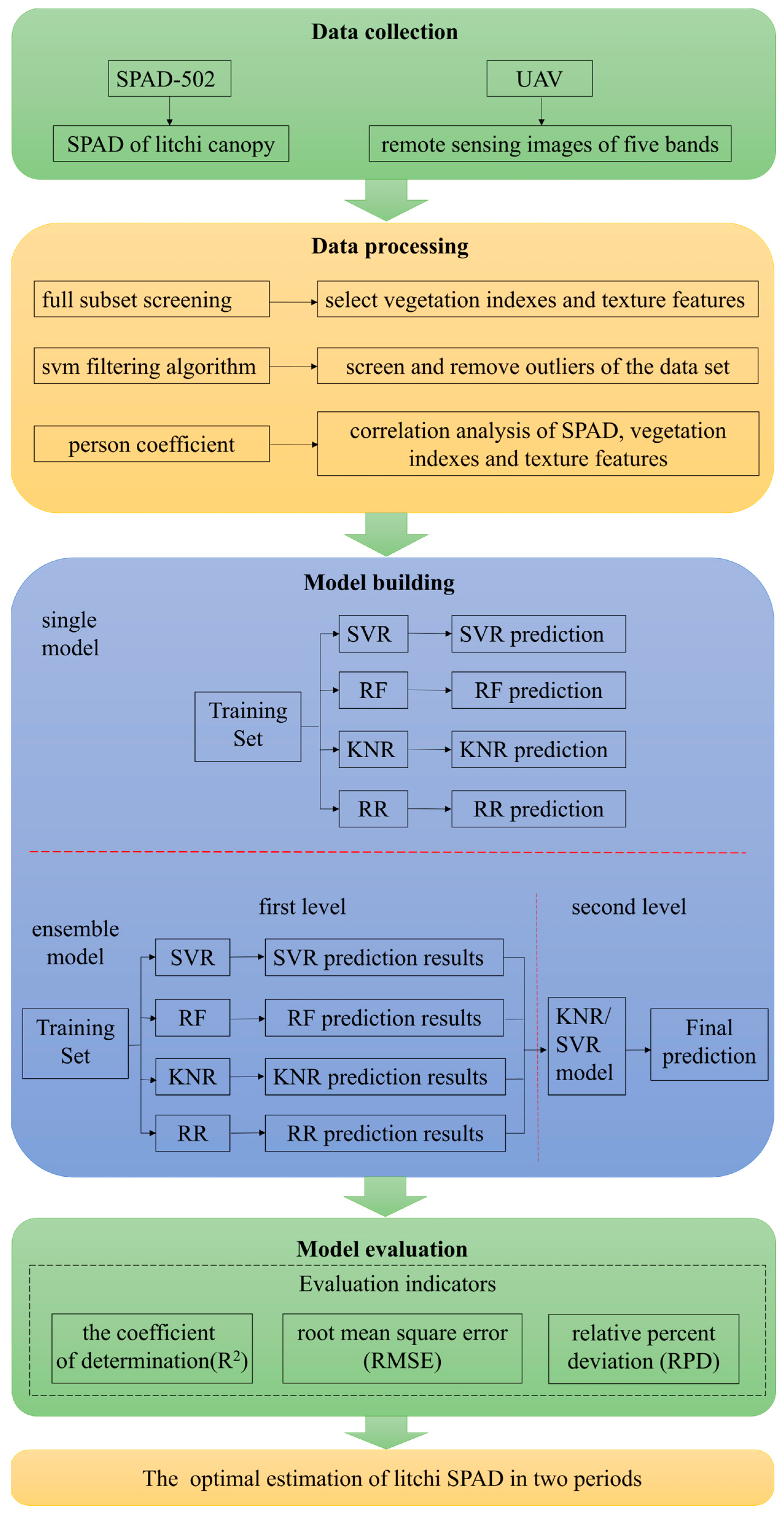
2. Materials and Methods
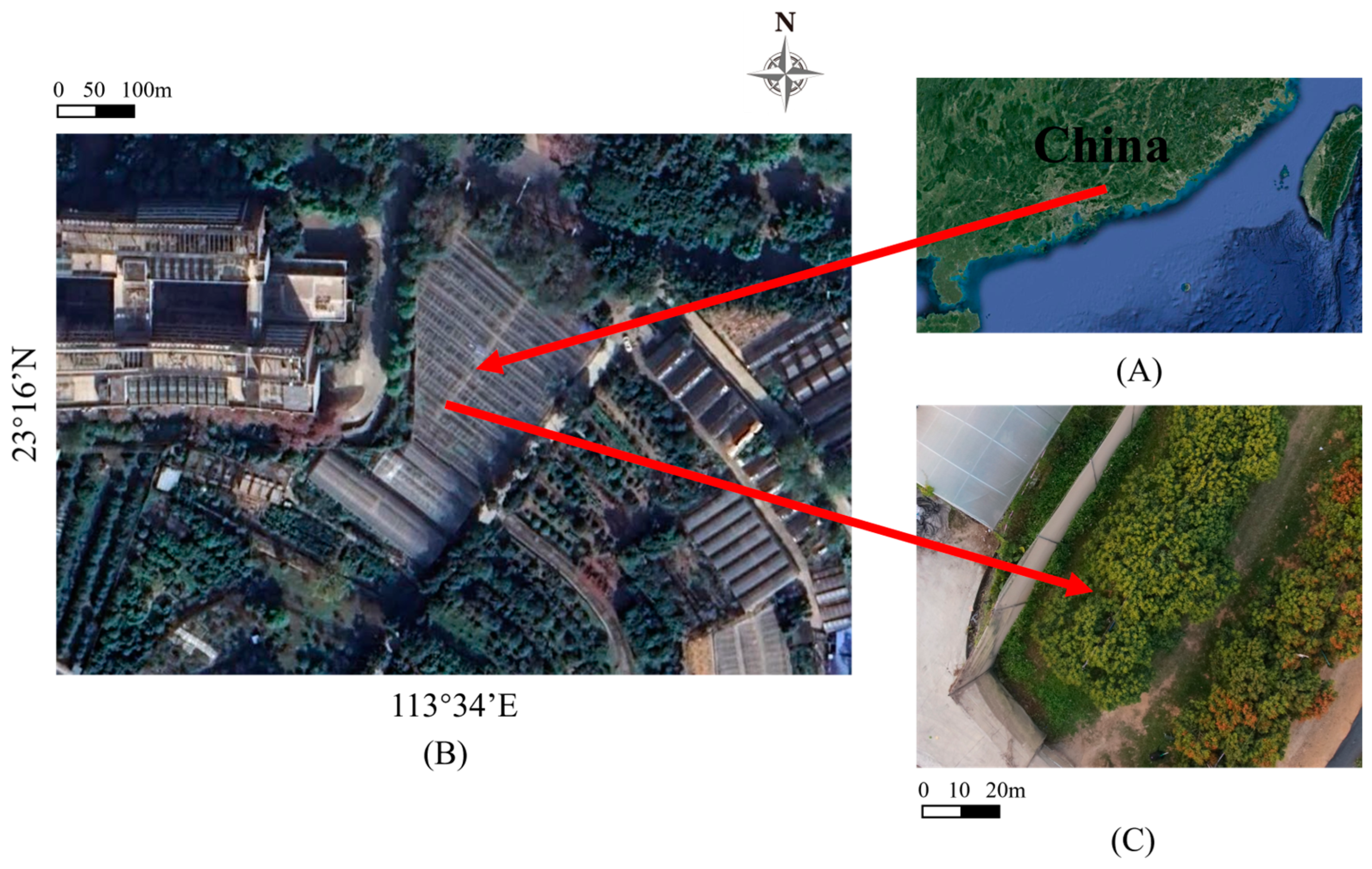
2.1. Overview of the Study Area
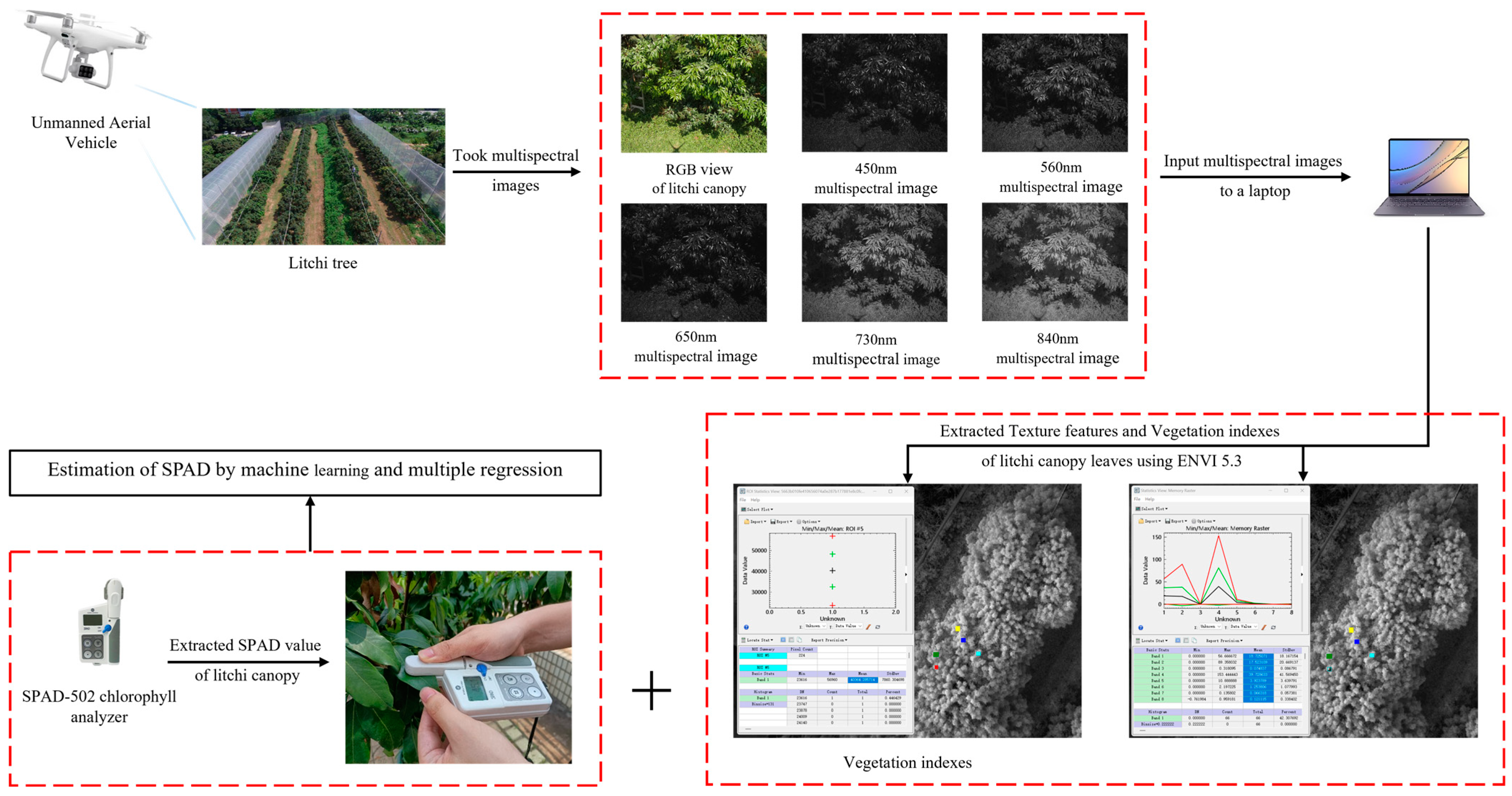
2.2. Measurement Method of the Litchi SPAD Value Based on the Integration of Space and Land
2.3. Spectral Reflectance Acquisition
2.4. Selection and Calculation of Vegetation Indexes and Texture Features
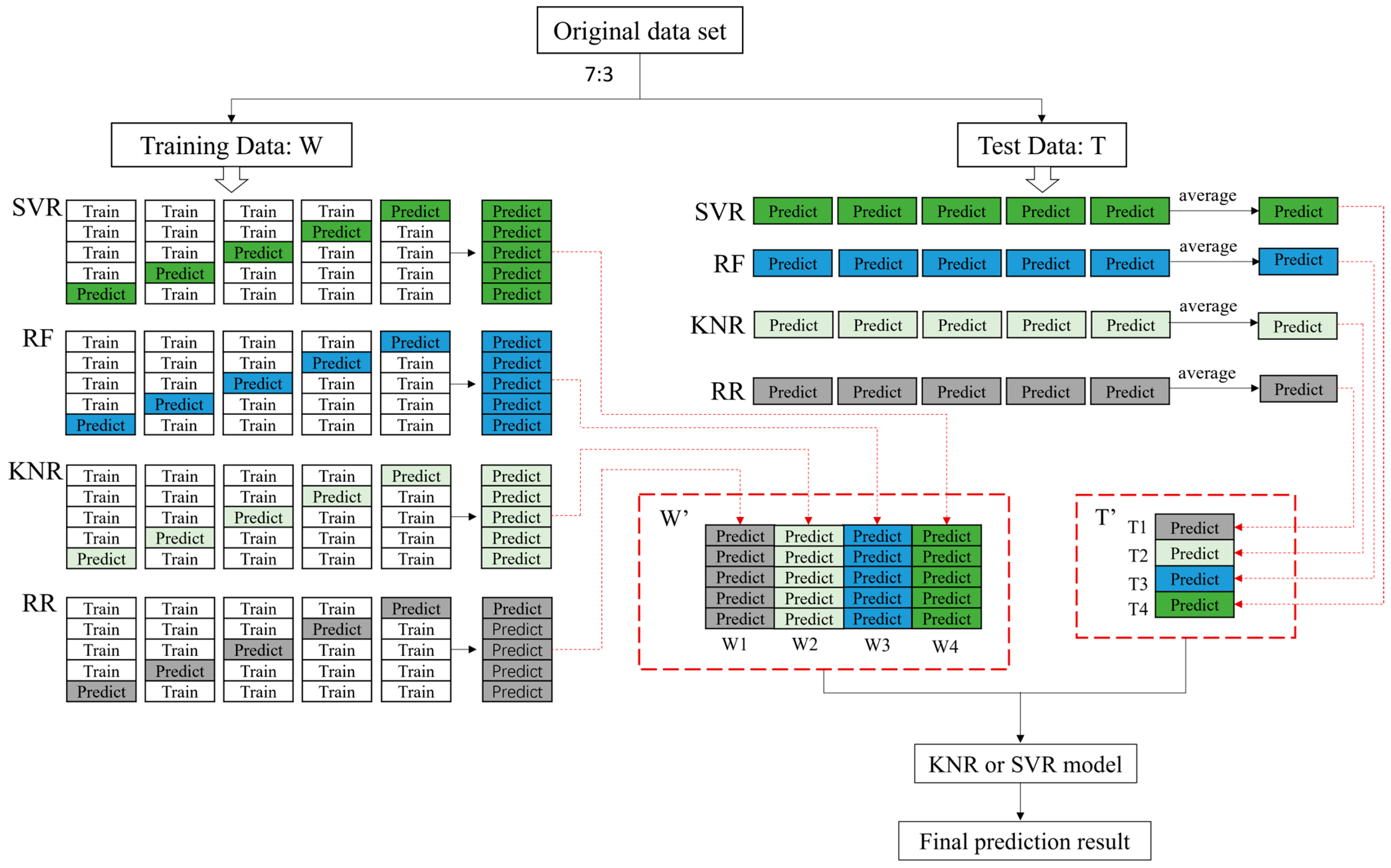
2.5. Machine Learning Model
2.6. Verification Methods for Model Performance Indicators
3. Results
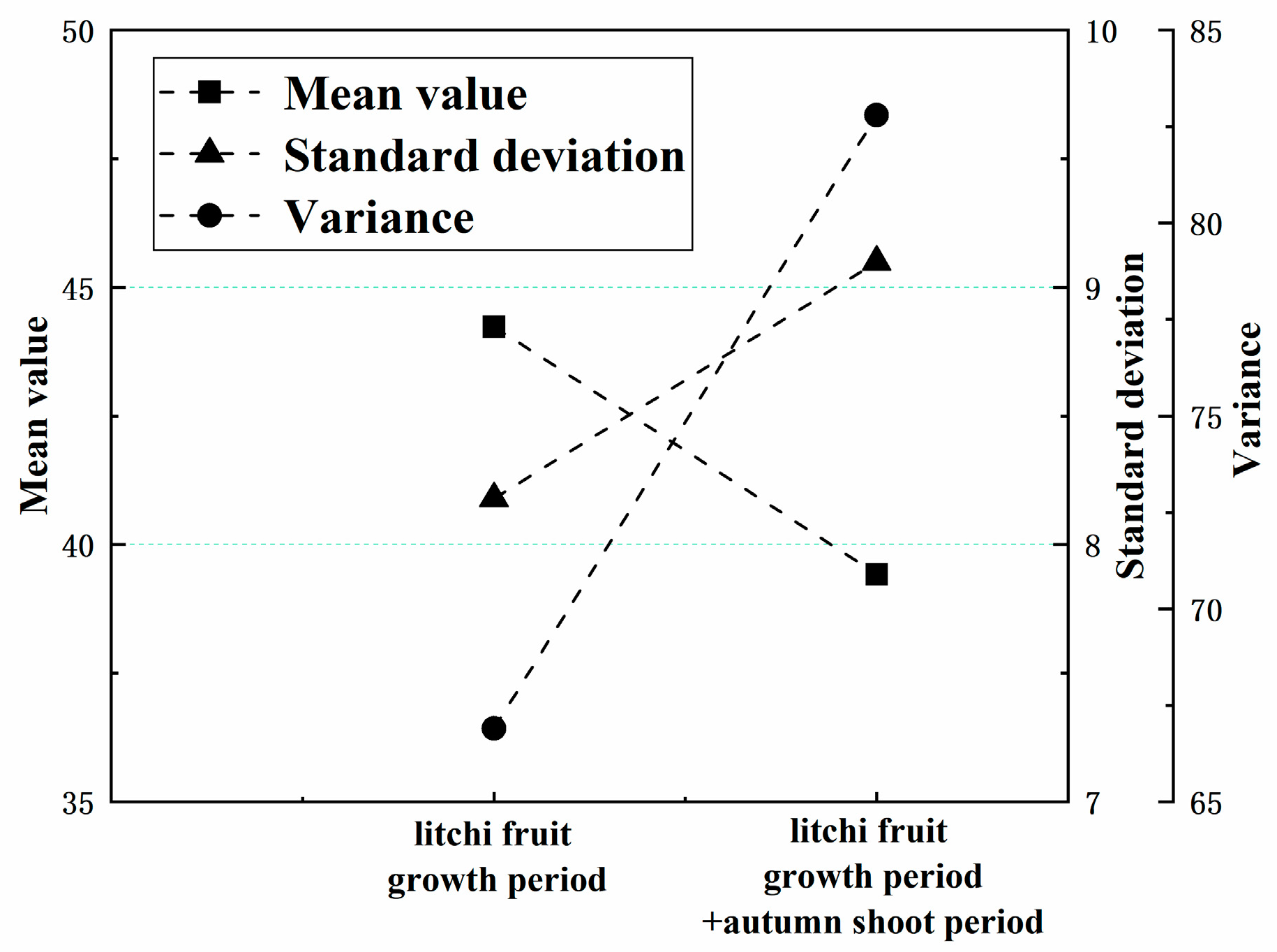
3.1. SPAD Data Analysis
3.2. Correlation Analysis of UAV Multi-Spectral Vegetation Indexes, Texture Features, and Litchi SPAD
3.3. Model Fitting Performance Results
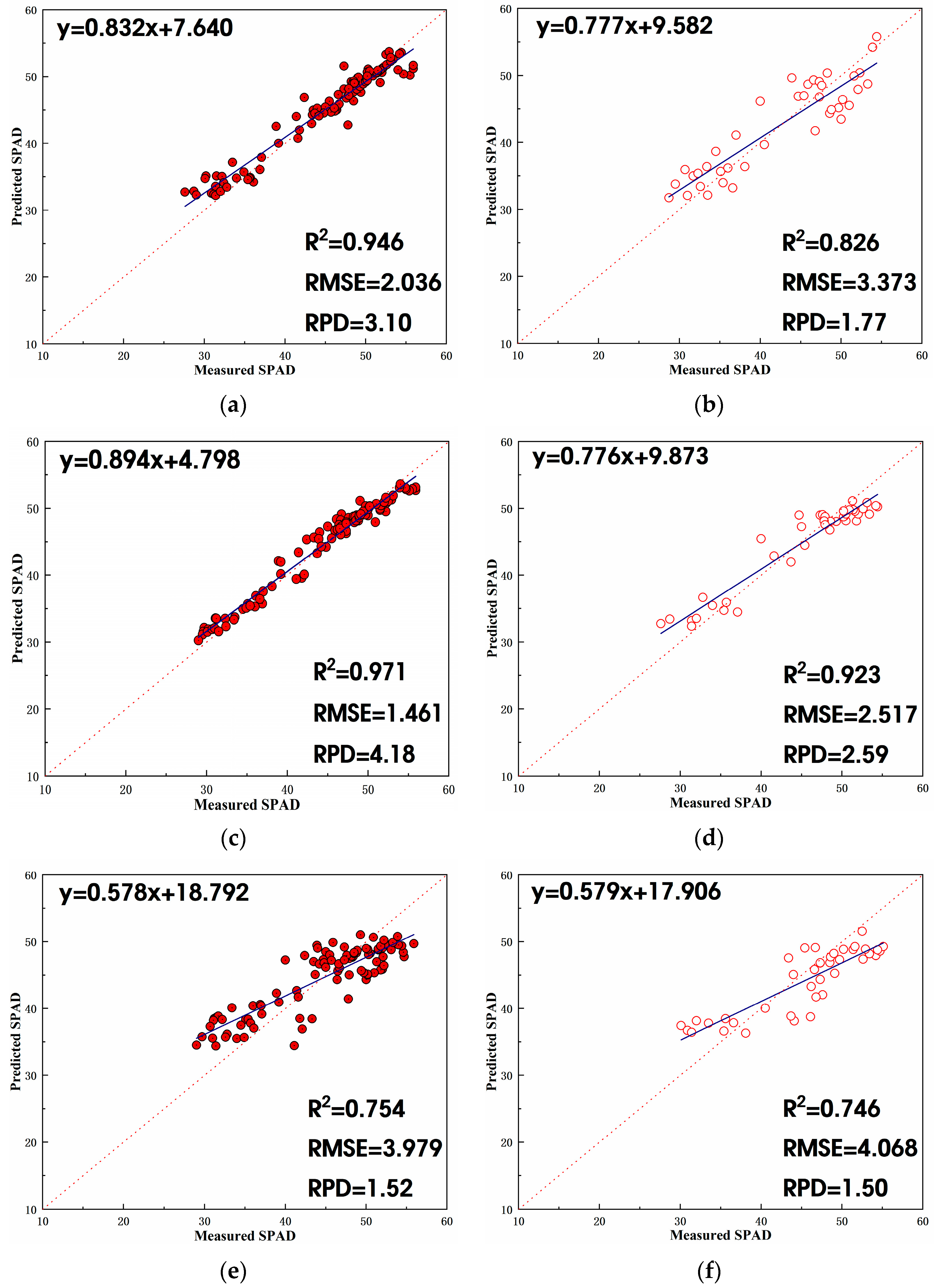
3.3.1. Estimation Model Based on Litchi Fruit Development Period
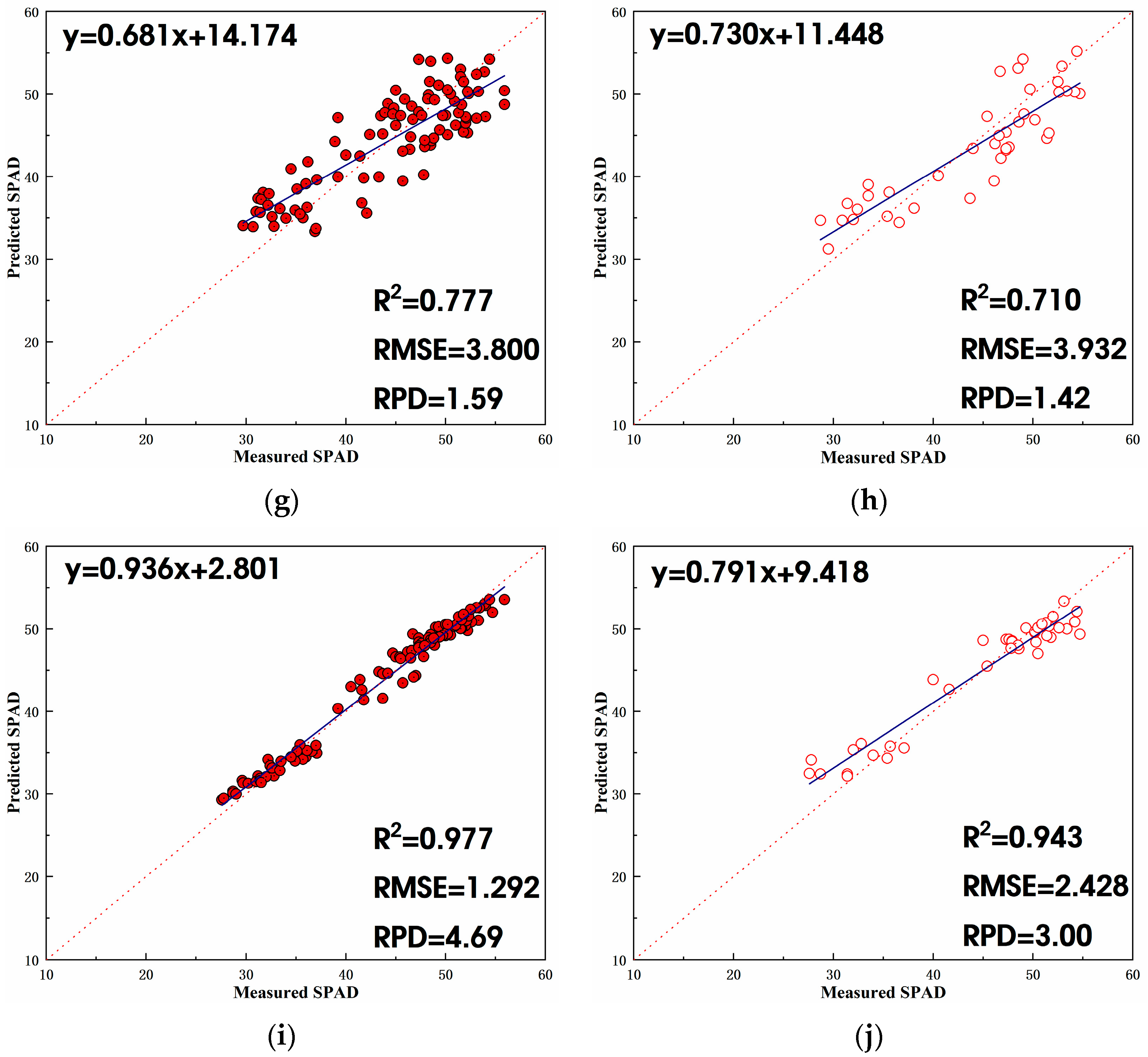
3.3.2. Estimation Model Based on Litchi Fruit Growth Period + Autumn Shoot Period
4. Discussion
5. Conclusions
- (1)
- For the litchi fruit growth period, three combinations of independent variables were investigated in this study: vegetation index, texture features, and vegetation index + texture features. Overall, the combination of vegetation index + texture features as independent variables exhibited the most effective estimation, followed by vegetation index alone and then texture features alone. In the SPAD estimation model developed in this study based on vegetation index + texture features during the fruit growth period, the stacking model demonstrated the highest R2 in the validation set, reaching 0.94. Following closely was the RF model with an R2 of 0.92. The stacking model also exhibited the lowest RMSE in the validation set, at 2.4, compared to 2.5 for the RF model. Additionally, the RPD of the validation set for the stacking model was the highest at 3.0, followed by 2.6 for the RF model. In summary, the stacking model proved to be the optimal choice for estimating the SPAD value of litchi fruit during its growth period based on vegetation index + texture features, followed by the RF model.
- (2)
- For the litchi fruit growth period + autumn shoot period, three combinations of independent variables were considered in this study: vegetation index, texture features, and vegetation index + texture features. Overall, the combination of vegetation index + texture features as independent variables demonstrated the most effective estimation, followed by vegetation index alone and then texture features alone. In the SPAD estimation model developed in this study based on vegetation index + texture features during the litchi fruit growth period + autumn shoot period, the stacking model exhibited the highest R2 in the validation set, reaching 0.84. Following closely was the RF model with an R2 of 0.81. The stacking model and RF model share the same lowest validation set RMSE, which is 3.9. The stacking model also showed the highest validation set RPD at 1.9, followed by 1.7 for the RF model. In summary, the stacking model was identified as the optimal choice for estimating the SPAD value of litchi fruit during its growth period + autumn shoot period based on vegetation index + texture features, followed by the RF model.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Vegetation Index | Calculation Formula | Reference |
|---|---|---|
| Chlorophyll Index of Red Edge, CIred Edge | [38] | |
| Modified Soil-Adjusted Vegetation Index, MSAVI | [39] | |
| Renormalized Vegetation Index, RDVI | [40] | |
| Structure Insensitive Pigment Index, SIPI | [41] | |
| Difference Vegetation Index, DVI | [42] | |
| Modified Chlorophyll Absorption Ratio Index, MCARI | [39] | |
| Optimized Soil and Adjusted Vegetation Index, OSAVI | [43] | |
| MERIS Terrestrial Chlorophyll Index, MTCI | [44] | |
| Ratio Vegetation Index 1, RVI1 | [45] | |
| Transformed Chlorophyll Absorption Reflectance Index, TCARI | [46] | |
| Non-Linear Index, NLI | [47] |
References
- Xie, J.; Peng, J.; Wang, J.; Chen, B.; Jing, T.; Sun, D.; Gao, P.; Wang, W.; Lu, J.; Yetan, R.; et al. Litchi Detection in a Complex Natural Environment Using the YOLOv5-Litchi Model. Agronomy 2022, 12, 3054. [Google Scholar] [CrossRef]
- Kuang, L.; Wang, Z.; Cheng, Y.; Li, Y.; Li, H.; Zhang, J.; Shen, Y.; Li, J.; Xu, G. Residue Levels and Risk Assessment of Pesticides in Litchi and Longan of China. J. Food Compos. Anal. 2023, 115, 104921. [Google Scholar] [CrossRef]
- Xiong, Z.; Wang, L.; Zhao, Y.; Lan, Y. Precision Detection of Dense Litchi Fruit in UAV Images Based on Improved YOLOv5 Model. Remote Sens. 2023, 15, 4017. [Google Scholar] [CrossRef]
- Liu, B.; Xue, W.; Guo, Z.; Liu, S.; Zhu, Q.; Pang, X.; Zhang, Z.; Fang, F. Water Loss and Pericarp Browning of Litchi (Litchi chinensis) and Longan (Dimocarpus longan) Fruit Maintain Seed Vigor. Sci. Hortic. 2021, 290, 110519. [Google Scholar] [CrossRef]
- Su, Z.; Liu, L.; Li, Y.; Chen, H. Predicting Flower Induction of Litchi (Litchi chinensis Sonn.) with Machine Learning Techniques. Comput. Electron. Agric. 2023, 205, 107572. [Google Scholar] [CrossRef]
- Fu, P.; Meacham-Hensold, K.; Siebers, M.H.; Bernacchi, C.J. The Inverse Relationship between Solar-Induced Fluorescence Yield and Photosynthetic Capacity: Benefits for Field Phenotyping. J. Exp. Bot. 2021, 72, 1295–1306. [Google Scholar] [CrossRef]
- Liu, P.; Huang, J.; Cai, Z.; Chen, H.; Huang, X.; Yang, S.; Su, Z.; Azam, M.; Chen, H.; Shen, J. Influence of Girdling on Growth of Litchi (Litchi chinensis) Roots during Cold-Dependent Floral Induction. Sci. Hortic. 2022, 297, 110928. [Google Scholar] [CrossRef]
- Fu, X.-Y.; Mo, W.-P.; Zhang, J.-Y.; Zhou, L.-Y.; Wang, H.-C.; Huang, X.-M. Shoot Growth Pattern and Quantifying Flush Maturity with SPAD Value in Litchi (Litchi chinensis Sonn.). Sci. Hortic. 2014, 174, 29–35. [Google Scholar] [CrossRef]
- Li, J.; Wijewardane, N.K.; Ge, Y.; Shi, Y. Improved Chlorophyll and Water Content Estimations at Leaf Level with a Hybrid Radiative Transfer and Machine Learning Model. Comput. Electron. Agric. 2023, 206, 107669. [Google Scholar] [CrossRef]
- Hassanijalilian, O.; Igathinathane, C.; Doetkott, C.; Bajwa, S.; Nowatzki, J.; Haji Esmaeili, S.A. Chlorophyll Estimation in Soybean Leaves Infield with Smartphone Digital Imaging and Machine Learning. Comput. Electron. Agric. 2020, 174, 105433. [Google Scholar] [CrossRef]
- Teshome, F.T.; Bayabil, H.K.; Hoogenboom, G.; Schaffer, B.; Singh, A.; Ampatzidis, Y. Unmanned Aerial Vehicle (UAV) Imaging and Machine Learning Applications for Plant Phenotyping. Comput. Electron. Agric. 2023, 212, 108064. [Google Scholar] [CrossRef]
- Yang, Y.; Wei, X.; Wang, J.; Zhou, G.; Wang, J.; Jiang, Z.; Zhao, J.; Ren, Y. Prediction of Seedling Oilseed Rape Crop Phenotype by Drone-Derived Multimodal Data. Remote Sens. 2023, 15, 3951. [Google Scholar] [CrossRef]
- Yu, T.; Zhou, J.; Fan, J.; Wang, Y.; Zhang, Z. Potato Leaf Area Index Estimation Using Multi-Sensor Unmanned Aerial Vehicle (UAV) Imagery and Machine Learning. Remote Sens. 2023, 15, 4108. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, Z.; Cao, Q.; Liang, Y.; Krienke, B.; Tian, Y.; Zhu, Y.; Cao, W.; Liu, X. Use of an Active Canopy Sensor Mounted on an Unmanned Aerial Vehicle to Monitor the Growth and Nitrogen Status of Winter Wheat. Remote Sens. 2020, 12, 3684. [Google Scholar] [CrossRef]
- Wan, L.; Zhu, J.; Du, X.; Zhang, J.; Han, X.; Zhou, W.; Li, X.; Liu, J.; Liang, F.; He, Y.; et al. A Model for Phenotyping Crop Fractional Vegetation Cover Using Imagery from Unmanned Aerial Vehicles. J. Exp. Bot. 2021, 72, 4691–4707. [Google Scholar] [CrossRef]
- Vélez, S.; Ariza-Sentís, M.; Valente, J. Mapping the Spatial Variability of Botrytis Bunch Rot Risk in Vineyards Using UAV Multispectral Imagery. Eur. J. Agron. 2023, 142, 126691. [Google Scholar] [CrossRef]
- Jiang, J.; Atkinson, P.M.; Zhang, J.; Lu, R.; Zhou, Y.; Cao, Q.; Tian, Y.; Zhu, Y.; Cao, W.; Liu, X. Combining Fixed-Wing UAV Multispectral Imagery and Machine Learning to Diagnose Winter Wheat Nitrogen Status at the Farm Scale. Eur. J. Agron. 2022, 138, 126537. [Google Scholar] [CrossRef]
- Huang, Y.; Ma, Q.; Wu, X.; Li, H.; Xu, K.; Ji, G.; Qian, F.; Li, L.; Huang, Q.; Long, Y.; et al. Estimation of Chlorophyll Content in Brassica Napus Based on Unmanned Aerial Vehicle Images. Oil Crop Sci. 2022, 7, 149–155. [Google Scholar] [CrossRef]
- Poudyal, C.; Sandhu, H.; Ampatzidis, Y.; Odero, D.C.; Arbelo, O.C.; Cherry, R.H.; Costa, L.F. Prediction of Morpho-Physiological Traits in Sugarcane Using Aerial Imagery and Machine Learning. Smart Agric. Technol. 2023, 3, 100104. [Google Scholar] [CrossRef]
- Zhang, L.; Han, W.; Niu, Y.; Chávez, J.L.; Shao, G.; Zhang, H. Evaluating the Sensitivity of Water Stressed Maize Chlorophyll and Structure Based on UAV Derived Vegetation Indices. Comput. Electron. Agric. 2021, 185, 106174. [Google Scholar] [CrossRef]
- Shen, L.; Gao, M.; Yan, J.; Wang, Q.; Shen, H. Winter Wheat SPAD Value Inversion Based on Multiple Pretreatment Methods. Remote Sens. 2022, 14, 4660. [Google Scholar] [CrossRef]
- Fei, S.; Chen, Z.; Li, L.; Ma, Y.; Xiao, Y. Bayesian Model Averaging to Improve the Yield Prediction in Wheat Breeding Trials. Agric. For. Meteorol. 2023, 328, 109237. [Google Scholar] [CrossRef]
- Li, Q.; Xu, S.; Zhuang, J.; Liu, J.; Zhou, Y.; Zhang, Z. Ensemble Learning Prediction of Soybean Yields in China Based on Meteorological Data. J. Integr. Agric. 2023, 22, 1909–1927. [Google Scholar] [CrossRef]
- Shao, G.; Han, W.; Zhang, H.; Zhang, L.; Wang, Y.; Zhang, Y. Prediction of Maize Crop Coefficient from UAV Multisensor Remote Sensing Using Machine Learning Methods. Agric. Water Manag. 2023, 276, 108064. [Google Scholar] [CrossRef]
- Wang, H.; Huo, Z.; Zhou, G.; Liao, Q.; Feng, H.; Wu, L. Estimating Leaf SPAD Values of Freeze-Damaged Winter Wheat Using Continuous Wavelet Analysis. Plant Physiol. Biochem. 2016, 98, 39–45. [Google Scholar] [CrossRef]
- Johansen, K.; Raharjo, T.; McCabe, M. Using Multi-Spectral UAV Imagery to Extract Tree Crop Structural Properties and Assess Pruning Effects. Remote Sens. 2018, 10, 854. [Google Scholar] [CrossRef]
- Xie, J.; Chen, Y.; Yu, Z.; Wang, J.; Liang, G.; Gao, P.; Sun, D.; Wang, W.; Shu, Z.; Yin, D.; et al. Estimating Stomatal Conductance of Citrus under Water Stress Based on Multispectral Imagery and Machine Learning Methods. Front. Plant Sci. 2023, 14, 1054587. [Google Scholar] [CrossRef]
- Islam, M.D.; Di, L.; Qamer, F.M.; Shrestha, S.; Guo, L.; Lin, L.; Mayer, T.J.; Phalke, A.R. Rapid Rice Yield Estimation Using Integrated Remote Sensing and Meteorological Data and Machine Learning. Remote Sens. 2023, 15, 2374. [Google Scholar] [CrossRef]
- Wang, Q.; Che, Y.; Shao, K.; Zhu, J.; Wang, R.; Sui, Y.; Guo, Y.; Li, B.; Meng, L.; Ma, Y. Estimation of Sugar Content in Sugar Beet Root Based on UAV Multi-Sensor Data. Comput. Electron. Agric. 2022, 203, 107433. [Google Scholar] [CrossRef]
- Wang, N.; Guo, Y.; Wei, X.; Zhou, M.; Wang, H.; Bai, Y. UAV-Based Remote Sensing Using Visible and Multispectral Indices for the Estimation of Vegetation Cover in an Oasis of a Desert. Ecol. Indic. 2022, 141, 109155. [Google Scholar] [CrossRef]
- Nasir Amin, M.; Iftikhar, B.; Khan, K.; Faisal Javed, M.; Mohammad AbuArab, A.; Faisal Rehman, M. Prediction Model for Rice Husk Ash Concrete Using AI Approach: Boosting and Bagging Algorithms. Structures 2023, 50, 745–757. [Google Scholar] [CrossRef]
- Das, B.; Rathore, P.; Roy, D.; Chakraborty, D.; Jatav, R.S.; Sethi, D.; Kumar, P. Comparison of Bagging, Boosting and Stacking Algorithms for Surface Soil Moisture Mapping Using Optical-Thermal-Microwave Remote Sensing Synergies. CATENA 2022, 217, 106485. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, X.; Liu, Z. State of Health Estimation of Power Batteries Based on Multi-Feature Fusion Models Using Stacking Algorithm. Energy 2022, 259, 124851. [Google Scholar] [CrossRef]
- Ouyang, Z.; Zhou, C.; Xie, J.; Zhu, J.; Zhang, G.; Ao, M. SRTM DEM Correction Using Ensemble Machine Learning Algorithm. Remote Sens. 2023, 15, 3946. [Google Scholar] [CrossRef]
- Qiu, Y. Complete Subset Least Squares Support Vector Regression. Econ. Lett. 2021, 200, 109737. [Google Scholar] [CrossRef]
- Martín, J.; Sáez, J.A.; Corchado, E. On the Suitability of Stacking-Based Ensembles in Smart Agriculture for Evapotranspiration Prediction. Appl. Soft Comput. 2021, 108, 107509. [Google Scholar] [CrossRef]
- Tao, S.; Zhang, X.; Feng, R.; Qi, W.; Wang, Y.; Shrestha, B. Retrieving Soil Moisture from Grape Growing Areas Using Multi-Feature and Stacking-Based Ensemble Learning Modeling. Comput. Electron. Agric. 2023, 204, 107537. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gritz†, Y.; Merzlyak, M.N. Relationships between Leaf Chlorophyll Content and Spectral Reflectance and Algorithms for Non-Destructive Chlorophyll Assessment in Higher Plant Leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef]
- Daughtry, C. Estimating Corn Leaf Chlorophyll Concentration from Leaf and Canopy Reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Roujean, J.-L.; Breon, F.-M. Estimating PAR Absorbed by Vegetation from Bidirectional Reflectance Measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- Blackburn, G.A. Spectral Indices for Estimating Photosynthetic Pigment Concentrations: A Test Using Senescent Tree Leaves. Int. J. Remote Sens. 1998, 19, 657–675. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of Leaf-Area Index from Quality of Light on the Forest Floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of Soil-Adjusted Vegetation Indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P.J. Evaluation of the MERIS Terrestrial Chlorophyll Index (MTCI). Adv. Space Res. 2007, 39, 100–104. [Google Scholar] [CrossRef]
- Xue, L.; Cao, W.; Luo, W.; Dai, T.; Zhu, Y. Monitoring Leaf Nitrogen Status in Rice with Canopy Spectral Reflectance. Agron. J. 2004, 96, 135–142. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated Narrow-Band Vegetation Indices for Prediction of Crop Chlorophyll Content for Application to Precision Agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Goel, N.S.; Qin, W. Influences of Canopy Architecture on Relationships between Various Vegetation Indices and LAI and Fpar: A Computer Simulation. Remote Sens. Rev. 1994, 10, 309–347. [Google Scholar] [CrossRef]




| Band Number | Band Name | Central Wave Length/nm | Wave Width/nm | Ash Plate Reflectance/% |
|---|---|---|---|---|
| 1 | Blue | 450 | 16 | 25.095 |
| 2 | Green | 560 | 16 | 26.648 |
| 3 | Red | 650 | 16 | 26.687 |
| 4 | Red edge | 730 | 16 | 26.680 |
| 5 | Near infrared | 840 | 26 | 28.000 |
| Period | Argument Type | Number of Arguments | Optimal Combination of Arguments |
|---|---|---|---|
| Fruit growth period | Vegetation index | 9 | CIred.edge, DVI, MCARI, MSAVI, OSAVI, RDVI, RVI2, SIPI, MTCI |
| Texture feature | 8 | Contrast (450 nm), Mean (540 nm), Mean (650 nm), Variancel (650 nm), Entropy (650 nm), Moment (650 nm), Homogeneity (730 nm), Contrast (840 nm) | |
| Vegetation index + texture feature | 17 | CIred.edge, DVI, MCARI, MSAVI, OSAVI, RDVI, RVI2, SIPI, MTCI, Contrast (450 nm), Mean (540 nm), Mean (650 nm), Variancel (650 nm), Entropy (650 nm), Moment (650 nm), Homogeneity (730 nm), Contrast (840 nm) | |
| Fruit growth period + autumn shoot period | Vegetation index | 9 | CIred.edge, DVI, MCARI, NLI, OSAVI, RDVI, SIPI, TCARI, MTCI |
| Texture feature | 8 | Mean (450 nm), Dissimilarity (450 nm), Contrast (540 nm), Mean (650 nm), Contrast (650 nm), Dissimilarity (650 nm), Mean (840 nm), Second Moment (840 nm) | |
| Vegetation index + texture feature | 17 | CIred.edge, DVI, MCARI, NLI, OSAVI, RDVI, SIPI, TCARI, MTCI, Mean (450 nm), Dissimilarity (450 nm), Contrast (540 nm), Mean (650 nm), Contrast (650 nm), Dissimilarity (650 nm), Mean (840 nm), Second Moment (840 nm) |
| Period | Argument | Model | Training Set | Validation Set | ||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | RPD | R2 | RMSE | RPD | |||
| Fruit growth period | Vegetation indexes | SVR | 0.87 | 2.7 | 2.0 | 0.82 | 3.8 | 1.7 |
| RF | 0.93 | 2.2 | 2.8 | 0.88 | 3.3 | 2.1 | ||
| KNR | 0.88 | 3.1 | 2.1 | 0.86 | 2.9 | 1.9 | ||
| RR | 0.67 | 4.4 | 1.3 | 0.64 | 5.3 | 1.3 | ||
| Stacking | 0.97 | 1.4 | 4.1 | 0.91 | 2.8 | 2.4 | ||
| Texture features | SVR | 0.81 | 3.0 | 1.7 | 0.65 | 4.7 | 1.3 | |
| RF | 0.93 | 3.2 | 2.8 | 0.63 | 4.5 | 1.3 | ||
| KNR | 0.44 | 5.0 | 1.1 | 0.36 | 6.30 | 1.1 | ||
| RR | 0.54 | 5.2 | 1.2 | 0.54 | 5.1 | 1.2 | ||
| Stacking | 0.96 | 1.6 | 3.5 | 0.69 | 4.6 | 1.4 | ||
| Vegetation indexes + texture features | SVR | 0.95 | 2.0 | 3.1 | 0.83 | 3.4 | 1.8 | |
| RF | 0.97 | 1.5 | 4.2 | 0.92 | 2.5 | 2.6 | ||
| KNR | 0.75 | 4.0 | 1.5 | 0.75 | 4.1 | 1.5 | ||
| RR | 0.78 | 3.8 | 1.6 | 0.71 | 3.9 | 1.4 | ||
| Stacking | 0.98 | 1.3 | 4.7 | 0.94 | 2.4 | 3.0 | ||
| Period | Argument | Model | Training Set | Validation Set | ||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | RPD | R2 | RMSE | RPD | |||
| Fruit growth period + autumn shoot period | Vegetation indexes | SVR | 0.77 | 4.4 | 1.6 | 0.70 | 4.9 | 1.39 |
| RF | 0.93 | 2.9 | 2.6 | 0.73 | 4.4 | 1.5 | ||
| KNR | 0.66 | 5.1 | 1.3 | 0.59 | 5.3 | 1.2 | ||
| RR | 0.61 | 5.4 | 1.3 | 0.59 | 5.4 | 1.2 | ||
| Stacking | 0.97 | 1.4 | 4.1 | 0.91 | 2.8 | 2.4 | ||
| Texture features | SVR | 0.50 | 5.8 | 1.2 | 0.38 | 6.9 | 1.1 | |
| RF | 0.70 | 6.1 | 1.4 | 0.39 | 7.1 | 1.1 | ||
| KNR | 0.30 | 6.9 | 1.1 | 0.29 | 6.9 | 1.0 | ||
| RR | 0.39 | 6.4 | 1.1 | 0.37 | 6.7 | 1.1 | ||
| Bagging | 0.55 | 5.7 | 1.2 | 0.42 | 6.7 | 1.1 | ||
| Vegetation indexes + texture features | SVR | 0.75 | 4.3 | 1.5 | 0.66 | 5.0 | 1.3 | |
| RF | 0.93 | 2.7 | 2.8 | 0.81 | 3.9 | 1.7 | ||
| KNR | 0.69 | 4.9 | 1.4 | 0.67 | 5.0 | 1.4 | ||
| RR | 0.68 | 4.6 | 1.4 | 0.64 | 5.4 | 1.3 | ||
| Stacking | 0.95 | 2.1 | 3.2 | 0.84 | 3.9 | 1.9 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, J.; Wang, J.; Chen, Y.; Gao, P.; Yin, H.; Chen, S.; Sun, D.; Wang, W.; Mo, H.; Shen, J.; et al. Estimating the SPAD of Litchi in the Growth Period and Autumn Shoot Period Based on UAV Multi-Spectrum. Remote Sens. 2023, 15, 5767. https://doi.org/10.3390/rs15245767
Xie J, Wang J, Chen Y, Gao P, Yin H, Chen S, Sun D, Wang W, Mo H, Shen J, et al. Estimating the SPAD of Litchi in the Growth Period and Autumn Shoot Period Based on UAV Multi-Spectrum. Remote Sensing. 2023; 15(24):5767. https://doi.org/10.3390/rs15245767
Chicago/Turabian StyleXie, Jiaxing, Jiaxin Wang, Yufeng Chen, Peng Gao, Huili Yin, Shiyun Chen, Daozong Sun, Weixing Wang, Handong Mo, Jiyuan Shen, and et al. 2023. "Estimating the SPAD of Litchi in the Growth Period and Autumn Shoot Period Based on UAV Multi-Spectrum" Remote Sensing 15, no. 24: 5767. https://doi.org/10.3390/rs15245767
APA StyleXie, J., Wang, J., Chen, Y., Gao, P., Yin, H., Chen, S., Sun, D., Wang, W., Mo, H., Shen, J., & Li, J. (2023). Estimating the SPAD of Litchi in the Growth Period and Autumn Shoot Period Based on UAV Multi-Spectrum. Remote Sensing, 15(24), 5767. https://doi.org/10.3390/rs15245767







