A Modified RNN-Based Deep Learning Method for Prediction of Atmospheric Visibility

Abstract

Accurate atmospheric visibility prediction is of great significance to public transport safety. However, since it is affected by multiple factors, there still remains difficulties in predicting its heterogenous spatial distribution and rapid temporal variation. In this paper, a recursive neural network (RNN) prediction model modified with the frame-hopping transmission gate (FHTG), feature fusion module (FFM) and reverse scheduled sampling (RSS), named SwiftRNN, is developed. The new FHTG is used to accelerate training, the FFM is used for extraction and fusion of global and local features, and the RSS is employed to learn spatial details and improve prediction accuracy. Based on the ground-based monitoring data of atmospheric visibility from the China Meteorological Information Center during 1 January 2018 to 31 December 2020, the SwiftRNN model and two traditional ConvLSTM and PredRNN models are performed to predict hourly atmospheric visibility in central and eastern China at a lead of 12 h. The results show that the SwiftRNN model has better performance in the skill scores of visibility prediction than those of the ConvLSTM and PredRNN model. The averaged structural similarity (SSIM) of predictions at a lead up to 12 h is 0.444, 0.425 and 0.399 for the SwiftRNN, PredRNN and ConvLSTM model, respectively, and the averaged image perception similarity (LPIPS) is 0.289, 0.315 and 0.328, respectively. The averaged critical success index (CSI) of predictions over 1000 m fog area is 0.221, 0.205 and 0.194, respectively. Moreover, the training speed of the SwiftRNN model is 14.3% faster than the PredRNN model. It is also found that the prediction effect of the SwiftRNN model over 1000 m medium grade fog area is significantly improved along with lead times compared with the ConvLSTM and PredRNN model. All above results demonstrate the SwiftRNN model is a powerful tool in predicting atmospheric visibility.

1. Introduction

Atmospheric visibility is one of the important indicators of atmospheric transparency; it is of great importance in influencing weather and climate, such as the effects on precipitation and radiation mentioned by Yang et al. [1,2]. Snow, rain, fog, and haze could usually reduce the visibility. Low visibility may affect the safety of aviation, navigation, and transportation, and cause significant economic losses. The atmospheric visibility prediction is of great significance to support government decision-making, maintain production and life order and protect citizens’ health and safety. However, the accurate visibility prediction even for short lead times of less than 12 h is challenging [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]. The visibility is not only affected by temperature, humidity, and wind, but also closely related to aerosol concentration and chemical composition. Atmospheric visibility is one of the most difficult elements of meteorological prediction.

Since most numerical weather prediction (NWP) models do not directly predict visibility, atmospheric visibility is usually derived from the other NWP model variables, such as relative humidity, dew point, cloud water content, wind, and precipitation. Model Out Statistics (MOS) is a popular approach to derive atmospheric visibility by estimating a multivariate linear regression with NWP model variables [22,23]. However, the traditional MOS approach has several limitations for the atmospheric visibility prediction. First, the linear regression is usually unsuccessful for the small probability events, such as a sudden low visibility. Second, the effect of MOS regression is based on the persistent and stable NWP model forecast data. Once the NWP model changes, the effect of MOS approach will decrease. Third, in the 0-6 h after the NWP model is started, the cloud water content and rainwater content in the NWP model are usually very small due to the spin-up problem, which seriously affects the short-term forecast of visibility by MOS approach [24,25].

With the increase in computing power, machine learning algorithms have generated a great deal of interest in short-term weather prediction research. Sara et al. [26] discussed short-term prediction of hourly low-visibility events using different methods, some of which come from persistence analysis via Markov chain models and others based on machine learning (ML) techniques. The results showed that a hybrid expert approach in-volving persistence-based methods and machine learning techniques provides the best results on this prediction problem. Driss et al. [27] investigated the use of supervised ma-chine learning regression techniques (tree-based ensembles, feedforward neural networks and generalized linear methods) to diagnose the visibility prediction effect of a large-area mesoscale model by hourly observations from 36 synoptic land stations in the northern region of Morocco. The tree-based ensemble approach showed significant improvements for the accuracy of visibility prediction compared to a practical visibility diagnostic scheme based on the Kunkel formula. A statistical model with a physical basis was con-structed to predict visibility in the Arctic based on a dynamic Bayesian network, and test-ed daily visibility prediction over a 1° × 1° grid area. The results show that the mean relative error of the predicted visibility from the dynamic Bayesian network is approximately 14.6% compared with the inferred visibility from the artificial neural network [28]. It is concluded that the dynamic Bayesian network is useful for predicting visibility in the Arctic. In addition, the previous studies using machine learning or deep learning methods are mostly based on one-dimensional sequences and rarely extract spatial features. In recent years, two-dimensional time-series prediction models have been used for precipitation or weather radar images prediction with good results. These models can be regarded as a spatiotemporal sequence prediction problem and often adopt the sequence of past meteorological images as input to output the sequence of future meteorological images. In this paper, such models considering spatiotemporal correlation are migrated and optimized for atmospheric visibility prediction models.

Recently, recursive neural network (RNN), including long-term and short-term memory (LSTM) based on encoding and decoding framework [29,30,31], are used in weather forecasting to capture sequence temporal correlation. Klein et al. [32] proposed a dynamic convolution method to extract spatiotemporal features to predict image sequence of rain and snow. Shi et al. [33] developed a convolution LSTM (ConvLSTM) model based on the traditional LSTM model. It could capture the dynamic features between image sequences. In addition, they further proposed the trajectory gated recursive unit (Trajgru) model [34], which is more flexible than the ConvLSTM model through the recursive connection structure of location variables and performs better in the task of shortening precipitation prediction. Wang et al. [35] proposed a predictive recurrent neural network (PredRNN) and used a unified memory pool to remember spatial appearance and temporal changes. The results revealed the PredRNN model obtained better performance than the previous Trajgru and ConvLSTM models. In addition, the hybrid method combining the effective information of observation data and NWP variables can further improve the prediction accuracy. A model based on the UNet [36] is proposed to improve the accuracy of high rainfall prediction by the fusion of rainfall radar image and wind speed generated by the NWP model. A dual encoder network structure is also proposed to extract NWP-based and observation-based prediction features [37,38].

Though the deep learning algorithms were widely utilized for weather forecasting, there are some problems of slow prediction speed and fuzzy prediction image [39,40,41]. In this paper, a modified SwiftRNN model based on the PredRNN model is proposed to improve the forecast accuracy and preserve the spatial details of the forecasted atmospheric visibility images. We design a new frame-hopping transmission gate (FHTG) unit to obtain faster training speed, use feature fusion module (FFM) to extraction and fusion global and local features and use reverse scheduled sampling (RSS) to obtain higher accuracy and more spatial details in the SwiftRNN model. In the following sections, we use the atmospheric visibility data set in central and eastern China to evaluate the SwiftRNN model and compare the performance with the traditional ConvLSTM and PredRNN model.

2. Method and Data

The atmospheric visibility prediction method needs to predict the future visibility image sequences from the previous visibility image sequences. In this section, we first introduce the basic formulation of prediction problem, then the shortcomings of the traditional PredRNN model are analyzed and the structure of the proposed SwiftRNN model are presented. Finally, the implementation of two models is also described.

2.1. Formulation of Prediction Problem

The prediction of atmospheric visibility can be seen as a spatiotemporal sequence prediction problem solved by deep learning methods. The basic formulation is to input a period of historical consecutive images into a deep learning system and to output the next period of consecutive images. In this paper, the input and output images are two-dimensional atmospheric visibility field color speckle maps (RGB image). The inferred sequence of the color spot map is a prediction as to the future atmospheric visibility. The observed image at time t can be expressed as a tensor X_t ∈ R^(P × M × N), where R represents the observed feature domain, P, M and N represent the RGB channels, width and height of atmospheric visibility maps, respectively. From the perspective of time, if the observations are recorded periodically, it will generate a tensor sequence. Therefore, the deep learning prediction problem of spatiotemporal sequence is to predict the K sequences in the future by giving the previous T sequences (including the current observation value), as shown in Equation (1).

$${\widehat{X}}_{T+1},\dots ,{\widehat{X}}_{T+K}=\underset{X_{T+1},\dots ,X_{T+K}}{argmax}\rho \left(X_{T+1},\dots ,X_{T+K}|X_t,\dots ,X_T\right)$$

(1)

In this paper, $T$ and $K$ are all set as 12. That is to say, we use the previous 12 h historical visibility field color spot map (12 consecutive images) to predict the future 12 h visibility field color spot map.

2.2. Network Structure

2.2.1. Challenges in the PredRNN Model

The PredRNN model is a kind of RNN neural network proposed based on the ConvLSTM model; it replaces the ConvLSTM model with a new spatiotemporal short-term memory (ST-LSTM) unit. This spatiotemporal storage unit is updated in a zigzag direction. The information is first transmitted upward across layers, and then forward with time to realize the efficient flow of spatial information. However, the gradient is easy to disappear in the transmitted process because the memory needs to flow a longer path between distant states. With the help of the ST-LSTM unit, the PredRNN model realizes the simultaneous extraction of standard temporal memory and recommended spatiotemporal memory. The PredRNN model structure is shown in Figure 1.

The equations of the ST-LSTM unit are shown as follows:

$$\begin{gathered} g_t=tanh\left(W_{xg}\ast X_t+W_{hg}\ast H_{t-1}^l+b_g\right) \\ {i}_t=\sigma \left(W_{xi}\ast X_t+W_{hi}\ast H_{t-1}^l+b_i\right) \\ {f}_t=\sigma \left(W_{xf}\ast X_t+W_{hf}\ast H_{t-1}^l+b_f\right) \\ {C}_t^l=f_t\circ C_{t-1}^l+i_t\circ g_t \\ {g}_t^{\prime }=tanh\left(W_{xg}^{\prime }\ast X_t+W_{mg}\ast M_t^{l-1}+b_g^{\prime }\right) \\ {i}_t^{\prime }=\sigma \left(W_{xi}^{\prime }\ast X_t+W_{mi}\ast M_t^{l-1}+b_i^{\prime }\right) \\ {f}_t^{\prime }=\sigma \left(W_{xf}^{\prime }\ast X_t+W_{mf}\ast M_t^{l-1}+b_f^{\prime }\right) \\ {M}_t^l=f_t^{\prime }\circ M_t^{l-1}+i_t^{\prime }\circ g_t^{\prime } \\ {o}_t=\sigma \left(W_{xo}\ast X_t+W_{ho}\ast H_{t-1}^l+W_{co}\ast C_t^l+W_{mo}\ast M_t^l+b_o\right) \\ {H}_t^l=o_t\circ tanh\left(W_{1\times 1}\ast \left[C_t^l,M_t^l\right]\right) \end{gathered}$$

(2)

In Equation (2), $W$ and $b$ are the learnable weight and bias parameters which should be optimized in the training process. The operator $\ast$ and $\circ$ donate the convolution operator and the Hadamard product. The $tanh$ and $\sigma$ represent tanh and sigmoid activation function, respectively. Maintain two memory cells, e.g., the standard temporal memory cell $C_t^l$ and the spatiotemporal memory cell $M_t^l$. $C_t^l$ horizontally conveys the temporal evolution at the current time step $t$ from the previous time step $t-1$. $M_t^l$ vertically transits the spatiotemporal memory in the current layer $l$ from the previous layer $l$ − 1. These storage cells from different directions are connected, and then the convolution layer is applied to extract spatial information across different time steps. The final hidden state $H_t^l$ depends on the fused spatiotemporal memory cell $M_t^l$ and standard temporal cell $C_t^l$, so that the hidden state is the same as the dimension of the storage cells. Different from the simple LSTM unit, the ST-LSTM unit can effectively extract the shape deformation and motion trajectory in spatiotemporal image sequences. However, there are three challenges in the PredRNN model. Firstly, the ST-LSTM unit is often difficult in transmitting gradient during back propagation process. Thus, the cyclic architecture of the ST-LSTM unit is unstable, especially for continuous images with periodic motion. Secondly, the PredRNN model follows a sequence-to-sequence architecture. In the training phase, it always takes the real images as the input of the encoding time step, which may affect the long-term dynamic learning process. Finally, the PredRNN does not capture the global and local features sufficiently, which leads to less than optimal final predictions of the model.

2.2.2. The SwiftRNN Model

To solve the above three challenges, we propose a new SwiftRNN model based on the PredRNN model. For the first challenge, we design a frame-hopping transmission gate (FHTG) to improve the difficulty of gradient transmission. In the new structure, the FHTG unit works seamlessly with the ST-LSTM unit to capture the dependence of long-term and short-term continuous images, respectively. By quickly updating the hidden state, the FHTG unit could carry out a fast route from any vertical steps of the first-time step to any vertical steps of the last time step (green line in Figure 2). It could realize the adaptive learning of the long-term and short-term image relationship.

The internal calculation formula of the SwiftRNN model integrating the FHTG unit is as follows.

$$\begin{gathered} Z_t^{l-1}=FHTG\left(H_t^{l-1},Z_{t-1}^{l-1}\right) \\ {H}_t^l,C_t^l,M_t^l=STLST{M}_l\left(Z_t^{l-1},H_{t-1}^l,C_{t-1}^l,M_t^{l-1}\right) \end{gathered}$$

(3)

The internal calculation formula of the FHTG unit is:

$$\begin{gathered} P_t=tanh\left(W_{px}\ast X_t+W_{pz}\ast Z_{t-1}\right) \\ {S}_t=\sigma \left(W_{sx}\ast X_t+W_{sz}\ast Z_{t-1}\right) \\ {Z}_t=S_t\circ P_t+\left(1-S_t\right)\circ Z_{t-1} \end{gathered}$$

(4)

For the second challenge, inspired by the PredRNN-v2 model [42], we employ the new curriculum learning strategy of the PredRNN-v2 model, which consists of two parts, e.g., reverse scheduled sampling (RSS) and scheduled sampling (SS). Figure 3 shows two possible strategies for combining RSS and SS strategies. The RSS strategy is employed at encoding timesteps to force the PredRNN model to learn long-term dynamics. The SS strategy is utilized to alleviate the inconsistency of data flow at forecasting timesteps between the training and inference process. The formula of encoder and forecaster is as follows:

$${\widehat{X}}_{t+1}=\{\begin{array}{c}\mathrm{SwiftRNN}\left({\widehat{X}}_t\stackrel{RSS}{\to }{X}_t,H_{t-1},Q_{t-1}\right) if t\le T,\hfill \\ \mathrm{SwiftRNN}\left(X_t\stackrel{SS}{\to }{\widehat{X}}_t,H_{t-1},Q_{t-1}\right) if t>T,\hfill \end{array}$$

(5)

where $Q_{t-1}=\left\{C_{t-1},M_{t-1}\right\}$ is a combination of memory cells at previous time step $t-1$. The main difference between encoding part (t $\le$ T) and forecasting part (t > T) is whether the observed image $X_t$ or the previous prediction image ${\widehat{X}}_t$ is used. In the encoder, the model mainly learns observed images because $X_t$ contains more accurate information than $H_{t-1}$ and $Q_{t-1}$. However, for the forecaster, due to the fact that there are no new observations in the future timestep, the model should learn long-term dynamics transmitted from $H_{t-1}$ and $Q_{t-1}$. Specifically, in encoder part, RSS gradually uses the observed image $X_t$ instead of the previous prediction image ${\widehat{X}}_t$ with an increasing probability $p_{RSS}$ during the training process. Conversely, for SS in the forecaster part, the previous prediction image ${\widehat{X}}_t$ will be used with an increasing probability $p_{SS}$ instead of the observed image $X_t$ during the training process. The increasing probability function $p_{RSS}$ and $p_{SS}$ used in this study are displayed in Equation (6). $p_{RSS}$ is an increasing function of the number of training iterations $k$, starting from ${ϵ}_s$ and increasing to ${ϵ}_e$, where ${\alpha }_l$, ${\alpha }_s$ > 0 denotes the increasing factors and ${\beta }_s>0$ denotes the starting point of the sigmoid function.

$$\begin{array}{c}{p}_{RSS}={ϵ}_e+({ϵ}_e-{ϵ}_s)\times \frac{1}{1+\exp (\frac{{\beta }_s-k}{{\alpha }_s})}\\ p_{SS}=\min ({ϵ}_s+{\alpha }_l\times k, {ϵ}_e)\end{array}$$

(6)

If the conventional training method is used, the inconsistent training between encoder and forecaster may lead to invalid optimization and hinder the long-term dynamics of model learning. Additionally, the RSS training strategy will effectively relieve the above problem.

For the final challenge, we intend to improve the sensitivity of the model to low atmospheric visibility by using global features. We use a transformer-based model to extract global information. Therefore, we propose a novel feature fusion module (FFM) that includes a local feature extraction unit, a global feature extraction unit, and then we fuse these two different scales of features. When predicting atmospheric visibility, in addition to global features, local features are also important. Therefore, we designed a local feature extraction unit, which can fully extract local features from the atmospheric visibility information. It is helpful for prediction of high and medium atmospheric visibility. Concretely, our local features extraction unit mainly consists of convolution block and attention mechanisms. The latter is composed of a convolutional block attention module (CBAM) [43].

The last step of this module is to fuse the extracted two parts of features as shown in Equation (7). It is similar to a gating mechanism. It empties what needs to be forgotten and keeps what needs to be remembered. By constraining the local and global features through the above gating mechanism, it greatly alleviates the numerical differences and avoids the problem that linear fusion does not work due to significant differences between them.

$$X_t^{\prime }=\sigma (global)\ast global+\sigma (local)\ast local$$

(7)

where $local$ and $global$ represent local features and global features, respectively.

2.3. Loss Function

The frequency of atmospheric visibility data with different levels is significantly unbalanced, so the weighted loss is used to alleviate this problem. Based on the principle that the lower visibility shares the greater importance, we define different weights for atmospheric visibility data with different levels by Equation (8):

$$\omega (X)=\{\begin{array}{c}25, X<1000 \mathrm{m}\hfill \\ 9, 1000 \mathrm{m}\le X<4000 \mathrm{m}\hfill \\ 4, 4000 \mathrm{m}\le X<10000 \mathrm{m}\hfill \\ 1, 10000 \mathrm{m}\le X\hfill \end{array}$$

(8)

where, $X$ represents the atmospheric visibility image in this study. The weighted loss function we designed is shown in Equation (9):

$$\begin{gathered} loss=\frac{1}{K}{{\displaystyle \sum }}_{t=1}^{k}MSE(X_t,{\widehat{X}}_t)+\frac{1}{2}(1-SSIM(X_t,{\widehat{X}}_t)+LPIPS(X_t,{\widehat{X}}_t)) \\ MSE(X_t,{\widehat{X}}_t)={{\displaystyle \sum }}_{i,j}{\omega }_{t,i,j}{(X_{t,i,j}-{\widehat{X}}_{t,i,j})}^2 \end{gathered}$$

(9)

where $K$ represents the number of all images in the predicted sequence, and ${\omega }_{t,i,j}$ represents the weight of the (i, j)th pixel at the $t$-th image. $X_{t,i,j}$ and ${\widehat{X}}_{t,i,j}$ are the value of (i, j)th of ground observed visibility field map $X_t$ and predicted visibility field map ${\widehat{X}}_t$ at the time step $t$. In the calculation of mean square error (MSE), more weight is given to the lower atmospheric visibility to improve the prediction performance of low visibility. By this way, the lack of low visibility samples can be compensated to some extent. The main purpose of training this network is to ensure that the predicted visibility field map is as close to the observed image as possible. The combination of structural similarity (SSIM) [44] and image perception similarity index (LPIPS) [45] in the loss function can enhance the details of the predicted image.

2.4. Implementation

All models are optimized using the Adam optimizer with a learning rate equal to 10⁻⁴. The parameters in Adam optimizer are set β1 = 0.9, β2 = 0.999. The formula for the Adam optimizer is shown in Equation (10), where $m_t$ represents past gradients, $v_t$ represents square of past gradient, ${\widehat{m}}_t$ and ${\widehat{v}}_t$ are the deviation correction of $m_t$ and $v_t$, ${\theta }_{t+1}$ represents the new gradient. The implementation details of the SwiftRNN model are shown in

Table 1. Implementation details of the proposed method.

Hyper-Parameter	Value
ST-LSTM layers	4
Kernel sizes of convolutional layers	5 × 5
Channels of convolutional layers	128
Optimizer	Adam (β1 = 0.9, β2 = 0.999)
Batch size	4
Learning rate	$1\times {10}^{-4}$
Framework	Pytorch 1.7
GPU	NVIDIA RTX 3090

. The training batch size in the SwiftRNN model is set to 4. The kernel sizes of all convolutional layers except that in the output operations (the kernel size is 1 × 1) are set as 5 × 5. Before the convolution operation, the boundary of the visibility field map is zero-filled to keep the size of the feature map unchanged. We implemented the SwiftRNN model using the Pytorch framework and trained this model with NVIDIA RTX 3090 GPU and CUDA 11.0.

$$\begin{gathered} m_t={\beta }_1{m}_{t-1}+(1-{\beta }_1)g_t \\ {v}_t={\beta }_2{v}_{t-1}+(1-{\beta }_2)g_t^2 \\ {\widehat{m}}_t=\frac{m_t}{1-{\beta }_1^t} \\ {\widehat{v}}_t=\frac{v_t}{1-{\beta }_2^t} \\ {\theta }_{t+1}={\theta }_t-\frac{\eta }{\sqrt{{\widehat{v}}_t}+ϵ}{\widehat{m}}_t \end{gathered}$$

(10)

2.5. Visibility Field Map Dataset

2.5.1. Introduction to the Dataset

Using the deep learning method to realize atmospheric visibility prediction requires a large amount of data. In this paper, the atmospheric visibility data is obtained from the meteorological station observed by China Meteorological Information Center. We collected the hourly visibility data from 1st January 2018 to 31st December 2020. The regional geographical scope covers the central and eastern regions of China, with longitude ranging from 100° to 120° E and latitude ranging from 20° to 40° N. A total of 2428 observation stations are selected in the area. Figure 4 shows the geographical area involved in the data set.

2.5.2. Pre-Process of the Visibility Field Map Dataset

Because the original observation data has outliers and defect values, the damaged data should be cleaned before training the model, including outliers’ deletion and missing data filling. For the data of outliers, e.g., 999,999, are directly deleted. Additionally, then two methods are used to fill missing data:

• If the number of continuous missing data does not exceed 1, the previous and behind two non-missing data are used for mean filling.
• If the number of continuous missing data exceeds 1, the previous and behind non-missing data are used for linear interpolation for filling.

The data set required for spatiotemporal sequence prediction is a set of continuous two-dimensional images. Therefore, this paper makes a user-defined color mapping on the longitude and latitude of the hourly site data, and finally generates the image in RGB picture. Because the number of ground observation stations is limited and cannot cover all grid points, linear interpolation is used to fill the values of grid points without station. We have used the bilinear interpolation method, which is a linear interpolation extension of the interpolation function with two variables, the core idea of which is to perform one linear interpolation in each of the two directions.

When sorting the pictures, it is found that some pictures are all-blue or all-green (indicating high visibility), but the pictures before and after them are not all-blue or all-green and have obvious low visibility. Therefore, it is speculated that these all-blue or all-green pictures are caused by the lack of collected station data. Therefore, delete these all-blue or all-green pictures, and then copy the adjacent pictures to the default place. This can avoid a negative impact on the training process. Considering the time and memory cost of deep learning training, compress the pictures to 128 × 128 pixels and 96 DPI.

In the time segment extraction function, we select the time segments with continuous time, and take corresponding pictures during the time segments as modelling samples. If there are any missing pictures in the time segment, this segment will not be considered. Among them, the modelling samples in 2018 and 2019 are used as training sets and validation sets, with a ratio of 8:2. Modelling samples in 2020 is used as a test set. Details of the visibility field map dataset is shown in

Table 2. Details of the visibility field map dataset.

Year	Number of Pictures
2018	8760
2019	8760
2020	8784

.

3. Experiments

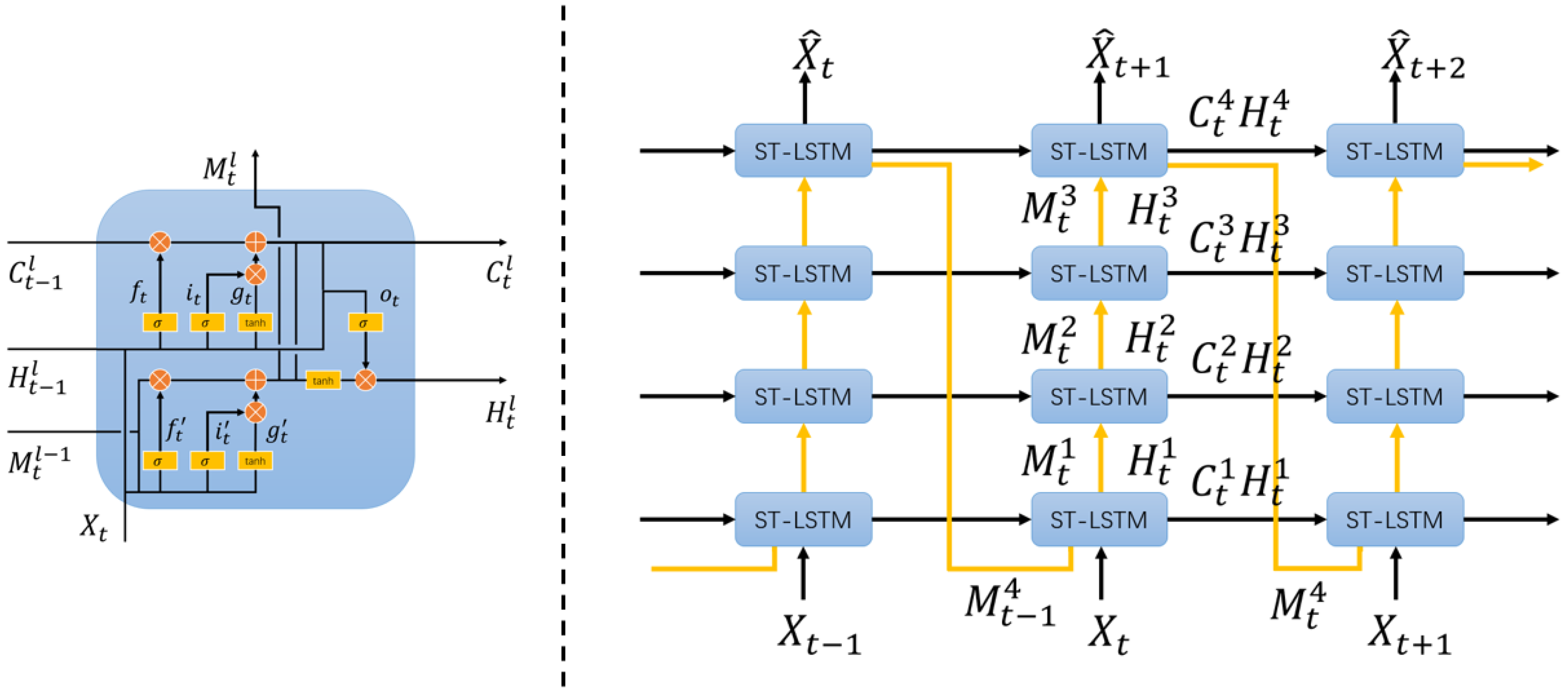
3.1. Evaluation

In this paper, we use a variety of metrics to quantify the prediction effect of three models, including SSIM (structural similarity), LPIPS (image perception similarity index) and CSI (critical success index). The SSIM and LPIPS metrics are used to quantify the image similarity based on the perspective of iconology, and the CSI metric is commonly used in the field of meteorology, which represents the success rate of prediction.

SSIM is an index to measure the similarity of two images. Given two images $x$ and $y$, the structural similarity of the two images can be calculated according to Equation (11), where ${\mu }_x$ is the average of $x$, ${\mu }_y$ is the average of $y$, ${\sigma }_x^2$ is the variance of $x$, ${\sigma }_y^2$ is the variance of $y$, and ${\sigma }_{xy}$ is the covariance of $x$ and $y$. $c_1={(k_{1}L)}^2$, $c_2={(k_{2}L)}^2$ is a constant used to maintain stability, $L$ is the dynamic range of pixel value, $k_1=0.01$, $k_2=0.03$.

$$SSIM(x,y)=\frac{(2{\mu }_x{\mu }_y+c_1)(2{\sigma }_{xy}+c_2)}{({\mu }_x^2+{\mu }_y^2+c_1)({\sigma }_x^2+{\sigma }_y^2+c_2)}$$

(11)

LPIPS learns to generate the reverse mapping from the image to the ground truth, forces the generator to learn to reconstruct the reverse mapping of the real image from the false image, and gives priority to processing the perceptual similarity between them, which is more in line with human perception. The lower the value of LPIPS, the more similar the two images are, where $d(x,x_0)$ represents the distance of $x$ and $x_0$ (d represents LPIPS), as shown in Equation (12), where $H_l$ and $W_l$ represent the height and width of the image, respectively in convolutional layer $l$, ${\widehat{y}}_{hw}^l$ and ${\widehat{y}}_{0hw}^l$ are the result of normalizing the output of each convolutional layer after activation, vector $w_l$ is used to deflate the number of active channels, and $⨀$ represents the multiplication of $w_l$ and $({\widehat{y}}_{hw}^l-{\widehat{y}}_{0hw}^l)$.

$$d(x,x_0)={\displaystyle \sum }_l\frac{1}{H_l{W}_l}{\displaystyle \sum }_{h,w}\parallel w_l⨀{({\widehat{y}}_{hw}^l-{\widehat{y}}_{0hw}^l)\parallel }_2^2$$

(12)

For the construction of the CSI metric in this study, since the prediction task is completed at the pixel level, they are projected back to the atmospheric visibility, and the atmospheric visibility of each pixel is calculated. This metric is like the classification metric and mainly focuses on whether the prediction of the location point is hit within a certain threshold range. For example, if the threshold is 1000 m, after binarization, 999 m will be converted to 0, 1001 m will be converted to 1. After converting each pixel value between the predicted value and the real value to 0/1, the $hits$ (true positive, predicted value = 1, real value = 1), $misses$ (false positive, predicted value = 1, real value = 0) and $false\_alarms$ (false negative, predicted value = 0, true value = 0) are calculated. To fully evaluate the performance of the algorithm, this paper calculates this metric under three thresholds, e.g., 1000 m, 4000 m and 10,000 m, corresponding to atmospheric visibility with different levels. The CSI metric is shown in Equation (13).

$$CSI=\frac{hits}{hits+misses+false\_alarms}$$

(13)

3.2. Results

In this section, we compare the SwiftRNN model with the classical ConvLSTM and PredRNN models based on the SSIM, LPIPS and CSI metrics.

To intuitively analyze the prediction effect, a group of individual cases are selected from the test set for analysis. Figure 5 shows the spatial distribution of atmospheric visibility images predicted by the ConvLSTM, PredRNN and SwiftRNN models at 12:00–17:00 on 31st October 2020; those results are also compared with the observed atmospheric visibility images. It can be seen that the spatial distribution of atmospheric visibility images predicted by the ConvLSTM, PredRNN and SwiftRNN models is in good agreement with the observed images. However, since the predictions of the ConvLSTM model are relatively unsatisfactory compared with the other two models, we only analyze the results of the proposed SwiftRNN model and the PredRNN model. Generally, the SwiftRNN and PredRNN model can well predict two large low-visibility areas in north and central China. Additionally, in some fine local characteristics, the low visibility in Wuhan, Tianjin, Shijiazhuang and other areas can also be well grasped. However, the overall intensity of the predicted images is slightly larger than the observed images, and the low visibility in Henan is underestimated in the next few hours. Compared with the PredRNN model, the visibility distribution predicted by the SwiftRNN model is closer to the observed images. For the example in Figure 5, the PredRNN model forecasts lower visibility in Shanxi, Shaanxi and the Yangtze River Delta, while the predicted results by the SwiftRNN model are more accurate and do not differ much from the observed images. In addition, the advantage of the SwiftRNN model is more obvious in the last 6 h. Figure 6 shows the comparison of the predicted results from 18:00 to 23:00 on 31st October 2020, the predicted results from the SwiftRNN model have a larger area of low visibility in central China and Guizhou, and a smaller area of low visibility in northern Jiangsu, northern Anhui, and Henan, which is closer to the observed images. However, the PredRNN model predicts heavier visibility over more areas, and the spatial details of the predictions are not as good as those of the SwiftRNN model. Overall, the PredRNN model is less accurate compared with the SwiftRNN model.

Table 3. The SSIM metric of visibility field map prediction for 4 months.

MODEL	January	April	July	October
ConvLSTM	0.381	0.398	0.431	0.389
PredRNN	0.394	0.431	0.461	0.415
SwiftRNN	0.415 (5.33%↑)	0.452 (4.87%↑)	0.472 (2.39%↑)	0.435 (4.82%↑)

‘↑’ means the improvement rate of the SSIM metric of SwiftRNN model in comparison to that of the PredRNN model.

and

Table 4. Same with Table 3, but for LPIPS metric.

MODEL	January	April	July	October
ConvLSTM	0.328	0.325	0.337	0.321
PredRNN	0.308	0.321	0.320	0.312
SwiftRNN	0.286 (7.14%↓)	0.278 (13.39%↓)	0.314 (1.86%↓)	0.277 (11.22%↓)

‘↓’ means the reduction rate of the LPIPS metric of SwiftRNN model in comparison to that of the PredRNN model.

show the SSIM metrics and LPIPS metrics of the 12 h predictions by the ConvLSTM, PredRNN and SwiftRNN model. It can be seen from these tables that the performance of the SwiftRNN model is better than the PredRNN model in four seasons. Thus, the proposed SwiftRNN model is conducive to predict clearer and more detailed atmospheric visibility images.

Figure 7 compares image similarity metrics in four seasons of the SwiftRNN and PredRNN model; we can see in winter, spring and autumn, the SSIM metrics of the predicted atmospheric visibility images by the SwiftRNN model are lower than those by the PredRNN model in the first four hours, but the SSIM metrics by the SwiftRNN model are higher than those by the PredRNN model in the following hours, which indicates that the SwiftRNN model can capture the characteristics of a longer time. Compared the SSIM metric in summer, the SwiftRNN model performs better than the PredRNN model in all hours. In terms of the LPIPS metric, the LPIPS metrics of the SwiftRNN model are lower than those of the PredRNN model. Therefore, in general, the images predicted by the SwiftRNN model are more detailed and closer to the observed images than those predicted by the PredRNN model.

Table 5. CSI-1000 of visibility field map prediction for 4 months.

MODEL	January	April	July	October
ConvLSTM	0.163	0.221	0.206	0.189
PredRNN	0.179	0.229	0.215	0.197
SwiftRNN	0.193 (7.82%↑)	0.243 (6.11%↑)	0.232 (7.91%↑)	0.213 (8.12%↑)

‘↑’ means the improvement rate of the CSI-1000 metric of SwiftRNN model to that of PredRNN model.

,

Table 6. Same with Table 5, but for CSI-4000 metric.

MODEL	January	April	July	October
ConvLSTM	0.417	0.465	0.501	0.458
PredRNN	0.433	0.483	0.520	0.477
SwiftRNN	0.460 (6.24%↑)	0.510 (5.29%↑)	0.552 (6.15%↑)	0.506 (6.08%↑)

‘↑’ means the improvement rate of the CSI-4000 metric of SwiftRNN model to that of PredRNN model.

and

Table 7. Same with Table 5, but for CSI-10000 metric.

MODEL	January	April	July	October
ConvLSTM	0.506	0.555	0.608	0.558
PredRNN	0.527	0.577	0.632	0.579
SwiftRNN	0.553 (4.93%↑)	0.603 (4.51%↑)	0.664 (5.06%↑)	0.609 (5.18%↑)

‘↑’ means the improvement rate of the CSI-10000 metric of SwiftRNN model to that of PredRNN model.

show the CSI metrics of the 12 h predictions by the ConvLSTM, PredRNN and SwiftRNN model. To fairly compare and fully evaluate the performance of the algorithm, we calculate the CSI metric under three atmospheric visibility thresholds in different seasons, including 1000 m, 4000 m and 10,000 m.

It can be seen that in the deep learning method, the nonlinear and convolutional structure of the network can learn some complex spatiotemporal patterns in the data set. Obviously, our proposed SwiftRNN model better achieves the CSI metric than the PredRNN model. At the threshold of 1000 m, the CSI metrics of the SwiftRNN model in winter, spring, summer, and autumn are increased by about 7.82%, 6.11%, 7.91% and 8.12%, respectively, compared with those of the PredRNN model. At the threshold of 4000 m, the CSI metrics of the SwiftRNN model in winter, spring, summer, and autumn are increased by about 6.24%, 5.59%, 6.15% and 6.08%, respectively compared with those of the PredRNN model. At the threshold of 10,000 m, the CSI metrics of the SwiftRNN model in winter, spring, summer, and autumn are increased by about 4.93%, 4.51%, 5.06% and 5.18%, respectively, compared with those of the PredRNN method. It can be concluded that although the SwiftRNN model obtains the promising performance at the threshold of 4000 m and 10,000 m, there is a maximum percentage increase at the threshold of 1000 m, which means that the proposed model has better prediction performance for low visibility. In addition, the improvement effect of atmospheric visibility prediction in winter, summer and autumn is relatively similar, and the improvement effect of atmospheric visibility prediction in spring is not obvious.

Figure 8 shows the CSI metrics of three models in four seasons. Comparing (a) January, (b) April, (c) July, and (d) October horizontally, it can be seen that the two models obtain the best predicted effect in summer and the worst predicted effect in winter. Vertical comparison of (a) January, (b) April, (c) July, and (d) October shows that the predicted effect of 10,000 m threshold is the best, the predicted effect of a 4000 m threshold is the second, and the predicted effect of 1000 m is the worst. Additionally, the SwiftRNN model performs better than the PredRNN model in all three thresholds.

Table 8. Model training speed.

MODEL	Seconds/Epoch (Seconds)
ConvLSTM	6.774
PredRNN	6.132
SwiftRNN	5.255 (14.3%↓)

‘↓’ means the reduction rate of the seconds/epoch metric of SwiftRNN model to that of PredRNN model.

indicates the training speed of three models. Based on 40,000 epochs, where the PredRNN model is about 6.132 s per epoch and the SwiftRNN model is about 5.255 s per epoch, the improvement effect is 14.3%.

4. Conclusions

In this paper, a SwiftRNN model for atmospheric visibility prediction based on the PredRNN model is proposed, and the atmospheric visibility in central and eastern China is predicted based on the station observation data of China Meteorological data network. This proposed model adds a multi-layer FHPG unit in the PredRNN model and uses the RSS strategy in the training process. This paper realizes the simultaneous spatiotemporal prediction of atmospheric visibility and improves the spatial details and accuracy of the predicted atmospheric visibility images. Compared with the PredRNN model, the SwiftRNN model has a more obvious improvement effect on the prediction effect of medium and low visibility along with the lead times. The training speed of the SwiftRNN model is also saved.

At present, the application of deep learning methods in the field of meteorology is still in the exploratory stage, and there is still much room for improvement. For example, the images predicted by the PredRNN and SwiftRNN model are relatively blurred, which will have a certain negative impact on the final test score. How to make the model produce finer prediction images as much as possible without losing the model test score is the focus of the next research. In addition, the accuracy deterioration of prediction effect along with the lead times is still an unsolved problem. In future research, the Attention Augmented TransUNet (AA-TransUNet) [46] model and muti-attention mechanism can be used to output finer prediction results and improve the prediction effect over time. In terms of atmospheric visibility prediction, how to effectively fuse radar, ground, satellite, and other multi-source data for prediction, and constantly incorporate the newly generated observation data into the neural network model training, to continuously improve the prediction effect with the passage of time still need more attention of researchers. In addition, how to organically combine the physical conceptual model into the deep learning algorithm is also worthy of in-depth research.