DOA Estimation in Impulsive Noise Based on FISTA Algorithm
Abstract
:1. Introduction
2. Signal Model
3. FISTA-Based DOA Estimation Method for Impulsive Noise
3.1. SSR Model and FISTA Algorithm
| Algorithm 1 Fast Iterative Shrinkage-Thresholding Algorithm |
|
3.2. DOA Estimation in Impulsive Noise
| Algorithm 2 Proposed FISTA-based method for DOA estimation in impulsive noise |
|
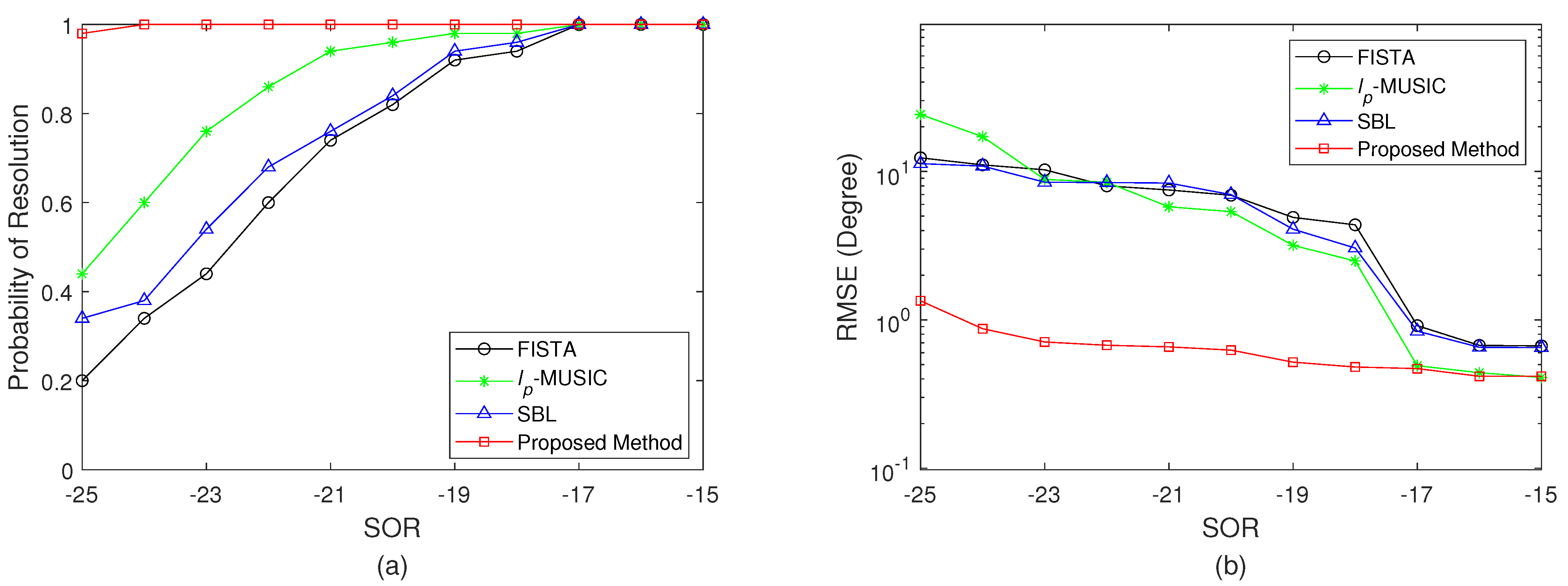
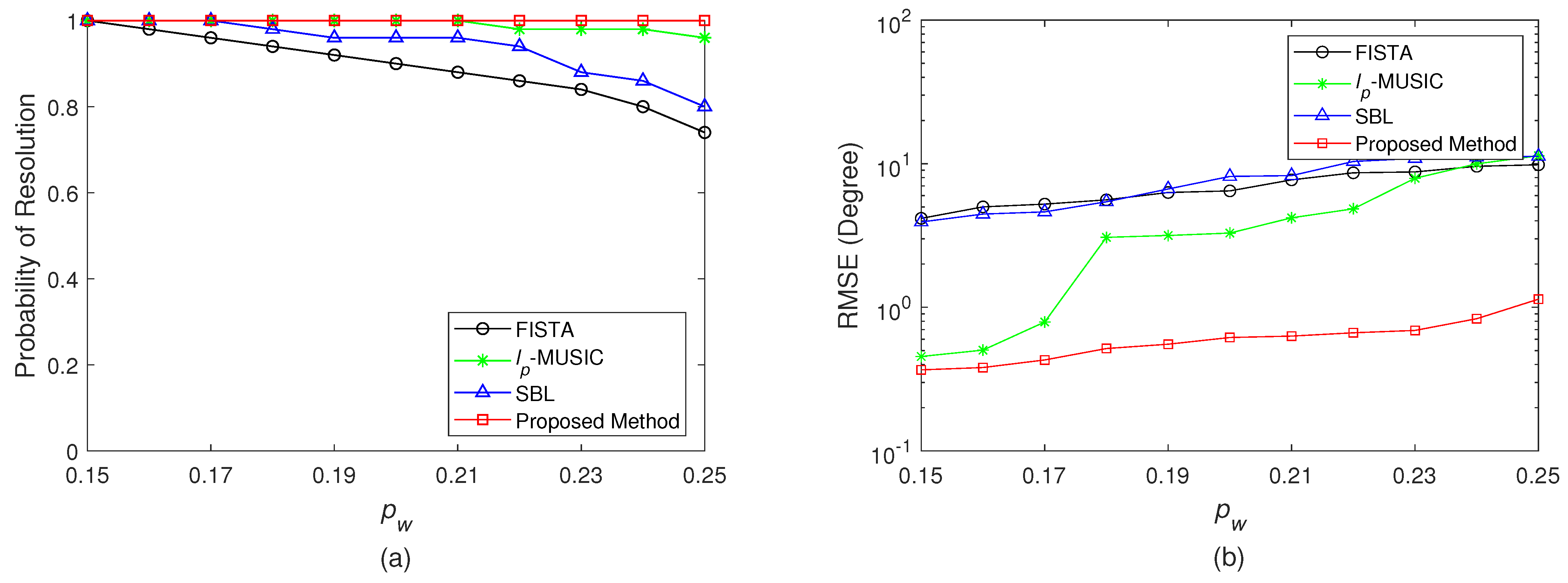
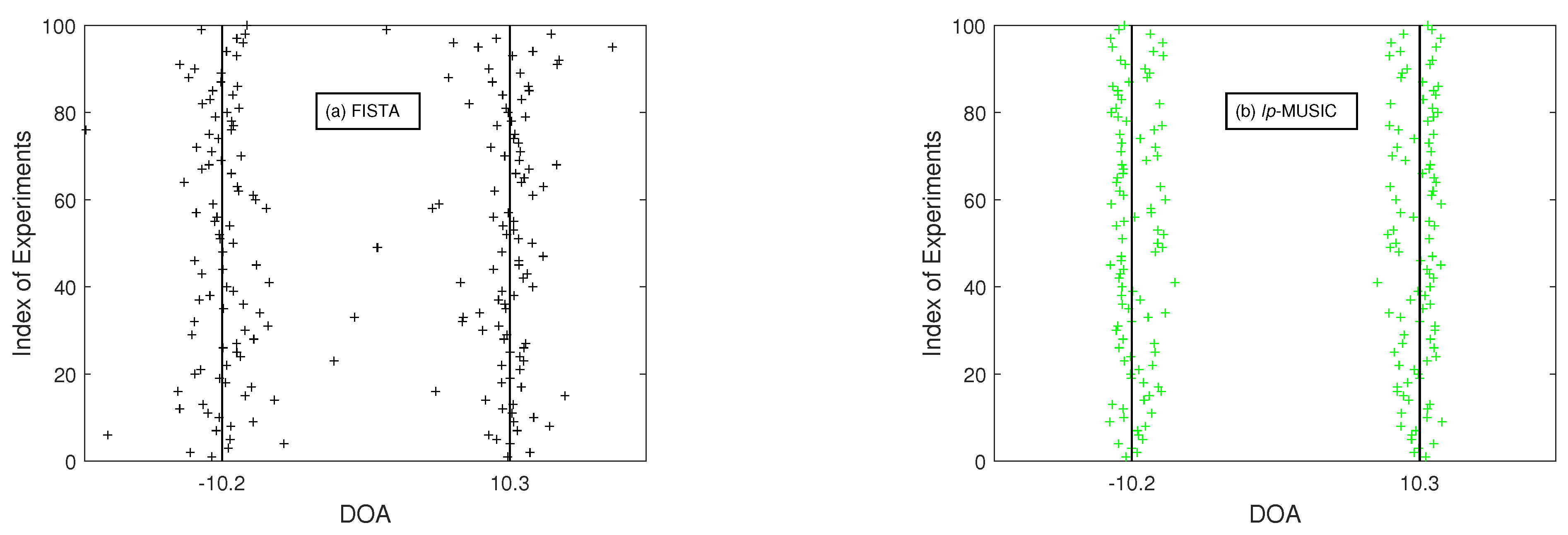
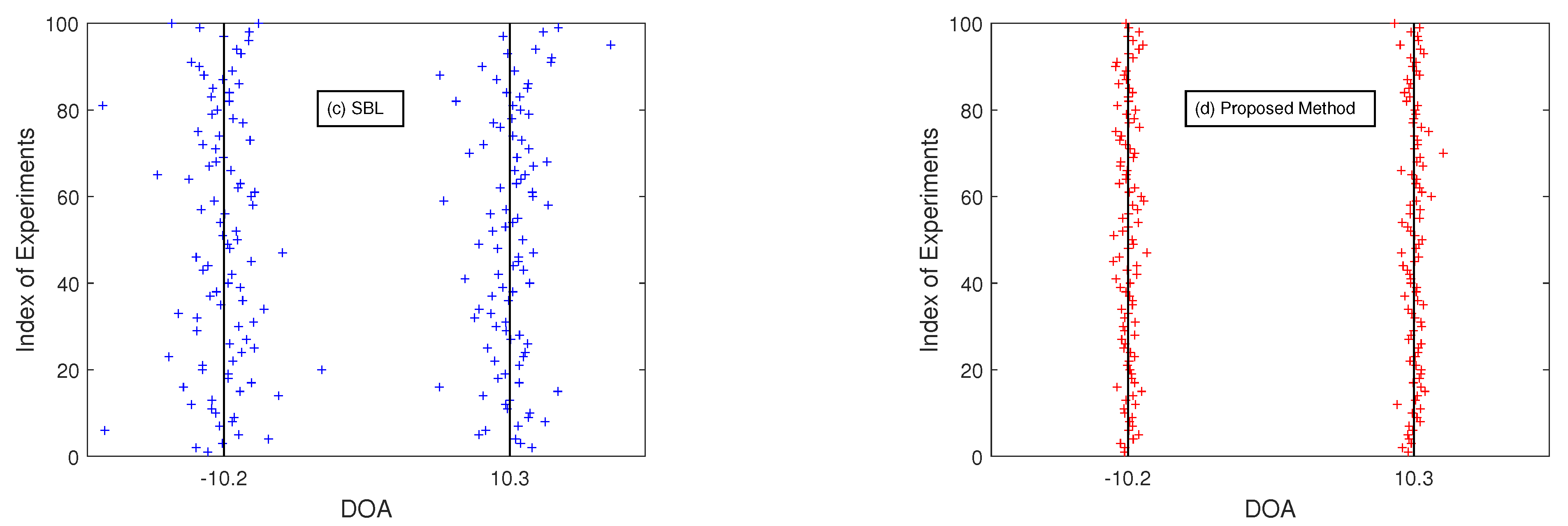
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Johnson, D.H.; Dan, E.D. Array Signal Processing: Concepts and Techniques; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef] [Green Version]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef] [Green Version]
- Rao, B.; Hari, K. Performance analysis of Root-Music. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 1939–1949. [Google Scholar] [CrossRef]
- Nikias, C.L.; Shao, M. Signal Processing with α-Stable Distributions and Applications; John Wiley & Sons: New York, NY, USA, 1995. [Google Scholar]
- Zhidkov, S.V. Analysis and comparison of several simple impulsive noise mitigation schemes for OFDM receivers. IEEE Trans. Commun. 2008, 56, 5–9. [Google Scholar] [CrossRef]
- Zeng, W.J.; So, H.C.; Huang, L. ℓp-MUSIC: Robust Direction-of-Arrival Estimator for Impulsive Noise Environments. IEEE Trans. Signal Process. 2013, 61, 4296–4308. [Google Scholar] [CrossRef]
- Tsakalides, P.; Nikias, C. The robust covariation-based MUSIC (ROC-MUSIC) algorithm for bearing estimation in impulsive noise environments. IEEE Trans. Signal Process. 1996, 44, 1623–1633. [Google Scholar] [CrossRef]
- Liu, T.H.; Mendel, J. A subspace-based direction finding algorithm using fractional lower order statistics. IEEE Trans. Signal Process. 2001, 49, 1605–1613. [Google Scholar] [CrossRef]
- Swami, A.; Bm, S. On some detection and estimation problems in heavy-tailed noise. Signal Process. 2002, 82, 1829–1846. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Statistics; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Lee, D.D.; Kashyap, R.L. Robust maximum likelihood bearing estimation in contaminated Gaussian noise. IEEE Trans. Signal Process. 1992, 40, 1983–1986. [Google Scholar] [CrossRef]
- Liao, B.; Zhang, Z.G.; Chan, S.C. A New Robust Kalman Filter-Based Subspace Tracking Algorithm in an Impulsive Noise Environment. IEEE Trans. Circuits Syst. II Express Briefs 2010, 57, 740–744. [Google Scholar] [CrossRef] [Green Version]
- Chan, S.; Wen, Y.; Ho, K. A robust past algorithm for subspace tracking in impulsive noise. IEEE Trans. Signal Process. 2006, 54, 105–116. [Google Scholar] [CrossRef] [Green Version]
- Visuri, S.; Oja, H.; Koivunen, V. Subspace-based direction-of-arrival estimation using nonparametric statistics. IEEE Trans. Signal Process. 2001, 49, 2060–2073. [Google Scholar] [CrossRef]
- Malioutov, D.; Cetin, M.; Willsky, A. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Process. 2005, 53, 3010–3022. [Google Scholar] [CrossRef] [Green Version]
- Hyder, M.M.; Mahata, K. Direction-of-Arrival Estimation Using a Mixed ℓ2,0 Norm Approximation. IEEE Trans. Signal Process. 2010, 58, 4646–4655. [Google Scholar] [CrossRef]
- Xu, X.; Wei, X.; Ye, Z. DOA Estimation Based on Sparse Signal Recovery Utilizing Weighted l1-Norm Penalty. IEEE Signal Process. Lett. 2012, 19, 155–158. [Google Scholar] [CrossRef]
- Yin, J.; Chen, T. Direction-of-Arrival Estimation Using a Sparse Representation of Array Covariance Vectors. IEEE Trans. Signal Process. 2011, 59, 4489–4493. [Google Scholar] [CrossRef]
- Dai, J.; So, H.C. Sparse Bayesian Learning Approach for Outlier-Resistant Direction-of-Arrival Estimation. IEEE Trans. Signal Process. 2018, 66, 744–756. [Google Scholar] [CrossRef]
- Lee, G.C.F.; Rawat, A.S.; Wornell, G.W. Robust Direction of Arrival Estimation in the Presence of Array Faults using Snapshot Diversity. In Proceedings of the 2019 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Ottawa, ON, Canada, 11–14 November 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, C.; Xie, L. Robustly Stable Signal Recovery in Compressed Sensing With Structured Matrix Perturbation. IEEE Trans. Signal Process. 2012, 60, 4658–4671. [Google Scholar] [CrossRef]
- Huang, T.; Liu, Y.; Meng, H.; Wang, X. Adaptive matching pursuit with constrained total least squares. EURASIP J. Adv. Signal Process. 2012, 1, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambrige University Press: Cambrige, UK, 2004. [Google Scholar]
- Beck, A.; Teboulle, M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef] [Green Version]
- Tan, Z.; Yang, P.; Nehorai, A. Joint Sparse Recovery Method for Compressed Sensing with Structured Dictionary Mismatches. IEEE Trans. Signal Process. 2014, 62, 4997–5008. [Google Scholar] [CrossRef] [Green Version]
- Carrillo, R.E.; Barner, K.E. Lorentzian Iterative Hard Thresholding: Robust Compressed Sensing with Prior Information. IEEE Trans. Signal Process. 2013, 61, 4822–4833. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Zhang, Y. Alternating Direction Algorithms for ℓ1-Problems in Compressive Sensing. SIAM J. Sci. Comput. 2011, 33. [Google Scholar] [CrossRef]
- Wen, F.; Liu, P.; Liu, Y.; Qiu, R.C.; Yu, W. Robust Sparse Recovery in Impulsive Noise via ℓp-ℓ1 Optimization. IEEE Trans. Signal Process. 2017, 65, 105–118. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Chu, P.; Liao, B. DOA Estimation in Impulsive Noise Based on FISTA Algorithm. Remote Sens. 2023, 15, 565. https://doi.org/10.3390/rs15030565
Zhang J, Chu P, Liao B. DOA Estimation in Impulsive Noise Based on FISTA Algorithm. Remote Sensing. 2023; 15(3):565. https://doi.org/10.3390/rs15030565
Chicago/Turabian StyleZhang, Jinfeng, Ping Chu, and Bin Liao. 2023. "DOA Estimation in Impulsive Noise Based on FISTA Algorithm" Remote Sensing 15, no. 3: 565. https://doi.org/10.3390/rs15030565
APA StyleZhang, J., Chu, P., & Liao, B. (2023). DOA Estimation in Impulsive Noise Based on FISTA Algorithm. Remote Sensing, 15(3), 565. https://doi.org/10.3390/rs15030565






