Imaging Simulation Method for Novel Rotating Synthetic Aperture System Based on Conditional Convolutional Neural Network
Abstract
:1. Introduction
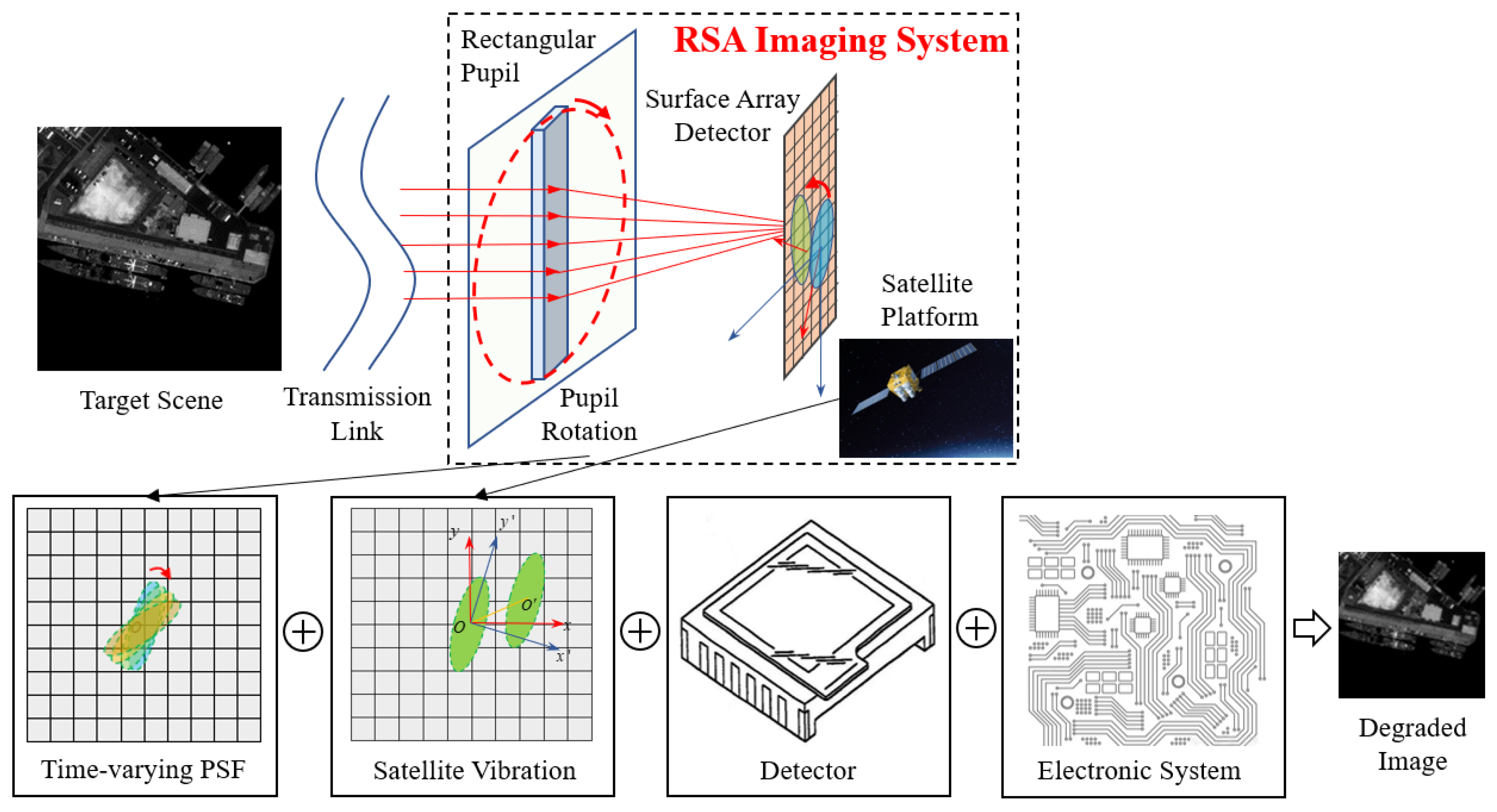
2. Imaging Simulation Method for the RSA System
2.1. Analysis of the Rectangular Rotary Pupil’s Imaging Characteristics
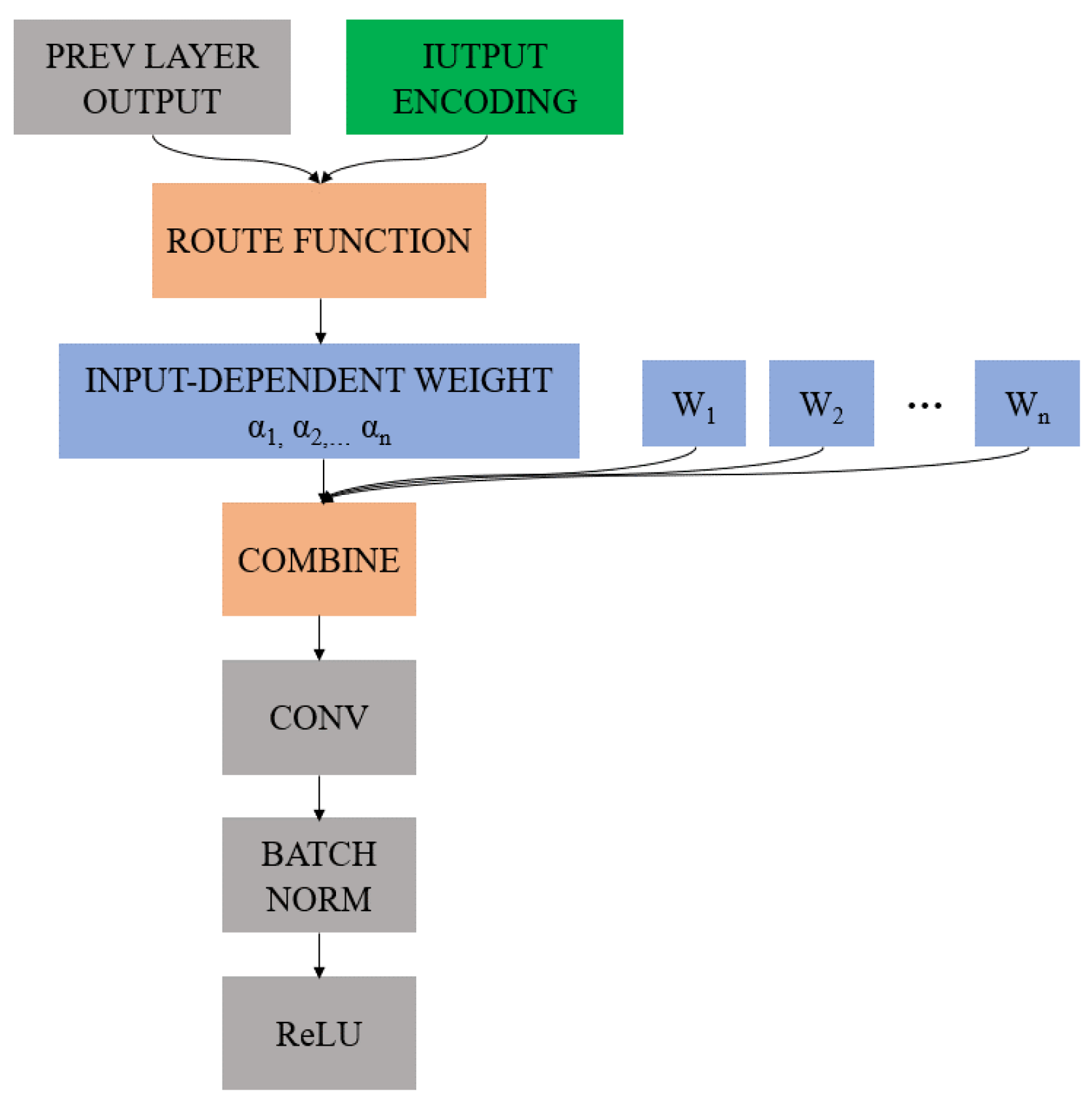
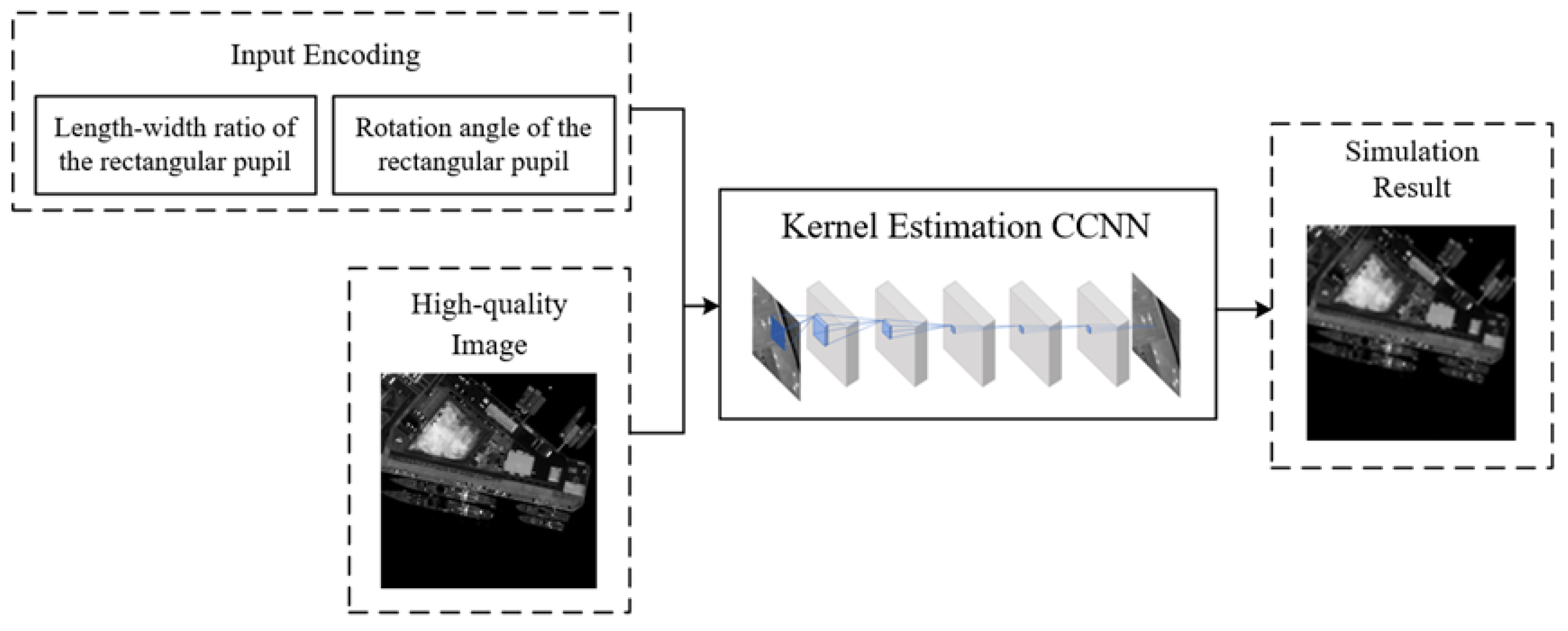
2.2. Simulation of the Rectangular Rotary Pupil’s Imaging Characteristics
3. Experiments
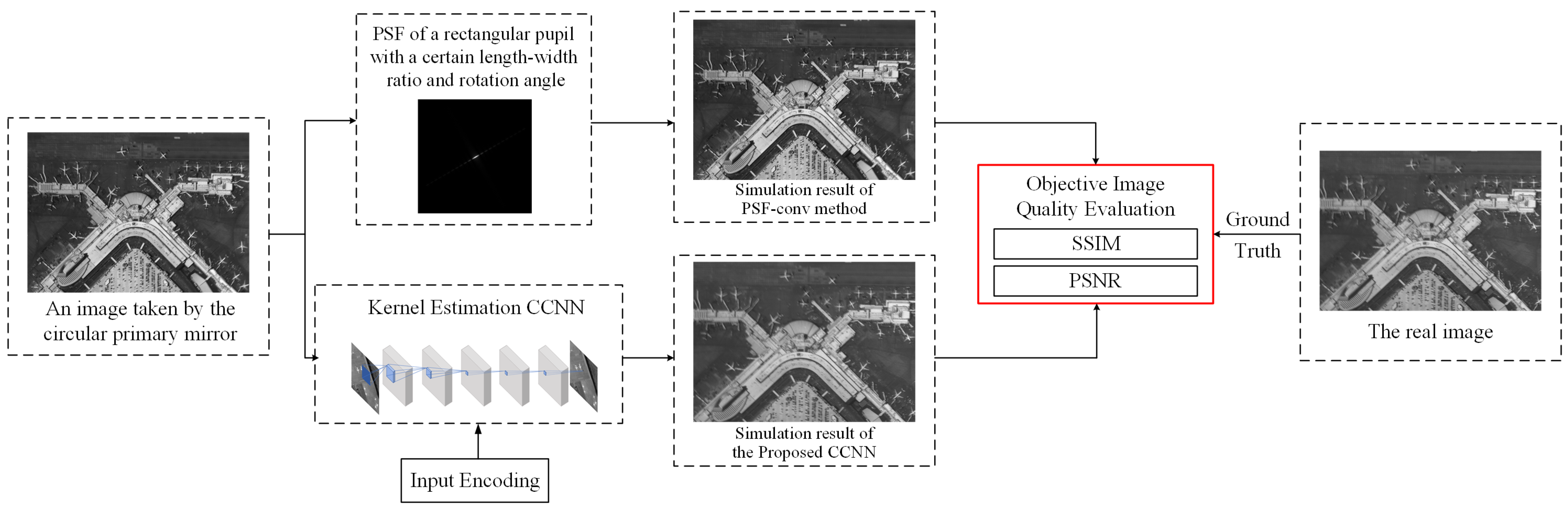
3.1. Experimental Scheme
3.2. Training Details
3.3. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Belward, A.S.; Skøien, J.O. Who launched what, when and why; trends in global land-cover observation capacity from civilian earth observation satellites. ISPRS J. Photogramm. Remote Sens. 2015, 103, 115–128. [Google Scholar] [CrossRef]
- Tong, X.; Wang, J.; Lai, G.; Shang, J.; Qiu, C.; Liu, C.; Ding, L.; Li, H.; Zhou, S.; Yang, L. Normalized projection models for geostationary remote sensing satellite: A comprehensive comparative analysis (January 2019). IEEE Trans. Geosci. Remote Sens. 2019, 57, 9643–9658. [Google Scholar] [CrossRef]
- Yang, X.; Li, F.; Xin, L.; Lu, X.; Lu, M.; Zhang, N. An improved mapping with super-resolved multispectral images for geostationary satellites. Remote Sens. 2020, 12, 466. [Google Scholar] [CrossRef] [Green Version]
- Tzortziou, M.; Mannino, A.; Schaeffer, B.A. Satellite Observations of Coastal Processes from a Geostationary Orbit: Application to estuarine, coastal, and ocean resource management. Am. Geophys. Union 2016, 2016, P54B–1756. [Google Scholar]
- Guo, J.; Zhao, J.; Zhu, L.; Gong, D. Status and trends of the large aperture space optical remote sensor. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation (ICMA), Changchun, China, 5–8 August 2018; pp. 1861–1866. [Google Scholar]
- Zhi, X.; Jiang, S.; Zhang, L.; Wang, D.; Hu, J.; Gong, J. Imaging mechanism and degradation characteristic analysis of novel rotating synthetic aperture system. Opt. Lasers Eng. 2021, 139, 106500. [Google Scholar] [CrossRef]
- Jiang, S.; Zhi, X.; Zhang, W.; Wang, D.; Hu, J.; Tian, C. Global Information Transmission Model-Based Multiobjective Image Inversion Restoration Method for Space Diffractive Membrane Imaging Systems. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–12. [Google Scholar] [CrossRef]
- Wang, D.; Zhi, X.; Zhang, W.; Yin, Z.; Jiang, S.; Niu, R. Influence of ambient temperature on the modulation transfer function of an infrared membrane diffraction optical system. Appl. Opt. 2018, 57, 9096–9105. [Google Scholar] [CrossRef] [PubMed]
- Zhi, X.; Zhang, S.; Yu, F.; Jiang, S.; Hu, J.; Chen, W. Imaging characteristics and image restoration method for large field circular scanning system. Results Phys. 2021, 31, 104884. [Google Scholar] [CrossRef]
- Rai, M.R.; Rosen, J. Optical incoherent synthetic aperture imaging by superposition of phase-shifted optical transfer functions. Opt. Lett. 2021, 46, 1712–1715. [Google Scholar] [CrossRef] [PubMed]
- Zhi, X.; Jiang, S.; Zhang, L.; Hu, J.; Yu, L.; Song, X.; Gong, J. Multi-frame image restoration method for novel rotating synthetic aperture imaging system. Results Phys. 2021, 23, 103991. [Google Scholar] [CrossRef]
- Tang, J.; Wang, K.; Ren, Z.; Zhang, W.; Wu, X.; Di, J.; Liu, G.; Zhao, J. RestoreNet: A deep learning framework for image restoration in optical synthetic aperture imaging system. Opt. Lasers Eng. 2021, 139, 106463. [Google Scholar] [CrossRef]
- Geng, T.; Liu, X.Y.; Wang, X.; Sun, G. Deep shearlet residual learning network for single image super-resolution. IEEE Trans. Image Process. 2021, 30, 4129–4142. [Google Scholar] [CrossRef] [PubMed]
- Courtrai, L.; Pham, M.-T.; Lefèvre, S. Small Object Detection in Remote Sensing Images Based on Super-Resolution with Auxiliary Generative Adversarial Networks. Remote Sens. 2020, 12, 3152. [Google Scholar] [CrossRef]
- Zhang, K.; Gool, L.V.; Timofte, R. Deep unfolding network for image super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 3217–3226. [Google Scholar]
- Zhang, K.; Zuo, W.; Zhang, L. Learning a single convolutional super-resolution network for multiple degradations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18 June–23 June 2018; pp. 3262–3271. [Google Scholar]
- Wang, X.; Xie, L.; Dong, C.; Shan, Y. Real-esrgan: Training real-world blind super-resolution with pure synthetic data. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, Canada, 11–17 October 2021; pp. 1905–1914. [Google Scholar]
- Liang, J.; Cao, J.; Sun, G.; Zhang, K.; Van Gool, L.; Timofte, R. Swinir: Image restoration using swin transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, Canada, 11–17 October 2021; pp. 1833–1844. [Google Scholar]
- Xu, Y.; Luo, W.; Hu, A.; Xie, Z.; Xie, X.; Tao, L. TE-SAGAN: An Improved Generative Adversarial Network for Remote Sensing Super-Resolution Images. Remote Sens. 2022, 14, 2425. [Google Scholar] [CrossRef]
- Liu, A.; Liu, Y.; Gu, J.; Qiao, Y.; Dong, C. Blind image super-resolution: A survey and beyond. arXiv 2021, arXiv:2107.03055. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Wright, J.; Huang, T.; Ma, Y. Image super-resolution as sparse representation of raw image patches. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Zeyde, R.; Elad, M.; Protter, M. On single image scale-up using sparse-representations. In Proceedings of the International Conference on Curves and Surfaces, Avignon, France, 24–30 June 2010; pp. 711–730. [Google Scholar]
- Mallat, S.; Yu, G. Super-resolution with sparse mixing estimators. IEEE Trans. Image Process. 2010, 19, 2889–2900. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Freeman, W.T.; Jones, T.R.; Pasztor, E.C. Example-based super-resolution. IEEE Comput. Graph. Appl. 2002, 22, 56–65. [Google Scholar] [CrossRef] [Green Version]
- Michaeli, T.; Irani, M. Nonparametric blind super-resolution. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 945–952. [Google Scholar]
- Zontak, M.; Irani, M. Internal statistics of a single natural image. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; pp. 977–984. [Google Scholar]
- Yang, B.; Bender, G.; Le, Q.V.; Ngiam, J. Condconv: Conditionally parameterized convolutions for efficient inference. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, Canada, 8–14 December 2019; pp. 1307–1318. [Google Scholar]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- Bell-Kligler, S.; Shocher, A.; Irani, M. Blind super-resolution kernel estimation using an internal-gan. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, Canada, 8–14 December 2019; pp. 284–293. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]








| Rotation Angles | Method | Length–Width Ratio 1 | Length–Width Ratio 3 | Length–Width Ratio 5 | Length–Width Ratio 10 | Average | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM (dB) | PSNR | SSIM (dB) | PSNR | SSIM (dB) | PSNR | SSIM (dB) | PSNR | SSIM (dB) | ||
| 0 | PSF-conv | 22.60 | 0.6896 | 22.86 | 0.7166 | 24.37 | 0.7876 | 24.60 | 0.7868 | 23.61 | 0.7451 |
| Proposed | 38.10 | 0.9177 | 36.85 | 0.8951 | 34.97 | 0.9022 | 32.72 | 0.8771 | 35.66 | 0.8980 | |
| 15 | PSF-conv | 22.83 | 0.7369 | 22.53 | 0.7296 | 24.55 | 0.7896 | 24.18 | 0.7751 | 23.52 | 0.7578 |
| Proposed | 37.94 | 0.9271 | 36.61 | 0.8979 | 33.73 | 0.8802 | 32.29 | 0.8631 | 35.14 | 0.8921 | |
| 30 | PSF-conv | 22.06 | 0.6765 | 22.49 | 0.7159 | 24.29 | 0.7871 | 24.13 | 0.7834 | 23.24 | 0.7407 |
| Proposed | 37.72 | 0.9210 | 37.06 | 0.9162 | 34.70 | 0.8780 | 32.04 | 0.8607 | 35.38 | 0.8939 | |
| 45 | PSF-conv | 22.20 | 0.7153 | 22.57 | 0.7417 | 24.21 | 0.7862 | 24.24 | 0.7908 | 23.31 | 0.7585 |
| Proposed | 38.11 | 0.9257 | 36.54 | 0.8916 | 34.17 | 0.8914 | 31.80 | 0.8621 | 35.15 | 0.8927 | |
| 60 | PSF-conv | 21.82 | 0.7158 | 22.22 | 0.7412 | 24.05 | 0.7849 | 23.73 | 0.7838 | 22.95 | 0.7564 |
| Proposed | 38.50 | 0.9289 | 35.95 | 0.8951 | 35.19 | 0.9040 | 31.71 | 0.8656 | 35.34 | 0.8984 | |
| 75 | PSF-conv | 22.22 | 0.7074 | 22.47 | 0.7363 | 23.91 | 0.7840 | 24.02 | 0.7838 | 23.15 | 0.7529 |
| Proposed | 38.90 | 0.9220 | 36.91 | 0.8920 | 34.74 | 0.9038 | 31.74 | 0.8749 | 35.57 | 0.8982 | |
| 90 | PSF-conv | 22.29 | 0.6990 | 22.72 | 0.7315 | 23.77 | 0.7832 | 24.32 | 0.7838 | 23.27 | 0.7493 |
| Proposed | 37.85 | 0.9267 | 36.98 | 0.8950 | 33.99 | 0.9041 | 32.06 | 0.8599 | 35.22 | 0.8964 | |
| 105 | PSF-conv | 22.06 | 0.7174 | 22.48 | 0.7363 | 23.91 | 0.7890 | 24.02 | 0.7888 | 23.12 | 0.7579 |
| Proposed | 37.91 | 0.9209 | 36.99 | 0.8919 | 34.29 | 0.8919 | 32.63 | 0.8873 | 35.46 | 0.8980 | |
| 120 | PSF-conv | 22.36 | 0.7103 | 22.84 | 0.7468 | 23.38 | 0.7812 | 23.63 | 0.7805 | 23.05 | 0.7547 |
| Proposed | 38.42 | 0.9112 | 36.94 | 0.8947 | 35.19 | 0.8896 | 32.79 | 0.8867 | 35.84 | 0.8955 | |
| 135 | PSF-conv | 22.40 | 0.6941 | 22.73 | 0.7075 | 23.46 | 0.7979 | 23.69 | 0.7958 | 23.07 | 0.7488 |
| Proposed | 37.62 | 0.9212 | 37.12 | 0.8979 | 34.95 | 0.8793 | 32.17 | 0.8731 | 35.47 | 0.8929 | |
| 150 | PSF-conv | 22.67 | 0.7090 | 22.12 | 0.7158 | 23.83 | 0.7917 | 23.74 | 0.7813 | 23.09 | 0.7495 |
| Proposed | 38.88 | 0.9165 | 36.02 | 0.8949 | 34.38 | 0.9025 | 31.94 | 0.8854 | 35.31 | 0.8998 | |
| 165 | PSF-conv | 22.23 | 0.6853 | 22.61 | 0.7147 | 23.88 | 0.7925 | 23.91 | 0.7896 | 23.16 | 0.7455 |
| Proposed | 38.49 | 0.9171 | 36.43 | 0.8950 | 34.68 | 0.9023 | 32.33 | 0.8812 | 35.48 | 0.8989 | |
| Average | PSF-conv | 22.31 | 0.7047 | 22.55 | 0.7278 | 23.97 | 0.7879 | 24.02 | 0.7853 | 23.21 | 0.7515 |
| Proposed | 38.20 | 0.9213 | 36.70 | 0.8964 | 34.58 | 0.8941 | 32.19 | 0.8731 | 35.42 | 0.8962 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Zhi, X.; Jiang, S.; Gong, J.; Shi, T.; Wang, N. Imaging Simulation Method for Novel Rotating Synthetic Aperture System Based on Conditional Convolutional Neural Network. Remote Sens. 2023, 15, 688. https://doi.org/10.3390/rs15030688
Sun Y, Zhi X, Jiang S, Gong J, Shi T, Wang N. Imaging Simulation Method for Novel Rotating Synthetic Aperture System Based on Conditional Convolutional Neural Network. Remote Sensing. 2023; 15(3):688. https://doi.org/10.3390/rs15030688
Chicago/Turabian StyleSun, Yu, Xiyang Zhi, Shikai Jiang, Jinnan Gong, Tianjun Shi, and Nan Wang. 2023. "Imaging Simulation Method for Novel Rotating Synthetic Aperture System Based on Conditional Convolutional Neural Network" Remote Sensing 15, no. 3: 688. https://doi.org/10.3390/rs15030688
APA StyleSun, Y., Zhi, X., Jiang, S., Gong, J., Shi, T., & Wang, N. (2023). Imaging Simulation Method for Novel Rotating Synthetic Aperture System Based on Conditional Convolutional Neural Network. Remote Sensing, 15(3), 688. https://doi.org/10.3390/rs15030688






