Next Article in Journal
Multiscale Variability of Hydrological Responses in Urbanizing Watershed
Next Article in Special Issue
Evaluation of Absolute Measurements and Normalized Indices of Proximal Optical Sensors as Estimators of Yield in Muskmelon and Sweet Pepper
Previous Article in Journal
An Increase of GNSS Data Time Rate and Analysis of the Carrier Phase Spectrum
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 15
Issue 3
10.3390/rs15030794
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Forecasting Table Beet Root Yield Using Spectral and Textural Features from Hyperspectral UAS Imagery

by
Mohammad S. Saif
1,*,
Robert Chancia
1,
Sarah Pethybridge
2,
Sean P. Murphy
2,
Amirhossein Hassanzadeh
1 and
Jan van Aardt
1
1
Chester F. Carlson Center for Imaging Science, Rochester Institute of Technology, Rochester, NY 14623, USA
2
Plant Pathology & Plant-Microbe Biology Section, School of Integrative Plant Science, Cornell AgriTech, Cornell University, Geneva, NY 14456, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2023, 15(3), 794; https://doi.org/10.3390/rs15030794
Submission received: 13 December 2022 / Revised: 19 January 2023 / Accepted: 26 January 2023 / Published: 31 January 2023
(This article belongs to the Special Issue Application of Hyperspectral Imagery in Precision Agriculture)
Browse Figures
Review Reports Versions Notes

Abstract

:
New York state is among the largest producers of table beets in the United States, which, by extension, has placed a new focus on precision crop management. For example, an operational unmanned aerial system (UAS)-based yield forecasting tool could prove helpful for the efficient management and harvest scheduling of crops for factory feedstock. The objective of this study was to evaluate the feasibility of predicting the weight of table beet roots from spectral and textural features, obtained from hyperspectral images collected via UAS. We identified specific wavelengths with significant predictive ability, e.g., we down-select >200 wavelengths to those spectral indices sensitive to root yield (weight per unit length). Multivariate linear regression was used, and the accuracy and precision were evaluated at different growth stages throughout the season to evaluate temporal plasticity. Models at each growth stage exhibited similar results (albeit with different wavelength indices), with the LOOCV (leave-one-out cross-validation) R2 ranging from 0.85 to 0.90 and RMSE of 10.81–12.93% for the best-performing models in each growth stage. Among visible and NIR spectral regions, the 760–920 nm-wavelength region contained the most wavelength indices highly correlated with table beet root yield. We recommend future studies to further test our proposed wavelength indices on data collected from different geographic locations and seasons to validate our results.

1. Introduction

Table beet (Beta vulgaris spp. vulgaris: Family Chenopodiaceae) consumption has increased recently, primarily due to an enhanced awareness of the potential health benefits [1], e.g., beets are a good source of dietary fiber and potassium [2]. Furthermore, Betalains from table beet roots represent a new class of dietary cationized antioxidants with excellent antiradical impact and antioxidant activity, and they have been linked to cancer prevention [3,4]. With the ever-increasing popularity and increasing production of table beets, our ability to predict root yield before harvest has become essential for both logistical planning and within-season crop inputs to manipulate yield.
Researchers have identified the suitability of unmanned aerial systems (UAS) to spectrally map large crop areas in a short duration, specifically for applications requiring high spatial resolution. The increased availability of UAS and miniaturized sensors [5] has also catalyzed various applications for UAS in agriculture [6]. Uses include, but are not limited to, the assessment of nutrient content [7,8], disease [9,10], above-ground biomass [11], leaf area index [12], evapotranspiration [13], water stress [14], weed presence [15], and yield [16,17,18] of various crops.
Hyperspectral sensors sample a wide range of narrow, contiguously spaced spectral information. As such, hyperspectral imagery (HSI) contains more detailed spectral characteristics than its multispectral counterpart, thus enabling extraction of actionable spectral information from data [19]. However, this increased information leads to a high dimensionality challenge [20]. The issue is further aggravated in precision agriculture, where the number of ground truth samples often is limited. One way to solve this is to use dimensionality reduction techniques [21]. However, algorithms developed from these techniques could hinder the detection of prominent wavelength regions indicative of a particular phenomenon. Results may also not be transferable to affordable, operational multispectral solutions. On the other hand, narrow-band indices often enable a more physiology-based understanding of specific crop applications [22,23,24].
An HSI data cube is a combination of spectral and spatial information. Analysis of narrow-band spectral indices alone does not harness the full scope of information available from such high-dimensional data. Texture features enable us to integrate spatial information, where texture represents the pattern of intensity variations in an image. After the development of texture measures [25,26,27,28], they were initially used for land use and land cover classification of satellite imagery [29,30,31,32,33,34]. Lu and Batistella [35] subsequently explored the relationship between texture measures and above-ground biomass (AGB) using Landsat Thematic Mapper (TM) data in Rondônia (Brazilian Amazon) and showed the importance of texture measures for estimating AGB, specifically for a mature forest. Sarker and Nichol [36] found stronger correlations for forest AGB using texture parameters than spectral parameters. More specifically, their best-performing model uses texture ratio indices. Eckert [37], Kelsey and Neff [38] found similar results applying texture parameters to a different dataset. These authors stressed that since vegetation indices saturate for medium to high canopy densities [39], adding texture indices often leads to these better-performing models.
While texture analysis has been used extensively with multispectral data in the remote sensing domain, its uses with hyperspectral imagery are more ubiquitous in food quality assessment utilizing in-house imaging techniques [40,41,42,43,44,45]. Furthermore, all studies showed better performance for their respective goals with the fusion of both textural and spectral features. However, in most of these papers [42,43,44], texture features were extracted from the principal components of HSI, preventing the identification of informative specific wavelengths. They were able to distinguish between fresh and frozen fish fillet [42], detecting yellow rust in wheat [43], and quantify water-holding capacity in chicken breast fillet [44]. Yang et al. [45], in turn, extracted texture features from select critical spectral bands, after first identifying the influential bands from relevant spectral signatures. Their model was able to predict water-holding capacity of chicken breast fillet with an R2 of 0.80 and RMSE of 0.80. Studies such as these hint at the potential utility of texture metrics from hyperspectral imagery.
UAS provides images of the crop canopy, while our goal is to measure the weight of subterranean table beet root biomass. However, since the yield of a root crop is the excess nutrient content stored in the root [46], it may be possible to estimate root yield from the above canopy imagery. However, the ratio of nutrient storage in the roots and top growth infrequently correlates [47], resulting in difficulty in determining root yield. Various vegetation indices were used to predict yields of potatoes [47,48,49,50] and carrots [51] with mixed success. Al-Gaadi et al. [47] and Suarez et al. [51] both used solely vegetation indices obtained from satellite imageries to predict potato and carrot, with the best-performing R2 values of 0.65 and 0.77, respectively. The addition of structural parameters, such as LAI (leaf area index) in the case of Luo et al. [48] and DSM for Li et al. [49], showed some improvement in model performance. Nevertheless, the full spectra of hyperspectral imagery proved to be more effective for Li et al. [49].
Previous B. vulgaris-specific studies are scarce, with Olson et al. [52] predicting sugar beet root yield with an R2 of 0.82 using multispectral imagery obtained from UAS. This study builds upon our previous study [53] by predicting table beet root weight (R2 = 0.89) with UAS-based multispectral imagery.
In this study, our objective was to assess the predictability of beet root yield (weight per unit length) entirely from HSI to determine the benefits of high-dimensional spectral data. A secondary objective was to quantify the effect of using both narrow-band spectral and textural features individually and in combination. Finally, we evaluate table beet root yield at five different growth stages during the season to assess the ideal flight timing and its impact on model performance.

2. Materials and Methods

2.1. Data Collection

Table beets (cv. Ruby Queen) were planted at Cornell AgriTech, Geneva, New York, USA. The beets were planted in a 60   m × 100   m field on 20 May 2021, representing 18 different plots where the root weight of the table beets was collected. Each of the plots was 1.52 m (5 ft) long. The roots were manually harvested on August 5, 2021, after which root weight was measured.
We collected hyperspectral imagery of the entire field using a Headwall Photonics Nano-Hyperspec imaging spectrometer (272 spectral bands; 400–1000 nm), which was fitted onto DJI Matrice 600 UAS. The ground sampling distance of our imagery was 3 cm. A hyperspectral image cube, captured from the UAS for all 18 plots, is shown in Figure 1. A MicaSense RedEdge-M camera [54] also was fitted to the drone, which captured five bands (475, 560, 668, 717 and 840 nm) of multispectral images. We flew our UAS at five different stages during the growing season, from the sowing date to harvest. The synopsis of the data collection is shown in Table 1. The first flight date was selected to align with canopy emergence. The second flight was chosen to correspond with canopy closure (last phase of the leaf development). The rest of the dates were chosen based on weather conditions.

2.2. Data Preprocessing

The raw digital count of the HSI was orthorectified and converted to radiance using Headwall’s Hyperspec III SpectralView V3.1 software [55]. Simultaneously, an orthorectified, spatially registered mosaic of the multispectral image was formed using Pix4D V4.6.3 [56]. Ten georegistered ground control points (AeroPoints) were deployed in the field to ensure accurate spatial registration of the multispectral images. These multispectral mosaics were then used to register the HSI spatially. All the study plots were marked in the field with orange plates, staked above the table beet canopy, which helped visually identify the plots from the HSI mosaics. The study plots were clipped from the mosaic via a rectangular per-plot shapefile. The shapefiles’ dimensions were 0.67 m (distance between two adjacent crop rows) across the row and 1.52 m (the length of the study plot) along the row. The box and HSI were spatially registered to ensure image analysis of the same crops across all the flights.
Since radiance data are susceptible to changes in illumination conditions, the HSI data were converted from radiance to reflectance [19]. Four panels (black, dark gray, medium gray, and light gray) were placed in the field to serve as calibration targets. The reflectance of each panel was measured using an SVC spectrometer. We also extracted the radiance of each panel from the HSI mosaic of the UAS data. The empirical line method tool in ENVI V5.3 [57] was used to convert the radiance HSI of the study plots to reflectance. We ignored the last 32 wavelength bands in the HSI imagery, given their noisy nature toward the detector fall-off range.

2.3. Denoising

Most UAS-based HSI data contain thermal noise, quantization noise and shot noise [58]. We suppressed as much noise from the image as possible to draw conclusive results before performing any analysis.
Our high-level denoising procedure was similar to Chen et al. [59]. This method hinges on the fact that most noise is contained in principal components with lower eigenvalues. As a result, a principal component analysis (PCA) was performed on the scene containing n bands, and the top-k components were retained and kept unaltered, with the remaining components being passed for denoising; k was determined by the minimum average partial (MAP) test [60]. Consecutively, n-k components were passed to dual-tree complex wavelet transformations [61] for denoising, after which an inverse PCA was performed to obtain the denoised image. We refer the reader to [18] for more information regarding this approach.

2.4. Feature Extraction

The high dimensionality of HSI is a well-documented problem across scientific literature [20]. Therefore, we carefully selected the bands, or a combination of bands, to derive a predictive model to reduce the complexity of analysis when dealing with a high number of bands.

2.4.1. Reflectance Features

Spectral angle mapper [62] was used to mask the vegetation from the soil in the imagery, after which the mean vegetation spectra for each plot were evaluated. Figure 2a shows the mean vegetation spectra across all flights. We observed the increase in reflectance in the NIR region with each successive flight, which was expected since as vegetation matures, canopy layering typically increases.
Huete et al. [63] examined cotton canopy spectra and concluded that the spectra of soil and vegetation mix interactively, and thus, normalization is crucial to remove the background effect. Normalized difference indices of various wavelength bands have been found to normalize soil background spectral variations [64] while simultaneously reducing the effect of sun and sensor view angle [65]. Additionally, the well-known normalized difference vegetation index (NDVI) has historically been used to map vegetation [66] while also being used to predict leaf area index (LAI) [67], crop biomass [68], and yield [69]. The shortcomings of using NDVI have also been well documented [70,71,72,73,74]. NDVI is restricted to just two specific band pairs, so instead, we evaluated normalized difference ratio indices (NDRI) of every possible combination of narrow-band reflectance, as follows:
N D R I = R 1 − R 2 R 1 + R 2  
This method of identifying wavelength pairs has been used in [75] to understand the relationship between evapotranspiration, to evaluate biophysical characteristics of cotton, potato, soybeans, corn and sunflower crops [76], and to estimate biomass and nitrogen concentrations in winter wheat [77].

2.4.2. Texture Features

The texture of a plot is another possible source of features for our model. Haralick et al. [25] documented the most widely used texture feature extraction method, which was also used in this study. It involves the calculation of the gray-level co-occurrence matrix (GLCM), followed by extracting descriptive statistics from the matrix. GLCM is a frequency table representing the number of times a specific tone occurs next to one another. The tone is the quantized level of pixel values for a particular spectral band. One of the many descriptive statistics is the mean of GLCM, and it is given by Equation (2), where N g   is the quantization level and P ( i ,   j ) is the probability of occurrence of pixel j next to i .
M e a n = ∑ i = 1 N g ∑ j = 1 N g i * P ( i , j )
In several previous studies [11,35,37,38,78], the top-performing models predominantly consisted of the mean of GLCM. Furthermore, the GLCM mean represents the value of the more frequently occurring mean tonal level within a particular window size. Thus, the GLCM means contains both spatial and spectral variation information.
The texture features were calculated over all 240 narrow wavelength bands. An 11 × 11 kernel size was used to calculate the GLCM mean for each kernel over each study plot. Both small [11] and large kernel sizes [35] have yielded promising results for their specific scenarios. For our case, using a smaller kernel size meant that the feature became more susceptible to noise, while too large a value could lead to over-smoothing of the data and loss of texture information. The GLCM was evaluated in eight directions (N, S, E, W, N-E, N-W, S-E, S-W) for each kernel. A quantization level of 16 was used to evaluate the GLCM mean for each kernel within a plot, after which the mean of GLCM means was taken as the texture feature for each plot. The texture features of an image depend on the canopy coverage of a plot [11,79], so we did not crop out the vegetation during the calculation.
Figure 2b is a plot of the mean of GLCM means over a particular plot at different flight times. We note the dip in spectra at around 680 nm due to the contrast in reflectance of vegetation and non-vegetation pixels at that wavelength band. Note that the contrast at 480 nm was not high enough; thus, there was no significant dip, even though there were absorption spectra in reflectance due to chlorophyll absorption. Vegetation shadow pixels result in variation of reflectance within the green and the NIR region, leading to a lower GLCM mean. We note that the relative uniformity of GLCM mean values for all the wavelength regions for flight 1, compared to other flights, was due to a greater number of soil pixels in the image.
In a study by Zheng et al. [11], textural measurements from individual wavelengths did not exhibit a high predictive capability of rice AGB. The authors therefore proposed a normalized difference texture index (NDTI). The texture feature extracted in this paper is also the NDTI, as defined by Equation (3). Here, T1 and T2 are the means of GLCM means at two different wavelengths. We also evaluated NDTI with each possible combination of narrow-band texture wavelengths, as follows:
N D T I = T 1 − T 2 T 1 + T 2  

2.5. Model Evaluation and Feature Search

Our goal was to identify the pair (or pairs) of wavelength bands that produced the most predictive NDRI and NDTI features, for an accurate and precise model for table beet root yield. Due to low sample size, we performed leave-one-out cross-validation (LOOCV) to evaluate our model [80]. Here, the dataset is divided into a number of subsets, which equals the number of instances in that dataset. In each subset, all but one instance was used to train models, while the omitted sample was used to test models. In our case, a model with the same feature was trained on 17 occasions and tested on one occasion with 18 combinations. Our model evaluation parameters were the coefficient of determination R2 and root mean square error (RMSE). The LOOCV R2 and RMSE for a model were calculated from these 18 unique occasion predictions.
We investigated the model performance for each flight individually, and the final models for each flight were evaluated in multiple ways. Firstly, we noted the top 10 LOOCV R2 features obtained from NDRI and NDTI. We also noted the models obtained using a combination of one NDRI and one NDTI feature. Finally, we fed the top-10 NDRI and NDTI features into a random forward-selected stepwise linear regression to obtain models that contained multiple features.

2.5.1. Single Feature Approach

To identify the wavelength bands that were best predictors of table beet root yield, the NDRI and NDTI for each possible wavelength pair in the spectrum were fitted with root yield in a simple linear regression (SLR). The predictive power from single features was identified for two purposes: to narrow down the feature search space for a general model and to evaluate the performance of a model that predicts root yield from just two wavelength bands. Additionally, we also wanted to monitor the change in predictive capabilities at each growth stage.

2.5.2. Double Feature Approach

We selected one feature from NDRI and one from NDTI and evaluated the model performances. Each model formed from all possible dual feature combinations of the top 10 NDRI and NDTI features was evaluated. Both feature extraction methods were used, as each signifies different properties of an image. NDRI is a placeholder for spectral characteristics, while NDTI provides information related to image texture. We selected one index from each, as the goal of the final model was to select just four wavelength bands, to ensure compatibility with inexpensive sensors.
Zheng et al. [11] showed that using spectral and textural measurements improved their rice AGB prediction model. Furthermore, Zheng et al. [78] showed significant improvements in the estimation of leaf nitrogen concentration when using VIs combined with NDTIs, compared to the indices alone. Yue et al. [79] also reported improved results when using vegetation indices in combination with image textures.

2.5.3. Modified Stepwise Regression

Finally, to find the best model derived from NDTI and NDRI features during each flight, stepwise regression offers a simple way to explore regression models over a large feature space without exhaustively interrogating every possible combination. In order to mitigate some of the concerns raised in the literature [81,82,83,84], we introduced some additional procedures in the stepwise regression algorithm.
Smith [81] argues the probability of choosing an explanatory variable decreases if the number of candidate variables is too large. Therefore, we restricted our procedure to pool 20 candidate variables. Grossman et al. [82] highlighted that the stepwise procedure features depend on the samples in the dataset, so LOOCV p-values were chosen to mitigate this issue. The LOOCV p-values are the mean of the p-values of a feature for each instance within LOOCV. Simple forward selection of features also does not account for interdependencies within the features [85], which can lead to the entry of redundant features into the final model, thus inflating its performance [86]. Therefore, we performed backward elimination after adding each new feature to discard all features with a p-value greater than 0.05.
In this process, the order of parameter entry affects the selection of features [83], while the stepwise regression algorithm only accounts for the interaction of a particular set of features at a fixed permutation [84]. The first feature for the stepwise regression algorithm was thus randomly selected, and each new feature was randomly added to the algorithm. The algorithm was repeated multiple times, ensuring that a broad range of sub-models was evaluated. Finally, multiple sets of features were obtained that could lead to predicting table beet root yield. Among the multiple models, we selected those exhibiting an R2adj value greater than 0.75 and the VIF for each feature as less than five. VIF is the variance inflation factor, a measure of the degree of inter-correlation of one feature with the rest of the features in a model [87]. A VIF greater than five shows high inter-correlation [88]. Models with features exhibiting the above criteria have the potential to be operational.
For extraction, analysis and visualization, we used python 3.9.7 and the following packages: numpy 1.21.4, matplotlib 3.5.0, scipy 1.7.3, scikit-learn 1.0.2, statsmodels 0.13.1, geopandas 0.9.0, gdal 3.4.0, rasterio 1.2.10 and rioxarray 0.9.0.

3. Results

In this section we report all the LOOCV R2, RMSE and relevant models’ performance parameters for each approach.

3.1. Single Features

The R2 values for each pair of narrow band wavelengths of NDRI and NDTI were recorded and shown in Figure 3. The top 10 R2 values for each flight can be found in Table A1 and Table A2 in Appendix A.
Figure 2a shows the changes to predictive narrow-band wavelengths for NDRI features. The 760 nm and NIR (770–900 nm) features show predictive abilities during the first three flights. The region of high R2 values shifts, but the NIR region remains most indicative for the last two flights. For flights 3 and 4, we observe a high coefficient of determination around the 450 nm and 650 nm regions. The top 10 R2 values and results are shown in Table A1 in Appendix A. The top 10 R2 values for the first two flights were between 0.49–0.61. Flights 3 and 4 had more predictive features, ranging from 0.63–0.73, while the top-10 R2 values of Flight 5 were all around 0.6. The most predictive features for all flights appear primarily in the NIR region (750–900 nm).
The predictive regions for NDTI are sparsely distributed, as seen in Figure 3b. For flight 1, the predictive features appear in the NIR pairs, with R2 values of around 0.4 and 0.5. With a maximum R2 of 0.36, the NDTI features of flight 2 perform poorly. There are some relatively high R2 regions around the 500–700 nm wavelength pairs for flights 3 and 4. Moreover, the features from flight 5 have a low predictive ability with table beet root yield, with the top R2 ranging in the range 0.25–0.30. Table A2 in Appendix A lists the top 10 NDTI features.

3.2. Double Features

The top five models (in terms of R2 values) obtained from combinations of each feature are reported in Table 2.
Incorporating both NDRI and NDTI features increased the R2 values of the model for all five flights. We also noted that each model’s VIF values are low, signifying the absence of correlation between the features. The dual features had better-performing models for flights 3 and 4 than the other flights. While the wavelength bands were different, there were some frequently occurring features; for example, for flight 4, the NDRI features were either 895 nm and 785.9 nm or 895 nm and 783.7 nm, while the NDTI features were around 850 nm and 760 nm. For flight 1, both NDRI and NDTI features were from wavelength pairs in the NIR, except for one pair of blue wavelengths. For flight 2, the NDRI features are from NIR pairs, but the NDTI features were at different wavelength pairs. For flight 3, we again observed the high R2 for blue wavelength pairs. Finally, for flight 5, we observed some texture features from blue and red pairs.

3.3. Multiple Features

Random stepwise regression with an alpha value of 0.05 was implemented. The summary of obtained models are shown in Table 3. Most of the models identified had an R2 value of greater than 0.80 and an RMSE of lower than 15.27% of the estimate, which is equivalent to around 0.28 kg/m. The top-performing models for each flight had similar R2 values, ranging from 0.85 to 0.90, with the best performing model occurring at flight 4, with an R2 of 0.90 and 10.81% (0.2 kg/m) RMSE. Flights 3 and 5, and 1 and 2 had similar performances compared to each other, albeit each with their own unique set of predictive features.
We identified select operational models as defined by our previously mentioned performance criteria (R2adj > 0.75 and VIF < 5) for all flights. However, we note the scarcity of models for flight 2 that meet this performance criteria. We emphasize that for the conditions we set to filter our models, flights 1 and 2 contained four features, while the rest of the top-performing models were obtained from just three features. For flight 1, most of the models are focused in the NIR region. For the fifth flight, however, there was a blue texture feature, while for the fourth flight, a red feature was present. We observed red and blue NDRI pairs, with NIR texture feature pairs, for the third flight. The fit of the best-performing models for each flight is shown in Figure 4.
The observed vs. predicted plots in Figure 4 gives us an idea of the range of table beet root yield values to evaluate the limitations of the model. For example, flight 1 overestimates values between 1.2 kg/m and 1.45 kg/m. Both flight 1 and flight 2 have a more significant number of outlier values, and the data points appear to be further apart from the 1:1 line, thereby signifying the increase in error variance. For flight 3, there is a trend for the model to overestimate between table beet root yields of 1.2–1.6 kg/m, while conversely, the model underestimates in the range 2.2–2.5 kg/m. The model from flight 4 shows underestimation of table beet root yield, especially in the range 2.3–2.7 kg/m.

3.4. Extrapolating Yield Modeling Results to the Field Scale

Yield maps are helpful tools for farmers to plan and make logistic decisions, and here we apply our model to provide insight into one such yield map. Figure 5 shows the predicted table beet root yield for plots in the northern region of the field. Each prediction was made by training the best-performing model on all 18 plots. In the plot, some boxes were empty, since the predicted root yields from the model were outside the labeled range. This occurred as some of the images within the plot appeared blurred in the mosaic, leading to an anomalous prediction. We observed similar regions or locally specific results, based on similar colors around the same plot. However, there was also some variability in growth factors across the field and across the growing season, which is understandable, since soil variability came into play, and the time-specific model performances, respectively, were different. The projection of the mosaic was not always uniform, and there were also missing crop locations in the plot. This resulted in some of the plots having anomalous results, which are shown as empty blocks in the image. We notice that, specifically for flights 3 and 4, the predicted table beet root yield is (spatially) similarly distributed.
Finally, by analyzing observed vs. predicted plots in Figure 4, we observe a higher error variability for our models, especially for flights 1, 2, and 5. Thus, we do not see a similar trend of predicted values that we observe for flights 3 and 4. As we do not possess the actual table beet root yield of the plot; i.e., it is difficult to verify the entire map’s accuracy, but we assume at least some validity in the table beet root yield map, since we hedged against the overall performance of flight 3 (growth stage).

4. Discussion

4.1. Significance of Obtained Features

An imaging system’s limitations must be considered before analyzing the prominent wavelength bands and the spectra for any given application. A number of critical factors include the band centers and the FWHM of the sensors in the imager, as well as flight shifts in airborne hyperspectral imaging systems due to vibrations [89]. These effects are further exacerbated by SMILE and keystone effects of the sensor [90], which lead to spectral absorption features appearing at slightly shifted locations. Furthermore, our sensor has a FWHM of around 6 nm, which is relatively broad compared to our spectral resolution of 2.2 nm [55]. These factors led to our observed absorption peaks appearing as relatively broad spikes, as seen in Figure 2a. We mention this as background to the discussion of the specific wavelength features and pairs, especially insofar as their specificity of location and combination is concerned.
The wavelength bands of each feature for the best-performing model (in terms of R2) of each flight are shown in Figure 6. We marked oxygen absorption at 760 nm and water vapor absorption at 820 nm and 910 nm [19] in the plot. Most of the spectral/texture features for all flights were located around the 900 and 800 nm pairs, attributable to the broad spectral spikes caused by oxygen and water absorption features. This has potential physiological implications. Table beet roots primarily consist of water [91]. The amount of water in the foliage could be an indication of the relative hydration of the roots and thus indicative of root weight. We contend that this is a type of normalized water absorption feature.
There also are feature pairs around 650 nm and 500 nm, even if only one feature appears around this region for the best-performing models for NDRI. However, from the heat map in Figure 3, we noted the significance of this region for predicting table beet root yield. Strong chlorophyll a and b absorptions can be found at around 440 nm and 680 nm, and 460 and 635 nm, respectively, while carotenoids have been shown to express as an absorption feature at around 470 nm [19,92].
Additionally, similar wavelength regions have been shown to have utility for the development of a broad range of crop physiological models. Thenkabail et al. [76] demonstrated the importance of 800 nm and 900 nm wavelength pairs, which significantly correlated with the wet biomass for soybean and cotton crops. The 672 nm and 448 nm combination also has been shown to be an indicator of evapotranspiration by Marshall et al. [75]. Finally, 900–700 nm and 750–400 nm wavelength pairs are predictive of AGB and LAI for paddy rice [93].

4.2. Model Performance

Several different models were developed to identify possible wavelength combinations that could lead to effective scalable solutions for the prediction of table beet root yield at each growth stage. However, we are aware of the relatively small sample size on which we performed our analysis. To mitigate the small number of samples, we evaluated our models by LOOCV. All our reported models arguably rely on a limited number of predictive features, thereby avoiding the challenge of over-fitting in the context of a limited sample set. Hyperspectral indices are highly susceptible to noise [58], so the top-reported wavelength indices may not be extrapolated to other locations and times. However, a broad range of models with LOOCV R2 greater than 0.80 and RMSE of less than 15% for table beet root crops have been documented in this study.
In our previous study [53], the best performing model had an R2 of 0.89 and RMSE of 2.5 kg at the canopy closing stage using VDVI (Visible Band Difference Vegetation Index) and canopy area obtained from multispectral imagery. Here, we obtained similar and sometimes better results for each growth stage. The R2 for predicting carrot yield by Wei et al. [94] using satellite imagery was around 0.80. The best performing model for predicting potato yield for Li et al. [49] had an R2 of 0.81, using spectral indices collected from UAS-based HSI. Therefore, our results outperform those analogous studies. However, we are aware of the sample size limitation of our study, as we only used 18 plots to establish our model. We therefore recommend that our models be verified with table beets grown at different geographic locations and across years, with a larger dataset encompassing multiple fields.
Although the top-performing models for each flight exhibit similar performances, the best performing model was from flight 4. In contrast, both flights 3 and 4 have the largest number of high performing models (12 and eight models with R2 value greater than 0.80, respectively). Flights 3 and 4 were performed within five days of each other, and as such, they exhibit similar feature sets, as well as model performances.
All the feature sets from each flight (as reported in Table 2 and Table 3) were assessed on the remaining four flights’ data, and their LOOCV R2 values are shown in Figure 7. Only the top five model performances across all flights are shown. From these plots, the top-performing feature for one flight does not necessarily perform well on other flight data, meaning the features’ foresight depended on the day the data was captured. Although the R2 values for flight 3 is relatively high with feature sets from all flights. This signifies the presence of abundant and broader wavelength features that potentially exhibit table beet root yield predictive ability during this period.
Moreover, the features obtained from flight 5 show relatively high coefficient of determinations for all flights, with R2 values ranging from 0.4–0.5 for flights 3 and 4, and 0.1–0.2 for flights 1 and 2. The features are close to the best-performing features of flights 3 and 4, leading to relatively higher R2 scores. In addition, some of the features were similar to the features of flights 1 and 2. However, their R2 values are lower, signifying that during the earlier stages of growth, the predictive ability was more in tune with the specific narrow-band indices, while as the crop matures and approaches harvest, a broader range of indices shows prognostic capability.

5. Conclusions

The goals of this study were to assess the utility of HSI to accurately/precisely model beet root yield and to identify the wavelength indices that exhibit a predictive capability for beet root weight. We developed a varied selection of wavelength indices at various growth stages, which farmers could utilize to design a system for predicting table beet root yield with parameters best suited to their means.
The potency of predicting root yield from NIR pairs, especially for spectral features, is highlighted in this study. These results are promising for developing cost-effective and operational sensing platforms, as most of the spectral/texture features were located in the spectral range that can be detected by relatively cheap silicon (Si) detector material. Furthermore, the addition of texture features showed significant improvement to our model, showing that HSI texture features could serve as an important tool for analysis. We explored its effectiveness with some specific hyperparameters for texture feature extraction. However, variation of hyperparameters leads to varying levels of performance, which are also dependent on the growth stage of a plant [35,78]. Therefore, this is a potential area for future research, i.e., to find the hyperparameters suitable for a particular study at a particular growth stage.
The flight that was performed 21 days prior to harvest (or equivalently, 56 days after planting) exhibited a more significant number of features that led to good-performing (LOOCV R2 > 0.80) models. Additionally, we noted that the features identified from other flights showed significant fit (R2 around 0.4) with data obtained from this flight. While flight 4 (which was performed five days after) had the best-performing model, with an R2 of 0.90 and a 10.81% RMSE. We thus surmise, with caution, that the time period of roughly 16 to 21 days from harvest (Rosette growth stage) is ideally the best time to fly for predicting table beet root yield. However, we also acknowledge the results to depend on the weather and growing condition of the 2021 harvest at Geneva, New York, USA. As such, the results are likely to vary for a different year and at different geographic locations. We thus recommend that future studies (i) expand the number of field samples, (ii) assess the efficacy of modeling for different regions and even different beet cultivars, and (iii) consider the inclusion of structure-related features, such as those derived from light detection and ranging (LiDAR) and structure-from-motion techniques. Nevertheless, we were encouraged by our models’performance in the variability in yield explained (R2) and the relatively low RMSE values.

Author Contributions

Conceptualization, M.S.S., R.C., S.P. and J.v.A.; methodology, M.S.S., R.C. and J.v.A.; software, M.S.S. and A.H.; validation, M.S.S., R.C. and J.v.A.; formal analysis, M.S.S., R.C., A.H. and J.v.A.; investigation, M.S.S., R.C. and J.v.A.; resources, S.P. and J.v.A.; data curation, M.S.S., S.P., S.P.M. and J.v.A.; writing—original draft preparation, M.S.S.; writing—review and editing, M.S.S., R.C., A.H., S.P., S.P.M. and J.v.A.; visualization, M.S.S. and R.C.; supervision, S.P. and J.v.A.; project administration, S.P. and J.v.A.; funding acquisition, S.P. and J.v.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research principally was supported by Love Beets USA and the New York Farm Viability Institute (NYFVI), as well as the United States Department of Agriculture (USDA), National Institute of Food and Agriculture Health project NYG-625424, managed by Cornell AgriTech at the New York State Agricultural Experiment Station (NYSAES), Cornell University, Geneva, New York. M.S.S. and J.v.A. also were supported by the National Science Foundation (NSF), Partnerships for Innovation (PFI) Award No. 1827551.

Data Availability Statement

Not applicable.

Acknowledgments

We credit Nina Raqueno and Tim Bauch of the RIT drone team, who were responsible for capturing the UAS imagery. We also thank Imergen Rosario and Kedar Patki for assistance with data collection.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A. Top Features from Each Feature Selection Method

Table
Table A1. Top 10 NDRI features.
Table A1. Top 10 NDRI features.
Flight 1Flight 2Flight 3Flight 4Flight 5
wavelength pair (nm)R2wavelength pair (nm)R2wavelength pair (nm)R2wavelength pair (nm)R2wavelength pair (nm)R2
[830.4, 765.9]0.61[897.2, 895.0]0.61[883.8, 832.6]0.73[872.7, 799.2]0.70[834.9, 770.3]0.68
[494.3, 485.4]0.60[899.4, 897.2]0.59[903.9, 897.2]0.70[881.6, 808.2]0.67[892.7, 814.8]0.67
[895.0, 765.9]0.54[801.5, 757.0]0.54[903.9, 852.7]0.68[895.0, 785.9]0.66[883.8, 794.8]0.66
[810.4, 736.9]0.53[897.2, 890.5]0.54[874.9, 788.1]0.68[895.0, 783.7]0.66[926.1, 823.7]0.65
[797.0 765.9]0.51[801.5, 761.4]0.52[618.9, 463.1]0.67[888.3, 790.3]0.65[895.0, 823.7]0.65
[785.9, 765.9]0.50[897.2, 892.7]0.51[886.1, 832.6]0.67[888.3, 832.6]0.64[886.1, 770.3]0.64
[826.0, 765.9]0.50[832.6, 812.6]0.51[897.2, 788.1]0.67[877.2, 785.9]0.63[910.5, 770.3]0.63
[821.5, 759.2]0.49[834.9, 812.6]0.50[892.7, 788.1]0.66[846.0, 785.9]0.63[912.8, 770.3]0.63
[765.9, 734.7]0.49[897.2, 826.0]0.49[485.4, 454.2]0.66[892.7, 808.2]0.63[926.1, 777.0]0.63
[895.0, 792.6]0.49[803.7, 761.4]0.49[886.1, 790.3]0.66[921.7, 834.9]0.63[923.9, 821.5]0.61
Table
Table A2. Top 10 NDTI features.
Table A2. Top 10 NDTI features.
Flight 1Flight 2Flight 3Flight 4Flight 5
wavelength pair (nm)R2wavelength pair (nm)R2wavelength pair (nm)R2wavelength pair (nm)R2wavelength pair (nm)R2
[850.4, 781.4]0.65[901.6, 897.2]0.36[469.8, 452.0]0.63[558.8, 541.0]0.50[610.0, 607.8]0.52
[805.9, 781.4]0.59[590.0, 581.1]0.33[701.3, 612.3]0.59[874.9, 763.6]0.49[681.3, 679.0]0.33
[908.3, 823.7]0.57[587.8, 583.3]0.33[890.5, 765.9]0.58[643.4, 639.0]0.49[618.9, 607.8]0.29
[850.4, 785.9]0.52[687.9, 654.6]0.32[817.1, 785.9]0.58[808.2, 765.9]0.48[478.7, 469.8]0.29
[850.4, 748.0]0.51[590.0, 583.3]0.31[699.1, 612.3]0.56[870.5, 763.6]0.47[614.5, 607.8]0.29
[850.4, 743.6]0.49[590.0, 576.7]0.31[590.0, 576.7]0.53[874.9, 777.0]0.47[505.4, 496.5]0.29
[805.9, 779.2]0.47[590.0, 585.6]0.30[701.3, 607.8]0.53[874.9, 765.9]0.46[420.8, 414.2]0.28
[805.9, 748.0]0.47[687.9, 656.8]0.28[890.5, 768.1]0.53[848.2, 765.9]0.45[505.4, 487.6]0.26
[850.4, 759.2]0.46[505.4, 496.5]0.27[518.8, 507.6]0.52[857.1, 792.6]0.44[681.3, 674.6]0.26
[797.0, 781.4]0.44[912.8, 910.5]0.26[701.3, 603.4]0.51[874.9, 812.6]0.43[708.0, 398.6]0.25

References

  1. Clifford, T.; Howatson, G.; West, D.J.; Stevenson, E.J. The Potential Benefits of Red Beetroot Supplementation in Health and Disease. Nutrients 2015, 7, 2801–2822. [Google Scholar] [CrossRef] [PubMed]
  2. Tanumihardjo, S.A.; Suri, D.; Simon, P.; Goldman, I.L. Vegetables of Temperate Climates: Carrot, Parsnip, and Beetroot. In Encyclopedia of Food and Health; Caballero, B., Finglas, P.M., Toldrá, F., Eds.; Academic Press: Oxford, UK, 2016; pp. 387–392. ISBN 978-0-12-384953-3. [Google Scholar]
  3. Pedreño, M.A.; Escribano, J. Studying the Oxidation and the Antiradical Activity of Betalain from Beetroot. J. Biol. Educ. 2000, 35, 49–51. [Google Scholar] [CrossRef]
  4. Gengatharan, A.; Dykes, G.A.; Choo, W.S. Betalains: Natural Plant Pigments with Potential Application in Functional Foods. LWT Food Sci. Technol. 2015, 64, 645–649. [Google Scholar] [CrossRef]
  5. Toth, C.; Jóźków, G. Remote Sensing Platforms and Sensors: A Survey. ISPRS J. Photogramm. Remote Sens. 2016, 115, 22–36. [Google Scholar] [CrossRef]
  6. Zhang, C.; Kovacs, J.M. The Application of Small Unmanned Aerial Systems for Precision Agriculture: A Review. Precis. Agric. 2012, 13, 693–712. [Google Scholar] [CrossRef]
  7. Chancia, R.; Bates, T.; Vanden Heuvel, J.; van Aardt, J. Assessing Grapevine Nutrient Status from Unmanned Aerial System (UAS) Hyperspectral Imagery. Remote Sens. 2021, 13, 4489. [Google Scholar] [CrossRef]
  8. Zheng, H.; Cheng, T.; Li, D.; Yao, X.; Tian, Y.; Cao, W.; Zhu, Y. Combining Unmanned Aerial Vehicle (UAV)-Based Multispectral Imagery and Ground-Based Hyperspectral Data for Plant Nitrogen Concentration Estimation in Rice. Front. Plant Sci. 2018, 9, 936. [Google Scholar] [CrossRef]
  9. Ahmad, A.; Aggarwal, V.; Saraswat, D.; El Gamal, A.; Johal, G.S. GeoDLS: A Deep Learning-Based Corn Disease Tracking and Location System Using RTK Geolocated UAS Imagery. Remote Sens. 2022, 14, 4140. [Google Scholar] [CrossRef]
  10. Oh, S.; Lee, D.-Y.; Gongora-Canul, C.; Ashapure, A.; Carpenter, J.; Cruz, A.P.; Fernandez-Campos, M.; Lane, B.Z.; Telenko, D.E.P.; Jung, J.; et al. Tar Spot Disease Quantification Using Unmanned Aircraft Systems (UAS) Data. Remote Sens. 2021, 13, 2567. [Google Scholar] [CrossRef]
  11. Zheng, H.; Cheng, T.; Zhou, M.; Li, D.; Yao, X.; Tian, Y.; Cao, W.; Zhu, Y. Improved Estimation of Rice Aboveground Biomass Combining Textural and Spectral Analysis of UAV Imagery. Precis. Agric. 2019, 20, 611–629. [Google Scholar] [CrossRef]
  12. Tao, H.; Feng, H.; Xu, L.; Miao, M.; Long, H.; Yue, J.; Li, Z.; Yang, G.; Yang, X.; Fan, L. Estimation of Crop Growth Parameters Using UAV-Based Hyperspectral Remote Sensing Data. Sensors 2020, 20, 1296. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  13. Simpson, J.E.; Holman, F.H.; Nieto, H.; El-Madany, T.S.; Migliavacca, M.; Martin, M.P.; Burchard-Levine, V.; Cararra, A.; Blöcher, S.; Fiener, P.; et al. UAS-Based High Resolution Mapping of Evapotranspiration in a Mediterranean Tree-Grass Ecosystem. Agric. For. Meteorol. 2022, 321, 108981. [Google Scholar] [CrossRef]
  14. de Oca, A.M.; Flores, G. A UAS Equipped with a Thermal Imaging System with Temperature Calibration for Crop Water Stress Index Computation. In Proceedings of the 2021 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 15–18 June 2021; pp. 714–720. [Google Scholar]
  15. Singh, V.; Rana, A.; Bishop, M.; Filippi, A.M.; Cope, D.; Rajan, N.; Bagavathiannan, M. Chapter Three—Unmanned Aircraft Systems for Precision Weed Detection and Management: Prospects and Challenges. In Advances in Agronomy; Sparks, D.L., Ed.; Academic Press: Cambridge, MA, USA, 2020; Volume 159, pp. 93–134. [Google Scholar]
  16. Yu, N.; Li, L.; Schmitz, N.; Tian, L.F.; Greenberg, J.A.; Diers, B.W. Development of Methods to Improve Soybean Yield Estimation and Predict Plant Maturity with an Unmanned Aerial Vehicle Based Platform. Remote Sens. Environ. 2016, 187, 91–101. [Google Scholar] [CrossRef]
  17. Zhou, X.; Zheng, H.B.; Xu, X.Q.; He, J.Y.; Ge, X.K.; Yao, X.; Cheng, T.; Zhu, Y.; Cao, W.X.; Tian, Y.C. Predicting Grain Yield in Rice Using Multi-Temporal Vegetation Indices from UAV-Based Multispectral and Digital Imagery. ISPRS J. Photogramm. Remote Sens. 2017, 130, 246–255. [Google Scholar] [CrossRef]
  18. Hassanzadeh, A.; Zhang, F.; van Aardt, J.; Murphy, S.P.; Pethybridge, S.J. Broadacre Crop Yield Estimation Using Imaging Spectroscopy from Unmanned Aerial Systems (UAS): A Field-Based Case Study with Snap Bean. Remote Sens. 2021, 13, 3241. [Google Scholar] [CrossRef]
  19. Eismann, M. Hyperspectral Remote Sensing; Society of Photo-Optical Instrumentation Engineers: Bellingham, WA, USA, 2012. [Google Scholar]
  20. Georganos, S.; Grippa, T.; Vanhuysse, S.; Lennert, M.; Shimoni, M.; Kalogirou, S.; Wolff, E. Less Is More: Optimizing Classification Performance through Feature Selection in a Very-High-Resolution Remote Sensing Object-Based Urban Application. GISci. Remote Sens. 2018, 55, 221–242. [Google Scholar] [CrossRef]
  21. Khodr, J.; Younes, R. Dimensionality Reduction on Hyperspectral Images: A Comparative Review Based on Artificial Datas. In Proceedings of the 2011 4th International Congress on Image and Signal Processing, Shanghai, China, 15–17 October 2011; Volume 4, pp. 1875–1883. [Google Scholar]
  22. Kokaly, R.F.; Clark, R.N. Spectroscopic Determination of Leaf Biochemistry Using Band-Depth Analysis of Absorption Features and Stepwise Multiple Linear Regression. Remote Sens. Environ. 1999, 67, 267–287. [Google Scholar] [CrossRef]
  23. Hassanzadeh, A.; van Aardt, J.; Murphy, S.P.; Pethybridge, S.J. Yield Modeling of Snap Bean Based on Hyperspectral Sensing: A Greenhouse Study. JARS 2020, 14, 024519. [Google Scholar] [CrossRef]
  24. Raj, R.; Walker, J.P.; Pingale, R.; Banoth, B.N.; Jagarlapudi, A. Leaf Nitrogen Content Estimation Using Top-of-Canopy Airborne Hyperspectral Data. Int. J. Appl. Earth Obs. Geoinf. 2021, 104, 102584. [Google Scholar] [CrossRef]
  25. Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
  26. He, D.-C.; Wang, L. Texture Unit, Texture Spectrum, and Texture Analysis. IEEE Trans. Geosci. Remote Sens. 1990, 28, 509–512. [Google Scholar]
  27. Unser, M. Texture Classification and Segmentation Using Wavelet Frames. IEEE Trans. Image Process. 1995, 4, 1549–1560. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  28. Riou, R.; Seyler, F. Texture Analysis of Tropical Rain Forest Infrared Satellite Images. Photogramm. Eng. Remote Sens. 1997, 63, 515–521. [Google Scholar]
  29. Podest, E.; Saatchi, S. Application of Multiscale Texture in Classifying JERS-1 Radar Data over Tropical Vegetation. Int. J. Remote Sens. 2002, 23, 1487–1506. [Google Scholar] [CrossRef]
  30. Nyoungui, A.N.; Tonye, E.; Akono, A. Evaluation of Speckle Filtering and Texture Analysis Methods for Land Cover Classification from SAR Images. Int. J. Remote Sens. 2002, 23, 1895–1925. [Google Scholar] [CrossRef]
  31. Marceau, D.J.; Howarth, P.J.; Dubois, J.M.M.; Gratton, D.J. Evaluation of the Grey-Level Co-Occurrence Matrix Method for Land-Cover Classification Using SPOT Imagery. IEEE Trans. Geosci. Remote Sens. 1990, 28, 513–519. [Google Scholar] [CrossRef]
  32. Franklin, S.E.; Hall, R.J.; Moskal, L.M.; Maudie, A.J.; Lavigne, M.B. Incorporating Texture into Classification of Forest Species Composition from Airborne Multispectral Images. Int. J. Remote Sens. 2000, 21, 61–79. [Google Scholar] [CrossRef]
  33. Augusteijn, M.F.; Clemens, L.E.; Shaw, K.A. Performance Evaluation of Texture Measures for Ground Cover Identification in Satellite Images by Means of a Neural Network Classifier. IEEE Trans. Geosci. Remote Sens. 1995, 33, 616–626. [Google Scholar] [CrossRef]
  34. Franklin, S.E.; Peddle, D.R. Spectral Texture for Improved Class Discrimination in Complex Terrain. Int. J. Remote Sens. 1989, 10, 1437–1443. [Google Scholar] [CrossRef]
  35. Lu, D.; Batistella, M. Exploring TM Image Texture and Its Relationships with Biomass Estimation in Rondônia, Brazilian Amazon. Acta Amaz. 2005, 35, 249–257. [Google Scholar] [CrossRef]
  36. Sarker, L.R.; Nichol, J.E. Improved Forest Biomass Estimates Using ALOS AVNIR-2 Texture Indices. Remote Sens. Environ. 2011, 115, 968–977. [Google Scholar] [CrossRef]
  37. Eckert, S. Improved Forest Biomass and Carbon Estimations Using Texture Measures from WorldView-2 Satellite Data. Remote Sens. 2012, 4, 810–829. [Google Scholar] [CrossRef]
  38. Kelsey, K.C.; Neff, J.C. Estimates of Aboveground Biomass from Texture Analysis of Landsat Imagery. Remote Sens. 2014, 6, 6407–6422. [Google Scholar] [CrossRef] [Green Version]
  39. Féret, J.-B.; Gitelson, A.A.; Noble, S.D.; Jacquemoud, S. PROSPECT-D: Towards Modeling Leaf Optical Properties through a Complete Lifecycle. Remote Sens. Environ. 2017, 193, 204–215. [Google Scholar] [CrossRef] [Green Version]
  40. Zheng, C.; Sun, D.-W.; Zheng, L. Recent Applications of Image Texture for Evaluation of Food Qualities—A Review. Trends Food Sci. Technol. 2006, 17, 113–128. [Google Scholar] [CrossRef]
  41. Xie, C.; He, Y. Spectrum and Image Texture Features Analysis for Early Blight Disease Detection on Eggplant Leaves. Sensors 2016, 16, 676. [Google Scholar] [CrossRef] [Green Version]
  42. Zhu, F.; Zhang, D.; He, Y.; Liu, F.; Sun, D.-W. Application of Visible and Near Infrared Hyperspectral Imaging to Differentiate Between Fresh and Frozen–Thawed Fish Fillets. Food Bioprocess Technol. 2013, 6, 2931–2937. [Google Scholar] [CrossRef]
  43. Guo, A.; Huang, W.; Ye, H.; Dong, Y.; Ma, H.; Ren, Y.; Ruan, C. Identification of Wheat Yellow Rust Using Spectral and Texture Features of Hyperspectral Images. Remote Sens. 2020, 12, 1419. [Google Scholar] [CrossRef]
  44. Jia, B.; Wang, W.; Yoon, S.-C.; Zhuang, H.; Li, Y.-F. Using a Combination of Spectral and Textural Data to Measure Water-Holding Capacity in Fresh Chicken Breast Fillets. Appl. Sci. 2018, 8, 343. [Google Scholar] [CrossRef] [Green Version]
  45. Yang, Y.; Wang, W.; Zhuang, H.; Yoon, S.-C.; Jiang, H. Fusion of Spectra and Texture Data of Hyperspectral Imaging for the Prediction of the Water-Holding Capacity of Fresh Chicken Breast Filets. Appl. Sci. 2018, 8, 640. [Google Scholar] [CrossRef] [Green Version]
  46. Olson, D.; Chatterjee, A.; Franzen, D.W. Can We Select Sugarbeet Harvesting Dates Using Drone-Based Vegetation Indices? Agron. J. 2019, 111, 2619–2624. [Google Scholar] [CrossRef]
  47. Al-Gaadi, K.A.; Hassaballa, A.A.; Tola, E.; Kayad, A.G.; Madugundu, R.; Alblewi, B.; Assiri, F. Prediction of Potato Crop Yield Using Precision Agriculture Techniques. PLoS ONE 2016, 11, e0162219. [Google Scholar] [CrossRef] [PubMed]
  48. Luo, S.; He, Y.; Li, Q.; Jiao, W.; Zhu, Y.; Zhao, X. Nondestructive Estimation of Potato Yield Using Relative Variables Derived from Multi-Period LAI and Hyperspectral Data Based on Weighted Growth Stage. Plant Methods 2020, 16, 150. [Google Scholar] [CrossRef] [PubMed]
  49. Li, B.; Xu, X.; Zhang, L.; Han, J.; Bian, C.; Li, G.; Liu, J.; Jin, L. Above-Ground Biomass Estimation and Yield Prediction in Potato by Using UAV-Based RGB and Hyperspectral Imaging. ISPRS J. Photogramm. Remote Sens. 2020, 162, 161–172. [Google Scholar] [CrossRef]
  50. Li, D.; Miao, Y.; Gupta, S.K.; Rosen, C.J.; Yuan, F.; Wang, C.; Wang, L.; Huang, Y. Improving Potato Yield Prediction by Combining Cultivar Information and UAV Remote Sensing Data Using Machine Learning. Remote Sens. 2021, 13, 3322. [Google Scholar] [CrossRef]
  51. Suarez, L.A.; Robson, A.; McPhee, J.; O’Halloran, J.; van Sprang, C. Accuracy of Carrot Yield Forecasting Using Proximal Hyperspectral and Satellite Multispectral Data. Precis. Agric. 2020, 21, 1304–1326. [Google Scholar] [CrossRef]
  52. Olson, D.; Chatterjee, A.; Franzen, D.W.; Day, S.S. Relationship of Drone-Based Vegetation Indices with Corn and Sugarbeet Yields. Agron. J. 2019, 111, 2545–2557. [Google Scholar] [CrossRef]
  53. Chancia, R.; van Aardt, J.; Pethybridge, S.; Cross, D.; Henderson, J. Predicting Table Beet Root Yield with Multispectral UAS Imagery. Remote Sens. 2021, 13, 2180. [Google Scholar] [CrossRef]
  54. RedEdge-M User Manual (PDF)—Legacy. Available online: https://support.micasense.com/hc/en-us/articles/115003537673-RedEdge-M-User-Manual-PDF-Legacy (accessed on 21 July 2022).
  55. Hyperspectral and Operational Software. Available online: https://www.headwallphotonics.com/products/software (accessed on 24 July 2022).
  56. PIX4Dmapper: Professional Photogrammetry Software for Drone Mapping. Available online: https://www.pix4d.com/product/pix4dmapper-photogrammetry-software (accessed on 24 July 2022).
  57. Atmospheric Correction. Available online: https://www.l3harrisgeospatial.com/docs/atmosphericcorrection.html#empirical_line_calibration (accessed on 24 July 2022).
  58. Rasti, B.; Scheunders, P.; Ghamisi, P.; Licciardi, G.; Chanussot, J. Noise Reduction in Hyperspectral Imagery: Overview and Application. Remote Sens. 2018, 10, 482. [Google Scholar] [CrossRef] [Green Version]
  59. Chen, G.; Qian, S.-E. Denoising of Hyperspectral Imagery Using Principal Component Analysis and Wavelet Shrinkage. IEEE Trans. Geosci. Remote Sens. 2011, 49, 973–980. [Google Scholar] [CrossRef]
  60. Velicer, W.F. Determining the Number of Components from the Matrix of Partial Correlations. Psychometrika 1976, 41, 321–327. [Google Scholar] [CrossRef]
  61. Chen, G.Y.; Zhu, W.-P. Signal Denoising Using Neighbouring Dual-Tree Complex Wavelet Coefficients. In Proceedings of the 2009 Canadian Conference on Electrical and Computer Engineering, St. John’s, NL, Canada, 3–6 May 2009; pp. 565–568. [Google Scholar]
  62. Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The Spectral Image Processing System (SIPS)—Interactive Visualization and Analysis of Imaging Spectrometer Data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
  63. Huete, A.R.; Jackson, R.D.; Post, D.F. Spectral Response of a Plant Canopy with Different Soil Backgrounds. Remote Sens. Environ. 1985, 17, 37–53. [Google Scholar] [CrossRef]
  64. Colwell, J.E. Vegetation Canopy Reflectance. Remote Sens. Environ. 1974, 3, 175–183. [Google Scholar] [CrossRef]
  65. Tucker, C.J. Red and Photographic Infrared Linear Combinations for Monitoring Vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
  66. Townshend, J.R.G.; Goff, T.E.; Tucker, C.J. Multitemporal Dimensionality of Images of Normalized Difference Vegetation Index at Continental Scales. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 888–895. [Google Scholar] [CrossRef]
  67. Zhu, Z.; Bi, J.; Pan, Y.; Ganguly, S.; Anav, A.; Xu, L.; Samanta, A.; Piao, S.; Nemani, R.R.; Myneni, R.B. Global Data Sets of Vegetation Leaf Area Index (LAI)3g and Fraction of Photosynthetically Active Radiation (FPAR)3g Derived from Global Inventory Modeling and Mapping Studies (GIMMS) Normalized Difference Vegetation Index (NDVI3g) for the Period 1981 to 2011. Remote Sens. 2013, 5, 927–948. [Google Scholar] [CrossRef] [Green Version]
  68. Schaefer, M.T.; Lamb, D.W. A Combination of Plant NDVI and LiDAR Measurements Improve the Estimation of Pasture Biomass in Tall Fescue (Festuca Arundinacea Var. Fletcher). Remote Sens. 2016, 8, 109. [Google Scholar] [CrossRef] [Green Version]
  69. Hassan, M.A.; Yang, M.; Rasheed, A.; Yang, G.; Reynolds, M.; Xia, X.; Xiao, Y.; He, Z. A Rapid Monitoring of NDVI across the Wheat Growth Cycle for Grain Yield Prediction Using a Multi-Spectral UAV Platform. Plant Sci. 2019, 282, 95–103. [Google Scholar] [CrossRef]
  70. Sun, Y.; Ren, H.; Zhang, T.; Zhang, C.; Qin, Q. Crop Leaf Area Index Retrieval Based on Inverted Difference Vegetation Index and NDVI. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1662–1666. [Google Scholar] [CrossRef]
  71. Li, F.; Miao, Y.; Feng, G.; Yuan, F.; Yue, S.; Gao, X.; Liu, Y.; Liu, B.; Ustin, S.L.; Chen, X. Improving Estimation of Summer Maize Nitrogen Status with Red Edge-Based Spectral Vegetation Indices. Field Crops Res. 2014, 157, 111–123. [Google Scholar] [CrossRef]
  72. Tan, C.-W.; Zhang, P.-P.; Zhou, X.-X.; Wang, Z.-X.; Xu, Z.-Q.; Mao, W.; Li, W.-X.; Huo, Z.-Y.; Guo, W.-S.; Yun, F. Quantitative Monitoring of Leaf Area Index in Wheat of Different Plant Types by Integrating NDVI and Beer-Lambert Law. Sci. Rep. 2020, 10, 929. [Google Scholar] [CrossRef] [PubMed]
  73. Hashimoto, N.; Saito, Y.; Maki, M.; Homma, K. Simulation of Reflectance and Vegetation Indices for Unmanned Aerial Vehicle (UAV) Monitoring of Paddy Fields. Remote Sens. 2019, 11, 2119. [Google Scholar] [CrossRef] [Green Version]
  74. Chen, S.; She, D.; Zhang, L.; Guo, M.; Liu, X. Spatial Downscaling Methods of Soil Moisture Based on Multisource Remote Sensing Data and Its Application. Water 2019, 11, 1401. [Google Scholar] [CrossRef] [Green Version]
  75. Marshall, M.; Thenkabail, P.; Biggs, T.; Post, K. Hyperspectral Narrowband and Multispectral Broadband Indices for Remote Sensing of Crop Evapotranspiration and Its Components (Transpiration and Soil Evaporation). Agric. For. Meteorol. 2016, 218–219, 122–134. [Google Scholar] [CrossRef] [Green Version]
  76. Thenkabail, P.S.; Smith, R.B.; De Pauw, E. Hyperspectral Vegetation Indices and Their Relationships with Agricultural Crop Characteristics. Remote Sens. Environ. 2000, 71, 158–182. [Google Scholar] [CrossRef]
  77. Koppe, W.; Li, F.; Gnyp, M.; Miao, Y.; Jia, L.; Chen, X.; Zhang, F.; Bareth, G. Evaluating Multispectral and Hyperspectral Satellite Remote Sensing Data for Estimating Winter Wheat Growth Parameters at Regional Scale in the North China Plain. Photogramm. Fernerkund. Geoinf. 2010, 2010, 167–178. [Google Scholar] [CrossRef] [Green Version]
  78. Zheng, H.; Ma, J.; Zhou, M.; Li, D.; Yao, X.; Cao, W.; Zhu, Y.; Cheng, T. Enhancing the Nitrogen Signals of Rice Canopies across Critical Growth Stages through the Integration of Textural and Spectral Information from Unmanned Aerial Vehicle (UAV) Multispectral Imagery. Remote Sens. 2020, 12, 957. [Google Scholar] [CrossRef] [Green Version]
  79. Yue, J.; Yang, G.; Tian, Q.; Feng, H.; Xu, K.; Zhou, C. Estimate of Winter-Wheat above-Ground Biomass Based on UAV Ultrahigh-Ground-Resolution Image Textures and Vegetation Indices. ISPRS J. Photogramm. Remote Sens. 2019, 150, 226–244. [Google Scholar] [CrossRef]
  80. Wong, T.-T. Performance Evaluation of Classification Algorithms by K-Fold and Leave-One-out Cross Validation. Pattern Recognit. 2015, 48, 2839–2846. [Google Scholar] [CrossRef]
  81. Smith, G. Step Away from Stepwise. J. Big Data 2018, 5, 32. [Google Scholar] [CrossRef]
  82. Grossman, Y.L.; Ustin, S.L.; Jacquemoud, S.; Sanderson, E.W.; Schmuck, G.; Verdebout, J. Critique of Stepwise Multiple Linear Regression for the Extraction of Leaf Biochemistry Information from Leaf Reflectance Data. Remote Sens. Environ. 1996, 56, 182–193. [Google Scholar] [CrossRef]
  83. Whittingham, M.J.; Stephens, P.A.; Bradbury, R.B.; Freckleton, R.P. Why Do We Still Use Stepwise Modelling in Ecology and Behaviour? J. Anim. Ecol. 2006, 75, 1182–1189. [Google Scholar] [CrossRef] [PubMed]
  84. Hegyi, G.; Garamszegi, L.Z. Using Information Theory as a Substitute for Stepwise Regression in Ecology and Behavior. Behav. Ecol. Sociobiol. 2011, 65, 69–76. [Google Scholar] [CrossRef]
  85. Karagiannopoulos, M.; Anyfantis, D.; Kotsiantis, S.; Pintelas, P. Feature Selection for Regression Problems. Educational Software Development Laboratory, Department of Mathematics, University of Patras: Patras, Greece, 2007; pp. 20–22. [Google Scholar]
  86. Jović, A.; Brkić, K.; Bogunović, N. A Review of Feature Selection Methods with Applications. In Proceedings of the 2015 38th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 25–29 May 2015; pp. 1200–1205. [Google Scholar]
  87. Craney, T.A.; Surles, J.G. Model-Dependent Variance Inflation Factor Cutoff Values. Qual. Eng. 2002, 14, 391–403. [Google Scholar] [CrossRef]
  88. Stine, R.A. Graphical Interpretation of Variance Inflation Factors. Am. Stat. 1995, 49, 53–56. [Google Scholar] [CrossRef]
  89. Gao, B.-C.; Montes, M.J.; Davis, C.O. Refinement of Wavelength Calibrations of Hyperspectral Imaging Data Using a Spectrum-Matching Technique. Remote Sens. Environ. 2004, 90, 424–433. [Google Scholar] [CrossRef]
  90. Wolfe, W.L. Introduction to Imaging Spectrometers; SPIE Press: Bellingham, WA, USA, 1997; ISBN 978-0-8194-2260-6. [Google Scholar]
  91. Ceclu, L.; Nistor, O.-V. Red Beetroot: Composition and Health Effects—A Review. J. Nutr. Med. Diet Care 2020, 6, 1–9. [Google Scholar] [CrossRef]
  92. Blackburn, G.A. Quantifying Chlorophylls and Caroteniods at Leaf and Canopy Scales: An Evaluation of Some Hyperspectral Approaches. Remote Sens. Environ. 1998, 66, 274–285. [Google Scholar] [CrossRef]
  93. Stroppiana, D.; Boschetti, M.; Brivio, P.A.; Bocchi, S. Plant Nitrogen Concentration in Paddy Rice from Field Canopy Hyperspectral Radiometry. Field Crops Res. 2009, 111, 119–129. [Google Scholar] [CrossRef]
  94. Wei, M.C.F.; Maldaner, L.F.; Ottoni, P.M.N.; Molin, J.P. Carrot Yield Mapping: A Precision Agriculture Approach Based on Machine Learning. AI 2020, 1, 229–241. [Google Scholar] [CrossRef]
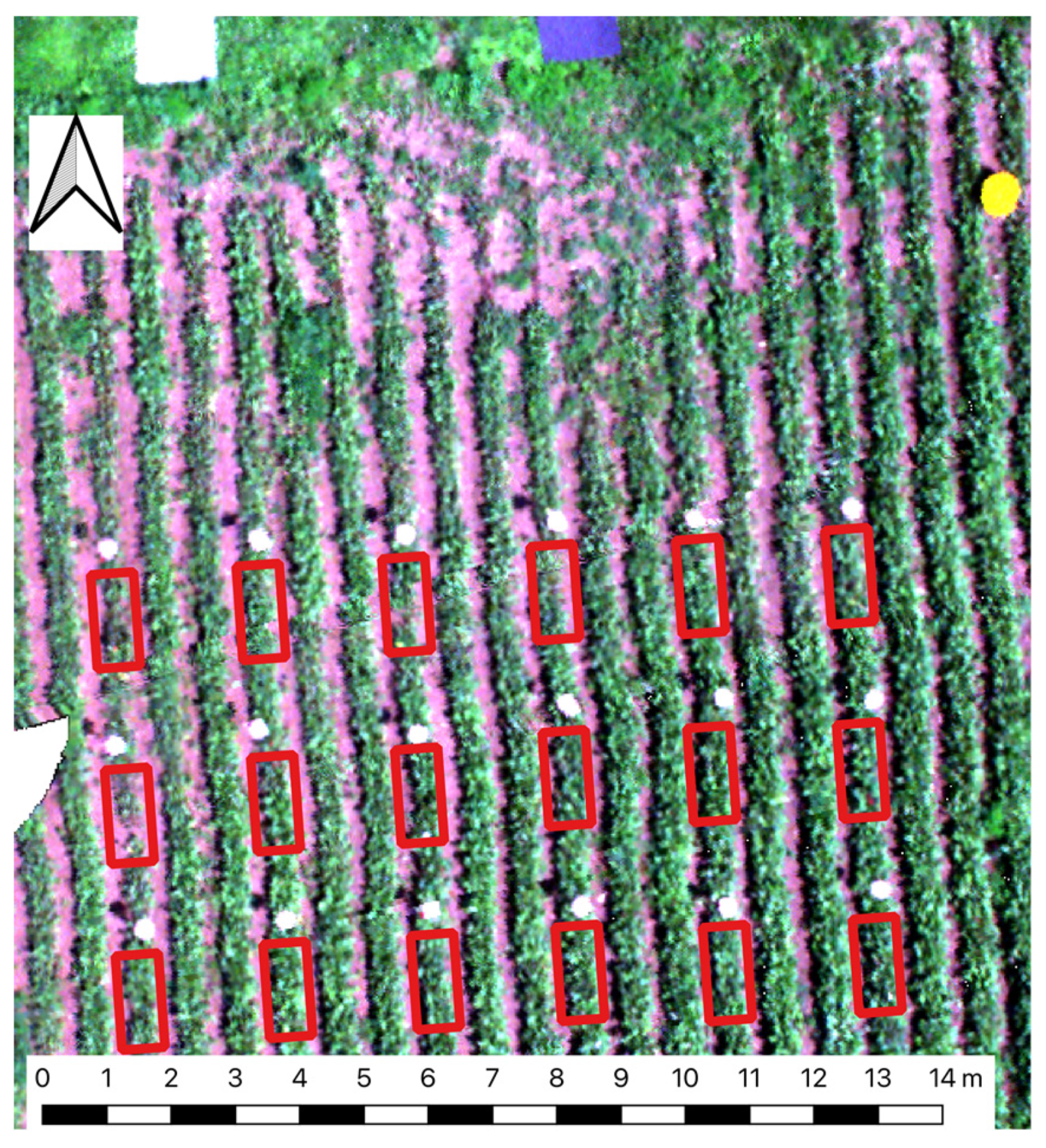
Remotesensing 15 00794 g001 550
Figure 1. Color mosaic of third flight hyperspectral image. The visualization bands are the following: red (639 nm), green (550 nm), and blue (470 nm). The crops in the red boxes in the figure were the plots under study.
Figure 1. Color mosaic of third flight hyperspectral image. The visualization bands are the following: red (639 nm), green (550 nm), and blue (470 nm). The crops in the red boxes in the figure were the plots under study.
Remotesensing 15 00794 g001
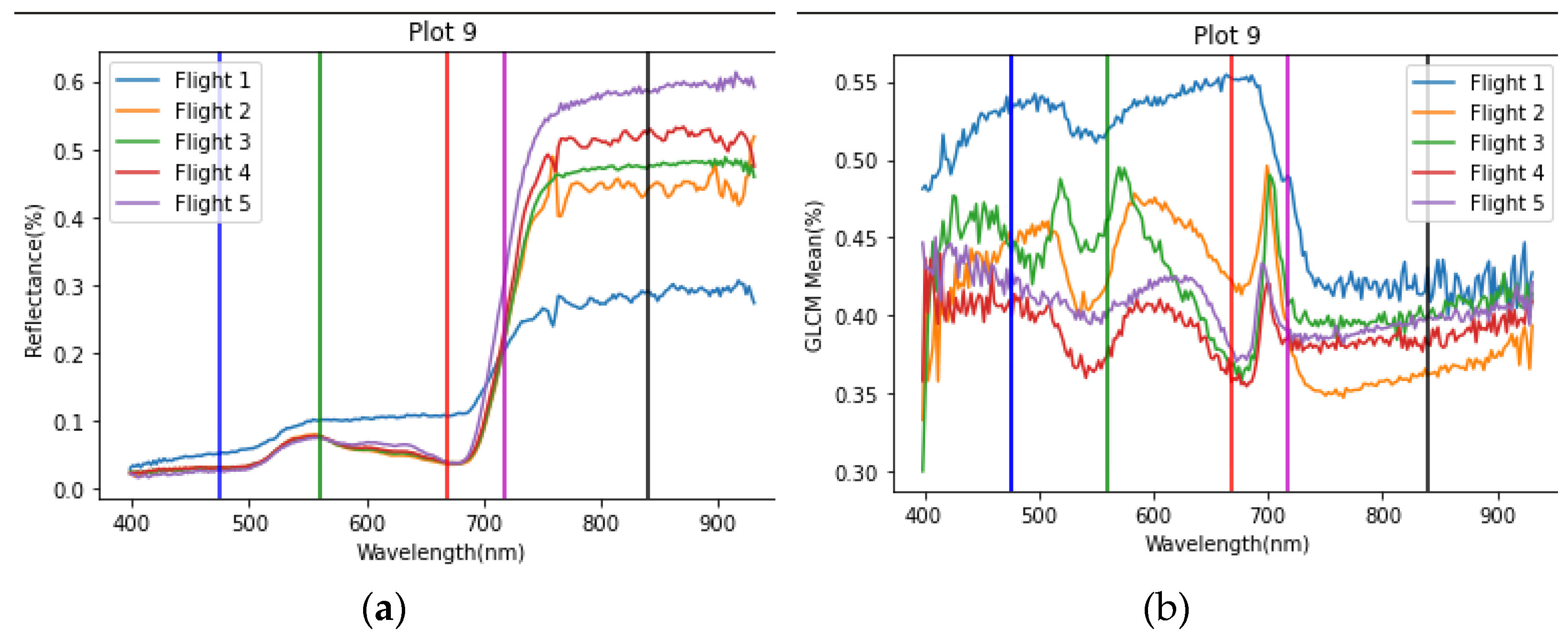
Remotesensing 15 00794 g002 550
Figure 2. The mean (a) reflectance and (b) GLCM mean of a selected plot for different flights.
Figure 2. The mean (a) reflectance and (b) GLCM mean of a selected plot for different flights.
Remotesensing 15 00794 g002
Remotesensing 15 00794 g003 550
Figure 3. Heat map of LOOCV R2 values at various wavelength pairs, using features obtained from (a) normalized difference reflectance index (NDRI) and (b) normalized difference texture index (NDTI).
Figure 3. Heat map of LOOCV R2 values at various wavelength pairs, using features obtained from (a) normalized difference reflectance index (NDRI) and (b) normalized difference texture index (NDTI).
Remotesensing 15 00794 g003
Remotesensing 15 00794 g004 550
Figure 4. Plot of observed vs. predicted yield for the best performing model for each flight. (a) flight 1, (b) flight 2, (c) flight 3, (d) flight 4 and (e) flight 5.
Figure 4. Plot of observed vs. predicted yield for the best performing model for each flight. (a) flight 1, (b) flight 2, (c) flight 3, (d) flight 4 and (e) flight 5.
Remotesensing 15 00794 g004
Remotesensing 15 00794 g005 550
Figure 5. An example of field-level estimated root yield using the best-performing model for each flight.
Figure 5. An example of field-level estimated root yield using the best-performing model for each flight.
Remotesensing 15 00794 g005
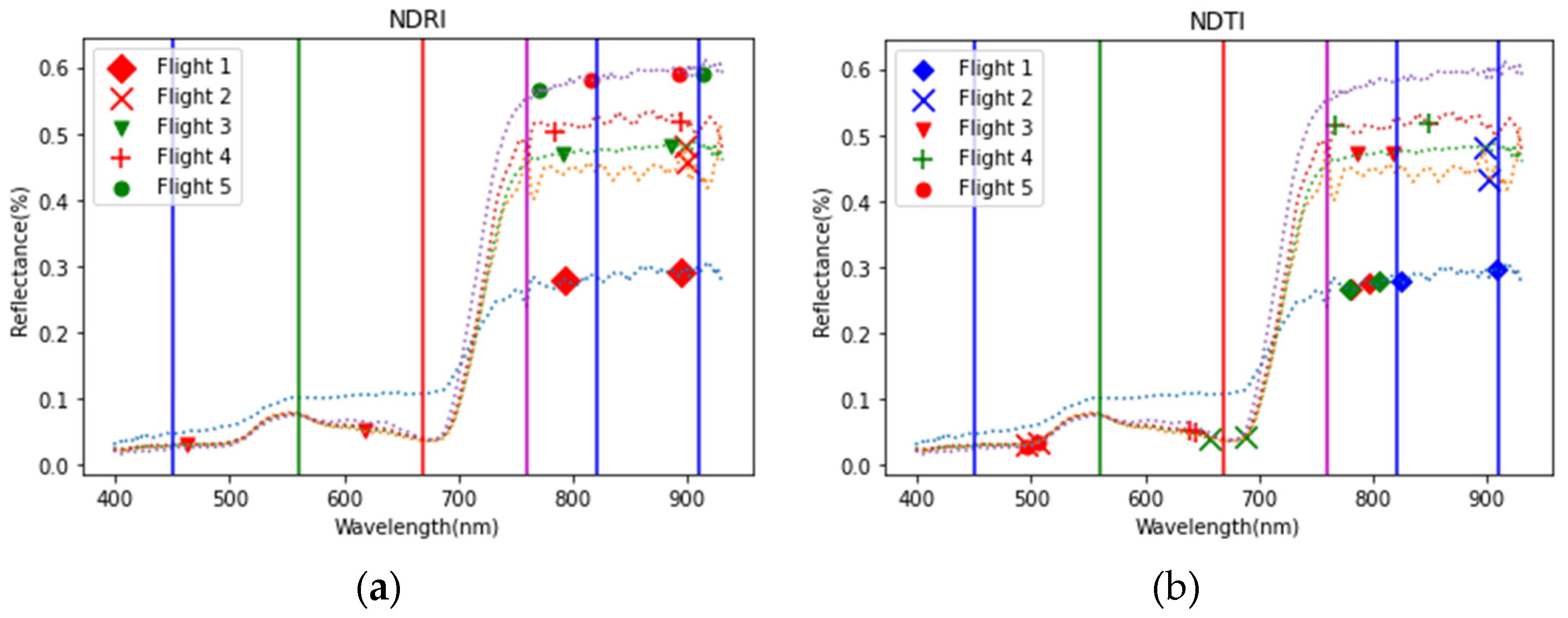
Remotesensing 15 00794 g006 550
Figure 6. (a) NDRI feature pairs and (b) NDTI feature pairs plotted over the mean vegetation spectra (dotted lines) of plot 9 for each flight. Each color signifies a unique feature for that flight.
Figure 6. (a) NDRI feature pairs and (b) NDTI feature pairs plotted over the mean vegetation spectra (dotted lines) of plot 9 for each flight. Each color signifies a unique feature for that flight.
Remotesensing 15 00794 g006
Remotesensing 15 00794 g007 550
Figure 7. Plot of LOOCV R2 values for models using the top performing features of (a) flight 1, (b) flight 2, (c) flight 3, (d) flight 4 and (e) flight 5. R2 values of less than or equal to 0 are not shown in the plot.
Figure 7. Plot of LOOCV R2 values for models using the top performing features of (a) flight 1, (b) flight 2, (c) flight 3, (d) flight 4 and (e) flight 5. R2 values of less than or equal to 0 are not shown in the plot.
Remotesensing 15 00794 g007
Table
Table 1. Data collection milestones. All data were collected in 2021.
Table 1. Data collection milestones. All data were collected in 2021.
DateMilestoneGrowth Stages
20-MayCrop plantedGermination
16-Jun1st FlightLeaf development (crop emergence)
7-Jul2nd FlightLeaf development (more than 9 leaves unfolded)
15-Jul3rd FlightRosette growth
20-Jul4th FlightRosette growth (cont’d)
2-Aug5th FlightHarvest-ready
5-AugHarvestHarvest-ready
Table
Table 2. The top five models obtained from one NDRI and one NDTI feature. ‘t’ represents the feature obtained from NDTI, while ‘d’ represents that from NDRI.
Table 2. The top five models obtained from one NDRI and one NDTI feature. ‘t’ represents the feature obtained from NDTI, while ‘d’ represents that from NDRI.
Flight 1
FeaturesR2R2adjRMSE (%)VIF
d [895.0, 792.6] t [908.3, 823.7]0.770.7416.13(1.241, 1.241)
d [826.0, 765.9] t [805.9, 779.2]0.760.7316.23(1.195, 1.195)
d [494.3, 485.4] t [908.3, 823.7]0.760.7316.32(1.496, 1.496)
d [895.0, 765.9] t [908.3, 823.7]0.750.7216.66(1.334, 1.334)
d [494.3, 485.4] t [797.0, 781.4]0.750.7216.73(1.324, 1.324)
Flight 2
FeaturesR2R2adjRMSE (%)VIF
d [897.2, 895.0] t [901.6, 897.2]0.730.6917.37(1.281, 1.281)
d [801.5, 761.4] t [687.9, 656.8]0.710.6718.16(1.103, 1.103)
d [899.4, 897.2] t [505.4, 496.5]0.710.6718.27(1.118, 1.118)
d [899.4, 897.2] t [687.9, 654.6]0.690.6518.66(1.264, 1.264)
d [803.7, 761.4] t [587.8, 583.3]0.670.6319.03(1.097, 1.097)
Flight 3
FeaturesR2R2adjRMSE (%)VIF
d [897.2, 788.1] t [469.8, 452.0]0.820.8014.23(1.651, 1.651)
d [886.1, 790.3] t [817.1, 785.9]0.810.7914.54(1.555, 1.555)
d [874.9, 788.1] t [469.8, 452.0]0.810.7814.72(1.77, 1.77)
d [903.9, 897.2] t [469.8, 452.0]0.800.7814.97(1.766, 1.766)
d [886.1, 790.3] t [469.8, 452.0]0.790.7615.32(1.756, 1.756)
Flight 4
FeaturesR2R2adjRMSE (%)VIF
d [895.0, 785.9] t [848.2, 765.9]0.850.8313.20(1.198, 1.198)
d [895.0, 785.9] t [808.2, 765.9]0.830.8113.70(1.226, 1.226)
d [895.0, 783.7] t [848.2, 765.9]0.830.8113.90(1.252, 1.252)
d [895.0, 785.9] t [874.9, 763.6]0.820.8014.15(1.341, 1.341)
d [895.0, 783.7] t [857.1, 792.6]0.820.8014.23(1.264, 1.264)
Flight 5
FeaturesR2R2adjRMSE (%)VIF
d [892.7, 814.8] t [505.4, 496.5]0.820.7914.41(1.108, 1.108)
d [883.8, 794.8] t [614.5, 607.8]0.790.7715.19(1.178, 1.178)
d [910.5, 770.3] t [505.4, 496.5]0.780.7515.71(1.146, 1.146)
d [886.1, 770.3] t [505.4, 496.5]0.760.7316.43(1.186, 1.186)
d [883.8, 794.8] t [610.0, 607.8]0.760.7316.46(1.694, 1.694)
Table
Table 3. Summary of results using multiple features. Random stepwise regression also generated models already found in the double feature case we did not report those models in this table.
Table 3. Summary of results using multiple features. Random stepwise regression also generated models already found in the double feature case we did not report those models in this table.
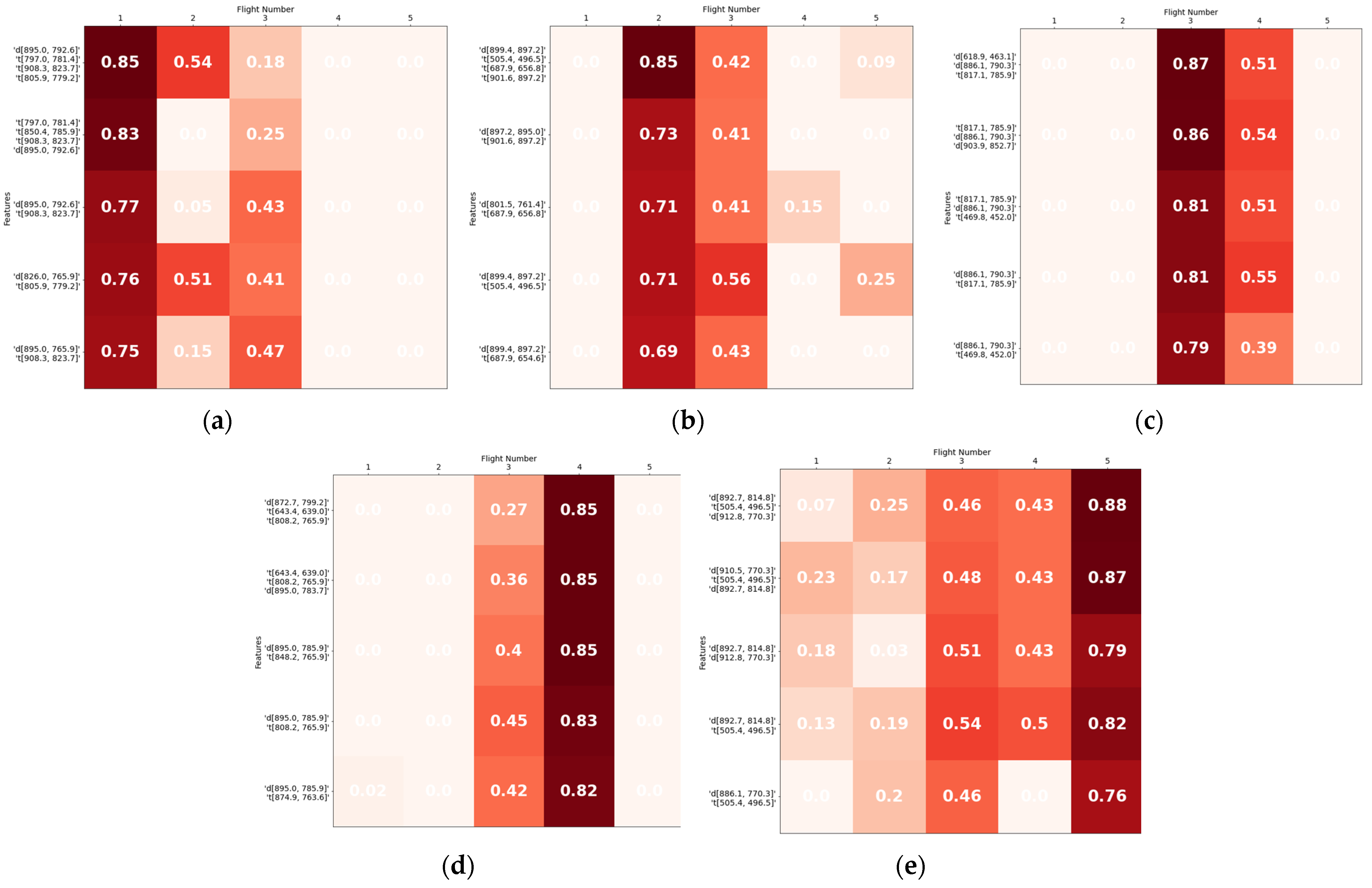
Flight 1
featuresR2R2adjRMSE (%)VIFp-values
['d [895.0, 792.6]', 't [797.0, 781.4]', 't [908.3, 823.7]', 't [805.9, 779.2]']0.850.8112.93[1.463, 1.632 2.136, 1.879][0.004, 0.027 0.019, 0.042]
['t [797.0, 781.4]', 'd [895.0, 792.6]', 't [850.4, 743.6]', 't [908.3, 823.7]']0.840.7913.59[1.648, 1.387 1.944, 2.205][0.043, 0.002 0.048, 0.026]
['t [797.0, 781.4]', 't [850.4, 785.9]', 't [908.3, 823.7]', 'd [895.0, 792.6]']0.830.7813.74[1.640, 1.959 1.938, 1.743][0.021, 0.046 0.010, 0.019]
['d [494.3, 485.4]', 't [797.0, 781.4]', 't [908.3, 823.7]']0.820.7814.28[1.589, 1.595 1.803][0.003, 0.041, 0.012]
Flight 2
FeaturesR2R2adjRMSE (%)VIFp-values
['d [899.4, 897.2]', 't [505.4, 496.5]', 't [687.9, 656.8]', 't [901.6, 897.2]']0.850.8112.93[1.813, 1.219 1.361, 1.586][0.006, 0.006 0.014, 0.019]
Flight 3
FeaturesR2R2adjRMSE (%)VIFp-values
['d [618.9, 463.1]', 'd [886.1, 790.3]', 't [817.1, 785.9]']0.870.8511.85[2.266, 1.839, 2.078][0.011, 0.002, 0.020]
['t [817.1, 785.9]', 'd [886.1, 790.3]', 'd [903.9, 852.7]']0.860.8312.63[2.070, 1.955, 2.457][0.021, 0.004, 0.020]
['d [903.9, 852.7]', 'd [886.1, 790.3]', 't [469.8, 452.0]']0.840.8113.46[2.405, 2.082, 2.289][0.022, 0.008, 0.023]
['t [817.1, 785.9]', 'd [886.1, 832.6]', 'd [618.9, 463.1]']0.840.8013.45[2.149, 2.044, 2.310][0.038, 0.006, 0.019]
['d [886.1, 790.3]', 't [469.8, 452.0]', 'd [618.9, 463.1]']0.830.8013.69[1.962, 2.379, 2.299][0.004, 0.027, 0.033]
['t [469.8, 452.0]', 'd [886.1, 790.3]', 'd [892.7, 788.1]']0.830.7913.92[2.026, 2.284, 2.293][0.008, 0.024, 0.024]
['t [817.1, 785.9]', 'd [886.1, 790.3]', 't [469.8, 452.0]']0.810.7714.51[2.276, 1.852, 2.569][0.045, 0.003, 0.049]
['t [817.1, 785.9]', 'd [886.1, 832.6]', 'd [874.9, 788.1]']0.810.7714.60[2.074, 2.370, 2.700][0.032, 0.022, 0.037]
Flight 4
FeaturesR2R2adjRMSE (%)VIFp-values
['t [643.4, 639.0]', 't [848.2, 765.9]', 'd [895.0, 783.7]']0.900.8710.81[1.666, 1.332, 1.672][0.007, 0.001, 0.000]
['d [872.7, 799.2]', 't [643.4, 639.0]', 't [808.2, 765.9]']0.850.8113.15[1.951, 1.603, 1.624][0.003, 0.008, 0.025]
['t [643.4, 639.0]', 't [808.2, 765.9]', 'd [895.0, 783.7]']0.850.8113.20[1.676, 1.413, 1.713][0.012, 0.003, 0.001]
Flight 5
FeaturesR2R2adjRMSE (%)VIFp-values
['d [892.7, 814.8]', 't [505.4, 496.5]', 'd [912.8, 770.3]']0.880.8511.80[1.680, 1.446, 2.184][0.000, 0.015, 0.016]
['d [910.5, 770.3]', 't [505.4, 496.5]', 'd [892.7, 814.8]']0.870.8412.14[2.929, 1.148, 2.833][0.036, 0.002, 0.009]
['d [926.1, 823.7]', 'd [883.8, 794.8]']0.810.7814.60[1.975, 1.975][0.004, 0.004]
['d [883.8, 794.8]', 'd [926.1, 777.0]']0.800.7715.08[1.884, 1.884][0.003, 0.008]
['d [892.7, 814.8]', 'd [912.8, 770.3]']0.790.7715.27[1.674, 1.674][0.001, 0.003]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Saif, M.S.; Chancia, R.; Pethybridge, S.; Murphy, S.P.; Hassanzadeh, A.; van Aardt, J. Forecasting Table Beet Root Yield Using Spectral and Textural Features from Hyperspectral UAS Imagery. Remote Sens. 2023, 15, 794. https://doi.org/10.3390/rs15030794

AMA Style

Saif MS, Chancia R, Pethybridge S, Murphy SP, Hassanzadeh A, van Aardt J. Forecasting Table Beet Root Yield Using Spectral and Textural Features from Hyperspectral UAS Imagery. Remote Sensing. 2023; 15(3):794. https://doi.org/10.3390/rs15030794

Chicago/Turabian Style

Saif, Mohammad S., Robert Chancia, Sarah Pethybridge, Sean P. Murphy, Amirhossein Hassanzadeh, and Jan van Aardt. 2023. "Forecasting Table Beet Root Yield Using Spectral and Textural Features from Hyperspectral UAS Imagery" Remote Sensing 15, no. 3: 794. https://doi.org/10.3390/rs15030794

APA Style

Saif, M. S., Chancia, R., Pethybridge, S., Murphy, S. P., Hassanzadeh, A., & van Aardt, J. (2023). Forecasting Table Beet Root Yield Using Spectral and Textural Features from Hyperspectral UAS Imagery. Remote Sensing, 15(3), 794. https://doi.org/10.3390/rs15030794

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop