Impact of the Antenna Spacing on the Brightness Temperature Maps Retrieved with a Synthetic Aperture Imaging Radiometer
Abstract
:1. Introduction
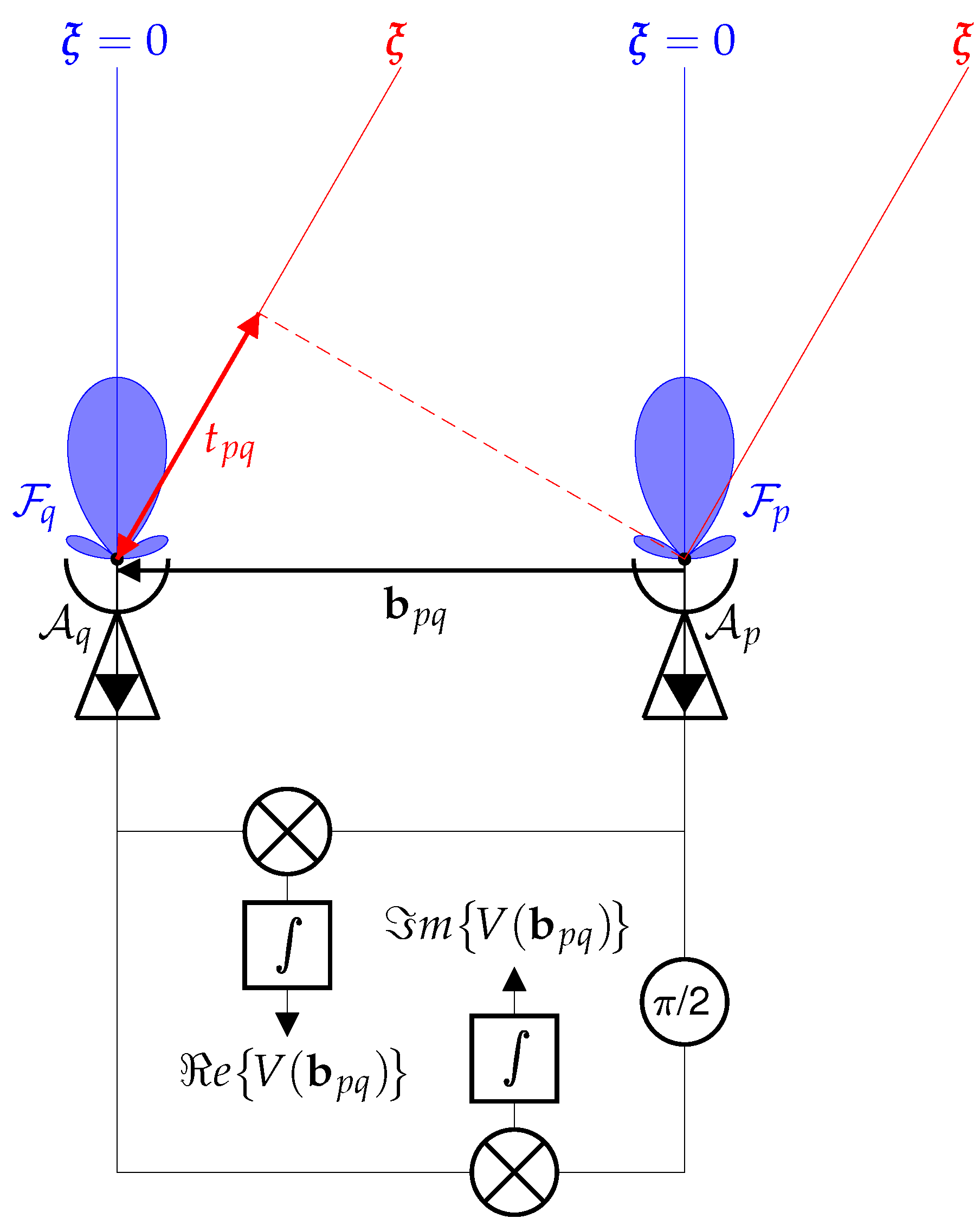
2. Observing Equation of Interferometric Arrays
3. Sky vs. Earth Observations with Antenna Arrays
3.1. The Radio Astronomy Point of View
3.2. The Remote Sensing Point of View
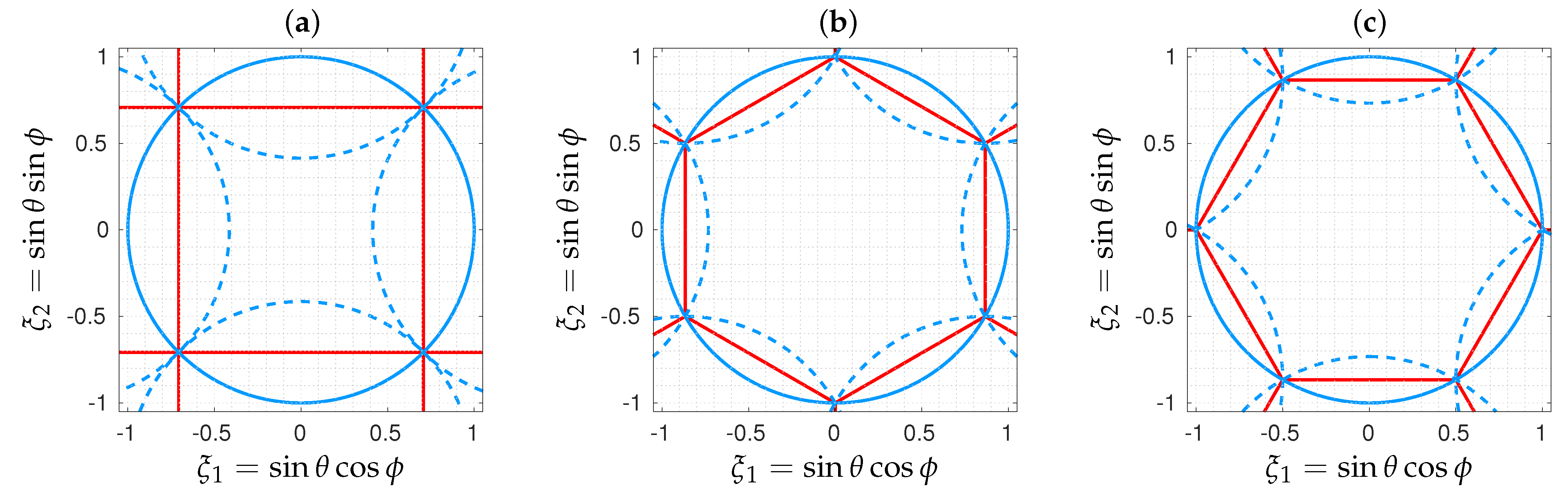
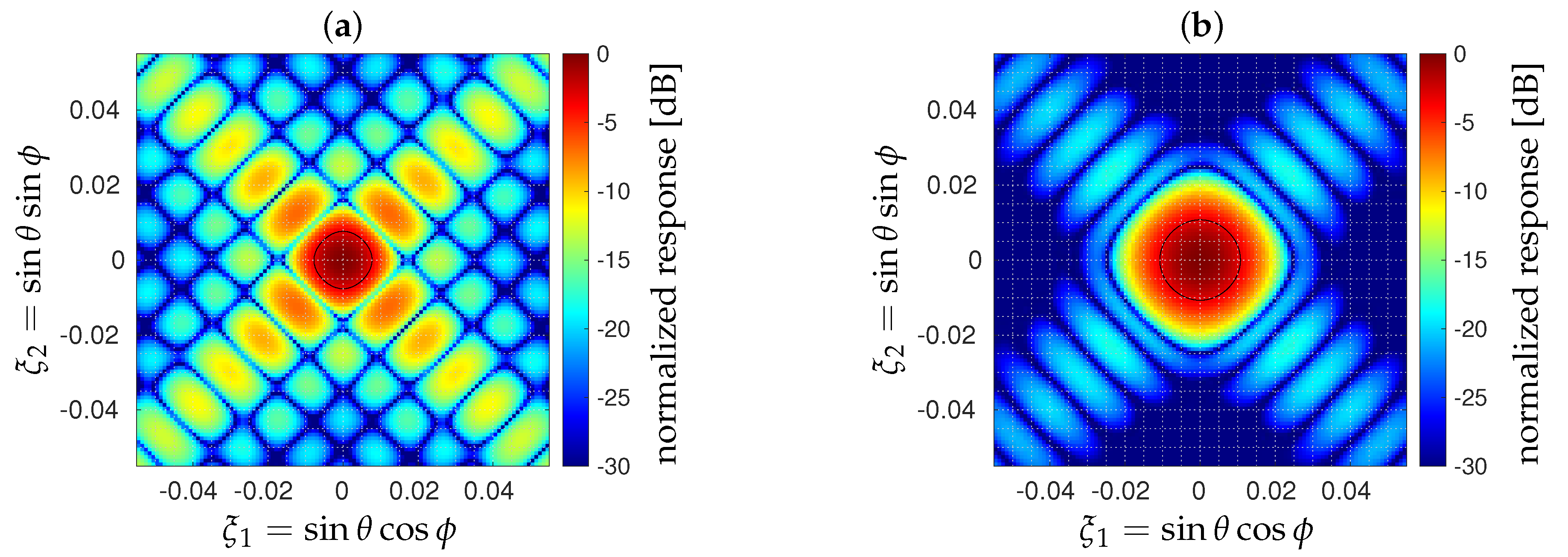
4. Geometrical Considerations
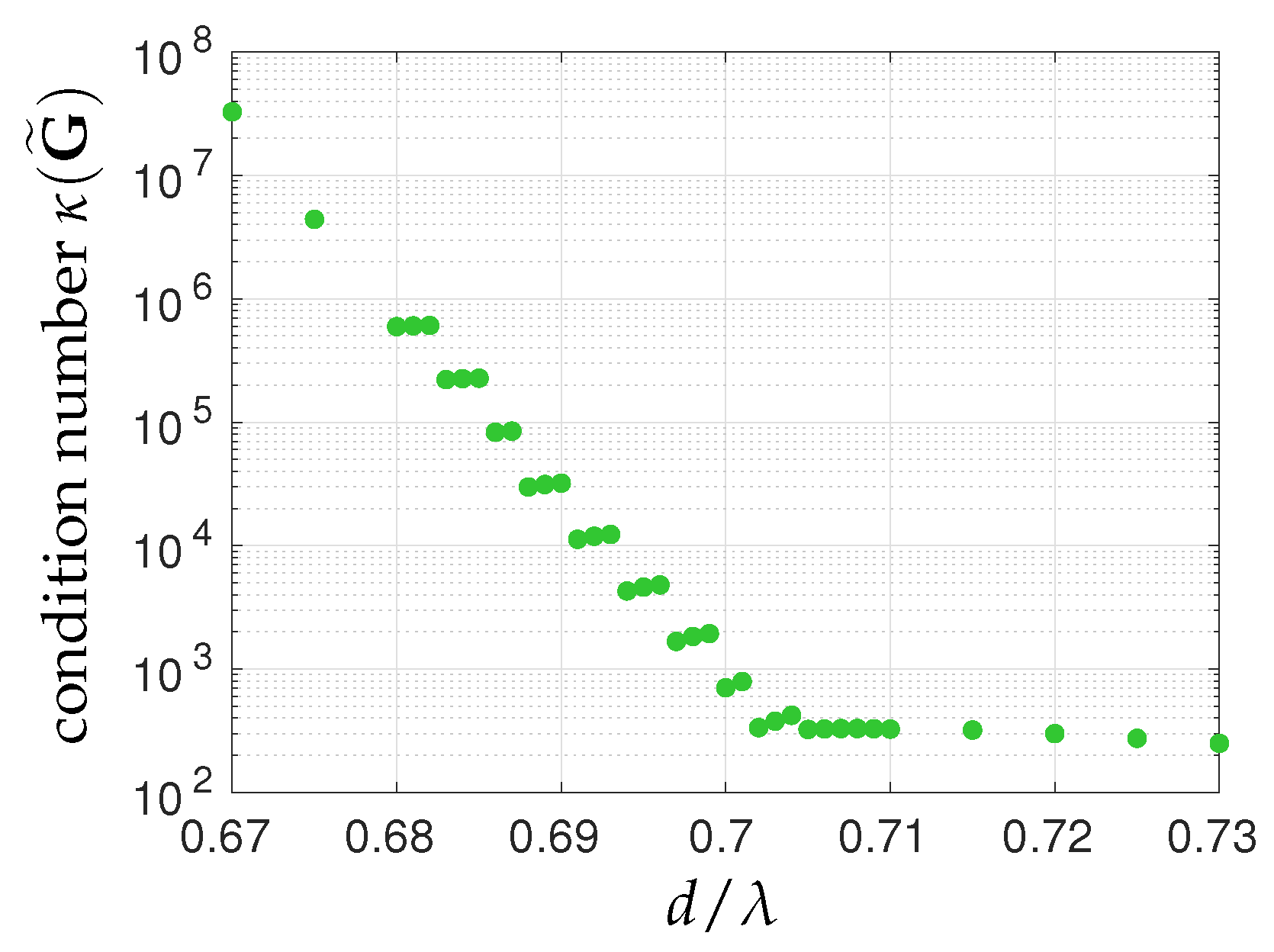
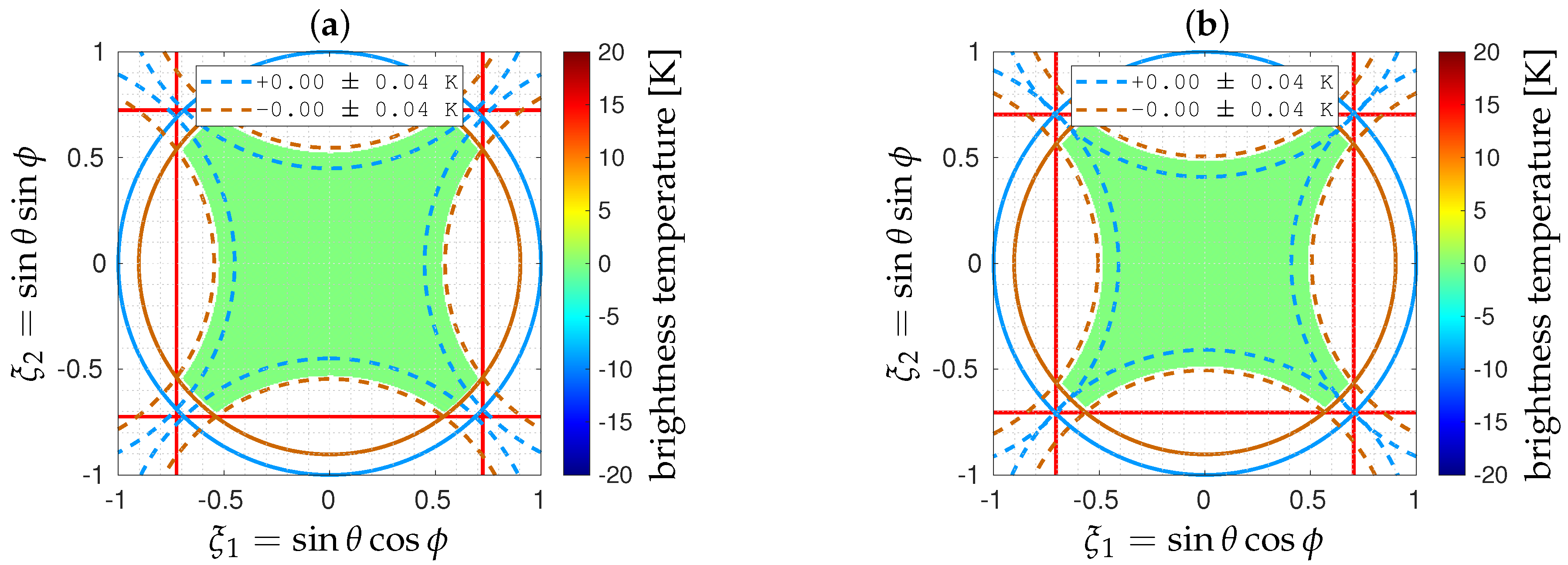
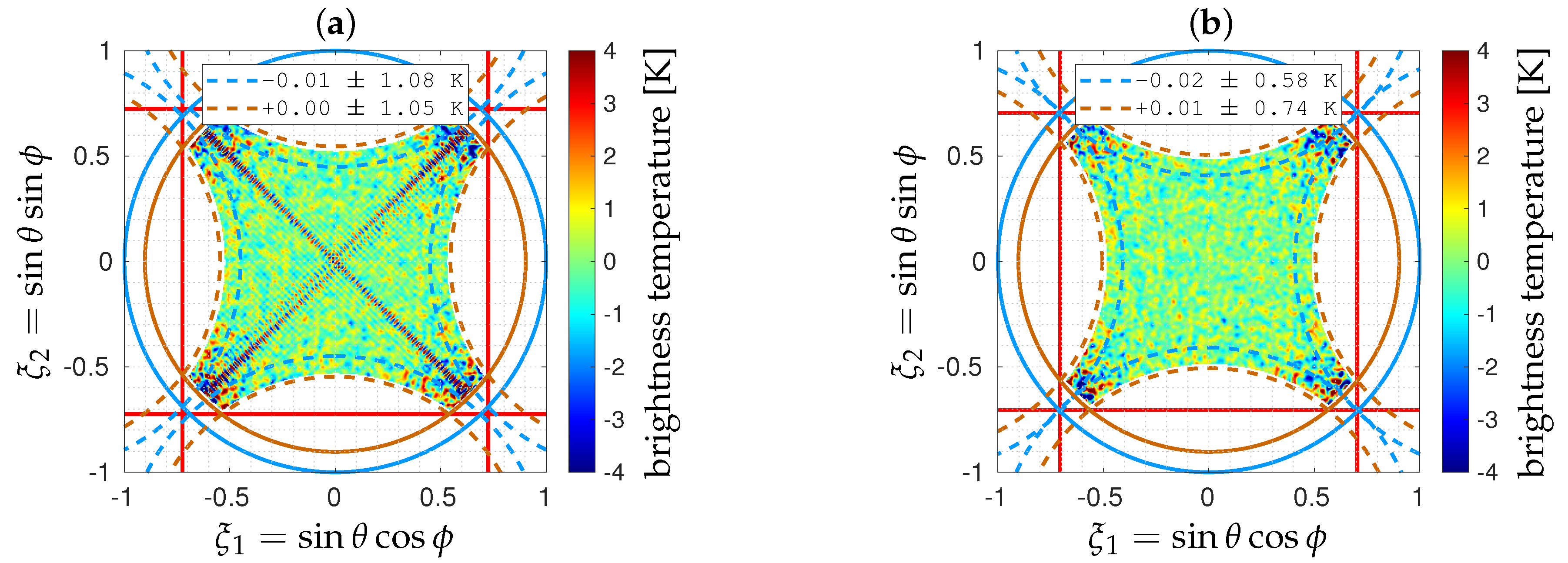
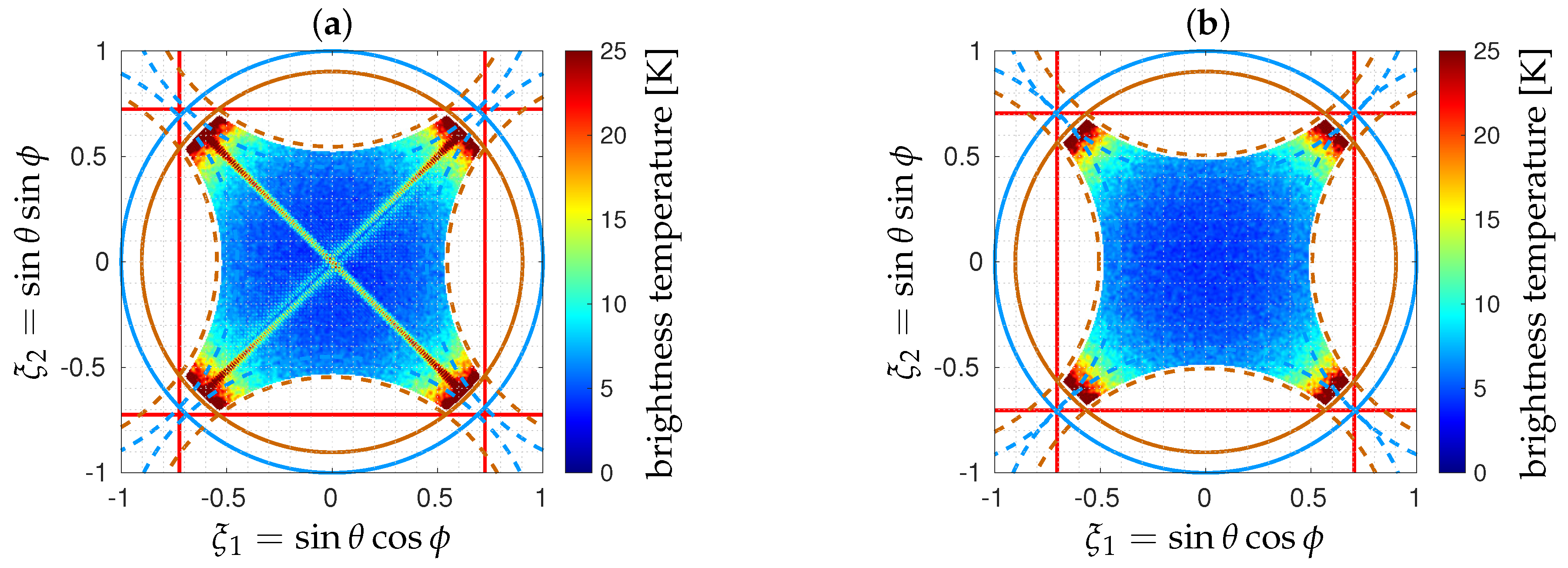
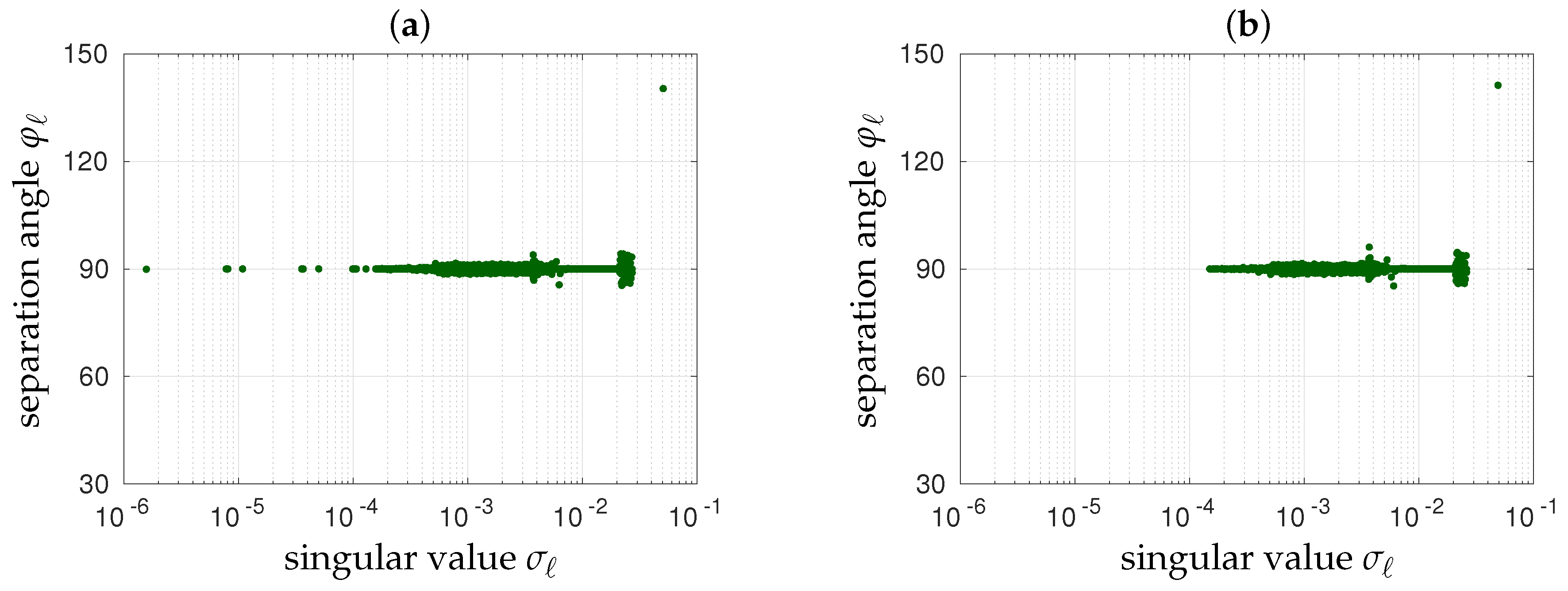
5. Numerical Simulations
5.1. Antenna Array
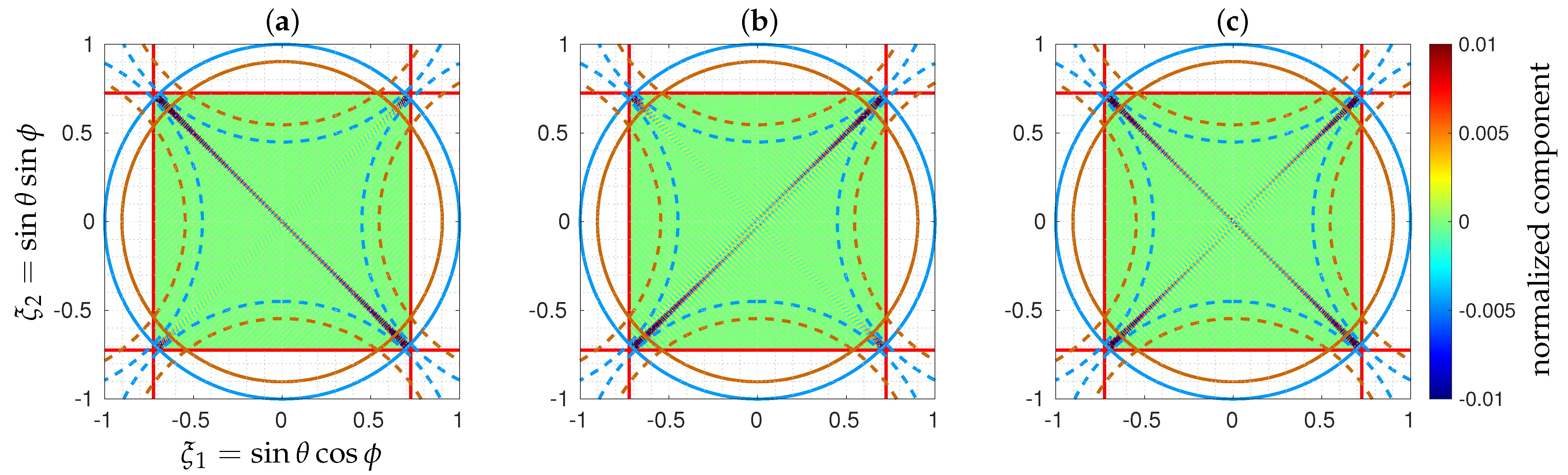
5.2. Modeling Matrix
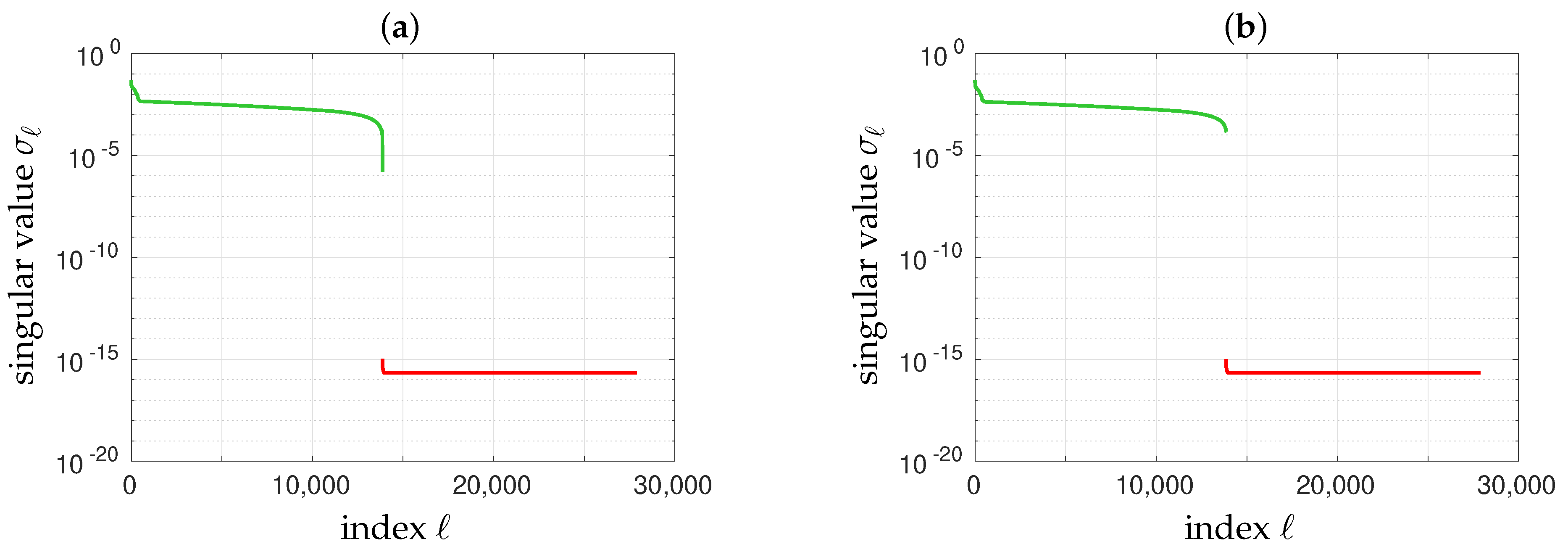
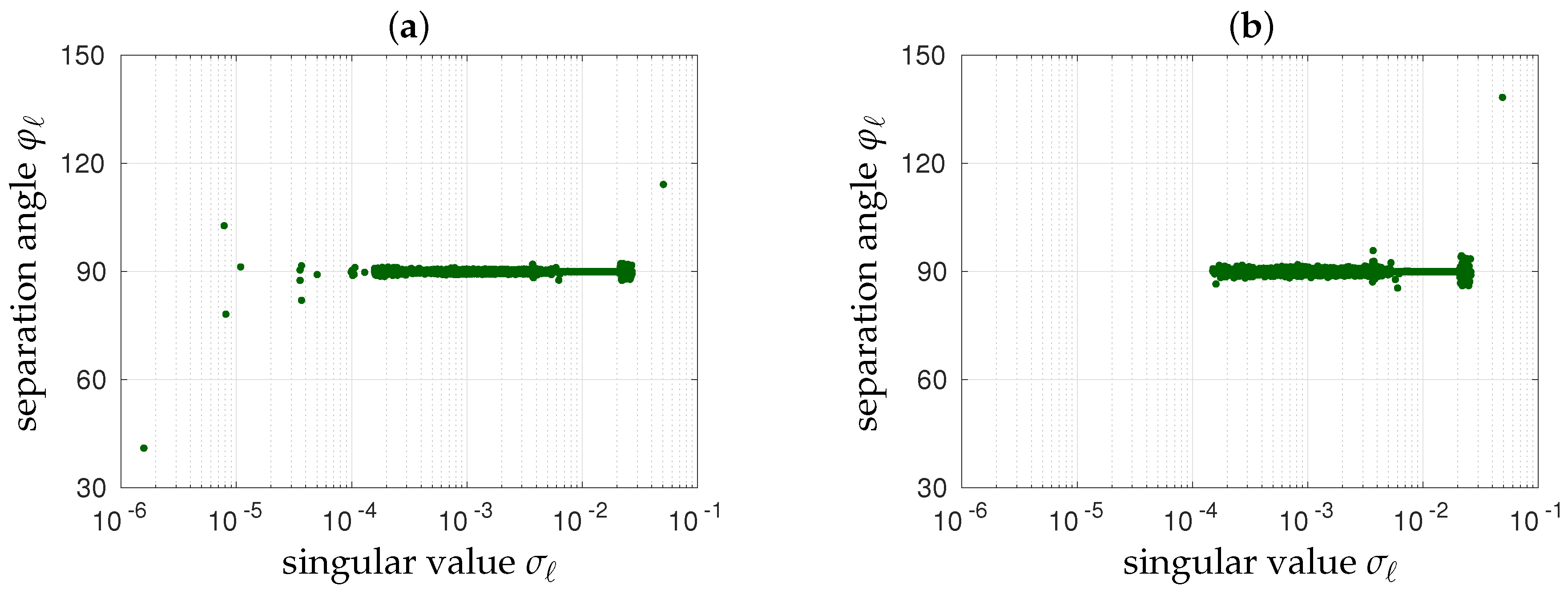
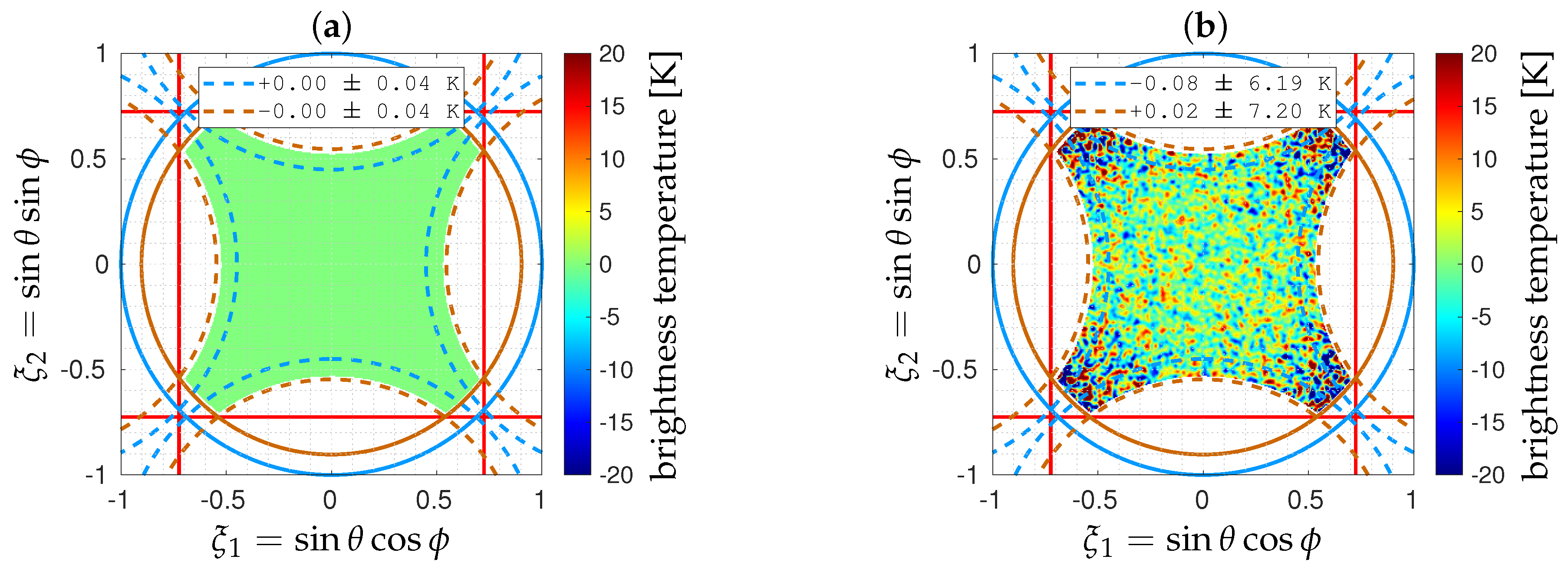
5.3. Noiseless Inversions
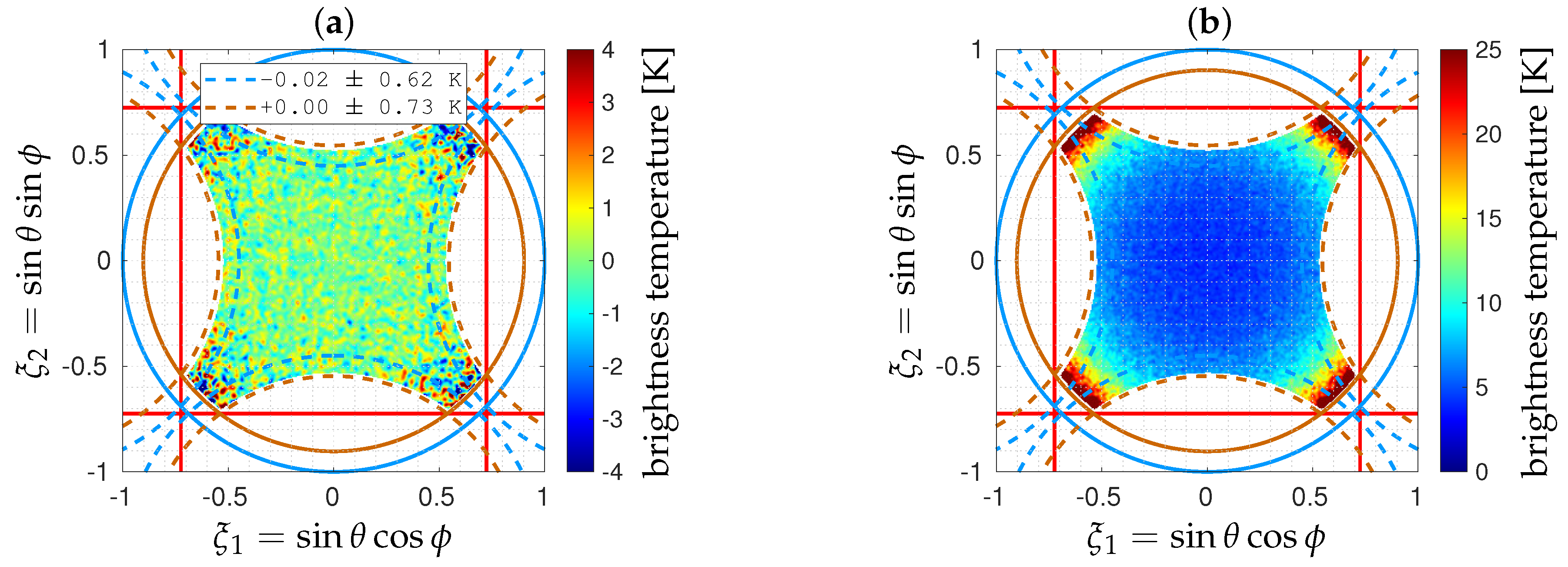
5.4. Noisy Inversions
6. Discussion and Remarks
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barré, H.; Duesmann, B.; Kerr, Y.H. SMOS: The Mission and the System. IEEE Trans. Geosci. Remote Sens. 2008, 46, 587–593. [Google Scholar] [CrossRef]
- McMullan, K.D.; Brown, M.A.; Martín-Neira, M.; Rits, W.; Ekholm, S.; Lemanczyk, J. SMOS: The Payload. IEEE Trans. Geosci. Remote Sens. 2008, 46, 594–605. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Wigneron, J.-P.; Ferrazzoli, P.; Mahmoodi, A.; Al Bitar, A.; Cabot, F.; Gruhier, C.; Enache Juglea, S.; et al. The SMOS Soil Moisture Retrieval Algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1384–1403. [Google Scholar] [CrossRef]
- Zine, S.; Boutin, J.; Font, J.; Reul, N.; Waldteufel, P.; Gabarró, C.; Tenerelli, J.; Petitcolin, F.; Vergely, J.-L.; Talone, M.; et al. Overview of the SMOS Sea Surface Salinity Prototype Processor. IEEE Trans. Geosci. Remote Sens. 2008, 46, 621–645. [Google Scholar] [CrossRef]
- de Rosnay, P.; Rodriguez-Fernandez, N.; Munoz-Sabater, J.; Albergel, C.; Fairbairn, D.; Lawrence, H.; English, S.; Drusch, M.; Kerr, Y.H. SMOS Data Assimilation for Numerical Weather Prediction. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS 2018), Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Thompson, A.R.; Moran, J.W.; Swenson, G.W. Interferometry and Synthesis in Radio Astronomy, 3rd ed.; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Thompson, A.R.; Clark, B.G.; Wade, C.M.; Napier, P.J. The Very Large Array. Astrophys. J. Suppl. Ser. 1980, 44, 151–167. [Google Scholar] [CrossRef]
- Padin, S.; Shepherd, M.C.; Cartwright, J.K.; Keeney, R.G.; Mason, B.S.; Pearson, T.J.; Readhead, A.C.S.; Schaal, W.A.; Sievers, J.; Udomprasert, P.S.; et al. The Cosmic Background Imager. Publ. Astron. Soc. Pac. 2002, 114, 83–97. [Google Scholar] [CrossRef] [Green Version]
- Anterrieu, É.; Rodriguez-Fernandez, N.J.; Rougé, B.; Cabot, F.; Richaume, P.; Khazâal, A.; Kerr, Y.H.; Morel, J.-M.; Colom, M.; Costeraste, J.; et al. Preliminary System Studies on a High-Resolution SMOS Follow-On: SMOS-HR. In Proceedings of the International Geoscience And Remote Sensing Symposium (IGARSS 2019), Yokohama, Japan, 28 July–2 August 2019. [Google Scholar]
- Jansen, S.; Pieters, M. The 7 Principles of Complete Co-Creation, 1st ed.; BIS Publishers: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Rodriguez-Fernandez, N.J.; Anterrieu, É.; Cabot, F.; Boutin, J.; Picard, G.; Pellarin, T.; Merlin, O.; Vialard, J.; Vivier, F.; Costeraste, J.; et al. A New L-Band Passive Radiometer for Earth Observation: SMOS-High Resolution (SMOS-HR). In Proceedings of the International Geoscience And Remote Sensing Symposium (IGARSS 2020), Virtual Symposium, 26 September–2 October 2020; 2020. [Google Scholar]
- Anterrieu, É.; Khazâal, A. Brightness Temperature Maps Reconstruction from Dual-Polarimetric Visibilities in Synthetic Aperture Imaging Radiometry. IEEE Trans. Geosci. Remote Sens. 2008, 46, 606–612. [Google Scholar] [CrossRef]
- Corbella, I.; Duffo, N.; Vall-llossera, M.; Camps, A.; Torres, A. The Visibility Function in Interferometric Aperture Synthesis Radiometry. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1677–1682. [Google Scholar] [CrossRef]
- Martín-Neira, M.; Ribó, S.; Martín-Polegre, A.J. Polarimetric Mode of MIRAS. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1755–1768. [Google Scholar] [CrossRef]
- Roederer, A.; Antennas Committee. IEEE Std 145-2013: IEEE Standard for Definitions of Terms for Antennas; IEEE Publishing: New York, NY, USA, 2014; pp. 1–50. [Google Scholar]
- Balanis, C.A. Antenna Theory: Analysis and Design, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Kainulainen, J.; Rautiainen, K.; Hallikainen, M. Experimental Verification of Fringe-washing Calibration Techniques in Large Aperture Synthesis Radiometers. In Proceedings of the 9th Specialist Meeting on Microwave Radiometry and Remote Sensing Applications (μRad-2006), Juan, PR, USA, 28 February–3 March 2006. [Google Scholar]
- Martín-Neira, M.; Suess, M.; Kainulainen, J.; Martin-Porqueras, F. The Flat Target Transformation. IEEE Trans. Geosci. Remote Sens. 2008, 46, 613–620. [Google Scholar] [CrossRef]
- Corbella, I.; Torres, F.; Camps, A.; Duffo, N.; Vall-llossera, M. Brightness-Temperature Retrieval Methods in Synthetic Aperture Radiometers. IEEE Trans. Geosci. Remote Sens. 2009, 47, 285–294. [Google Scholar] [CrossRef]
- Hadamard, J. Sur les problèmes aux dérivés partielles et leur signification physique. Princet. Univ. Bull. 1902, 13, 49–52. [Google Scholar]
- Picard, B.; Anterrieu, É. Comparison of Regularized Inversion Methods in Synthetic Aperture Imaging Radiometry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 218–224. [Google Scholar] [CrossRef]
- Goodberlet, M.A. Improved Image Reconstruction Techniques for Synthetic Aperture Radiometers. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1362–1366. [Google Scholar] [CrossRef]
- Moore, E.H. On the Reciprocal of the General Algebraic Matrix. Bull. Am. Math. Soc. 1920, 26, 394–395. [Google Scholar]
- Penrose, R. A Generalized Inverse for Matrices. Math. Proc. Camb. Philos. Soc. 1955, 51, 406–413. [Google Scholar] [CrossRef] [Green Version]
- Hewitt, E.; Hewitt, R.E. The Gibbs-Wilbraham Phenomenon: An Episode in Fourier Analysis. Arch. Hist. Exact Sci. 1979, 21, 129–160. [Google Scholar] [CrossRef]
- Anterrieu, É.; Waldteufel, P.; Lannes, A. Apodization Functions for 2D Hexagonally Sampled Synthetic Aperture Imaging Radiometers. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2531–2542. [Google Scholar] [CrossRef]
- Brouw, W.N. Aperture Synthesis. Methods Comput. Phys. 1975, 14, 131–175. [Google Scholar]
- Omont, A.; Pety, J.; Guelin, M. NOEMA-Une fenêtre sur les mondes en formation. L’Astronomie 2017, 131, 12–21. [Google Scholar]
- Shannon, C.E. Communication in the Presence of Noise. Proc. IRE 1949, 37, 10–21. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Font, J.; Waldteufel, P.; Camps, A.; Bara, J.; Corbella, I.; Torres, F.; Duffo, N.; Vall-llossera, M.; Caudal, G. New Radiometers: SMOS-a Dual Pol L-band 2D Aperture Synthesis Radiometer. In Proceedings of the 2000 IEEE Aerospace Conference, Big Sky, MT, USA, 25 March 2000. [Google Scholar]
- Arnot, N.R.; Atherton, P.D.; Greeaway, A.H.; Noordam, J.E. Phase Closure in Optical Astronomy. Trait Signal 1985, 2, 129–136. [Google Scholar]
- Colliander, A.; Tauriainen, S.; Auer, T.I.; Kainulainen, J.; Uusitalo, J.; Toikka, M.; Hallikainen, M.T. MIRAS Reference Radiometer: A Fully Polarimetric Noise Injection Radiometer. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1135–1143. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Khazâal, A.; Cabot, F.; Rougé, B.; Lesthievent, G.; Monjid, Y.; Suere, C.; Rodriguez-Fernandez, N.; Anterrieu, É.; Richaume, P. Système d’Imagerie Radiométrique; Publication Number 3 071 068, Registration Number 17 58533; Institut National de la Propriété Industrielle: Paris, France, 2017. [Google Scholar]
- Golub, G.; Kahan, W. Calculating the Singular Values and Pseudo-Inverse of a Matrix. J. Soc. Ind. Appl. Math. Ser. B 1965, 2, 205–224. [Google Scholar] [CrossRef]
- Roy, O.; Vetterli, M. The Effective Rank: A Measure of Effective Dimensionality. In Proceedings of the 15th European Signal Processing Conference, Poznan, Poland, 3–7 September 2007; pp. 606–610. [Google Scholar]
- Hansen, P.C. Rank-Deficient and Discrete Ill-Posed Problems, 1st ed.; Society for Industrial & Applied Mathematics: Philadelphia, PA, USA, 1998. [Google Scholar]
- Matlab Function Reference. Available online: https://fr.mathworks.com/help/matlab/ref/eps.html (accessed on 1 January 2023).
- Hansen, P.C. The Truncated SVD as a Method for Regularization. BIT Numer. Math. 1987, 27, 534–553. [Google Scholar] [CrossRef]
- Cline, A.K.; Moler, C.B.; Stewart, G.W.; Wilkinson, J.H. An Estimate for the Condition Number of a Matrix. SIAM J. Numer. Anal. 1979, 16, 368–375. [Google Scholar] [CrossRef]
- Klein, L.; Swift, C. An Improved Model for the Dielectric Constant of Sea Water at Microwave Frequencies. IEEE J. Ocean. Eng. 1977, 2, 104–111. [Google Scholar] [CrossRef]
- Camps, A.; Corbella, I.; Barà, J.; Torres, F. Radiometric Sensitivity Computation in Aperture Synthesis Interferometric Radiometry. IEEE Trans. Geosci. Remote Sens. 1998, 36, 680–685. [Google Scholar] [CrossRef] [Green Version]
- Spiegel, M.; Lipschutz, S.; Spellman, D. Vector Analysis, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2009. [Google Scholar]
- Zurita, A.M.; Corbella, I.; Martín-Neira, M.; Plaza, M.A.; Torres, F.; Benito, F.J. Towards a SMOS Operational Mission: SMOSOps-Hexagonal. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1769–1780. [Google Scholar] [CrossRef]
- Anterrieu, É.; Palacin, B.; Costes, L. A New Metric for Estimating the Disparity of Antenna Patterns in Synthetic Aperture Imaging Radiometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5800–5906. [Google Scholar] [CrossRef]
- Pivnenko, S.; Nielsen, J.M.; Cappellin, C.; Lemanczyk, G.; Breinbjerg, O. High-Accuracy Calibration of the SMOS Radiometer Antenna Patterns at the DTU-ESA Spherical Near-Field Antenna Test Facility. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS 2007), Barcelona, Spain, 1–7 July 2007. [Google Scholar]
- Camps, A.; Skou, S.; Torres, F.; Corbella, I.; Duffo, N.; Vall-llossera, M. Considerations About Antenna Pattern Measurements of 2-D Aperture Synthesis Radiometers. IEEE Geosci. Remote Sens. Lett. 2006, 3, 259–261. [Google Scholar] [CrossRef]
- Fischman, M.A.; England, A.W. A Technique for Reducing Fringe Washing Effects in L-band Aperture Synthesis Radiometry. In Proceedings of the International Geoscience And Remote Sensing Symposium (IGARSS 2000), Honolulu, HI, USA, 24–28 July 2000. [Google Scholar]
- Subbaram, H.; Abend, K. Interference Suppression via Orthogonal Projections: A Performance Analysis. IEEE Trans. Antennas Propag. 1993, 41, 1187–1194. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anterrieu, E.; Yu, L. Impact of the Antenna Spacing on the Brightness Temperature Maps Retrieved with a Synthetic Aperture Imaging Radiometer. Remote Sens. 2023, 15, 805. https://doi.org/10.3390/rs15030805
Anterrieu E, Yu L. Impact of the Antenna Spacing on the Brightness Temperature Maps Retrieved with a Synthetic Aperture Imaging Radiometer. Remote Sensing. 2023; 15(3):805. https://doi.org/10.3390/rs15030805
Chicago/Turabian StyleAnterrieu, Eric, and Louise Yu. 2023. "Impact of the Antenna Spacing on the Brightness Temperature Maps Retrieved with a Synthetic Aperture Imaging Radiometer" Remote Sensing 15, no. 3: 805. https://doi.org/10.3390/rs15030805




