Risk Evaluation of the Sanalona Earthfill Dam Located in Mexico Using Satellite Geodesy Monitoring and Numerical Modeling
Abstract
:1. Introduction
2. Case Study: The Sanalona Dam
3. Methodology
3.1. MT-InSAR Displacements
3.2. Finite Element Model of the Sanalona Dam
3.3. GPS Displacements
3.3.1. Data Acquisition
3.3.2. GPS Processing Strategies
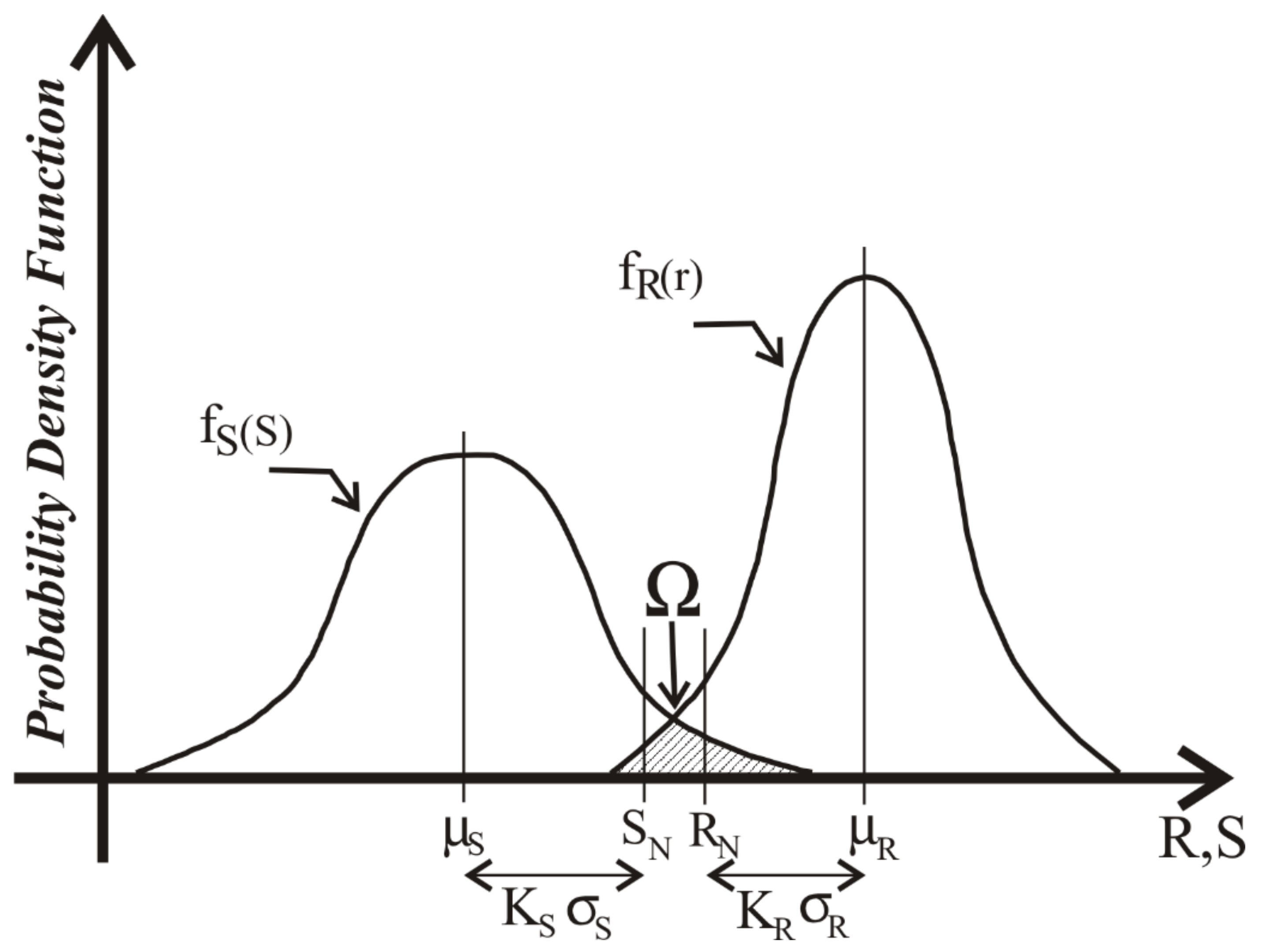
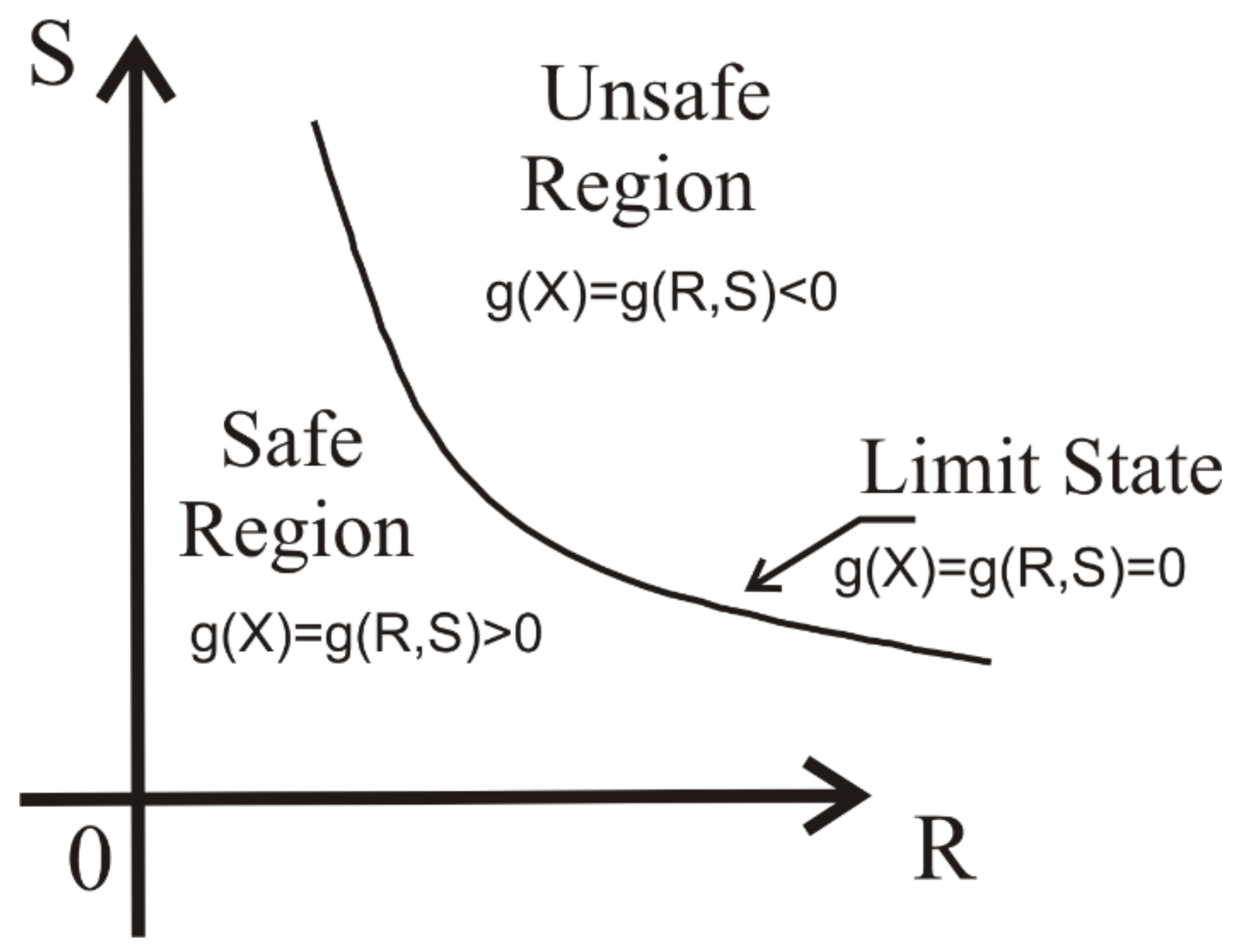
3.4. Probability of Failure Calculation Considering Dam Sliding
Analysis of Variables
4. Results
4.1. Displacements
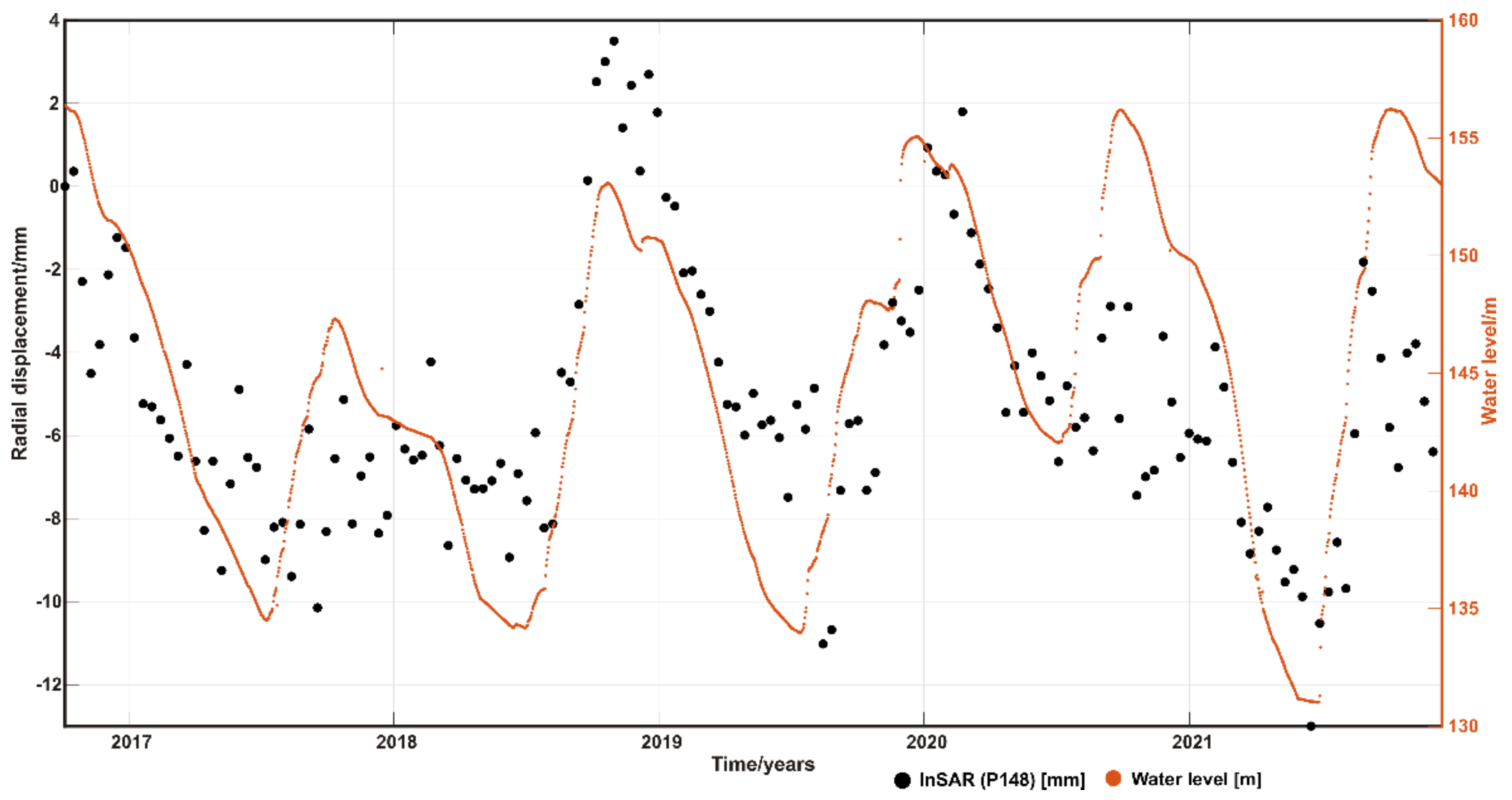
4.1.1. MT-InSAR Displacements
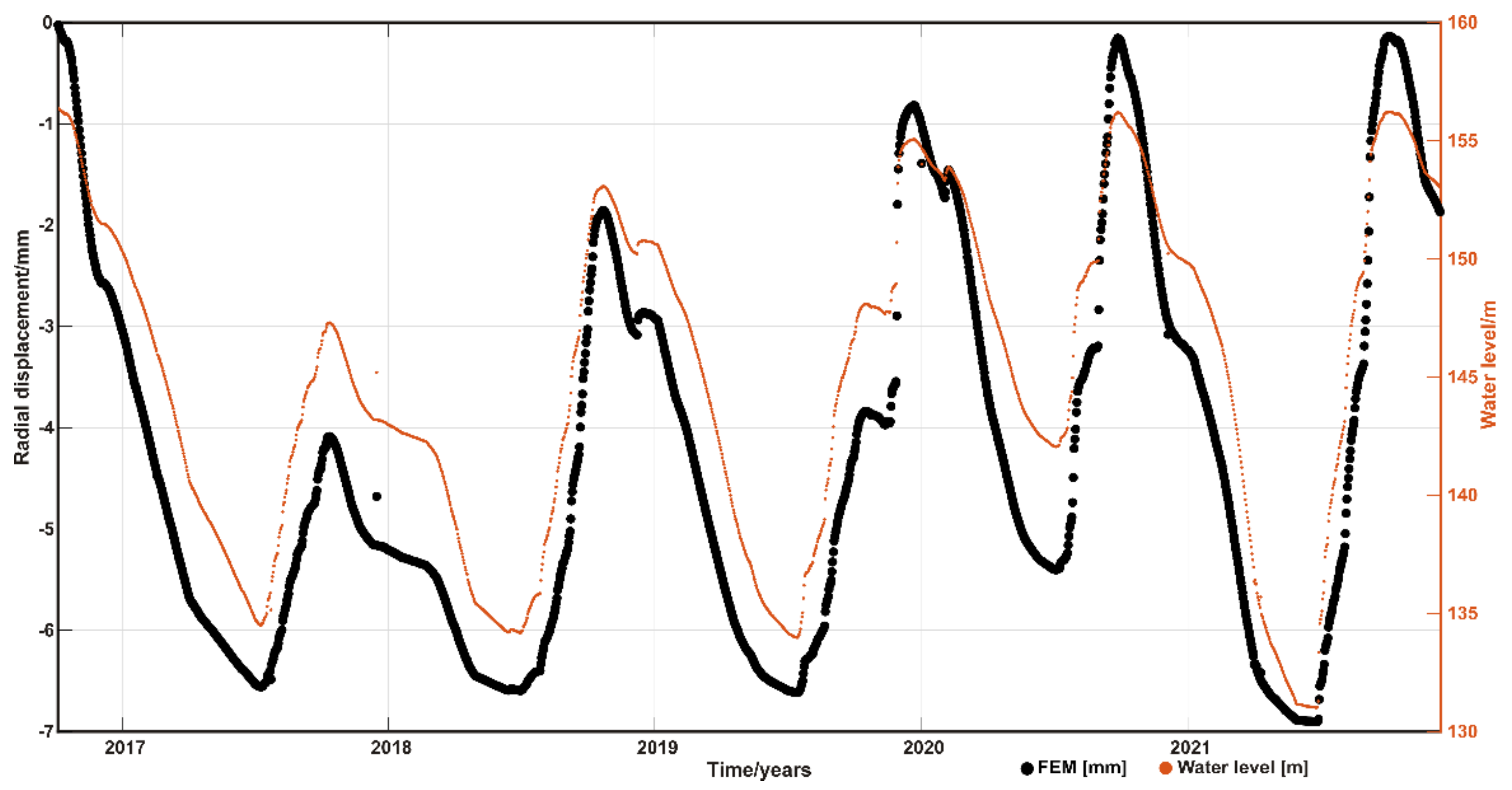
4.1.2. FEM Displacements
4.1.3. GPS Displacements
4.2. Accuracy Analysis of Radial Displacements
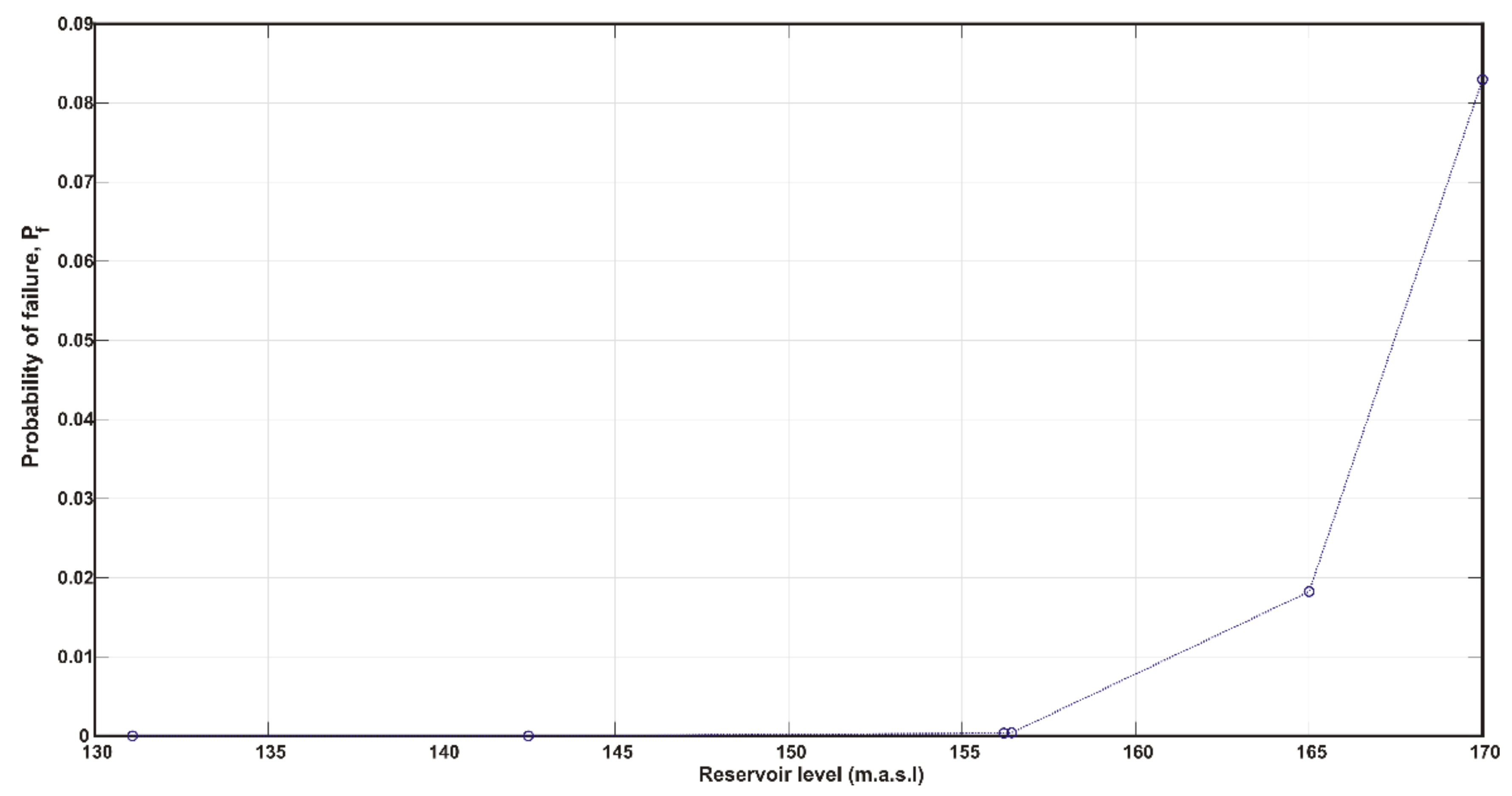
4.3. Probability of Failure by Sliding
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jänichen, J.; Schmullius, C.; Baade, J.; Last, K.; Bettzieche, V.; Dubois, C. Monitoring of Radial Deformations of a Gravity Dam Using Sentinel-1 Persistent Scatterer Interferometry. Remote Sens. 2022, 14, 1112. [Google Scholar] [CrossRef]
- Vazquez-Ontiveros, J.R.; Martinez-Felix, C.A.; Vazquez-Becerra, G.E.; Gaxiola-Camacho, J.R.; Melgarejo-Morales, A.; Padilla-Velazco, J. Monitoring of local deformations and reservoir water level for a gravity type dam based on GPS observations. Adv. Space Res. 2022, 69, 319–330. [Google Scholar] [CrossRef]
- Alcay, S.; Yigit, C.O.; Inal, C.; Ceylan, A. Analysis of displacements response of the Ermenek dam monitoring by an integrated geodetic and pendulum system. Int. J. Civ. Eng. 2017, 16, 1279–1291. [Google Scholar] [CrossRef]
- Altarejos-Garcia, L. Contribution to the Estimation of the Probability of Failure of Concrete Gravity Dams in the Risk Analysis Context. Ph.D. Thesis, Universidad Politécnica de Valencia, Valencia, Spain, 2009. [Google Scholar]
- Altarejos-Garcia, L.; Escuder-Bueno, I.; Serrano-Lombillo, A.; Membrillera-Ortuño, M.G. Methodology for estimating the probability of failure by sliding in concrete gravity dams in the context of risk analysis. Struct. Saf. 2012, 36, 1–13. [Google Scholar] [CrossRef]
- Maltese, A.; Pipitone, C.; Dardanelli, G.; Capodici, F.; Muller, J.P. Toward a comprehensive dam monitoring: On-site and remote-retrieved forcing factors and resulting displacements (gnss and ps–insar). Remote Sens. 2021, 13, 1543. [Google Scholar] [CrossRef]
- Scaioni, M.; Marsella, M.; Crosetto, M.; Tornatore, V.; Wang, J. Geodetic and remote-sensing sensors for dam deformation monitoring. Sensors 2018, 18, 3682. [Google Scholar] [CrossRef] [Green Version]
- Pytharouli, S.I.; Stiros, S.C. Ladon dam (Greece) deformation and reservoir level fluctuations: Evidence for a causative relationship from the spectral analysis of a geodetic monitoring record. Eng. Struct. 2005, 27, 361–370. [Google Scholar] [CrossRef]
- Guler, G.; Kilic, H.; Hosbas, G.; Ozaydin, K. Evaluation of the Movements of the Dam Embankments by Means of Geodetic and Geotechnical Methods. J. Surv. Eng. 2006, 132, 31–39. [Google Scholar] [CrossRef]
- Casaca, J.; Braz, N.; Conde, V. Combined adjustment of angle and distance measurements in a dam monitoring network. Surv. Rev. 2015, 47, 181–184. [Google Scholar] [CrossRef]
- Barzagui, R.; Cazzaniga, N.E.; De Gaetani, C.I.; Pinto, L.; Tornatore, V. Estimation and comparing dam deformation using classical and gnss techniques. Sensors 2018, 18, 756. [Google Scholar] [CrossRef] [Green Version]
- De Lacy, M.C.; Ramos, M.I.; Gil, A.J.; Franco, O.D.; Herrera, A.M.; Aviles, M.; Dominguez, A.; Chica, J.C. Monitoring of vertical displacements by means high-precision geodetic levelling. Test case: The Arenoso dam (South of Spain). J. Appl. Geod. 2017, 11, 31–41. [Google Scholar] [CrossRef]
- Xi, R.; Zhou, X.; Jiang, W.; Chen, Q. Simultaneous estimation of dam displacements and reservoir level variation from GPS measurements. J. Int. Meas. Confed. 2018, 122, 247–256. [Google Scholar] [CrossRef]
- Yigit, C.O.; Alcay, S.; Ceylan, A. Displacement response of a concrete arch dam to seasonal temperature fluctuations and reservoir level rise during the first filling period: Evidence from geodetic data. Geomat. Nat. Hazards Risk 2016, 7, 1489–1505. [Google Scholar] [CrossRef] [Green Version]
- Acosta, L.E.; De lacy, M.C.; Ramos, M.I.; Cano, J.P.; Herrera, A.M.; Aviles, M.; Gil, A.J. Displacements study of an earth fill dam based on high precision geodetic monitoring and numerical modeling. Sensors 2018, 18, 1369. [Google Scholar] [CrossRef] [Green Version]
- Xiao, R.; Shi, H.; He, X.; Li, Z.; Jia, D.; Yang, Z. Deformation monitoring of reservoir dams using GNSS: An aplication to south-to-north water diversion proyect, China. IEEE Access 2019, 7, 54981–54992. [Google Scholar] [CrossRef]
- Reguzzoni, M.; Rossi, L.; Gaetani, C.L.; Caldera, S.; Barzaghi, R. GNSS-based dam monitoring: The application of a statistical approach for time series analysis to a case study. Appl. Sci. 2022, 12, 9981. [Google Scholar] [CrossRef]
- Montillet, J.-P.; Szeliga, W.M.; Melbourne, T.I.; Flake, R.M.; Schrock, G. Critical infrastrcture monitoring with global navigation satellite systems. J. Surv. Eng. 2016, 142, 4016014. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Chen, B.; Gong, H.; Lei, K.; Shi, M.; Zhou, C. Three-dimensional surface displacement of the eastern beijing plain, china, using ascending and descending sentinel-1a/b images and levelling data. Remote Sens. 2021, 13, 2809. [Google Scholar] [CrossRef]
- Macias-Valadez, D.; Santerre, R.; Larochelle, S.; Landry, R. Improving vertical GPS precision with a GPS-over fiber architecture and real-time relative delay calibration. GPS Solut. 2012, 16, 449–462. [Google Scholar] [CrossRef]
- Guilhot, D.; Martinez del Hoyo, T.; Bartoli, A.; Ramakrishnan, P.; Leemans, G.; Houtepen, M.; Salzer, J.; Metzger, J.S.; Maknavicius, G. Internet-of-things-based geotechnical monitoring boosted by satellite insar data. Remote Sens. 2021, 13, 2757. [Google Scholar] [CrossRef]
- Qu, C.; Qiao, X.; Shan, X.; Zhao, D.; Zhao, L.; Gong, W.; Li, Y. InSAR 3-D coseismic displacement field of the 2015 Mw 7.8 Nepal earthquake: Insights into complex fault kinematics during the event. Remote Sens. 2020, 12, 3982. [Google Scholar] [CrossRef]
- Pawluszek-Filipiak, K.; Borkowski, A. Monitoring mining-induced subsidence by integrating differential radar interferometry and persistent scatterer techniques. Eur. J. Remote Sens. 2021, 54, 18–30. [Google Scholar] [CrossRef]
- Ruiz-Armenteros, A.M.; Marchamalo-Sacrsitán, M.; Bakon, M.; Lamas-Fernández, F.; Delgado, J.M.; Sánchez-Ballesteros, J.P.; González-Rodrigo, B.; Lazecky, M.; Perissin, D.; Sousa, J.J. Monitoring of an embankment dam in southern Spain based on Sentinel-1 time-series InSAR. Procedia Comput. Sci. 2021, 181, 353–359. [Google Scholar] [CrossRef]
- Xiao, R.; He, X. Deformation monitoring of reservoirs and dam using time-series InSAR. Geo. Inf. Sci. Wuhan Univer. 2019, 44, 1334–1341. [Google Scholar] [CrossRef]
- Tomas, R.; Cano, M.; Garcia-Barba, J.; Vicente, F.; Herrera, G.; Lopez-Sanchez, J.M.; Mallorqui, J.J. Monitoring an earthfill dam using differential SAR interferometry: La Pedrera dam, Alicante, Spain. Eng. Geol. 2013, 157, 21–32. [Google Scholar] [CrossRef]
- Milillo, P.; Perissin, D.; Salzer, J.T.; Lundgren, P.; Lcava, G.; Milillo, G.; Serio, C. Monitoring dam structural health from space: Insights from novel InSAR techniques and multi-parametric modeling applied to the pertusillo dam basilicata, Italy. Int. J. Earth Obs. Geoinf. 2016, 52, 221–229. [Google Scholar] [CrossRef]
- Maierhifer, C.; Reinhard, H.W.; Dobmann, G. Non-Destructive Evaluation of Reinforced Concrete Structural; Woodhead Publishing CRC Press: Cambridge, UK, 2010. [Google Scholar]
- Hariri-Ardebili, M.A. Risk, Reliability, Resilience (R3) and deyond in dam engineering: A state-of-the-art review. Int. J. Dis. Risk Reduct. 2018, 31, 806–831. [Google Scholar] [CrossRef]
- Perissin, D. Sarproz Software Manual. 2009. Available online: https://www.sarproz.com/software-manual/ (accessed on 1 November 2022).
- CSI. SAP2000 Integrated Software for Structural Analysis and Design; Computers and Structures Inc: Berkeley, CA, USA, 2013. [Google Scholar]
- Estey, L.H.; Meertens, C.M. TEQC: The Multi-Purpose Toolkit for GPS/GLONASS Data. GPS Solut. 1999, 3, 42–49. [Google Scholar] [CrossRef]
- CSRS-PPP. Canadian Spatial Reference System Precise Point Positioning. 2022. Available online: https://webapp.csrs-scrs.nrcan-rncan.gc.ca/geod/tools-outils/ppp.php?locale=en (accessed on 8 October 2022).
- Banville, S. CSRS-PPP Version 3: Tutorial. 2020. Available online: https://webapp.csrs-scrs.nrcan-rncan.gc.ca/geod/tools-outils/sample_doc_filesV3/NRCanCSRS-PPP-v3_TutorialEN.pdf (accessed on 8 October 2022).
- Yigit, C.O. Experimental assessment of post-processed kinematic Precise Point Positioning method for structural health monitoring. Geomat. Nat. Hazards Risk. 2016, 7, 360–383. [Google Scholar] [CrossRef] [Green Version]
- Gaxiola-Camacho, J.R.; Azizsoltani, F.J.; Villegas-Mercado, F.J.; Haldar, A. A novel reliability technique for implementation of Performance-Based Seismic Design of structures. Eng. Struct. 2017, 142, 137–147. [Google Scholar] [CrossRef] [Green Version]
- Haldar, A.; Mahadevan, S. Probability, Realibility and Statistical Methods in Engineering Design; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Melchers, R.E.; Beck, A.T. Structural Reliability Analysis and Prediction, 3rd ed.; Wiley: New York, NY, USA, 2018. [Google Scholar]
- Selvakumaran, S.; Plank, S.; GeiB, C.; Rossi, C.; Middleton, C. Remote monitoring to predict bridge scour failure using Interferometric Synthetic Aperture Radar (InSAR) stacking techniques. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 463–470. [Google Scholar] [CrossRef]
- Milillo, P.; Giardina, G.; Perissin, D.; Milillo, G.; Coletta, A.; Terranova, C. Pre-collapse space geodetic observations of critical infrastructure: The morandi bridge, genoa, italy. Remote Sens. 2019, 11, 1403. [Google Scholar] [CrossRef] [Green Version]

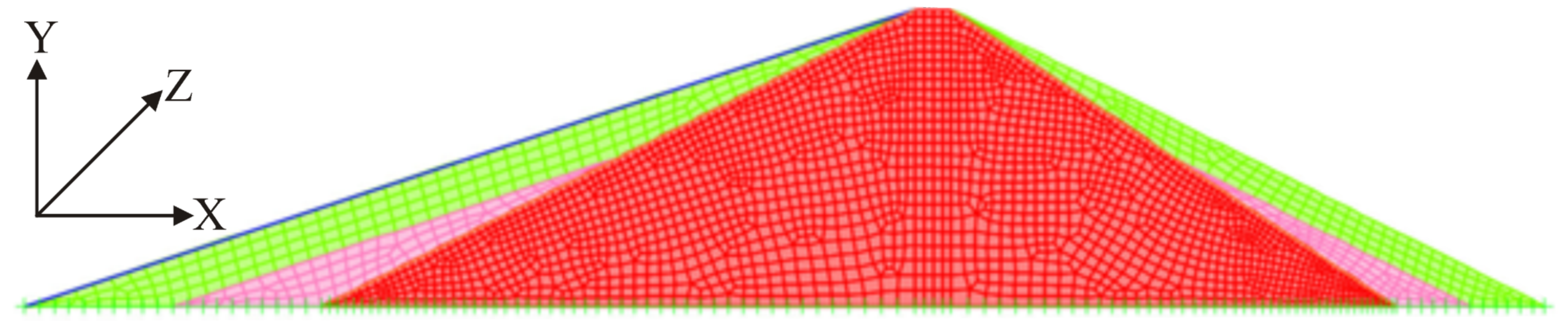





| Material Type | V | ||||
|---|---|---|---|---|---|
| Clay | 1.9-2.1 | 0.4 | 69 | 27 | 50 |
| Coronation(gravel) | 2.2 | 0.3 | 200 | 42 | - |
| Coronation (Sand) | 1.9 | 0.3 | 45 | 36 | - |
| Conglomerate | 2.3 | 0.25 | 1350 | 35 | 15 |
| Foundation(bedrock) | 2.9 | 0.2 | 8400 | - | - |
| GNSS System | GPS |
| Observations | Code & Phase |
| Frequency Observed | L1, L2 |
| Satellite Orbits | Precise (IGS) |
| Satellite Product Type | IGS Final |
| Sample rate | 30 s |
| Cut of Elevation | 10° |
| Ocean Tide Model | FES2014b |
| Tropospheric Model | VMF1 Model |
| Ionospheric Model | L1 & L2 |
| Reference Frame | IGb14 |
| Variable | Abbreviation | Probability Density Function | Mean | Standard Deviation | Min Value | Max value | Unit |
|---|---|---|---|---|---|---|---|
| Conglomerate density | Normal | 2300 | 50 | 2100 | 2500 | ||
| Cohesion in the dam-foundation contact | Lognormal | 0.418 | 0.298 | 0 | 3.5 | ||
| Friction angle in the dam-foundation contact | Normal | 50 | 8.79 | 30 | 76 | ° |
| Reservoir Level | Displacements in mm | ||
|---|---|---|---|
| GPS | FEM | InSAR (P148) | |
| 13 October 2016 (101.5%) | 0 (origin) | 0 (origin) | 0 (origin) |
| 18 October 2018 (81.1%) | 1.4 (7.3) * | −1.86 (4.7) | 3.5 (12.4) |
| 23 December 2019 (92.81%) | 4.167 (4.9) | −0.8 (5.7) | −0.93 (11.9) |
| 27 September 2020(99.93%) | 0.45 | −0.14 (5.5) | −2.89 (3.7) |
| 15 October 2021(100.13%) | −1.9 | −0.11 (6.7) | −1.82 (11.1) |
| Reservoir Level (m.a.s.l) | Number of Simulation (N) | Number of Failures | Probability of Failure |
|---|---|---|---|
| 131.09 (7.73%) | 100,000,000 | 0 | |
| 142.5 (81.1%) | 100,000,000 | 8 | |
| 156.2 (100%) | 100,000,000 | 35,624 | |
| 156.43 (101.5%) | 100,000,000 | 40,109 | |
| 165 (132.76%) | 100,000,000 | 1,824,720 | |
| 170 (151.2%) | 100,000,000 | 8,297,482 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vázquez-Ontiveros, J.R.; Ruiz-Armenteros, A.M.; de Lacy, M.C.; Gaxiola-Camacho, J.R.; Anaya-Díaz, M.; Vázquez-Becerra, G.E. Risk Evaluation of the Sanalona Earthfill Dam Located in Mexico Using Satellite Geodesy Monitoring and Numerical Modeling. Remote Sens. 2023, 15, 819. https://doi.org/10.3390/rs15030819
Vázquez-Ontiveros JR, Ruiz-Armenteros AM, de Lacy MC, Gaxiola-Camacho JR, Anaya-Díaz M, Vázquez-Becerra GE. Risk Evaluation of the Sanalona Earthfill Dam Located in Mexico Using Satellite Geodesy Monitoring and Numerical Modeling. Remote Sensing. 2023; 15(3):819. https://doi.org/10.3390/rs15030819
Chicago/Turabian StyleVázquez-Ontiveros, J. René, Antonio Miguel Ruiz-Armenteros, M. Clara de Lacy, J. Ramon Gaxiola-Camacho, Miguel Anaya-Díaz, and G. Esteban Vázquez-Becerra. 2023. "Risk Evaluation of the Sanalona Earthfill Dam Located in Mexico Using Satellite Geodesy Monitoring and Numerical Modeling" Remote Sensing 15, no. 3: 819. https://doi.org/10.3390/rs15030819
APA StyleVázquez-Ontiveros, J. R., Ruiz-Armenteros, A. M., de Lacy, M. C., Gaxiola-Camacho, J. R., Anaya-Díaz, M., & Vázquez-Becerra, G. E. (2023). Risk Evaluation of the Sanalona Earthfill Dam Located in Mexico Using Satellite Geodesy Monitoring and Numerical Modeling. Remote Sensing, 15(3), 819. https://doi.org/10.3390/rs15030819








