Urbanization Trends Analysis Using Hybrid Modeling of Fuzzy Analytical Hierarchical Process-Cellular Automata-Markov Chain and Investigating Its Impact on Land Surface Temperature over Gharbia City, Egypt
Abstract
:1. Introduction
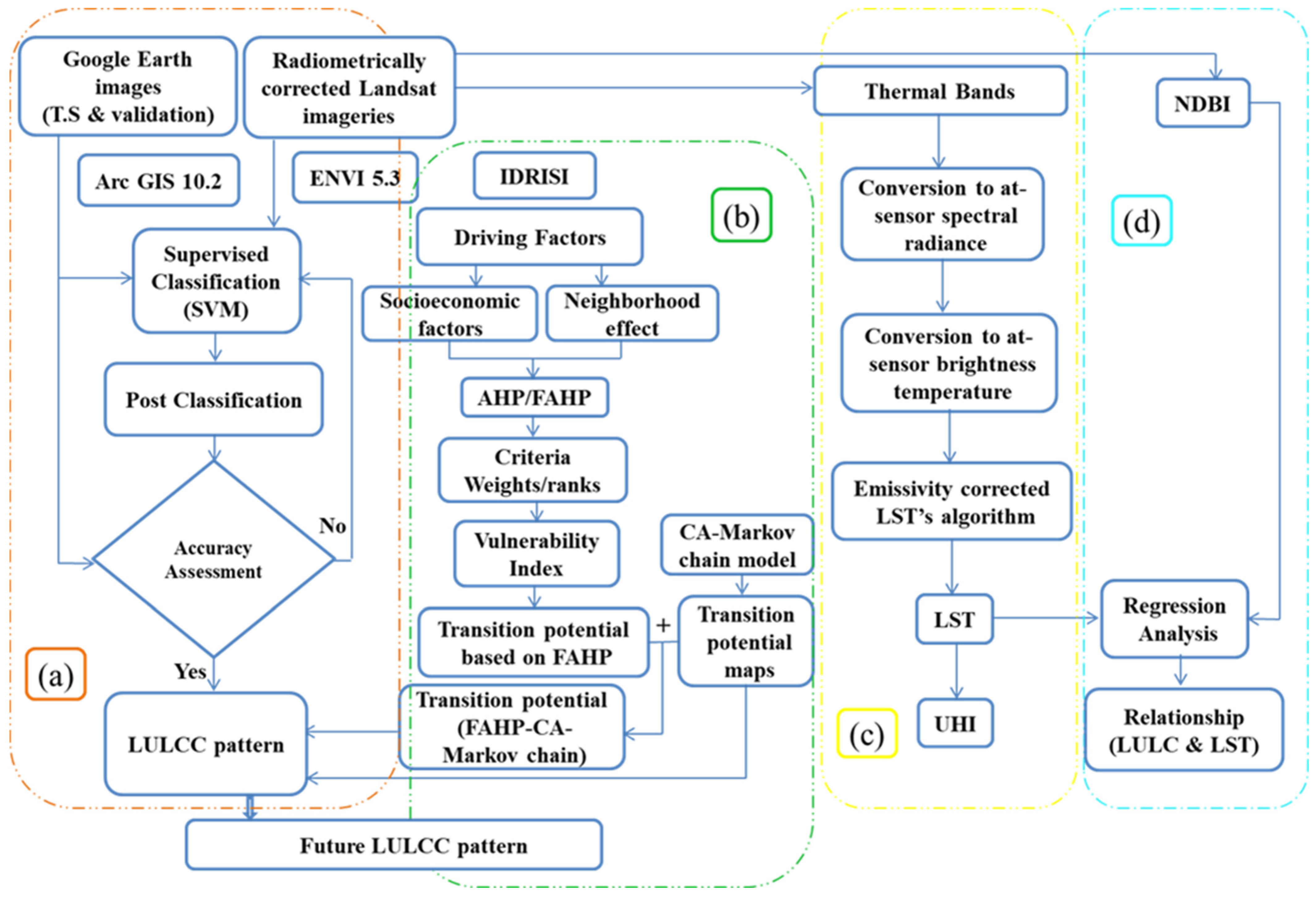
2. Materials and Methods
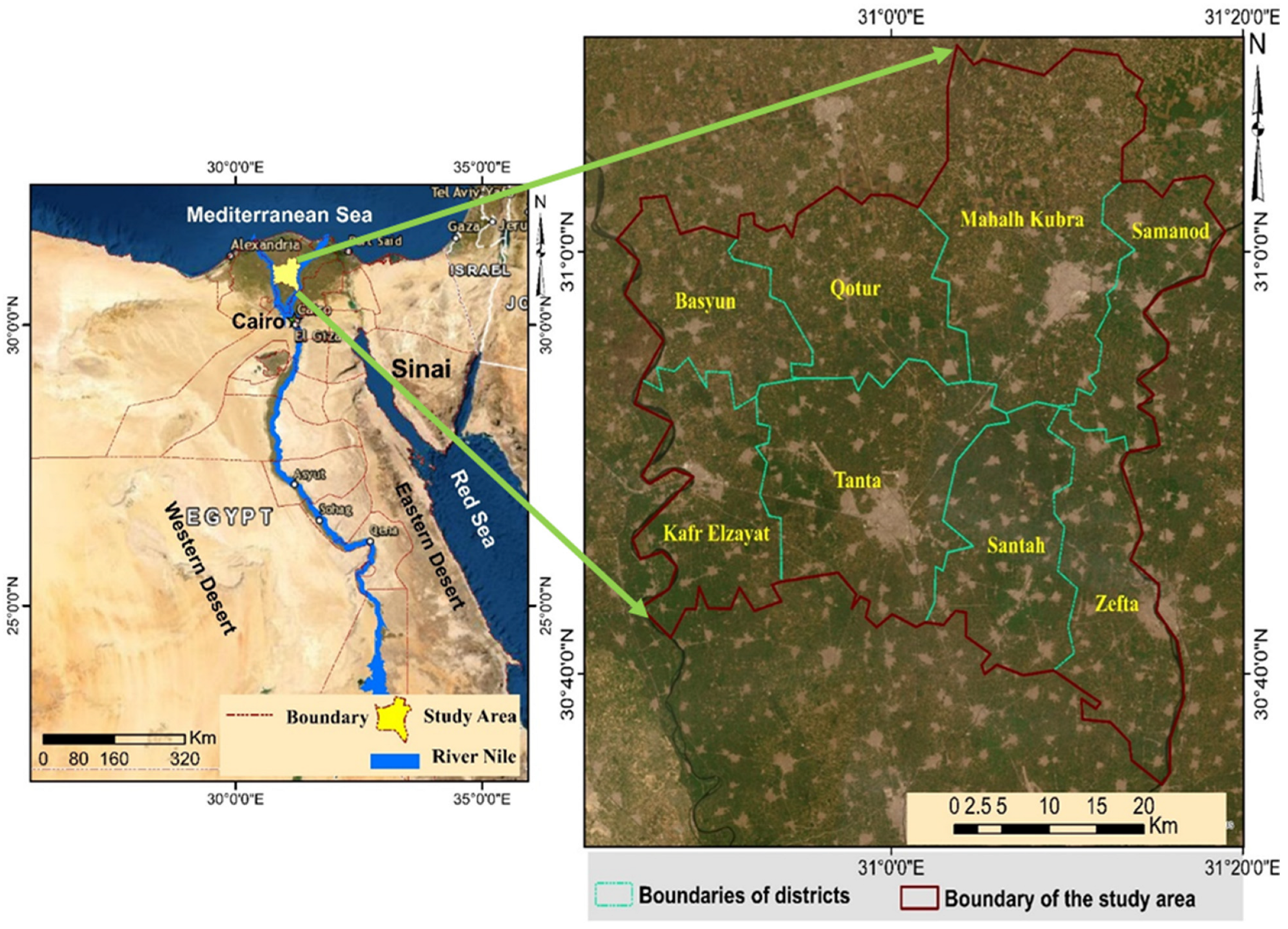
2.1. Study Area
2.2. Data Collection and Processing
2.3. LULC Classification
2.4. LULC Change Modeling
- (1)
- Model Calibration
- (2)
- LULC Simulation and Model Validation
- (3)
- Model Projection
2.4.1. CA-Markov Chain Model
2.4.2. FAHP-CA-Markov Chain Hybrid Model
- a.
- Driving factors
- b.
- Steps of applying the FAHP model [64] based on the aforementioned criteria:
2.5. Estimation of Land Surface Temperature
2.5.1. LST Estimation from Landsat Imageries
- L = spectral radiance at the sensor’s aperture (Watts m−2 sr−1 μm−1);
- Qcal = the quantized calibrated pixel value in DN;
- LMINλ = the spectral radiance scaled to QCALMIN in (Watts m−2 sr−1 μm−1);
- LMAXλ = the spectral radiance scaled to QCALMAX in (Watts m−2 sr−1 μm−1);
- Qcalmin = the minimum quantized calibrated pixel value (corresponding to LMIN) in DN;
- Qcalmax = the maximum quantized calibrated pixel value (corresponding to LMAX) in DN.
- TB—is the satellite brightness temperature in degrees Kelvin;
- K1_constant_band_6 of TM 5 = 607.76;
- K2_constant_band_6 of TM 5 = 1260.56;
- K1_constant_band_10 of TIRS 8 = 774.8853;
- K2_constant_band_10 of TIRS 8 = 1321.0789;
- Lλ—is TOA spectral radiance.
- St—is the emissivity-corrected land surface temperature in degrees Kelvin;
- TB—is the satellite brightness temperature in degrees Kelvin recaptured earlier;
- λ = 11.457 µm;
- = 1.438 × 10−2 m k= 1.438 × 104 µm k;
- h—is Planck’s constant = 6.626 × 10−34 J s−1;
- c is velocity of light = 2.998 × 108 m s−1;
- δ is Boltzmann’s constant = 1.38 × 10−23J k−1.
2.5.2. Computation of LSE ε
2.6. Regression Analysis
3. Results
3.1. Accuracy of LULC Maps
3.2. Spatiotemporal Analysis of LULCC
3.3. LULCC Modeling, Simulation, and Projection
3.3.1. Analysis of the CA-Markov Chain Model
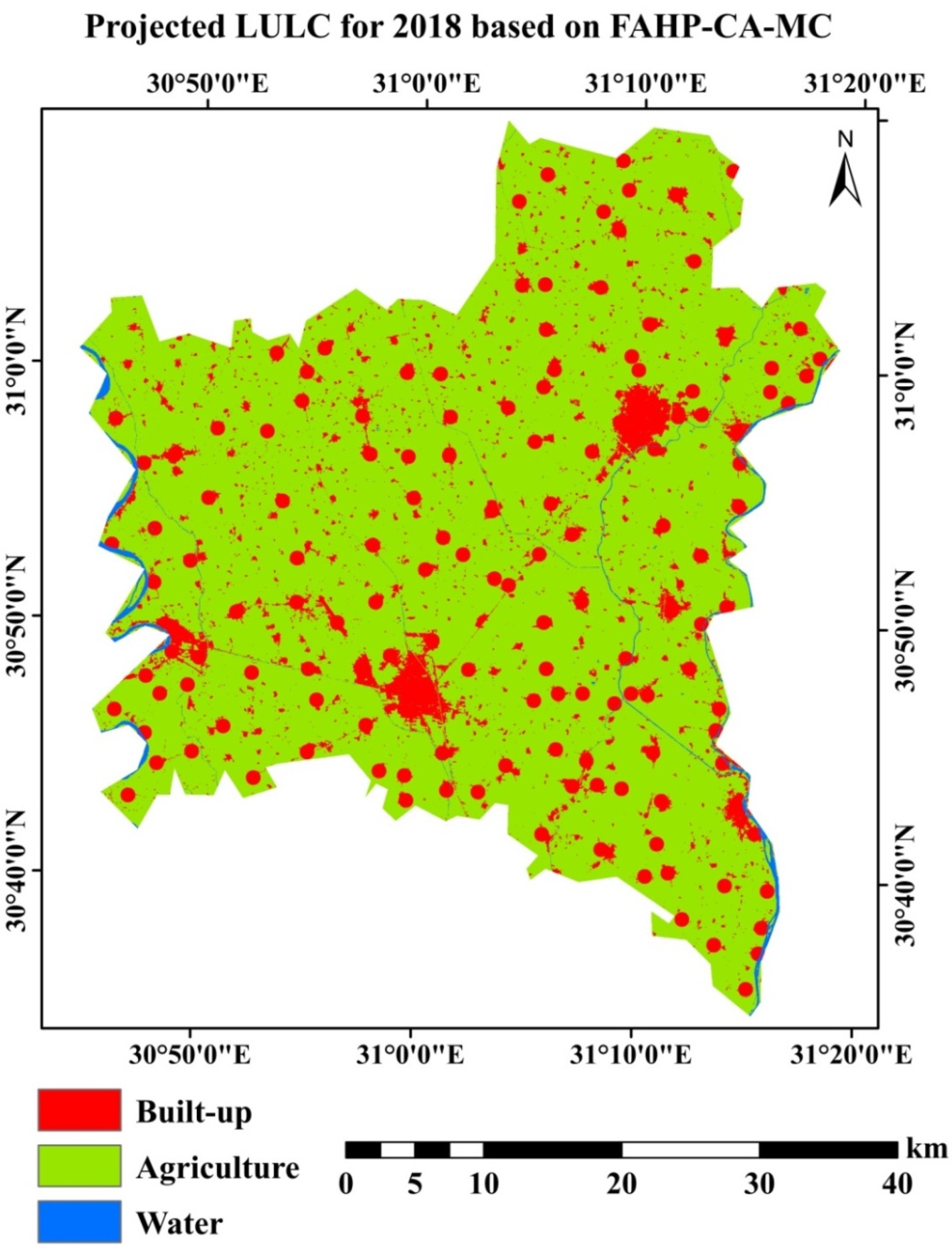
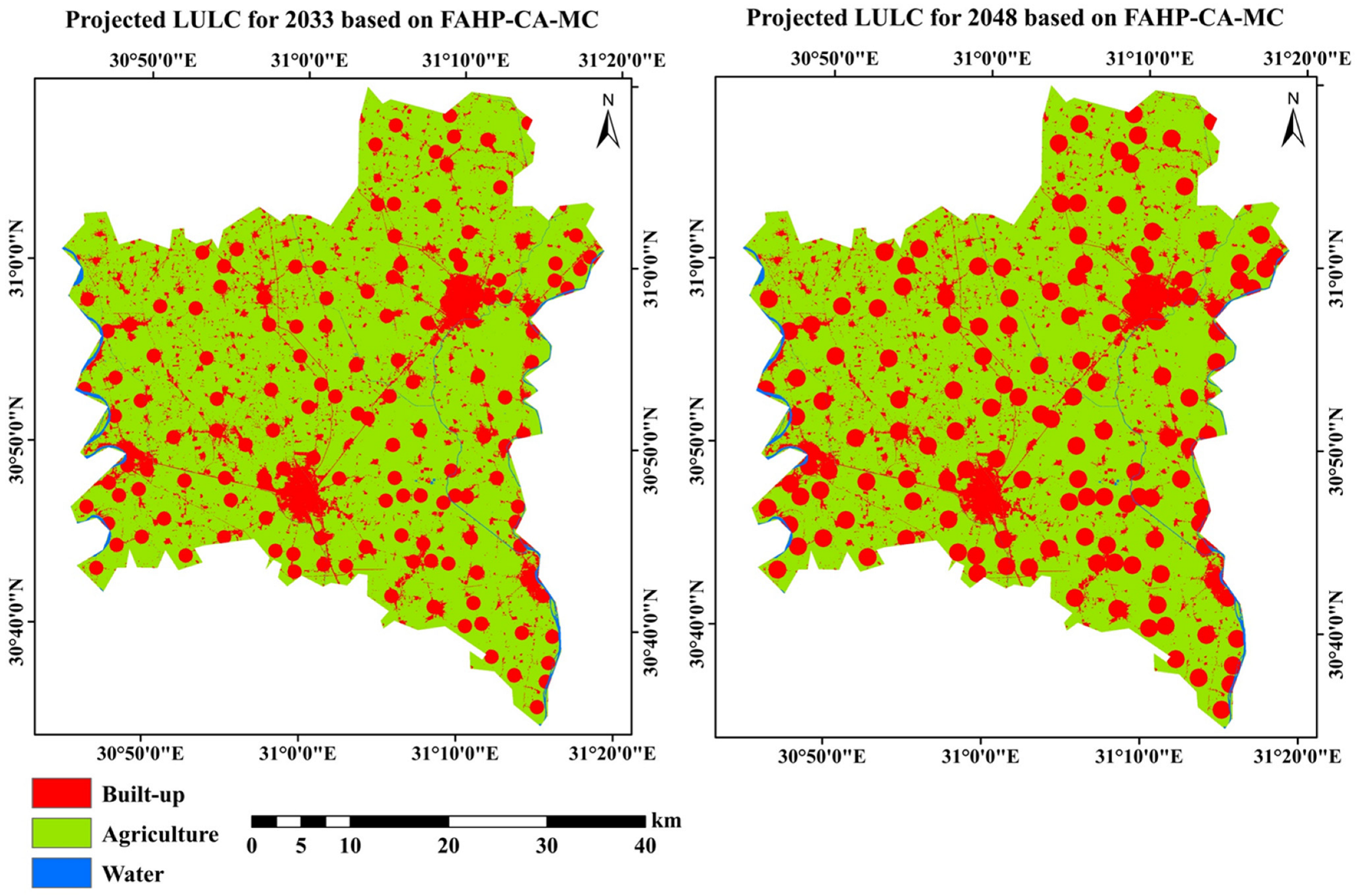
3.3.2. Analysis of FAHP-CA-Markov Chain Model
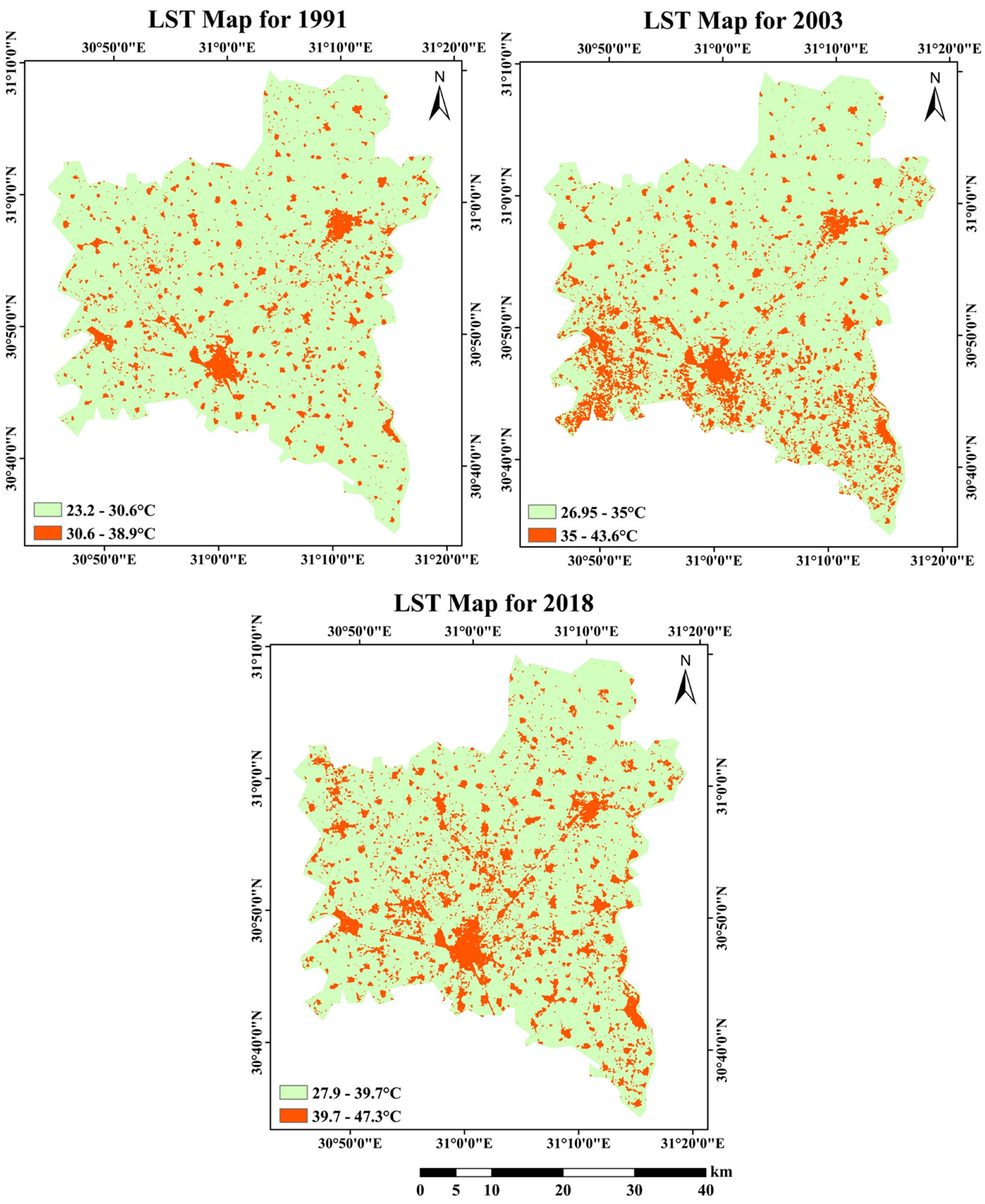
3.4. Analysis of LST
3.5. Analysis of the UHI
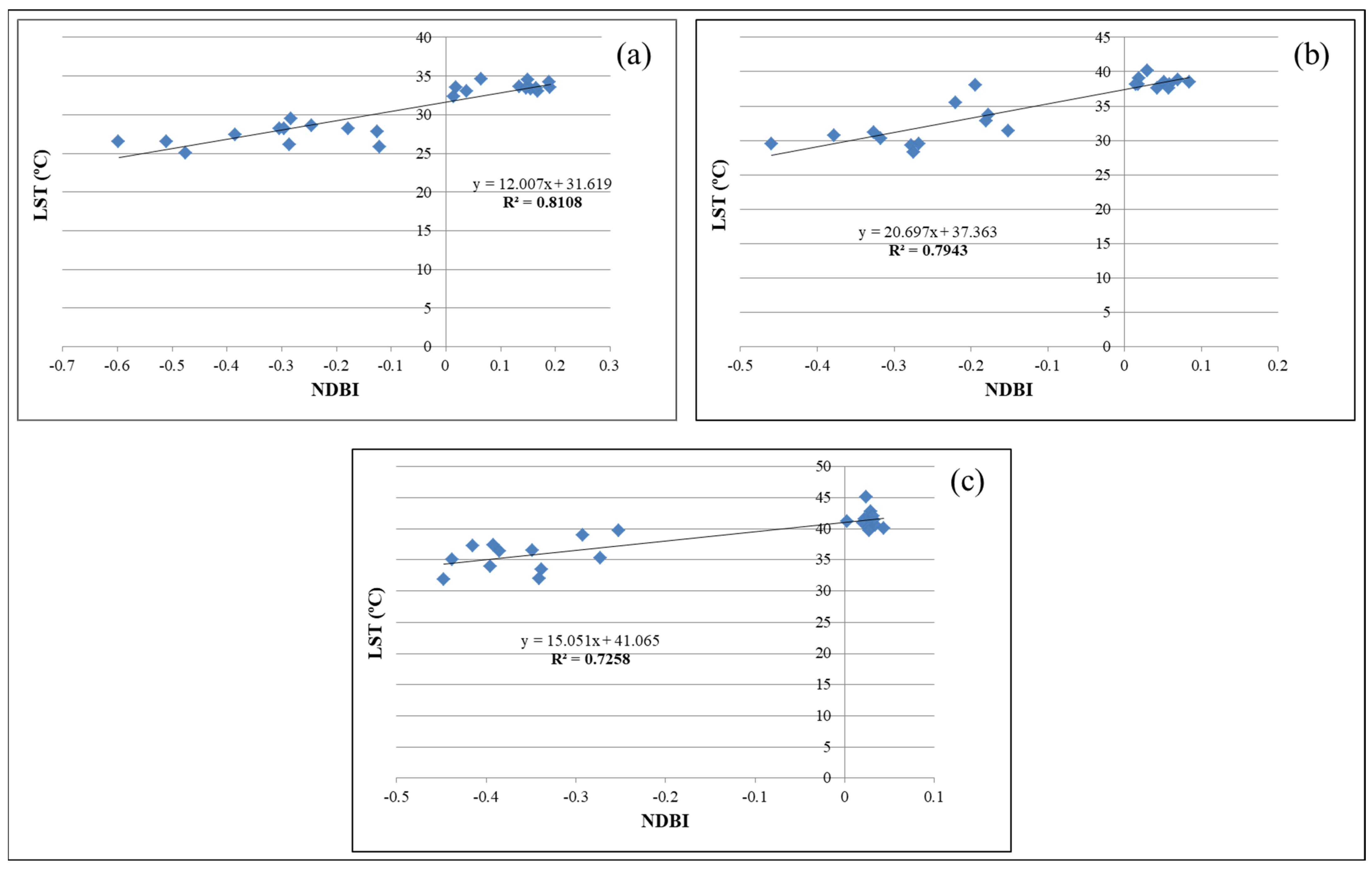
3.6. Relationship between LULC and LST
4. Discussion
4.1. Current Study Compared to Previous LULC and Corresponding LST Studies
4.2. Current and Possible Future Alternative Land-Use Strategies
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, L.; Ren, C.; Zhang, B.; Wang, Z.; Liu, M. Quantifying Urban Land Sprawl and its Driving Forces in Northeast China from 1990 to 2015. Sustainability 2018, 10, 188. [Google Scholar] [CrossRef]
- Abd El-Kawy, O.R.; Rød, J.K.; Ismail, H.A.; Suliman, A.S. Land use and land cover change detection in the western Nile delta of Egypt using remote sensing data. Appl. Geogr. 2011, 31, 483–494. [Google Scholar] [CrossRef]
- Bakr, N.; Bahnassy, M.H. Egyptian Natural Resources. In The Soils of Egypt, 1st ed.; El-Ramady, H., Alshaal, T., Bakr, N., Elbana, T., Mohamed, E., Belal, A.A., Eds.; Springer: Cham, Switzerland, 2019; pp. 33–49. [Google Scholar]
- Li, C. Monitoring and Analysis of Urban Growth Process Using Remote Sensing, GIS and Cellular Automata Modeling: A Case Study of Xuzhou City, China. Ph.D. Thesis, Universitätsbibliothek, Dortmund, Germany, September 2014. [Google Scholar]
- Li, G.; Sun, S.; Fang, C. The varying driving forces of urban expansion in China: Insights from a spatial-temporal analysis. Landsc. Urban Plan. 2018, 174, 63–77. [Google Scholar] [CrossRef]
- Bratley, K.; Ghoneim, E. Modeling Urban Encroachment on the Agricultural Land of the Eastern Nile Delta Using Remote Sensing and a GIS-Based Markov Chain Model. Land 2018, 7, 114. [Google Scholar] [CrossRef]
- El-Eraqi, M.B.; Shehata, M.S. The Urban Sprawl on Agricultural Lands in Gharbia Govornorate. Arab Univ. J. Agric. Sci. 2019, 27, 1771–1781. [Google Scholar]
- Sahana, M.; Hong, H.; Sajjad, H. Analyzing urban spatial patterns and trend of urban growth using urban sprawl matrix: A study on Kolkata urban agglomeration, India. Sci. Total Environ. 2018, 628–629, 1557–1566. [Google Scholar] [CrossRef] [PubMed]
- Van Vliet, J.; Eitelberg, D.A.; Verburg, P.H. A global analysis of land take in cropland areas and production displacement from urbanization. Glob. Environ. Chang. 2017, 43, 107–115. [Google Scholar] [CrossRef]
- United Nations, Department of Economic and Social Affairs, Population Division. World Urbanization Prospects: The 2018 Revision; United Nations, Department of Economic and Social Affairs, Population Division: New York, NY, USA, 2019. [Google Scholar]
- Zhang, X.M.; Zhu, F. Group size and incentives to contribute: A natural experiment at Chinese Wikipedia. Am. Econ. Rev 2011, 101, 1601–1615. [Google Scholar] [CrossRef]
- Lillesand, T.M.; Kiefer, R.W.; Chipman, J.W. Remote Sensing and Image Interpretation, 5th ed.; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Han, D.; Chan, L.; Zhu, N. Flood forecasting using support vector machines. J. Hydroinform. 2007, 9, 267–276. [Google Scholar] [CrossRef]
- Moghaddamnia, A.; Gosheh, M.; Nuraie, M.; Mansuri, M.; Han, D.; Schmitter, E. Performance evaluation of LLR, SVM, CGNN and BFGSNN models to evaporation estimation. Water Geosci. 2010, 9, 108–113. [Google Scholar]
- Gutiérrez, S.; Tardaguila, J.; Fernández-Novales, J.; Diago, M.P. Support vector machine and artificial neural network models for the classification of grapevine varieties using a portable NIR spectrophotometer. PLoS ONE 2015, 10, e0143197. [Google Scholar] [CrossRef]
- Clarke, K.C. Land use change modeling with sleuth: Improving calibration with a genetic algorithm. In Geomatic Approaches for Modeling Land Change Scenarios; Camacho Olmedo, M.T., Paegelow, M., Mas, J.-F., Escobar, F., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 139–161. [Google Scholar]
- Theobald, D. Landscape patterns of exurban growth in the USA from 1980 to 2020. Ecol. Soc. 2005, 10, 34. [Google Scholar] [CrossRef] [Green Version]
- Sloan, S.; Pelletier, J. How accurately may we project tropical forest-cover change? Glob. Environ. Chang. 2012, 22, 440–453. [Google Scholar] [CrossRef]
- Rodrigues, H.; Soares-Filho, B. A short presentation of dinamica ego. In Geomatic Approaches for Modeling Land Change Scenarios; Camacho Olmedo, M.T., Paegelow, M., Mas, J.-F., Escobar, F., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 493–498. [Google Scholar]
- Yang, X.; Chen, R.; Zheng, X.Q. Simulating land use change by integrating ann-ca model and landscape pattern indices. Geomat. Nat. Hazards Risk 2016, 7, 918–932. [Google Scholar] [CrossRef]
- Kuo, H.-F.; Tsou, K.-W. Modeling and simulation of the future impacts of urban land use change on the natural environment by sleuth and cluster analysis. Sustainability 2018, 10, 72. [Google Scholar] [CrossRef]
- Baig, M.F.; Mustafa, M.R.U.; Baig, I.; Takaijudin, H.B.; Zeshan, M.T. Assessment of land use land cover changes and future predictions using CA-ANN simulation for selangor, Malaysia. Water 2022, 14, 402. [Google Scholar] [CrossRef]
- Chen, C.; Son, N.; Chang, N.; Chen, C.; Chang, L.; Valdez, M.; Centeno, G.; Thompson, C.A.; Aceituno, J.L. Multi-decadal mangrove forest change detection and prediction in Honduras, Central America, with Landsat imagery and a Markov Chain Model. Remote Sens. 2013, 5, 6408–6426. [Google Scholar] [CrossRef]
- Weiguo, J.; Zheng, C.; Xuan, L.E.I.; Kai, J.I.A.; Yongfeng, W.U. Simulating urban land use change by incorporating an autologistic regression model into a CLUE-S model. J. Geogr. Sci. 2015, 25, 836–850. [Google Scholar]
- Arsanjani, J.J.; Helbich, M.; Kainz, W.; Darvishi Boloorani, A. Integration of logistic regression, markov chain and cellular automata models to simulate urban expansion. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 265–275. [Google Scholar] [CrossRef]
- Wang, S.W.; Munkhnasan, L.; Lee, W.K. Land use and land cover change detection and prediction in Bhutan’s high altitude city of Thimphu, using cellular automata and Markov chain. Environ. Chall. 2021, 2, 100017. [Google Scholar] [CrossRef]
- Koko, A.F.; Han, Z.; Wu, Y.; Abubakar, G.A.; Bello, M. Spatiotemporal Land Use/Land Cover Mapping and Prediction Based on Hybrid Modeling Approach: A Case Study of Kano Metropolis, Nigeria (2020–2050). Remote Sens. 2022, 14, 6083. [Google Scholar] [CrossRef]
- Samat, N.; Mahamud, M.A.; Tan, M.L.; Maghsoodi Tilaki, M.J.; Tew, Y.L. Modelling Land Cover Changes in Peri-Urban Areas: A Case Study of George Town Conurbation, Malaysia. Land 2020, 9, 373. [Google Scholar] [CrossRef]
- Sun, X.; Crittenden, J.C.; Li, F.; Lu, Z.; Dou, X. Urban expansion simulation and the spatio-temporal changes of ecosystem services, a case study in Atlanta Metropolitan area, USA. Sci. Total Environ. 2018, 622–623, 974–987. [Google Scholar] [CrossRef] [PubMed]
- Liping, C.; Yujun, S.; Saeed, S. Monitoring and predicting land use and land cover changes using remote sensing and GIS techniques—A case study of a hilly area, Jiangle, China. PLoS ONE 2018, 13, e0200493. [Google Scholar] [CrossRef]
- Wang, S.; Zheng, X. Dominant transition probability: Combining CA-Markov model to simulate land use change. Environ. Dev. Sustain. 2022, 1–19. [Google Scholar] [CrossRef]
- Pal, S.; Ziaul, S. Detection of land use and land cover change and land surface temperature in English Bazar urban centre. Egypt. J. Remote Sens. Space Sci. 2017, 20, 125–145. [Google Scholar] [CrossRef]
- Effat, H.A.; Taha, L.G.; Mansour, K.F. Change detection of land cover and urban heat islands using multi-temporal landsat images, application in Tanta City, Egypt. Open J. Remote Sens. Position. 2014, 1, 1–15. [Google Scholar] [CrossRef]
- Negm, A.M.; Saavedra, O.; El-Adawy, A. Nile Delta Biography: Challenges and Opportunities. In The Nile Delta; Negm, A., Ed.; The Handbook of Environmental Chemistry; Springer: Cham, Switzerland, 2016; Volume 55. [Google Scholar]
- Mostafa, E.; Li, X.; Sadek, M.; Dossou, J. Monitoring and Forecasting of Urban Expansion Using Machin Learning-Based Techniques and Remotely Sensed Data: A Case Study of Gharbia Governorate, Egypt. Remote Sens. 2021, 132, 4498. [Google Scholar] [CrossRef]
- Erkan, U.; Gökrem, L. A new method based on pixel density in salt and pepper noise removal. Turk. J. Electr. Eng. Comput. Sci. 2018, 26, 162–171. [Google Scholar] [CrossRef]
- Sakthidasan, K.; Nagappan, N.V. Noise free image restoration using hybrid filter with adaptive genetic algorithm. Comput. Electr. Eng. 2016, 54, 382–392. [Google Scholar] [CrossRef]
- Taati, A.; Sarmadian, F.; Mousavi, A.; Pour, C.T.H.; Shahir, A.H.E. Land use classification using support vector machine and maximum likelihood algorithms by Landsat 5 TM images. Walailak J. Sci. Technol. (WJST) 2015, 12, 681–687. [Google Scholar]
- Sadek, M.; Li, X. Low-cost solution for assessment of urban flash flood impacts using sentinel-2 satellite images and fuzzy analytic hierarchy process: A case study of Ras Ghareb city, Egypt. Adv. Civ. Eng. 2019, 2019, 2561215. [Google Scholar] [CrossRef]
- Almouctar, M.A.S.; Wu, Y.; Kumar, A.; Zhao, F.; Mambu, K.J.; Sadek, M. Spatiotemporal analysis of vegetation cover changes around surface water based on NDVI: A case study in Korama basin, Southern Zinder, Niger. Appl. Water Sci. 2020, 11, 4. [Google Scholar] [CrossRef]
- Rousta, I.; Sarif, M.O.; Gupta, R.D.; Olafsson, H.; Ranagalage, M.; Murayama, Y.; Zhang, H.; Mushore, T.D. Spatiotemporal analysis of land use/land cover and its effects on surface urban heat island using Landsat data: A case study of metropolitan city Tehran (1988–2018). Sustainability 2018, 10, 4433. [Google Scholar] [CrossRef] [Green Version]
- Sadek, M.; Li, X.; Mostafa, E.; Freeshah, M.; Kamal, A.; Sidi Almouctar, M.A.; Mustafa, E.K. Low-Cost Solutions for Assessment of Flash Flood Impacts Using Sentinel-1/2 Data Fusion and Hydrologic/Hydraulic Modeling: Wadi El-Natrun Region, Egypt. Adv. Civ. Eng. 2020, 2020, 1039309. [Google Scholar] [CrossRef]
- Dissanayake, D.; Morimoto, T.; Murayama, Y.; Ranagalage, M. Impact of landscape structure on the variation of land surface temperature in sub-saharan region: A case study of Addis Ababa using Landsat data (1986–2016). Sustainability 2019, 11, 2257. [Google Scholar] [CrossRef]
- Hamdy, O.; Zhao, S.; Salheen, M.A.; Eid, Y.Y. Analyses the driving forces for urban growth by using IDRISI® Selva Models Abouelreesh Aswan as a Case Study. Int. J. Eng. Technol. 2017, 9, 226. [Google Scholar] [CrossRef]
- Eastman, J.R. Manual for Using Terrset; Clark Labs, Clark University: Worcester, MA, USA, 2018. [Google Scholar]
- Landis, J.R.; Koch, G.G. The measurement of observer agreement for categorical Data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [PubMed]
- Van Vliet, J.; Bregt, A.K.; Hagen-zanker, A. Revisiting Kappa to account for change in the accuracy assessment of land-use change models. Ecol. Model. 2011, 222, 1367–1375. [Google Scholar] [CrossRef]
- Flo, J.; Landmark, B.; Hatlevik, O.E.; Fagerström, L. Using a new interrater reliability method to test the modified oulu patient classification instrument in home health care. Nurs. Open 2018, 5, 167–175. [Google Scholar] [CrossRef]
- Pontius, R.G., Jr.; Millones, M. Death to Kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- Sadek, M.; Li, X.; Mostafa, E.; Dossou, J. Monitoring Flash Flood Hazard Using Modeling-Based Techniques and Multi-Source Remotely Sensed Data in Ras Ghareb City, Egypt. Arab. J.Geosci. 2021, 14, 2030. [Google Scholar] [CrossRef]
- Mustafa, E.K.; Co, Y.; Liu, G.; Kaloop, M.R.; Beshr, A.A.; Zarzoura, F.; Sadek, M. Study for Predicting Land Surface Temperature (LST) Using Landsat Data: A Comparison of Four Algorithms. Adv. Civ. Eng. 2020, 2020, 7363546. [Google Scholar] [CrossRef]
- Kampanart, P.A. Dynamic Settlement Simulation Model: Application to Urban Growth in Thailand. Ph.D. Thesis, University College London, London, UK, 2005. [Google Scholar]
- Takeyama, M.; Couclelis, H. Map dynamics: Integrating cellular automata and GIS through Geo-Algebra. Int. J. Geogr. Inf. Sci. 1997, 11, 73–91. [Google Scholar] [CrossRef]
- Li, X.; Yeh, A.G.O. Neural-network-based cellular automata for simulating multiple land use changes using GIS. Int. J. Geogr. Inf. Sci. 2002, 16, 323–343. [Google Scholar] [CrossRef]
- Saaty, T.L.; Peniwati, K. Group Decision Making: Drawing Out and Reconciling Differences; RWS Publications: Pittsburgh, PA, USA, 2013. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process, Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Chen, C.T. Extension of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Nădăban, S.; Dzitac, S.; Dzitac, I. Fuzzy TOPSIS: A general view. Procedia Comput. Sci. 2016, 91, 823–831. [Google Scholar] [CrossRef]
- Dubovyk, O.; Sliuzas, R.; Flacke, J. Spatio-temporal modeling of informal settlement development in Sancaktepe district, Istanbul, Turkey. ISPRS J. Photogramm. Remote Sens. 2011, 66, 235–246. [Google Scholar] [CrossRef]
- Thapa, R.B.; Murayama, Y. Drivers of urban growth in the Kathmandu valley, Nepal: Examining the efficacy of the analytic hierarchy process. Appl. Geogr. 2010, 30, 70–83. [Google Scholar] [CrossRef]
- Wu, K.; Zhang, H. Land use dynamics, built-up land expansion patterns, and driving forces analysis of the fast-growing Hangzhou metropolitan area, eastern China (1978–2008). Appl. Geogr. 2012, 34, 137–145. [Google Scholar] [CrossRef]
- Ahmed, B.; Ahmed, R.; Zhu, X. Evaluation of model validation techniques in land cover dynamics. ISPRS Int. J. Geo-Inf. 2013, 2, 577–597. [Google Scholar] [CrossRef]
- Subasinghe, S.; Estoque, R.C.; Murayama, Y. Spatiotemporal analysis of urban growth using GIS and remote sensing: A case study of the Colombo Metropolitan Area, Sri Lanka. ISPRS Int. J. Geo-Inf. 2016, 5, 197. [Google Scholar] [CrossRef]
- Kore, N.B.; Ravi, K.; Patil, S.B. A simplified description of fuzzy TOPSIS method for multi criteria decision making. Int. Res. J. Eng. Technol (IRJET) 2017, 4, 2047–2050. [Google Scholar]
- Malczewski, J. Gis and Multicriteria Decision Analy; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Artis, D.A.; Carnahan, W.H. Survey of emissivity variability in thermography of urban areas. Remote Sens. Environ. 1982, 12, 313–329. [Google Scholar] [CrossRef]
- Liu, H.; Xu, L.; Ding, J.; Zhuoma, B.; Deng, X.; Liu, Z. Notice of Retraction Atmospheric correction and land surface temperature retrieval method for FY-3 IR observations. In Proceedings of the Geoscience and Remote Sensing (IITA-GRS), 2010 Second IITA International Conference on Geoscience and Remote Sensing, Qingdao, China, 28–31 August 2010; Volume 2, pp. 131–134. [Google Scholar]
- Li, Z.L.; Becker, F.; Stoll, M.P.; Wan, Z. Evaluation of six methods for extracting relative emissivity spectra from thermal infrared images. Remote Sens. Environ. 1999, 69, 197–214. [Google Scholar] [CrossRef]
- Pieper, M.L.; Manolakis, D.; Truslow, E.; Cooley, T.W.; Brueggeman, M.; Jacobson, J.; Weisner, A. Performance limitations of temperature–emissivity separation techniques in long-wave infrared hyperspectral imaging applications. Opt. Eng. 2017, 56, 081804. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Sòria, G.; Romaguera, M.; Guanter, L.; Moreno, J.; Martínez, P. Land surface emissivity retrieval from different VNIR and TIR sensors. IEEE Trans.Geosci. Remote Sens. 2008, 46, 316–327. [Google Scholar] [CrossRef]
- Jin, M.; Dickinson, R.E.; Vogelmann, A.M. A comparison of CCM2–BATS skin temperature and surface-air temperature with satellite and surface observations. J. Clim. 1997, 10, 1505–1524. [Google Scholar] [CrossRef]
- Van de Griend, A.A.; Owe, M. On the relationship between thermal emissivity and the normalized difference vegetation index for natural surfaces. Int. J. Remote Sens. 1993, 14, 1119–1131. [Google Scholar] [CrossRef]
- Valor, E.; Caselles, V. Mapping land surface emissivity from NDVI: Application to European, African, and South American areas. Remote Sens. Environ. 1996, 57, 167–184. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Raissouni, N. Toward remote sensing methods for land cover dynamic monitoring: Application to Morocco. Int. J. Remote Sens. 2000, 21, 353–366. [Google Scholar] [CrossRef]
- Skoković, D.; Sobrino, J.A.; Jimenez-Munoz, J.C.; Soria, G.; Juşien, Y.; Mattar, C.; Cristóbal, J. Calibration and validation of land surface temperature for landsat8-tirs sensor. In LPVE (Land Product Validation and Evolution); ESA/ESRIN: Frascati, Italy, 2014. [Google Scholar]
- Senanayake, I.P.; Welivitiya, W.D.D.P.; Nadeeka, P.M. Remote sensing based analysis of urban heat islands with vegetation cover in Colombo city, Sri Lanka using Landsat-7 ETM+ data. Urban Clim. 2013, 5, 19–35. [Google Scholar] [CrossRef]
- Ma, Y.; Kuang, Y.; Huang, N. Coupling urbanization analyses for studying urban thermal environment and its interplay with biophysical parameters based on TM/ETM+ imagery. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 110–118. [Google Scholar] [CrossRef]
- Sánchez, J.M.; Galve, J.M.; González-Piqueras, J.; López-Urrea, R.; Niclòs, R.; Calera, A. Monitoring 10-m LST from the Combination MODIS/Sentinel-2, Validation in a High Contrast Semi-Arid Agroecosystem. Remote Sens. 2020, 12, 1453. [Google Scholar] [CrossRef]
- S2-PDGS-TAS-DI-PSD-V14.9.pdf. Available online: https://sentinel.esa.int/documents/247904/4756619/S2-PDGS-TAS-DIPSD-V14.9.pdf/3d3b6c9c-4334-dcc4-3aa7-f7c0deffbaf7 (accessed on 14 May 2022).
- Gascon, F.; Bouzinac, C.; Thépaut, O.; Jung, M.; Francesconi, B.; Louis, J.; Lonjou, V.; Lafrance, B.; Massera, S.; Gaudel-Vacaresse, A.; et al. Copernicus Sentinel-2A calibration and products validation status. Remote Sens. 2017, 9, 584. [Google Scholar] [CrossRef] [Green Version]
- Athukorala, D.; Murayama, Y. Urban heat island formation in Greater Cairo: Spatio-temporal analysis of daytime and nighttime land surface temperatures along the urban–rural gradient. Remote Sens. 2021, 13, 1396. [Google Scholar] [CrossRef]
- Zhang, Q.; Ban, Y.; Liu, J.; Hu, Y. Simulation and analysis of urban growth scenarios for the Greater Shanghai Area, China. Comput. Environ. Urban Syst. 2011, 35, 126–139. [Google Scholar] [CrossRef]
- Li, X.; Zhou, W.; Ouyang, Z. Forty years of urban expansion in Beijing: What is the relative importance of physical, socioeconomic, and neighborhood factors? Appl. Geogr. 2013, 38, 110. [Google Scholar] [CrossRef]
- Aburas, M.M.; Ho, Y.M.; Ramli, M.F.; Ash’aari, Z.H. Improving the capability of an integrated CA-Markov model to simulate spatio-temporal urban growth trends using an Analytical Hierarchy Process and Frequency Ratio. Int. J. Appl. Earth Obs. Geoinf. 2017, 59, 65–78. [Google Scholar] [CrossRef]
- Radwan, T.M.; Blackburn, G.A.; Whyatt, J.D.; Atkinson, P.M. Dramatic loss of agricultural land due to urban expansion threatens food security in the Nile Delta, Egypt. Remote Sens. 2019, 11, 332. [Google Scholar] [CrossRef]
- Arsanjani, J.J.; Helbich, M.; Vaz, E.D.N. Spatiotemporal simulation of urban growth patterns using agent-based modeling: The case of Tehran. Cities 2013, 32, 33–42. [Google Scholar] [CrossRef]



| Data Type | Capture Date | Resolution | Source | Output |
|---|---|---|---|---|
| Landsat 1991™ | 27 June 1991 | 30 m | USGS | LULC map |
| Landsat 2003™ | 28 June 2003 | 30 m | USGS | LULC map |
| Landsat 2018OLI-TIRS | 21 June 2018 | 30 m | USGS | LULC map |
| Google Earth historical images | June 1991, 2003, 2018 | Google Earth Pro | Training/validation | |
| Road network layer | OSM | Distance to nearest road |
| Criteria | LULC | Dist. to Persist. Built-Up | Dist. to Urban Centers | Dist. to Railway Stations | Dist. to Near Road | Neighbor. Effect | Population Density | Local Develop. | Employment |
|---|---|---|---|---|---|---|---|---|---|
| LULC | (1,1,1) | ||||||||
| Dist. to persist. built-up | (7,8,9) | (1,1,1) | (1,1,1) | (4,5,6) | (2,3,4) | (1,1,1) | (2,3,4) | (2,3,4) | (2,3,4) |
| Dist. to urban centers | (7,8,9) | (1,1,1) | (1,1,1) | (2,3,4) | (1,2,3) | (1,1,1) | (2,3,4) | (3,4,5) | (2,3,4) |
| Dist. to railway stations | (6,7,8) | (1,1,1) | (1,1,1) | (2,3,4) | (1,1,1) | ||||
| Dist. to nearest road | (7,8,9) | (2,3,4) | (1,1,1) | (2,3,4) | (3,4,5) | (2,3,4) | |||
| Neighborhood effect | (6,7,8) | (1,1,1) | (1,1,1) | (4,5,6) | (2,3,4) | (1,1,1) | (1,1,1) | (2,3,4) | (2,3,4) |
| Population density | (4,5,6) | (1,1,1) | (1,1,1) | (1,1,1) | (1,1,1) | ||||
| Local development | (4,5,6) | (2,3,4) | (1,1,1) | ||||||
| Employment | (6,7,8) | (1,1,1) | (1,1,1) | (1,2,3) | (1,1,1) |
| Accuracy | LULC Class | 1991 | 2003 | 2018 |
|---|---|---|---|---|
| User’s accuracy (%) | Built-up | 80.7 | 85.7 | 91.8 |
| Water | 82.1 | 82.6 | 94.7 | |
| Agricultural land | 97.0 | 96.4 | 95.1 | |
| Producer’s accuracy (%) | Built-up | 80.0 | 80.9 | 81.3 |
| Water | 82.1 | 86.4 | 85.7 | |
| Agricultural land | 97.1 | 97.2 | 98.1 | |
| Overall accuracy (%) | 94.9 | 94.7 | 94.6 | |
| Kappa coefficient | 0.78 | 0.81 | 0.84 |
| LULC | 1991 | 2003 | 2018 | |||
|---|---|---|---|---|---|---|
| Area (km2) | % | Area (km2) | % | Area (km2) | % | |
| Built-up | 156.75 | 7.8 | 193.37 | 9.7 | 303.75 | 15.2 |
| Water | 19.57 | 1.0 | 24.48 | 1.2 | 21.56 | 1.1 |
| Agricultural land | 1832.01 | 91.2 | 1781.48 | 89.1 | 1674.02 | 83.7 |
| Total | 1999.33 | 100 | 1999.33 | 100 | 1999.33 | 100 |
| Model Criteria | AHP | FAHP |
|---|---|---|
| LULC | 0.017 | 0 |
| Dist. to persistent built-up area | 0.202 | 0.260 |
| Dist. to urban centers | 0.185 | 0.238 |
| Dist. to railway stations | 0.07 | 0.040 |
| Dist. to nearest road | 0.134 | 0.206 |
| Neighborhood effect | 0.186 | 0.226 |
| Population density | 0.071 | 0 |
| Local development | 0.065 | 0 |
| Employment | 0.07 | 0.030 |
| LULC | 2018 | 2033 | 2048 | RD% 2018–2033 | RD% 2018–2033 | |||
|---|---|---|---|---|---|---|---|---|
| Area (km2) | % | Area (km2) | % | Area (km2) | % | |||
| Built-up | 251.62 | 12.6 | 414.90 | 20.7 | 514.00 | 25.7 | 64.9 | 104.3 |
| Water | 24.48 | 1.2 | 21.56 | 1.1 | 21.56 | 1.1 | −11.9 | −11.9 |
| Agricultural land | 1723.23 | 86.2 | 1562.87 | 78.2 | 1463.77 | 73.2 | −9.3 | −15.1 |
| Total | 1999.33 | 100 | 1999.33 | 100 | 1999.33 | 100 | ||
| Image Acquisition Date | Mean Urban LST (°C) | Mean Rural LST (°C) | UHI (°C) |
|---|---|---|---|
| 1991 | 32.48 | 29.23 | 3.25 |
| 2003 | 37.29 | 32.57 | 4.72 |
| 2018 | 41.50 | 37.46 | 4.04 |
| Urban LST (°C) | Rural LST (°C) | UHI (°C) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Districts | Mean Temperature (μ) 1991 | Mean Temperature (μ) 2003 | Mean Temperature (μ) 2018 | Mean Temperature (μ) 1991 | Mean Temperature (μ) 2003 | Mean Temperature (μ) 2018 | 1991 | 2003 | 2018 |
| Mahalla Kubra | 32.16 | 36.62 | 40.63 | 28.65 | 31.09 | 36.26 | 3.51 | 5.53 | 4.37 |
| Tanta | 32.87 | 37.95 | 41.29 | 29.77 | 33.30 | 37.38 | 3.10 | 4.65 | 3.91 |
| Basyun | 32.80 | 36.77 | 40.42 | 29.89 | 32.44 | 38.19 | 2.91 | 4.33 | 2.23 |
| Zefta | 32.32 | 37.84 | 41.50 | 29.29 | 33.86 | 38.26 | 3.03 | 3.98 | 3.24 |
| Santah | 32.41 | 37.65 | 41.02 | 29.32 | 33.31 | 37.44 | 3.09 | 4.34 | 3.58 |
| Kafr Elzayat | 32.74 | 38.03 | 41.40 | 29.43 | 34.44 | 39.48 | 3.31 | 3.59 | 1.92 |
| Samanod | 31.72 | 36.53 | 40.53 | 28.52 | 31.92 | 36.58 | 3.2 | 4.61 | 3.95 |
| Qotur | 32.74 | 36.70 | 41.04 | 29.45 | 31.76 | 37.77 | 3.29 | 4.94 | 3.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mostafa, E.; Li, X.; Sadek, M. Urbanization Trends Analysis Using Hybrid Modeling of Fuzzy Analytical Hierarchical Process-Cellular Automata-Markov Chain and Investigating Its Impact on Land Surface Temperature over Gharbia City, Egypt. Remote Sens. 2023, 15, 843. https://doi.org/10.3390/rs15030843
Mostafa E, Li X, Sadek M. Urbanization Trends Analysis Using Hybrid Modeling of Fuzzy Analytical Hierarchical Process-Cellular Automata-Markov Chain and Investigating Its Impact on Land Surface Temperature over Gharbia City, Egypt. Remote Sensing. 2023; 15(3):843. https://doi.org/10.3390/rs15030843
Chicago/Turabian StyleMostafa, Eman, Xuxiang Li, and Mohammed Sadek. 2023. "Urbanization Trends Analysis Using Hybrid Modeling of Fuzzy Analytical Hierarchical Process-Cellular Automata-Markov Chain and Investigating Its Impact on Land Surface Temperature over Gharbia City, Egypt" Remote Sensing 15, no. 3: 843. https://doi.org/10.3390/rs15030843
APA StyleMostafa, E., Li, X., & Sadek, M. (2023). Urbanization Trends Analysis Using Hybrid Modeling of Fuzzy Analytical Hierarchical Process-Cellular Automata-Markov Chain and Investigating Its Impact on Land Surface Temperature over Gharbia City, Egypt. Remote Sensing, 15(3), 843. https://doi.org/10.3390/rs15030843







