An Iterative Algorithm for Predicting Seafloor Topography from Gravity Anomalies
Abstract
:1. Introduction
2. Theory and Methods
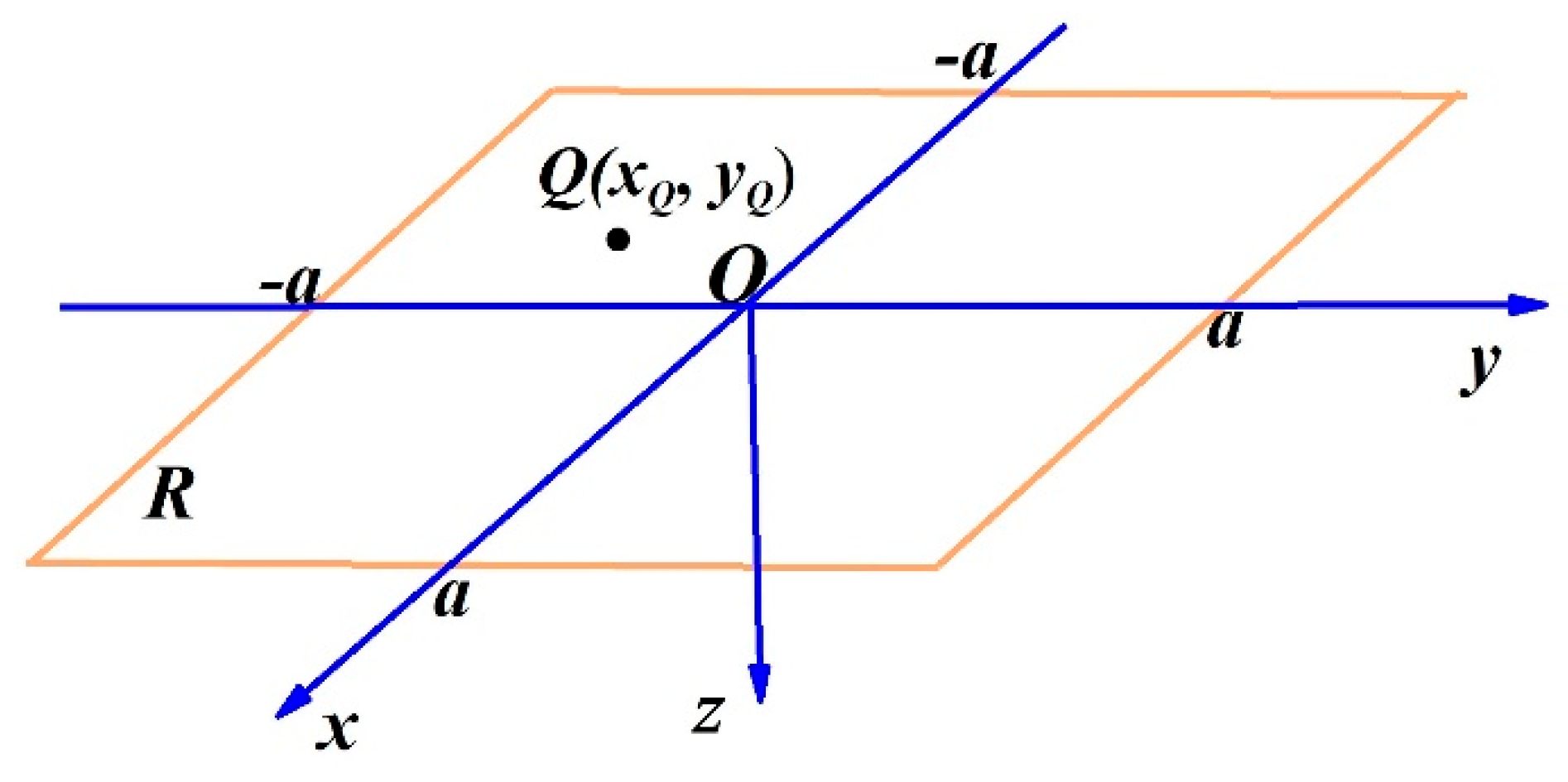
2.1. Computational Formula of Gravity Generated by a Prism
2.2. Establishment of the Observation Equations for Sea Depth from the Gravity Anomaly
2.2.1. Observation Equations Only for the Target Area
2.2.2. Observation Equations by Considering the Boundary Region
2.2.3. Effect of the Deep Region: Correction for the Moho Undulation
2.2.4. System of Observation Equations in the General Case
2.3. Regularization Method for the Solving Equations
3. Simulation Experiment
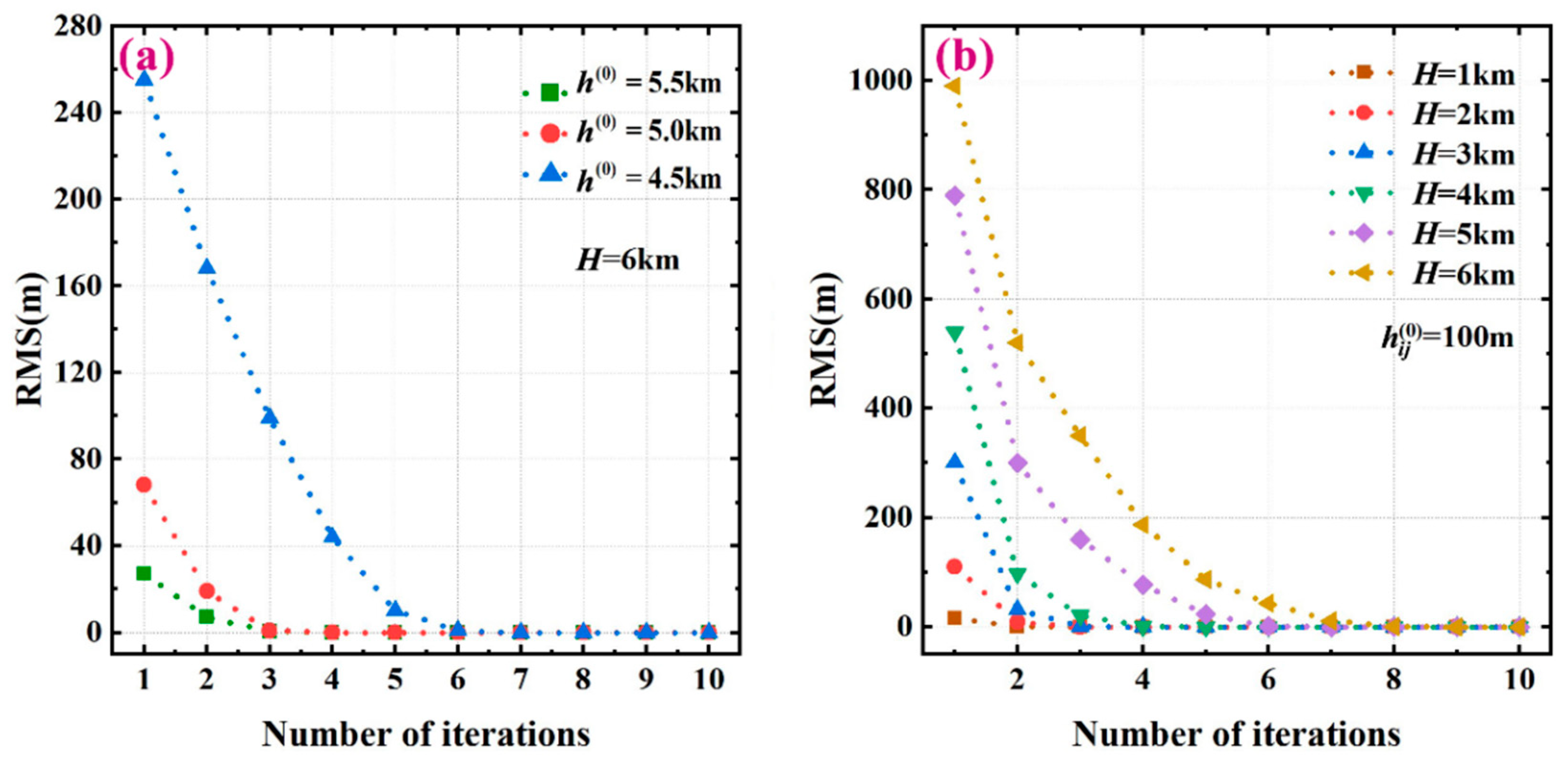
3.1. Selection of Some Parameters
3.2. Selection of Regularization Factors
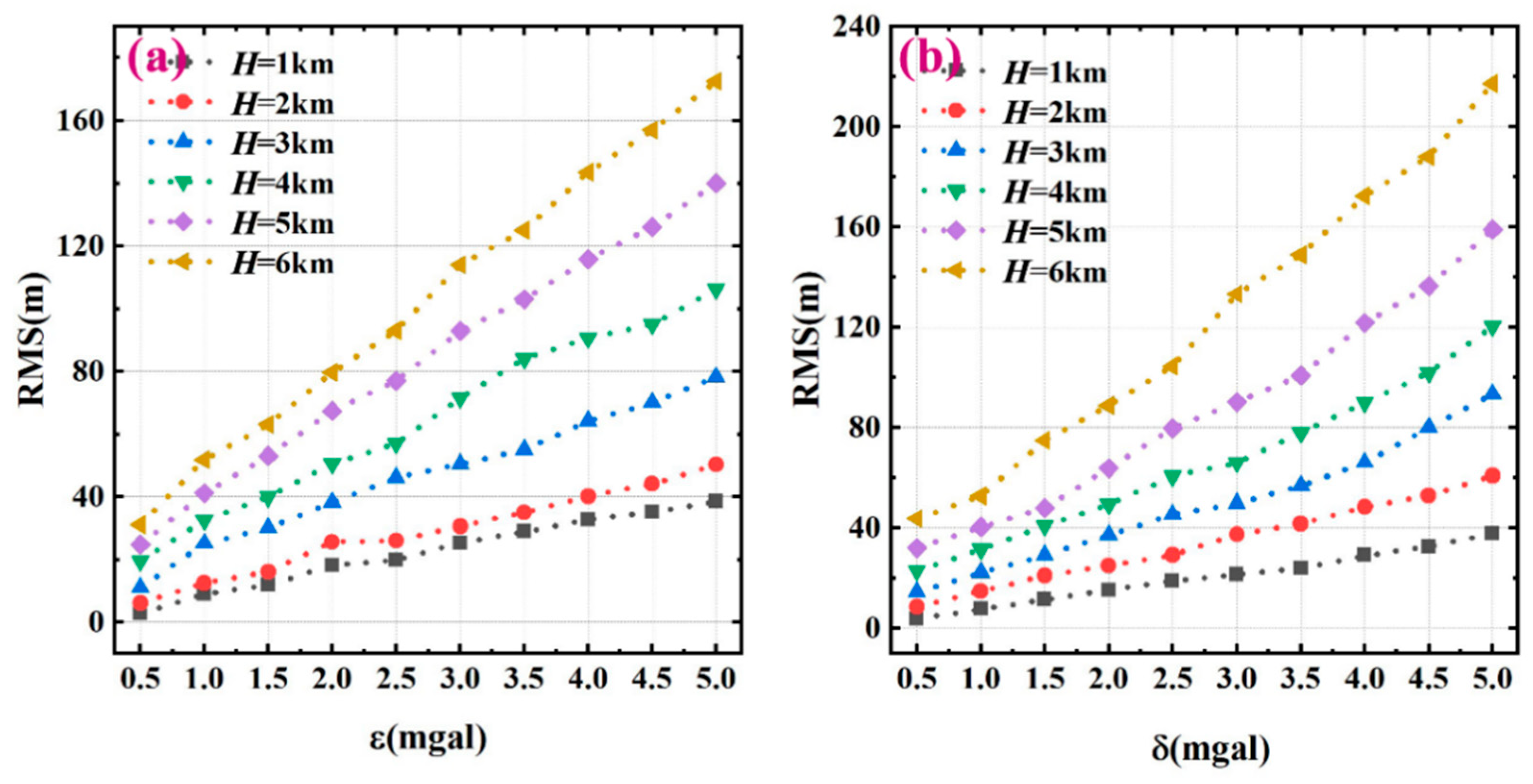
3.3. Anti-Error Characteristics of the Linearized Systems of Equations
3.4. Assessment for the Far Effect
4. Actual Application
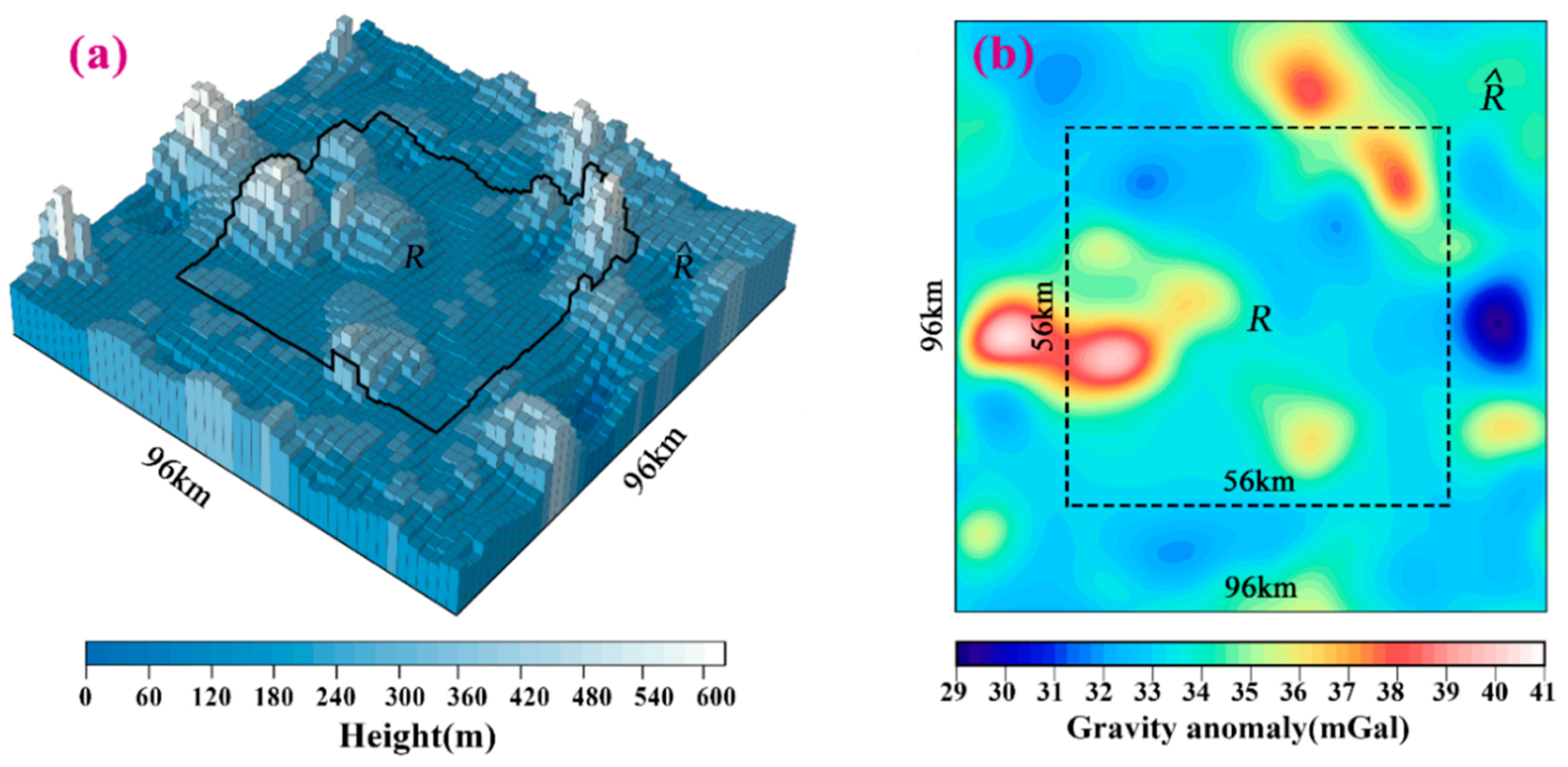
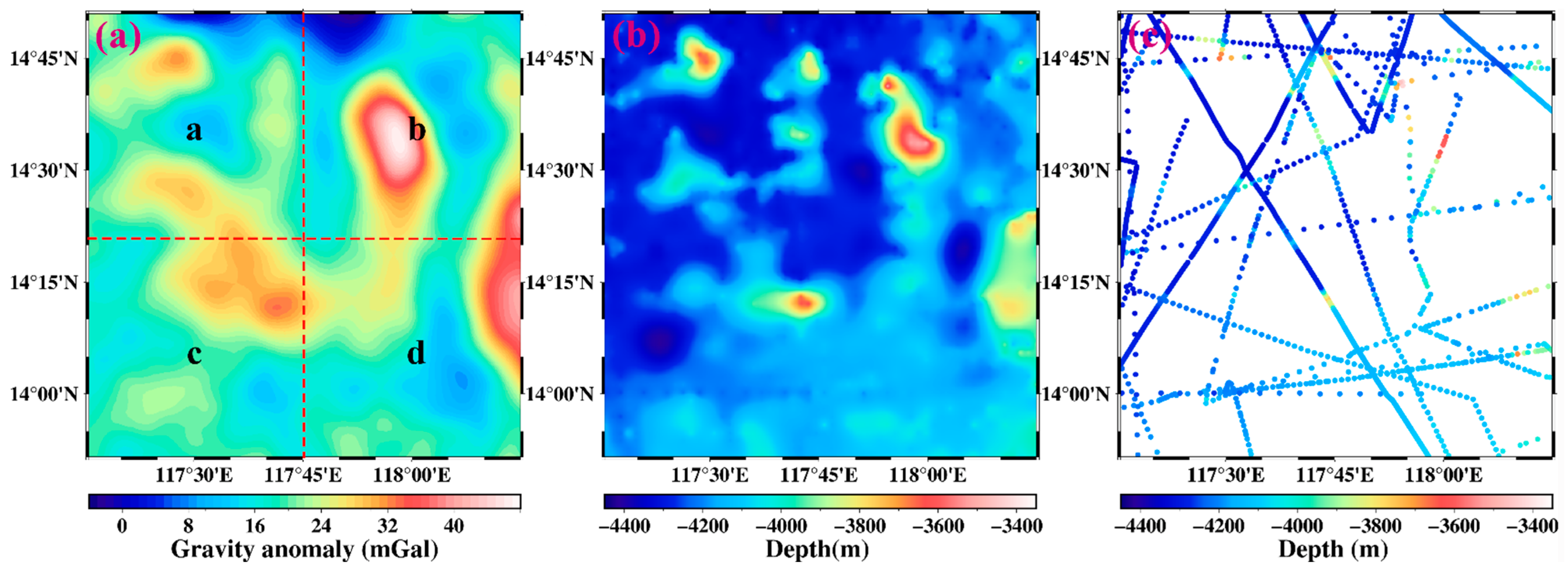
4.1. Target Area and Datasets
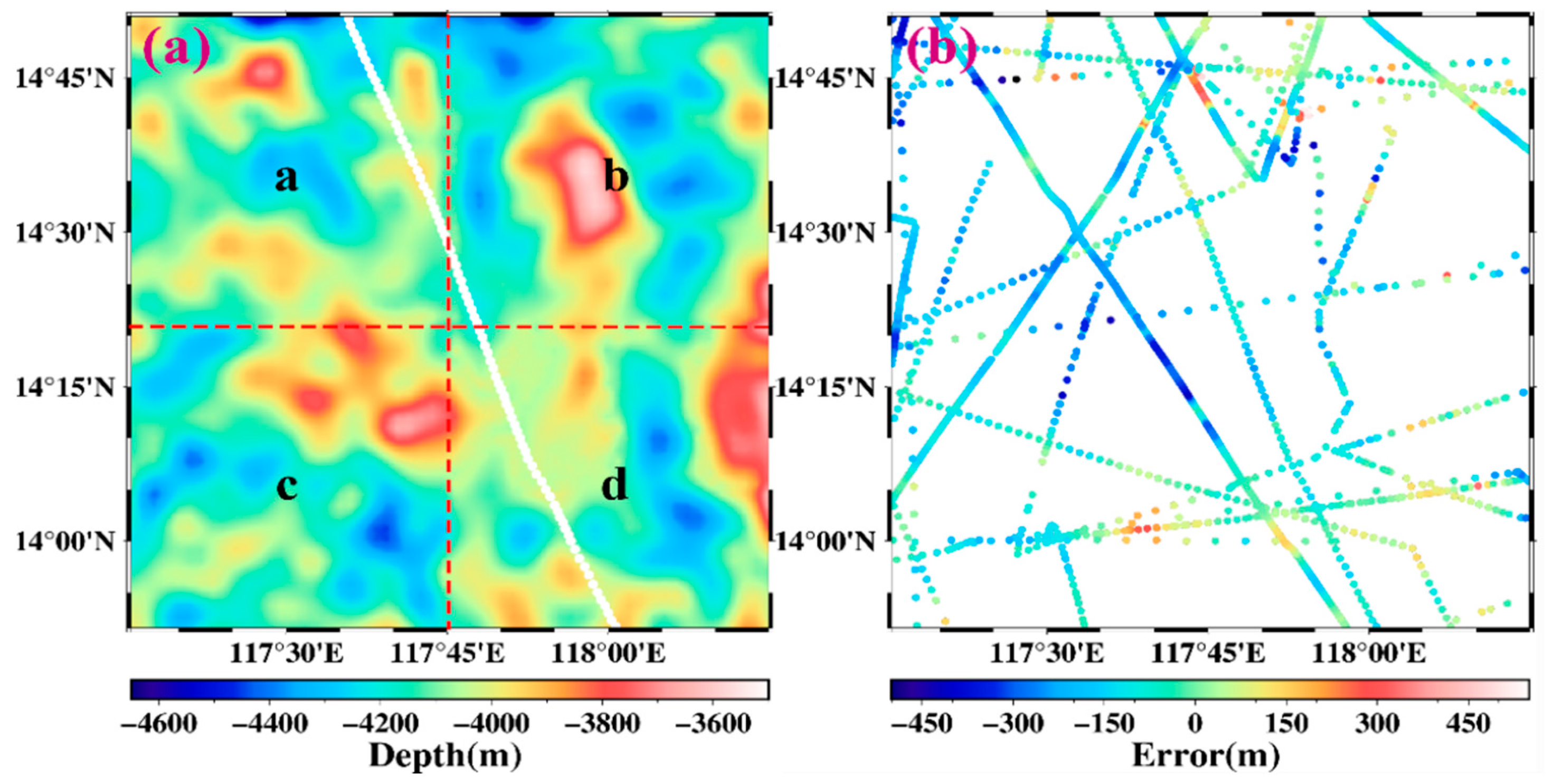
4.2. Results and Comparisons
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baudry, N.; Calmant, S. Seafloor mapping from high-density satellite altimetry. Mar. Geophys. Res. 1996, 18, 135–146. [Google Scholar] [CrossRef]
- Becker, J.J.; Sandwell, D.T.; Smith, W.H.F.; Braud, J.; Binder, B.; Depner, J. Global bathymetry and elevation data at 30 arcseconds resolution: SRTM30_PLUS. Mar. Geod. 2009, 32, 355–371. [Google Scholar] [CrossRef]
- Hsiao, Y.S.; Kim, K.; Kim, J.W.; Lee, B.Y.; Hwang, C. Bathymetry estimation using the gravity-geologic method: An investigation of density contrast predicted by the downward continuation method. Terr. Atmos. Ocean. Sci. 2011, 22, 347–358. [Google Scholar] [CrossRef] [Green Version]
- Sandwell, D.T.; Smith, W.H.F.; Gille, S.; Kappel, E.; Jayne, S.; Soofi, K. Bathymetry from space: Rationale and requirements for a new high-resolution altimetric mission. Comptes. Rendus. Geosci. 2006, 338, 1049–1062. [Google Scholar] [CrossRef] [Green Version]
- Jekeli, C. Spectral Methods in Geodesy and Geophysics; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Abulaitijiang, A.; Andersen, O.B.; Sandwell, D. Improved Arctic Ocean Bathymetry Derived from DTU17 Gravity Model. Earth Space Sci. 2019, 6, 1336–1347. [Google Scholar] [CrossRef] [Green Version]
- Lyzenga, D.R. Passive remote sensing techniques for mapping water depth and bottom features. Appl. Opt. 1978, 17, 379–383. [Google Scholar] [CrossRef] [PubMed]
- Stumpf, R.P.; Kristine, H.; Mark, S. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48 Pt 2, 547–556. [Google Scholar] [CrossRef]
- Caballero, I.; Richard, P.S. Towards Routine Mapping of Shallow Bathymetry in Environments with Variable Turbidity: Contribution of Sentinel-2A/B Satellites Mission. Remote Sens. 2020, 12, 451. [Google Scholar] [CrossRef] [Green Version]
- Smith, W.H.F.; Sandwell, D.T. Global seafloor topography from satellite altimetry and ship depth soundings. Science 1997, 277, 1956–1962. [Google Scholar] [CrossRef] [Green Version]
- Rasheed, S.; Warder, S.C.; Plancherel, Y.; Piggott, M.D. An improved gridded bathymetric data set and tidal model for the Maldives archipelago. Earth Space Sci. 2021, 8, e2020EA001207. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Müller, R.D.; Smith, W.H.F.; Garcia, E.; Francis, R. New global marine gravity model from CryoSat-2 and Jason-1 reveals buried tectonic structure. Science 2014, 346, 65–67. [Google Scholar] [CrossRef] [PubMed]
- Andersen, O.B.; Knudsen, P. The DTU17 Global Marine Gravity Field: First Validation Results. In Fiducial Reference Measurements for Altimetry; Mertikas, S.P., Pail, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 83–87. [Google Scholar]
- Yu, D.C.; Hwang, C.; Andersen, O.B.; Chang, E.T.Y.; Gaultier, L. Gravity recovery from SWOT altimetry using geoid height and geoid gradient. Remote Sens. Environ. 2021, 265, 112650. [Google Scholar] [CrossRef]
- Calmant, S. Seamount topography by least-squares inversion of altimetric geoid heights and shipborne profiles of bathymetry and/or gravity anomalies. Geophys. J. Int. 1994, 119, 428–452. [Google Scholar] [CrossRef] [Green Version]
- Sandwell, D.T.; Smith, W.H.F. Marine gravity anomaly from Geosat and ERS 1 satellite altimetry. J. Geophys. Res. 1997, 105, 10039–10054. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.W.; Frese, R.; Lee, B.Y.; Roman, D.R.; Doh, S. Altimetry-derived gravity predictions of bathymetry by gravity-geologic method. Pure Appl. Geophys. 2011, 168, 815–826. [Google Scholar] [CrossRef]
- Hu, M.Z.; Li, J.C.; Li, H.; Xin, L. Bathymetry predicted from vertical gravity gradient anomalies and ship soundings. Geod. Geodyn. 2014, 5, 41–46. [Google Scholar]
- Kim, S.; Wessel, P. New analytic solutions for modeling vertical gravity gradient anomalies. Geochem. Geophys. Geosyst. 2016, 17, 1915–1924. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.J.; Jekeli, C.; Liu, L. Seafloor topography estimation from gravity gradients using simulated annealing. J. Geophys. Res. 2018, 123, 6958–6975. [Google Scholar] [CrossRef]
- Xu, H.; Yu, J.H. Using an iterative algorithm to predict topography from vertical gravity gradients and ship soundings. Earth Space Sci. 2022, 9, e2022EA002437. [Google Scholar] [CrossRef]
- Ibrahim, A.; Hinze, W.J. Mapping buried bedrock topography with gravity. Ground Water 1972, 10, 18–23. [Google Scholar] [CrossRef]
- Hwang, C. A bathymetric model for the South China sea from satellite altimetry and depth data. Mar. Geod. 1999, 22, 37–51. [Google Scholar] [CrossRef]
- Parker, R.L. The rapid calculation of potential anomalies. Geophys. J. R. Astron. Soc. 1972, 31, 447–455. [Google Scholar] [CrossRef] [Green Version]
- Dixon, T.H.; Naraghi, M.; McNutt, M.K.; Smith, S.M. Bathymetric prediction from Seasat altimeter data. J. Geophys. Res. 1983, 88, 1563–1571. [Google Scholar] [CrossRef]
- Baudry, N.; Diament, M.; Albouy, Y. Precise location of unsurveyed seamounts in the Austral archipelago area using SEASAT data. Geophys. J. R. Astron. Soc. 1987, 89, 869–888. [Google Scholar] [CrossRef] [Green Version]
- Nagy, D. The gravitational attraction of a right rectangular prism. Geophysics 1966, 31, 362–371. [Google Scholar] [CrossRef]
- Nagy, D.; Papp, G.; Benedek, J. The gravitational potential and its derivatives for the prism. J. Geod. 2000, 74, 552–560. [Google Scholar] [CrossRef]
- Blakely, R.J. Potential Theory in Gravity & Magnetic Applications. In Potential Theory in Gravity and Magnetic Applications; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Zhu, L.Z. Gradient Modeling with Gravity and GEM; OSU Report; OSU: Columbus, OH, USA, 2007. [Google Scholar]
- Fan, D.; Li, S.; Li, X.; Yang, J.; Wan, X.Y. Seafloor Topography Estimation from Gravity Anomaly and Vertical Gravity Gradient Using Nonlinear Iterative Least Square Method. Remote Sens. 2021, 13, 64. [Google Scholar] [CrossRef]
- Calmant, S.; Baudry, N. Modelling bathymetry by inverting satellite altimetry data: A review. Mar. Geophys. Res. 1996, 18, 123–134. [Google Scholar] [CrossRef]
- Heiskanen, W.; Moritz, H. Physical Geodesy; San Francisco W. H. Freeman and Company: San Francisco, CA, USA, 1967. [Google Scholar]
- Yu, J.H.; Xu, H.; Wan, X.Y. An analytical method to invert the seabed depth from the vertical gravitational gradient. Mar. Geod. 2021, 44, 306–326. [Google Scholar] [CrossRef]
- Fan, D.; Li, S.; Meng, S.; Lin, Y.; Xing, Z.; Zhang, C. Applying Iterative Method to Solving High-Order Terms of Seafloor Topography. Mar. Geod. 2020, 43, 63–85. [Google Scholar] [CrossRef]
- Luis, J.F.; Neves, M.C. The isostatic compensation of the Azores Plateau: A 3D admittance and coherence analysis. J. Volcanol. Geotherm. Res. 2006, 156, 10–22. [Google Scholar] [CrossRef]
- Bouman, J.; Bosch, W.; Sebera, J. Assessment of systematic errors in the computation of gravity gradients from satellite altimeter data. Mar. Geod. 2011, 34, 85–107. [Google Scholar] [CrossRef]





| Main Indicators | Max Depth | Min Depth | Mean Depth | Max Abs Error | Sys Error | RMS Error | Relative Error | Model Error |
|---|---|---|---|---|---|---|---|---|
| Sub-area a | 4590.9 | 3698.2 | 4063.6 | 480.4 | 25.2 | 140.6 | 3.45% | 148.0 |
| Sub-area b | 4531.4 | 3570.1 | 4018.3 | 533.9 | 17.9 | 116.8 | 2.91% | 134.3 |
| Sub-area c | 4484.8 | 3608.3 | 4011.5 | 437.5 | 22.9 | 144.4 | 3.59% | 153.4 |
| Sub-area d | 4473.0 | 3596.3 | 4007.6 | 426.5 | 13.1 | 107.8 | 2.68% | 110.8 |
| Region R | 4590.9 | 3570.1 | 4025.3 | 533.9 | 19.8 | 127.4 | 3.16% | 136.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; An, B.; Xu, H.; Sun, Z.; Tian, Y.; Wang, Q. An Iterative Algorithm for Predicting Seafloor Topography from Gravity Anomalies. Remote Sens. 2023, 15, 1069. https://doi.org/10.3390/rs15041069
Yu J, An B, Xu H, Sun Z, Tian Y, Wang Q. An Iterative Algorithm for Predicting Seafloor Topography from Gravity Anomalies. Remote Sensing. 2023; 15(4):1069. https://doi.org/10.3390/rs15041069
Chicago/Turabian StyleYu, Jinhai, Bang An, Huan Xu, Zhongmiao Sun, Yuwei Tian, and Qiuyu Wang. 2023. "An Iterative Algorithm for Predicting Seafloor Topography from Gravity Anomalies" Remote Sensing 15, no. 4: 1069. https://doi.org/10.3390/rs15041069





