Evaluation of Airborne HySpex and Spaceborne PRISMA Hyperspectral Remote Sensing Data for Soil Organic Matter and Carbonates Estimation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Soil Sampling and Chemical Analysis
2.3. Laboratory Spectral Measurements
2.4. HySpex Data Acquisition
2.5. PRISMA Data Acquisition
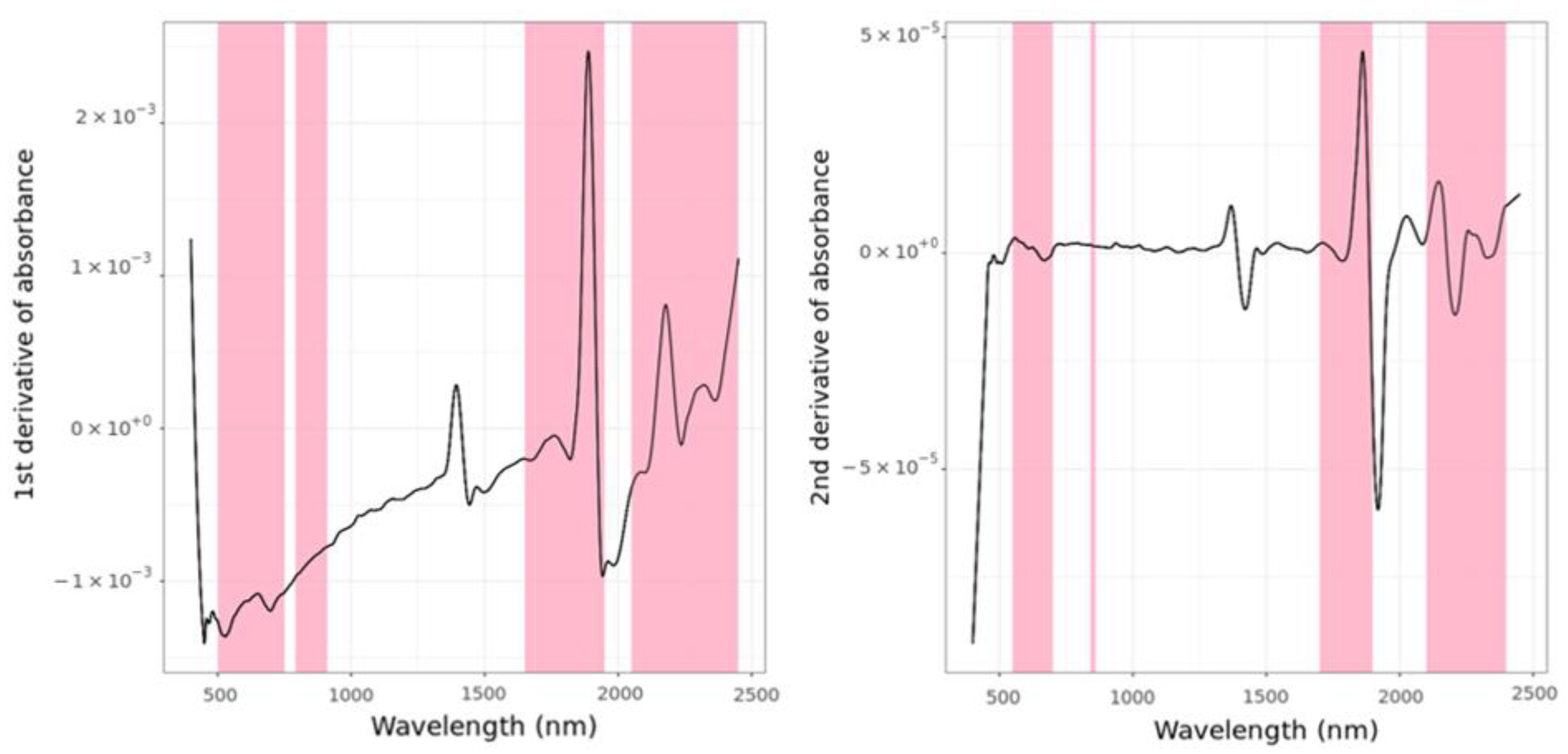
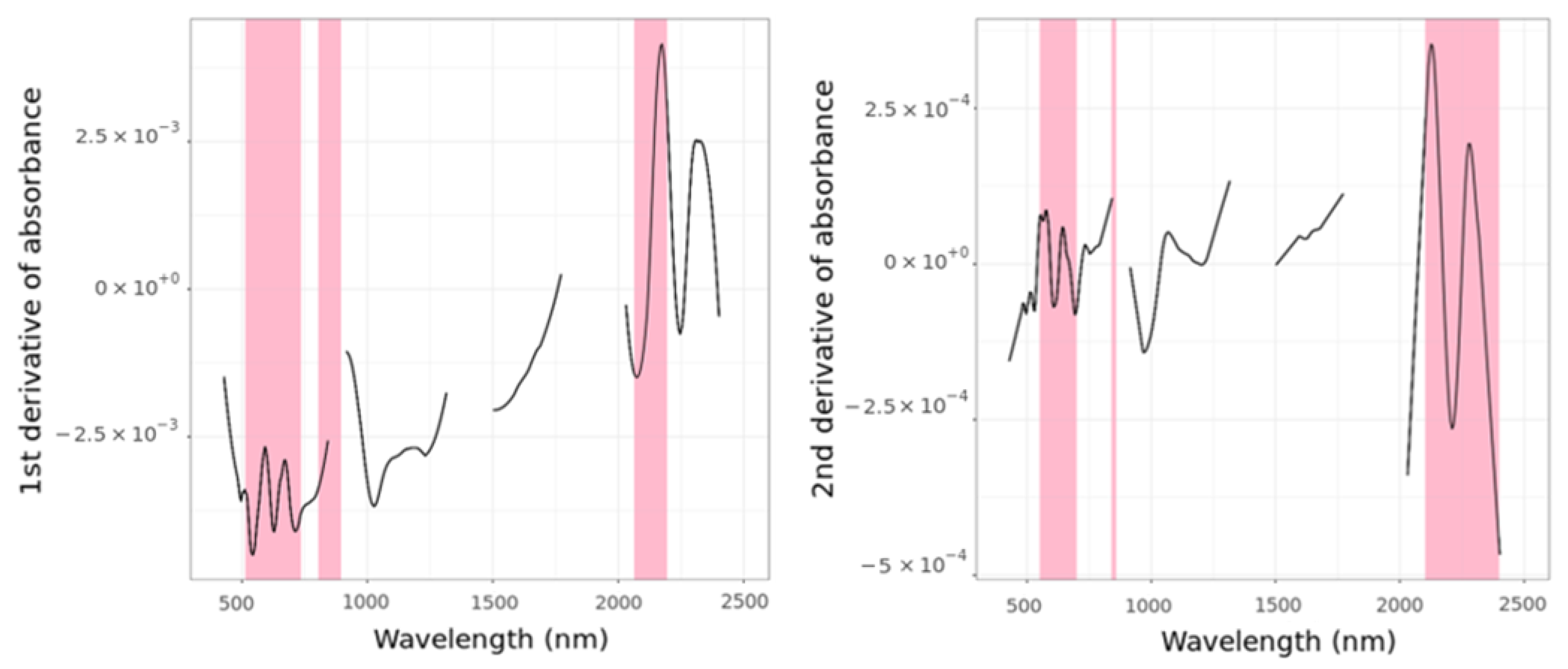
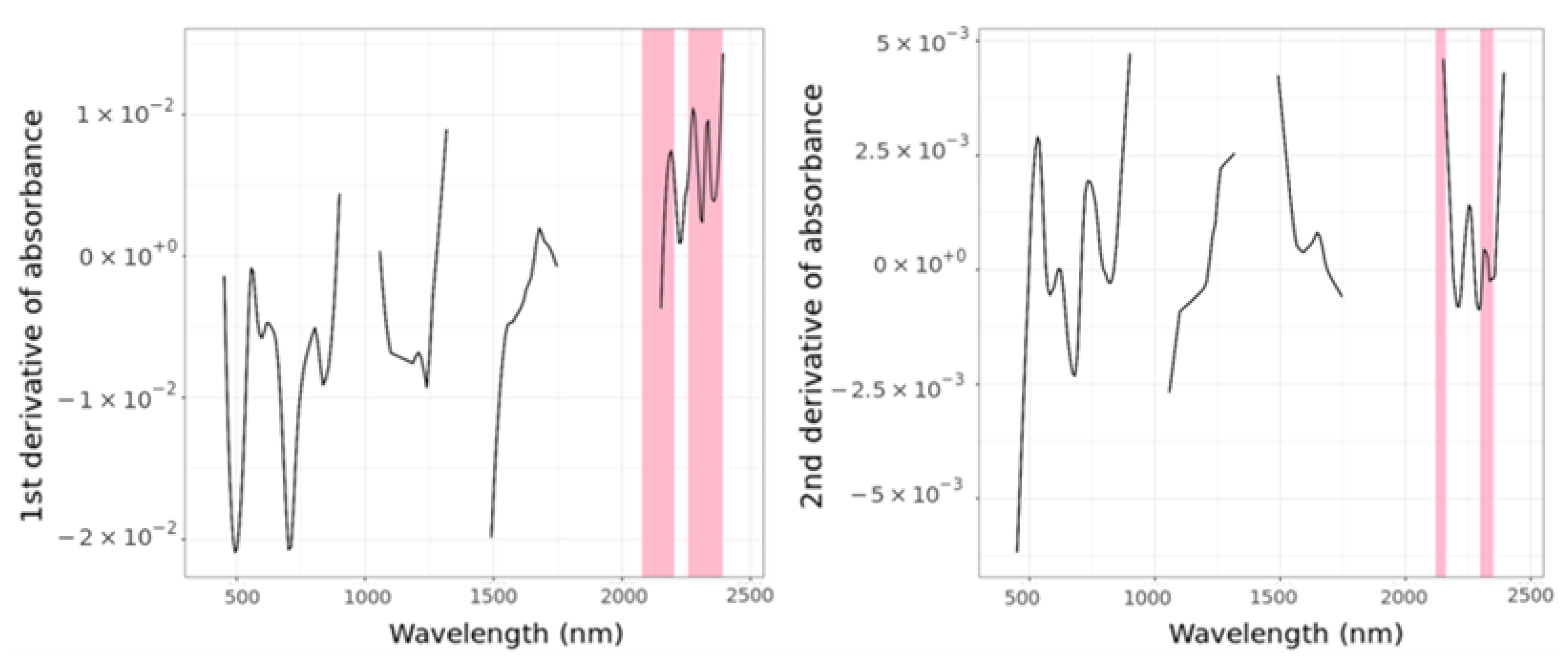
2.6. Data Preprocessing
2.7. Predictive Algorithms
2.8. Datasets Used for Modeling
3. Results and Discussion
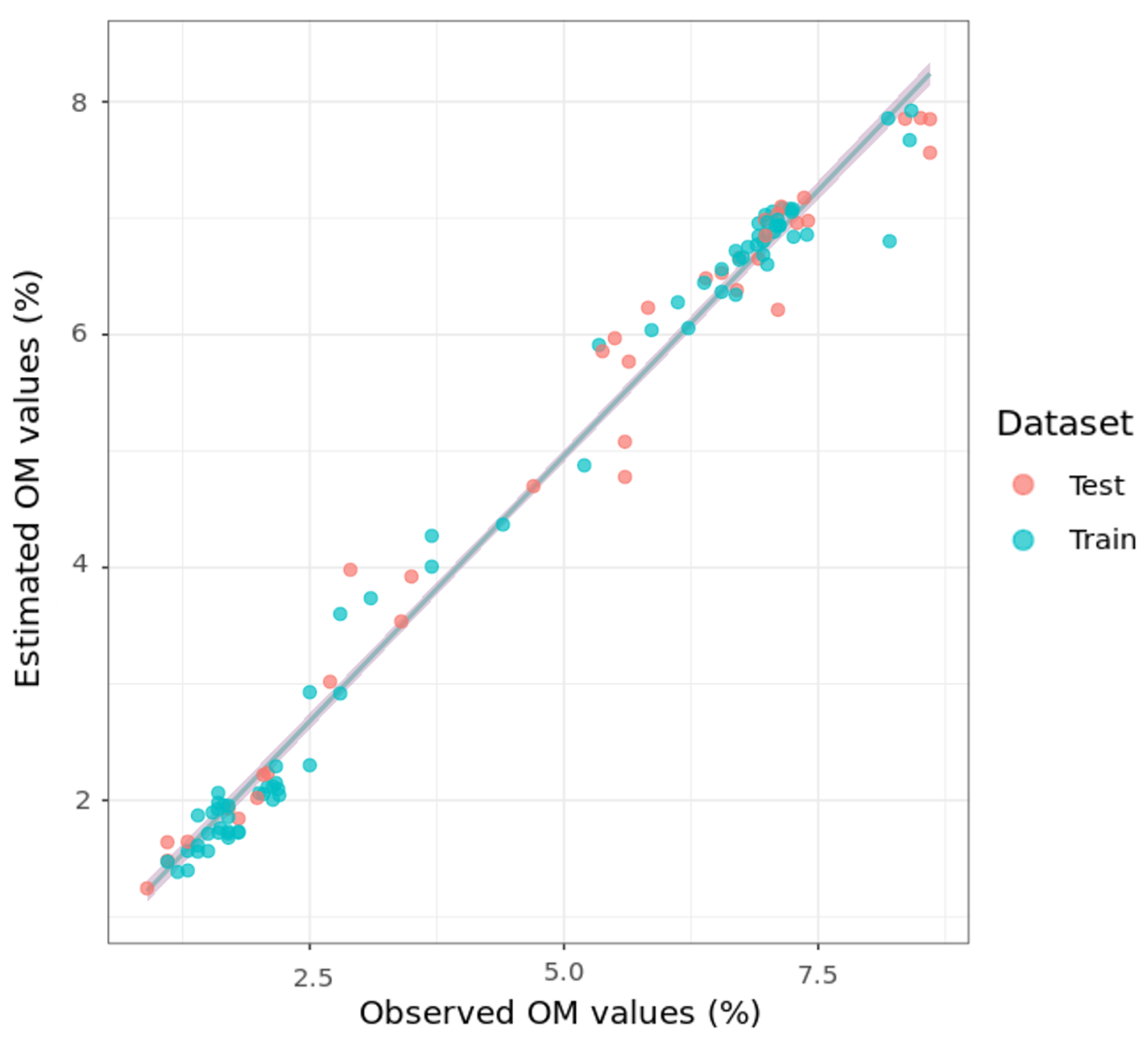
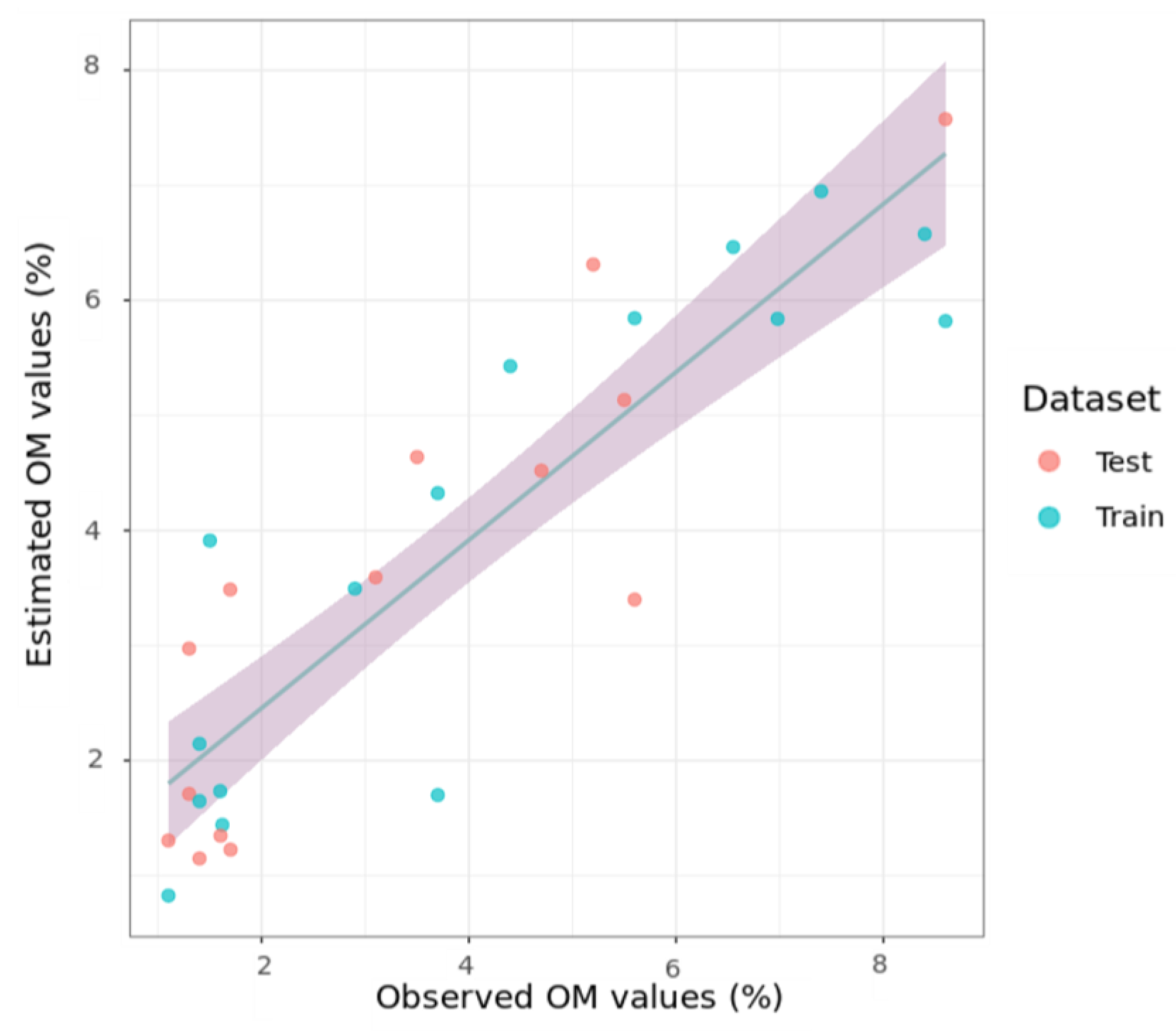
3.1. Soil Property Estimation
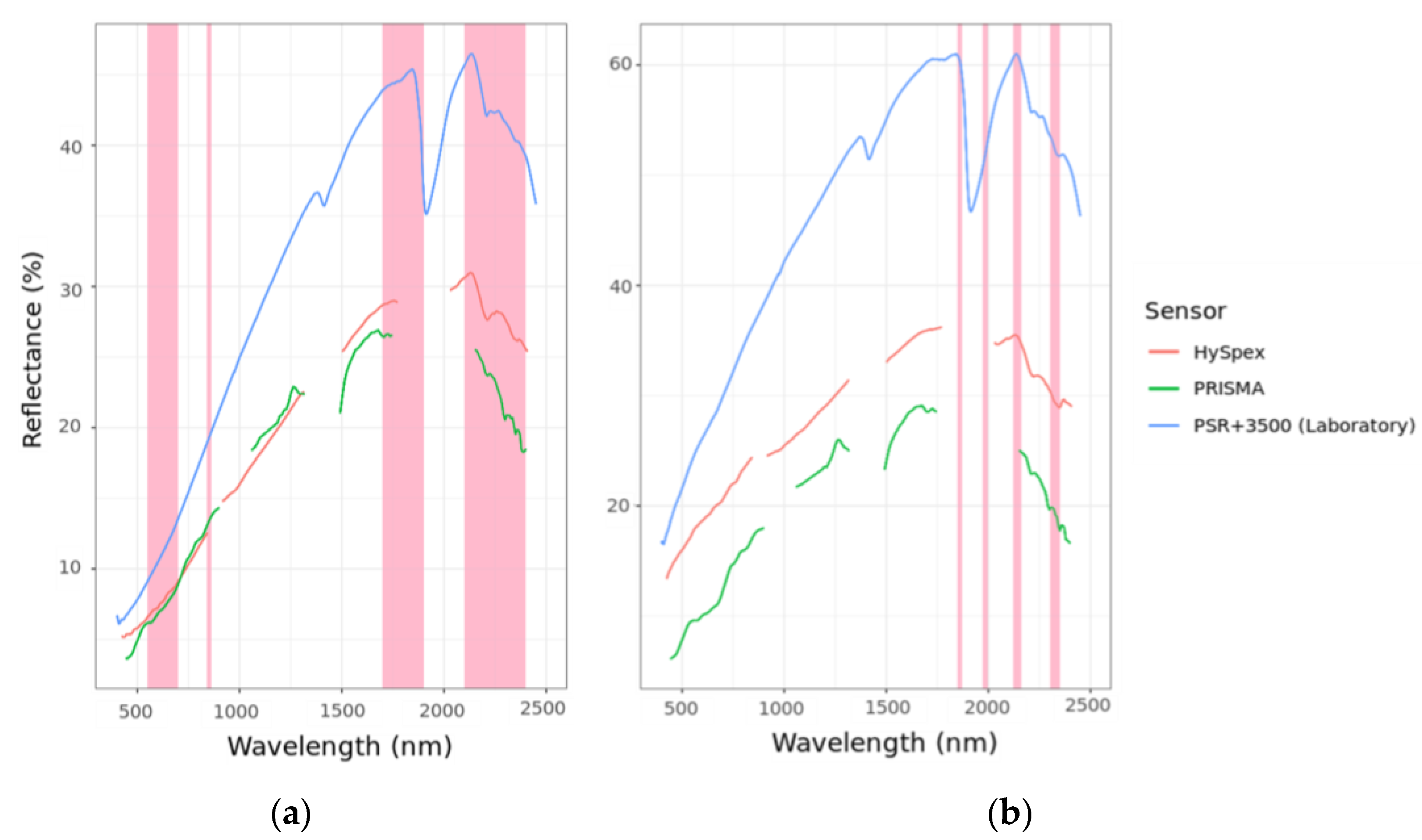
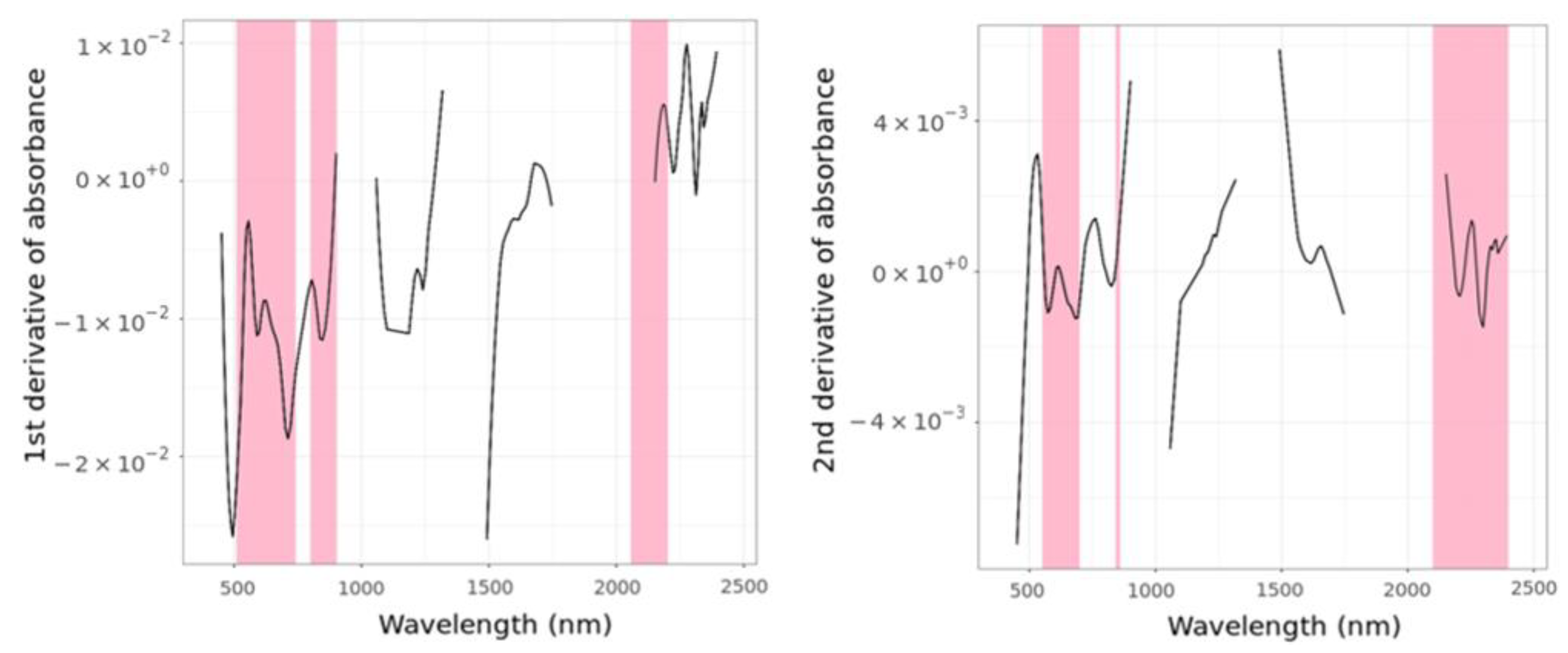
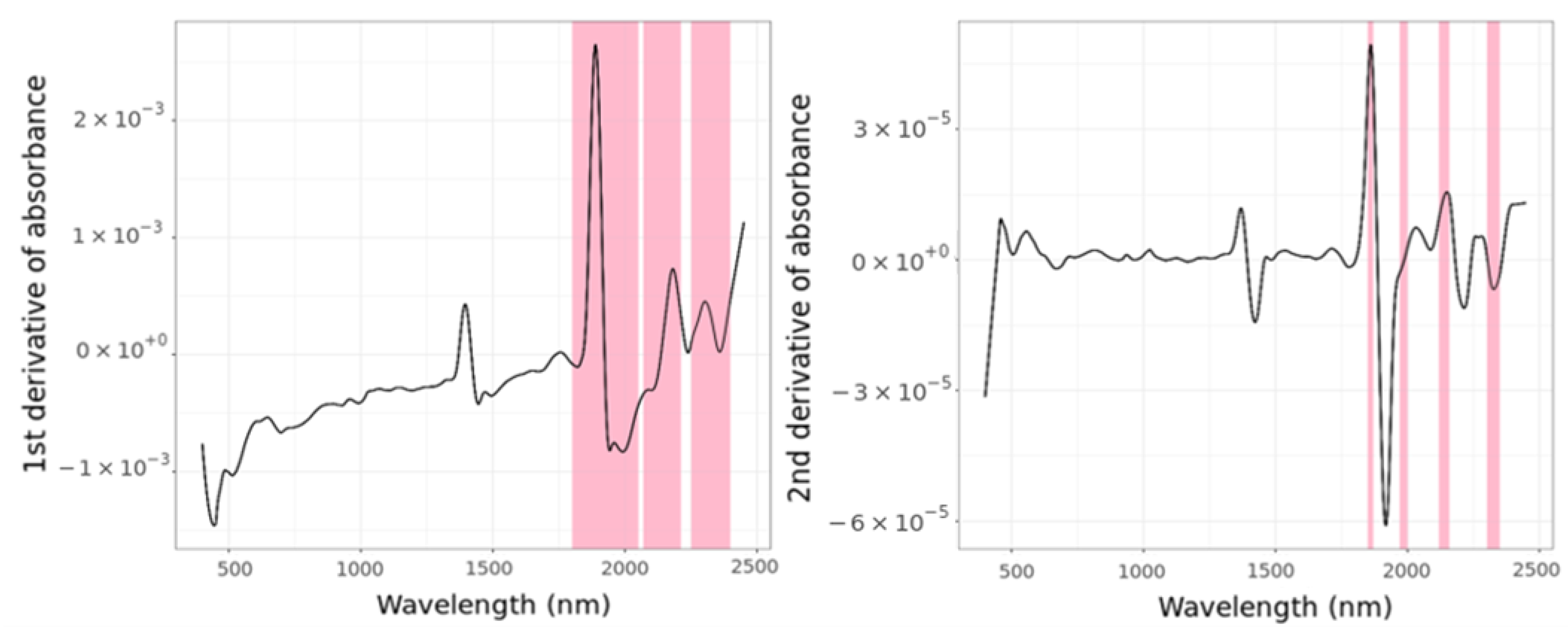
3.2. Spectral Data from the Three Different Sensors
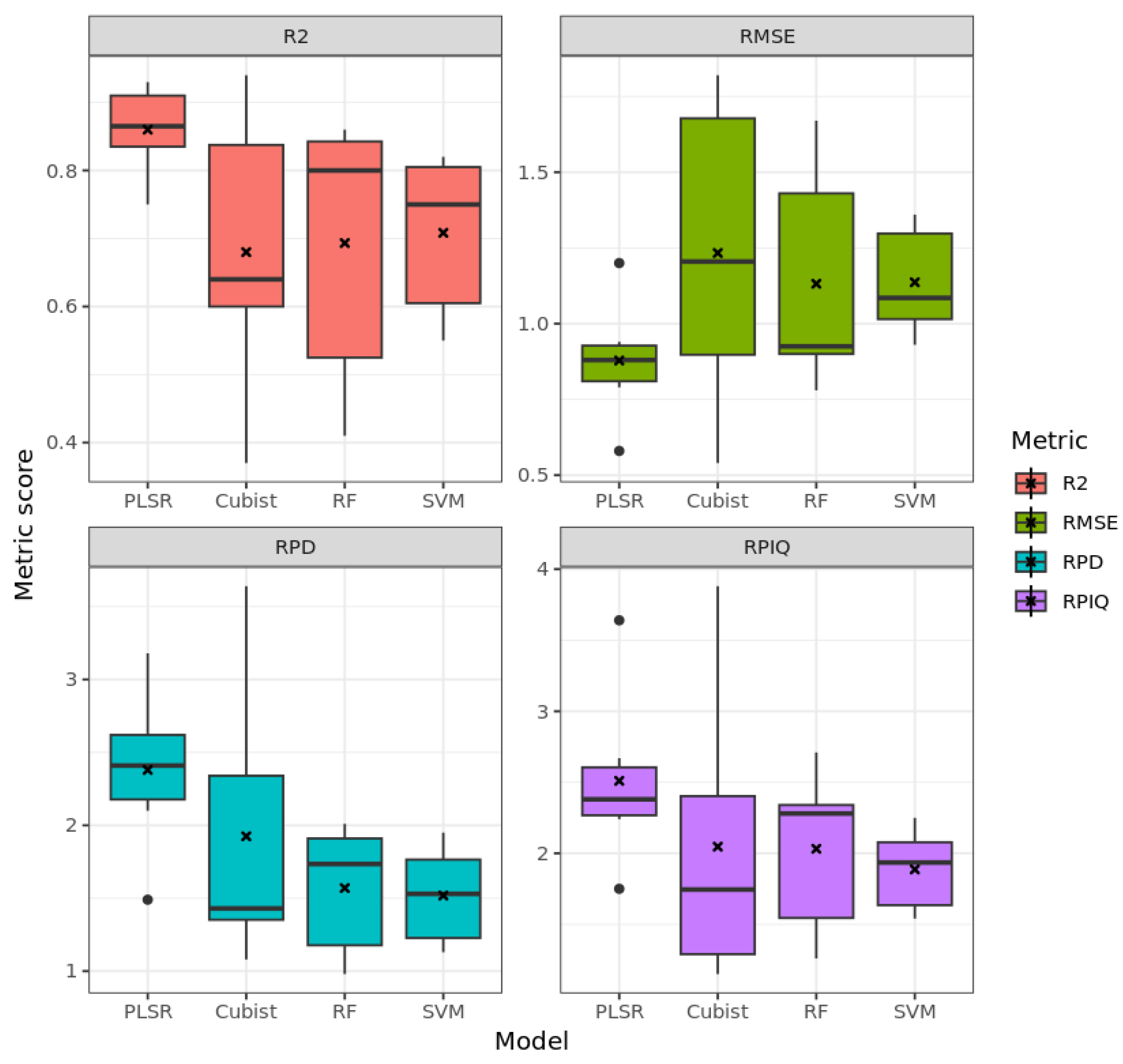
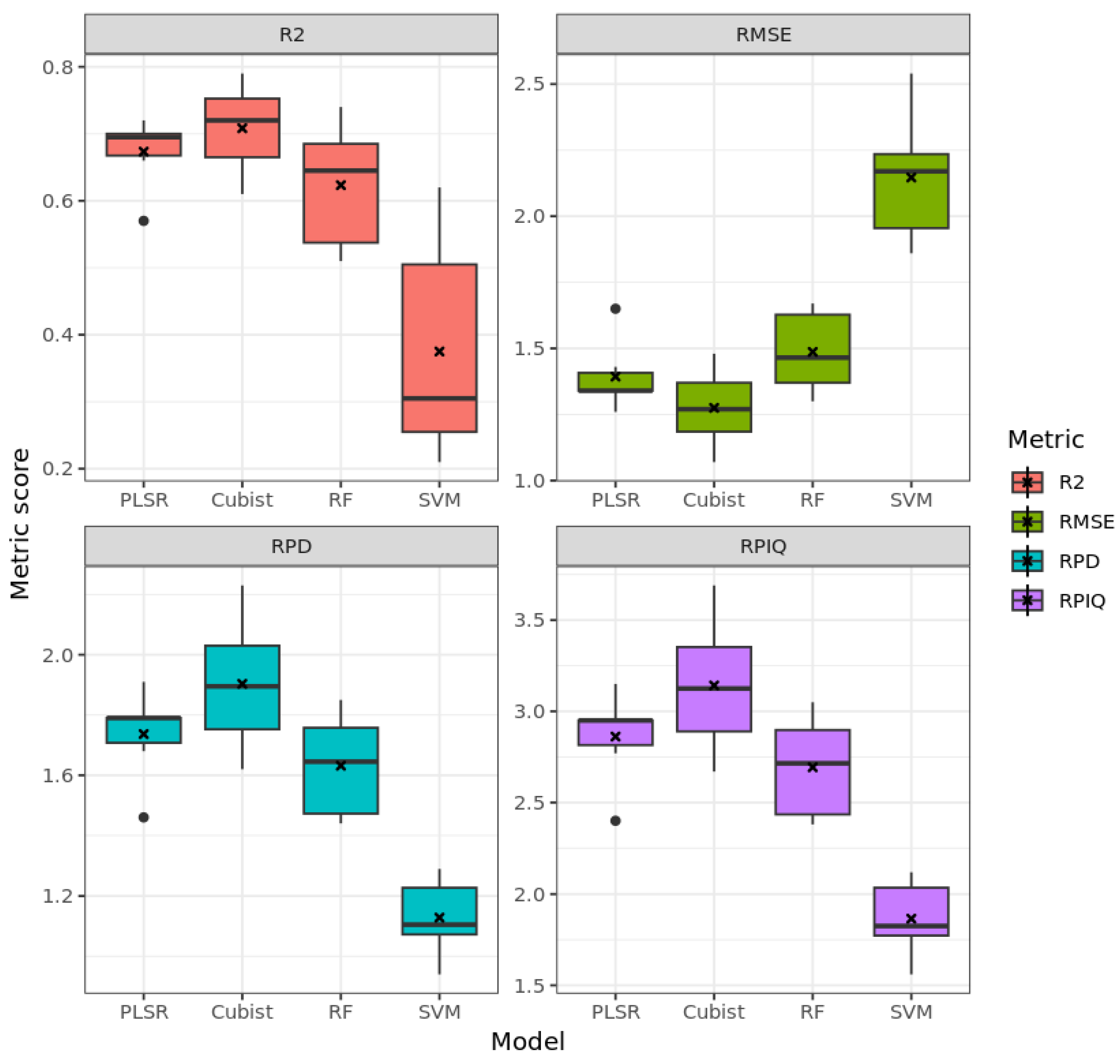
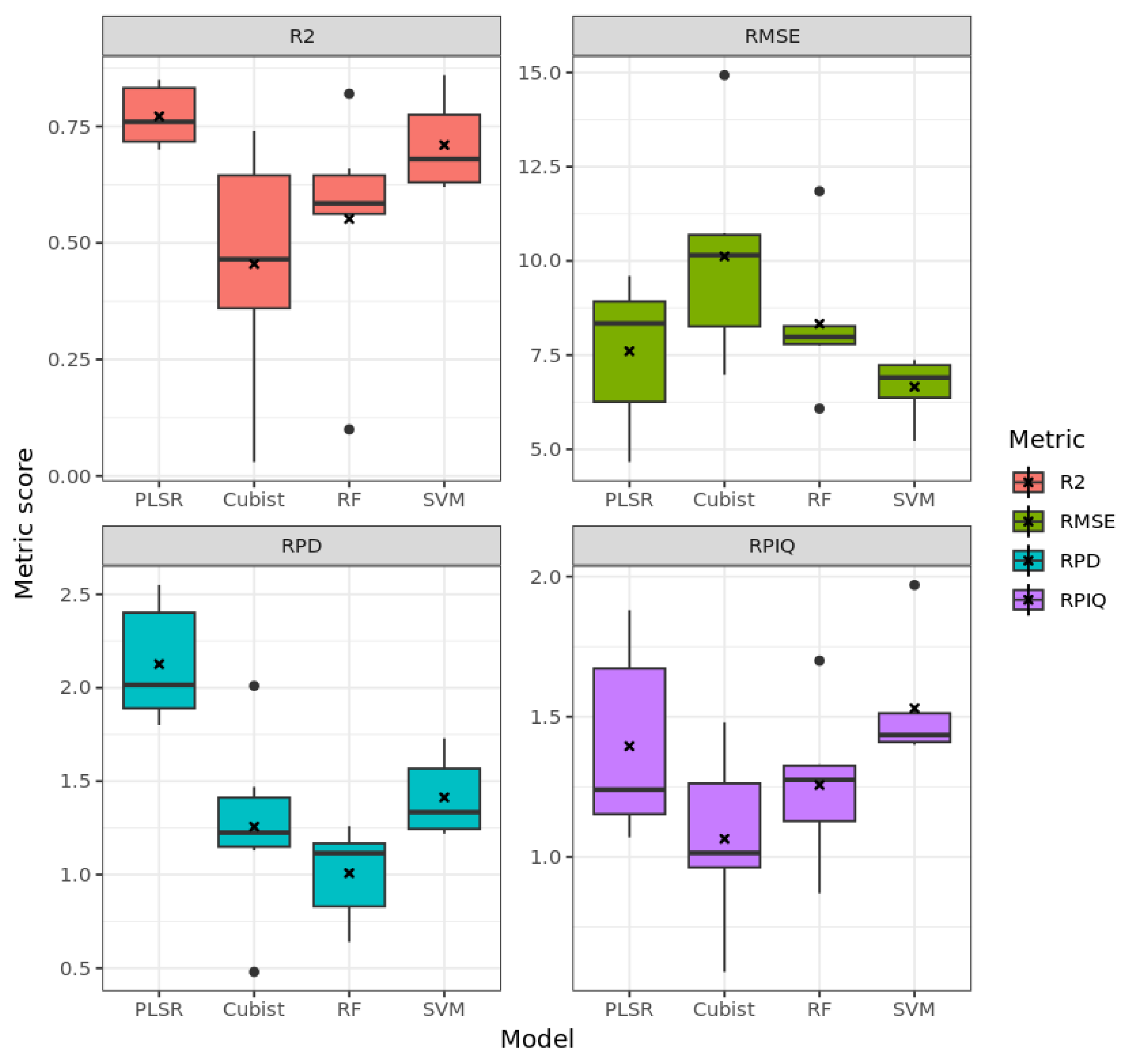
3.3. Model Performance for SOM
3.3.1. Laboratory Measurements
3.3.2. HySpex Data
3.3.3. PRISMA Data
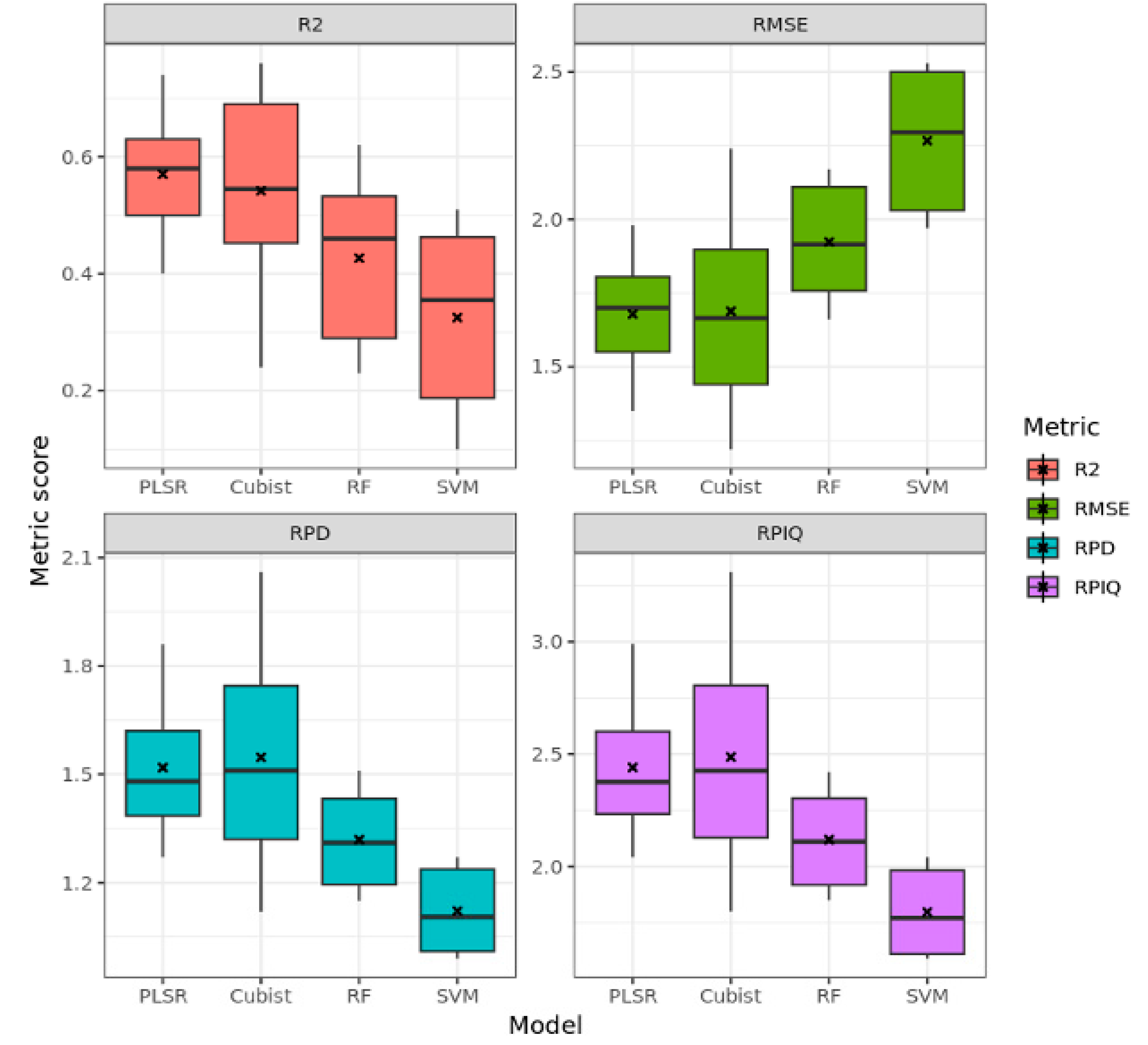
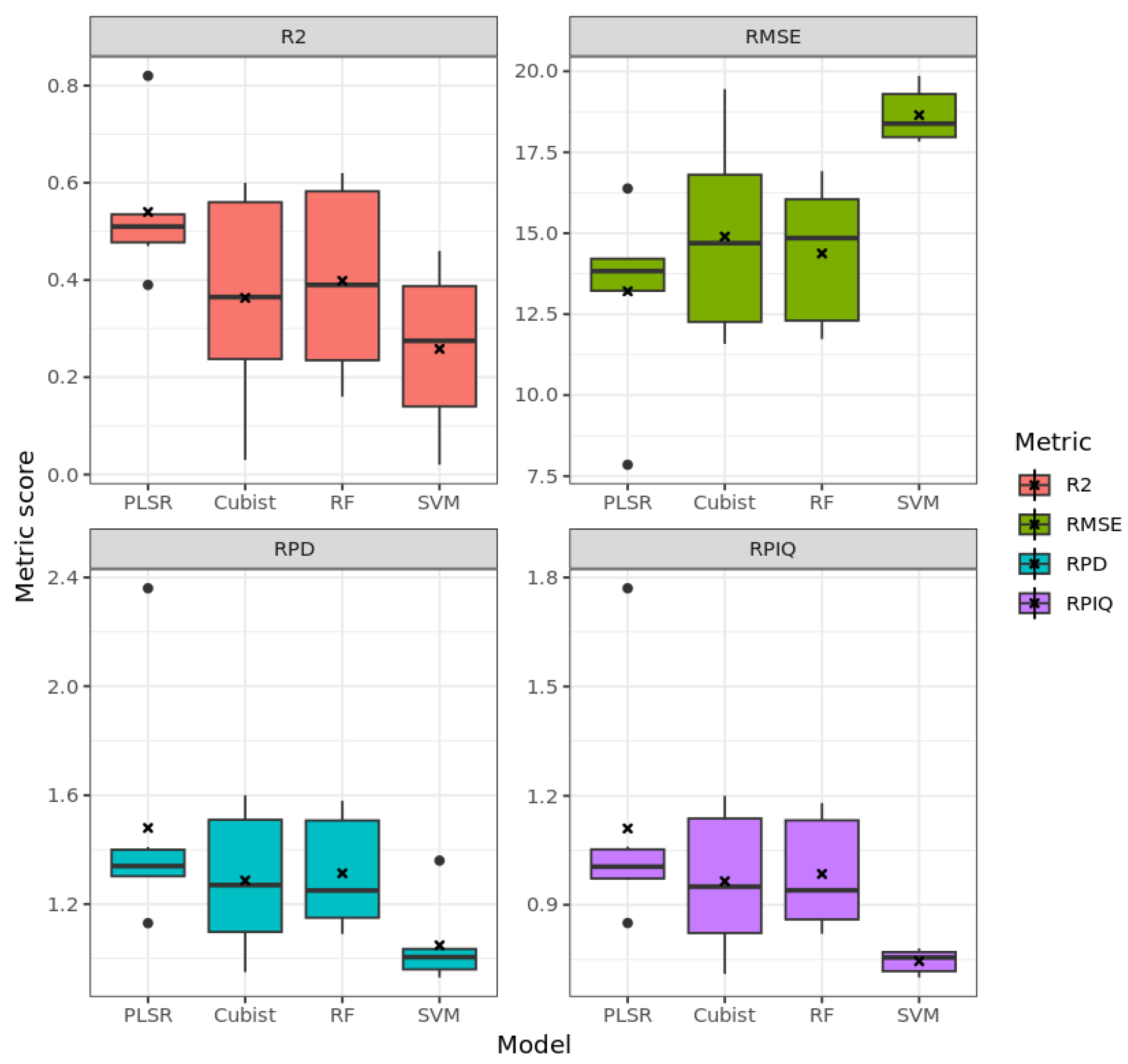
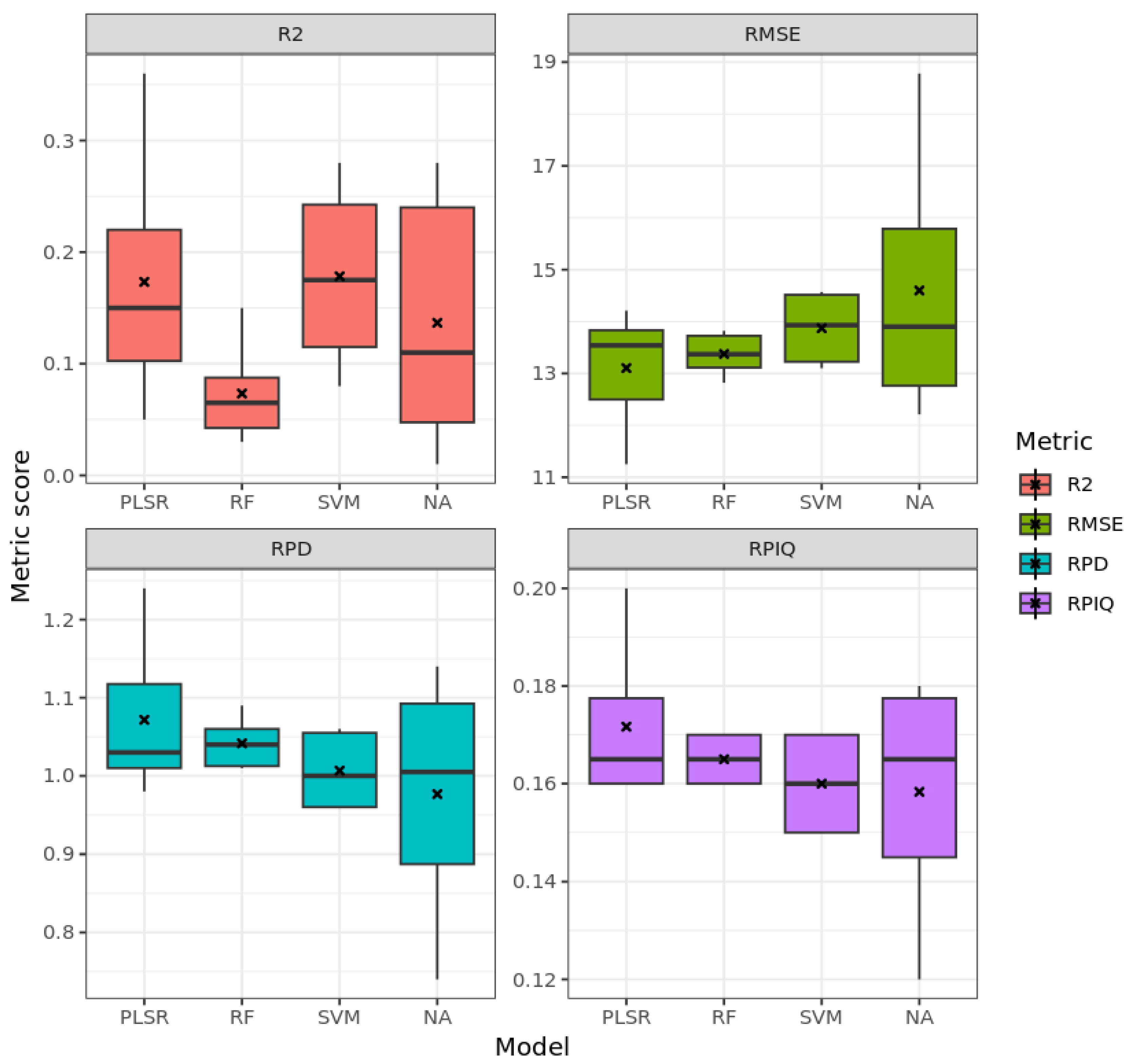
3.4. Model Performance for Carbonate Estimation (CaCO3)
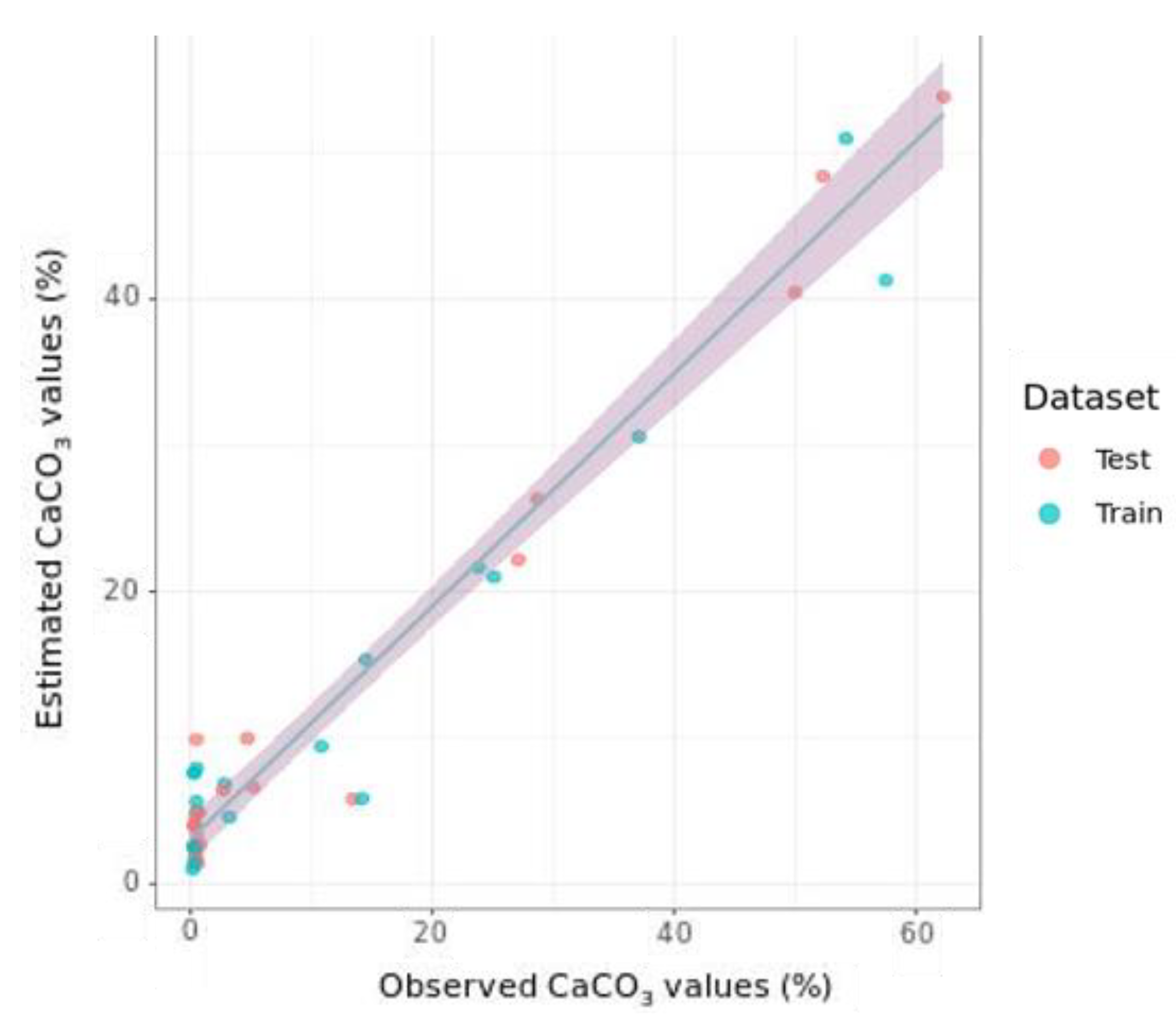
3.4.1. Laboratory Data
3.4.2. HySpex Data
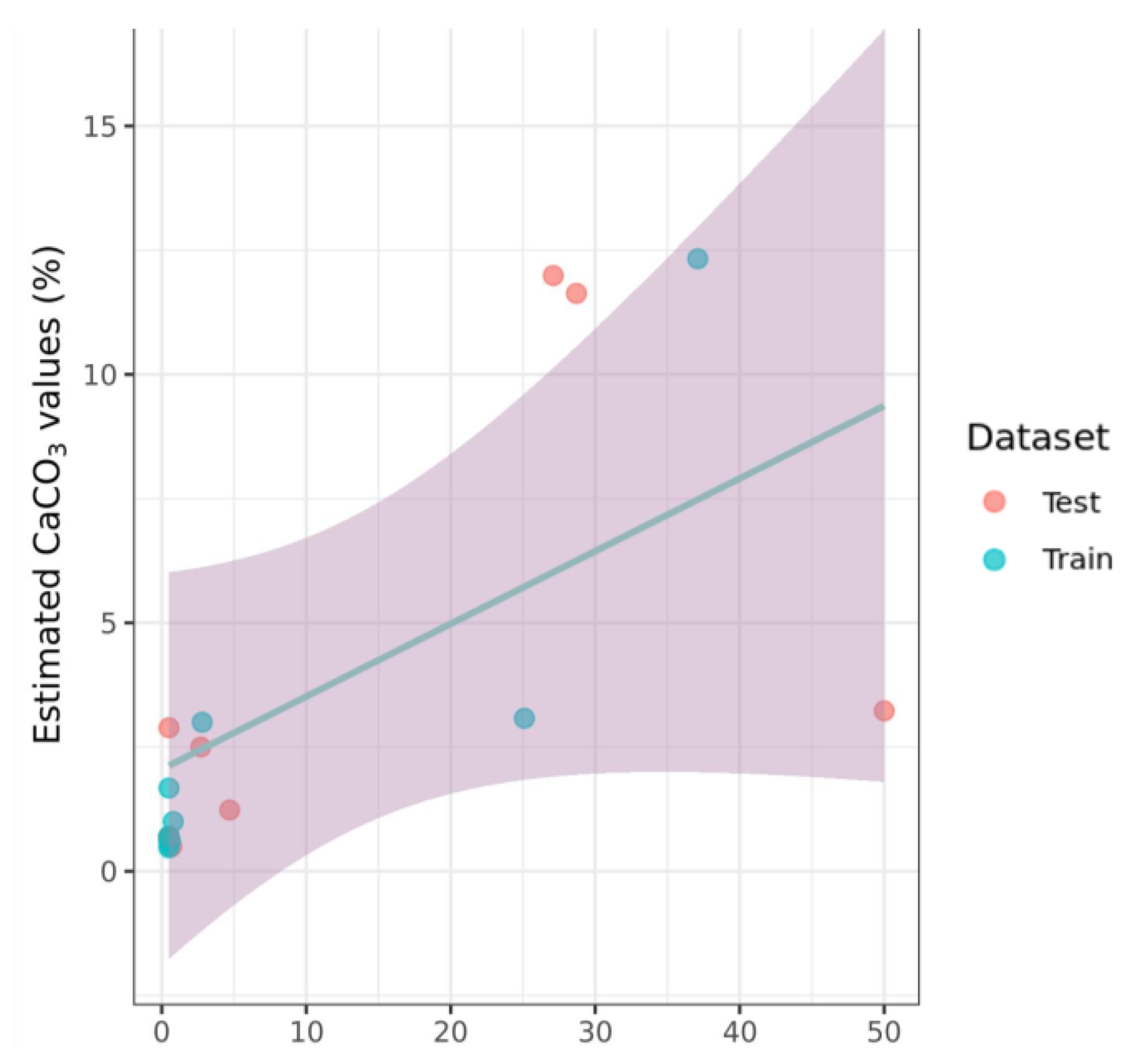
3.4.3. PRISMA Data
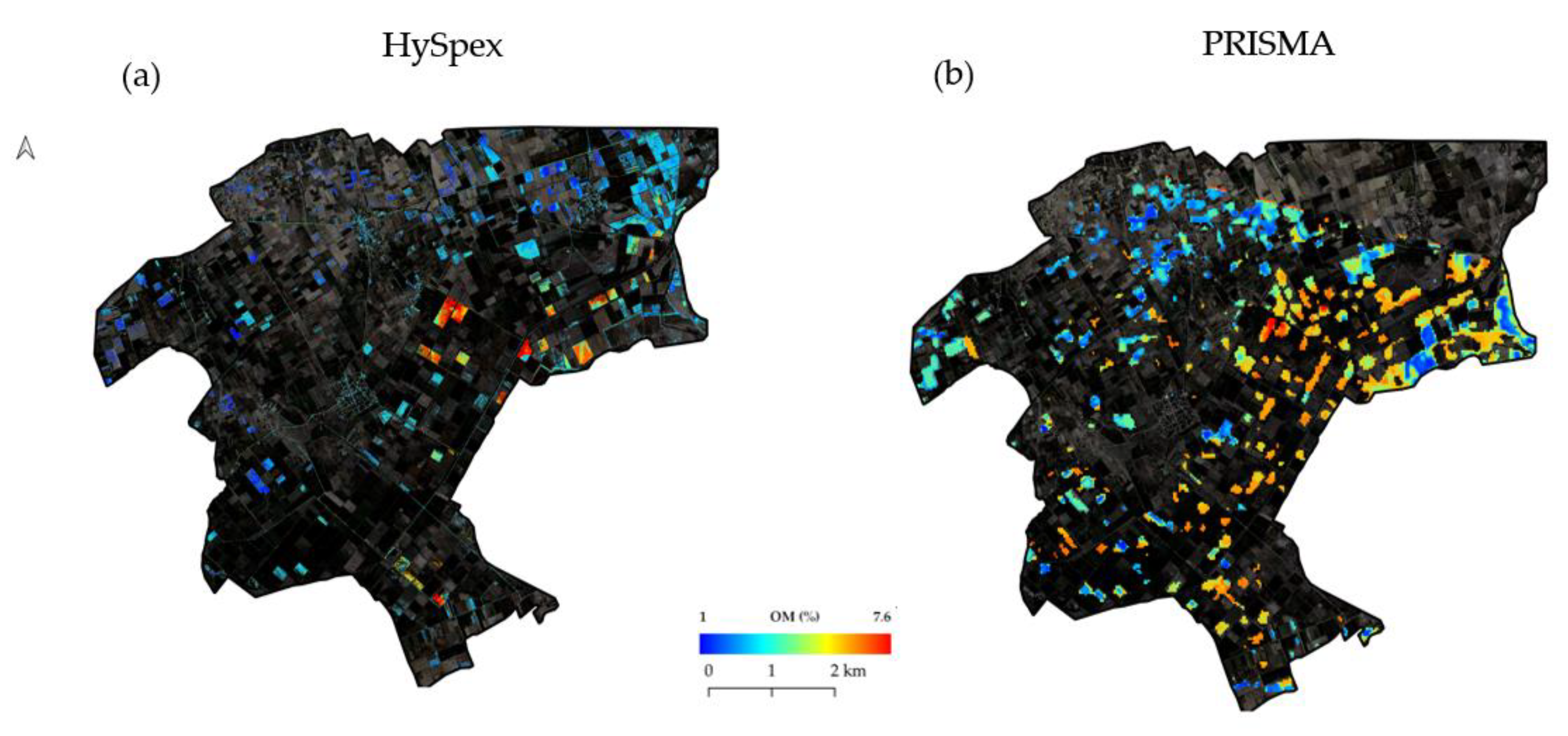
3.5. Spatial Distribution of Soil Properties
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Laboratory (PSR+ 3500) (SOM) | |||||
|---|---|---|---|---|---|
| Preprocessing | Model | RMSE | R2 | RPD | RPIQ |
| 1 | PLSR | 1.2 | 0.75 | 1.49 | 1.75 |
| 2 | PLSR | 0.89 | 0.83 | 2.1 | 2.35 |
| 3 | PLSR | 0.87 | 0.85 | 2.41 | 2.41 |
| 4 | PLSR | 0.94 | 0.88 | 2.41 | 2.24 |
| 5 | PLSR | 0.79 | 0.92 | 2.69 | 2.67 |
| 6 | PLSR | 0.58 | 0.93 | 3.18 | 3.64 |
| 1 | Cubist | 1.82 | 0.63 | 1.42 | 1.15 |
| 2 | Cubist | 1.82 | 0.37 | 1.08 | 1.16 |
| 3 | Cubist | 1.16 | 0.65 | 1.44 | 1.81 |
| 4 | Cubist | 0.54 | 0.94 | 3.64 | 3.88 |
| 5 | Cubist | 0.81 | 0.9 | 2.64 | 2.6 |
| 6 | Cubist | 1.25 | 0.59 | 1.33 | 1.68 |
| 1 | RF | 1.59 | 0.44 | 1.02 | 1.32 |
| 2 | RF | 1.67 | 0.41 | 0.98 | 1.26 |
| 3 | RF | 0.78 | 0.86 | 2.01 | 2.71 |
| 4 | RF | 0.9 | 0.85 | 1.94 | 2.34 |
| 5 | RF | 0.95 | 0.78 | 1.65 | 2.22 |
| 6 | RF | 0.9 | 0.82 | 1.82 | 2.34 |
| 1 | SVM | 1.36 | 0.56 | 1.13 | 1.54 |
| 2 | SVM | 1.36 | 0.55 | 1.18 | 1.55 |
| 3 | SVM | 1.06 | 0.76 | 1.79 | 1.98 |
| 4 | SVM | 1.11 | 0.74 | 1.37 | 1.89 |
| 5 | SVM | 0.93 | 0.82 | 1.95 | 2.25 |
| 6 | SVM | 1 | 0.82 | 1.69 | 2.11 |
| HySPEX (SOM) | |||||
|---|---|---|---|---|---|
| Preprocessing | Model | RMSE | R2 | RPD | RPIQ |
| 1 | PLSR | 1.43 | 0.66 | 1.68 | 2.77 |
| 2 | PLSR | 1.34 | 0.7 | 1.79 | 2.95 |
| 3 | PLSR | 1.34 | 0.7 | 1.79 | 2.95 |
| 4 | PLSR | 1.65 | 0.57 | 1.46 | 2.4 |
| 5 | PLSR | 1.26 | 0.72 | 1.91 | 3.15 |
| 6 | PLSR | 1.34 | 0.69 | 1.79 | 2.95 |
| 1 | Cubist | 1.48 | 0.61 | 1.62 | 2.67 |
| 2 | Cubist | 1.4 | 0.65 | 1.71 | 2.82 |
| 3 | Cubist | 1.07 | 0.79 | 2.23 | 3.69 |
| 4 | Cubist | 1.28 | 0.71 | 1.88 | 3.1 |
| 5 | Cubist | 1.16 | 0.76 | 2.07 | 3.42 |
| 6 | Cubist | 1.26 | 0.73 | 1.91 | 3.15 |
| 1 | RF | 1.67 | 0.51 | 1.44 | 2.38 |
| 2 | RF | 1.66 | 0.51 | 1.44 | 2.38 |
| 3 | RF | 1.36 | 0.69 | 1.77 | 2.92 |
| 4 | RF | 1.53 | 0.62 | 1.57 | 2.6 |
| 5 | RF | 1.4 | 0.67 | 1.72 | 2.83 |
| 6 | RF | 1.3 | 0.74 | 1.85 | 3.05 |
| 1 | SVM | 2.24 | 0.25 | 1.07 | 1.77 |
| 2 | SVM | 2.22 | 0.27 | 1.08 | 1.78 |
| 3 | SVM | 1.86 | 0.62 | 1.29 | 2.12 |
| 4 | SVM | 2.54 | 0.21 | 0.94 | 1.56 |
| 5 | SVM | 1.9 | 0.56 | 1.26 | 2.09 |
| 6 | SVM | 2.12 | 0.34 | 1.13 | 1.87 |
| PRISMA (OM) | |||||
|---|---|---|---|---|---|
| Preprocessing | Model | RMSE | R2 | RPD | RPIQ |
| 1 | PLSR | 1.82 | 0.49 | 1.37 | 2.21 |
| 2 | PLSR | 1.76 | 0.53 | 1.43 | 2.3 |
| 3 | PLSR | 1.35 | 0.74 | 1.86 | 2.99 |
| 4 | PLSR | 1.52 | 0.63 | 1.65 | 2.65 |
| 5 | PLSR | 1.64 | 0.63 | 1.53 | 2.45 |
| 6 | PLSR | 1.98 | 0.4 | 1.27 | 2.04 |
| 1 | Cubist | 2.24 | 0.24 | 1.12 | 1.8 |
| 2 | Cubist | 1.56 | 0.6 | 1.61 | 2.58 |
| 3 | Cubist | 1.77 | 0.49 | 1.41 | 2.27 |
| 4 | Cubist | 1.4 | 0.72 | 1.79 | 2.88 |
| 5 | Cubist | 1.94 | 0.44 | 1.29 | 2.08 |
| 6 | Cubist | 1.22 | 0.76 | 2.06 | 3.31 |
| 1 | RF | 2.17 | 0.24 | 1.16 | 1.86 |
| 2 | RF | 2.17 | 0.23 | 1.15 | 1.85 |
| 3 | RF | 1.71 | 0.55 | 1.47 | 2.36 |
| 4 | RF | 1.66 | 0.62 | 1.51 | 2.42 |
| 5 | RF | 1.93 | 0.44 | 1.3 | 2.09 |
| 6 | RF | 1.9 | 0.48 | 1.32 | 2.13 |
| 1 | SVM | 2.5 | 0.16 | 1.01 | 1.61 |
| 2 | SVM | 2.53 | 0.1 | 0.99 | 1.59 |
| 3 | SVM | 1.97 | 0.51 | 1.27 | 2.04 |
| 4 | SVM | 2.5 | 0.27 | 1.01 | 1.61 |
| 5 | SVM | 2.01 | 0.47 | 1.25 | 2.00 |
| 6 | SVM | 2.09 | 0.44 | 1.2 | 1.93 |
| Laboratory (PSR+ 3500) (CaCO3) | |||||
|---|---|---|---|---|---|
| Preprocessing | Model | RMSE | R2 | RPD | RPIQ |
| 1 | PLSR | 8.87 | 0.7 | 1.85 | 1.16 |
| 2 | PLSR | 5.74 | 0.85 | 2.55 | 1.79 |
| 3 | PLSR | 7.81 | 0.74 | 2.01 | 1.32 |
| 4 | PLSR | 9.6 | 0.71 | 1.8 | 1.07 |
| 5 | PLSR | 8.94 | 0.78 | 2.02 | 1.15 |
| 6 | PLSR | 4.66 | 0.85 | 2.53 | 1.88 |
| 1 | Cubist | 6.98 | 0.69 | 1.24 | 1.48 |
| 2 | Cubist | 7.77 | 0.74 | 2.01 | 1.33 |
| 3 | Cubist | 10.57 | 0.51 | 1.47 | 0.97 |
| 4 | Cubist | 10.73 | 0.34 | 1.13 | 0.96 |
| 5 | Cubist | 9.73 | 0.42 | 1.21 | 1.058 |
| 6 | Cubist | 14.93 | 0.03 | 0.48 | 0.59 |
| 1 | RF | 7.88 | 0.56 | 1.1 | 1.31 |
| 2 | RF | 7.76 | 0.57 | 1.13 | 1.33 |
| 3 | RF | 6.08 | 0.82 | 1.26 | 1.7 |
| 4 | RF | 8.33 | 0.66 | 1.18 | 1.24 |
| 5 | RF | 11.85 | 0.1 | 0.64 | 0.87 |
| 6 | RF | 8.08 | 0.6 | 0.74 | 1.09 |
| 1 | SVM | 7.29 | 0.62 | 1.26 | 1.41 |
| 2 | SVM | 6.75 | 0.7 | 1.24 | 1.53 |
| 3 | SVM | 7.06 | 0.66 | 1.62 | 1.46 |
| 4 | SVM | 5.22 | 0.86 | 1.73 | 1.97 |
| 5 | SVM | 7.37 | 0.62 | 1.22 | 1.4 |
| 6 | SVM | 6.24 | 0.8 | 1.41 | 1.41 |
| HySPEX (CaCO3) | |||||
|---|---|---|---|---|---|
| Preprocessing | Model | RMSE | R2 | RPD | RPIQ |
| 1 | PLSR | 7.85 | 0.82 | 2.36 | 1.77 |
| 2 | PLSR | 13.12 | 0.54 | 1.41 | 1.06 |
| 3 | PLSR | 13.53 | 0.5 | 1.37 | 1.03 |
| 4 | PLSR | 16.38 | 0.39 | 1.13 | 0.85 |
| 5 | PLSR | 14.24 | 0.47 | 1.3 | 0.97 |
| 6 | PLSR | 14.13 | 0.52 | 1.31 | 0.98 |
| 1 | Cubist | 11.91 | 0.59 | 1.55 | 1.17 |
| 2 | Cubist | 11.58 | 0.6 | 1.6 | 1.2 |
| 3 | Cubist | 13.32 | 0.47 | 1.39 | 1.04 |
| 4 | Cubist | 17.05 | 0.23 | 1.08 | 0.81 |
| 5 | Cubist | 16.07 | 0.26 | 1.15 | 0.86 |
| 6 | Cubist | 19.45 | 0.03 | 0.95 | 0.71 |
| 1 | RF | 11.85 | 0.6 | 1.56 | 1.17 |
| 2 | RF | 11.73 | 0.62 | 1.58 | 1.18 |
| 3 | RF | 13.66 | 0.53 | 1.35 | 1.02 |
| 4 | RF | 16.92 | 0.16 | 1.09 | 0.82 |
| 5 | RF | 16.04 | 0.23 | 1.15 | 0.86 |
| 6 | RF | 16.05 | 0.25 | 1.15 | 0.86 |
| 1 | SVM | 17.83 | 0.39 | 1.04 | 0.78 |
| 2 | SVM | 17.93 | 0.38 | 1.36 | 0.77 |
| 3 | SVM | 19.5 | 0.46 | 0.95 | 0.71 |
| 4 | SVM | 19.86 | 0.17 | 0.93 | 0.7 |
| 5 | SVM | 18.08 | 0.13 | 1.02 | 0.77 |
| 6 | SVM | 18.69 | 0.02 | 0.99 | 0.74 |
| PRISMA (CaCO3) | |||||
|---|---|---|---|---|---|
| Preprocessing | Model | RMSE | R2 | RPD | RPIQ |
| 1 | PLSR | 11.25 | 0.36 | 1.24 | 0.2 |
| 2 | PLSR | 12.23 | 0.24 | 1.14 | 0.18 |
| 3 | PLSR | 13.3 | 0.16 | 1.05 | 0.17 |
| 4 | PLSR | 14.21 | 0.05 | 0.98 | 0.16 |
| 5 | PLSR | 13.78 | 0.14 | 1.01 | 0.16 |
| 6 | PLSR | 13.85 | 0.09 | 1.01 | 0.16 |
| 1 | Cubist | 12.54 | 0.27 | 1.11 | 0.18 |
| 2 | Cubist | 12.21 | 0.28 | 1.14 | 0.18 |
| 3 | Cubist | 16.26 | 0.04 | 0.86 | 0.14 |
| 4 | Cubist | 18.78 | 0.01 | 0.74 | 0.12 |
| 5 | Cubist | 13.43 | 0.15 | 1.04 | 0.17 |
| 6 | Cubist | 14.37 | 0.07 | 0.97 | 0.16 |
| 1 | RF | 13.82 | 0.04 | 1.01 | 0.16 |
| 2 | RF | 13.77 | 0.05 | 1.01 | 0.16 |
| 3 | RF | 12.82 | 0.15 | 1.09 | 0.17 |
| 4 | RF | 13.59 | 0.03 | 1.02 | 0.16 |
| 5 | RF | 13.1 | 0.09 | 1.06 | 0.17 |
| 6 | RF | 13.15 | 0.08 | 1.06 | 0.17 |
| 1 | SVM | 14.5 | 0.13 | 0.96 | 0.15 |
| 2 | SVM | 14.57 | 0.08 | 0.96 | 0.15 |
| 3 | SVM | 13.18 | 0.28 | 1.06 | 0.17 |
| 4 | SVM | 14.52 | 0.11 | 0.96 | 0.15 |
| 5 | SVM | 13.1 | 0.25 | 1.06 | 0.17 |
| 6 | SVM | 13.36 | 0.22 | 1.04 | 0.17 |
References
- FAO. Soil Organic Carbon the Hidden Potential; Food and Agriculture Organization: Rome, Italy, 2017; ISBN 9789251096819. [Google Scholar]
- Keesstra, S.D.; Bouma, J.; Wallinga, J.; Tittonell, P.; Smith, P.; Cerdà, A.; Montanarella, L.; Quinton, J.N.; Pachepsky, Y.; Van Der Putten, W.H.; et al. The significance of soils and soil science towards realization of the United Nations sustainable development goals. Soil 2016, 2, 111–128. [Google Scholar] [CrossRef] [Green Version]
- Osland, M.J.; Gabler, C.A.; Grace, J.B.; Day, R.H.; McCoy, M.L.; McLeod, J.L.; From, A.S.; Enwright, N.M.; Feher, L.C.; Stagg, C.L.; et al. Climate and plant controls on soil organic matter in coastal wetlands. Glob. Chang. Biol. 2018, 24, 5361–5379. [Google Scholar] [CrossRef]
- Scharlemann, J.P.; Tanner, E.V.; Hiederer, R.; Kapos, V. Global soil carbon: Understanding and managing the largest terrestrial carbon pool. Carbon Manag. 2014, 5, 81–91. [Google Scholar] [CrossRef]
- Wang, C.; Li, W.; Yang, Z.; Chen, Y.; Shao, W.; Ji, J. An invisible soil acidification: Critical role of soil carbonate and its impact on heavy metal bioavailability. Sci. Rep. 2015, 5, 12735. [Google Scholar] [CrossRef] [Green Version]
- Martin, J.B. Carbonate minerals in the global carbon cycle. Chem. Geol. 2017, 449, 58–72. [Google Scholar] [CrossRef]
- Goovaerts, P. Estimation or simulation of soil properties? An optimization problem with conflicting criteria. Geoderma 2000, 97, 165–186. [Google Scholar] [CrossRef]
- Ladoni, M.; Bahrami, H.A.; Alavipanah, S.K.; Norouzi, A.A. Estimating soil organic carbon from soil reflectance: A review. Precis. Agric. 2010, 11, 82–99. [Google Scholar] [CrossRef]
- Chabrillat, S.; Ben-Dor, E.; Rossel, R.A.V.; Demattê, J.A.M. Quantitative soil spectroscopy. Appl. Environ. Soil Sci. 2013, 2013, 1–3. [Google Scholar] [CrossRef] [Green Version]
- Stenberg, B.; Viscarra Rossel, R.A.; Mouazen, A.M.; Wetterlind, J. Visible and near infrared spectroscopy in soil science. Adv. Agron. 2010, 107, 163–215. [Google Scholar]
- Nocita, M.; Stevens, A.; van Wesemael, B.; Aitkenhead, M.; Bachmann, M.; Barthès, B.; Ben Dor, E.; Brown, D.J.; Clairotte, M.; Csorba, A.; et al. Soil Spectroscopy: An Alternative to Wet Chemistry for Soil Monitoring. Adv. Agron. 2015, 132, 139–159. [Google Scholar]
- Terra, F.S.; Demattê, J.A.M.; Viscarra Rossel, R.A. Spectral libraries for quantitative analyses of tropical Brazilian soils: Comparing vis-NIR and mid-IR reflectance data. Geoderma 2015, 255, 81–93. [Google Scholar] [CrossRef]
- Chabrillat, S.; Ben-Dor, E.; Cierniewski, J.; Gomez, C.; Schmid, T.; van Wesemael, B. Imaging Spectroscopy for Soil Mapping and Monitoring. Surv. Geophys. 2019, 40, 361–399. [Google Scholar] [CrossRef] [Green Version]
- Stevens, A.; Nocita, M.; Tóth, G.; Montanarella, L.; van Wesemael, B. Prediction of Soil Organic Carbon at the European Scale by Visible and Near InfraRed Reflectance Spectroscopy. PLoS ONE 2013, 8, e66409. [Google Scholar] [CrossRef]
- Rossel, R.A.V.; Behrens, T. Using data mining to model and interpret soil diffuse reflectance spectra. Geoderma 2010, 158, 46–54. [Google Scholar] [CrossRef]
- Castaldi, F.; Hueni, A.; Chabrillat, S.; Ward, K.; Buttafuoco, G.; Bomans, B.; Vreys, K.; Brell, M.; van Wesemael, B. Evaluating the capability of the Sentinel 2 data for soil organic carbon prediction in croplands. ISPRS J. Photogramm. Remote Sens. 2019, 147, 267–282. [Google Scholar] [CrossRef]
- Castaldi, F.; Chabrillat, S.; van Wesemael, B. Sampling Strategies for Soil Property Mapping Using Multispectral Sentinel-2 and Hyperspectral EnMAP Satellite Data. Remote Sens. 2019, 11, 309. [Google Scholar] [CrossRef] [Green Version]
- Angelopoulou, T.; Tziolas, N.; Balafoutis, A.; Zalidis, G.; Bochtis, D. Remote sensing techniques for soil organic carbon estimation: A review. Remote Sens. 2019, 11, 676. [Google Scholar] [CrossRef] [Green Version]
- Angelopoulou, T.; Balafoutis, A.; Zalidis, G.; Bochtis, D. From laboratory to proximal sensing spectroscopy for soil organic carbon estimation-A review. Sustainability 2020, 12, 443. [Google Scholar] [CrossRef] [Green Version]
- Ben-Dor, E.; Patkin, K.; Banin, A.; Karnieli, A. Mapping of several soil properties using DAIS-7915 hyperspectral scanner data—A case study over soils in Israel. Int. J. Remote Sens. 2002, 23, 1043–1062. [Google Scholar] [CrossRef]
- Vohland, M.; Ludwig, M.; Thiele-Bruhn, S.; Ludwig, B. Quantification of Soil Properties with Hyperspectral Data: Selecting Spectral Variables with Different Methods to Improve Accuracies and Analyze Prediction Mechanisms. Remote Sens. 2017, 9, 1103. [Google Scholar] [CrossRef] [Green Version]
- Steinberg, A.; Chabrillat, S.; Stevens, A.; Segl, K.; Foerster, S. Prediction of common surface soil properties based on Vis-NIR airborne and simulated EnMAP imaging spectroscopy data: Prediction accuracy and influence of spatial resolution. Remote Sens. 2016, 8, 613. [Google Scholar] [CrossRef] [Green Version]
- Castaldi, F.; Palombo, A.; Santini, F.; Pascucci, S.; Pignatti, S.; Casa, R. Evaluation of the potential of the current and forthcoming multispectral and hyperspectral imagers to estimate soil texture and organic carbon. Remote Sens. Environ. 2016, 179, 54–65. [Google Scholar] [CrossRef]
- Ward, K.J.; Chabrillat, S.; Brell, M.; Castaldi, F.; Spengler, D.; Foerster, S. Mapping Soil Organic Carbon for Airborne and Simulated EnMAP Imagery Using the LUCAS Soil Database and a Local PLSR. Remote Sens. 2020, 12, 3451. [Google Scholar] [CrossRef]
- Van Der Meer, F. Spectral reflectance of carbonate mineral mixtures and bidirectional reflectance theory: Quantitative analysis techniques for application in remote sensing. Remote Sens. Rev. 1995, 13, 67–94. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Banin, A. Near-Infrared Reflectance Analysis of Carbonate Concentration in Soils. Appl. Spectrosc. 1990, 44, 1064–1069. [Google Scholar] [CrossRef]
- Summers, D.; Lewis, M.; Ostendorf, B.; Chittleborough, D. Visible near-infrared reflectance spectroscopy as a predictive indicator of soil properties. Ecol. Indic. 2011, 11, 123–131. [Google Scholar] [CrossRef]
- Ostovari, Y.; Ghorbani-Dashtaki, S.; Bahrami, H.-A.; Abbasi, M.; Dematte, J.A.M.; Arthur, E.; Panagos, P. Towards prediction of soil erodibility, SOM and CaCO3 using laboratory Vis-NIR spectra: A case study in a semi-arid region of Iran. Geoderma 2018, 314, 102–112. [Google Scholar] [CrossRef]
- Khayamim, F.; Wetterlind, J.; Khademi, H.; Robertson, A.H.J.; Cano, A.F.; Stenberg, B. Using visible and near infrared spectroscopy to estimate carbonates and gypsum in soils in arid and subhumid regions of Isfahan, Iran. J. Near Infrared Spectrosc. 2015, 23, 155–165. [Google Scholar] [CrossRef] [Green Version]
- Gomez, C.; Coulouma, G. Importance of the spatial extent for using soil properties estimated by laboratory VNIR/SWIR spectroscopy: Examples of the clay and calcium carbonate content. Geoderma 2018, 330, 244–253. [Google Scholar] [CrossRef]
- Lagacherie, P.; Baret, F.; Feret, J.B.; Madeira Netto, J.; Robbez-Masson, J.M. Estimation of soil clay and calcium carbonate using laboratory, field and airborne hyperspectral measurements. Remote Sens. Environ. 2008, 112, 825–835. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Boruvka, L.; Saberioon, M.M.; Kozák, J.; Vašát, R.; Nemecek, K. Comparing different data preprocessing methods for monitoring soil heavy metals based on soil spectral features. Soil Water Res. 2015, 10, 218–227. [Google Scholar] [CrossRef] [Green Version]
- Viscarra Rossel, R.A.; Behrens, T.; Ben-Dor, E.; Brown, D.J.; Demattê, J.A.M.; Shepherd, K.D.; Shi, Z.; Stenberg, B.; Stevens, A.; Adamchuk, V.; et al. A global spectral library to characterize the world’s soil. Earth-Sci. Rev. 2016, 155, 198–230. [Google Scholar] [CrossRef] [Green Version]
- Samarinas, N.; Tziolas, N.; Zalidis, G. Improved Estimations of Nitrate and Sediment Concentrations Based on SWAT Simulations and Annual Updated Land Cover Products from a Deep Learning Classification Algorithm. ISPRS Int. J. Geo-Inf. 2020, 9, 576. [Google Scholar] [CrossRef]
- Tziolas, N.; Tsakiridis, N.; Ben-Dor, E.; Theocharis, J.; Zalidis, G. Employing a Multi-Input Deep Convolutional Neural Network to Derive Soil Clay Content from a Synergy of Multi-Temporal Optical and Radar Imagery Data. Remote Sens. 2020, 12, 1389. [Google Scholar] [CrossRef]
- Allison, L.E.; Black, C. Methods of soil analysis. Part 2. Chemical and microbiological properties. Agron. Monogr. 1965, 9, 1367–1378. [Google Scholar]
- Jackson, M.L. Soil chemical analysis-Advanced course, published by the author. Madison Wis. 1956, 991, 96. [Google Scholar]
- Bouyoucos, G.J. Hydrometer method improved for making particle size analyses of soils 1. Agron. J. 1962, 54, 464–465. [Google Scholar] [CrossRef]
- Ben Dor, E.; Ong, C.; Lau, I.C. Reflectance measurements of soils in the laboratory: Standards and protocols. Geoderma 2015, 245, 112–124. [Google Scholar] [CrossRef]
- Brell, M.; Rogass, C.; Segl, K.; Bookhagen, B.; Guanter, L. Improving Sensor Fusion: A Parametric Method for the Geometric Coalignment of Airborne Hyperspectral and Lidar Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3460–3474. [Google Scholar] [CrossRef] [Green Version]
- Richter, R.; Schläpfer, D. Geo-atmospheric processing of airborne imaging spectrometry data. Part 2: Atmospheric/topographic correction. Int. J. Remote Sens. 2002, 23, 2631–2649. [Google Scholar] [CrossRef]
- Coppo, P.; Brandani, F.; Faraci, M.; Sarti, F.; Dami, M.; Chiarantini, L.; Ponticelli, B.; Giunti, L.; Fossati, E.; Cosi, M. Leonardo spaceborne infrared payloads for Earth observation: SLSTRs for Copernicus Sentinel 3 and PRISMA hyperspectral camera for PRISMA satellite. Appl. Opt. 2020, 59, 6888–6901. [Google Scholar] [CrossRef]
- Cogliati, S.; Sarti, F.; Chiarantini, L.; Cosi, M.; Lorusso, R.; Lopinto, E.; Miglietta, F.; Genesio, L.; Guanter, L.; Damm, A.; et al. The PRISMA imaging spectroscopy mission: Overview and first performance analysis. Remote Sens. Environ. 2021, 262, 112499. [Google Scholar] [CrossRef]
- Pignatti, S.; Amodeo, A.; Carfora, M.F.; Casa, R.; Mona, L.; Palombo, A.; Pascucci, S.; Rosoldi, M.; Santini, F.; Laneve, G. PRISMA L1 and L2 Performances within the PRISCAV Project: The Pignola Test Site in Southern Italy. Remote Sens. 2022, 14, 1985. [Google Scholar] [CrossRef]
- Rogass, C.; Guanter, L.; Mielke, C.; Scheffler, D.; Boesche, N.K.; Lubitz, C.; Brell, M.; Spengler, D.; Segl, K. An automated processing chain for the retrieval of georeferenced reflectance data from hyperspectral EO-1 HYPERION acquisitions. In Proceedings of the 34th EARSeL Symposium 2014, Warsaw, Poland, 16–20 June 2014; Volume 16, pp. 3.1–3.7. [Google Scholar]
- Milewski, R.; Chabrillat, S.; Behling, R. Analyses of Recent Sediment Surface Dynamic of a Namibian Kalahari Salt Pan Based on Multitemporal Landsat and Hyperspectral Hyperion Data. Remote Sens. 2017, 9, 170. [Google Scholar] [CrossRef] [Green Version]
- Guanter, L.; Richter, R.; Kaufmann, H. On the application of the MODTRAN4 atmospheric radiative transfer code to optical remote sensing. Int. J. Remote Sens. 2009, 30, 1407–1424. [Google Scholar] [CrossRef]
- Van der Linden, S.; Rabe, A.; Held, M.; Jakimow, B.; Leitão, P.J.; Okujeni, A.; Schwieder, M.; Suess, S.; Hostert, P. The EnMAP-Box—A Toolbox and Application Programming Interface for EnMAP Data Processing. Remote Sens. 2015, 7, 11249–11266. [Google Scholar] [CrossRef] [Green Version]
- Guanter, L.; Segl, K.; Sang, B.; Alonso, L.; Kaufmann, H.; Moreno, J. Scene-based spectral calibration assessment of high spectral resolution imaging spectrometers. Opt. Express 2009, 17, 11594–11606. [Google Scholar] [CrossRef] [Green Version]
- Rinnan, Å.; van den Berg, F.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. TrAC Trends Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Minasny, B.; McBratney, A.B. A conditioned Latin hypercube method for sampling in the presence of ancillary information. Comput. Geosci. 2006, 32, 1378–1388. [Google Scholar] [CrossRef]
- Soriano-Disla, J.M.; Janik, L.J.; Viscarra Rossel, R.A.; Macdonald, L.M.; McLaughlin, M.J. The Performance of Visible, Near-, and Mid-Infrared Reflectance Spectroscopy for Prediction of Soil Physical, Chemical, and Biological Properties. Appl. Spectrosc. Rev. 2014, 49, 139–186. [Google Scholar] [CrossRef]
- Williams, P. Near-Infrared Technology: Getting the Best out of Light: A Short Course in the Practical Implementation of Near-Infrared Spectroscopy for the User; PDK Projects, Incorporated: Nanaimo, BC, Canada, 2004; ISBN 0975216708. [Google Scholar]
- Saeys, W.; Mouazen, A.M.; Ramon, H. AE—Automation and Emerging Technologies Potential for Onsite and Online Analysis of Pig Manure using Visible and Near Infrared Reflectance Spectroscopy. Biosyst. Eng. 2005, 91, 393–402. [Google Scholar] [CrossRef]
- Kuhn, M. Building predictive models in R using the caret package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Chabrillat, S.; Guillaso, S.; Rabe, A.; Foerster, S.; Guanter, L. From HYSOMA to ENSOMAP—A New Open Source Tool for Quantitative Soil Properties Mapping Based on Hyperspectral Imagery from Airborne to Spaceborne Applications; EGU: Munich, Germany, 2016; Volume 18. [Google Scholar]
- Pietrzykowski, M.; Chodak, M. Near infrared spectroscopy—A tool for chemical properties and organic matter assessment of afforested mine soils. Ecol. Eng. 2014, 62, 115–122. [Google Scholar] [CrossRef]
- Guerrero, C.; Wetterlind, J.; Stenberg, B.; Mouazen, A.M.; Gabarrón-Galeote, M.A.; Ruiz-Sinoga, J.D.; Zornoza, R.; Viscarra Rossel, R.A. Do we really need large spectral libraries for local scale SOC assessment with NIR spectroscopy? Soil Tillage Res. 2016, 155, 501–509. [Google Scholar] [CrossRef]
- Jiang, Q.; Li, Q.; Wang, X.; Wu, Y.; Yang, X.; Liu, F. Estimation of soil organic carbon and total nitrogen in different soil layers using VNIR spectroscopy: Effects of spiking on model applicability. Geoderma 2017, 293, 54–63. [Google Scholar] [CrossRef]
- Sithole, N.J.; Ncama, K.; Magwaza, L.S. Robust Vis-NIRS models for rapid assessment of soil organic carbon and nitrogen in Feralsols Haplic soils from different tillage management practices. Comput. Electron. Agric. 2018, 153, 295–301. [Google Scholar] [CrossRef]
- Xu, S.; Zhao, Y.; Wang, M.; Shi, X. Comparison of multivariate methods for estimating selected soil properties from intact soil cores of paddy fields by Vis–NIR spectroscopy. Geoderma 2018, 310, 29–43. [Google Scholar] [CrossRef]
- Liu, Y.; Shi, Z.; Zhang, G.; Chen, Y.; Li, S.; Hong, Y.; Shi, T.; Wang, J.; Liu, Y.; Liu, Y.; et al. Application of Spectrally Derived Soil Type as Ancillary Data to Improve the Estimation of Soil Organic Carbon by Using the Chinese Soil Vis-NIR Spectral Library. Remote Sens. 2018, 10, 1747. [Google Scholar] [CrossRef] [Green Version]
- Ng, W.; Minasny, B.; Malone, B.; Filippi, P. In search of an optimum sampling algorithm for prediction of soil properties from infrared spectra. PeerJ 2018, 2018, e5722. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- de Santana, F.B.; de Souza, A.M.; Poppi, R.J. Visible and near infrared spectroscopy coupled to random forest to quantify some soil quality parameters. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2018, 191, 454–462. [Google Scholar] [CrossRef] [PubMed]
- Vohland, M.; Besold, J.; Hill, J.; Fründ, H.-C. Comparing different multivariate calibration methods for the determination of soil organic carbon pools with visible to near infrared spectroscopy. Geoderma 2011, 166, 198–205. [Google Scholar] [CrossRef]
- Xuemei, L.; Jianshe, L. Measurement of soil properties using visible and short wave-near infrared spectroscopy and multivariate calibration. Meas. J. Int. Meas. Confed. 2013, 46, 3808–3814. [Google Scholar] [CrossRef]
- Jiang, G.; Zhou, S.; Cui, S.; Chen, T.; Wang, J.; Chen, X.; Liao, S.; Zhou, K. Exploring the Potential of HySpex Hyperspectral Imagery for Extraction of Copper Content. Sensors 2020, 20, 6325. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, Y.; Yu, L.; Liu, Y.; Liu, Y.; Zhang, Y.; Liu, Y.; Cheng, H. Combining fractional order derivative and spectral variable selection for organic matter estimation of homogeneous soil samples by VIS-NIR spectroscopy. Remote Sens. 2018, 10, 479. [Google Scholar] [CrossRef] [Green Version]
- Stevens, A.; Udelhoven, T.; Denis, A.; Tychon, B.; Lioy, R.; Hoffmann, L.; van Wesemael, B. Measuring soil organic carbon in croplands at regional scale using airborne imaging spectroscopy. Geoderma 2010, 158, 32–45. [Google Scholar] [CrossRef]
- Mzid, N.; Castaldi, F.; Tolomio, M.; Pascucci, S.; Casa, R.; Pignatti, S. Evaluation of Agricultural Bare Soil Properties Retrieval from Landsat 8, Sentinel-2 and PRISMA Satellite Data. Remote Sens. 2022, 14, 714. [Google Scholar] [CrossRef]
- Gomez, C.; Viscarra, R.A.; Mcbratney, A.B. Soil organic carbon prediction by hyperspectral remote sensing and fi eld vis-NIR spectroscopy: An Australian case study. Geoderma 2008, 146, 403–411. [Google Scholar] [CrossRef]
- Mirzaee, S.; Ghorbani-Dashtaki, S.; Mohammadi, J.; Asadi, H.; Asadzadeh, F. Spatial variability of soil organic matter using remote sensing data. Catena 2016, 145, 118–127. [Google Scholar] [CrossRef]
- Vaudour, E.; Gomez, C.; Fouad, Y.; Lagacherie, P. Sentinel-2 image capacities to predict common topsoil properties of temperate and Mediterranean agroecosystems. Remote Sens. Environ. 2019, 223, 21–33. [Google Scholar] [CrossRef]
- Asgari, N.; Ayoubi, S.; Demattê, J.A.M.; Dotto, A.C. Carbonates and organic matter in soils characterized by reflected energy from 350–25000 nm wavelength. J. Mt. Sci. 2020, 17, 1636–1651. [Google Scholar] [CrossRef]
- Massimo Conforti; Gabriele Buttafuoco Vis-NIR Spectroscopy for Determining Physical and Chemical Soil Properties: An Application to an Area of Southern Italy. Glob. J. Agric. Innov. Res. Dev. 2014, 1, 17–26. [CrossRef]
- Mammadov, E.; Denk, M.; Riedel, F.; Lewinska, K.; Kaźmierowski, C.; Glaesser, C. Visible and Near-Infrared Reflectance Spectroscopy for Assessment of Soil Properties in the Caucasus Mountains, Azerbaijan. Commun. Soil Sci. Plant Anal. 2020, 51, 2111–2136. [Google Scholar] [CrossRef]
- Qi, Y.; Qie, X.; Qin, Q.; Shukla, M.K. Prediction of soil calcium carbonate with soil visible-near-infrared reflection (Vis-NIR) spectral in Shaanxi province, China: Soil groups vs. spectral groups. Int. J. Remote Sens. 2020, 42, 2502–2516. [Google Scholar] [CrossRef]
- Gomez, C.; Lagacherie, P.; Coulouma, G. Continuum removal versus PLSR method for clay and calcium carbonate content estimation from laboratory and airborne hyperspectral measurements. Geoderma 2008, 148, 141–148. [Google Scholar] [CrossRef]
- Mitran, T.; Sreenivas, K.; Janakirama Suresh, K.G.; Sujatha, G.; Ravisankar, T. Spatial Prediction of Calcium Carbonate and Clay Content in Soils using Airborne Hyperspectral Data. J. Indian Soc. Remote Sens. 2021, 49, 2611–2622. [Google Scholar] [CrossRef]
- Castaldi, F. Sentinel-2 and landsat-8 multi-temporal series to estimate topsoil properties on croplands. Remote Sens. 2021, 13, 3345. [Google Scholar] [CrossRef]
- Gaffey, S. Spectral reflectance of carbonate minerals in the visible and near infrared (0.35–2.55 um). Anhydrous carbonate minerals. J. Geophys. Res. 1987, 92, 1429–1440. [Google Scholar] [CrossRef]






| Requirements | VNIR | SWIR | PAN | |
|---|---|---|---|---|
| Spectral range | 400–2500 nm | 400–1010 nm | 920–2500 nm | 400–700 nm |
| FWHM | <15 nm | 9–13 nm | 9–14.5 nm | - |
| Spectral bands | 66 | 171 | 1 | |
| SNR | ≥160–200 (400–450 nm) | 161–209 (400–450 nm) | ||
| ≥200 (450–1000 nm) | 200–450 (450–1000 nm) | |||
| ≥200 (1000–1750 nm) | ||||
| ≥100 (1950–2350 nm) | ||||
| ≥100 (PAN) | ||||
| Swath width | 30 km; 2.77° | |||
| Ground Sampling Distance (GSD) | 30 m | 30 m | 5 m | |
| Abbreviation | Description of the Preprocessing Method |
|---|---|
| 1 | no-preprocessing |
| 2 | log10(1/R) reflectance to absorbance |
| 3 | log10(1/R) and Savitzky–Golay 1st derivative, w = 101/29/11, p = 3 |
| 4 | log10(1/R) and Savitzky–Golay 2nd derivative, w = 101/29/11, p = 3 |
| 5 | log10(1/R) and Savitzky–Golay 1st derivative, w = 101/29/11, p = 3 and SNV |
| 6 | log10(1/R) and Savitzky–Golay 2nd derivative, w = 101/29/11, p = 3 and SNV |
| Sensor | SOM | CaCO3 |
|---|---|---|
| PSR+ 3500 | 55 | 43 |
| HySpex | 55 | 43 |
| PRISMA | 30 | 25 |
| SOM% (55) | SOM% (30) | CaCO3 (43) | CaCO3 (25) | Clay% | |
|---|---|---|---|---|---|
| Min | 0.9 | 1.1 | 0.5 | 0.5 | 5 |
| Max | 8.6 | 8.6 | 62.3 | 50 | 59.9 |
| Average | 3.5 | 3.8 | 11.68 | 7.5 | 30.39 |
| Standard Deviation | 2.4 | 2.5 | 18.52 | 14 | 19.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Angelopoulou, T.; Chabrillat, S.; Pignatti, S.; Milewski, R.; Karyotis, K.; Brell, M.; Ruhtz, T.; Bochtis, D.; Zalidis, G. Evaluation of Airborne HySpex and Spaceborne PRISMA Hyperspectral Remote Sensing Data for Soil Organic Matter and Carbonates Estimation. Remote Sens. 2023, 15, 1106. https://doi.org/10.3390/rs15041106
Angelopoulou T, Chabrillat S, Pignatti S, Milewski R, Karyotis K, Brell M, Ruhtz T, Bochtis D, Zalidis G. Evaluation of Airborne HySpex and Spaceborne PRISMA Hyperspectral Remote Sensing Data for Soil Organic Matter and Carbonates Estimation. Remote Sensing. 2023; 15(4):1106. https://doi.org/10.3390/rs15041106
Chicago/Turabian StyleAngelopoulou, Theodora, Sabine Chabrillat, Stefano Pignatti, Robert Milewski, Konstantinos Karyotis, Maximilian Brell, Thomas Ruhtz, Dionysis Bochtis, and George Zalidis. 2023. "Evaluation of Airborne HySpex and Spaceborne PRISMA Hyperspectral Remote Sensing Data for Soil Organic Matter and Carbonates Estimation" Remote Sensing 15, no. 4: 1106. https://doi.org/10.3390/rs15041106
APA StyleAngelopoulou, T., Chabrillat, S., Pignatti, S., Milewski, R., Karyotis, K., Brell, M., Ruhtz, T., Bochtis, D., & Zalidis, G. (2023). Evaluation of Airborne HySpex and Spaceborne PRISMA Hyperspectral Remote Sensing Data for Soil Organic Matter and Carbonates Estimation. Remote Sensing, 15(4), 1106. https://doi.org/10.3390/rs15041106










